第五章异方差ppt课件
异方差的检验PPT课件

第21页/共27页
5.对给定的显著水平α,查 分布表,得临界值2
,若
,则否定 ,表明原模型
的随机2 (项5)中存在异方差n R。2
2
(5)
H0
例5.3.5我们以例5.3.1中给出的数据表5.3.1为例, 检验随机项的异方差性。 首先建立方程LS y c x ,在此方程的窗口点击 View \ Residual Test \ White Heteroskedasticity , 便可直接给出结果如图5.3.7所示。
;
2.计算模型(5.3.15)的残差序列 ,并计算 ; ˆ 0 , ˆ1, ˆ 2
3. 用 代替模型(5.3.16)中的 ,再用OLS估计
模型(5.3.16),计算R2;
i
2 i
2 i
2 ui
4.计算统计量nR2。在假设 H0 :不存在异方差(也就 是模型5.3.16中的所有斜率都为零)条件下,nR2服 从自由度为k = 5 的分布;
第四步,对β进行t检验。如果β不显著,则表明 β的真值为0,此时 实际上与xi无关,即没有异
方差性。否则,表明有异方差性存u2i在。
(5.3.10) (5.3.11)
第2页/共27页
帕克检验法的优点是不但能确定有无异方差性,而且 一旦确定有异方差性时,还能给出异方差性的具体函 数结构。它的缺点是(5.3.9)中的随机项vi仍可能有异方 差性,因而使帕克方法的使用效果受到影响。
第11页/共27页
五、布罗特-帕甘检验(Breusch-Pagan test for heteroskeda-sticity, BP test )
基本思想:模型
y 0 1 x1 2 x2 k xk u
(5.3.12)
《异方差的概念》PPT课件

主要包括:
(1)随机误差项序列存在异方差性; (2)随机误差项序列存在序列相关性; (3)解释变量之间存在多重共线性; (4)解释变量是随机变量且与随机误差项相关 (随机解释变量);
在进行计量经济学模型的回归分析时,必须对模型是否 满足基本假定进行检验,这种检验称为计量经济学检验。
第一节 异方差的概念
一、异方差的概念
对于模型
Yi 0 1X1i 2 X 2i k X ki ui
如果出现
Var
(ui
)
2 i
即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,则认为模型出现了异方 差性(Heteroskedasticity)。
概
率
异方差一般可归结为三种类型:
(1)单调递增型: i2随X的增大而增大; (2)单调递减型: i2随X的增大而减小; (3)复 杂 型: i2与X的变化呈复杂形式。
图5.1 异方差的类型
三、实际经济问题中的异方差性
例5.1:截面资料下研究居民家庭的储蓄行为
Yi 0 1Xi ui
Yi : 第i个家庭的储蓄额; Xi : 第i个家庭的可支配收入
高收入家庭:储蓄的差异较大 低收入家庭:储蓄则更有规律性,差异较小 高收入家庭随机误差项的方差明显大于低收入家 庭。
例5.2:截面资料下研究企业的成本函数
Yi 0 1Xi ui
Yi : 第i个企业的生产成本; Xi : 第i个企业的总产值
密
Y
度
X1
X2
X3
X
异方差性干扰
存在异方差时U的方差 协方差矩阵为:
第五讲 异方差和自相关ppt课件

42
Cochrane-Orcutt(1949) 估计(舍弃第一期观察 值)
prais D.rs LD.r20,corc
prais D.rs LD.r20,rho(dw) corc Prais-Winsten(1954) 估计(对第一期观察值进行 处理 sqrt(1-rho^2)*y1)
prais D.rs LD.r20
estat hettest,rhs (使用方程右边的解释变量,而
不是yˆ )
最初的BP 检验假设扰动项服从正态分布,有一定局
限性。Koenker(1981)将此假定放松为iid,在
实际中较多采用,其命令为:
estat hettest, iid
estat hettest, rhs iid
整理版课件
16
系数完全相同,但标准差和t值不同。
整理版课件
40
可行广义最小二乘法(FGLS):广义差分法:
CO-PW方法Cochrane-Orcutt(1949) 估计 (舍弃第一期观察值)
Prais-Winsten(1954) 估计(对第一期观察值 进行处理 sqrt(1-rho^2)*y1)
整理版课件
41
整理版课件
1
n
E
121n nn1n2va1 r)( co1 v ,(n) 2 0
2I
con v,(1) varn)( 0 2
整理版课件
2
此时可得:
Var()2(X'X)1
在存在异方差的情况下:
V a r ()2 (X 'X ) 1 X ' X (X 'X ) 1
estat hettest,normal
整理版课件
计量经济学课件-异方差

PPT文档演模板
2020/12/8
计量经济学课件-异方差
PPT文档演模课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
3rew
演讲完毕,谢谢听讲!
再见,see you again
PPT文档演模板
2020/12/8
计量经济学课件-异方差
计量经济学课件:第五章-异方差性汇总
第五章异方差性本章教学要求:根据类型,异方差性是违背古典假定情况下线性回归模型建立的另一问题。
通过本章的学习应达到,掌握异方差的基本概念包括经济学解释,异方差的出现对模型的不良影响,诊断异方差的方法和修正异方差的方法。
经过学习能够处理模型中出现的异方差问题。
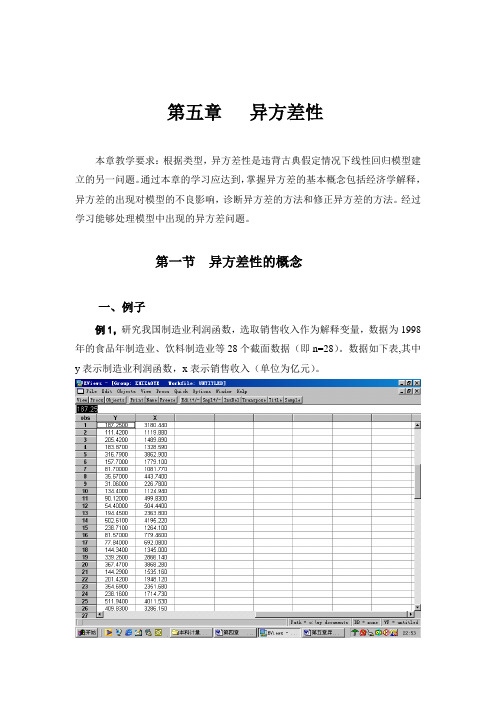
第一节异方差性的概念一、例子例1,研究我国制造业利润函数,选取销售收入作为解释变量,数据为1998年的食品年制造业、饮料制造业等28个截面数据(即n=28)。
数据如下表,其中y表示制造业利润函数,x表示销售收入(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较小,有的点分散幅度较大。
因此,这种分散幅度的大小不一致,可以认为是由于销售收入的影响,使得制造业利润偏离均值的程度发生了变化,而这种偏离均值的程度大小不同是一种什么现象?如何定义?如果非线性,则属于哪类非线性,从图形所反映的特征看并不明显。
下面给出制造业利润对销售收入的回归估计。
模型的书写格式为2ˆ12.03350.1044(0.6165)(12.3666)0.8547,..84191.34,152.9322213.4639,146.4905Y YX R S E FY s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在一种系统性的表现。
例2,改革开放以来,各地区的医疗机构都有了较快发展,不仅政府建立了一批医疗机构,还建立了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,而医疗服务需求与人口数量有关。
为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
根据四川省2000年21个地市州医疗机构数与人口数资料对模型估计的结果如下:i iX Y 3735.50548.563ˆ+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表示卫生医疗机构数(个),X 表示人口数量(万人)。
计量经济学第五章 异方差

X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
(一般把异方差看成是由于解释变量的变化而引起的)
5.1异方差的概念
三、异方差产生的原因 模型设定误差:省略了重要的解释变量
例:真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响,则 该影响体现在扰动项中。
测量误差: 一方面,测量误差常常在一定时间内逐渐增加,如X 越大,测量误差就会趋于增大 另一方面,测量误差随时间变化趋于减少,如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型: 200
递增型异方差:
150
100
递减型异方差:
50
条件异方差(略):
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
《异方差教学》课件

基于最小二乘法的残差,通过构造统计量检验异方差的存在 性。该方法适用于多种类型的数据,尤其适用于面板数据。
非参数检验法
Park检验
利用数据中的信息,通过比较不同阶数的自回归模型对数据的拟合效果,判断 是否存在异方差。该方法不需要预设模型形式,较为灵活。
ARCH模型
利用自回归条件异方差模型进行异方差的检验,通过比较不同滞后阶数的模型 拟合效果,判断是否存在异方差。该方法适用于波动性较大的数据。
Box-Cox变换法
总结词
Box-Cox变换法是一种通用的修正异方 差的方法,通过选择适当的λ值进行变换 ,使数据的方差变得相等。
VS
详细描述
Box-Cox变换法是一种灵活的修正异方差 的方法,适用于不同类型的异方差数据。 通过选择适当的λ值进行变换,可以使数 据的方差变得相等,从而消除异方差的影 响。Box-Cox变换法的优点在于能够自动 选择最佳的λ值进行变换,使得数据的同 方差性得到最大程度的保持。在回归模型 中,可以使用Box-Cox变换法来处理因变 量的异方差问题。
PART 03
异方差的修正
对数变换法
总结词
对数变换法是一种常用的修正异方差的方法,通过取对数将异方差转化为同方差 。
详细描述
对数变换法适用于正态分布的异方差数据,通过取自然对数或对数变换,可以使 方差变得相等,从而消除异方差的影响。在回归模型中,可以使用对数变换法来 处理因变量的异方差问题。
平方根变换法
提出相应的解决策略。
PART 06
总结与展望
异方差研究的意义
揭示数据内在规律
异方差研究有助于揭示数据分布的内在规律,为数据分析和预测 提供更准确的模型。
提高统计推断的准确性
5 异方差

异方差性的后果
(heteroskedasticity :Consequences)
计量经济学模型一旦出现异方差性(heteroskedasticity ),如 果仍采用OLS估计模型参数,会产生下列不良后果: 1、参数估计量仍然具有无偏性(unbiased) ) 2、参数估计量非有效(does not have minimum variance) 由于非有效, 3、由于非有效,因而变量的显著性检验失去意义 (t statistics are unreliable) )
1
ˆ 如果出现了异方差,se(β1) 出现偏误(偏大或偏小), t检验失真。
三、异方差诊断
(heteroskedasticity detection)
? 用什么来表示随机误差项的方差 用什么来表示随机误差项的方差? (how to indicate the variance of stochasic?) • 在同方差假定下(homoskedasticity assumption),随机误差项的方差用 σ 2 表示。 • 事实上,关于模型是否满足同方差假定,我们 在估计模型时并不知道,是需要通过异方差性 诊断(detecting heteroskedasticity)才能知道的。 • 要诊断模型是否存在异方差,首先需要找到一 个用以表示随机误差项方差的“量”。
第五章 异方差性 (Heteroskedasticity)
本章内容
• 异方差性的含义及异方差产生的原因(Nature and causes) • 异方差性对模型的影响(Practical consequences) • 检验异方差性方法(Detection) • 处理和消除异方差的办法(Remedies)
OLS估计结果
Dependent Variable: TX Method: Least Squares Date: 05/27/09 Time: 00:37 Sample: 1 30 Included observations: 30 Variable C SR R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient 38.75161 0.041419 0.544467 0.528198 67.01587 125751.5 -167.6811 2.009705 Std. Error 39.64001 0.007160 t-Statistic 0.977588 5.785021 Prob. 0.3366 0.0000 256.8727 97.56583 11.31208 11.40549 33.46646 0.000003
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f
ˆ 2
2
w i (Yˆ ( ˆ1 ˆ2 X i ))( X i ) 0
ˆ2
wi xi* yi*
w
i
x
* i
2
ˆ1 Y * ˆ 2 X *
其中, X * w i X i , Y * w iYi
wi
wi
xi*
Xi
X
* i
,
yi*
Yi
Yi*
Econometrics 2005
将是不可靠的。
Econometrics 2005
13
5.3 异方差的检验
方法有 (1)图示法( X _ e2); (2)解析法:
戈德菲尔德-匡特检验 怀特检验 ARCH检验
Econometrics 2005
14
5.3.1 图示法及其类型
1. 异方差指u的方差随着x的变化而变化。 2. 故可以根据x-e2的散点图,对异方差是否
Y的预测值的精度降低;
2
(2)由于 i 难以确定, Y的方差也就难以确定, Y
的预测区间的确定也出 现困难;
2
(3)在 = ei2 /( n k )是 2的无偏的证明中用到了
2
同方差的假定,由于异 方差性,使得 = ei2 /( n k )
是有偏的。在此区间估 计基础上区间估计和假 设检验
基本思路:
(以二元回归为例Y:t 1 2 X2t 3X3t ut)
如果有异方差,则i2与解释变量有关系。:如
i2=0
1X2i
3 X3i
2
X
2 2i
4 X32i
5 X2i
X3i+vi
但是i2一般未知,用模型回剩归余ei2作为i2的渐进
估计值,进行以上辅回助归,判断其变化是与否解
释变量有关.
Econometrics 2005
Econometrics 2005
25
G-Q检验在EViews上的实现
1. 用SORT X 以X为条件排序 2. 用SMPL命令定义两个子样 3. 用LS命令进行两次回归,计算出残差
平方和(可以直接读出)与自由度 4. 进行F检验
Econometrics 2005
26
解析法2:White检验(大样本下)
35
在EViews中实现加权最小二乘法
1. 假定以某个序列(权数序列通常都是某个 自变量的表达式)为权数,在EViews中, 可以在LS命令中使用加权处理方式来完成 加权的最小二乘法估计。
2. 实例。就用上实验课的数据演示一下!
Econometrics 2005
36
异方差修正(法2):模型变换法
i
2
i
E
( ˆ2
)
即线性无偏。
2
但,var( ˆ2 )
(
xi xi2
)2
var(
i
)
(
xi 2 i 2
xi2 )
Econometrics 2005
10
异方差影响2: t检验失效
首先是确定参数方差有 困难。例如上例中 ,
var( ˆ2 )
(
x i 2 xi2
2 i
)
,
2是未知的,也不能
i
点的 ei2的重要性程度一视同仁 。
( 2)
异方差时,
散程度越小,越应受到 重视,对回归线的决定 作用越
大。反之,当
ei的方差
2 i
越大,
ei所起的作用应当越小。
(3) 由此可选择加权:min wiei2 , 例如,取
w i
1
i2
, 其中
i
1,...,
n,由
min
27
White检验的具体做法
(1)用OLS法估计原模型,得到ei ,计算ei2;
(2)用ei2代替
2,作对解释变量的辅助回归;
i
(3)计算统计量nR2。n为样本容量,R2为辅助回归的
可决系数;nR2渐近服从自由度等于辅助回归中的回归元
(不包括常数项)个数的卡方分布。
Econometrics 2005
32
5.4 异方差的修正
补救异方差的基本思路 1. 变异方差为同方差 2. 尽量缓解方差变异的程度
以补救异方差造成的严重后果
Econometrics 2005
33
法1,加权最小二乘法WLS
(1) 在一元线性回归分析中 ,用 OLS 估计参数用
min ei2 (Yi ( 1 2 X i )) 2,此隐含假设:对各
et;
( 2 ) 计算
e
2 t
,
e
2 t
1
,
e
2 t
2
,...,
e
2 t
p
;
( 3 ) 作辅助回归:
e
2 t
0
1e
2 t1
...
e2
p t p
vt
计算 nR 2
( 4 ) 提出原假设:
H
0
:
0 ,...,
全为
p
0;
在
H
成立时,
0
nR 2 ~ (2 p ).
( 5 ) 给定显著水平
,查表得:
(2
p)
Econometrics 2005
20
Goldfeld-Quant检验适用条件
1. 样本容量较大(一般不低于参数个数的两倍 以上)
2. 异方差递增; i2 2Xi2
3. 其他古典假定满足。
Econometrics 2005
21
Goldfeld-Quant检验的思路
1. 递增异方差,方差之比就会大于1;递 减异方差,方差之比小于1;同方差, 方差之比趋近于1
. . . .. . .. . . .
. .
Xi
Xi
Econometrics 2005
16
e
2 i
e
2 i
. ..
. ..
.. . ..
Xi
e
2 i
Xi
Econometrics 2005
Xi
17
怎样通过Eviews作x- e2 散点图
1. 键入 LS y c x 作回归; 2. 键入 GENR E1=resid 调用残差; 3. 键入 GENR E2=E1^2 生成残差平方序列; 4. 键入 SCAT E2 X
项的方差可能减少。 3. 模型设置不正确; 4. 经济结构发生了变化,但模型参数没作相应调整。比
如按照边错边改学习模型,人们在学习的过程中,其 行为误差随时间而减少。 5. 异常值的出现也会产生。 (通常,截面数据较时间序列数据更易产生异方差) Why?比如成员的大小不一,收入有大中小之分!
Econometrics 2005
第五章异方差ppt课件
Econometrics 2005
1
本章主要介绍
1. 异方差的含义和产生的背景 2. 异方差性对模型的影响 3. 异方差性的检验 4. 异方差性补救措施
Econometrics 2005
2
Econometrics 2005
3
Econometrics 2005
4
(A)与(B)的比较:
( 6 ) 判断:若 nR 2 (2 p ), 认为有异方差, 否则无异方差。
Econometrics 2005
31
异方差检验:小结
以上各个检验方法,很难说哪个更有 效。为保险起见,一般将White检验和 ARCH检验结合使用,当两者都认为有 异方差时,一般可以很有把握认为异 方差存在。
Econometrics 2005
2. 先将样本一分而二,对子样1和子样2 分别作回归,然后利用两个子样的残 差的方差之比构造检验统计量F进行异 方差检验。这个检验统计量服从F分布。
Econometrics 2005
22
图示: Goldfeld-Quant检验的思路
e
样本1
3n/8
n/4
样本2
3n/8
x
Econometrics 2005
在时间序列数据中认为存在的异方差为ARCH
(自回归条件异方差)过程:
2 t
0
1
2 t 1
2
2 t 2
...
p
2 t
p
vt
因为各个t2未知,用对原模型OLS估计的剩余项ei2
去近似估计。
在此基础上进行假设检验,判断上述回归成立否。
Econometrics 2005
30
ARCH检验的具体做法
( 1)用 OLS 估计原模型,得残差
ei2 估计系数。
i2
Econometrics 2005
34
具体做法举例:一元回归的WLS过程和结果
残差平方和:
w
i
uˆ
2 i
w i Yˆi ( ˆ1 ˆ 2 X i ) 2 f ( ˆ1 , ˆ 2 )
f
ˆ1
2
w i (Yˆ ( ˆ1 ˆ2 X i ))( 1) 0
7
5.2 异方差对模型的影响
Econometrics 2005
8
影响1:OLS参数估计不再是BLUE估计
(1) 参数OLS估计仍然是线性无偏的
(2) 参数OLS 估计的方差不再具有最小性 (常用的OLS,相对于顾及异方差性的OLS而言,其
标准差或者偏之于过大(对截距而言)或者一般偏之于过 小(对斜率系数而言))。
5. 进行F检验,根据结果判断是否有异 方差。
Econometrics 2005
24
G-Q检验统计量F及其检验
ee ee F
2 i2
