形状相同的图形ppt课件一
合集下载
华东师大版九年级数学上册第23章《图形的相似》PPT课件

AB AB
与
BC 之间的关系是什么?
BC
AB BC A' B' B'C'
归纳
两条线段的比就是它们长度的比;
像这样,对于四条线段a、b、c、d,如果其中两条线段的
长度的比等于另外两条线段的比, 如 a c (或a∶b=
bd
c∶d),那么,这四条线段叫做成比例线段,简称比例线 段.此时也称这四条线段成比例.
∴ ac bd
∴ 线段a、b、c、d是成比例线段.
• 注意:
• 1.若a:b=k , 说明a是b的k倍;
• 2.两条线段的比与所采用的长度单位无关,但求比时两 条线段的长度单位必须一致;
• 3.两条线段的比值是一个没有单位的正数;
•
4.除了a=b外,a:b≠b:a,
a b
与
b a
互为倒数.
三 比例的基本性质
k.
第23章 图形的相似
23.2 相似图形
学习目标
1.理解相似多边形的定义,并能根据定义判断两个多边形是 否相似;(重点)
2.掌握相似比的概念并会求相似比; (重点) 3.理解并且掌握相似多边形的性质与判定.(难点)
观察与思考 请观察下面几组图片,是我们前面学过的相似图形吗?
一 相似多边形的性质
a c ab cd bd b d
ab cd ab cd
等比性质:
a
c
...
n
a c ... n
a
(b+d+···+m≠0)
bd
m b d ... m b
当堂练习
1.下列各组数中一定成比例的是( B )
A.2,3,4,5
相似图形的概念ppt课件
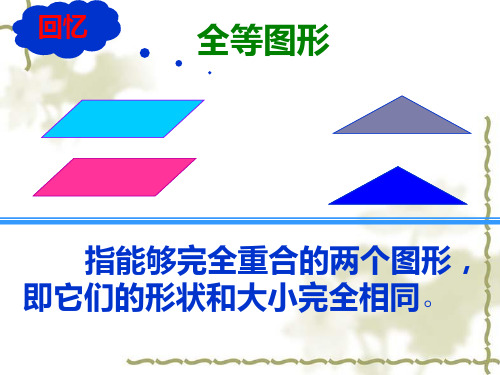
观察下面的图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(B)
(1)所有的圆都是形状相同的图形; (2)所有的正方形都是形状相同的图形; (3)所有的等腰三角形都是形状相同的图形; (4)所有的矩形都是形状相同的图形;
A、1个 B、2个 C、3个 D、4个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
4、下列说法中正确的是 (D ) A、所有平行四边形都是相似图形 B、所有菱形都是相似图形 C、所有等腰梯形都是相似图形 D、所有全等三角形都是相似图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想:我们刚才所见到的图形有什么相同 和不同的地方?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(B)
(1)所有的圆都是形状相同的图形; (2)所有的正方形都是形状相同的图形; (3)所有的等腰三角形都是形状相同的图形; (4)所有的矩形都是形状相同的图形;
A、1个 B、2个 C、3个 D、4个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
4、下列说法中正确的是 (D ) A、所有平行四边形都是相似图形 B、所有菱形都是相似图形 C、所有等腰梯形都是相似图形 D、所有全等三角形都是相似图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想:我们刚才所见到的图形有什么相同 和不同的地方?
形状相同的图形

2
-1
倍 (x, y) (2x, 2y)
议一议
你能利用刚才所学到的方法, 将“A”字形缩小吗?
一个图形各点的坐标经过怎样的变化, 可以使所得到的图形与原图形的形状相 同?
答:一个图形各点的横坐标、纵坐标都乘以 或除以同一个不为零的数,可以使所得的新 图形与原图形的形状相同。
议一议:
学习了《形状相同的图形》之后,小 明和小张就一直在争论:小明说: “任意两个矩形都是形状相同的图 形。 ”而小张说:“不对,任意两 个圆形才是形状相同的图形。”
所有的圆柱真的都是形状相同的吗?
所有的菱形真的都是形状相同的图形吗?
所有的等腰三角形真的都是形状相同的图 形吗?
1、什么是形状相同的图形?两个形状 相同的图形与这两个图形本身的大小 与位置有关吗?
2、形状相同的图形与全等的区别与 联系. 3、利用坐标系怎样使一个图形与 已知图形形状相同?
你还有其他的方法吗?
请观察以下图形
篮球巨星姚明同一张底片冲洗出来的2 寸照片和4寸照片中,人物的形状改变 了吗?大小呢?
符合国家标准的两面中国国 旗的形状相同吗?大小呢?
蕨类植物的整张叶片和它上面的小 叶片形状相同吗?大小呢?
四阶魔方和三阶魔方形状 相同吗?大小呢?
(四阶)
(三阶)
这些足球和正方体的的形 状和大小怎么样?
(14)
请在下列图形中找出形状相同的图形
4
1
2
5
3
7 6
8 10
9
14
11 12
13
一起来探索一下吧! 随堂练习
在直角坐标系中描出点O(0,0)、 A(1,2)、B(2,4)、C(3,2)、 D(4,0)。先用线段顺次连接点O、 A、B、C、D,然后再用线段连接A、 C两点。
《形状相同的图形》相似图形PPT 图文

我们一路怀揣着爱,脚踏着万物,一声 绝唱, 飘然落 尘!也 许,你 我曾是 几百年 前的一 株草, 一朵花 ,一粒 尘,经 过几世 轮回的 转换变 成了今 生的亲 人,朋 友,爱 人…… 也许, 我们只 是来兑 现前世 的一场 盟约。 也许, 在百年 之后, 你我又 都化为 世间的 生灵, 守候在 天地之 间,彼 此相望 ,相顾 无言。 然而, 你我却 心灵相 犀,甘 为绿叶 ,守护 着这世 间一朵 花开的 时光!
时光就是这么不经用,很快自己做了母 亲,我 才深深 的知道 ,这样 的爱, 不带任 何附加 条件, 不因万 物毁灭 而更改 。只想 守护血 浓于水 的旧时 光,即 便峥嵘 岁月将 容颜划 伤,相 信一切 都是最 好的安 排。那 时的时 光无限 温柔, 当清水 载着陈 旧的往 事,站 在时光 这头, 看时光 那头, 一切变 得分明 。执笔 书写, 旧时光 的春去 秋来, 欢喜也 好,忧 伤也好 ,时间 窖藏, 流光曼 卷里所 有的宠 爱,疼 惜,活 色生香 的脑海 存在。
这世间,有一种相逢叫做缘份。如若有 缘,你 我会迎 着月, 奔着光 ,在人 生的某 个岔路 口相见 ,然后 又悄悄 离别。 像一朵 洁白似 雪的梨 花,轻 轻被风 吹落, 好像从 未被时 光染上 任何颜 色,永 远素雅 洁净。
有些人,在你生命里,走着走着就散了 ,走着 走着就 远了, 转身是 刹那, 离别早 已是天 涯。有 些人, 如同在 你的世 界打马 而过, 走时如 春风拂 面,未 曾留下 一丝一 痕。有 些人, 走时却 如惊涛 骇浪, 让你痛 彻心扉 ,就像 长在你 心里的 一根刺 ,怎么 拨也拨 不出来 ,只留 下浅浅 淡淡的 伤痕, 也许, 是思念 ;也许 ,是怨 念;也许 ,只是 记得… …
“十年生死两茫茫,不思量,自难忘。 千里孤 坟,无 处话凄 凉。纵 使相逢 应不识 ,尘满 面,鬓 如霜“ 。如若 今生, 你我遇 到一个 愿意为 自己陪 伴一生 的人, 那么, 请握紧 现在手 中的幸 福,珍 惜彼此 ,别等 失去, 再话凄 凉……
《形状相同的图形》相似图形PPT课件4

( x, y ) O(0 , 0) A (1 , 2) B (2 , 4) C (3 , 2) D(4 , 0) (2 x,2 y ) O3( 0, 0) A3( 2, 4) B3( 4 , 8 ) C3( 6 , 4 ) D3( 8 , 0 )
O(0,0 )
A(2,2 ) B(4,4 ) C(6,2 ) D(8,0 )
y
B7
4 2 A7
A
B
C7
C
-6 -5 D7-4 -3 -2 -1 O -2
1
2
3
4 D 5
6 x
( x, y ) ( x, y )
下列图形在原图形的基础上作了哪些变化,变化 后的图形和原图形形状相同吗?
补充练习(一):
(1)、油桶和杯子都是圆柱体,因此 这两个物体形状相同( )
(2)、课桌都是由桌面和四条腿构成 ,所有课桌形状相同( ) (3)、中国象棋和国际象棋棋盘都是 矩形,所以它们形状相同( ) (4)、所有正方体的形状相同( )
练 习:
指出下列图形中,形状 相同的图形是 (1)所有的三角形 (2)所有的等腰三角形
练 习:
(3)所有的等边三角形 (4)所有的直角三角形 (5)所有的边长之比是 3:4:5的三角形
练 习:
(6)所有等腰直角三角形 (7)所有的正方形 (8)所有的菱形
练 习:
(9)所有的矩形 (10)所有的梯形 (11)所有的正六边形 (12)所有的五边形
找一找:下列图形哪些形状相 同?用线连起来。 D
E F
A
B C
辨一辨
图中有哪些图 形的形状相同?
答:(1)与(3), (2)与(13) (4)与(11) (5)与(10) (6)、(7) (8)、(9) (14)与(16)
上海沪科版初中数学九年级上册22.1 第1课时 相似图形ppt课件

AB
F
C
E1
D1
E
D
问题1 这两个多边形相似吗? 问题2 在这两个多边形中,是否有对应相等的内角? 问题3 在这两个多边形中,夹相等内角的两边否成 比例?
A1 F1
B1 C1
AB
F
C
E1
D1
E
D
归纳: ◑相似多边形的定义: 各角分别相等、各边成比例的两个多边形 叫做相似多边形.
◑相似多边形的特征: 相似多边形的对应角相等,对应边成比例.
归纳:任意两个边数相等的正多边形都相似.
思考: 任意的两个菱形(或矩形)是否相似?为什么?
典例精析
例1 如图,四边形 ABCD 和 EFGH 相似,求角α,β 的大小和EH的长度 x.
H x
21 D
A
β
18
E 118°
24
78° 83°
B
C
F
α G
解:∵ 四边形 ABCD 和 EFGH 相似,∴ 它们的对 应角相等.由此可得
思考:你见过哈哈镜吗?哈哈镜与平面镜中的形 象哪一个与你本人相似?
练一练 放大镜下的图形和原来的图形相似吗?
放大镜下的角与原图 形中角是什么关系?
三 相似多边形与相似比
观察与思考
多边形 ABCDEF 是显示在电脑屏幕上的,而多 边形 A1B1C1D1E1F1 是投射到银幕上的.
A1 F1
B1 C1
◑相似比: 相似多边形的对应边的比叫作相似比.
议一议
任意两个等边三角形相似吗?任意两个正方形 呢?任意两个正 n 边形呢?
…
a1
a2
a3
an
分析:已知等边三角形的每个角都为60°, 三边都相 等. 所以满足边数相等,对应角相等,以及对应边的 比相等.
27.1 图形的相似课件(共30张PPT)

比)与另两条线段的比相等,如
a b
c
d(即
ad
=
bc),我们就说这四
条线段成比
27.1 图形的相似
观察与思考 1.观察多面体模型与五棱柱教具中的正五边形回答下列问题
27.1 图形的相似
问题1 这些正五边形两两之间相似吗?
相似
问题2 在这两个正五边形中,是否有对应相等的内角?
是
问题3 在这两个正五边形中,对应内角的两边是否成比例?
78° 83°
B
C
F
α G
27.1 图形的相似
解:∵ 四边形 ABCD 和 EFGH 相似, ∴ 它们的对应角相等.由此可得
∠α = ∠C = 83°,∠A = ∠E=118°.
在四边形 ABCD 中,
β = 360°-(78°+83°+118°) = 81°.
21 D
A
β
18
78° 83°
B
C
x E
27.1 图形的相似 如果放在教室最后面展示又有什么不同? 2. 图形的放大:
两个图形相似,其中一个图形可以 看作由另一个图形放大或缩小得到.
通过上面两 组图形的观 察,发现了 什么?
27.1 图形的相似 例1 放大镜观察学具的一个角和原来的角有什么关系?
放大之后的角与原来的 角是相似关系
27.1 图形的相似
118° 24
F
H
α G
27.1 图形的相似
∵ 四边形 ABCD 和四边形 EFGH 相似, ∴它们的对应边成比例,由此可得
EH AD
EF AB
,即
x 21
24 18
.
解得 x = 28 cm.
九下数学课件相似图形 课件(共27张PPT)

为 AA'BB'=BB'CC'=AA'CC'
= k′,因此k =
1 k'
.
感悟新知
要点提醒: 判断两个三角形相似的条件: (1)三角形的三组角分别对应相等; (2)三角形的三组边对应成比例. ●相似三角形的性质:相似三角形的对应角相等,对
应边成比例. ●在相似多边形中,最简单的就是相似三角形.
感悟新知
感悟新知
特别解读 : ①“形状相同”是判定相似图形的唯一条件. ②两个图形相似是指它们的形状相同,与它们的位置、
大小无关.
感悟新知
例 1
[模拟·南通] 下列图形不是相似图形的是(
C)
A. 同一底片打印出来的两张大小不同的照片
B. 用放大镜将一个细小物体图案放大过程中原图案
和放大图案
C. 某人的侧身照片和正面照片
相似多边 形的性质
相似图形 相似图形
相似三角 形的定义
相似三角 形的性质
感悟新知
新知二 相似多边形
1. 相似多边形的定义 各角分别相等,各边成比例的两个多边形,它们的形状相
同,称为相似多边形. 2. 相似比的定义 相似多边形的对应边的比叫做相似比.
感悟新知
3. 相似多边形的性质 相似多边形的对应边的比相等,对应 角相等.
(1)相似比与两个多边形的先后顺序有关. (2)相似多边形的定义可用来判断两个多边形是否相似. (3)相似多边形的性质常用来求相似多边形未知边的长度或
感悟新知
(1)求梯形ABCD与梯形A′B′C′D′ 的相似比k;
解题秘方:紧扣“相似多边形的性质及相似比的定义”
进行计算.
解:相似比k=
AD 4 2 A'D'=6=3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O2( ) A2( ) B2(
3, 2) C(3 , 4
) C2( C(3 , 2)
4, 0 D(4 , 0)
) D2( D(4 , 0) )
表3
( x, y )
O(0 , 0) A(1 , 2)
B(2 , 4)
( 2 x , 2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
它们形状相同 , 大小不一定相同
请从下图中找出形状相同的图形.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)与(3),(2)与(13),(4)与(11), (5)与(10),(6)(7)(8)(9)分别是形状 相同的图形。
做一做:利用下面的方法可以近似地将一个图形放大. 1.将2根长短相同的橡皮筋系在一起,联结处形成一 个结点. 2.选取一个图形,在图形外取一个定点. 3.将系在一起的橡皮筋的一端固定在定点,把一枝 铅笔固定在橡皮筋的另一端. 4.拉动铅笔,使2个橡皮筋的结 点沿所选图形的边缘运动,当 结点在已知图形上运动一圈时, 铅笔就画出了一个新的图形. 这个新图形与已知图形形状 相同.
y 4 B
⑶在上述得到的图形中, 2 A C C A O 哪些图形与原图形的形 -2 -1O 1 2 3 4D5 6 7 8D x -2 状相同?
1
B1
1
1
1
-4
( x ,y ) ( 2x ,y )
y 8 6 4 2
B2 A B
2
A C
y 8 6
B
3
C2
4 2
A
A3
B C
C
3
D -2 -1 O 1 2 3 D 5 6 7 8 x 4 2 -1
O2
O -2 -1 O 1
3 -1
D D 2 3 4 5 6 7 8x 3
( x ,y ) (x , 2y )
( x ,y ) (2x , 2y )
这节课你有什么收获?
习题 4.4
第2,3小题.
谢谢!
在直角坐标系中描出点O(0,0),A(1,2), B(2,4),C(3,2),D(4,0).先用线段 顺次连接点O,A,B,C,D,然后再用线段连接 A,C两点. ⑴你得到了一个什么图形?
⑵填写表1,在直角坐标系中描出点O1,A1,B1, C1,D1,并按同样的方式连接各点,你得到了一 个什么图形?填写表2,你又得到了一个什么图 形?填写表3呢?
B2(2,8)
2
C2(3,4)
A
O2
-2 -1 O 1 -1
D2(4,0)
( x, y ) ( x , 2 y )
y 8
B3 O3(0,0)6 4来自A3AB
C3
C
A3(2,4) B3(4,8) C3(6,4)
2
O3
-2 -1 O 1 -1 2 3
D 4 5
D3
6 7 8 x
D3(0,8)
( x, y ) (2x , 2y )
y 4 A B
B1
C D
O1(0,0)
2
A1
2
C1
D1
5 6 7 8 x 4
A1(2,2)
O1
-2 -1 O -2 1 3
B1(4,4)
C1(6,2)
D1(8,0)
-4
( x, y ) ( 2x , y)
y
8
B2 O2(0,0) A2
6 4 B
A2(1,4)
C2
C 2 D 3 4 5 D2 6 7 8 x
表1
( x, y )
(2 x, y )
0, 0
O1(
O(0 , 0) A(1 , 2)
2, 2
4, 4
B(2 , 4)
C(3 , 2)
6, 2
D(4 , 0)
8, 0
表2
) A1(
) B1(
) C1(
) D1(
)
( x, y )
( x ,2 y )
0, 0 1, 4 2, 8 O(0 , 0) A(1 , 2) B(2 , 4)
第四章 相似图形
在放大镜中看到的字和原来的字有 什么关系?
生活中丰富的图形
你看到形状相同的图形了吗?
用同一张底片洗出的不同尺寸的照片 中,人物的形状改变了吗?
两个足球的形状相同吗?它们的大小呢?
两个正方体物体的形状相同吗?
复印前后纸上对应图形之间分别有 什么关系?
你能发现每一对图形中有什么共同特征吗?
3, 2) C(3 , 4
) C2( C(3 , 2)
4, 0 D(4 , 0)
) D2( D(4 , 0) )
表3
( x, y )
O(0 , 0) A(1 , 2)
B(2 , 4)
( 2 x , 2 y ) O3( 0, 0 ) A3( 2, 4) B3( 4, 8 ) C3( 6, 4 ) D3( 8, 0 )
它们形状相同 , 大小不一定相同
请从下图中找出形状相同的图形.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)与(3),(2)与(13),(4)与(11), (5)与(10),(6)(7)(8)(9)分别是形状 相同的图形。
做一做:利用下面的方法可以近似地将一个图形放大. 1.将2根长短相同的橡皮筋系在一起,联结处形成一 个结点. 2.选取一个图形,在图形外取一个定点. 3.将系在一起的橡皮筋的一端固定在定点,把一枝 铅笔固定在橡皮筋的另一端. 4.拉动铅笔,使2个橡皮筋的结 点沿所选图形的边缘运动,当 结点在已知图形上运动一圈时, 铅笔就画出了一个新的图形. 这个新图形与已知图形形状 相同.
y 4 B
⑶在上述得到的图形中, 2 A C C A O 哪些图形与原图形的形 -2 -1O 1 2 3 4D5 6 7 8D x -2 状相同?
1
B1
1
1
1
-4
( x ,y ) ( 2x ,y )
y 8 6 4 2
B2 A B
2
A C
y 8 6
B
3
C2
4 2
A
A3
B C
C
3
D -2 -1 O 1 2 3 D 5 6 7 8 x 4 2 -1
O2
O -2 -1 O 1
3 -1
D D 2 3 4 5 6 7 8x 3
( x ,y ) (x , 2y )
( x ,y ) (2x , 2y )
这节课你有什么收获?
习题 4.4
第2,3小题.
谢谢!
在直角坐标系中描出点O(0,0),A(1,2), B(2,4),C(3,2),D(4,0).先用线段 顺次连接点O,A,B,C,D,然后再用线段连接 A,C两点. ⑴你得到了一个什么图形?
⑵填写表1,在直角坐标系中描出点O1,A1,B1, C1,D1,并按同样的方式连接各点,你得到了一 个什么图形?填写表2,你又得到了一个什么图 形?填写表3呢?
B2(2,8)
2
C2(3,4)
A
O2
-2 -1 O 1 -1
D2(4,0)
( x, y ) ( x , 2 y )
y 8
B3 O3(0,0)6 4来自A3AB
C3
C
A3(2,4) B3(4,8) C3(6,4)
2
O3
-2 -1 O 1 -1 2 3
D 4 5
D3
6 7 8 x
D3(0,8)
( x, y ) (2x , 2y )
y 4 A B
B1
C D
O1(0,0)
2
A1
2
C1
D1
5 6 7 8 x 4
A1(2,2)
O1
-2 -1 O -2 1 3
B1(4,4)
C1(6,2)
D1(8,0)
-4
( x, y ) ( 2x , y)
y
8
B2 O2(0,0) A2
6 4 B
A2(1,4)
C2
C 2 D 3 4 5 D2 6 7 8 x
表1
( x, y )
(2 x, y )
0, 0
O1(
O(0 , 0) A(1 , 2)
2, 2
4, 4
B(2 , 4)
C(3 , 2)
6, 2
D(4 , 0)
8, 0
表2
) A1(
) B1(
) C1(
) D1(
)
( x, y )
( x ,2 y )
0, 0 1, 4 2, 8 O(0 , 0) A(1 , 2) B(2 , 4)
第四章 相似图形
在放大镜中看到的字和原来的字有 什么关系?
生活中丰富的图形
你看到形状相同的图形了吗?
用同一张底片洗出的不同尺寸的照片 中,人物的形状改变了吗?
两个足球的形状相同吗?它们的大小呢?
两个正方体物体的形状相同吗?
复印前后纸上对应图形之间分别有 什么关系?
你能发现每一对图形中有什么共同特征吗?
