数学九上课时作业本
2024九年级上册数学课时作业本

章节1:有理数一、有理数概念及性质1.1 有理数的定义1.2 有理数的性质1.3 有理数的大小比较二、有理数的四则运算2.1 有理数的加法2.2 有理数的减法2.3 有理数的乘法2.4 有理数的除法三、绝对值3.1 绝对值的概念3.2 有理数的绝对值性质3.3 求解绝对值不等式章节2:代数基础一、代数式及代数式的基本性质1.1 代数式的概念1.2 代数式的分类1.3 代数式的基本性质二、一元一次方程2.1 一元一次方程的概念2.2 一元一次方程的解法2.3 一元一次方程的应用三、一元一次不等式3.1 一元一次不等式的概念3.2 一元一次不等式的解法3.3 一元一次不等式的应用章节3:平面图形的认识一、平面图形的基本概念1.1 点、线、面的概念1.2 角的概念及性质1.3 三角形的定义二、相似三角形2.1 相似三角形的概念2.2 相似三角形的判定2.3 相似三角形的性质三、勾股定理3.1 勾股定理的概念3.2 勾股定理的证明3.3 勾股定理的应用本册数学课时作业本主要围绕有理数、代数基础和平面图形的认识展开。
通过对有理数的概念和性质的学习,使学生初步掌握有理数的特点和运算规律;通过对代数式、方程、不等式的学习,培养学生的代数思维和解决实际问题的能力;通过对平面图形的学习,使学生掌握平面图形的基本概念和性质,为以后的几何学习打下良好的基础。
在学习过程中,学生需要按部就班地完成习题,逐步提高对数学知识的掌握和运用能力。
老师应给予学生及时的指导和教育,帮助他们在数学领域获得更好的成绩,实现知识的全面提升和素质的全面发展。
希望《2024九年级上册数学课时作业本》能够成为学生们在数学学习过程中的得力助手,激发他们的学习兴趣,提高他们的学习成绩,为未来的学习和生活打下坚实的基础。
由于有理数、代数基础和平面图形的认识是数学学习中的基础知识,因此这些知识的掌握对学生的数学学习至关重要。
在学习有理数的过程中,学生需要了解有理数的定义和性质,掌握有理数的大小比较规则,以及进行有理数的四则运算。
2021年九年级数学上册 课时作业本 一元二次方程解法-直接开方法与配方法(含答案)

2021年九年级数学上册课时作业本一元二次方程解法-直接开方法与配方法一、选择题1.用直接开平方的方法解方程(2x﹣1)2=x2做法正确的是( )A.2x﹣1=xB.2x﹣1=﹣xC.2x﹣1=±xD.2x﹣1=±x22.x1,x2是一元二次方程3(x-1)2=15的两个解,且x1<x2,下列说法正确的是( )A.x1小于-1,x2大于3B.x1小于-2,x2大于3C.x1,x2在-1和3之间D.x1,x2都小于33.方程x2﹣4=0的根是()A.x=2B.x=﹣2C.x1=2,x2=﹣2D.x=44.解下列方程:①2x2-18=0;②9x2-12x-1=0;③3x2+10x+2=0;④2(5x-1)2=2(5x-1).用较简便的方法依次是( )A.①直接开平方法,②配方法,③公式法,④因式分解法B.①直接开平方法,②公式法,③、④因式分解法C.①因式分解法,②公式法,③配方法,④因式分解法D.①直接开平方法,②、③公式法,④因式分解法5.用配方法解下列方程,其中应在两边都加上16的是( )A.x2﹣4x+2=0B.2x2﹣8x+3=0C.x2﹣8x=2D.x2+4x=26.将方程x2+8x+9=0左边配方后,正确的是( )A.(x+4)2=﹣9B.(x+4)2=25C.(x+4)2=7D.(x+4)2=﹣77.将方程2x2﹣4x﹣3=0配方后所得的方程正确的是( )A.(2x﹣1)2=0B.(2x﹣1)2=4C.2(x﹣1)2=1D.2(x﹣1)2=58.用配方法解方程x2+1=8x,变形后的结果正确的是( )A.(x+4)2=15B.(x+4)2=17C.(x-4)2=15D.(x-4)2=179.用配方法解下列方程,配方正确的是( )A.2y2﹣4y﹣4=0可化为(y﹣1)2=4B.x2﹣2x﹣9=0可化为(x﹣1)2=8C.x2+8x﹣9=0可化为(x+4)2=16D.x2﹣4x=0可化为(x﹣2)2=410.用配方法解下列方程时,配方有错误的是()A.x2-2x-99=0化为(x-1)2=100B.x2+8x+9=0化为(x+4)2=25C.2t2-7t-4=0化为D.3y2-4y-2=0化为二、填空题11.方程x2﹣16=0的解为.12.一元二次方程9(x-1)2-4=0的解是 .13.若将方程x2+6x=7化为(x+m)2=16,则m=________.14.若(m+n)(m+n+5)=6,则m+n的值是________.15.用配方法将方程x2+10x﹣11=0化成(x+m)2=n的形式(m、n为常数),则m+n= .16.将方程x2-4x-1=0化为(x-m)2=n的形式,其中m,n是常数,则m+n= .17.一元二次方程x2﹣8x﹣1=0的解为.18.若(2m+n)2+2(2m+n)+1=0,则2m+n的值是________.三、解答题19.解方程:(2x﹣1)2=(3﹣x)2(直接开平方法)20.解方程:(x﹣5)2=16 (直接开平方法)21.解方程:4(x-1)2=9(x-5)222.解方程:(1-2x)2=x2-6x+9.23.解方程:x2+2x-399=0.(配方法)24.解方程:x2﹣6x﹣9=0(配方法)25.解方程:x2+3x﹣4=0;(用配方法)26.解方程:2x2﹣4x+1=0.(用配方法)27.解方程:x2﹣5x+1=0;(用配方法)28.解方程:2x2﹣5x+2=0(配方法)参考答案1.答案为:C.2.A3.C.4.D5.答案为:C.6.C7.D.8.C9.D.10.B11.答案为:x=±4.12.答案:x1=5/3,x2=1/313.答案为:314.答案为:-6或115.答案为:41.16.答案为:717.答案是:x 1=4+,x2=4﹣.18.答案为:-119.答案为:20.(x﹣5)2=16 (直接开平方法)x﹣5=±4x=5±4∴x1=1,x2=9;21.答案为:x1=13,x2=-3.4.22.答案为:x1=,x2=-2.23.答案为:x1=-21,x2=19.24.答案为:x1=3+3,x2=3﹣3;25.答案为:x1=﹣4,x2=1;26.答案为:x1=1+,x2=1﹣.27.答案为:28.答案为:x1=2,x2=0.5.。
苏科版九年级上册数学课时作业

7.如图,边长为1的正方形ABCD绕点A逆时针旋转300到正方形AB/C/D/,图中阴影部分的面积为
8.如图,四边形ABCD是正方形,△ADE绕A点顺时针旋转一定度数能与△ABF重合,则△AEF是
三角形.
第5题第6题第7题第8题
9.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是.
3.若使平行四边形ABCD成为正方形,则需添加的条件是()
A.对角线垂直B.对角线互相垂直且相等C.对角线相等D.对角互补
4.下列说法中,正确的个数有()
①四边都相等的四边形是正方形;②四个内角都相等的四边形是正方形;③有三个角是直角且有一组邻边相等的四边形是正方形;④对角线与一边夹角为450的四边形是正方形.
12.如图所示,在正方形ABCD中,M是CD的中点,E是CD上一点,且∠BAE=2∠DAM.
求证:AE=BC+CE.
13.如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.
(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;
(2)连接AE,试判断AE与DF的位置关系,并证明你的结论;
14.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°.证明你的结论.
课时作业
初 三 数 学(1.3.6矩形的判定)
1.四边形ABCD的对角线相交于点O,在下列条件中不能判断它是矩形的是()
课时提优计划作业本数学九年级上

课时提优计划作业本数学九年级上一、一元二次方程。
1. 定义。
- 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程。
- 一般形式:ax^2+bx + c = 0(a≠0),其中ax^2是二次项,a是二次项系数;bx 是一次项,b是一次项系数;c是常数项。
2. 解法。
- 直接开平方法。
- 对于方程x^2=k(k≥0),解得x = ±√(k)。
- 例如方程(x - 3)^2=16,则x - 3 = ±4,解得x = 7或x=-1。
- 配方法。
- 步骤:先将方程化为ax^2+bx = - c的形式;然后在方程两边加上一次项系数一半的平方((b)/(2a))^2;将左边配成完全平方式(x+(b)/(2a))^2,再进行求解。
- 例如用配方法解方程x^2+6x - 7 = 0。
- 移项得x^2+6x = 7。
- 配方:x^2+6x + 9 = 7+9,即(x + 3)^2=16。
- 解得x = 1或x=-7。
- 公式法。
- 对于一元二次方程ax^2+bx + c = 0(a≠0),其求根公式为x=frac{-b±√(b^2)-4ac}{2a}。
- 例如解方程2x^2-5x + 1 = 0,其中a = 2,b=-5,c = 1。
- 先计算判别式Δ=b^2-4ac=(-5)^2-4×2×1 = 17。
- 代入公式得x=(5±√(17))/(4)。
- 因式分解法。
- 将方程化为一边是两个一次因式乘积,另一边为零的形式,使每个一次因式等于零,分别解这两个一元一次方程,得到的解就是原一元二次方程的解。
- 例如方程x^2-3x + 2 = 0,因式分解为(x - 1)(x - 2)=0,解得x = 1或x = 2。
3. 根的判别式。
- 对于一元二次方程ax^2+bx + c = 0(a≠0),判别式Δ=b^2-4ac。
- 当Δ>0时,方程有两个不相等的实数根;当Δ = 0时,方程有两个相等的实数根;当Δ<0时,方程没有实数根。
新人教版九年级数学上册课时作业24.4 扇形面积
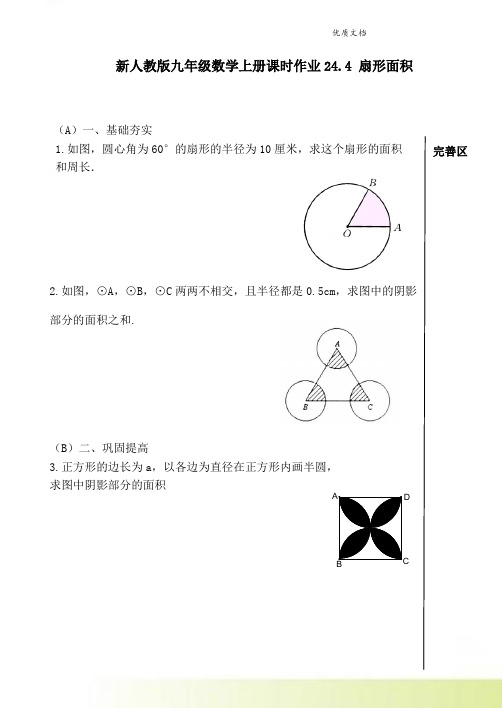
新人教版九年级数学上册课时作业24.4 扇形面积
(A )一、基础夯实
1.如图,圆心角为60°的扇形的半径为10
厘米,求这个扇形的面积
和周长.
2.如图,⊙A ,⊙B ,⊙C 两两不相交,且半径都是0.5cm ,求图中的阴影
部分的面积之和.
(B )二、巩固提高
3.正方形的边长为a ,以各边为直径在正方形内画半圆, 求图中阴影部分的面积
完善区
图23.3.5 D A B C
4.如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,
AB的长为30cm,贴纸部分BD的长为20cm,求贴纸部分的面积。
(C)三、拓展创新
5.如图,大半圆O与小半圆O
1
相切于点C,大半圆的弦AB与小半圆
相切于F,且AB∥CD,AB=4cm,求阴影部分的面积.
6.有一座正方形房子边长为4米,房子外面一个屋角用一根6米长的
绳子系着一条狗,求狗活动的范围?
师生交流:
完善区
D E
A
B C
等级: 整洁_________正确_________ 日期:____月____日。
课时作业本九上数学答案【四篇】

精心整理 ∴∠CEB=∠CBE, ∴∠OBC=∠OBA+∠CBE=∠A+∠CEB=∠A+∠AED=90°, ∴BC 是⊙O 的切线; (2)连接 OF,AF,△AOF 为等边三角形, ∴∠AOF=60°,∠ABF=30° 3.4 直线与圆的位置关系第 3 课时答案
1、3 2、75° 3、25 4、C 5、D 6、∵∠B=90°,BC=2•OB=AB, ∴∠A=∠C=45°, ∴BD 的度数为 90°,D 为 AB 的中点, ∴OD∥BC,OD⊥AB. 7、∵∠ACB=90°,∠BAC=2∠B,
精心整理
课时作业本九上数学答案【四篇】 【导语:】这篇关于课时作业本九上数学答案【四篇】的文章,是特 地为大家整理的,希望对大家有所帮助!
3.4 直线与圆的位置关系第 1 课时答案
1、略
Байду номын сангаас
2、8≤AB≤10
3、4
4、D
5、t=3,5 时,⊙P 与 CD 相切;在 3 6、3≤BP≤4(提示:作 点 A 关于直线 BC 的对称点 A′,求△AA′C 的内切圆半径)
精心整理 ∴∠B=30°, ∴△AOC 是等边三角形, ∴∠AOC=60°,在 Rt△OAP 中, OA=PAtan60°=6, ∴AC=6. 8、(1)连接 OC,OC⊥l,OC∥AD, ∴∠BAC=∠OCA=∠DAC=30°; (2)连接 BF,∠AFB=90°, ∵∠AED=∠ABF,∠AED=90°-∠DAE,∠ABF=90°-∠BAF, ∴∠BAF=∠DAE=18° 3.4 直线与圆的位置关系第 4 课时答案
7、(1)(2,3),(6,3);
(2)作 PE⊥OX,垂足为 E,连 OP,
作 AD⊥OP,垂足为 D,
数学课时作业本九上答案

数学课时作业本九上答案【篇一:苏科版九年级上册数学课时作业】class=txt>设计:张春丽审校:顾利荣时间:班级学号姓名一、选择题1.在下列图形的性质中,平行四边形不一定具有的是() a.对角相等 b.对角互补 c.邻角互补 d.内角和是360?2.平行四边形abcd中,ab=3,bc=5,ac的垂直平分线交ad于e,则△cde的周长是() a.6 b.8c.9d.103.在△abc中,ab=ac=5,d是bc上的中点,de∥ab交ac于点e,df∥ac交ab于点f,那么四边形afde的周长是() a. 5 b. 10 c. 15d. 204.在□abcd中,ac=10,bd=6,则边长ab,ad的可能取值为()a.ab=4,ad=4b.ab=4,ad=7 c.ab=9,ad=2d.ab=6,ad=2 二、填空题5.如果□abcd中,∠a—∠b=240,则∠a= 度,∠b= 度,∠c= 度,∠d= 度. 6.如果□abcd的周长为28cm,且ab:bc=2∶5,那么ab= cm,bc= cm,cd= cm,ad= cm. 7.平行四边形的周长为30,两邻边的差为5,则其较长边是.ae∥bd,ef⊥bc,df=2,则ef的长为.ad三、解答题bcf11.已知四边形abcd是平行四边形,ab=10cm,ad=8cm,ac⊥bc,求bc、cd、ac、oa的长以及□abcd的面积.13.已知:如图,在□abcd中,ac,bd交于点o,ef过点o,分别交cb,ad?的延长线于点e,f,求证:ae=cf .14.如图,已知四边形abcd是平行四边形,∠bcd的平分线cf交ab于点f,∠adc的平分线dg交边ab于点g.(1)求证:af=gb;(2)请你在已知条件的基础上再添加一个条件,使得△efg为等腰直角三角形,并说明理由.1初三数学(1.3.2矩形的性质)设计:张春丽审校:顾利荣时间:班级学号姓名一、选择题 1.如图,ef过矩形对角线的交点o,且分别交abcd于ef,那么阴影部分的面积是矩形abcd面积的()1113a.5b.4c.3d.10()a. 1.5b. 3c. 6d. 9 3.如图,点p是矩形abcd的边ad上的一个动点,矩形的两条边ab、ac的长分别为3和4,那么点p到矩形的两条对角线ac和bd的距离之和是()a12.6 c.24.不确定5554.如图1,周长为68的矩形abcd被分成7个全等的矩形,则矩形abcd的面积为()(a)98 (b)196 (c)280 (d)284(1) (2) (3) 二、填空题5.如图2,根据实际需要,要在矩形实验田里修一条公路(小路任何地方水平宽度都相等),则剩余实验田的面积为________.6.如图3,在矩形abcd中,m是bc的中点,且ma⊥md.?若矩形abcd?的周长为48cm,则矩形abcd的面积为_______cm210.已知,如图,矩形abcd的对角线ac,bd相交于点o,e,f分别是oa,ob的中点.(1)求证:△ade≌△bcf;(2)若ad=4cm,ab=8cm,求of的长.11.已知,在矩形abcd中,ae⊥bd,e是垂足,∠dae∶∠eab=2∶1,求∠cae的度数。
2023课时作业本人教版数学九年级上册

第一单元:数与代数
1.有理数的性质与运算
2.一元一次方程
3.一元一次不等式组
4.简单的函数
第二单元:几何
1.三角形和四边形
2.圆
3.圆的度量
4.轴对称图形和中心对称图形
第三单元:统计与概率
1.数据的收集与整理
2.数据的分析与处理
3.简单的概率
第四单元:数学与实践
1.直线与方程的应用
2.三角形与四边形面积的应用
3.圆面积和圆周长的应用
4.数据的应用
期末复习
1.数与代数
2.几何
3.统计与概率
4.数学与实践
课时作业
1.(填空题)一个三角形的三边长分别为3、4、5,则这个三角形是()三
角形。
2.(判断题)一个一元一次方程有唯一解,即()。
3.(选择题)一个圆的半径为5,则这个圆的面积是()。
4.(计算题)一个班级有30名学生,其中男生占60%,则这个班级中有多少
名男生?
5.(应用题)某商店销售一种商品,原价为100元,现在打八折销售,则这
种商品现在售价为多少元?
答案
1.直角
2.正确
3.25π
4.18
5.80。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3课时圆的对称性(1)
知识梳理
1.圆是中心对称图形,是它的对称中心。
2.(1)在同圆或等圆中,相等的圆心角所对的弧,所对的弦;
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有组量相等,那么它们所对应的其余各组量都分别
3.圆心角的度数与它所对的弧的度数
课后作业
1.如图,在⊙O中,AB、CD为弦,且AB=CD,则AC BD(填“>””<”或“=”)。
2.已知⊙O的一条弦AB把圆的周长分成1:4的两部分,则弦AB所对的圆心角的度数为
3.下列说法中,正确的是()
A.相等的弦所对的弧相等
B.相等的弧所对的圆心角相等
C.在同圆或等圆中,较长的弧所对的弦较长
D.相等的圆心角所对的弧相等
4.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为()
A.30°
B.60°
C.75°
D.120°
5.如图,△ABC内接于⊙O,点A、B、C把⊙O的周长三等分。
(1)试判断△ABC的形状,并说明理由;
(2)求∠AOB的度数。
课后作业
6.如图,AB和DE是⊙O的直径,弦AC∥DE。
若弦BE=3,则弦CE=
7.如图,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向行走。
按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α= 。
8.如图,在⊙O中,,则弦AB与2CD的数量关系是()
A.AB>2CD
B.AB=2CD
C.AB<2CD
D.AB≤2CD
9.如图,在⊙O 中⌒AB =⌒AC , 若∠B=75°,则∠A 的度数为 ( )
A.15°
B.30°
C.45°
D.60°
10.如图,半圆O 直径AB=10cm ,弦AC =6cm ,AD 平分∠BAC ,则AD 的长为( ) A.cm 54 B. cm 53 C. cm 55 D. cm 4
11.如图,点O 在∠APB 的平分线PN 上,以点O 为圆心的⊙O 分别交直线PN 于点M 、N ,那么⌒AM 与⌒BM 相等吗?并说明理由。
12.如图,AB 是⊙O 的直径,弦CD 交AB 于点M ,且OM=CM ,试确定⌒BD 与⌒AC 之间的数量关系,并说明理由。
13.如图,AB 是⊙O 的直径,C 、D 是⊙O 上的两点,且AC=CD 。
(1)求证:OC ∥BD ;
(2)若BC 将四边形OBDC 分成面积相等的两个三角形,试确定四边形OBDC 的形状。
答案:
知识梳理
1.圆心
2.(1)相等 相等 (2)一 相等
3.相等
课堂作业
1.=
2.72°
3.B
4. B
5.(1)△ABC 是等边三角形 理由略 (2)∠AOB 的度数为120°
6. 3
7. 52°
8.C
9.B 10.A 11.相等 点拨:过点O 分别作OH ⊥PA ,OI ⊥PB ,垂足分别为H 、I ,连接AO 、BO 。
可以得到△AHO ≌△BIO ,△PHO ≌△PIO ,则有∠PHO=∠POI ,∠AOH=∠BOI ,即可得∠POA=∠POB ,则有⌒AM =与⌒BM 。
12. ⌒BD =3⌒AC 理由:连接OD 、OC 。
∵OM=CM ,∠COA=∠C. ∴∠OMD=2∠COA 。
∵OD=OC ,∴∠D=∠C 。
又∵∠BOD=∠D+∠OMD ,∴∠BOD=3∠COA. ∴⌒BD =3⌒AC .
13.(1)在⊙O 中,又∵AC=CD ,∴∠ABC=∠DBC 。
∵OC=OB ,∴∠ABC=∠OCB 。
∴∠OCB=∠DBC 。
∴OC ∥BD
(2)设平行线OC 与BD 之间的距离为h ,则S △OBC =S h OC ,21∙△DBC =h BD ∙2
1.∵BC 将四边形OBDC 分成面积相等的两个三角形,即S △OBC =S △DBC ,∴OC=BD 。
又∵OC ∥BD ,∴四边形OBDC 为平行四边形。
又∵OC=OB ,∴四边形OBDC 为菱形。
