《刚体的角动量守恒》PPT课件
合集下载
角动量守恒 教学ppt课件

i
12
M外 Mi外 ri Fi
i
i
----各质点所受外力矩的矢量 和称为质点系所受合外力矩
M内 Mi内 (ri fij ) 0
i
i
ji
----各质点所受内力矩 的矢量和
(证明如下:)
Fi
m2
m1
mi
fij ri
f ji m j
0
rj
13
内力总是成对出现的,所以内力矩也是成对出
:质量线密度
线积分
对质量面分布的刚体: dm dS
:质量面密度
对质量体分布的刚体:dm dV
:质量体密度
面积分
体积分 26
计算转动惯量 I 的三条有用的定理:
(1)叠加定理:对同一转轴 I 有可叠加性
I Ii
I mr mr mr
m2
I
r1
m1
r2 r3
m3
转轴
(2)平行轴定理: I Ic md 2
常矢量
7
若 M 0 ,则 L 常矢量
M 0
的条件是
— 质点角动量守恒定律
F 0
或 F 过固定点:有心力
(如行星受的万有引力)
角动量守恒定律是物理学的基本定
律之一,它不仅适用于宏观体系,也 适用于微观体系,而且在高速低速范 围均适用。
8
角动量守恒定律可导出行星运动的开
普勒第二定律:
L
(书P79页例3.1)
i
与内力矩无关 v
守恒条件 M i 0 i
20
§3.3 定轴转动刚体的角动量 转动惯量 一、定轴转动刚体的角动量
把刚体看作非常多质元构成 的质点系,第i个质元对原点o
z v vvi
角动量角动量守恒PPT课件
M M1 M2 M3
(2)刚体内作用力和反作用力的力矩互相抵消.
M ij
rj
j
O
d ri
i Fji
Fij
Mij M ji
M ji
(3)力矩必须明确是对哪个点(或轴) 8
三、角动量定理 角动量守恒
1.质点的角动量定理
将角动量 L r p 两边对时间求导
14
角动量守恒定律是一条普遍的规律,存在
于很多自然现象中,例如,行星受恒星引力作
用作椭圆轨道运动,引力的作用线始终通过恒
星中心,这样的力称为有心力。由于有心力对
力心的力矩恒为零,因此,受有心力作用的质
点对力心的角动量守恒。 掠面速度
·m
f
r
dS 1 r v dt 2
o r
vdt
12
将角动量定理的微分形式 M dL 两边乘以
dt 并积分得
t
dt
0 M dt L L0
t
0 M
dt :
质点或质点系的合外力矩的冲量矩;
L0 与L 分别是质点或质点系始末状态的角动量。
在一段时间内,质点(系)角动量的增量
等于作用于质点(系)的合外力矩的冲量
矩——质点(系)角动量定理的积分形式
Lrp
(xi yj zk ) (pxi py j pzk )
各坐标轴的分量
Lx ypz zpy Ly zpx xpz Lz xpy ypx
分别称为对 x、y 、z 轴的角动量
2
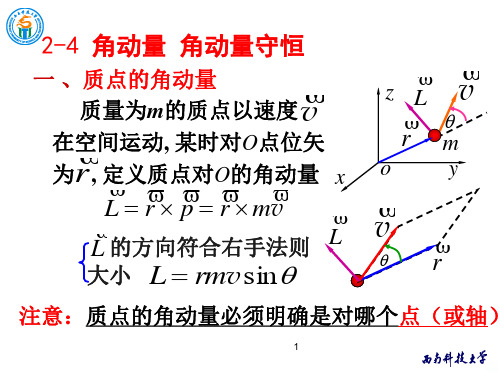
例 质点L沿某r一 p方向r作 m直v线运动,对O点的角动量 角动量大小为
L rm vsin m v d
角动量守恒定律.pptx

角动量守恒定律
一、角动量定理
由转动定律
4-3 角动量守恒定律
M dL dt
Mdt dL
L L t2 Mdt L2 dL
t1
L1
21
系统所受合外力矩的冲量矩等于系统 角动量的增量。
4-3 角动量守恒定律
二、角动量守恒定律
由角动量定理:
t2 t1
M
d
t
L2
L1
若 M 0,则 L J =恒矢量
4-3 角动量守恒定律
一、角动量定理:
t2 tL1
二、角动量守恒定律:
若 M 0,则 L J =恒量
1、刚体: J不变, 也不变(大小、方向) 2、非刚体: J变, 变 → J ,;J ,
课后思考:
4-3 角动量守恒定律
试分析为什么直升机要安装尾翼螺旋桨呢?
4-3 角动量守恒定律
内容:当系统所受合外力矩为零时,则 系统的总角动量保持不变。
应用:
4-3 角动量守恒定律
1、刚体: J不变, 也不变 (大小、方向)
应用:
4-3 角动量守恒定律
2、非刚体: J变, 变 → J ,;J ,
4-3 角动量守恒定律
2、非刚体: J变, 变 → J ,;J ,
J ,
J ,
小结:
刚体转动及角动量守恒ppt

匀直细杆对端垂轴旳
平行移轴定理
对质心轴旳转动惯量 对新轴旳转动惯量
质心
例如:
时
新轴对心轴旳平移量
新轴 质心轴
代入可得 端
匀质薄圆盘对圆心垂盘轴算旳 例
取半径为 微宽为 旳窄环带旳质量为质元
球体算例 匀质实心球对心轴旳 可看成是许多半径不同旳共轴 薄圆盘旳转动惯量 旳迭加 距 为 、半径为 、微厚为 旳薄圆盘旳转动惯量为
a = Rb
T2 – m2 g = m2a ( T1 – T2 ) R = Ib
及
I
=
1 2
mR2
得
b=
(m1-m2)g
R(m1+ m2+ m
2)
常量
故
由
m2
a
G2
m1
a
G1
(m1-m2)g
R(m1+ m2+ m 2)
t (m1-m2)g
g 2 (rad)
R(m1+ m2+ m 2)
两匀直细杆
q
转动定两律者瞬例时题角加五速度之比
与 时刻相应,何时
则何时
,
何时 恒定 则何时 恒定。
匀直 细杆一 端为轴 水平静 止释放
转动定律例转题动 二( T2 – T1 ) R = Ib
I=mR2 2
R
m
T2
T1
a
m2
m1
b
平动 m2 g – T2 = m2a
T2
T1
T1 – m1 g = m1a
线-角 a = Rb
T2
T1
联立解得
a
G2
力矩旳功算例 拨动圆盘转一周,摩擦阻力矩旳功旳大小
第3章 角动量守恒定律 PPT课件

若转轴不动,称定轴转动。 O
1. 定轴转动特征
(1) 刚体上各点都在垂直于固定轴的平面内(转动平面) 做圆周运动.其圆心都在一条固定不动的直线(转轴)上.
(2) 刚体上各点到转轴的垂直线在同样的时间内所转过 的角度都相同。因而用角量描述刚体的运动.
www. ******.com
3.3 刚体的运动
2. 定轴转动的描述
解:
N
R
T
Mg
T' M.
a R
mg
m
www. ******.com
3.4 刚体的角动量 转动定律 转动惯量
根据转动定律 根据牛顿第二定律
TR=Jβ
1 MR2
2
mg-T=ma
因绳与滑轮间无滑动,所以 a=Rβ
解以上三式得
a mg mM /2
a
mg
R R( m M / 2 )
rF
www. ******.com
3.1 质点的角动量 力矩
3.1.2 质点的角动量定理
力矩定义:
M rF
力矩大小:
M r F sinθ 式中 rsinθ d 为力臂,则
M Fd
因 Fsin θ F ,即合力切向分量,所以:
M r F
www. ******.com
3.2 质点的角动量守恒定律
(1) 角坐标 称角位置或角坐标。
规定逆时针转向 为正。
p x
O
刚体定轴转动的运动学方程
= (t) (2) 角位移
为 t时间内刚体所转过的角度。
p x O
www. ******.com
3.3 刚体的运动
(3) 角速度 角速度 lim Δ d Δt0 Δt dt 在定轴转动中,转向只可能有
刚体定轴转动的角动量定理和角动量守恒定律课件

转动惯量的特性
只与刚体的质量和各质点到转动轴 的距离有关,与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ,等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量,具有方向和大小;对 于定轴转动,角动量位于转轴上;角 动量是相对量,与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种,一种是基于牛顿第二定律和转动定理推导,另一种是通过分析系统的能 量变化来证明。通过这些证明方法,可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明,对于不受外力矩或所受外力矩的矢量和为零的系统,其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用,如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例,其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时,可以将其视为 刚体定轴转动,这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时,也是一个刚体定 轴转动的例子,其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时,可以通过改变身体的姿势来改变转动惯量,从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
只与刚体的质量和各质点到转动轴 的距离有关,与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ,等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量,具有方向和大小;对 于定轴转动,角动量位于转轴上;角 动量是相对量,与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种,一种是基于牛顿第二定律和转动定理推导,另一种是通过分析系统的能 量变化来证明。通过这些证明方法,可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明,对于不受外力矩或所受外力矩的矢量和为零的系统,其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用,如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例,其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时,可以将其视为 刚体定轴转动,这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时,也是一个刚体定 轴转动的例子,其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时,可以通过改变身体的姿势来改变转动惯量,从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
角动量守恒PPT

i 1
可见即使对定轴转动,角动量L也不一定与方向相同
(本例中方向还一直在改变)。
第 49 页
z
本章中我们感兴趣的是定
L
ri
D Li
轴转动,即要研究角动量
v i 在z轴的分量Lz
q
Dmi
Ri
DLiz DLi cosq
O
Dmi Rivi cosq
Dmiri2
Lz DLiz (Dmiri2)
JZ
r 2dm
m
r2 r r (r h) (r h)
r2 h2 2h r
rdm 0 质心的定义 m
Jz
r2dm
m
h2dm 2h
m
m r2dm JC mh2
第 21 页
例3 一质量为 m ,半径为 R 的均匀薄圆盘,求通 过盘中心并与盘面垂直的轴的转动惯量。
解 dm 2 rdr
特别要注意: 转动惯量与转轴的位置有关。
转动惯量具有可相加性。
第 17 页
第 18 页
例2 计算质量为 m ,长为 l 的细棒绕通过其端点的 垂直轴的转动惯量。
解 J r2dm
dm dx m dx
l
J l x2 m dx 1 m x3 l
0l
3l 0
J 1 ml2 3
第 19 页
J r2dm
J 2 R r3dr 0 R4 1 mR2 22
r dr Ro
第 22 页
例4 质量m1、半径为 R的实心滑轮,可绕通过其质心 的轴无摩擦的转动。一根轻绳绕在其上,绳端挂一质
量为 m2的物体,绳子与滑轮间无相对滑动。求物体下 落的加速度和绳子的张力。
解
T
R
刚体的角动量PPT课件

应该理解和掌握。 如果忽略滑轮的质量,则有
T1
T2
m1m2 g m1 m2
15
第15页/共59页
例题6 长度为l、质量为m 的均匀棒悬挂在通过
其顶端的水平轴上,并可绕此轴在竖直平面内作
无摩擦的摆动。如果棒自由摆动通过平衡位置时,
低端的速率为v,试求:
(1)棒通过平衡位置时的转动动能;
(2)棒摆动的最大偏角m ; (3)在从平衡位置到达最大偏角m 的过程中, 在任一位置时棒的角加速度。
M z
dM z
l g m ldl 1 Lmg
0
L
2
(2)求角加速度
根据转动定律 Mz J
其中,棒相对一端的转动惯量
3 g
2L
J 1 mL2 3
角加速度为负值,表示为减速转动
22
第22页/共59页
(3)求外力矩撤去后棒转过的转数 选求转过的总角度。根据匀变速定轴转动规律
0 02 2
m2R2 )1
1 2
m1R22
2
1 2
m1R2 m2R2
1 2
m1R2
1
1 2
m1 1 2
m2 m1
1
2.31rad
s1
38
第38页/共59页
例3如图所示,细杆(l,m)可绕端点O的水平轴转动,从水 平位置自由释放,在竖直位置与物体M相碰,物体与地面摩擦 系数为μ,相撞后,物体沿水平地面滑行一段s 后停止。 求:碰后杆质心C离地最大高度,并说明杆向左右摆的条件。 解(1) 自由下落过程 (E守恒)
将 代入上式: o2 1 o2L
2 3 g
转动的转数为: n 1 o2L 2 6 g
(4)求摩擦力矩所作的功
