小学求阴影部分面积经典78题(提高题)
六年级上册第五单元圆和扇形奥数提高题
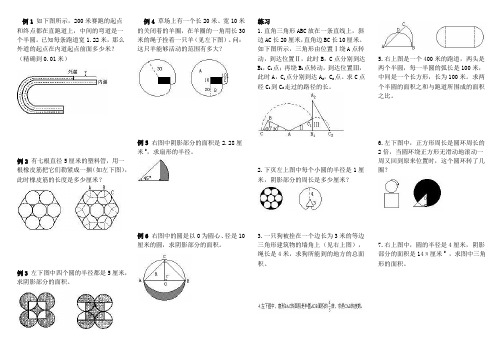
例1如下图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)例2有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下图),此时橡皮筋的长度是多少厘米?例3左下图中四个圆的半径都是5厘米,求阴影部分的面积。
例4 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?例5 右图中阴影部分的面积是2.28厘米2,求扇形的半径。
例6 右图中的圆是以O为圆心、径是10厘米的圆,求阴影部分的面积。
练习1.直角三角形ABC放在一条直线上,斜边AC长20厘米,直角边BC长10厘米。
如下图所示,三角形由位置Ⅰ绕A点转动,到达位置Ⅱ,此时B,C点分别到达B1,C1点;再绕B1点转动,到达位置Ⅲ,此时A,C1点分别到达A2,C2点。
求C点经C1到C2走过的路径的长。
2.下页左上图中每个小圆的半径是1厘米,阴影部分的周长是多少厘米?3.一只狗被拴在一个边长为3米的等边三角形建筑物的墙角上(见右上图),绳长是4米,求狗所能到的地方的总面积。
5.右上图是一个400米的跑道,两头是两个半圆,每一半圆的弧长是100米,中间是一个长方形,长为100米。
求两个半圆的面积之和与跑道所围成的面积之比。
6.左下图中,正方形周长是圆环周长的2倍,当圆环绕正方形无滑动地滚动一周又回到原来位置时,这个圆环转了几圈?7.右上图中,圆的半径是4厘米,阴影部分的面积是14π厘米2,求图中三角形的面积。
练习111.68厘米。
2.62.8厘米。
解:大圆直径是6厘米,小圆直径是2厘米。
阴影部分周长是6π+2π×7=62.8(厘米)。
3.43.96米2。
解:如下页右上图所示,可分为半径为4米、圆心角为300°的扇形与两个半径为1米、圆心角为120°的扇形。
六年级下册奥数试题-几何专题 全国通用(含答案) (1)

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料, 本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位: 厘米)分析: 阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答: $(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案: 阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算, 这里考查了梯形和圆的面积公式的灵活应用。
2.如图, 求阴影部分的面积。
(单位: 厘米)分析:根据图形可以看出, 阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米, 4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答: 扇形的半径是: $10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案: 阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系, 特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
4.求出如图阴影部分的面积: 单位: 厘米。
解答:该题缺少图形, 无法回答。
5.求如图阴影部分的面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
6.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
7.计算如图中阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
8.求阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
9.如图是三个半圆, 求阴影部分的周长和面积。
(单位: 厘米)分析: 阴影部分可以看成是两个半圆和一个矩形组成的, 可以分别计算各部分的周长和面积再相加。
阴影部分面积专题复习经典例题(含答案)

小升初阴影部分面积专题姓名:1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积.()3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:cm)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
阴影部分的周长与面积

阴影部分的周长与面积执教:姚久龙 2010-1-6 教学目标:1.通过求图形中阴影部分的周长与面积,进一步熟练圆的周长与面积、弧长及扇形的周长与面积的计算.2.在通过割补法求图形的周长与面积的过程中,体验将所求图形转化成熟悉的图形的方法给解题带来的简便.3.激发学生学习几何图形问题的兴趣,培养善于观察、独立思考、敢于质疑的良好学习习惯.教学重点:求图形中阴影部分的周长与面积难点:通过“割、补”将所求图形转化成熟悉的图形教学过程:一、复习思考:1.提问:请同学们回忆一下圆的周长与面积计算公式?弧长的计算公式?2.扇形的面积的计算公式是什么?如何计算扇形的周长?3.思考:如图1:用一个边长为2cm 的正方形纸片剪一个面积最大的圆,剩余部分的面积是多少?剩余图形的周长呢?二、问题探究:1.问题1:如图2,用一个边长为2cm 的正方形纸片,剪去两个面积最大的半圆,剩余部分的面积是多少?剩余图形的周长呢?分析:图形中的阴影部分的面积与思考题有何关系?你是如何看出的?周长是由哪些线组成的?阴影部分的面积=正方形的面积—圆的面积阴影部分的周长=正方形的两边+圆的周长解:r=221⨯=1(cm ) S=22114.3⨯=r π=3.14 C=114.322⨯⨯=⋅r π=6.28S 阴=4-3.14=0.86,C 阴=28.1028.622=+⨯答:阴影部分的面积为0.86平方厘米,周长为10.28 厘米.变式1:如图3,用一个边长为2cm 的正方形纸片,剪去4个面积相等的扇形,如果扇形的半径都是1cm ,圆心角都是90°,那么剩余部分的面积是多少?剩余图形的周长呢?变式2:如图4,正方形的边长为2,求阴影部分的面积与周长?图2图3图1图42.问题2:如图5,正方形边长为10cm ,求阴影部分的面积和周长? 解:r=10cm , n=90°l =1014.318090180⨯⨯=⋅r n π=15.7 S =221014.336090360⨯⨯=⋅r n π=78.5 S 阴=100-78.5=21.5,C 阴=7.357.1520=+答:阴影部分的面积为21.5平方厘米,周长为35.7厘米.变式1:如图6,正方形边长为10cm ,求阴影部分的面积和周长? 变式2:如图7,正方形边长为10cm ,求阴影部分的面积和周长?变式3:如图8,正方形边长为10cm ,求阴影部分的面积和周长?三、课堂练习1.如图10,大圆的直径为20cm ,半圆的直径等于大圆的半径,求阴影部分的面积和周长?2.如图11,长方形的长是20cm ,宽是长的一半,求阴影部分的面积和周长?四、师生小结:通过这节课的学习,你有何收获?有何疑惑?五、布置作业:基础题:如图11,长方形的长30cm ,宽为20cm ,求图中阴影部分的面积和周长?提高题:如图12,两条互相垂直的半径长为20cm ,求图中阴影部分的面积和周长?图5图8图9图10图11图6。
苏教版小学数学五年级上册计算题强化训练(专项突破)【含答案】

苏教版小学数学五年级上册计算题强化训练(专项突破)一、图形计算1.计算下面各图形的面积。
(单位:厘米)2.计算下面图形的面积。
(单位:厘米)3.求第一个图形的面积,求第二个图形的阴影部分的面积。
4.计算下面图形的面积。
(单位:厘米)5.计算下图的面积。
6.计算下面图形的面积。
7.计算图形面积。
(有阴影部分的计算阴影部分,单位:厘米)8.求下列阴影部分的面积。
(单位:分米)二、竖式计算9.列竖式计算,打★的要验算.8.4+12.68=20﹣5.67=★4.98+5.2=10.竖式计算3.76+4.53= 6.92-1.48=24.08+1.7= 6.28+5.32=11.竖式计算.16.37+20.9=50-43.67=8.96+13.9=49.5-23.67=12.列竖式计算。
(1)57.08-8.19=(2)6.2+14.98=(3)16.05-9.7=13.用竖式计算.(带★的要验算)(1)413÷3(2)★283÷4(3)0.3+7.7(4)24×68(5)★600÷5(6)4.1-2.814.用竖式计算,带★的要验算.8.65-6.31=★10-7.64=13.6+8.46=0.99+1.1=12.9+5.01=★141.2-48.98=15.列竖式计算.(前两个验算)7.55+5.68=10-9.57=11.35+64.5=19.08-4.28=16.用竖式计算。
(1)5.08×0.65(2)30.807÷6.3(3)54.68-12.8(4)19.92+420.26三、脱式计算17.用简便方法计算下列各题。
14.62-(6.62+1.54)13.7×0.125×817.29÷0.5÷214.4×4.8+5.2×14.418.计算,能简算的要写出简算过程。
★12.8×8.6-2.8×8.6★15.29+4.2+4.71+5.8★38÷12.5÷0.8★0.42×[(3.2-0.5)÷9]19.脱式计算。
六年级下册奥数试题-几何专题 全国通用(含答案)

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版)(含答案).doc

(期末真题精选)07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版)试卷说明:本试卷试题精选自广东省广州市各区县2020-2022近三年的四年级期末真题试卷,难易度均衡,适合广东省广州市各区县和使用人教版教材的四年级学生期末复习备考使用!一、图形计算1.求出下图的周长。
2.下面是一张纸折起来以后形成的图形,已知∠1=50°,你能求出∠2的度数吗?3.一张直角三角形纸片,剪去直角后得到一个四边形(如下图),求12∠+∠的度数。
4.算出下面未知角的度数。
5.算一算。
在一个三角形中∠2=65°,∠3=73°,求∠1。
6.求出下面未知角的度数。
7.如图,已知∠1=72°,∠2=32°,∠3=45°,求∠5。
8.已知∠1=105°,求∠2的度数。
9.算出下面各个未知角的度数。
10.求下面各未知角的度数。
(1)(2)(3)11.求出图中未知角的度数。
(1)(2)12.求出下面∠1的度数。
13.已知∠1=75°,求∠2的度数。
14.计算下面图形的周长。
(单位:厘米)(1)(2)15.列式计算角的度数。
16.下图中每个正方形的边长是4cm,求阴影部分的面积。
17.小兔家的屋顶是一个等腰三角形(如图),请你算出顶角的度数。
18.算一算。
在三角形中∠1=72°,∠2=90°,求∠3。
19.算一算角的度数。
①②20.求出下面三角形各个角的度数。
21.求出下面三角形各个角的度数。
(1)(2)(3)22.求出下图中∠1的度数。
23.计算如图图形的周长。
(单位:厘米)24.计算下面图形中阴影部分的面积。
(图中每个小方格的面积是1cm2)25.求图中∠1的度数.26.求阴影部分的面积。
(单位:cm)27.算出下面各个未知角的度数(写出计算过程)。
28.计算下面图形的周长和面积。
29.计算下面未知角的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学求阴影部分面积经典78题(提高题)1、平行四边形ABCD 的对角线上一点E,AE=EC,BF=F G=GC,三角形EFG的面积等于3平方厘米,求平行四边形面积是多少?2、正方形ABCD和EFGC 分别是边长6厘米和8厘米,求阴影面积。
3、用55米的竹篱笆靠墙围成一个花圃,求花圃的面积是多少?20米ABDECFGABCDEFG4、计算图形面积。
(单位:分米)5、求图形面积。
(单位:厘米。
)6、一块长方形草坪,长是16米,宽是10米,中间有两条交叉的人行道,一条是长方形,一条是平行四边形,人行道宽2米,那么,有草部分(阴影部分)的面积有多大?7、右图是由9个长方形组成,其中编号为1,2,3,4,5的长方形的面积分别为1m 2, 2m 2, 3m 2, 4m 2, 5m 2,求6号图形面积是多少?5512541 2 3456CADE 5 12135o68、三角形AOB的面积是15平方米,OB=3OD,求梯形ABCD的面积。
9、如图:是一个边长为4厘米的正方形,我们称它为第一个正方形,依次连结四条边的中点,得到第二个正方形,继续这样下去,得到第三个,第四个,第五个正方形,那么第五个正方形是多少?10、在长方形ABCD中,E为宽的中点,F为长的中点,求阴影面积占长方形面积的几分之几?A BDOCCE FA BD11、三角形ABC 是等腰直角三角形,E 、F 分别是AB 和AC 的中点,AE =FC =1厘米,三角形AEF 的面积是1平方厘米,四边形BCFE 的面积是多少平方厘米?12、两个相同的直角三角形如图重叠在一起,求阴影部分的面积。
13、长方形ABCD 的长为7厘米,宽是4厘米,另一个长方形DEFG 的长为10厘米,宽是2厘米,求三角形BCO 与三角形EFO 的面积之差。
AB D GCE F O5cm 2cm12cmABC D 10cm E 24cm 45010cm 14、求阴影部分面积。
FAE CB15、图中长方形ABCD 中AB =5cm,BC=8cm.三角形DEF (甲)的面积比三角形ABF (乙)的面积大8平方厘米。
求DE 的长。
16、四边形ABCD 中,AC 和BD 互相垂直,AC =20厘米,BD =15厘米。
求四边形的面积。
17、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B =∠E =900.求四边形ACDF 的面积。
BCAEFD甲乙D ABcAC EB DF2cm4cm 8cm5cm18、在四边形ABCD 中,∠C =450,∠B =900,∠D =900,AD=4cm,BC=12cm.求四边形ABCD 的面积。
19、三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米。
AB 长40厘米,BC 长多少厘米?20、在右图中(单位:厘米),两个阴影部分面积的和是多少平方厘米?21、ABC 是等腰直角三角形。
D 是半圆周的中点,BC 是半圆的直径,已知:AB =BC =10厘米,那么阴影部分的面积是多少?ABDC450①②②②CB A20 1612DAC22、在三角形ABC 中,AD =BD ,CE =3BE 。
若三角形BED 的面积是1平方厘米,则三角形ABC 的面积是多少平方厘米?23、如图所示,平行四边形ABCD 的面积是40平方厘米,求图中阴影部分的面积。
24、图中阴影部分的面积是25平方厘米,求圆环的面积。
DB CAABDCO25、算出圆内正方形的面积为多少?26、如图,以B ,C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米。
(保留小位小数)27、图中扇形的半径OA =OB =6cm.∠AOB =45o ,AC 垂直OB 于C ,那么图中阴影部分的面积是多少平方厘米。
(π=3.14)28、半圆S1的面积是14.13平方厘米,圆S2的面积是19.625平方厘米。
那么长方形(阴影部分的面积)是多少平方厘米?6厘米DCEA E450ADcB6 S2S129、三角形ABC 面积是31.2平方厘米。
圆的直径AC =6厘米;BD :DC =3:1;求阴影部分面积。
30、O 是小圆的圆心,OC 垂直于AB ;三角形ABC 的面积是45平方厘米。
求阴影部分的面积。
31、求阴影部分的面积32、求阴影部分的面积CD BAoACBo 8cm633、正方形周长是24米,求阴影面积。
4米5厘米10cm10cm37、求阴影部分的面积(单位:厘米。
)38、已知,在矩形ABCD中,三角形EFD的面积是4平方米,三角形EDC的面积为6平方米,求阴影部分面积?39、长方形ABCD中,AE=EB,BC=3BF,CG=GD,H是AD上的任一点,则图中阴影部分的面积是几分之几?AEBHF DG CA BDCFE42 2 241、求阴影部分的面积,单位:厘米。
43,求阴影部分的面积,正方形的边长是10厘米。
2085 40、正方形ABCD 边长为10cm,BO ⊥AE,BO 长8cm 。
AE =?DACBo E42、如图,以OA 为斜边的直角三角形的面积是24平方厘米,斜边长10厘米,将它以0点为中心旋转900,问三角形扫过的面积是多少?π=3oA44、求阴影部分的面积。
22cm10cm8cm45、一个三角形底长6米,如果底延长1米,面积就增加2平方米,原三角形的面积是多少平方米?42平方米6米1米46、图中平行四边形面积是20平方厘米,求阴影面积是多少?5847、求阴影部分的面积(单位:厘米。
)ABEFFCD49、四边形ABCD 的对角线AC 和BD相交于E ,F ,G 分别是AC ,BD 延长线上的点且CF =AE ,DG =BE 。
如果四边形ABCD 的面积为10平方厘米,求三角形EFG 的面积。
ADBC FEO48、如图正方形的边长为6厘米,E ,F 分别是CD ,BC 的中点,求阴影部分的面积。
BA50、由点A 向三角形的三条边作出三条垂线,并且量出三条垂线的总长是多由点B 向三角形的三条边作出三条垂线,并且量出三条垂线的总长是多少。
51、已知三角形ABC 面积为1平方厘米,延长AB 至D ,使BD =AB ;延长BC 至E ,使CE =2BC ;延长CA 至F ,使AF =3AC ,求三角形DEF 的面积。
52、E 是长方形ABCD 的AB 边中点,CE 和BD 相交于F ,如果三角形EBF 的面积是1平方厘米,那么三角形DFC 的面积是多少?53、梯形ABCD 的面积是90平方厘米,AC =3AO ,阴影部分的面积是多少平方厘米?EDFAB CDACBFEAB CDo54、两个正方形的周长相差12厘米,面积相差69平方厘米,两个正方形的面积各是多少平方厘米?55、大中小三个正方形,边长都是整厘米数,小正方形的周长比中正方形的边长大,把两个正方形叠放在大正方形上,大正方形露出部分(阴影部分)的面积为28平方厘米。
大正方形的面积是多少平方厘米?FG AD E BC56、等腰三角形ABC 的面积为240平方厘米,AB =AC =30厘米,D ,E 为AB 边上的两点,且AD =15厘米,DE =10厘米,EB =5厘米;F ,G 为AC 边上的两点,且AF =5厘米,FG =10厘米,GC =15厘米。
那么,阴影部分面积是多少平方厘米?红黄绿57、有红,黄,绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间相互叠合,已知露在外面部分中,红色面积是20,黄色面积是12,绿色面积是8,那么正方形盒的底面积是多少?58、一个长方形若能分割成大小不一样的小正方形,则称它为完美长方形。
右图完美长方形可以分割成9个小正方形,其中小正方形A和B的边长分别为5厘米和9厘米,那么大长方形的面积是多少平方厘米?59、图中5个阴影所示的图形都是正方形,所标数字是邻近线段的长度。
那么,阴影所示的5个正方形的面积之和是多少?(单位:厘米)60、左图是用七巧板拼成的边长为20厘米的正方形,求阴影部分的面积?61、在梯形ABCD中,CD的长是AB的2倍,BC长5厘米,DE长8厘米,梯形ABCD的面积是多少平方厘米?62、ABCD和BEFG是两个正方形有,EF=18分米,阴影部分的面积是多少平方分米?63、在边长为6的正方形内有一个三角形DEF,线段AE=3,BF=2,三角形DEF的面积是多少?64、梯形ABCD的下底是上底的1.5倍,梯形中阴影面积和空白面积相等。
三角形AOD的面积是12,那么三角形BOC的面积是多少?65、图中每个小正方形的面积是4平方厘米,阴影部分的面积是多少平方厘米?66、在三角形ABC中,画有一个最大的正方形BEFG,已知AG=3,EC=15,那么正方形BEFG的面积是多少?67、在图中直角三角形ABC中,AB=10厘米,BC=15厘米,在其内画一个正方形BDEF,正方形BDEF的面积是多少平方厘米?68、三角形ABC是等腰直角三角形,D,E是AB边上两点,AD=50厘米,DE=30厘米,EB=20厘米;F,G是AC边上的两点,AF=20厘米,FG=30厘米,GC=50厘米。
阴影部分的面积与空白部分面积相差多少平方厘米?69、一个大长方形被分成9个面积不相等的小长方形。
其中A,B,C,D,E的面积分别是A=160,B=172,C=215,D=240,E=300(单位:平方厘米)。
原来大长方形的面积是多少平方厘米?70、用一张斜边为29厘米的兰色直角三角形纸片,一张斜边为49厘米的红色直角三角形纸片,一张黄色正方形纸片,恰好拼成一个直角三角形。
问:红,蓝两张三角形片的面积和是多少?71、一条白色的正方形手帕,它的边长是18厘米,手帕上横,竖各有两道红条,红条宽都是2厘米,问这条手帕白色部分的面积是多少?72、三角形ABC的面积为1平方分米,其中AE=3AB,BD=2BC,那么三角形BED的面积是多少平方分米?73、在长方形内画了一些直线,已知边上有三块面积分别是13平方厘米,35平方厘米,49平方厘米。
图中阴影部分的面积是多少?74、已知图中长方形长8厘米,宽4厘米,图中阴影部分的面积是10平方厘米。
那么,OD长多少厘米?ABO DC75、ABCD是长方形,面积为48,三角形ADF面积为8,三角形ABE 面积为6,求三角形AEF的面积?76、长方形ABCD中,EF与BC平行,HG与AB平行,如果长方形AEOH,HOFD,OGCF的面积分别为9平方厘米,4平方厘米,7平方厘米,那么三角形HBF的面积为多少平方厘米?77、ABCG是4*7的长方形,DEFG是2*10的长方形,那么三角形BCM的面积与三角形D EM的面积之差是多少?78、左图是由9个小正方形组成的完美长方形。
图中正方形A和B 的边长分别是7和4,那么这个完美长方形的面积分别是( )。
