多项式数据结构c语言实现
数据结构(C语言)用单链表存储一元多项式,并实现两个多项式的相加运算

#include<stdio.h>#include<stdlib.h>#include<malloc.h>typedef int ElemType;/*单项链表的声明*/typedef struct PolynNode{int coef; // 系数int expn; // 指数struct PolynNode *next;}PolynNode,*PolynList;/*正位序(插在表尾)输入n个元素的值,建立带表头结构的单链线性表*/ /*指数系数一对一对输入*/void CreatePolyn(PolynList &L,int n){int i;PolynList p,q;L=(PolynList)malloc(sizeof(PolynNode)); // 生成头结点L->next=NULL;q=L;printf("成对输入%d个数据\n",n);for(i=1;i<=n;i++){p=(PolynList)malloc(sizeof(PolynNode));scanf("%d%d",&p->coef,&p->expn); //指数和系数成对输入q->next=p;q=q->next;}p->next=NULL;}// 初始条件:单链表L已存在// 操作结果: 依次对L的每个数据元素调用函数vi()。
一旦vi()失败,则操作失败void PolynTraverse(PolynList L,void(*vi)(ElemType, ElemType)){PolynList p=L->next;while(p){vi(p->coef, p->expn);if(p->next){printf(" + "); //“+”号的输出,最后一项后面没有“+” }p=p->next;}printf("\n");}/*ListTraverse()调用的函数(类型要一致)*/void visit(ElemType c, ElemType e){if(c != 0){printf("%dX^%d",c,e); //格式化输出多项式每一项}}/* 多项式相加,原理:归并 *//* 参数:两个已经存在的多项式 *//* 返回值:归并后新的多项式的头结点 */PolynList MergeList(PolynList La, PolynList Lb){PolynList pa, pb, pc, Lc;pa = La->next;pb = Lb->next;Lc = pc = La; // 用La的头结点作为Lc的头结点while(pa&&pb){if(pa->expn < pb->expn){pc->next = pa; //如果指数不相等,pc指针连上指数小的结点,pc = pa;pa = pa->next; //指向该结点的指针后移}else if(pa ->expn > pb->expn ){pc->next = pb; //pc指针连上指数小的结点,pc = pb;pb = pb->next; //指向该结点的指针后移}else//(pa ->expn = pb->expn ){pa->coef = pa->coef + pb->coef; //指数相等时,系数相加 pc->next = pa;pc = pa;pa = pa->next; //两指针都往后移pb = pb->next;}}pc->next = pa ? pa:pb; // 插入剩余段return Lc;}void main(){PolynList ha,hb,hc;printf("非递减输入多项式ha, ");CreatePolyn(ha,5); // 正位序输入n个元素的值printf("非递减输入多项式hb, ");CreatePolyn(hb,5); // 正位序输入n个元素的值printf("多项式ha :");PolynTraverse(ha, visit); printf("\n");printf("多项式hb :"); PolynTraverse(hb, visit); printf("\n");hc = MergeList(ha,hb); PolynTraverse(hc, visit); }。
数据结构多项式求和实验报告

1.实验题目设计一种用单链表存储多项式的结构(每个结点存储一项的系数和指数,类型都为int),并编写一个产生多项式链表的函数和一个实现两个多项式相加的函数。
2 .实验内容顺序存储结构的实现。
先输入多项式最高项数,然后按照(系数,指数)的格式输入顺序表类型定义如下:typedef struct term{int coef;int expn;struct term *next;}term,*Polynomial;3.实验要求(1)利用C语言完成算法设计和程序设计。
(2)上机调试通过实验程序。
(3)输入数据,检验程序运行结果。
(4)给出具体的算法分析,包括时间复杂度和空间复杂度。
(5)撰写实验报告。
4.实验步骤与源程序⑴实验步骤首先分析实验内容,要实现多项式求和,必须创建两个函数,然后先建立一个多项式a和多项式b,接着输入每个多项式的系数和指数,再实现多项式a和b的求和将求出的多项式放在多项式a中,最后输出求出的多项式的结果。
⑵源代码#include<stdio.h>#include<stdlib.h>#include<string.h>#include<time.h>#include<malloc.h>/*定义存储结构,用单链表存储多项式,链表中每个结点存储多项式中的一项。
*/typedef struct term{int coef;//定义多项式系数为coefint expn;//定义多项式指数为expnstruct term *next;}term,*Polynomial;void Create_Polynomial(Polynomial *P,int n){ /*建立多项式*/int i;term *t1,*t2;(*P)=(term *)malloc(sizeof(term));(*P)->coef=0;(*P)->expn=0;(*P)->next=NULL;t1=(*P);for(i=0;i<=n;i++){ /*输入每一项的系数和指数*/ t2=(term *)malloc(sizeof(term));scanf("%d,%d",&(t2->coef),&(t2->expn));t1->next=t2;t1=t1->next;}t2->next=NULL;}void Add_Polynomial(Polynomial *a,Polynomial *b){ /*多项式a和多项式b求和,结果存放在a中。
数据结构C语言实现之一元多项式的表示及相加(2)

数据结构 C 语言实现之一元多项式的表示及相加(2)
一元多项式的表示及相加 对于符号多项式的各种操作,实际上都可以利用线性表来处理。比较典型的是关于一元多项式的处理。在
} } e>next; /*将 q 结点加入到和多项式中*/ q =q->next; } }
} if(p!=NULL)/*多项式 A 中还有剩余,则将剩余的结点加入到和多项式中*/
pre->next=p;
else /*否则,将 B 中的结点加入到和多项式中*/ pre->next=q; }
算法 2.24 多项式相加 假设 A 多项式有 M 项,B 多项式有 N 项,则上述算法的时间复杂度为 O(M+N) 图 2.20 所示为图 2.19 中两个多项式的和,其中孤立的结点代表被释放的结点。
通过对多项式加法的介绍,我们可以将其推广到实现两个多项式的相乘,因为乘法可以分解为一系列的加 法运算。
“中的结点无需另生成,则可看成是将多项式 B 加到多项式 A 中,由此得到下列运算规则(设 p、q 分别 指向多项式 A,B 的一项,比较结点的指数项)
若 p->exp< q->exp,则结点 p 所指的结点应 是“和多项式”中的一项,令指针 p 后移;若 p>exp>q->exp,则结点 q 所指的结点应是“和多项式”中的一项,将结点 q 插入在结点 p 之前, 且令指针 q 在原来的链表上后移;
(1)用单链表存储多项式的结点结构如下: struct Polynode { int coef; int exp; Polynode *next; } Polynode , * Polylist;
C语言编写牛顿插值多项式的实现

1实验名称:Newton 插值多项式实验目的了解Newton 插值多项式实验类型设计型实验环境Windows XP TC实验内容相关知识:通过n+1个节点的次数不超过n 的Newton 插值多项式为:)())(](,,,[))(](,,[)](,[)()(11010102100100----++--+-+=n n n x x x x x x x x x f x x x x x x x f x x x x f x f x N数据结构:两个一维数组或一个二维数组算法设计:(略)实验用例: 已知函数y=f(x)的一张表(同上一个试验)试验要求:利用Newton 插值多项式)(x N n 求被插值函数f(x)在点x=65处的近似值。
建议:画出Newton 插值多项式)(x N n 的曲线。
编写代码:#include<stdio.h>#include <graphics.h>double Juncha(double a[13][2],int f,int l){double m;if((l-f)>1){m=(Juncha(a,f+1,l)-Juncha(a,f,l-1))/(a[l][0]-a[f][0]); }elsem=(a[l][1]-a[f][1])/(a[l][0]-a[f][0]);return m;}double Newton(double a[13][2],double x) {double m,n,y;int i,j;y=a[0][1];i=j=1;while(i!=13){j=0;m=n=1.0;m=Juncha(a,j,i);while(j!=i){n=(x-a[j][0])*n;j++;}y=y+m*n;i++;}return y;}double Lglr(double a[13][2],double x) {double m,n,y;int i,j;m=n=1.0;i=j=y=0;while(i!=13){j=0;m=n=1;while(j<13){if(j!=i)m=(x-a[j][0])*m;j++;}j=0;while(j<13){if(j!=i)n=(a[i][0]-a[j][0])*n;j++;}y=y+m/n*a[i][1];i++;}return y;}void main(){double a[13][2]={0,5,10,1,20,7.5,30,3,40,4.5,50,8.8,60,15.5,70,6.5,80,-5,90,-10,100,-2,110,4.5,120,7}; double x,x1;int arw[6]={515,235,520,240,515,245};int arw1[6]={315,45,320,40,325,45};int gdriver=VGA;int gmode=VGAHI;initgraph(&gdriver, &gmode, "c:\\TC20\\BGI");c leardevice();printf("input x:\n");scanf("%lf",&x);x1=x;printf("y=%f\n",Newton(a,x));s etbkcolor(7);s etcolor(14);s etlinestyle(0,0,3);d rawpoly(3,arw);d rawpoly(3,arw1);l ine(120,240,520,240);l ine(320,40,320,440);s etlinestyle(1,0,1);line(320,150,320,340);line(330,150,330,340);line(340,150,340,340);line(350,150,350,340);line(360,150,360,340);line(370,150,370,340);line(380,150,380,340);line(390,150,390,340);line(400,150,400,340);line(410,150,410,340);line(420,150,420,340);line(430,150,430,340);line(440,150,440,340);setcolor(3);outtextxy(320,30,"Y");outtextxy(310,245,"O");outtextxy(525,240,"X");settextstyle(4,0,4);outtextxy(450,400,"Newton...");x=0;s etcolor(2);s etlinestyle(0,0,3);m oveto((x+320),(240-Newton(a,x)));w hile(x<=119){x=x+1;lineto((x+320),(240-Newton(a,x)));}x=0;s etcolor(6);s etlinestyle(0,0,1);m oveto((x+320),(240-Lglr(a,x)));w hile(x<=119){x=x+1;lineto((x+320),(240-Lglr(a,x)));}s etcolor(4);s etlinestyle(1,0,1);l ine((x1+320),((240-Newton(a,x1))-80),(x1+320),((240-Newton(a,x1))+120)); getch();c losegraph();}实验结果(测试用例、实验结果)实验总结与心得通过本次实验,对Newton插值多项式有了更深刻的了解!。
数据结构实验多项式计算器

数据结构实验多项式计算器1.实验目的本次实验的目的是使用C语言实现一个多项式计算器,分析其计算性能,并对计算结果进行验证。
2.实验内容(1)多项式计算器的原理多项式计算器是指利用多项式的定义,结合多项式的加法、减法、乘法、除法等运算,实现多项式进行计算的一类计算器。
多项式定义:当n>=0时,若存在一个多项式P(x)=a(0)+(x)+a(1)(x^1)+...+a(n)(x^n),且其中有一个a(i)!=0,则称多项式P(x)为a(0)+(x)+a(1)(x^1)+...+a(n)(x^n)。
其中a(i)称为多项式P(x)的系数,并且n+1称为多项式P(x)的次数。
多项式运算:(1)多项式加法:若存在多项式A(x)和B(x),则A(x)+B(x)的值为:A(x)+B(x)=a(0)+(x)+a(1)(x^1)+...+a(i)(x^i)+...+a(n)(x^n)+b(0)+(x)+b(1)(x^1)+...+b(i)(x^i)+...+b(n)(x^n)=c(0)+(x)+c(1)(x^1)+. ..+c(i)(x^i)+...+c(n)(x^n)其中c(i)=(a(i)+b(i))(0<=i<=n),即多项式A(x)+B(x)=C(x),其中C(x)的次数=max{A(x)的次数,B(x)的次数}。
(2)多项式减法:若存在多项式A(x)和B(x),则A(x)-B(x)的值为:A(x)-B(x)=a(0)+(x)+a(1)(x^1)+...+a(i)(x^i)+...+a(n)(x^n)-b(0)+(x)-b(1)(x^1)-...-b(i)(x^i)-...-b(n)(x^n)=c(0)+(x)+c(1)(x^1)+...+c(i)(x^i)+...+c(n)(x^n)其中c(i)=(a(i)-b(i))(0<=i<=n),即多项式A(x)-x)=C(x),其中C(x)的次数=max{A(x)的次数。
数据结构C语言实现多项式源代码

一、一元稀疏多项式计算器#include<stdio.h>#include<stdlib.h>#include<malloc.h>#define OK 1#define ERROR 0#define OVERFLOW -1typedef int Status;#define LIST_INIT_SIZE 51 //假设次数不超过50typedef struct{//coef表示系数,expo表示指数。
float coef;int expo;}ElemType;typedef struct LNode{ //结点类型ElemType data;struct LNode *next;}LNode,*LinkList;//记:Link与Position均为指向LNode的指针类型typedef LinkList Polynomail;//在单链表的基础上定义并实现//多项式用链表存储Status CreateList_L(LinkList &L){int n;printf("请输入需创建的多项式的长度:\n");scanf("%d",&n);LNode *CurPtr,*PrePtr;//创建递增链表L=(LinkList) malloc(sizeof(LNode));L->next=NULL;if(!L) exit(OVERFLOW);PrePtr=L;for(int i=1;i<=n;++i){CurPtr=(LNode *)malloc(sizeof(LNode));printf("请输入不同的多项式的非0系数:");scanf("%f",&(CurPtr->data).coef );printf("请输入不同的多项式的指数:");scanf("%d",&(CurPtr->data).expo );CurPtr->next=NULL;PrePtr->next=CurPtr;PrePtr=PrePtr->next;//插入到表头}CurPtr->next =L;//冒泡排序法对多项式按指数由大到小排列。
数据结构C语言描述——用单链表实现多项式的相加
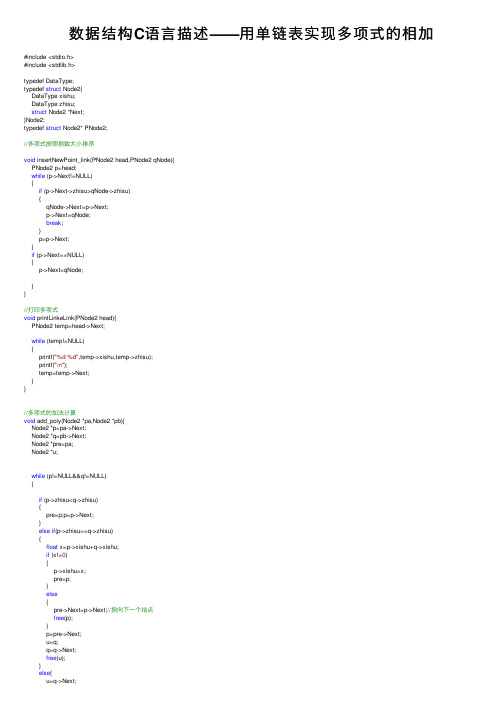
数据结构C语⾔描述——⽤单链表实现多项式的相加#include <stdio.h>#include <stdlib.h>typedef DataType;typedef struct Node2{DataType xishu;DataType zhisu;struct Node2 *Next;}Node2;typedef struct Node2* PNode2;//多项式按照指数⼤⼩排序void insertNewPoint_link(PNode2 head,PNode2 qNode){PNode2 p=head;while (p->Next!=NULL){if (p->Next->zhisu>qNode->zhisu){qNode->Next=p->Next;p->Next=qNode;break;}p=p->Next;}if (p->Next==NULL){p->Next=qNode;}}//打印多项式void printLinkeLink(PNode2 head){PNode2 temp=head->Next;while (temp!=NULL){printf("%d %d",temp->xishu,temp->zhisu);printf("\n");temp=temp->Next;}}//多项式的加法计算void add_poly(Node2 *pa,Node2 *pb){Node2 *p=pa->Next;Node2 *q=pb->Next;Node2 *pre=pa;Node2 *u;while (p!=NULL&&q!=NULL){if (p->zhisu<q->zhisu){pre=p;p=p->Next;}else if(p->zhisu==q->zhisu){float x=p->xishu+q->xishu;if (x!=0){p->xishu=x;pre=p;}else{pre->Next=p->Next;//指向下⼀个结点free(p);}p=pre->Next;u=q;q=q->Next;free(u);}else{u=q->Next;q->Next=p;pre->Next=q;pre=q;q=u;}}if (q){pre->Next=q;}free(pb);}void main( ){int zhishu;float xishu;PNode2 head1=(PNode2)malloc(sizeof(struct Node2));PNode2 head2=(PNode2)malloc(sizeof(struct Node2));PNode2 tem=NULL;head1->Next=NULL;head2->Next=NULL;printf("输⼊链表⼀的系数和指数,如:3,2 以0,0结束输⼊:\n"); scanf("%f,%d",&xishu,&zhishu);while (xishu!=0||zhishu!=0){tem=(PNode2)malloc(sizeof(struct Node2));tem->xishu=xishu;tem->zhisu=zhishu;tem->Next=NULL;insertNewPoint_link(head1,tem);scanf("%f,%d",&xishu,&zhishu);}printf("链表⼀按指数升序排序后的多项式为:\n");printLinkeLink(head1);printf("\n");printf("输⼊链表⼀的系数和指数,如:3,2 以0,0结束输⼊:\n"); scanf("%f,%d",&xishu,&zhishu);while (xishu!=0||zhishu!=0){tem=(PNode2)malloc(sizeof(struct Node2));tem->xishu=xishu;tem->zhisu=zhishu;tem->Next=NULL;insertNewPoint_link(head2,tem);scanf("%f,%d",&xishu,&zhishu);}printf("链表⼆按指数升序排序后的多项式为:\n");printLinkeLink(head2);printf("\n");add_poly(head1,head2);printf("多项式相加后的结果为:\n");printLinkeLink(head1);}。
c语言数据结构实现——一元多项式的基本运算

c语言数据结构实现——一元多项式的基本运算在C语言中,一元多项式的表示与运算是常见的数据结构操作之一。
一元多项式由一系列具有相同变量的单项式组成,每个单项式由系数和指数组成。
本文将介绍如何使用C语言实现一元多项式的基本运算,包括多项式的创建、求和、差、乘积等操作。
首先,我们需要定义一个结构体来表示单项式。
每个单项式由一个系数和一个指数组成,我们可以将其定义如下:```cstruct term{float coefficient; // 系数int exponent; // 指数};typedef struct term Term;```接下来,我们可以定义一个结构体来表示一元多项式。
一元多项式由一系列单项式组成,可以使用一个动态数组来存储这些单项式。
```cstruct polynomial{Term* terms; // 单项式数组int num_terms; // 单项式数量};typedef struct polynomial Polynomial;```现在,我们可以开始实现一元多项式的基本运算了。
1. 创建一元多项式要创建一元多项式,我们需要输入每个单项式的系数和指数。
我们可以使用动态内存分配来创建一个适应输入的单项式数组。
```cPolynomial create_polynomial(){Polynomial poly;printf("请输入多项式的项数:");scanf("%d", &poly.num_terms);poly.terms = (Term*)malloc(poly.num_terms * sizeof(Term));for(int i = 0; i < poly.num_terms; i++){printf("请输入第%d个单项式的系数和指数:", i+1);scanf("%f %d", &poly.terms[i].coefficient, &poly.terms[i].exponent);}return poly;}```2. 求两个一元多项式的和两个一元多项式的和等于对应指数相同的单项式系数相加的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PLTerm * PolyMult(PLTerm * a,PLTerm * b)
{
/*多项式乘法*/
PLTerm * p;
PolyZero(&p);
while(a->next !=NULL)
{
p=PolyAdd(p,PolySMult(b,a->next->coef,a->next->expon));
p->coef =c;
p->expon =e;
p->next =NULL;
(* rear)->next=p;
(* rear)=p;
return 1;
}
int PolyRead(PLTerm * head)
{
PLTerm ** rear= &head;
int i , n;
int e;
float c;
printf("请输入待操作多项式的项数:\n");
{
PolyAttach(&rear,(a->next->coef)*c,(a->next->expon)+e);
a=a->next;
}
rear->next =NULL;
return p;
}
PLTerm * PolySub(PLTerm * a,PLTerm * b)
{
/*多项式减法*/
return PolyAdd(a,PolySMult(b,-1,0));
{
sum=a->next->coef + b->next->coef;
if(sum) PolyAttach(&rear,sum,a->next->expon);
a= a->next;
b= b->next;
}
else
{
PolyAttach(&rear,b->next->coef,b->next->expon);
}
*head=NULL;
}
else
printf("%.2f,%d",p->coef,p->expon);
printf("\n");
}
PLTerm * PolyAdd(PLTerm * a,PLTerm * b)
{
/*多项式加法*/
PLTerm * p ,* rear;
float sum;
PolyZero(&p);
rear= p;
b= b->next;
}
}
}
for(;a->next !=NULL;a= a->next) PolyAttach(&rear,a->next->coef,a->next->expon);
for(;b->next !=NULL;b= b->next) PolyAttach(&rear,b->next->coef,b->next->expon);
typedef struct PTerm
{
float coef;
int expon;
struct PTerm * next;
} PLTerm;
void PolyZero(PLTerm ** head)
{
if((* head=(PLTerm *)malloc(sizeof(PLTerm)))==NULL)
scanf("%d",&n);
printf("\n");
for(i=1;i<=n;i++)
{
printf("请输入多项式第%d项的系数:c ,指数:e\n",i);
scanf("%f,%d",&c,&e);
if(PolyAttach(rear,c,e)==0) return 0;
}
return 1;
term*=x;
term*=a->next->coef;
sum+=term;
a=a->next;
}
return sum;
}
void PolyErase(PLTerm ** head)
{
PLTerm * p, * p1;
p= * head;
while(p!=NULL)
{
p1=p;
p=p->next;
free(p1);
return -1;
}
else
return head->next->expon;
}
int PolyAttach(PLTerm ** rear,float c,int e)
{
PLTerm * p;
if((p=(PLTerm *)malloc(sizeof(PLTerm)))==NULL) return 0;
exit(1);
(* head)->next=NULL;
(* head)->coef=0;
(* head)->expon=0;
}
int PolyNotZero(PLTerm * head)
{
if(head->next==NULL) return 0;
else
return 1;
}
int PolyLength(PLTerm * head)
}
void PolyWrite(PLTerm * head)
{
PLTerm * p=head;
if(PolyNotZero(head))
while(p->next !=NULL)
{
printf("%.2f,%d ",p->next->coef,p->next->expon);
p= p->next;
}
while(a->next !=NULL && b->next !=NULL)
{
if(a->next->expon > b->next->expon)
{
PolyAttach(&rear,a->next->coef,a->next->expon);
a= a->next;
}
else
{
if(a->next->expon == b->next->expon)
a=a->next;
}
return p;
}
float PolyEval(PLTerm * a,float x)
{
/*求多项式a在x处的值*/
float sum=0, term;
int i;
wh(i=0,term=1;i< a->next->expon;i++)
{
PLTerm * p=head;
int size=0;
while(p->next !=NULL)
{
p=p->next;
size++;
}
return size;
}
int PolyLeadExp(PLTerm * head)
{
/*求多项式阶数*/
if(!PolyNotZero(head))
{
printf("error\n");
rear->next =NULL;
return p;
}
PLTerm * PolySMult(PLTerm * a,float c,int e)
{
/*多项式a乘系数为c指数为e的项*/
PLTerm * p, * rear;
PolyZero(&p);
rear=p;
while(a->next !=NULL)
