小升初组合图形面积计算(1)
专题17：《平面几何的面积(一)》小升初数学专题讲练 (思维导图+知识点精讲+例题分析+变式训练
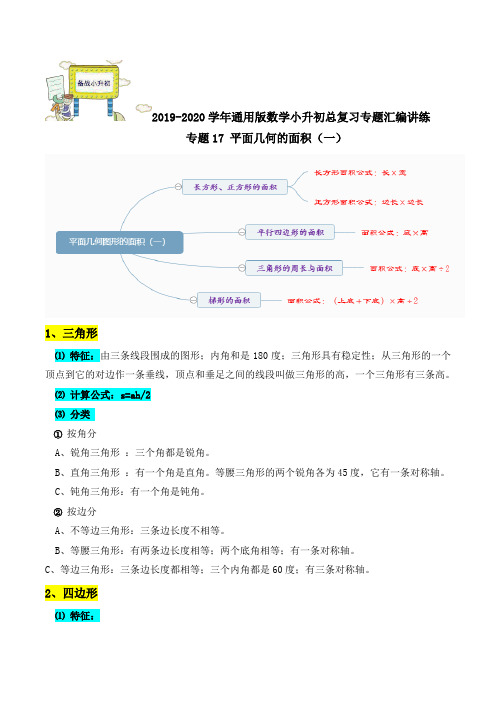
2019-2020学年通用版数学小升初总复习专题汇编讲练专题17 平面几何的面积（一）1、三角形⑴特征：由三条线段围成的图形；内角和是180度；三角形具有稳定性；从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，一个三角形有三条高。
⑵计算公式：s=ah/2⑶分类①按角分A、锐角三角形：三个角都是锐角。
B、直角三角形：有一个角是直角。
等腰三角形的两个锐角各为45度，它有一条对称轴。
C、钝角三角形：有一个角是钝角。
②按边分A、不等边三角形：三条边长度不相等。
B、等腰三角形：有两条边长度相等；两个底角相等；有一条对称轴。
C、等边三角形：三条边长度都相等；三个内角都是60度；有三条对称轴。
2、四边形⑴特征：①四边形是由四条线段围成的图形。
②任意四边形的内角和是360度。
③只有一组对边平行的四边形叫梯形。
④两组对边分别平行的四边形叫平行四边形，它简洁变形。
长方形、正方形是特殊的平行四边形；正方形是特殊的长方形。
⑵分类①长方形A、特征：对边相等，4个角都是直角的四边形。
有两条对称轴。
B、计算公式：c=2(a+b) s=ab②正方形A、特征：四条边都相等，四个角都是直角的四边形。
有4条对称轴。
B、计算公式：c=4a s=a²③平行四边形A、特征：两组对边分别平行的四边形；相对的边平行且相等；对角相等；相邻的两个角的度数之和为180度；平行四边形简洁变形。
B、计算公式：s=ah④梯形A、特征：只有一组对边平行的四边形；中位线等于上下底和的一半；等腰梯形有一条对称轴。
B、计算公式：s=(a+b)h/2=mh3、圆⑴圆的生疏圆是平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o表示。
半径：连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里，有很多条半径，每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有很多条直径，全部的直径都相等。
【新版】小升初组合图形面积计算
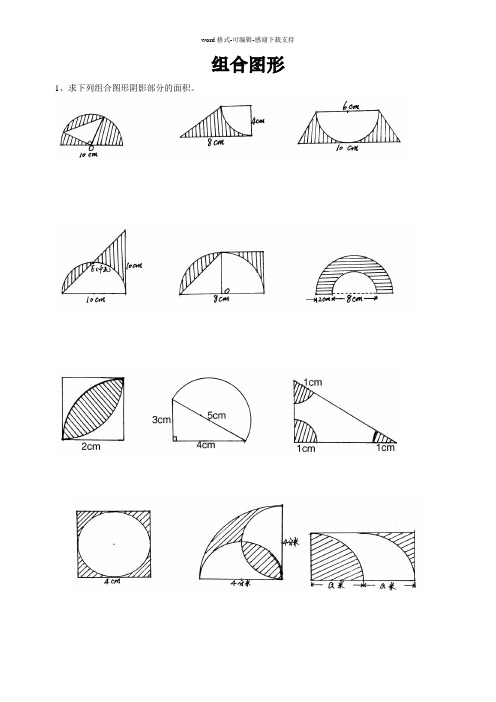
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。
③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。
的半径是3cm，求阴影部分的周长和面积。
（单位：分米）⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，①比阴影②面积少3cm2，求EC的长。
⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求三角形AEF的面积。
⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。
（单位：cm）部分面积64cm2，求梯形面积。
⑿梯形面积是48平方厘米，阴影部分比空白 ⒀阴影部分比空白部分大6cm 2，求S 阴。
部分少12平方厘米，求阴影部分面积。
一、求出阴影部分面积：（6分）。
4、下图中大小正方形的边长分别是9厘米和5厘米，求阴影部分的面积（10分）16、下图中阴影部分的面积是（ ）平方厘米。
8 4m 48m25、如图（3），有两个边长是2厘米的正方形，其中一个正方形的一个顶点在另一个的中心2、右图中阴影部分的面积为（单位：厘米）。
如图，等腰直角三角形ABC 的面积是8平方厘米。
求阴影部分的面积。
（8分）图（3）5 5 4 422. 求阴影部分的面积。
（单位：厘米）1、求右图中阴影部分面积（单位：厘米）。
1. 下图是由正方形和半圆形组成的图形，其中P 点为半圆周的中点，Q 点为正方形一边的中点，求阴影部分面积。
（单位：厘米）631、下图中三角形的面积等于梯形的面积，求五边形的面积。
（单位：厘米）16、下图中阴影部分的面积是（）平方厘米。
666 611、如图：阴影三角形的面积是 。
12、用一块面积为36平方厘米的圆形铝板下料，如图，裁出7个同样大小的圆铝板，则余下的边角料的总面积是 平方厘米。
数学(小升初) 组合图形周长、面积的计算
第2讲组合图形面积的计算一、计算公式例1、如图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.例2、下图，求阴影部分的面积。
其他常用的基本方法有：一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。
例如：求下图整个图形的面积二、相减法这方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例如：下图，求阴影部分的面积。
一句话：正方形面积减去圆的面积即可。
三、直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积。
例如：下图，求阴影部分的面积。
一句话：通过分析发现阴影部分就是一个底是2、高是4的三角形。
四、重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可。
例如：下图，求阴影部分的面积。
一句话：拆开图形，使阴影部分分布在正方形的4个角处，如下图。
五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可例如：下图，若求阴影部分的面积。
六、割补法法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决。
例如：求阴影部分的面积．七、平移法这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积。
例如：下图，求阴影部分的面积。
一句话：可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。
八、旋转法这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积。
例如图（1），求阴影部分的面积。
一句话：左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半。
小升初数学每日一练：组合图形面积的巧算练习题及答案_2020年压轴题版
小升初数学每日一练：组合图形面积的巧算练习题及答案_2020年压轴题版答案答案答案答案2020年小升初数学：空间与图形_四边形及多边形_组合图形面积的巧算练习题
~~第1题~~(2017
东莞.小升初真题) 三角形ABC 中,三角形ABC 的面积为36平方厘米，CF=4AF,BD=DF,求阴影部分的面积。
考点： 组合图形面积的巧算;~~第
2题~~
(2017杭州.小升初模拟) 正方形ABCD 的边长为1cm ，图中4个弓形面积之和是多少？
考点： 组合图形面积的巧算;~~第3题~~
(2015潍坊.小升初真题) 如图，在半径为
R 的圆形钢板上，冲去半径为r 的四个圆，请列出阴影部分面积S 的计算式子，并利用因式分解计算当R=6.5，r=3.2时S 的值（π≈3.14结果保留两个有效数字）．
考点： 组合图形面积的巧算;~~第
4题~~
(2019.小升初模拟) 如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣，图中的黑点是这些圆的圆心．如果圆周π率取3.1416，那么花瓣图形的面积是多少平方厘米？
考点： 组合图形面积的巧算;~~第5题~~
(2018浙江.小升初模拟) 下面两题任意选做一题。
（1） 如图，长方形的长是8厘米，宽6厘米。
阴影部分甲比乙大多少平方厘米?
答案（
2） 如图，长方形的长是6厘米，宽是4厘米，阴影部分三角形的面积是9平方厘米，求BD 的长度。
考点： 组合图形面积的巧算;
2020年小升初数学：空间与图形_
四边形及多边形_组合图形面积的巧算练习题答案1.
答案：
2.答案：
3.答案：
4.答案：
5.答案：。
小升初专题之组合图形面积
一、几种常用求组合图形面积的方法： 1、旋转的思想方法。
将所给图形中的某一部分绕一个固定点旋转一定（或适当）的角度，变为较明显的简单而又直观的图形。
2．移动的思想方法。
A ．点的移动：将图中的某一点看作一个“动点”沿直线移动，使原来分着的空白部分合并在一起变成一个简单明了的图形。
B ．面的移动：将所给图形中的某个图形沿直线上下左右移动，把复杂的图形转化成简单的图形，使原来面积不等变成相等。
3．翻折的思想方法。
将所给图形的某一部分以某一直线为对称轴翻折，使原来复杂的图形变为直观图形。
【例题讲解】例1、如图，长方形的长是8厘米、宽是6厘米、A 和B 是宽的中点，求长方形内阴影部分的面积。
例2、下面的长方形是一块草坪，中间有两条宽1米的走道。
求植草的面积。
BB例3、下图是一块长方形草地。
长方形长16米、宽10米，中间有两条宽2米的道路，两条都是平行四边形。
求有草部分的面积。
【知识反馈】1、求图中阴影部分的面积。
（单位：厘米）2、梯形草坪(如下图),有一平形四边形人行道,求人行道的面积是多少平方米?80米50米16102203、一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道红条，如下图阴影所示部分，红条宽都是2厘米。
问：这条手帕白色部分的面积是多少？7、下图是一块长方形草地。
长方形长30米、宽15米，中间有两条宽3米的道路，一条是长方形，另一条是平行四边形。
求有草部分的面积。
8、如图，ABCD 是直角梯形，AD=4cm,BC=6cm,AB=3cm 求阴影部分的面积和。
（单位：厘米）3033DA 439、下图中，边长为10和15的两个正方形并放在一起，求三角形ABC （阴影部分）的面积。
(小升初培优讲义)专题27 组合图形的面积计算-六年级一轮复习(知识点精讲+达标检测)(教师版)
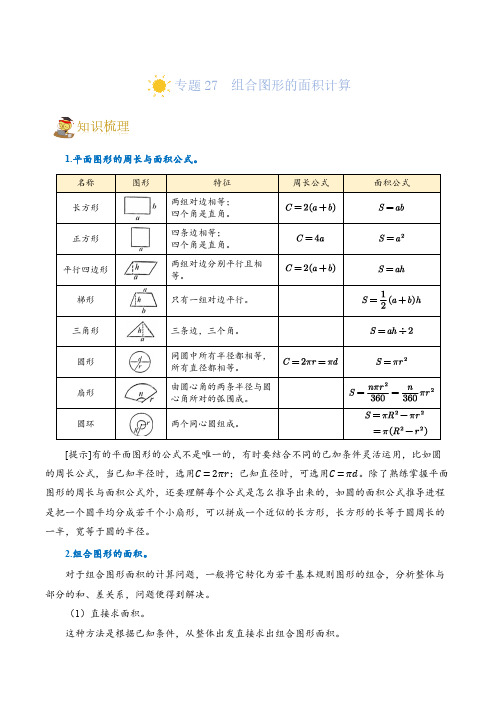
专题27 组合图形的面积计算知识梳理1.平面图形的周长与面积公式。
[提示]有的平面图形的公式不是唯一的，有时要结合不同的已加条件灵活运用，比如圆的周长公式，当已知半径时，选用C=2πr；已知直径时，可选用C=πd。
除了熟练掌握平面图形的周长与面积公式外，还要理解每个公式是怎么推导出来的，如圆的面积公式推导进程是把一个圆平均分成若干个小扇形，可以拼成一个近似的长方形，长方形的长等于圆周长的一半，宽等于圆的半径。
2.组合图形的面积。
对于组合图形面积的计算问题，一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决。
（1）直接求面积。
这种方法是根据已知条件，从整体出发直接求出组合图形面积。
（2）相加、相减求面积。
这种方法是将组合图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加或相减求出该图形的面积。
（3）等量代换求面积。
一个图形可以用与它相等的另一个图形替换，如果甲、乙大小相等，那么求出乙的大小，就知道甲的大小；两个图形同时增加或减少相同的面积，它们的差不变。
（4）借助辅助线求面积。
这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法求面积。
【例1】计算右面图形的面积。
（单位:厘米）【点拨分析】 求梯形的面积，必须知道上底、下底和高这三个条件。
从圆中可以看出，此梯形的高是6厘米，那么解题的关键就是求出上底和下底的长或求出它们的长度和。
在左边的直角三角形中，一个内角是45°，可知它是等腰直角三角形，所以高的左边部分与下底相等。
同样，右边的三角形也是一个等腰直角三角形，所以梯形的上底和高的右边部分相等。
这样就可推和梯形上、下底的长度和就是梯形高的长度6厘米。
【答 案】 6×6÷2＝18（平方厘米）例题精讲1.计算下面图形的面积。
（单位:厘米）2.如图，长方形的面积是45平方米，求阴影部分的面积。
小升初组合图形面积计算(1)
权威小升初之-—-阴影部分面积计算【知识精讲】1。
常用公式长方形面积= 正方形面积= 平行四边形面积=三角形面积= 梯形面积=长方形周长= 正方形周长=2。
等积代换最常用的等积变换是三角形，要熟记下面的结论：①等底等高的两个三角形面积相等；②两条平行线间的距离处处相等；③底在同一条直线上并且相等,两底分别所对的两个三角形的两个角的顶点是同一个点或在与底平行的直线上，则这两个三角形面积相等；④若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形的几倍。
一、扇形、环形的面积计算1、（2010成外一）甲乙两人分别绕右图的内圆(半径为30米)和外圆（半径为50米）跑步．①两人各跑一圈相差多少米?(π≈3）②求图中阴影部分的面积？（π≈3)2、右图所示是人行道的转弯处，已知弧AA’和BB'都是45°圆心角所对的弧，AA1的半径为8米，人行道宽为2米，求ABB’A'的面积。
. 3、求下图中阴影部分的面积。
（单位：米)4、(2012成外)圆的半径是4cm，阴影部分的面积是14πcm2，求图中三角形的面积．二、割补法1、(2010成外一)图中阴影部分的面积是（）平方厘米.2、（2012成都西川中学)如图所示，正方形ABCD的边长为10cm，以CD为直径作半圆,E为半圆周上的中点，F为BC的中点，求阴影部分的面积。
3、（2009成都西川中学）求下列图形中阴影部分的面积.4、（2009成都西川中学)图中正方形ABCD的边长为3厘米,正方形CEFG的边长为4 厘米。
5、（2012成都七中嘉祥）如图是边长6的正方形和梯形拼成的“火炬"，梯形的上底长9m，A为上底的中点，B为下底的中点，线段AB恰好是梯形的高且长为3m，CD长为2m。
那么，图中阴影部分的面积是多少㎡？6、（2010成都七中嘉祥）如图，若长方形APHM、BNHP、CQHN的面积分别为7、4、6，则阴影部分的面积是多少？7、(2010成都实外一）如图,是大小两个正方形组成的图形，大正方形边长是8厘米,小正方形边长为6厘米，求阴影部分的面积。
小升初数学专题2：图形与几何(1)图形的认识及计算-附答案
A. 圆的周长
B. 圆的直径
C. 圆的半径
D. 圆的面积
12. ( 2 分 ) 小圆与大圆的半径之比是 1：3，小圆与大圆的面积之比是( )。
A. 1：3
B. 1：6
C. 1：9
D. 1：9.42
13. ( 6 分 ) 在一个大正方形上挖去一个棱长是 1cm 的小正方体，大正方体的表面积发生怎样的变化？
【解析】【解答】甲的面积=2×2× =2；
乙的面积=2×1=2； 甲的面积=乙的面积. 故答案为：C.
【分析】甲图是一个三角形，底是 2，高是 2，根据面积公式：三角形的面积=底×高× ， 可以求出这个
三角形的面积；
乙图是一个平行四边形，底是 2，高是 1，根据面积公式：平行四边形的面积=底×高，可以求出这个平行
50. ( 5 分 ) 画一个直径是 12 厘米的圆，并在圆中画一个圆心角是 100°的扇形。求这个扇形的面积。
51. ( 5 分 ) 计算阴影部分的面积
52. ( 10 分 ) 安居小区门前的水池长 9m，长是宽的 1.5 倍，深 1.2m。 （1）这个水池的占地面积是多少平方米？ （2）如果把水池四周和底面贴上瓷砖，贴瓷砖的面积是多少平方米？ 53. ( 5 分 ) 一根铁丝可以围成一个直径是 6cm 的圆，如果用它围成一个等边三角形，每边的长是多少厘米? 54. ( 5 分 ) 长青桥小学有一块面积是 490 平方米的长方形苗圃，苗圃长 35 米，宽是多少米？周长是多少 米？ 55. ( 5 分 ) 有一块平行四边形麦田，底是 200 米，高是 45 米，平均每公顷收获小麦 7.05 吨，这块地共收 获小麦多少吨？ 56. ( 5 分 ) 李爷爷把牛栓在草原的木桩上，木桩到牛鼻的绳子长 6 米，牛能吃到草的面积有多大? 57. ( 5 分 ) 压路机的滚筒是一个圆柱体，它的底面直径是 1 米，长 2 米。每滚动一周能压多大面积的路面？ 58. ( 5 分 ) 有一个近似圆锥形的小麦堆，测得麦堆底面直径 4 米，高 1.5 米，如果每立方米小麦重 740 千 克，这堆小麦大约重多少千克？
小升初几何-用割补法巧求面积
小升初几何之---用割补法求面积在组合图形中，除了多边形外，还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形，为了计算它们的面积，常常需要变动图形的位置或对图形进行分割、旋转、拼补，使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中，为了计算面积，有时也要用到割补的方法。
例1求下列各图中阴影部分的面积：分析与解：（1）如左下图所示，将左下角的阴影部分分为两部分，然后按照右下图所示，将这两部分分别拼补在阴影位置。
可以看出，原题图的阴影部分等于右下图中AB 弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
（2）在题图虚线分割的两个正方形中，右边正方形的阴影部分是半径为5的四分之一个圆，在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示，将右边的阴影部分平移到左边正方形中。
可以看出，原题图的阴影部分正好等于一个正方形的面积，为5×5=25。
例2在一个等腰三角形中，两条与底边平行的线段将三角形的两条边等分成三段（见右图），求图中阴影部分的面积占整个图形面积的几分之几。
分析与解：阴影部分是一个梯形。
我们用三种方法解答。
（1）割补法从顶点作底边上的高，得到两个相同的直角三角形。
将这两个直角三角（2）拼补法将两个这样的三角形拼成一个平行四边形（下页左上图）。
积和平行四边行面积同时除以2，商不变。
所以原题阴影部分占整个图形面（3）等分法将原图等分成9个小三角形（见右上图），阴影部分占3个小三角形，注意，后两种方法对任意三角形都适用。
也就是说，将例题中的等腰三角形换成任意三角形，其它条件不变，结论仍然成立。
例3如左下图所示，在一个等腰直角三角形中，削去一个三角形后，剩下一个上底长5厘米、下底长9厘米的等腰梯形（阴影部分）。
求这个梯形的面积。
分析与解：因为不知道梯形的高，所以不能直接求出梯形的面积。
小升初数学图形与几何知识点分类复习《图形拼组问题》大题量附答案
小升初数学图形与几何知识点分类复习《图形拼组问题》一、选择题1．想要把一个长方形纸板剪成2个长方形纸板后，剪成的两个长方形纸板周长的和与原来长方形纸板的周长相比（）。
A．增加了B．减少了C．与原来相等2．用两个完全一样的直角三角形拼成一个平行四边形，可以拼成两种平行四边形，问拼成的两个平行四边形面积相等吗？（）A．相等B．不相等C．无法确定3．两个（）的三角形可以拼成一个平行四边形。
A．形状相同B．面积相等C．周长相等D．等底等高4．两个周长是12厘米的正方形，拼成一个长方形，这个长方形的周长是（）厘米。
A．24B．96C．185．把一个长10cm、宽8cm、高6cm的长方体，切成两个相等的长方体，它们的表面积之和比原来最多增加（）平方厘米。
A．480B．160C．96D．806．先放两个正方体，在两个正方体的上面放两个圆柱，在两个圆柱的上面放一个长方体，在长方体上面放一个球，放对了的是（）。
A．①B．①C．①7．在一张长方形纸上剪一刀，把它分成两部分，这两部分的形状不可能是（）。
A．直角三角形B．等边三角形C．正方形D．直角梯形8．用20个相同的小正方形可以拼成（）种长方形，20的因数有（）个。
A．3；6B．4；5C．4；6D．5；69．左边的图形是用（）个组成的。
A．4B．5C．610．把一张长方形的纸对折三次，折痕间的关系是（）。
A．互相平行B．互相垂直C．可能互相平行，也可能互相垂直11．两个（）的梯形一定能拼成一个平行四边形。
A．面积相等B．形状相同C．完全一样12．认真观察下图，共有（）个。
A．6B．7C．813．以下几个图形中，不能单独密铺的是（）。
A．B．C．D．14．下图中的大长方形是由4个完全相同的长方形拼成的，那么阴影部分与空白部分的面积比是（）。
A．3①4B．4①5C．3①8D．3①515．一根绳子对折2次后，每段长4米，对折3次后，每段长（）。
A．2米B．4米C．8米16．把一张圆形纸片剪拼成一个近似的梯形（如图），这个梯形的上、下底之和相当于圆的（）。
小升初数学专题2：图形与几何(1)图形的认识及计算 经典题型及详细解析
小升初数学专题二：图形与几何--图形的认识及计算一、选择题（共16题；共36分）1.(2分)在一个三角形中，有两个锐角的和是90°，那么这个三角形是（）。
A.直角三角形B.锐角三角形C.钝角三角形D.无法确定2.(2分)一张长8厘米、宽5厘米的长方形纸，从中剪出一个最大的正方形，正方形的边长是()。
A.8厘米B.5厘米C.6厘米3.(2分)从如图的长方形纸上剪下一个最大的正方形，这个正方形的周长是（）厘米．A.12B.16C.204.(2分)下列图中，甲乙两部分的周长不相同的是（）A. B. C.5.(2分)下图中，甲和乙两部分面积的关系是()。
A.甲>乙B.甲<乙C.甲=乙6.(2分)射线()端点。
A.没有B.有一个C.有两个7.(2分)如图,中有()条线段。
A.3B.4C.5D.68.(2分)把半圆平均分成180份，每一份所对的角的度数是（）A.10°B.1°C.18°9.(2分)如图阴影部分的面积是（）A.39.25B.38.35C.38.58D.39.4810.(2分)以下哪个选项是弧（）A.半径AO+BOB.半径AO+BO+圆上ABC.圆上ABD.都不是11.(2分)把一个圆平均分成若干份，沿半径剪开后，拼成一个近似的长方形，长方形的宽相当于()。
A.圆的周长B.圆的直径C.圆的半径D.圆的面积12.(2分)小圆与大圆的半径之比是1：3，小圆与大圆的面积之比是()。
A.1：3B.1：6C.1：9D.1：9.4213.(6分)在一个大正方形上挖去一个棱长是1cm的小正方体，大正方体的表面积发生怎样的变化？（1）表面积不变的是（）A. B. C.（2）表面积增加2的是（）A. B. C.（3）表面积增加4的是（）A. B. C.14.(2分)一个圆柱的侧面展开图是一个正方形，这个圆柱的高与底面半径的比值是()。
A.πB.2πC.r15.(2分)把一个圆锥沿底面直径到顶点切开，切面是一个()。
2022小升初专题练 第16讲 组合图形的周长与面积(通用版,含详解) (1)
第16讲组合图形的周长与面积一、精挑细选（共5题；每题2分，共10分）1. 下面三幅图中，正方形一样大，则三个阴影部分的面积（）A.一样大B.第一幅图最大C.第二幅图最大D.第三幅图最大2. 如下图，甲部分的周长和乙部分相比（）A.甲大B.乙大C.一样大3. （2021六上·海安期末）一个木匠用32米木围栏材料把一块花园围起来，花园有四种可能的设计，其中不能用32米的木围栏围起来的是（）。
A. B.C. D.4. （2021六上·温江期末）如图，大圆内有3个大小不等的小圆，这四个圆的圆心都在同一直线上，若大圆的直径是5厘米，则三个小圆的周长之和是（）厘米.A.7.85B.15.7C.31.4D.78.55. （2020六上·福田月考）如图：这两个图形中涂色的部分周长和面积的大小关系是（）A.周长相等，面积不相等B.周长和面积都相等C.周长不相等，面积相等二、判断正误（共3题；每题2分，共6分）6. 用8个1立方厘米的小方块拼成一个正方体．如果拿去一个小方块，它的表面积不变．（）7. （2012·广州）右图中的阴影部分面积占长方形的。
（）8. 右图的阴影部分的周长是圆的周长+长方形的周长。
（）三、填空题（共10题；每空1，共12分）9. 求下面图中阴影部分的面积．面积是________ ．10. 一张长方形纸片，长10厘米，宽8厘米．在这张纸片上剪去一个最大的圆后，剩下部分的面积是________平方厘米？（保留两位小数）11. 一座隧道的入口上部是半圆，下部是个长方形(如下图)．已知长方形的长是10米，宽是5米．这个隧道横截面的周长是________米？面积是________平方米？（保留一位小数）12. 用一张长8厘米、宽6厘米的长方形纸，剪一个尽可能大的圆后，剩下部分的面积是________平方厘米？(用一张纸剪一剪，再算一算)13. 小玲要在一个长6厘米、宽4厘米的长方形纸片上剪下一个最大的圆．（1）圆的面积是________平方厘米？(结果用小数表示)（2）剩下部分的面积是________平方厘米？(结果用小数表示)14. （2020六上·福田月考）如图，半圆的半径是2分米，则封闭图形的周长为________分米。
六年级数学小升初重点题型组合图形面积带答案
如下图长方形ABCD的面积是16平方厘米，E、F都是所在边的中 点，求三角形AEF的面积。
16÷2=8（平方厘米）
16÷4÷2=2（平方厘米） 8-2=6（平方厘米）
三角形ABC的面积是24平方厘米，且DC=2AD，E、F分别 是AF、BC的中点，那么阴影部分的面积是多少？
24÷6=4（平方厘米）
求阴影部分的面积。
6×6÷2=18（平方厘米） （6-4）×4÷2=4（平方厘米）
18-4=14（平方厘米）
差不变原理
图中两个完全一样的三角形重叠在一起，求阴影部分 的面积。（单位：厘米）
12-4=8（厘米） （8+12）×2÷2=20（平方厘米）
差不变原理
平行四边形ABCD的边长BC长为8厘米，直角三角形BCE的 直角边CE长为6厘米。已知两块阴影部分的面积和比三角形 EFG的面积大8平方厘米，求CF的长度？
S△BDE=8×6÷2=24（平方厘米）
S平行四边形ABCD=24+8=32（平方厘米）
CF=32÷8=4（厘米）
三角形ABC的面积是56平方米，BD=CD.求阴影部分的面 积.
56÷2=28（平方米）
如图阴影部分的面积是6平方厘米，OC=2AO，求梯形的面积。
6×2=12（平方厘米） 12×2=24（平方厘米） 6+12+12+24=54平方厘米）
2.5×4=10（平方厘米）
蝴蝶定理：梯形两翼三角形面积相等。
S△ABC=BC×h÷2 S△BCD=பைடு நூலகம்C×h÷2 S△ABC=S△BCD
B S△ABC-S△OBC=S△BCD-S△OBC
即 S△ABO=S△CDO
A
D
O
小升初数学组合图形的面积+数学趣题+分数计算技巧+奥数题训练及答案解析
小升初数学组合图形的面积+数学趣题+分数计算技巧+奥数题训练及答案解析组合图形的面积一、 知识要点：1. 我们学过的常见多边形的周长和面积求法:2.计算不规则图形的面积，常用到哪些方法？二、知识运用典型例题。
例题1：如图，两条对角线把梯形ABCD 分割成四个三角形，（1） 请写出图中面积相等的三角形？（2） 已知两个三角形的面积，求另两个三角形的面积各是多少？ （3） 求梯形ABCD 的面积？B C例2：长方形ABCD 的面积是24平方厘米，三角形EBC 的面积是30平方厘米，两块阴影部分的面积相差多少?例3：如下图，长方形ABCD 的面积是20平方厘米，三角形ADF 的面积为5平方厘米，三角形ABE 的面积为7平方厘米，求三角形AEF 的面积。
例4：如下图，已知四条线段长分别是AB=2，CE=6，CD=5，AF=4，并有两个直角，求四边形ABCD 的面积。
D BCA D三、知识运用课堂练习。
1、三角形EBC的面积是40平方厘米，且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形ABCD的面积？2、如下图，长方形的长和宽分别是12和9，把三角形的三条边分别平均分成三段，得到A，B，C，D，E，F六个点，连接AF、BC、DE，得到一个六边形。
这个六边形的面积是多少？3、在右图中，AB=8厘米，CD=4厘米，BC=6厘米，三角形AFB比三角形EFD 的面积大18厘米2。
求ED的长。
4、下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积。
课后练习 等级1、下图中的甲和乙都是正方形，求阴影部分的面积。
2、下图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形E DF 的面积大9厘米2，求ED 的长。
3、（动手操作题）右图是一个4×4的方格纸，请在保持每个小方格完整的情况下，将它分割成大小、形状完全相同的两部分。
（至少要有4种不同的方法）甲乙生活中的数学趣题一、知识要点。
小升初专题平面组合图形的面积计算
平面图形面积————圆的面积专题简析：在进行组合图形的面积计算时,要仔细观察,认真思考,看清组合图形是由几个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系;并且同学们应该牢记几个常见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的错误!,而在圆内的最大正方形占所在圆的面积的错误!,这些知识点都应该常记于心,并牢牢掌握例题1;求图中阴影部分的面积单位：厘米;分析如图所示的特点,阴影部分的面积可以拼成1/4圆的面积;62××1/4＝平方厘米练习11.求下面各个图形中阴影部分的面积单位：厘米;2.求下面各个图形中阴影部分的面积单位：厘米;例题2;求图中阴影部分的面积单位：厘米;分析阴影部分通过翻折移动位置后,构成了一个新的图形如图所示;从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半;×42×1/4－4×4÷2÷2＝平方厘米练习21、计算下面图形中阴影部分的面积单位：厘米,正方形边长4;2、计算下面图形中阴影部分的面积单位：厘米,正方形边长4;1 2例题3;如图19－10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等;求长方形ABO1O的面积;分析因为两圆的半径相等,所以两个扇形中的空白部分相等;又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半如图19－10右图所示;所以×12×1/4×2＝平方厘米练习31、如图所示,圆的周长为厘米,AC两点把圆分成相等的两段弧,阴影部分1的面积与阴影部分2的面积相等,求平行四边形ABCD的面积;2、如图所示,AB＝BC＝8厘米,求阴影部分的面积;例题4;如图所示,图中圆的直径AB是4厘米,平行四边形ABCD的面积是7平方厘米,∠ABC＝30度,求阴影部分的面积得数保留两位小数;分析阴影部分的面积等于平行四边形的面积减去扇形AOC的面积,再减去三角形BOC的面积;半径：4÷2＝2厘米扇形的圆心角：180－180－30×2＝60度扇形的面积：2×2××60/360≈平方厘米三角形BOC的面积：7÷2÷2＝平方厘米7－+＝平方厘米练习41、如图,三角形ABC的面积是平方厘米,圆的直径AC＝6厘米,BD：DC＝3：1;求阴影部分的面积;2、如图所示,求阴影部分的面积单位：厘米;得数保留两位小数;3、如图所示,求阴影部分的面积单位：厘米;得数保留两位小数;1 2 3例题5;如图所示,求图中阴影部分的面积;分析解法一：阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形如图,等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2＝10厘米×102×1/4－10×10÷2×2＝107平方厘米解法二：以等腰三角形底的中点为中心点;把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差;20÷22×1/2－20÷22×1/2＝107平方厘米练习51、如图所示,求阴影部分的面积单位：厘米2、如图所示,用一张斜边为29厘米的红色直角三角形纸片,一张斜边为49厘米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形;求红蓝两张三角形纸片面积之和是多少例题6如图所示,求图中阴影部分的面积单位：厘米;分析解法一：先用长方形的面积减去小扇形的面积,得空白部分a的面积,再用大扇形的面积减去空白部分a的面积;如图所示;×62×1/4－6×4－×42×1/4＝平方厘米解法二：把阴影部分看作1和2两部分如图20－8所示;把大、小两个扇形面积相加,刚好多计算了空白部分和阴影1的面积,即长方形的面积;×42×1/4+×62×1/4－4×6＝平方厘米练习61、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米;以AC、BC为直径画半圆,两个半圆的交点在AB边上;求图中阴影部分的面积;2、如图所示,图中平行四边形的一个角为600,两条边的长分别为6厘米和8厘米,高为厘米;求图中阴影部分的面积;例题7;在图中,正方形的边长是10厘米,求图中阴影部分的面积;分析先用正方形的面积减去一个整圆的面积,得空部分的一半如图所示,再用正方形的面积减去全部空白部分;空白部分的一半：10×10－10÷22×＝平方厘米阴影部分的面积：10×10－×2＝57平方厘米练习71、求下面各图形中阴影部分的面积单位：厘米;2、求右面各图形中阴影部分的面积单位：厘米;3、求右面各图形中阴影部分的面积单位：厘米;例题8;在正方形ABCD中,AC＝6厘米;求阴影部分的面积;分析这道题的难点在于正方形的边长未知,这样扇形的半径也就不知道;但我们可以看出,AC是等腰直角三角形ACD的斜边;根据等腰直角三角形的对称性可知,斜边上的高等于斜边的一半如图所示,我们可以求出等腰直角三角形ACD的面积,进而求出正方形ABCD的面积,即扇形半径的平方;这样虽然半径未求出,但可以求出半径的平方,也可以把半径的平方直接代入圆面积公式计算;既是正方形的面积,又是半径的平方为：6×6÷2×2＝18平方厘米 阴影部分的面积为：18－18×÷4＝平方厘米答：阴影部分的面积是平方厘米;练习81、 如图所示,图形中正方形的面积是50平方厘米,分别求出每个图形中阴影部分的面积;2、 如图所示,正方形中对角线长10厘米,过正方形两个相对的顶点以其边长为半径分别做弧;求图形中阴影部分的面积试一试,你能想出几种办法;例题9;在图的扇形中,正方形的面积是30平方厘米;求阴影部分的面积;分析阴影部分的面积等于扇形的面积减去正方形的面积;可是扇形的半径未知,又无法求出,所以我们寻求正方形的面积与扇形面积的半径之间的关系;我们以扇形的半径为边长做一个新的正方形如图所示,从图中可以看出,新正方形的面积是30×2＝60平方厘米,即扇形半径的平方等于60;这样虽然半径未求出,但能求出半径的平方,再把半径的平等直接代入公式计算;×30×2×1/4－30＝平方厘米答：阴影部分的面积是平方厘米;练习91、 如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积;2、如图所示,O 是小圆的圆心,CO 垂直于AB,三角形ABC 的面积是45平方厘米,求阴影部分的面积;上面所举的例子只是常见的圆的组合图形面积解法,在以后的练习中,还希望同学们能举一反三,总结自己的学习方法与心得与体会,达到举一反三的效果圆的面积与组合圆积专题训练一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是3.,,这个正方形E D C B A 4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.保留两位小数5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B 长40厘米, BC 长 厘米. 6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 . 7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中单位:厘米,两个阴影部分面积的和是 平方厘米. 11.如图,阴影部分的面积是 .12.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.13.在一个半径是厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.π取,结果精确到1平方厘米 14.右图中三角形是等腰直角三角形,阴影部分的面积是 平方厘米.15.如图所求,圆的周长是厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π16.如图,151=∠的圆的周长为厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .17.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18.图中,ADB 的面积的311倍,那么,CAB ∠是 度. 20.,以圆弧为分界线的甲、乙两部分的面6C B A O 4512 15 20 C ② ① A B 2 1 211., BC 是半圆的直径,已知:AB =BC 14.3=π12.如图2的面积是平方厘米.那么长方形阴影 13.如图1521=∠=,那么阴影部分的面积是多少平方厘米)14.3(≈π4个顶点,它们的公共点是该正方形的1厘米,那么阴影部分的总面积是多少平方厘米。
圆、组合图形面积-小升初立体图形训练-圆、组合图形面积-无答案
圆、组合图形的面积第一部分 知识梳理字母意义：O 圆心，r 半径，d 直径，π 圆周率,C 周长，S 面积 特征：同一圆内，所有的半径、直径都分别相等，直径等于半径的2倍 对称性：圆是轴对称图形，圆的直径所在的直线是圆的对称轴1.圆 圆的周长计算公式：C=πd=2πr ，半圆周长计算公式：C 半圆=πr+2r=(π+2)r 圆的面积计算公式推导过程：将圆沿着直径等分成若干个扇形（偶数份），再拼成一 个近似的长方形（分成的扇形越多，越接近长方形），长方形的长相当于圆的周 长一半（πr ），宽相当与圆的半径，圆的面积等于长方形的面积。
所以：S 圆=S 长方形=πr ×r=πr 2概念：两个半径不等的同心圆之间的部分称之为圆环。
各部分名称：①外圆：圆环中较大的圆叫做外圆，其半径通常用R 表示。
2.圆环 ②内圆：圆环中较小的圆叫做内圆，其半径通常用r 表示。
③环宽：外圆到内圆的距离叫做环宽 环宽=R —r圆环的面积计算方法：外圆的面积与内圆的面积之差是圆环的面积。
即：S 圆环=S 外圆—S 内圆 ,S 圆环=π(R 2 — r 2)弧：圆上任意两点间的部分叫做弧3.扇形 圆心角：弧的两个端点与圆心连结，所得两条半径的夹角叫圆心角 扇形：由圆心角的两条半径和圆心角所对的弧组成的图形叫扇形割补（平移）法 组合图形的面积 加减法计算策略1 旋转、对称法4.组合图形的 要求阴影先求空白 面积计算 包含与排除组合图形的面积 总面积=两部分面积和-重叠部分面积 计算策略2 巧添辅助线 等积转化（代换）第二部分精讲点拨例1判断下列各题是否正确：（1）圆的周长是直径的3.14倍。
（）（2）圆是轴对称图形，直径是圆的对称轴。
（）（3）世界上第一位把圆周率精确到七位小数的人物是祖冲之。
（）举一反三：1.填空题：（1）经过圆心并且两端都在圆上的线段叫做圆的（），圆有（）条直径。
（2）圆的面积推导公式是：将圆分成若干个扇形，再拼成一个近似的长方形，长方形的长相当于圆的（），长方形的宽相当于圆的（），所以圆的面积公式为（）。
六年级下册数学试题-小升初专题培优：第十一讲 组合图形的面积(一)(无答案)全国通用
第十一讲 组合图形的面积（一）【学习锦囊】许多图形是由两个或两个以上的图形组合而成的，我们称之为组合图形，组合图形具有图形不规则，图形重叠，条件隐蔽或缺少条件等特点，计算组合图形的面积，首先要掌握基本的图形面积计算公式，公式如下：三角形面积=底⨯高÷2=21ah正方形面积=边长⨯边长=a 2 长方形面积=长⨯宽=ab 平行四边形面积=底⨯高=ah梯形面积=（上底+下底）⨯高÷2=21（a+b ）h圆面积=半径⨯半径⨯π=πr 2 扇形面积=半径⨯半径⨯π⨯圆心角的角度÷360°=︒360n ⨯πr 2组合图形往往不能直接用公式计算，需要通过观察，分析把组合图形转化为基本的图形来计算，对于千变万化的组合图形，我们要学会多种的解题思路和方法，常用的方法有：等分法，等量代换法，做辅助线法，设数法，列方程法，利用比设参数法，割补法，包含与排除法，用勾股定理等，在本节和下节两讲中，我们学习用这些方法来解答组合图形的面积。
【典题1】如右图，已知长方形ABCD 的面积是88平方厘米，E和F 分别是长和宽的中点。
（1）画出长方形ABCD 所有的对称轴。
（2）求出阴影部分面积 典题分析：通过观察四边形ACFE 是一个梯形，求梯形的面积缺少必要的条件，我们可以把长方形利用等分法把它等分成八个相等的三角形，阴影有三个三角形组成，占长方形的八分之三，从而可以求出阴影部分的面积【典题分析】解：画出长方形两条对称轴交于点O,连结BOS 阴影=88×83 =33（cm 2）答：阴影部分的面积是33平方厘米。
【典题2】如右图有三个正方形ABCD,BEFG 和CHIJ ，其中正方形ABCD 的边长是10，正方形BEFG 的边长是6，那么三角形DFI的面积是多少?【典题分析】求三角形DFI 的面积，缺少底和高的条件，试图能不能找一个和三角形DFI 等底等高的三角形呢? 通过做辅助线连结CI,CF.三角形CDF 和DFI 等底等高，我们利用等量代换的方法，可以求出三角形DFI 的面积AB CD EFABDFG HI J解题过程 解：连结CI,CF ∵∠CIF=∠FDC=450∴CI∥DF ∴S △DFI =S △CDF =10×(10-6)÷2=20 答：三角形DFI 的面积是20.【典题3】三角形ABC 的面积为10平方厘米，AE=21AD,BD=3DC,求阴影部分的面积。
小升初真题专练组合图形的面积小学数学六年级下册人教版(含答案)
小升初真题特训：组合图形的面积-小学数学六年级下册人教版学校:___________姓名：___________班级：___________考号：___________1A．（1）号面积最大B．（2）号面积最大二、填空题7．（2020·江苏南通·统考小升初真题）如图，大正方形被分成了4个相同的三角形和一个小正方形。
大正a b ，则小正方形的面积是()平方厘米。
方形的周长为24厘米，已知:2:18．（2021·全国·小升初真题）（汉阳区）如图，将两个正三角形重叠作出一个星形，在重叠的图形中再作出一个小星形，即阴影部分，已知大星形的面积是40cm2，那么小星形的面积是_____．9．（2020·北京海淀·小升初真题）如图，已知大正方形的面积是a，则小正方形的面积是___________。
10．（2020·北京海淀的面积的面积＝的面积＝，由此发现，，15．（2020·全国·小升初真题）5平方分米．三、图形计算20．（2022·湖北十堰·统考小升初真题）如图，两个正方形的边长分别是10cm和4cm，求阴影部分的面积。
21．（2022·山东临沂·统考小升初真题）求如图阴影部分的面积。
四、解答题22．（2022·湖南长沙·长沙市开福区青竹湖湘一外国语学校校考小升初真题）如图，大小正方形的边长分别是5厘米、3厘米，求三角形DBF的面积。
23．（2020·江苏常州·校考小升初真题）如下图所示，把三角形DBE沿线段AC折叠，得到一个多边形27．（2021·浙江宁波·小升初真题）28．（2020春·辽宁·六年级统考小升初模拟）如下图，一张边长为4cm的正方形纸，从相邻两边的中点连一条线段，沿这条线段剪去一个角，剩余部分面积是多少？29．（2021春·江苏·六年级统考小升初模拟）如图，一块长方形绿地中有一条弯曲的小路，准备在小路的两侧铺上草坪．草坪的面积是多少平方米？（单位：米）30．（2020·河北·小升初真题）李大爷家承包了如图所示的一块地，请你帮他计算一下这块地的面积（单位，米）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
权威小升初之---阴影部分面积计算
【知识精讲】
1.常用公式
长方形面积= 正方形面积= 平行四边形面积=
三角形面积= 梯形面积=
长方形周长= 正方形周长=
2.等积代换
最常用的等积变换是三角形，要熟记下面的结论：
①等底等高的两个三角形面积相等；
②两条平行线间的距离处处相等；
③底在同一条直线上并且相等，两底分别所对的两个三角形的两个角的顶点是同一个点或在与底平行的
直线上，则这两个三角形面积相等；
④若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍，那么这个三
角形的面积也是另一个三角形的几倍。
一、扇形、环形的面积计算
1、（2010成外一）甲乙两人分别绕右图的内圆（半径为30米）和外圆（半径为50米）跑步．
①两人各跑一圈相差多少米？（π≈3）
②求图中阴影部分的面积？（π≈3）
2、右图所示是人行道的转弯处，已知弧AA’和BB’都是45°圆心角所对的弧，AA1的半径为8米，人行道宽为2米，求ABB’A’的面积。
. 3、求下图中阴影部分的面积。
（单位：米）
4、（2012成外）圆的半径是4cm，阴影部分的面积是14πcm2，求图中三角形的面积．
二、割补法
1、(2010成外一)图中阴影部分的面积是（）平方厘米。
2、（2012成都西川中学）如图所示，正方形ABCD的边长为10cm，以CD为直径作半圆，E为半圆周上的中点，F为BC的中点，求阴影部分的面积。
3、（2009成都西川中学）求下列图形中阴影部分的面积。
4、（2009成都西川中学）图中正方形ABCD的边长为3厘米，正方形CEFG的边长为4 厘米。
5、（2012成都七中嘉祥）如图是边长6的正方形和梯形拼成的“火炬”，梯形的上底长9m，A为上
底的中点，B为下底的中点，线段AB恰好是梯形的高且长为3m，CD长为2m。
那么，图中阴影部分的面积是多少㎡？
6、（2010成都七中嘉祥）如图，若长方形APHM、BNHP、CQHN的面积分别为
7、4、6，则阴影部分的
面积是多少？
7、（2010成都实外一）如图，是大小两个正方形组成的图形，大正方形边长是8厘米，小正方形边长
为6厘米，求阴影部分的面积。
8、（2009七中嘉祥）如图，由正方形和半圆形组成的图形。
正方形的边长为10，其中P点为半圆周的中点，Q为正方形一边的中点。
那么阴影部分的面积是多少？（圆周率=3.14）
9、（2009七中嘉祥）计算图形的面积：如图两个正方形的边长分别是4厘米、6厘米，
求阴影部分的面积是多少平方厘米？
10、（2011实外西区）求阴影部分的面积（单位：厘米）
11、（2010实外西区）求出周长和面积。
12、（2012师大一中）求图中阴影部分的面积。
（单位：厘米）
13、（2011七中实验）图中的阴影部分面积等于多少。
14、（2011七中实验）如图，求阴影部分的面积。
（单位：厘米）（π取3.14）
15、（2013成华区）如图，已知圆的周长是25.12厘米，圆的面积与长方形的面积相等，则阴影部分面积为多少平方厘米？
16、（2010成都实外二）求图中阴影部分的面积。
（图中的三角形是等腰直角三角形，π=3.14）
17、下图中，大圆半径为6，则其阴影部分的面积为多少？
18、求下图中阴影部分的面积。
（单位：米）
19、（2011太原市四十八中分班卷）如右图，阴影部分的面积是（）平方厘米。
（π取3.14，单位：
厘米）
20、如下图，四边形ABCD的面积是（）平方厘米。
（单位：厘米）
三、等积变形、蝴蝶原理
（1）等积变形
1、如右图，在平行四边形ADFG中，AB=BC=CD,DE=EF,则甲、乙两个三角形面积的比是（）。
.2、下图中AB＝3厘米，CD＝12厘米，ED＝8厘米，AF＝7厘米，则四边形ABDE的面积是多少平方厘米？
3、如右图，图中数据表示该长方形各块的面积，求阴影面积。
4、（2013师大一中）如图，点EF,分别是平行四边形ABCD边AB，BC的中点，若阴影部分的面积为6，求平行四边形ABCD的面积。
5、（2012师大一中）如图，AF=3FB,FD=3EF,直角三角形ABC的面积是48平方厘米。
求平行四边形EBCD和三角形AFD的面积。
8、（2011成都实外二）如图,长方形ABCD的面积为2平方厘米,EG=2DE,F是DG的中点，则阴影部分的面积是多少？
9、（2009成都实外）如图，△ABC中，AB=3AD，AC=3CG，BE=EF=FC，且△FCG的面积为1平方厘米，求阴影部分的面积。
10、（2012成外）在正方体ABCD中，E，F分别是所在边的中点，求四边形AGCD的面积占正方形面积的几分之几？
11、如右图，ABCD为任意四边形，其中AE=2
3
AB,BF=
2
3
BC,CG=
2
3
CD,DH=
2
3
DA,连接E、F、G、H,求四边形
EFGH的面积与四边形ABCD的面积之比。
12、如图，在直角三角形ABC中，∠BAC=90°， AC= 6cm， BA= 8cm，点E在边BC上，四边形ADEF是正方形，求正方形ADEF的边长。
13、ABCD为直角梯形,AD=6,DC=10,三角形BEC面积为6,求ABCD的面积？
14、如图,在角MON的两边上分别有A C E及B D F六个点,并且△OAB△ABC,△BCD,△CDE,△DEF的面积都等于1,则△DCF的面积等于多少?
（2）蝴蝶原理
1、（2010成外一）如图，BD、CF将长方形ABCD分成4块，△DEF的面积是4cm2，△CED的面积是6cm2，
则四边形ABEF的面积是（）平方厘米．
2、（2010成外二）如右图所示，长方形ABCD中，△ABP的面积为20平方厘米，△CDQ的面积为35平方
厘米，求阴影四边形的面积。
3、（2010成都七中嘉祥）如图，在长方形ABCD中，AB=6厘米，BC=8厘米，四边形EFHG
的面积是3平方厘米，阴影部分的面积是多少平方厘米？
四、同加同减
1、求下列图形中两阴影部分的面积之差。
2.如下图，正方形ABCD的面积比三角形ABF的面积小6平方厘米，线段AB长8厘米，CF长（）厘米。
3、如右图，三角形ABC是直角三角形，AC长4厘米，BC长2厘米，以AC、BC分别为直径画圆，两个半圆的交点D在AB上，求阴影部分的面积。
4、如图是两个同样大的圆，半径为1厘米，而且两个阴影部分的面积相等，那么，连接两个圆心的的线段O1O2的长是多少厘米？
五、特殊题型
1.(2013成外)将如图所示的三角形沿虚线折叠，得到到如图所示的多边形，这个多边形的面积是原三角形
面积的5
7
，已知图中阴影部分的面积为6平方厘米，求原三角形的面积。
2、一个等腰直角三角形，它的斜边长20厘米，它的面积是多少平方厘米？
3、（2013成都实外）如图，在梯形ABCD内有两个三角形的面积分别是10与12，已知梯形的上底AB
的长是下底DC的长的2
3,那么余下的阴影部分的面积是多少？
4、正方形ABCD边长是8厘米,长方形DEFG的长DG=10厘米,求他的宽DE长多少厘米?。