计算光学作业.(DOC)
光学例题2012。12.9

1.有一玻璃球,折射率为,今有一光线射到球面上,入射角为60°,求反射光线和折射光线的夹角。
2. 水槽有水20cm深,槽底有一个点光源,水的折射率为1.33,水面上浮一不透明的纸片,使人从水面上任意角度观察不到光,则这一纸片的最小面积是多少?3. 空气中的玻璃棒,n’=1.5163,左端为一半球形,r=-20mm。
轴上有一点光源,L=-60mm。
求U=-2°的像点的位置。
4. 简化眼把人眼的成像归结为只有一个曲率半径为5.7mm,介质折射率为1.333的单球面折射,求这种简化眼的焦点的位置和光焦度。
5. 有一玻璃球,折射率为n=1.5,半径为R,放在空气中。
(1)物在无穷远时,经过球成像在何处?(2) 物在球前2R处时像在何处?像的大小如何?6. 一个半径为100mm的玻璃球,折射率为1.53。
球内有两个气泡,看来一个恰好在球心,另一个在球的表面和球心之间,求两个气泡的实际位置。
7. 一个玻璃球直径为60mm,折射率为1.5,一束平行光入射在玻璃球上,其会聚点应该在什么位置?8. 一球面反射镜,r=-100mm,求β=0,-0.1,-1,5,10情况下的物距和像距。
9. 一球面镜对其前面200mm处的物体成一缩小一倍的虚像,求该球面镜的曲率半径。
10. 垂直下望池塘水底的物时,若其视见深度为1m,求实际水深,已知水的折射率为4/3。
11. 有一等边折射率三棱镜,其折射率为1.65,求光线经该棱镜的两个折射面折射后产生最小偏向角时的入射角和最小偏向角。
12. 身高为1.8m的人站在照相机前3.6m处拍照,若拟拍成100mm高的像,照相机镜头的焦距为多少?13. 单透镜成像时,若共轭距为250mm,求下列情况下透镜的焦距:(1) 实物,β=-4;(2) 实物,β=-1/4;(3) 虚物,β=-4。
14. 设一个光学系统处于空气中,β=-10,由物面到像面的距离为7200mm,物镜两焦点距离为1140mm,求透镜的焦距。
光学计算题

一、几何光学部分1、孔径都等4cm 的两个薄透镜组成同轴光具组,一个透镜是会聚的,其焦距为5cm ;另一个是发散的,其焦距为10cm 。
两个透镜中心间的距离为4cm 。
对于会聚透镜前面6cm 处的一个物点,试问:(1)哪一个透镜是有效光阑?(s '=f sf s ''+=5454cm cm cm cm-⨯-⨯=20cm y '=s y s '=2044cm cm cm ⨯=20cm (2分) 所以发散透镜经会聚透镜所成的像对物点所张的孔径角为2Lu '=26y arctg s cm''+=1026arctg =21230''' (1分) 会聚透镜对物点所张孔径角1Lu '=26yarctg cm=26arctg =1826' (1分) 因为2Lu '>1L u ',所以会聚透镜1L 为同轴光具组的有效光阑。
(1分) (2)1L 为入射光瞳,其直径为4cm 。
(1分)1L 经2L 成的像为出射光瞳,光瞳的位置s '及大小y '分别计算如下:s =-4cm ,f '=-10cms '=f sf s ''+=4(10)410cm cm cm cm -⨯---=207-cm=-2.857cmy '=s y s '=20744-⨯-=2.857cm (2分) 2、(1)显微镜用波长为250nm 的紫外光照射比用波长为500nm 的可见光照射时,其分辨本领增大多少倍?(2)它的物镜在空气中的数值孔径约为0.75,用紫外光时所能分辨的两条线之间的距离是多少?(3)用折射率为1.56的油浸系统时,这个最小距离为多少? (1)显微镜的分辨极限为:y ∆=0.61sin n uλ(2分)在其他条件一样,而用以不同波的光照射时,有12y y ∆∆=12λλ 则1y ∆=12λλ2y ∆=500250nm nm 2y ∆=22y ∆,即用紫外光250nm 时显微镜的分辨本领增至2倍,即增大1倍。
光纤光学作业精选全文

可编辑修改精选全文完整版Homework 11. 用射线方程求出各向同性介质中光线轨迹。
解:由射线方程 对于各向同性介质,n 是一个常数,即其轨迹函数表明光线在各向同性介质中传输时轨迹是直线。
2. 导出折射率平方律分布的渐变型光纤射线方程,并求其光纤中光线轨迹。
解:由射线方程:由于光纤折射率仅以径向变化,沿圆周方向和z 轴方向不变, 与z 无关,与径向r 有关,所以由折射率平方律分布型函数:通解为:3. 从麦克斯韦方程组出发,导出磁场的波动方程。
)()(r n dz rd n dz d ∇=⇒=0)(dz r d n dz d C dz r d n = bz nC r += )()(r n dz r d n dz d ∇=drdn r n ˆ=∇⇒=dr dn r dz r d n ˆ22 r drdn n dz r d ˆ122= r an dr dna r n n 2])(1[2020∆-=⇒∆-=∆⋅-=∴20222a n r n dz rd )2()2()(21z aCos C z a Sin C z r ∆+∆=4. 计算突变型多模光纤中最大时延。
Homework 21.证明(说明)光波导中不可能存在TEM模。
2.什么是TE、TM模式?什么是HE、EH模式?它们与本征值方程的关系是什么?3.简述u,w,V的定义及物理意义。
homework 31.一光纤的纤芯折射率为1.52,包层折射率为1.45,则其数值孔径为多少?2. 对于芯径为8um的阶跃折射率单模光纤,纤芯折射率为1.5,包层折射率为1.495,截止波长为多少?3. 衰减为0.3dB/km,长为100km的光纤,在输出端得到的光占输入光能的百分比为多少?Homework 41.简述色度色散,模间色散和偏振模色散的概念。
(请看ppt)2.简述光纤损耗的机制。
3.说明利用材料色散与波导色散制作色散位移光纤的原理。
答:对于石英系光纤,其材料色散()在=1.3um附近为零,在<1.3um时材料色散为正,在大于1.3um时,材料色散为负。
全部光学作业解答Word版
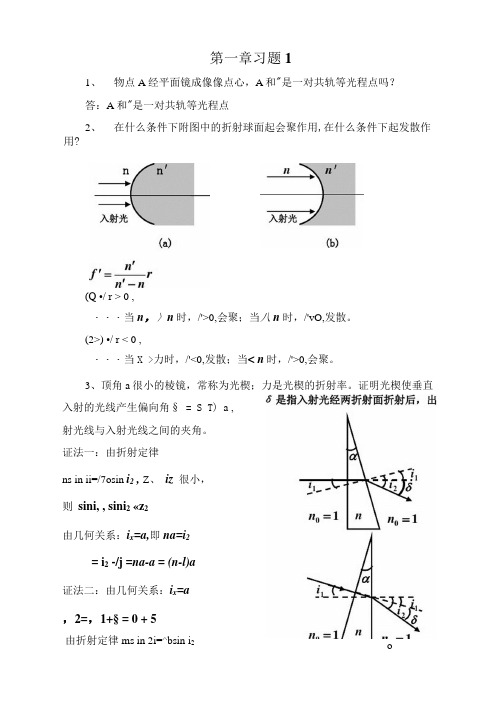
第一章习题11、物点A经平面镜成像像点心,A和"是一对共轨等光程点吗?答:A和"是一对共轨等光程点2、在什么条件下附图中的折射球面起会聚作用,在什么条件下起发散作用?(Q •/ r > 0 ,・・・当n,〉n时,/'>0,会聚;当八n时,/'vO,发散。
(2>) •/ r < 0 ,・・・当X >力时,/'<0,发散;当< n时,/'>0,会聚。
3、顶角a很小的棱镜,常称为光楔;力是光楔的折射率。
证明光楔使垂直入射的光线产生偏向角§ = S T) a ,射光线与入射光线之间的夹角。
证法一:由折射定律ns in ii=/7osin i2 , Z、iz很小,则sini, , sini2 «z2由几何关系:i x=a,即na=i2= i2 -/j =na-a = (n-l)a证法二:由几何关系:i x=a,2=,1+§ = 0 + 5由折射定律ms in 2i=^bsin i2o _V N 很小,sinq =a, sin/2 »i2, 且n0 «1则有na-a + 5, /• 8 = na-a = (n- l)a4>若空气中一均匀球形透明体能将平行光束会聚于其背面顶点上.此透明体的折射率应等于多少?解:设球形透明体的半径为r,其折射率为川已知H =1,p = -g, p' = 2r根据单球面折射成像公式= 得:工=上1 :. n f = 2p p r 2r r5、试证明:一束平行光相继经过几个平行分界面的多层介质折射时,出射光线的方向只与入射光的方向及入射空间和出射空间介质的折射率有关,与中间各层介质无关。
证明:V 坷sinh = //o sin/on2 sini2 = n l smi xn3 sin匚=n2 sin/2ii■g】sinL ijsini—n k sini* sini AU:.n k sini k =n o sin«o即sin/x = (/i0 sini0)/«A,命题成立。
光学计算题及答案分析

1、一人正对竖直平面镜站立,人的脸宽为20cm,两眼的距离为10cm,欲使自己无论闭上左眼还是右眼,都能用另一只眼睛从镜中看到自己的整个脸,则镜子的宽度至少为____________cm。
分析:根据平面镜成像特点先作出身体的像,再根据光路可逆,分别把人的两只眼睛与身体像的边界相连,镜子的有效范围刚好是两只眼睛和身体像组成的梯形的中位线.解:如图所示,人的脸宽为AB等于20cm,两眼为C、D,CD=10cm,如果用左眼看完整的像需用PR之间的平面镜,如果用右眼看完整的像需用QS之间的平面镜,所以无论闭上左眼或右眼都能看到完整的像需用PS之间的平面镜因PS=是梯形CDB′A′的中位线,则PS=1/2(A′B′+CD).因AB=A′B′=20cm.CD=10cm,所以PS=1/2(20cm+10cm)=15cm某人身高1.5米,站在离河岸3米处,他向水中看去,恰好看到对岸河边一根电线杆在水中的“倒影”,已知水面低于河岸0.5米,河宽15米,试求电线杆的高度。
2、一个身高1.8m的人站在河岸看到对岸的一根电线杆在水中的像,当人离开河岸后退,距离超过6m时,就不能看到完整的电线杆的像.已知河岸高出水面1m,河宽40m,求电线杆的高一束平行光从天花板A处沿竖直方向投射到一块水平放置的平面镜上,如果把平面镜转过30度角,则天花板上得到的光斑离A处5.2米。
求:(1)天花板与水平镜面相距几米?(2)A点与其在水平放置的平面镜里的虚像面相距几米?3.某人通过焦距为9.0cm,直径为6.0cm的凸透镜看报纸。
此时眼睛距离报纸15.0cm,凸透镜距离报纸6.0cm。
设眼睛在透镜主轴上,报纸平面垂直于主轴。
(1)此时报纸的像距离眼睛多远?(2)若报纸上密排着宽、高均为0.30cm的字,则他通过透镜,至多能看清同一行几个完整的字?(忽略眼睛瞳孔大小)4、一位同学看到远方的闪电开始计时时,过了△t时间后听到雷击声。
如果已知光在空气中的传播速度为c,声音在空气中的传播速度为v,若用△t,v,c这三个物理量表示该同学离打雷处的距离s。
光学计量单位计算

多年来,感光材料的感光度计算方法是以使感光材料产生一定密度值所需曝光量为计算依据的,而曝光量又是以烛光.米.秒或勒克司*秒为计量单位的。
曝光量的计算公式是;H(曝光量)=E(照度)×t(时间)照度与光源的发光强度(光强I)成正比:E=I(光强)×D-2(D为距离)光强的单位:(旧)烛光:又名国际烛光,国际标准照明协会(CIE)早期规定的,以特定的鲸鱼油蜡烛的单位发光强度为单位,这也是烛光一词命名的由来。
显然,当时主要是以光源的亮度为依据的(亮度的定义是:单位面积发光体的光强)。
(新)烛光,法定名称坎德拉candela.cd,CIE(1942)定义为一平方厘米绝对黑体在金属铂的凝固温度(2045K)时发光强度的六十分之一,这个规定既确定了其亮度,又确定了其色温。
新烛光=0.981旧烛光1979年,CIE又对坎德拉规定了新的标准:定义频率为540×1012Hz(即波长555nm)的单色光源每单位立体角(1个球面度)辐射能为1/683W时的发光强度。
这个定义把光强单位和能量绝对单位联系起来了,含义覆盖面更广了。
特别规定单色光源的波长,进一步把光的波长和机械能与亮度和光强联系起来。
在通常的感光测定工作中,都采用白光作为感光仪的光源和施照光,严格规定其色温和光强,并以烛光为光强单位,以勒克司lx为照度单位,以lx*s为曝光量单位,并以这些单位为基础的数据评价照相性能,计算感光材料的感光度,这无疑是很实用的常规方法。
这个方法检测的数据和通常感光材料在应用时的实用性能是一致的,但是这仅适用于在实际应用时用白光曝光的感光材料。
对于实际应用时,用红外线或紫外线曝光的感光材料,或只对可见光谱中某个范围曝光的感光材料,则必须采用红外线、紫外线或特定光谱成分色光作为感光测定曝光时的施照光,才能反映其在实际应用时的性能。
若尚采用白光作为感光测定时曝光的施照光,则根本不能反映这类感光材料的实用性能。
光学课后作业

练习36 双缝干涉班级 姓名 学号一、选择题1.把双缝干涉实验装置放在折射率为n 的水中,两缝间距为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中波长为λ,则屏上干涉条纹两相邻明纹之间的距离为:( )(A )nd Dλ (B )d D n λ (C )nD d λ (D )ndD 2λ2.双缝间距为2 mm ,双缝与幕相距300 cm 。
用波长为6000Å的光照射时,幕上干涉条纹的相邻两条纹距离(单位为mm )是( )(A )4.5 (B )0.9 (C )3.12 (D )4.15 (E )5.183.在双缝干涉实验中,初级单色光源S 到两缝1s 2s 距离相等,则观察屏上中央明条纹位于图中O 处。
现将光源S 向下移动到示意图中的S ′位置,则( )(A )中央明条纹也向下移动,且条纹间距不变。
(B )中央明条纹向上移动,且条纹间距不变。
(C )中央明条纹向下移动,且条纹间距增大。
(D )中央明条纹向上移动,且条纹间距增大。
二、填空题1.在双缝干涉实验中,若使两缝之间的距离增大,则屏幕上干涉条纹间距 ,若使单色光波长减少,则干涉条纹间距 。
2.如图所示,在双缝干涉实验中S 1S =S 2S 用波长为λ的光照射双缝1S 和2S ,通过空气后在屏幕E 上形成干涉条纹。
已知P 点处为第三级明条纹,则1S 和2S 到P 点的光程差为 。
若将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率n = 。
3.在杨氏干涉装置中,双缝至幕的垂直距离为2.00 m ,测得第10级干涉亮纹到零级亮纹间的距离为3.44 cm ,双缝间距为0.342 mm ,那么入射单色光的波长为 Å。
三、计算题1.在双缝干涉实验中,D =2 m ,若用波长λ=5500Å的单色光垂直入射,在屏幕上距中心O 点2.2 mm处可观察到第4级明纹,求:(1)双缝间距。
光学试卷打印

一、填空1、光的折射定律(1) (2)2、发生全反射的条件为(1) (2)3、费马原理4、用垂轴放大率判断物、像虚实关系方法:当β>0时 β<0时5、物、像位置相对于光学系统的 来确定的称为牛顿公式,相对于光学系统的 来确定的称为高斯公式,如已知光学系统的物、像方的介质折射率分别为n 及n`,则理想光学系统中两焦距间的关系为6、光学系统的垂轴放大率β、轴向放大率α及角放大率γ之间的关系为7、一光学系统由焦距分别为:`,`,2211f f f f 和的两光组组成,两光组间光学间隔为∆=21`F F ,则组合系统的物、像方焦距分别为8、平面反射镜成像的垂轴放大率为 ,物像位置关系为 ,如果反射镜转过α角,则反射光线方向改变9、限制进入光学系统的成像光束口径的光阑称为 ,限制成像范围的光阑称为 , 经前面光组在光学系统物空间所成像称为 ,经后面光组在光学系统的像空间所成的像称为 ,主光线是指过 中心的光线10、单色光成像会产生性质不同的五种像差,分别为 ,白光产生的色差有两种,即1、厦门大学《工程光学》课程试卷物理与机电学院机电系三年级测控/机电专业主考教师:张建寰 试卷类型:(试卷)二、计算题1、 一厚度为200mm 的平行平板玻璃,n=1.5,其下面放一直径为1mm 的金属片,若在玻璃板上盖一圆形纸片,要求在玻璃上方任何方向上都看不到该金属片,问纸片最小直径为多少?2、 一束平行光束入射到一半径为r=30mm ,折射率n=1.5的玻璃球上,球的一半镀反射层,光从未镀侧入射,求平行光束的会聚点位置,并判断像的虚实。
3、 一光学系统由两薄透镜组组成,焦距分别为mm d mm f mm f 350,50,10021===,一物位于离第一透镜250mm 处,求光学系统所成像位置及垂轴放大率。
4、 如图所示的光学测微系统,光学透镜的焦距为`f ,当聚焦光斑在标尺上刻度为y 时,试推导其测量微小角位移原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
王新柯07B911020 物理系时域有限差分算法对于生物电磁学的应用博士研究生:王新柯学号:07B911020导师:张岩所在单位:物理系- I -王新柯07B911020 物理系目录第1章时域有限差分算法简介 (3)第2章时域有限差分方法的基本理论 (7)2.1 麦克斯韦方程和Yee元胞 (7)2.2 直角坐标中的三维FDTD (10)第3章FDTD对于生物电磁学的应用 (19)3.1 生物组织的电磁特性和人体的电磁模型 (19)3.2 平面波照射下人体内的电磁效应 (23)3.3 动力电的人体效应 (30)3.4 高压EMP的生物效应 (34)第4章结论 (38)参考文献 (39)- II -王新柯07B911020 物理系第1章时域有限差分算法简介自1873年麦克斯韦建立电磁场基本方程以来,电磁波理论和应用的发展已经有一百多年的历史。
目前,电磁波的研究已深入到各个领域,应用十分广泛,例如无线电波传播、光纤通信和移动通信、雷达技术、微波、天线、电磁成像、地下电磁探测、电磁兼容,等等。
电磁波在实际环境中的传播过程十分复杂,例如各种复杂目标的散射,复杂结构天线的影响,等等。
具体实际地研究电磁波的特性有着十分重要的意义。
实验和理论分析技术是相辅相成的重要手段。
分析计算途径需要结合实际环境电磁参数求解麦克斯韦方程边值问题,通常只有一些经典问题有解析解。
应当说,解析解具有重要的指导意义。
然而,由于实际环境的复杂性,往往需要通过数值解得到具体环境下的电磁波特性。
随着计算机技术的发展,已经提出求解麦克斯韦方程的很多有意义的数值解方法,例如矩量法、有限元法、边界元法已经时域有限差分方法等等。
并且,随着电磁波应用的广泛和计算机技术的发展,各种方法的研究也更加深入。
1966年K. S. Yee首次提出了一种电磁场数值计算的新方法——时域有限差分(Finite Difference Time Domain, FDTD)方法[1]。
对电磁场E、H分量在空间和时间上采用交替抽样的离散方式,每一个E(或H)场分量周围有四个H(或E)分量环绕,应用这种离散方式将含有时间变量的麦克斯韦旋度方程转化为一组差分方程,并在时间轴上逐步推进地求解空间电磁场。
Yee提出的这种抽样方式后来被称为Yee元胞。
FDTD方法是求解麦克斯韦微分方程的直接时域方法。
在计算中将空间某一样本点的电场或磁场与- 3 -王新柯07B911020 物理系周围格点的磁场或电场直接相关联,且介质参数已赋值给空间每一个元胞,因此这一方法可以处理复杂形状目标和非均匀介质物体的电磁散射、辐射等问题。
同时,FDTD的随时间推进可以方便地给出电磁场的时间演化过程,在计算机上以伪彩色方式显示,这种电磁场可视化结果清楚地显示了物理过程,便于分析和设计。
FDTD方法是求解麦克斯韦方式的直接时域方法,经过三十多年的发展已成为一种成熟的数值方法,目前已被广泛研究和应用。
以下只是简单回顾FDTD的发展:1966年,Yee首次提出麦克斯韦方程的差分离散方式,并用来处理电磁脉冲的传播和反射问题[1]。
1969年,Taylor等用FDTD分析非均匀介质的电磁散射,提出用吸收边界来吸收外向行波,吸收边界采用的是最简单插值方法[2]。
1971年,Merewether用FDTD计算旋转体上有入射脉冲所引起的感生电流,采用了辐射边界条件[3]。
1975年,Taflove等用FDTD计算非均匀介质在正弦波入射的时谐场(稳态)电磁散射,讨论了时谐场情况的近—远场外推,以及数值稳定性条件[4]。
Holland在1977年和Kunz在1978年,分别独立采用FDTD计算F117飞机这种复杂目标的电磁波散射[5,6]。
1981年,Mur提出在计算区域截断边界处的一阶和二阶吸收边界条件及其在FDTD的离散形式。
这是FDTD的一种十分有效的吸收边界条件,获得广泛应用[7]。
- 4 -王新柯07B911020 物理系1982年,Umashankar和Taflove用FDTD计算目标雷达散射截面,提出将FDTD区划分成总场区和散射场区,并提出连接边界条件,是散射计算中入射波设置的一种简便有效方法[8]。
Umashankar和Taflove等在1987年和1988年,利用FDTD分析了自由空间及腔体中导线上的感应电流,讨论了FDTD中细导线的处理方法[9,10]。
Choi和Hoefer于1986年,用FDTD分析了波导腔体的谐振问题,计算其谐振频率[11]。
Kasher和Yee在1987年,提出亚网格技术[12],Mei等人在1984年提出共形网络技术[13]。
Zhang和Mei在1988年,Liang等在1989年,Gwarek在1988年,Sheen和Kong等在1990年,用FDTD分析计算了波导、同轴线、微带天线及微带不连续性问题,得到相应的阻抗、传播常数及S参数[14,15,16,17]。
Maloney等在1990年,用圆柱坐标下FDTD分析了柱状和锥状天线位于理想导体平面上的辐射,得到宽带天线的输入阻抗及瞬态辐射场的直观可视化显示[18]。
Sullivan在1990年,用FDTD计算了60-70 MHz电磁波照射下透入到人体内部的电磁场,研究了生物电磁学问题[19]。
Britt在1989年,首次给出了时域远场结果[20];Yee等和Luebbers等分别在1991年提出了三维FDTD时域近—远场外推方法[21,22];随后,Luebbers等在1992年提出了二维FDTD时域近—远场外推方法[23]。
Larson, Perlik和Taflove等分别在1989年提出了研究适用于FDTD的专用计算机,以便计算电磁波与大尺寸物体的相互作用[24,25]。
- 5 -王新柯07B911020 物理系Luebbers和Hunsberger等在1990年,研究了色散介质在FDTD中的处理方法[26]。
Maloney和Smith在1992年,提出将阻抗边界条件应用于FDTD[27]。
Sui等于1992年,提出用二维FDTD计算有集中参数元件的数字和微波电路模型,包括电阻、电容、电感、二极管、晶体管等元件[28]。
Berenger在1994年,提出将麦克斯韦方程扩展为场分量分裂形式,并构成完全匹配层(PML),这是一种全新的吸收边界[29];Sacks等人在1995年和Gedney在1996年分别提出各向异性介质的PML,其支配方程是各向异性介质麦克斯韦方程[30,31];在FDTD计算中这两种PML作为吸收边界已得到广泛应用。
Prather和Shi在1999年,分析轴对称衍射透镜,给出波长为平面波和高斯波入射时,直径衍射透镜的光波传播特性[32]。
- 6 -王新柯 07B911020 物理系- 7 -第2章 时域有限差分方法的基本理论2.1 麦克斯韦方程和Yee 元胞麦克斯韦方程组是支配宏观电磁现象的一组基本方程。
这组方程即可以写成微分形式,又可以写成积分形式。
FDTD 方法是由微分形式的麦克斯韦方程出发进行差分离散。
众所周知,麦克斯韦为旋度方程可写为,D H J t ∂∇⨯=+∂ (1) B E J t∂∇⨯=--∂ (2) 其中,E 为电场强度,D 为电通量密度,H 为磁场强度,B 为磁通量密度,J 为电流密度,m J 为磁流密度。
各向同性线性介质中的本构关系为,,,,.m m D E B H J E J H εμσσ==== (3) 其中ε表示介质介电系数,μ表示磁导系数,σ表示电导率,m σ表示磁导率。
σ和m σ分别为介质的电损耗和磁损耗。
由于真空中,有0,0m σσ==,以及1208.8510/F m εε-==⨯和70410/H m μμπ-==⨯。
在真空中,式(1)和(2)可以写为差分方程,王新柯 07B911020 物理系 - 8 -y x z x y x z y y x z z H E H E y z tE H H E z x tH H E E x y tεσεσεσ∂∂∂-=+∂∂∂∂∂∂-=+∂∂∂∂∂∂-=+∂∂∂ (4) 以及y x z m x y x z m y y x z m z E H E H y z tH E E H z x tE E H H x y tμσμσμσ∂∂∂-=--∂∂∂∂∂∂-=--∂∂∂∂∂∂-=--∂∂∂ (5) 下面考虑式(4)和(5)的FDTD 的差分离散。
令(),,,f x y z t 表示E 或H 在直角坐标系中某一分量,在时间和空间域中的离散取以下符号表示:()()(),,,,,,,,n f x y z t f i x j y k z n t f i j k =∆∆∆∆= (6)对(),,,f x y z t 关于时间和空间的一阶偏导数取中心差分近似,即()()()()()()1/21/211,,,,,,,22|11,,,,,,,22|11,,,,,,,22|,,,,,,,|n n x i x n n y j y n n z k z n n t n t f i j k f i j k f x y z t x xf i j k f i j k f x y z t y y f i j k f i j k f x y z t z tf x y z t f i j k f i j k t =∆=∆=∆+-=∆⎛⎫⎛⎫+-- ⎪ ⎪∂⎝⎭⎝⎭≈∂∆⎛⎫⎛⎫+-- ⎪ ⎪∂⎝⎭⎝⎭≈∂∆⎛⎫⎛⎫+-- ⎪ ⎪∂⎝⎭⎝⎭≈∂∆∂-≈∂t∆ (7)王新柯 07B911020 物理系- 9 -在FDTD 离散中电场和磁场各节点的空间排布如图1所示,这就是著名的Yee 元胞。
由图可见每一个磁场分量由四个电场分量环绕;同样,每一个电场分量由四个磁场分量环绕。
这种电磁场分量的空间取样方式不仅符合法拉第电磁感应定律和安培环路定理得自然结构,而且这种电磁场各分量的空间相对位置也适合于麦克斯韦方程的差分计算,能够恰当地描述电磁场的传输特性。
此外,电场和磁场在时间顺序上交替抽样,抽样时间间隔彼此相差半个时间步长,使麦克斯韦旋度方程离散以后构成显示差分方程,从而可以在时间上迭代求解,而不需要进行矩阵求逆运算。
因此,由给定相应电磁问题的初始值,FDTD 方法就可以逐步推进地求得以后各个时刻空间电磁场的分布。
图1 FDTD 离散中的Yee 元胞。
Yee 元胞中,E H 各个分量空间节点与时间步取值的整数和半整数约定如表1所示。
王新柯 07B911020 物理系- 10 - 表1 Yee 元胞中,E H 各分量节点位置2.2 直角坐标中的三维FDTD现在考虑三维情况下的FDTD 形式。
先看(4)式中第一式,设观察点(),,x y z 为x E 的节点,即()1/2,,i j k +,以及时刻()1/2t n t =+∆,于是,(4)式中第一式的离散形式为,王新柯 07B911020 物理系 - 11 -111/21/21/211,,,,122,,211,,,,122 ,,221111,,,,222211,,22 n n x x n n x x n n z z n n y y E i j k E i j k i j k t E i j k E i j k i j k H i j k H i j k yH i j k H εσ++-++-⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪∆⎝⎭⎛⎫⎛⎫+++ ⎪ ⎪⎛⎫⎝⎭⎝⎭++ ⎪⎝⎭⎛⎫⎛⎫++-+- ⎪ ⎪⎝⎭⎝⎭=∆⎛⎫++- ⎪⎝⎭-1/211,,22i j k z⎛⎫+- ⎪⎝⎭∆ (8) 其中用了平均值近似,即11/211,,,,122,,22n n x x n x E i j k E i j k E i j k ++⎛⎫⎛⎫+++ ⎪ ⎪⎛⎫⎝⎭⎝⎭+= ⎪⎝⎭(9) 这样处理是为了在离散式中只出现表1所示的各个场分量节点。
