2019版一轮创新思维文数(人教版A版)练习：第十章 第四节 变量间的相关关系与统计案例 Word版含解析
人教版A版2019版一轮创新思维文科数学练习：第十章第四节变量间的相关关系与统计案例
课时规范练 A 组 基础对点练1．(2018·大连双基测试)已知x ，y 的取值如表所示：如果y 与x 线性相关，且线性回归方程为y ^＝b ^x ＋2，则b ^的值为( )A ．－12B.12 C ．－110D.110解析：计算得x ＝3，y ＝5，代入到y ^＝b ^x ＋132中，得b ^＝－12.故选A.答案：A2．四名同学根据各自的样本数据研究变量x ，y 之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且y ^＝2.347x －6.423；②y 与x 负相关且y ^＝－3.476x ＋5.648；③y 与x 正相关且y ^＝5.437x ＋8.493；④y 与x 正相关且y ^＝－4.326x －4.578. 其中一定不正确的结论的序号是( ) A ．①② B ．②③ C ．③④D ．①④解析：y ^＝b ^x ＋a ^，当b >0时，为正相关，b <0为负相关，故①④错误． 答案：D3．在一组样本数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )(n ≥2，x 1，x 2，…，x n 不全相等)的散点图中，若所有样本点(x i ，y i )(i ＝1,2，…，n )都在直线y ＝12x ＋1上，则这组样本数据的样本相关系数为( ) A ．－1 B ．0 C.12D ．1解析：所有点均在直线上，则样本相关系数最大即为1，故选D. 答案：D4．已知变量x 与y 正相关，且由观测数据算得样本平均数x ＝3，y ＝3.5，则由该观测数据算得的线性回归方程可能是( )A.y ^＝0.4x ＋2.3 B.y ^＝2x －2.4 C.y ^＝－2x ＋9.5D.y ^＝－0.3x ＋4.4解析：依题意知，相应的回归直线的斜率应为正，排除C 、D.且直线必过点(3,3.5)，代入A 、B 得A 正确． 答案：A5．经调查某地若干户家庭的年收入x (万元)和年饮食支出y (万元)具有线性相关关系，并得到y 关于x 的回归直线方程：y ^＝0.245x ＋0.321，由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加________万元．解析：x 变为x ＋1，y ^＝0.245(x ＋1)＋0.321＝0.245x ＋0.321＋0.245，因此家庭年收入每增加1万元，年饮食支出平均增加0.245万元． 答案：0.2456．某炼钢厂废品率x (%)与成本y (元/吨)的线性回归方程为y ^＝105.492＋42.569x .当成本控制在176.5元/吨时，可以预计生产的1 000吨钢中，约有________吨钢是废品(结果保留两位小数)．解析：因为176.5＝105.492＋42.569x ，解得x ≈1.668，即当成本控制在176.5元/吨时，废品率约为1.668%，所以生产的1 000吨钢中，约有1 000×1.668%＝16.68吨是废品． 答案：16.687．(2018·合肥模拟)某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间(x 个月)和市场占有率(y %)的几组相关对应数据：(1)(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%(精确到月)．附：b ^＝∑i ＝1nx i y i －n x·y∑i ＝1nx 2i －n x 2，a ^＝y －b ^x .解析：(1)由题意知x ＝3，y ＝0.1，∑i ＝15x i y i ＝1.92，∑i ＝15x 2i ＝55，所以b ^＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x 2＝1.92－5×3×0.155－5×32＝0.042， a ^＝y －b ^x ＝0.1－0.042×3＝－0.026， 所以线性回归方程为y ^＝0.042x －0.026.(2)由(1)中的回归方程可知，上市时间与市场占有率正相关，即上市时间每增加1个月，市场占有率约增加0.042个百分点．由y ^＝0.042x －0.026>0.5，解得x ≥13，故预计上市13个月时，该款旗舰机型市场占有率能超过0.5%.8．某校数学课外兴趣小组为研究数学成绩是否与性别有关，先统计本校高三年级每个学生一学期数学成绩的平均分(采用百分制)，剔除平均分在30分以下的学生后，共有男生300名，女生200名．现采用分层抽样的方法，从中抽取了100名学生，按性别分为两组，并将两组学生成绩分为6组，得到如下所示频数分布表.数学成绩与性别是否有关；(2)规定80分以上为优分(含80分)，请你根据已知条件作出2×2列联表，并判断是否有90%以上的把握认为“数学成绩与性别有关”.附表及公式K 2＝a ＋bc ＋d a ＋cb ＋d.解析：(1)x 男＝45×0.05＋55×0.15＋65×0.3＋75×0.25＋85×0.1＋95×0.15＝71.5，x 女＝45×0. 15＋55×0.1＋65×0.125＋75×0.25＋85×0.325＋95×0.05＝71.5，从男、女生各自的平均分来看，并不能判断数学成绩与性别有关．(2)由频数分布表可知：在抽取的100名学生中，“男生组”中的优分有15人，“女生组”中的优分有15人，据此可得2×2列联表如下：可得K 2＝60×40×30×70≈1.79，因为1.79<2.706，所以没有90%以上的把握认为“数学成绩与性别有关”．B 组能力提升练1．为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y ＝b x ＋a ，其中b ＝0.76，a ＝y －b x .据此估计，该社区一户年收入为15万元家庭的年支出为( ) A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元解析：∵x ＝10.0，y ＝8.0，b ^＝0.76，∴a ^＝8－0.76×10＝0.4，∴回归方程为y ^＝0.76x ＋0.4，把x ＝15代入上式得，y ^＝0.76×15＋0.4＝11.8(万元)，故选B. 答案：B2．根据如下样本数据：得到的回归方程为y ＝b x ＋a .若样本点的中心为(5,0.9)，则当x 每增加1个单位时，y ( )A ．增加1.4个单位B ．减少1.4个单位C ．增加7.9个单位D ．减少7.9个单位解析：依题意得，y ＝a ＋b －25＝0.9，故a ＋b ＝6.5①；又样本点的中心为(5,0.9)，故0.9＝5b ＋a ②，联立①②，解得b ＝－1.4，a ＝7.9，即y ^＝－1.4x ＋7.9，可知当x 每增加1个单位时，y 减少1.4个单位，故选B. 答案：B3．(2018·岳阳模拟)某考察团对全国10个城市进行职工人均工资水平x (千元)与居民人均消费水平y (千元)统计调查，y 与x 具有相关关系，回归方程y ^＝0.66x ＋1.562.若某城市居民人均消费水平为7.675(千元)，估计该城市人均消费占人均工资收入的百分比约为________．解析：由y ^＝0.66x ＋1.562知，当y ＝7.675时，x ＝6 113660，故所求百分比为7.675x ＝7.675×6606 113≈83%.答案：83%4．(2018·唐山质检)为了研究某种细菌在特定环境下随时间变化的繁殖规律，得到了下表中的实验数据，计算得回归直线方程为y ^＝0.85x －0.25.由以上信息，可得表中c 的值为________.解析：x ＝3＋4＋5＋6＋75＝5，y ＝2.5＋3＋4＋4.5＋c 5＝14＋c5，代入回归直线方程得14＋c5＝0.85×5－0.25，解得c ＝6. 答案：65．为了研究男羽毛球运动员的身高x (单位：cm)与体重y (单位：kg)的关系，通过随机抽样的方法，抽取5名运动员测得他们的身高与体重关系如下表：(1)从这5 2 kg 的概率； (2)求回归直线方程y ^＝b ^x ＋a ^.解析：(1)从这5个人中随机地抽取2个人的体重的基本事件有(74,73)，(74,76)，(74,75)，(74,77)；(73,76)，(73,75)，(73,77)；(76,75)，(76,77)；(75,77)．满足条件的有(74,76)，(74,77)，(73,76)，(73,75)，(73,77)，(75,77)6种情况，故2个人体重之差的绝对值不小于2 kg 的概率为610＝35.(2)x ＝176，y ＝75，b ^＝∑5i ＝1 xi －xy i －y∑5i ＝1x i －x2＝－－＋－－＋0×1＋2×0＋4×2－2＋－2＋02＋22＋42＝0.4， a ^＝y －b ^x ＝4.6， ∴y ^＝0.4x ＋4.6.6．(2018·郑州一中检测)为了解某地区观众对某大型综艺节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．下面是根据调查结果绘制的观众观看该节目的场数与所对应的人数的表格：10名女性． (1)根据已知条件完成如下2×2列联表，并判断我们能否有95%的把握认为是否为“歌迷”与性别有关？(2)2名女性，若从“超级歌迷”中任意选取2人，求至少有1名女性观众的概率． 注：K 2＝n ad －a ＋bc ＋d a ＋cb ＋d，n ＝a ＋b ＋c ＋d .解析：(1)由统计表可知，在抽取的100人中，“歌迷”有25人，从而完成2×2列联表如下：将2×2K 2＝－275×25×45×55＝10033≈3.030<3.841 所以我们没有95%的把握认为是否为“歌迷”与性别有关．(2)由统计表可知，“超级歌迷”有5人，其中2名女性，3名男性，设2名女性分别为a 1，a 2,3名男性分别为b 1，b 2，b 3，从中任取2人所包含的基本事件有：(a1，a2)，(a1，b1)，(a1，b2)，(a1，b3)，(a2，b1)，(a2，b2)，(a2，b3)，(b1，b2)，(b1，b3)，(b2，b3)，共10个，用A表示“任意选取的2人中，至少有1名女性观众”这一事件，A包含的基本事件有：(a1，a2)，(a1，b1)，(a1，b2)，(a1，b3)，(a2，b1)，(a2，b2)，(a2，b3)，共7个，所以P(A)＝710.。
2019版一轮创新思维文数(人教版A版)练习：对数函数
课时规范练 A 组 基础对点练1．函数y ＝1log 2(x －2)的定义域是( )A ．(－∞，2)B ．(2，＋∞)C ．(2,3)∪(3，＋∞)D ．(2,4)∪(4，＋∞)解析：要使函数有意义，应满足⎩⎪⎨⎪⎧x －2＞0，log 2(x －2)≠0，即⎩⎪⎨⎪⎧x ＞2，x －2≠1，解得x ＞2且x ≠3.故选C. 答案：C2．设a ＝⎝⎛⎭⎫1213，b ＝log 132，c ＝log 123，则( )A ．a ＞b ＞cB ．a ＞c ＞bC ．b ＞c ＞aD ．c ＞a ＞b解析：∵b ＝－log 32∈(－1,0)，c ＝－log 23＜－1，a ＝⎝⎛⎭⎫1213＞0，∴a ＞b ＞c ，选A. 答案：A3．(2016·高考全国卷Ⅱ)下列函数中，其定义域和值域分别与函数y ＝10lg x 的定义域和值域相同的是( ) A ．y ＝x B ．y ＝lg x C ．y ＝2xD ．y ＝1x解析：函数y ＝10lg x 的定义域为(0，＋∞)，又当x >0时，y ＝10lg x ＝x ，故函数的值域为(0，＋∞)．只有D 选项符合． 答案：D4．函数y ＝⎩⎪⎨⎪⎧3x ，x ∈(－∞，1)，log 2x ，x ∈[1，＋∞)的值域为( )A ．(0,3)B ．[0,3]C ．(－∞，3]D ．[0，＋∞)解析：当x ＜1时，0＜3x ＜3；当x ≥1时，log 2x ≥log 21＝0，所以函数的值域为[0，＋∞)． 答案：D5．(2018·焦作模拟)若函数y ＝a |x |(a ＞0，且a ≠1)的值域为{y |y ≥1}，则函数y ＝log a |x |的图象大致是( )解析：若函数y ＝a |x |(a ＞0，且a ≠1)的值域为{y |y ≥1}，则a ＞1，故函数y ＝loga |x |的大致图象如图所示． 故选B. 答案：B6.已知函数y ＝log a (x ＋c )(a ，c 为常数，其中a ＞0，a ≠1)的图象如图，则下列结论成立的是( ) A ．a ＞1，c ＞1 B ．a ＞1,0＜c ＜1 C ．0＜a ＜1，c ＞1 D ．0＜a ＜1,0＜c ＜1解析：由对数函数的性质得0<a <1，因为函数y ＝log a (x ＋c )的图象在c >0时是由函数y ＝log a x 的图象向左平移c 个单位得到的，所以根据题中图象可知0<c <1. 答案：D7．(2018·吉安模拟)如果log 12x ＜log 12y ＜0，那么( )A ．y ＜x ＜1B ．x ＜y ＜1C ．1＜x ＜yD ．1＜y ＜x解析：因为y ＝log 12x 在(0，＋∞)上为减函数，所以x ＞y ＞1.答案：D8．函数y ＝x 2ln|x ||x |的图象大致是( )解析：易知函数y ＝x 2ln |x ||x |是偶函数，可排除B ，当x >0时，y ＝x ln x ，y ′＝ln x ＋1，令y ′>0，得x >e －1，所以当x >0时，函数在(e －1，＋∞)上单调递增，结合图象可知D 正确，故选D.答案：D9．已知f (x )是定义在R 上的偶函数，且在区间(－∞，0]上单调递增，若实数a 满足f (2log 3a )>f (－2)，则a 的取值范围是( ) A ．(－∞，3) B ．(0，3) C ．(3，＋∞)D ．(1，3)解析：本题主要考查函数的奇偶性及单调性．∵f (x )是定义在R 上的偶函数，且在区间(－∞，0]上单调递增，∴f (x )在区间[0，＋∞)上单调递减．根据函数的对称性，可得f (－2)＝f (2)，∴f (2log 3a )>f (2)．∵2log 3a >0，f (x )在区间[0，＋∞)上单调递减，∴0<2log 3a <2⇒log 3a <12⇒0<a <3，故选B.答案：B10．已知函数y ＝f (x )是定义在R 上的偶函数，当x ∈(－∞，0]时，f (x )为减函数，若a ＝f (20.3)，b ＝f (log 124)，c ＝f (log 25)，则a ，b ，c 的大小关系是( )A ．a ＞b ＞cB ．c ＞b ＞aC ．c ＞a ＞bD ．a ＞c ＞b解析：函数y ＝f (x )是定义在R 上的偶函数， 当x ∈(－∞，0]时，f (x )为减函数， ∴f (x )在[0，＋∞)上为增函数， ∵b ＝f (log 124)＝f (－2)＝f (2)，又1<20.3<2<log 25，∴c >b >a .故选B. 答案：B11．已知b ＞0，log 5b ＝a ，lg b ＝c,5d ＝10，则下列等式一定成立的是( ) A ．d ＝ac B ．a ＝cd C ．c ＝adD ．d ＝a ＋c解析：由已知得5a ＝b,10c ＝b ，∴5a ＝10c ，∵5d ＝10，∴5dc ＝10c ，则5dc ＝5a ，∴dc ＝a ，故选B. 答案：B12．已知函数f (x )＝ln(1＋4x 2－2x )＋3，则f (lg 2)＋f ⎝⎛⎭⎫lg 12＝( ) A ．0 B ．－3 C ．3D ．6解析：由函数解析式，得f (x )－3＝ln(1＋4x 2－2x )，所以f (－x )－3＝ln(1＋4x 2＋2x )＝ln11＋4x 2－2x＝－ln(1＋4x 2－2x )＝－[f (x )－3]，所以函数f (x )－3为奇函数，则f (x )＋f (－x )＝6，于是f (lg 2)＋f ⎝⎛⎭⎫lg 12＝f (lg 2)＋f (－lg 2)＝6.故选D. 答案：D13．已知4a ＝2，lg x ＝a ，则x ＝________. 解析：∵4a ＝2，∴a ＝12，又lg x ＝a ，x ＝10a ＝10.答案：1014．已知f (x )是定义在R 上的奇函数，当x ＞0时，f (x )＝log 2x －1，则f ⎝⎛⎭⎫－22＝________. 解析：因为f (x )是定义在R 上的奇函数，所以f ⎝⎛⎭⎫－22＝－f ⎝⎛⎭⎫22＝－⎝⎛⎭⎫log 222－1＝32. 答案：3215．函数f (x )＝log 2(－x 2＋22)的值域为________．解析：由题意知0＜－x 2＋22≤22＝232，结合对数函数图象(图略)，知f (x )∈⎝⎛⎦⎤－∞，32，故答案为⎝⎛⎦⎤－∞，32. 答案：⎝⎛⎦⎤－∞，32 16．若log 2a 1＋a 21＋a ＜0，则a 的取值范围是________．解析：当2a ＞1时，∵log 2a 1＋a 21＋a ＜0＝log 2a 1，∴1＋a 21＋a ＜1.∵1＋a ＞0，∴1＋a 2＜1＋a ， ∴a 2－a ＜0，∴0＜a ＜1，∴12＜a ＜1.当0＜2a ＜1时，∵log 2a 1＋a 21＋a ＜0＝log 2a 1，∴1＋a 21＋a＞1. ∵1＋a ＞0，∴1＋a 2＞1＋a .∴a 2－a ＞0，∴a ＜0或a ＞1，此时不合题意． 综上所述，a ∈⎝⎛⎭⎫12，1. 答案：⎝⎛⎭⎫12，1B 组 能力提升练1．已知函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x ，x ≥4f (x ＋1)，x ＜4，则f (1＋log 25)的值为( )A.14 B.⎝⎛⎭⎫1221log 5＋ C.12D.120解析：∵2＜log 25＜3，∴3＜1＋log 25＜4，则4＜2＋log 25＜5，f (1＋log 25)＝f (1＋1＋log 25)＝f (2＋log 25)＝⎝⎛⎭⎫1222log 5＋＝14×⎝⎛⎭⎫122log 5＝14×15＝120，故选D. 答案：D2．(2018·四川双流中学模拟)已知a ＝log 29－log 23，b ＝1＋log 27，c ＝12＋log 213，则( )A ．a ＞b ＞cB ．b ＞a ＞cC ．c ＞a ＞bD ．c ＞b ＞a解析：a ＝log 29－log 23＝log 233，b ＝1＋log 27＝log 227，c ＝12＋log 213＝log 226，因为函数y ＝log 2x 是增函数，且27＞33＞26，所以b ＞a ＞c ，故选B. 答案：B3．设f (x )＝lg ⎝⎛⎭⎫21－x ＋a 是奇函数，则使f (x )＜0的x 的取值范围是( )A ．(－1,0)B ．(0,1)C ．(－∞，0)D ．(－∞，0)∪(1，＋∞)解析：∵f (x )＝lg ⎝⎛⎭⎫21－x ＋a 是奇函数，∴对定义域内的x 值，有f (0)＝0， 由此可得a ＝－1，∴f (x )＝lg 1＋x1－x， 根据对数函数单调性，由f (x )＜0，得0＜1＋x1－x ＜1，∴x ∈(－1,0)．答案：A4．已知a ，b ＞0，且a ≠1，b ≠1.若log a b ＞1，则( ) A ．(a －1)(b －1)＜0 B ．(a －1)(a －b )＞0 C ．(b －1)(b －a )＜0D ．(b －1)(b －a )＞0解析：根据题意，log a b ＞1⇔log a b －log a a ＞0⇔log a ba＞0⇔⎩⎪⎨⎪⎧ 0＜a ＜10＜ba ＜1或⎩⎪⎨⎪⎧a ＞1b a＞1，即⎩⎪⎨⎪⎧ 0＜a ＜10＜b ＜a 或⎝ ⎛ a ＞1b ＞a .当⎩⎪⎨⎪⎧0＜a ＜10＜b ＜a 时，0＜b ＜a ＜1，∴b －1＜0，b －a ＜0；当⎩⎪⎨⎪⎧a ＞1b ＞a 时，b ＞a ＞1，∴b －1＞0，b －a ＞0. ∴(b －1)(b －a )＞0.故选D. 答案：D5．已知函数f (x )是定义在(－∞，＋∞)上的奇函数，若对于任意的实数x ≥0，都有f (x ＋2)＝f (x )，且当x ∈[0,2)时，f (x )＝log 2(x ＋1)，则f (2 014)＋f (－2 015)＋f (2 016)的值为( ) A ．－1 B ．－2 C ．2D ．1解析：∵当x ≥0时，f (x ＋2)＝f (x )，∴f (2 014)＝f (2 016)＝f (0)＝log 21＝0，∵f (x )为R 上的奇函数，∴f (－2 015)＝－f (2 015)＝－f (1)＝－1.∴f (2 014)＋f (－2 015)＋f (2 016)＝0－1＋0＝－1.故选A. 答案：A6．设函数f (x )＝ln(1＋x )－ln(1－x )，则f (x )是( ) A ．奇函数，且在(0,1)上是增函数 B ．奇函数，且在(0,1)上是减函数 C ．偶函数，且在(0,1)上是增函数 D ．偶函数，且在(0,1)上是减函数解析：由题意可得，函数f (x )的定义域为(－1,1)，且f (x )＝ln1＋x 1－x ＝ln ⎝⎛⎭⎫21－x －1，易知y ＝21－x－1在(0,1)上为增函数，故f (x )在(0,1)上为增函数，又f (－x )＝ln(1－x )－ln(1＋x )＝－f (x )，故f (x )为奇函数，选A. 答案：A7．已知f (x )是偶函数，且在[0，＋∞)上是减函数，若f (lg x )＞f (2)，则x 的取值范围是( ) A.⎝⎛⎭⎫1100，1 B.⎝⎛⎭⎫0，1100∪(1，＋∞) C.⎝⎛⎭⎫1100，100 D ．(0,1)∪(100，＋∞)解析：不等式可化为⎩⎪⎨⎪⎧ lg x ≥0lg x ＜2或⎩⎪⎨⎪⎧lg x ＜0－lg x ＜2，解得1≤x ＜100或1100＜x ＜1.∴1100＜x ＜100.故选C. 答案：C8．已知函数f (x )＝|log 12x |，若m <n ，有f (m )＝f (n )，则m ＋3n 的取值范围是( )A ．[23，＋∞)B ．(23，＋∞)C ．[4，＋∞)D ．(4，＋∞)解析：由f (x )＝|log 12x |，m <n ，f (m )＝f (n )可知，log 12m ＝－log 12n >0，从而0<m ＝1n<1，m ＋3n ＝m ＋3m (0<m <1)，若直接利用基本不等式，则m ＋3m ≥23(当且仅当m ＝3m ＝3时取得最小值，但这与0<m <1矛盾)，利用函数g (x )＝x ＋3x 的单调性(定义或导数)判断当0<x <1时g (x )单调递减，故g (x )>g (1)＝4，可知选D. 答案：D9．已知函数y ＝f (x )(x ∈D )，若存在常数c ，对于∀x 1∈D ，存在唯一x 2∈D ，使得f (x 1)＋f (x 2)2＝c ，则称函数f (x )在D 上的均值为c .若f (x )＝lg x ，x ∈[10,100]，则函数f (x )在[10,100]上的均值为( ) A ．10 B.34 C.710D.32解析：因为f (x )＝lg x (10≤x ≤100)，则f (x 1)＋f (x 2)2＝lg x 1x 22等于常数c ，即x 1x 2为定值，又f (x )＝lg x (10≤x ≤100)是增函数，所以取x 1＝10时，必有x 2＝100，从而c 为定值32.选D.答案：D10．已知函数f (x )＝(e x －e －x )x ，f (log 5x )＋f (log 15x )≤2f (1)，则x 的取值范围是( )A.⎣⎡⎦⎤15，1 B ．[1,5] C.⎣⎡⎦⎤15，5D.⎝⎛⎦⎤－∞，15∪[5，＋∞) 解析：∵f (x )＝(e x －e －x )x ，∴f (－x )＝－x (e －x －e x )＝(e x －e －x )x ＝f (x )(x ∈R)，∴函数f (x )是偶函数．∵f ′(x )＝(e x －e －x )＋x (e x ＋e －x )>0在(0，＋∞)上恒成立．∴函数f (x )在(0，＋∞)上单调递增．∵f (log 5x )＋f (log 15x )≤2f (1)，∴2f (log 5x )≤2f (1)，即f (log 5x )≤f (1)， ∴|log 5x |≤1，∴15≤x ≤5.故选C.答案：C11．设方程log 2x －⎝⎛⎭⎫12x＝0与log 14x －⎝⎛⎭⎫14x ＝0的根分别为x 1，x 2，则( ) A ．0＜x 1x 2＜1 B ．x 1x 2＝1 C ．1＜x 1x 2＜2D ．x 1x 2≥2解析：方程log 2x －⎝⎛⎭⎫12x＝0与log 14x －⎝⎛⎭⎫14x ＝0的根分别为x 1，x 2，所以log 2x 1＝⎝⎛⎭⎫12x 1，log 14x 2＝⎝⎛⎭⎫14x 2，可得x 2＝12，令f (x )＝log 2x －⎝⎛⎭⎫12x ，则f (2)f (1)＜0，所以1＜x 1＜2，所以12＜x 1x 2＜1，即0＜x 1x 2＜1.故选A. 答案：A12．(2017·江西红色七校模拟)已知函数f (x )＝ln e x e －x，若f ⎝⎛⎭⎫e 2 013＋f ⎝⎛⎭⎫2e 2 013＋…＋f ⎝⎛⎭⎫2 012e 2 013＝503(a ＋b )，则a 2＋b 2的最小值为( ) A ．6 B ．8 C ．9D ．12解析：∵f (x )＋f (e －x )＝ln e x e －x ＋ln e (e －x )x ＝ln e 2＝2，∴503(a ＋b )＝f ⎝⎛⎭⎫e 2 013＋f ⎝⎛⎭⎫2e 2 013＋…＋f ⎝⎛⎭⎫2 012e 2 013＝12⎣⎡f ⎝⎛⎭⎫e 2 013＋f ⎝⎛⎭⎫2 012e 2 013＋f ⎝⎛⎭⎫2e 2 013＋f ⎝⎛⎭⎫2 011e 2 013＋…＋f ⎝⎛⎭⎫2 012e 2 013＋f⎦⎤⎝⎛⎭⎫e 2 013＝12×(2×2 012)＝2 012， ∴a ＋b ＝4，∴a 2＋b 2≥(a ＋b )22＝422＝8，当且仅当a ＝b ＝2时取等号．∴a 2＋b 2的最小值为8. 答案：B13．若函数f (x )＝⎩⎪⎨⎪⎧log a x ， x ＞2，－x 2＋2x －2， x ≤2(a ＞0，且a ≠1)的值域是(－∞，－1]，则实数a 的取值范围是________． 解析：x ≤2时，f (x )＝－x 2＋2x －2＝－(x －1)2－1， f (x )在(－∞，1)上递增，在(1,2]上递减，∴f (x )在(－∞，2]上的最大值是－1，又f (x )的值域是(－∞，－1]，∴当x ＞2时， log a x ≤－1，故0＜a ＜1，且log a 2≤－1， ∴12≤a ＜1. 答案：⎣⎡⎭⎫12，114．(2018·湘潭模拟)已知函数f (x )＝ln x 1－x ，若f (a )＋f (b )＝0，且0<a <b <1，则ab 的取值范围是________．解析：由题意可知ln a 1－a ＋ln b1－b＝0，即ln ⎝⎛⎭⎫a 1－a ×b 1－b ＝0，从而a 1－a ×b1－b ＝1，化简得a ＋b ＝1，故ab ＝a (1－a )＝－a 2＋a ＝－⎝⎛⎭⎫a －122＋14，又0<a <b <1，∴0<a <12，故0<－⎝⎛⎭⎫a －122＋14<14. 答案：⎝⎛⎭⎫0，14 15．已知函数f (x )＝log a (8－ax )(a ＞0，且a ≠1)，若f (x )＞1在区间[1,2]上恒成立，则实数a 的取值范围为________．解析：当a ＞1时，f (x )＝log a (8－ax )在[1,2]上是减函数，由于f (x )＞1恒成立，所以f (x )min ＝log a (8－2a )＞1，故1＜a ＜83.当0＜a ＜1时，f (x )＝log a (8－ax )在[1,2]上是增函数， 由于f (x )＞1恒成立， 所以f (x )min ＝log a (8－a )＞1， 且8－2a ＞0，∴a ＞4，且a ＜4， 故这样的a 不存在． ∴1<a <83.答案：⎝⎛⎭⎫1，83 16．若函数f (x )＝log a (x 2－ax ＋5)(a ＞0，且a ≠1)满足对任意的x 1，x 2，当x 1＜x 2≤a2时，f (x 2)－f (x 1)＜0，则实数a 的取值范围为________．解析：当x 1＜x 2≤a 2时，f (x 2)－f (x 1)＜0，即函数在区间(－∞，a2]上为减函数，设g (x )＝x 2－ax＋5，则⎩⎪⎨⎪⎧a ＞1g ⎝⎛⎭⎫a 2＞0，解得1＜a ＜2 5.答案：(1,25)。
新人教版高中数学选择性必修一课件：8.1.1变量的相关关系
sy
sx
( xi x) 上
说明成对样本数据的两个分量之间满足一种线性关系
新人教A版高中数学精品教学课件
由此可见，样本相关系数r的取值范围为[-1，1].样本相关系数
r的绝对值大小可以反映成对数据之间线性相关的程度。
问题5：样本相关系数r的取值与成对样本数据的相关程度
有什么内在联系？
答 当|r|越接近1时，成对数据的线性相关程度越强;
也呈现减少的趋势
线性相关：两个变量呈正相关或负相关，且散点图落在一条直线附近
新人教A版高中数学精品教学课件
40
35
脂肪含量%
30
25
20
15
10
5
0
0
10
20
30
40
50
结论：脂肪含量与年龄成线性正相关关系
60
70
年龄/岁
练习.下列四个散点图中，变量x与y之间具有负的线性相关关系的是（ D ）
新人教A版高中数学精品教学课件
新人教A版高中数学精品教学课件
解：先画出散点图,可以看出样本点都集中在一条直线附近，
由此推断脂肪含量和年龄线性相关。
∴ ≈
19403.2 − 14 × 48.07 × 27.26
34181 − 14 ×
48.072
× 11051.77 − 14 ×
27.262
≈ 0.97
类似于平面或空间向量的坐标表示，对于向量
a (a1 , a2 ,, an )
b (b1 , b2 ,, bn )
我们有 a b a1b1 a2b2 anbn
设“标准化”处理后的成对数据 ( x , y ), ( x2 , y2 ),, ( xn , yn )
2018-2019学年高中新创新一轮复习文数江苏专版讲义：第十章+算法、复数、推理与证明+Word版含答案
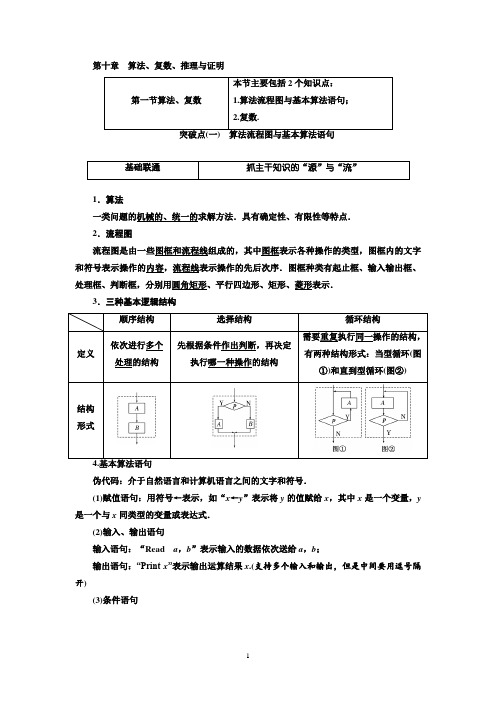
第十章算法、复数、推理与证明第一节算法、复数本节主要包括2个知识点：1.算法流程图与基本算法语句；2.复数.基础联通抓主干知识的“源”与“流”1．算法一类问题的机械的、统一的求解方法．具有确定性、有限性等特点．2．流程图流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框内的文字和符号表示操作的内容，流程线表示操作的先后次序．图框种类有起止框、输入输出框、处理框、判断框，分别用圆角矩形、平行四边形、矩形、菱形表示．3．三种基本逻辑结构顺序结构选择结构循环结构定义依次进行多个处理的结构先根据条件作出判断，再决定执行哪一种操作的结构需要重复执行同一操作的结构，有两种结构形式：当型循环(图①)和直到型循环(图②)结构形式伪代码：介于自然语言和计算机语言之间的文字和符号．(1)赋值语句：用符号←表示，如“x←y”表示将y的值赋给x，其中x是一个变量，y 是一个与x同类型的变量或表达式．(2)输入、输出语句输入语句：“Read a，b”表示输入的数据依次送给a，b；输出语句：“Print x”表示输出运算结果x.(支持多个输入和输出，但是中间要用逗号隔开)(3)条件语句(4)循环语句对应当型循环对应直到型循环考点贯通抓高考命题的“形”与“神”顺序结构和选择结构 路较多，容易出现错误．解决此类问题，可按下列步骤进行：第一步：弄清变量的初始值；第二步：按照流程图从上到下或从左到右的顺序，依次对每一个语句、每一个判断框进行读取，在读取判断框时，应注意判断后的结论分别对应着什么样的结果，然后按照对应的结果继续往下读取；第三步：输出结果．[例1] (1)定义运算a ⊗b 为执行如图所示的算法流程图输出的S 值，则⎝⎛⎭⎫2cos 5π3⊗⎝⎛⎭⎫2tan 5π4的值为________．(2)(2017·江苏高考)如图是一个算法流程图．若输入x 的值为116，则输出y 的值是________．[解析] (1)由算法流程图可知，S ＝⎩⎪⎨⎪⎧a (a －b )，a ≥b ，b (a ＋1)，a ＜b ，因为2cos 5π3＝1,2tan 5π4＝2,1＜2，所以⎝⎛⎭⎫2cos 5π3⊗⎝⎛⎭⎫2tan 5π4＝2×(1＋1)＝4. (2)由流程图可知其功能是运算分段函数y ＝⎩⎪⎨⎪⎧2x ，x ≥1，2＋log 2x ，0＜x ＜1，所以当输入的x 的值为116时，y ＝2＋log 2116＝2－4＝－2.[答案] (1)4 (2) －2 [方法技巧]顺序结构和选择结构的运算方法(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可．(2)选择结构中条件的判断关键是明确选择结构的功能，然后根据“Y ”的分支成立的条件进行判断．(3)对选择结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．循环结构考法(一) 由流程图求输出结果[例2] (1)如图所示，算法流程图的输出结果是________．(2)(2018·苏州高三暑假测试)运行如图所示的流程图，则输出的结果S 是________．[解析] (1)第一次循环：n ＝2＜8，S ＝12，n ＝4；第二次循环：n ＝4＜8，S ＝12＋14，n ＝6；第三次循环：n ＝6＜8，S ＝12＋14＋16，n ＝8;第四次循环：n ＝8＜8不成立，输出S ＝12＋14＋16＝1112.(2)S ＝2，i ＝1，进入循环，S ＝12，i ＝2，进入循环，S ＝－1，i ＝3，进入循环，S ＝2，i ＝4，进入循环，…，S ＝12，i ＝35，输出S .[答案] (1)1112 (2)12[方法技巧]循环结构流程图求输出结果的注意事项解决此类问题最常用的方法是列举法，即依次执行循环体中的每一步，直到循环终止，但在执行循环体的过程中：第一，要明确是当型循环结构还是直到型循环结构，根据各自特点执行循环体； 第二，要明确流程图中的累加变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；第三，要明确循环终止的条件是什么，什么时候要终止执行循环体．考法(二)完善流程图[例3](2018·苏州模拟)按如下算法流程图，若输出结果为273，则判断框内循环变量i 应补充的条件为________．[解析]由算法流程图可知：第一次循环，S＝0＋31＝3，i＝3；第二次循环，S＝3＋33＝30，i＝5；第三次循环，S＝30＋35＝273，i＝7.故判断框内可填i≥7.[答案]i≥7(答案不唯一也可以填i＝7)[方法技巧]解决算法流程图填充问题的思路(1)要明确算法流程图的顺序结构、选择结构和循环结构．(2)要识别、执行算法流程图，理解算法流程图所解决的实际问题．(3)按照题目的要求完成解答并验证．基本算法语句(2)执行如图所示的伪代码，输出的结果是________．(3)根据如图所示的伪代码，最后输出的S的值为________．[解析](1)第一次循环：x＝7，k＝1；第二次循环：x＝15，k＝2；第三次循环：x＝31，k＝3；终止循环，输出k的值是3.(2)根据循环结构可得，第一次：S＝1×3＝3，i＝3＋2＝5，由3≤200，则循环；第二次：S＝3×5＝15，i＝5＋2＝7，由15≤200，则循环；第三次：S＝15×7＝105，i＝7＋2＝9，由105≤200，则循环；第四次：S＝105×9＝945，i＝9＋2＝11，由945＞200，则循环结束，故此时i＝11.(3)这是一个1＋2＋3＋…＋10的求和，所以输出的S的值为55.[答案](1)3(2)11(3)55[方法技巧]解决伪代码问题的步骤及解题规律(1)解决伪代码问题有三个步骤：首先通读全部语句，把它翻译成数学问题；其次领悟该语句的功能；最后根据语句的功能运行程序，解决问题．(2)解题时应注意以下规律：①赋值语句在给出变量赋值时，先计算赋值号右边的式子，然后赋值给赋值号左边的变量；给一个变量多次赋值时，变量的取值只与最后一次赋值有关．②条件语句必须以If开始，以End If结束，一个If必须和一个End If对应，尤其对条件语句的嵌套问题，应注意每一层结构的完整性，不能漏掉End If.Else后面操作无内容，可以省略．③循环语句的格式要正确，要保证有结束循环的语句，切忌死循环．三种循环语句停止循环的条件不同，注意它们的区别．能力练通抓应用体验的“得”与“失”为________．解析：当满足条件⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1时，由线性规划的图解法(图略)知，目标函数S ＝2x ＋y的最大值为2；当不满足条件⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1时，S 的值为1.所以输出的S 的最大值为2.答案：22.[考点二·考法(一)]执行如图所示的算法流程图，输出的x 值为________．解析：执行算法流程图可知，x 的值依次为2,3,5,6,7,9,10,11,13，故输出的x 值为13. 答案：133.[考点二·考法(一)](2017·苏锡常镇二模)据记载，在公元前3世纪，阿基米德已经得出了前n 个自然数平方和的一般公式．如图是一个求前n 个自然数平方和的算法流程图，若输入x 的值为1，则输出S 的值为________．解析：模拟执行程序，可得，输入x 的值为1，S ＝1，不满足条件S ＞5，x ＝2，S ＝5；不满足条件S ＞5，x ＝3，S ＝14；满足条件S ＞5，退出循环，输出S 的值为14.答案：144.[考点二·考法(二)](2018·太原模拟)执行如图所示的算法流程图，若输出的S ＝2524，则判断框内填入的条件可以是________．解析：由算法流程图可知，k ＝2，S ＝0＋12＝12，满足循环条件；k ＝4，S ＝12＋14＝34，满足循环条件；k ＝6，S ＝34＋16＝2224，满足循环条件；k ＝8，S ＝2224＋18＝2524，符合题目条件，结束循环，故可填k ＜8(或k ≤7)．答案：k ＜8(k ≤7亦可)5.[考点三]运行如图所示的伪代码，若输入a ，b 分别为3,4，则输出m ＝________.解析：由已知中的伪代码，可知其功能是计算并输出分段函数m ＝⎩⎪⎨⎪⎧a ，a ＞b ，b ，a ≤b 的值．当a ＝3，b ＝4时，满足a ≤b .故m ＝b ＝4.答案：4突破点(二) 复 数基础联通抓主干知识的“源”与“流”(1)复数的定义：形如a ＋b i(a ，b ∈R)的数叫做复数，其中实部是a ，虚部是b . (2)复数的分类：复数z ＝a ＋b i(a ，b ∈R )⎩⎨⎧实数(b ＝0)，虚数(b ≠0)⎩⎪⎨⎪⎧纯虚数(a ＝0，b ≠0)，非纯虚数(a ≠0，b ≠0).2．复数的有关概念 复数相等a ＋b i ＝c ＋d i ⇔a ＝c 且b ＝d (a ，b ，c ，d ∈R)共轭复数 a ＋b i 与c ＋d i 共轭⇔a ＝c 且b ＝－d (a ，b ，c ，d ∈R)复数的模向量OZ ―→的模叫做复数z ＝a ＋b i 的模，记作|z |或|a ＋b i|，即|z |＝|a ＋b i|＝r ＝a 2＋b 2(r ≥0，a ，b ∈R)复平面的概念 建立直角坐标系来表示复数的平面叫做复平面实轴、虚轴 在复平面内，x 轴叫做实轴，y 轴叫做虚轴，实轴上的点都表示实数；除原点以外，虚轴上的点都表示纯虚数复数的几何表示 复数z ＝a ＋b i 一一对应复平面内的点Z (a ，b )一一对应平面向量OZ ―→4．复数的运算法则设z 1＝a ＋b i ，z 2＝c ＋d i(a ，b ，c ，d ∈R)，则： (1)z 1＋z 2＝(a ＋b i)＋(c ＋d i)＝(a ＋c )＋(b ＋d )i ； (2)z 1－z 2＝(a ＋b i)－(c ＋d i)＝(a －c )＋(b －d )i ； (3)z 1·z 2＝(a ＋b i)(c ＋d i)＝(ac －bd )＋(ad ＋bc )i ；(4)z 1z 2＝a ＋b i c ＋d i ＝(a ＋b i )(c －d i )(c ＋d i )(c －d i )＝ac ＋bd c 2＋d 2＋bc －ad c 2＋d 2i(c ＋d i ≠0). 考点贯通抓高考命题的“形”与“神”复数的有关概念[例1] (1)设i 是虚数单位，若复数z ＝a －103－i(a ∈R)是纯虚数，则a 的值为________． (2)(2018·无锡期末)已知复数z ＝21－i，其中i 为虚数单位，则复数z 的共轭复数为________．(3)若复数 z 满足z (1＋i)＝2i(i 为虚数单位)，则|z |＝________. [解析] (1)∵z ＝a －103－i ＝a －10(3＋i )(3－i )(3＋i )＝(a －3)－i 为纯虚数，∴a －3＝0，即a ＝3. (2)因为复数z ＝21－i ＝2(1＋i )(1－i )(1＋i )＝1＋i ，所以复数z 的共轭复数z ＝1－i. (3)法一：设z ＝a ＋b i(a ，b ∈R)，则由z (1＋i)＝2i ，得(a ＋b i)·(1＋i)＝2i ，所以(a －b )＋(a ＋b )i ＝2i ，由复数相等的条件得⎩⎪⎨⎪⎧a －b ＝0，a ＋b ＝2，解得a ＝b ＝1，所以z ＝1＋i ，故|z |＝12＋12＝ 2.法二：由z (1＋i)＝2i ，得z ＝2i 1＋i＝2i (1－i )2＝i －i 2＝1＋i ，所以|z |＝12＋12＝ 2.[答案] (1)3 (2)1－i (3) 2 [方法技巧]求解与复数概念相关问题的技巧复数的分类、复数的相等、复数的模及共轭复数的概念都与复数的实部、虚部有关，所以解答与复数相关概念有关的问题时，需把所给复数化为代数形式，即a ＋b i(a ，b ∈R)的形式，再根据题意求解．复数的几何意义[例2] (1)(2018·徐州调研)复数z ＝3＋i1＋i＋3i 在复平面内对应的点在第________象限． (2)(2017·北京高考改编)若复数(1－i)(a ＋i)在复平面内对应的点在第二象限，则实数a 的取值范围是________．[解析] (1)z ＝3＋i 1＋i ＋3i ＝(3＋i )(1－i )(1＋i )(1－i )＋3i ＝4－2i2＋3i ＝2－i ＋3i ＝2＋2i ，故z 在复平面内对应的点在第一象限．(2)因为z ＝(1－i)(a ＋i)＝a ＋1＋(1－a )i ， 所以它在复平面内对应的点为(a ＋1,1－a )，又此点在第二象限，所以⎩⎪⎨⎪⎧a ＋1＜0，1－a ＞0，解得a ＜－1.[答案] (1)一 (2)(－∞，－1)复数的运算1.(实部与实部相加减，虚部与虚部相加减)计算即可．2．在进行复数的乘法运算时：(1)复数的乘法类似于两个多项式相乘，即把虚数单位i 看作字母，然后按多项式的乘法法则进行运算，最后只要在所得的结果中把i 2换成－1，并且把实部和虚部分别结合即可，但要注意把i 的幂写成简单的形式；(2)实数范围内的运算法则在复数范围内仍然适用，如交换律、结合律以及乘法对加法的分配律、正整数指数幂的运算律，这些对复数仍然成立．3．在进行复数的除法运算时，关键是分母“实数化”，其一般步骤如下： (1)分子、分母同时乘分母的共轭复数； (2)对分子、分母分别进行乘法运算；(3)整理、化简成实部、虚部分开的标准形式．[例3] (1)(2018·镇江模拟)已知z ＝2＋i1－2i(i 为虚数单位)，则复数z ＝________. (2)(2018·长沙模拟)已知(a ＋b i)(1－2i)＝5(i 为虚数单位，a ，b ∈R)，则a ＋b 的值为________．(3)若复数z 满足z－1－i ＝i ，其中i 为虚数单位，则z ＝________.[解析] (1)由题意得2＋i 1－2i ＝(2＋i )(1＋2i )(1－2i )(1＋2i )＝2＋4i ＋i ＋2i 25＝i.(2)因为(a ＋b i)(1－2i)＝a ＋2b ＋(b －2a )i ＝5，故⎩⎪⎨⎪⎧a ＋2b ＝5，b －2a ＝0，解得a ＝1，b ＝2，故a ＋b ＝3.(3)由已知得z －＝i(1－i)＝1＋i ，则z ＝1－i. [答案] (1)i (2)3 (3)1－i [易错提醒]在乘法运算中要注意i 的幂的性质：(1)区分(a ＋b i)2＝a 2＋2ab i －b 2(a ，b ∈R)与(a ＋b )2＝a 2＋2ab ＋b 2(a ，b ∈R); (2)区分(a ＋b i)(a －b i)＝a 2＋b 2(a ，b ∈R)与(a ＋b )(a －b )＝a 2－b 2(a ，b ∈R)．1.[考点三]若z ＝1＋2i ，则4iz z －－1＝________. 解析：因为z ＝1＋2i ，则z －＝1－2i ，所以z z －＝(1＋2i)·(1－2i)＝5，则4i z z －－1＝4i 4＝i.答案：i2.[考点三](2018·武汉模拟)已知(1＋2i)z －＝4＋3i(其中i 是虚数单位，z －是z 的共轭复数)，则z 的虚部为________．解析：因为z －＝4＋3i 1＋2i ＝(4＋3i )(1－2i )(1＋2i )(1－2i )＝10－5i 5＝2－i ，所以z ＝2＋i ，则其虚部为1.答案：13.[考点二]已知z ＝(m ＋3)＋(m －1)i 在复平面内对应的点在第四象限，则实数m 的取值范围是________．解析：由题意知⎩⎪⎨⎪⎧m ＋3＞0，m －1＜0，即－3＜m ＜1.故实数m 的取值范围为(－3,1)．4.[考点一]若复数z ＝a 2－1＋(a ＋1)i(a ∈R)是纯虚数，则1z ＋a的虚部为________．解析：由题意得⎩⎪⎨⎪⎧a 2－1＝0，a ＋1≠0，所以a ＝1，则z ＝2i ，所以1z ＋a ＝11＋2i ＝1－2i (1＋2i )(1－2i )＝15－25i ，根据虚部的概念，可得1z ＋a的虚部为－25. 答案：－255.[考点二]如图，若向量OZ ―→对应的复数为z ，则z ＋4z 表示的复数为________．解析：由题图可得Z (1，－1)，即z ＝1－i ，所以z ＋4z ＝1－i ＋41－i ＝1－i ＋4(1＋i )(1－i )(1＋i )＝1－i ＋4＋4i2＝1－i ＋2＋2i ＝3＋i.答案：3＋i6.[考点一]设复数a ＋b i(a ，b ∈R)的模为3，则(a ＋b i)·(a －b i)＝________. 解析：∵|a ＋b i|＝a 2＋b 2＝3，∴(a ＋b i)(a －b i)＝a 2＋b 2＝3. 答案：37.[考点三]已知复数z ＝3＋i (1－3i )2，z －是z 的共轭复数，则z ·z ＝________.解析：∵z ＝3＋i (1－3i )2＝3＋i －2－23i ＝3＋i －2(1＋3i )＝(3＋i )(1－3i )－2(1＋3i )(1－3i )＝23－2i－8＝－34＋14i ， ∴z ＝－34－14i ， ∴z ·z ＝⎝⎛⎭⎫－34＋14i ⎝⎛⎭⎫－34－14i ＝316＋116＝14. 答案：148.[考点三]已知i 是虚数单位，⎝ ⎛⎭⎪⎫21－i 2 018＋⎝ ⎛⎭⎪⎫1＋i 1－i 6＝________.解析：原式＝⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫21－i 2 1 009＋⎝ ⎛⎭⎪⎫1＋i 1－i 6＝⎝⎛⎭⎫2－2i 1 009＋i 6＝i 1 009＋i 6＝i 4×252＋1＋i 4＋2＝i ＋i 2＝－1＋i.[课时达标检测] 基础送分课时——精练“14小题”，求准求快不深挖1.(2018·南京市高三年级学情调研)如图所示的算法流程图，若输出y 的值为12，则输入x 的值为________．解析：此算法程序表示一个分段函数y ＝⎩⎪⎨⎪⎧2x ，x ≥0，log 2(－x )，x ＜0， 由f (x )＝12得x ＝－ 2.答案：－ 22．(2018·常州模拟)设复数z 满足(z ＋i)(2＋i)＝5(i 为虚数单位)，则z ＝________. 解析：由(z ＋i)(2＋i)＝5，得z ＋i ＝52＋i，即z ＋i ＝2－i ，所以z ＝2－2i. 答案： 2－2i3．(2018·徐州模拟)已知复数z 满足z 2＝－4，若z 的虚部大于0，则z ＝________. 解析：由z 2＝－4得z ＝±2i ，而z 的虚部大于0，所以z ＝2i. 答案：2i4．(2018·连云港模拟)运行如图所示的伪代码，则输出的结果S 为________．解析：本题的算法功能是在累加变量S 初值为1的基础上连续加2四次，所以S ＝9. 答案：95．(2018·扬州调研)如图给出的是计算12＋14＋16＋18＋…＋1100的一个算法流程图，其中判断框内应填入的条件是________．解析：因为该循环体需要运行50次，i的初始值是1，间隔是1，所以i＝50时不满足判断框内的条件，而i＝51时满足判断框内条件，所以判断框内的条件可以填入i＞50(或i≥51)．答案：i＞50(i≥51亦可)6．(2018·宿迁期中)若复数z＝1＋2i3－i(i为虚数单位)，则z的模为________．解析：由z＝1＋2i3－i两边同时取模得|z|＝|1＋2i||3－i|＝510＝22.答案：2 27．(2018·盐城模拟)若复数z＝(1＋m i)(2－i)(i是虚数单位)是纯虚数，则实数m的值为________．解析：因为z＝(1＋m i)(2－i)＝2＋m＋(2m－1)i是纯虚数，所以2＋m＝0，所以m＝－2.答案：－28．设(1＋i)x＝1＋y i，其中x，y是实数，则|x＋y i|＝________.解析：∵(1＋i)x＝1＋y i，∴x＋x i＝1＋y i.又∵x，y∈R，∴x＝1，y＝1.∴|x＋y i|＝|1＋i|＝ 2.答案： 29．(2016·江苏高考)如图是一个算法的流程图，则输出的a的值是________．解析：由a ＝1，b ＝9，知a ＜b ， 所以a ＝1＋4＝5，b ＝9－2＝7，a ＜b . 所以a ＝5＋4＝9，b ＝7－2＝5，满足a ＞b . 所以输出的a ＝9. 答案：910．(2018·南通期中)在如图所示的算法流程图中，若输出的y 的值为26，则输入的x 的值为________．解析：本题算法功能是求分段函数y ＝⎩⎪⎨⎪⎧x 2－2x ＋2，x ＜4，5，x ≥4的函数值，因为输出值为26，所以⎩⎪⎨⎪⎧x 2－2x ＋2＝26，x ＜4，解得x ＝－4.答案：－411．(2017·镇江期中)根据如图所示的伪代码，若输出的y 值为2，则输入的x 值为________．解析：本题算法功能是利用条件语句求分段函数y ＝⎩⎪⎨⎪⎧x ＋1，x ＞0，1－x ，x ≤0的函数值．因为输出的y 值为2，所以⎩⎪⎨⎪⎧ x ＋1＝2，x ＞0或⎩⎪⎨⎪⎧1－x ＝2，x ≤0，所以x ＝±1.答案：±112．(2018·泰州中学高三年级学情调研)根据如图的伪代码，输出的结果T 为________．解析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出满足条件的T ＝1＋3＋5＋7＋...＋19的值，因为T ＝1＋3＋5＋7＋ (19)(1＋19)×102＝100，故输出的T 值为100. 答案：10013．(2018·淮安期中)根据如图所示的伪代码，则输出的S 的值为________．解析：本题算法功能是求积，S ＝1×2×5×8×11＝880. 答案：88014．(2018·苏州模拟)执行如图所示的算法流程图，输出的x 值为________．解析：a ＝2，x ＝4，此时y ＝16，判断不满足条件，循环；x ＝5，所以y ＝32，判断不满足条件，再循环；x ＝6，所以y ＝64，再判断满足条件，结束循环，所以此时x ＝6.答案：6第二节合情推理与演绎推理本节主要包括2个知识点：1.合情推理；2.演绎推理.基础联通抓主干知识的“源”与“流”类型定义特点归纳推理从个别事实中推演出一般性的结论的推理由部分到整体、由个别到一般类比推理由两类对象具有某些类似特征和其中一类对象的某些已知特征，推演出另一类对象也具有这些特征的推理由特殊到特殊考点贯通抓高考命题的“形”与“神”归纳推理(1)通过观察特例发现某些相似性(特例的共性或一般规律)；(2)把这种相似性推广到一个明确表述的一般命题(猜想)；(3)对所得出的一般性命题进行检验．类型(一)与数字有关的推理[例1]给出以下数对序列：(1,1)(1,2)(2,1)(1,3)(2,2)(3,1)(1,4)(2,3)(3,2)(4,1)……记第i行的第j个数对为a ij，如a43＝(3,2)，则a n m＝________.[解析]由前4行的特点，归纳可得：若a n m＝(a，b)，则a＝m，b＝n－m＋1，∴a n m ＝(m，n－m＋1)．[答案](m，n－m＋1)[易错提醒]解决此类问题时，需要细心观察，寻求相邻项及项与序号之间的关系，同时还要联系相关的知识，如等差数列、等比数列等．类型(二)与式子有关的推理[例2](2018·常熟中学模拟)已知cos π3＝12，cosπ5cos2π5＝14，cosπ7cos2π7cos3π7＝18，….(1)根据以上等式，可猜想出的一般结论是________；(2)若数列{a n}中，a1＝cosπ3，a2＝cosπ5cos2π5，a3＝cosπ7cos2π7cos3π7，…的前n项和S n＝1 0231 024，则n＝________.[解析](1)从题中所给的几个等式可知，第n个等式的左边应有n个余弦相乘，且分母均为2n＋1，分子分别为π，2π，…，nπ，右边应为12n，故可以猜想出结论为cosπ2n＋1·cos 2π2n＋1·…·cosnπ2n＋1＝12n(n∈N*)．(2)由(1)可知a n＝12n，故S n＝12⎣⎡⎦⎤1－⎝⎛⎭⎫12n1－12＝1－12n＝2n－12n＝1 0231 024，解得n＝10.[答案](1)cosπ2n＋1cos2π2n＋1·…·cosnπ2n＋1＝12n(n∈N*)(2)10[方法技巧]与式子有关的推理类型及解法(1)与等式有关的推理．观察每个等式的特点，找出等式左右两侧的规律及符号后可解．(2)与不等式有关的推理．观察每个不等式的特点，注意是纵向看，找到规律后可解．类型(三)与图形有关的推理[例3]某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为1,1,2,3,5，则预计第10年树的分枝数为________．[解析]因为2＝1＋1,3＝2＋1,5＝3＋2，即从第三项起每一项都等于前两项的和，所以第10年树的分枝数为21＋34＝55.[答案]55[方法技巧]与图形有关的推理的解法与图形变化相关的归纳推理，解决的关键是抓住相邻图形之间的关系，合理利用特殊图形，找到其中的变化规律，得出结论，可用赋值检验法验证其真伪性．类比推理1类比定义在求解由某种熟悉的定义产生的类比推理型试题时，可以借助原定义来求解类比性质从一个特殊式子的性质、一个特殊图形的性质入手，提出类比推理型问题，求解时要认真分析两者之间的联系与区别，深入思考两者的转化过程是求解的关键类比方法有一些处理问题的方法具有类比性，我们可以把这种方法类比应用到其他问题的求解中，注意知识的迁移2．平面中常见的元素与空间中元素的类比：平面点线圆三角形角面积周长…空间线面球三棱锥二面角体积表面积…[例4]如图，在梯形ABCD中，AB∥CD，AB＝a，CD＝b(a＞b)．若EF∥AB，EF到CD与AB的距离之比为m∶n，则可推算出：EF＝ma＋nbm＋n.用类比的方法，推想出下面问题的结果．在上面的梯形ABCD中，分别延长梯形的两腰AD和BC交于O点，设△OAB，△ODC的面积分别为S1，S2，则△OEF的面积S0与S1，S2的关系是________．[解析]在平面几何中类比几何性质时，一般是由平面几何中点的性质类比推理线的性质；由平面几何中线段的性质类比推理面积的性质．故由EF＝ma＋nbm＋n类比到关于△OEF的面积S0与S1，S2的关系是S0＝m S1＋n S2m＋n.[答案]S0＝m S1＋n S2m＋n[方法技巧]类比推理的步骤和方法(1)类比推理是由特殊到特殊的推理，其一般步骤为：①找出两类事物之间的相似性或一致性；②用一类事物的性质去推测另一类事物的性质，得出一个明确的命题(猜想)．(2)类比推理的关键是找到合适的类比对象．平面几何中的一些定理、公式、结论等，可以类比到立体几何中，得到类似的结论．1.[考点二]由代数式的乘法法则类比推导向量的数量积的运算法则： ①“mn ＝nm ”类比得到“a·b ＝b·a ”；②“(m ＋n )t ＝mt ＋nt ”类比得到“(a ＋b )·c ＝a·c ＋b·c ”； ③“(m ·n )t ＝m (n ·t )”类比得到“(a·b )·c ＝a·(b·c )”；④“t ≠0，mt ＝xt ⇒m ＝x ”类比得到“p ≠0，a·p ＝x·p ⇒a ＝x ”； ⑤“|m ·n |＝|m |·|n |”类比得到“|a·b|＝|a|·|b|”； ⑥“ac bc ＝a b ”类比得到“a·c b·c ＝ab”．以上的式子中，类比得到的结论中正确的序号是________． 答案：①②2.[考点二]在平面几何中有如下结论：正三角形ABC 的内切圆面积为S 1，外接圆面积为S 2，则S 1S 2＝14，推广到空间可以得到类似结论：已知正四面体P -ABC 的内切球体积为V 1，外接球体积为V 2，则V 1V 2＝________. 解析：正四面体的内切球与外接球的半径之比为1∶3，故V 1V 2＝127.答案：1273．[考点一·类型(一)](2018·海门中学月考) 有一个奇数组成的数阵排列如下：则第30解析：先求第30行的第1个数，再求第30行的第3个数．观察每一行的第一个数，由归纳推理可得第30行的第1个数是1＋4＋6＋8＋10＋…＋60＝30×(2＋60)2－1＝929.又第n 行从左到右的第2个数比第1个数大2n ，第3个数比第2个数大2n ＋2，所以第30行从左到右的第2个数比第1个数大60，第3个数比第2个数大62，故第30行从左到右第3个数是929＋60＋62 ＝1 051.答案：1 0514．[考点一·类型(二)]设n 为正整数，f (n )＝1＋12＋13＋…＋1n ，计算得f (2)＝32，f (4)＞2，f (8)＞52，f (16)＞3，观察上述结果，可推测一般的结论为________．解析：∵f (21)＝32，f (22)＞2＝42，f (23)＞52，f (24)＞62，∴归纳得f (2n )≥n ＋22(n ∈N *)．答案：f (2n )≥n ＋22(n ∈N *)5．[考点一·类型(三)]蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，以f (n )表示第n 个图的蜂巢总数．则f (4)＝________，f (n )＝________.解析：因为f (1)＝1，f (2)＝7＝1＋6，f (3)＝19＝1＋6＋12，所以f (4)＝1＋6＋12＋18＝37，所以f (n )＝1＋6＋12＋18＋…＋6(n －1)＝3n 2－3n ＋1.答案：37 3n 2－3n ＋1突破点(二) 演绎推理基础联通抓主干知识的“源”与“流”定义：从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理．(2)模式：“三段论”是演绎推理的一般模式，包括： ①大前提——已知的一般性的原理； ②小前提——所研究的特殊对象；③结论——根据一般原理，对特殊对象做出的判断． (3)特点：演绎推理是由一般到特殊的推理．考点贯通抓高考命题的“形”与“神”演绎推理[典例] 数列{a n }的前n 项和记为S n ，已知a 1＝1，a n ＋1＝n ＋2n S n (n ∈N *)．证明：(1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列；(2)S n ＋1＝4a n .[证明] (1)∵a n ＋1＝S n ＋1－S n ，a n ＋1＝n ＋2n S n， ∴(n ＋2)S n ＝n (S n ＋1－S n )，即nS n ＋1＝2(n ＋1)S n . 故S n ＋1n ＋1＝2·S nn ，(小前提)故⎩⎨⎧⎭⎬⎫S n n 是以2为公比，1为首项的等比数列．(结论)(大前提是等比数列的定义)(2)由(1)可知数列⎩⎨⎧⎭⎬⎫S n n 是等比数列，(大前提)所以S n ＋1n ＋1＝4·S n －1n －1(n ≥2)，即S n ＋1＝4(n ＋1)·S n －1n －1＝4·n －1＋2n －1·S n －1＝4a n (n ≥2)．又a 2＝3S 1＝3，S 2＝a 1＋a 2＝1＋3＝4＝4a 1，(小前提) 所以对于任意正整数n ，都有S n ＋1＝4a n .(结论) [方法技巧]演绎推理的推证规则(1)演绎推理是从一般到特殊的推理，其一般形式是三段论，应用三段论解决问题时，应当首先明确什么是大前提和小前提，如果前提是显然的，则可以省略，本例中，等比数列的定义在解题中是大前提，由于它是显然的，因此省略不写．(2)在推理论证过程中，一些稍复杂一点的证明题常常要由几个三段论才能完成．(1)证明：函数y ＝f (x )的图象关于点⎝⎛⎭⎫12，－12对称； (2)求f (－2)＋f (－1)＋f (0)＋f (1)＋f (2)＋f (3)的值．解：(1)证明：函数f (x )的定义域为全体实数，任取一点(x ，y )，它关于点⎝⎛⎭⎫12，－12对称的点的坐标为(1－x ，－1－y )．(大前提)由已知y ＝－aa x ＋a，则－1－y ＝－1＋a a x ＋a ＝－a xa x ＋a，f (1－x )＝－a a 1－x ＋a ＝－a a a x ＋a＝－a ·a x a ＋a ·a x ＝－a xa x ＋a ，(小前提) ∴－1－y ＝f (1－x )，即函数y ＝f (x )的图象关于点⎝⎛⎭⎫12，－12对称．(结论) (2)由(1)知－1－f (x )＝f (1－x )， 即f (x )＋f (1－x )＝－1.∴f (－2)＋f (3)＝－1，f (－1)＋f (2)＝－1，f (0)＋f (1)＝－1. 故f (－2)＋f (－1)＋f (0)＋f (1)＋f (2)＋f (3)＝－3.2．已知函数y ＝f (x )满足：对任意a ，b ∈R ，a ≠b ，都有af (a )＋bf (b )＞af (b )＋bf (a )，试证明：f (x )为R 上的单调增函数．证明：设任意x 1，x 2∈R ，取x 1＜x 2， 则由题意得x 1f (x 1)＋x 2f (x 2)＞x 1f (x 2)＋x 2f (x 1)，所以x 1[f (x 1)－f (x 2)]＋x 2[f (x 2)－f (x 1)]＞0，[f (x 2)－f (x 1)](x 2－x 1)＞0， 因为x 1＜x 2， 即x 2－x 1＞0， 所以f (x 2)－f (x 1)＞0， 即f (x 2)＞f (x 1)．(小前提)所以y ＝f (x )为R 上的单调增函数．(结论)[练基础小题——强化运算能力]1．(1)已知a 是三角形一边的长，h 是该边上的高，则三角形的面积是12ah ，如果把扇形的弧长l ，半径r 分别看成三角形的底边长和高，可得到扇形的面积为12lr ；(2)由1＝12,1＋3＝22,1＋3＋5＝32，可得到1＋3＋5＋…＋2n －1＝n 2，则(1)(2)两个推理过程分别属于________推理．解析：(1)由三角形的性质得到扇形的性质有相似之处，此种推理为类比推理；(2)由特殊到一般，此种推理为归纳推理．答案：类比，归纳2．“因为指数函数y ＝a x 是增函数(大前提)，而y ＝⎝⎛⎭⎫13x是指数函数(小前提)，所以y ＝⎝⎛⎭⎫13x是增函数(结论)”，上面推理的错误在于________错而导致结论错．解析：y ＝a x 是增函数这个大前提是错误的，从而导致结论错误． 答案：大前提3．(2018·如东高级中学模拟)观察(x 2)′＝2x ，(x 4)′＝4x 3，(cos x )′＝－sin x ，由归纳推理得：若定义在R 上的函数f (x )满足f (－x )＝f (x )，记g (x )为f (x )的导函数，则g (－x )＝________.解析：由已知得函数的导函数为奇函数，故g (－x )＝－g (x )． 答案：－g (x )4．下面图形由小正方形组成，请观察图①至图④的规律，并依此规律，写出第n 个图形中小正方形的个数是________．解析：由题图知第1个图形的小正方形个数为1，第2个图形的小正方形个数为1＋2，第3个图形的小正方形个数为1＋2＋3，第4个图形的小正方形个数为1＋2＋3＋4，…，则第n 个图形的小正方形个数为1＋2＋3＋…＋n ＝n (n ＋1)2. 答案：n (n ＋1)25．在平面几何中：△ABC 中∠C 的角平分线CE 分AB 所成线段的比为 AC BC ＝AEBE .把这个结论类比到空间：在三棱锥A -BCD 中(如图)，DEC 平分二面角A -CD -B 且与AB 相交于E ，则得到类比的结论是_____________________．解析：由平面中线段的比转化为空间中面积的比可得AE EB ＝S △ACDS △BCD .答案：AE EB ＝S △ACDS △BCD[练常考题点——检验高考能力]一、填空题1．已知圆：x 2＋y 2＝r 2上任意一点(x 0，y 0)处的切线方程为x 0x ＋y 0y ＝r 2，类比以上结论有：双曲线：x 2a 2－y 2b2＝1上任意一点(x 0，y 0)处的切线方程为________________．解析：设圆上任一点为(x 0，y 0)，把圆的方程中的x 2，y 2替换为x 0x ，y 0y ，则得到圆的切线方程；类比这种方式，设双曲线x 2a 2－y 2b 2＝1上任一点为(x 0，y 0)，则有切线方程为x 0x a 2－y 0yb 2＝1.答案：x 0x a 2－y 0y b 2＝1 2．已知“整数对”按如下规律排成一列：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，…，则第60个“整数对”是________．解析：依题意，把“整数对”的和相同的分为一组，不难得知第n 组中每个“整数对”的和均为n ＋1，且第n 组共有n 个“整数对”，这样的前n 组一共有n (n ＋1)2个“整数对”，注意到10×(10＋1)2＜60＜11×(11＋1)2，因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置，结合题意可知每个“整数对”的和为12的组中的各对数依次为：(1,11)，(2,10)，(3,9)，(4,8)，(5,7)，…，因此第60个“整数对”是(5,7)．答案：(5,7)3．(2018·常州模拟)观察下列各式：55＝3 125,56＝15 625，57＝78 125,58＝390 625，59＝1 953 125，……，则52 019的末四位数字为________．解析：55＝3 125,56＝15 625,57＝78 125,58＝390 625，59＝1 953 125，……，可得59与55的后四位数字相同，由此可归纳出5m＋4k与5m (k ∈N *，m ＝5,6,7,8)的后四位数字相同，又2 019＝4×503＋7，所以52 019与57的后四位数字相同，为8 125.答案：8 1254．若数列{a n }是等差数列，则数列{b n }⎝⎛⎭⎫b n ＝a 1＋a 2＋…＋a n n 也为等差数列．类比这一性质可知，若正项数列{c n }是等比数列，且{d n }也是等比数列，则d n 的表达式应为________．解析：若{a n }是等差数列，则a 1＋a 2＋…＋a n ＝na 1＋n (n －1)2d ，∴b n ＝a 1＋(n －1)2d ＝d2n＋a 1－d 2，即{b n }为等差数列；若{c n }是等比数列，则c 1·c 2·…·c n ＝c n 1·q 1＋2＋…＋(n －1)＝c n 1·q n (n －1)2，∴d n ＝nc 1·c 2·…·c n ＝c 1·q n －12，即{d n }为等比数列．答案：d n ＝nc 1·c 2·…·c n5．(2017·全国卷Ⅱ改编)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，下列说法正确的序号是________．①乙可以知道四人的成绩； ②丁可以知道四人的成绩； ③乙、丁可以知道对方的成绩； ④乙、丁可以知道自己的成绩．解析：依题意，四人中有2位优秀，2位良好，由于甲知道乙、丙的成绩，但还是不知道自己的成绩，则乙、丙必有1位优秀，1位良好，甲、丁必有1位优秀，1位良好，因此，乙知道丙的成绩后，必然知道自己的成绩；丁知道甲的成绩后，必然知道自己的成绩，故④正确．答案：④6．某市为了缓解交通压力，实行机动车辆限行政策，每辆机动车每周一到周五都要限行一天，周末(周六和周日)不限行．某公司有A ，B ，C ，D ，E 五辆车，保证每天至少有四辆车可以上路行驶．已知E 车周四限行，B 车昨天限行，从今天算起，A ，C 两车连续四天都能上路行驶，E 车明天可以上路，由此可知下列推测一定正确的是________．(填序号)①今天是周六；②今天是周四； ③A 车周三限行；④C 车周五限行．解析：因为每天至少有四辆车可以上路行驶，E 车明天可以上路，E 车周四限行，所以今天不是周三；因为B 车昨天限行，所以今天不是周一，也不是周日；因为A ，C 两车连续四天都能上路行驶，所以今天不是周五，周二和周六，所以今天是周四．答案：②7．对于实数x ，[x ]表示不超过x 的最大整数，观察下列等式： [ 1 ]＋[ 2 ]＋[ 3 ]＝3，[ 4 ]＋[ 5 ]＋[ 6 ]＋[7 ]＋[8 ]＝10，[9 ]＋[10 ]＋[11 ]＋[12 ]＋[13 ]＋[14 ]＋[15 ]＝21， ……按照此规律第n 个等式的等号右边的结果为________．解析：因为[ 1 ]＋[ 2 ]＋[ 3 ]＝1×3，[ 4 ]＋[ 5 ]＋[ 6 ]＋[7 ]＋[8 ]＝2×5，[9 ]＋[10 ]＋[11 ]＋[12 ]＋[13 ]＋[14 ]＋[15 ]＝3×7，……，以此类推，第n 个等式的等号右边的结果为n (2n ＋1)，即2n 2＋n .答案：2n 2＋n8．(2018·江苏省通州高级中学高三月考)如果函数f (x )在区间D 上是凸函数，那么对于区间D 内的任意x 1，x 2，…，x n ，都有f (x 1)＋f (x 2)＋…＋f (x n )n ≤f⎝⎛⎭⎫x 1＋x 2＋…＋x n n .若y ＝sinx 在区间(0，π)上是凸函数，那么在△ABC 中，sin A ＋sin B ＋sin C 的最大值是________．解析：由题意知，凸函数满足f (x 1)＋f (x 2)＋…＋f (x n )n ≤f ⎝⎛⎭⎫x 1＋x 2＋…＋x n n ，又y ＝sin x 在区间(0，π)上是凸函数，则sin A ＋sin B ＋sin C ≤3sin A ＋B ＋C 3＝3sin π3＝。
2019版一轮创新思维语文(人教版)练习：板块一 专题二 第一讲 情节结构的三种考法
规范练一、阅读下面的文字，完成1～3题。
喊山葛水平炕上的孩子翻了一下身，蹬开了盖着的被子，哑巴伸手给孩子盖好，就听得大从外面蹦蹦跳跳地进来了。
大说：“我有名字了，韩冲叔起的，叫小书。
他还说要我念书，人要是不念书，就没有出息，就一辈子被人打，和娘一样。
”哑巴抬起头望了望窗外，幽黑的天光吊挂下来，她看到大手里拿着一包蜡烛，她知道是韩冲给的。
她用麻秆点燃了蜡烛，找来一个空酒瓶子把蜡烛套进去，有些松。
她想找一块纸，大给她拿过来一张纸，她准备卷蜡烛往里塞时，发现了那张纸是王胖孩给她打的条子[注]，上面有她的签字。
她抬起手打了大一下，大扯开嗓子哭，把炕上的孩子也吓醒了，也开始哭。
哑巴不管，把卷在蜡烛上的纸小心缠下来，又找了一张纸卷好蜡烛塞进酒瓶里，放到炕头上。
她拿起那张条子看了半天，抚展了，走到破旧的木板箱前，打开找出一个几年前的红色塑料笔记本，很慎重地压进去。
哑巴就指望这条子要韩冲养活她娘仨哩，哑巴什么也不要！哑巴返回来摸了大的头一下，抱起了炕上的孩子。
这时候就听得院子里走进来一个人，不可能是其他人，是韩冲。
韩冲用篮子提着秋天的玉米棒子放到屋子里的地上，韩冲说：“地里的嫩玉米煮熟了好吃，给孩子们解个心焦。
”韩冲说完从怀里又掏出半张纸的蚕种放到哑巴的炕上，韩冲说：“一半天蚕就出来了，你没有见过，半张蚕能养一屋子，到时候还得搭架子。
蚕见不得一点儿脏东西，哑巴，你爱干净，蚕更爱干净，好生伺候着这小东西。
”韩冲说完走了。
哑巴想，我哪里还知道什么叫干净呀，我这日子叫爱干净吗？夜暗下来了，月亮像一弯眉毛挂在中天上，半明半暗的光影加上阒寂的氛围，让哑巴有点嗒然伤心起来。
潜沉于被时间流走的世界里，哑巴就打了个颤抖，觉得丈夫腊宏是死了，又觉得腊宏还活着，惊惊地四下里看了一遍，她的思维在清明和混沌中半醒半梦着。
现在刚入秋，天到晚上有点夜凉。
哑巴摸索着从窗台上找到一块手掌大的镜子来，举了镜子看到了自己的脸，好久了不知道自己长了个啥样，好久了自己长了个啥样并不重要，重要的是挨了丈夫的上顿打，想着丈夫的下顿打，眼睛盯着个地方就不敢到处看，哪还敢看镜子嘛，那个是要找死吆。
2019版 创新设计 高考总复习 数学 人教A版 理科 第十章 第3节
C正确.由图知2006年以来我国二氧化硫年排放量与年份负相关，D不正确.
法叫做最小二乘法. (2)回归方程：两个具有线性相关关系的变量的一组数据：(x1，y1)，(x2，y2)，…， ^ ^x＋a ^ y＝b (xn，yn)，其回归方程为_________ ，则 ^是回归方程的______ ^是在 y 轴上的截距. 斜率 ，a 其中，b 回归直线一定过样本点的中心( x ， y ).
第3节
变量间的相关关系与统计案例
最新考纲
1.会作两个有关联变量的数据的散点图，会利用散点图认识变量间的相
关关系；2.了解最小二乘法的思想，能根据给出的线性回归方程系数公式建立线性 回归方程(线性回归方程系数公式不要求记忆)；3.了解独立性检验(只要求2×2列联 表)的基本思想、方法及其简单应用；4.了解回归分析的基本思想、方法及其简单应
A.逐年比较，2008年减少二氧化硫排放量的效果最显著 B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关 解析 对于A选项，由图知从2007年到2008年二氧化硫排放量下降得最多，故A正 确.对于B选项，由图知，由2006年到2007年矩形高度明显下降，因此B正确.对于C 选项，由图知从2006年以后除2011年稍有上升外，其余年份都是逐年下降的，所以
(2)在散点图中，点散布在从_________ 右下角 的区域，两个变量的这种相关关系 左上角 到________ 称为负相关. 一条直线 (3) 如果散点图中点的分布从整体上看大致在 ____________ 附近，称两个变量具有线 性相关关系.
2.线性回归方程
距离的平方和 (1)最小二乘法：使得样本数据的点到回归直线的___________________ 最小的方
2020年一轮创新思维文数(人教版A版)练习：第十章第一节算法与程序框图、基本算法语句Word版含解
课时规范练 A 组基础对点练1执行如图所示的程序框图，若输入的a ,b , k 分别为1,2,3,则输出的M =(7 C.7解析：第一次循环：M = 2 3, a = 2,b = 2, n = 2;第二次循环:M =号，a = 4 5 6, b = 3 n = 3; 第三次循环：15 8 15 15M = --, a = 8, b = 丁，n = 4.则输出的 M = 丁，选 D.8 3 8 8答案：D2.执行如图所示的程序框图，如果输入的 x , t 均为2,则输出的S =()C . 61解析：k = 1 w 2,执行第一次循环， M = 1X 2 = 2, S = 2 + 3 = 5, k = 1 + 1 = 2; k = 2< 2,执2行第二次循环， M = |X 2 = 2, S = 2+ 5 = 7, k = 2 + 1 = 3 ; k = 3>2，终止循环，输出 S = 7. 故选D. 答案：D3•阅读如图所示的程序框图，运行相应程序，则输出的20 i 的值为()15B . 5、 * ____/输丸砒A . 3B . 4C . 5D . 6解析：第一次执行，i = 1, a = 2;第二次执行，i = 2, a = 5;第三次执行，i = 3, a = 16;第 四次执行，i = 4, a = 65,此时满足条件a>50,跳出循环，故选 B. 答案：B4•执行如图所示的程序框图，如果输入的x 的值是407, y 的值是259，那么输出的x 的值解析：输入x 的值是407, y 的值是259，第一次循环后，S = 148, x = 259, y = 148;第二次 循环后，S = 111, x = 148, y = 111;第三次循环后，S = 37, x = 111, y = 37;第四次循环后， S = 74, x = 74, y = 37;第五次循环后，S = 37, x = 37, y = 37,结束循环，所以输出的 x 的值是37.故选B. 答案：B5. （2018唐山统考）执行如图所示的程序框图，若输入的 a 0= 4, a 1=— 1, a ?= 3, a 3=— 2, a 4= 1,则输出的t 的值为（）A . 2 849 C . 74 〔结朿CW}/输人On円，叫阿阿/卓-fl厂「（篩）B . 10D . 14解析：第一次循环，得t = 2X 1 —2 = 0, i = 2;第二次循环，得t = 0+ 3= 3, i = 3;第三次循环，得t = 2X 3 — 1 = 5, i = 4;第四次循环，得t= 2 X 5 + 4= 14, i = 5，不满足循环条件, 退出循环，输出的t= 14,故选D.答案：DA . [ —3,4]C. [ —4,3]3t, t<1 ,解析：作出分段函数s= 2I—t2+ 4t, t> 1在[2 , + )上单调递减，••• t € [—1,3]时,答案：AB . [—5,2]D . [ —2,5]的图象（图略），可知函数s在[—1,2]上单调递增,s€ [ —3,4].7•执行如图所示的程序框图，若输出的结果为21,则判断框中应填（）6•执行如图所示的程序框图，如果输入的t€ [ —1,3]，则输出的s属于（C. 121+1A . i<5?B . i<6?C . i<7?D . i<8?解析：第一次执行，S =— 1, i = 2;第二次执行，S = 3, i = 3;第三次执行，S =— 6, i = 4; 第四次执行，S = 10, i = 5;第五次执行，S =— 15, i = 6;第六次执行，S = 21, i = 7.此时 不满足条件，跳出循环，判断框中应填入的条件是 “i<7? ”，故选C.答案：C&执行如图所示的程序框图，若输入n 的值为8，则输出S 的值为 ___________ .（开的］/输入n /*1巨忘1而I否*L 输护7解析：第一次循环：S = 2, i = 4, k = 2;第二次循环：S = 4, i = 6, k = 3;第三次循环：S =8, i = 8, k = 4,当i = 8时不满足i<n ,退出循环，故输出 S 的值为8. 答案：89•执行如图所示的程序框图，则输出的k 值是 _________时（5制〔/朿］ \^\解析：由不等式k2—6k+ 5>0可得k>5或k<1，所以，执行程序框图可得k= 6.答案：6‘一x , 1<x W 4,10.关于函数f(x)=*的程序框图如图所示，现输入区间[a , b ],则输出的cos x ,— 1 < x < 1区间是 _________解析：由程序框图的第一个判断条件为 f(x)>0 ,当f(x) = cos x , x € [ — 1,1]时满足•然后进入第二个判断框，需要解不等式 f (x)=— sin x < 0,即0w x < 1•故输出区间为[0,1].答案：[0,1]B 组能力提升练1.(2017长沙模拟)执行如图所示的程序框图， 若输出的结果为43,则判断框内应填入的条件B . z w 20? D . z w 52?解析：运行程序：x = 0, y = 1,因为z = 1不满足输出结果，则 x = 1, y = 1;因为z = 2 x1 + 1 = 3不满足输出结果，则 x = 1, y = 3;因为z =2 x 1 + 3= 5不满足输出结果，则 x = 3, y =5;因为z = 2 x3 + 5= 11不满足输出结果，则 x = 5, y = 11;因为z = 2X 5+ 11 = 21不满 足输出结果，则x = 11, y = 21;因为z = 2X 11 + 21 = 43满足输出结果，此时需终止循环， 结合选项可知，选 A. 答案：AA . z w 42? C . z w 50?i 输人区间|dh] /a 值为1，则输出的k 值为（_N/ 输 Aa/C . 3B . 30,3答案：D（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法， 至今仍是比较先进的算法. 如图所示的程序框图给出了2•执行如图所示的程序框图，若输入的 Z+1足/输出未/结束解析：输入a= J 则b= X 第一次循环，a「* 1—1 12, k = 1;第二次循环,—1 a =1 1 —- 2—12, k = 2；第三次循环，a = 口 = 1，此时a = b ，结束循环，输出k = 2.故选 B.答案：B3.执行如图所示的程序框图，若输入 p = 5, q = 6,则输出a , i 的值分别为（A . 5,1 C . 15,3解析：执行程序框图可知，当i = 1时, D . 30,6a = 5X 1；当 i = 2 时，a = 5X 2;…；当 i = 6 时，a=5 X 6，此时a 能被q 整除，退出循环,输出 a , i 的值分别为30,6.査.-1利用秦九韶算法求某多项式值的一个实例，若输入n,x的值分别为4,3,则输出v的值为（）A. 20C. 183解析：初始值n, x的值分别为4,3，程序运行过程如下所示：v = 1, i = 3; v= 1 x 3 + 3= 6, i = 2; v = 6x 3+ 2= 20, i = 1, v = 20x 3+ 1= 61, i = 0; v= 61 x 3+ 0= 183, i = —1;跳出循环，输出v的值为183，故选C.答案：C5. 执行如图所示的程序框图，如果输入的t= 50,则输出的S=0,a：=2n=0n =（A . 5B . 6C. 7 D . 8解析：第一次运行后，S= 2, a = 3, n= 1;第二次运行后，S= 5, a= 5, n = 2;第三次运行后，S= 10, a = 9, n= 3;第四次运行后，S= 19, a = 17, n = 4;第五次运行后，S = 36, a = 33, n = 5; 第六次运行后，S = 69, a = 65, n = 6, 此时不满足S<t ,输出n =6,故选B. 答案：B6. （2018郑州一中质检）执行如图所示的程序框图，若输出 y =—•. 3，则输入的0=（）（站束J冗 冗 A.:B .—；6 6冗 冗C.3D• — 3解析：对于A ，当0=n时，y = sin 0= sin n 1，则输出y = 2，不合题意；对于 B ,当0=—訓时y = sin = sin （ — f ） = — 2，则输出丫=一 2，不合题意；对于 C ,当0=守寸，y = tan 0=tan n= ,3,则输出y = .3,不合题意；对于3 则输出y =— .3,符合题意•故选 D. 答案：D7. （2018临沂模拟）某程序框图如图所示，若判断框内是 k >n ,且n € N 时，输出的S = 57, 则判断框内的n 应为 __________ .解析：由程序框图，可得：S = 1, k = 1;S = 2X 1 + 2= 4, k = 2; S = 2 X 4+ 3= 11, k = 3;D ，当 0= —,y = tan 0= ta n (-n =-V 3,W+1s= 2X 11 + 4 = 26, k= 4;S= 2 X 26 + 5 = 57, k= 5.答案：5&执行如图所示的程序框图, 则输出的实数m的值为实数m的值为11.答案：11此时|a— 1.414|= |1.5- 1.414|= 0.086>0.005 ;第二次执行循环体a= 7, n = 3;5此时|a— 1.414|= |1.4— 1.414|= 0.014>0.005 ;n= 4.答案：44 •秦九韶是我国南宋时期的数学家，普州解析：分析框图可知输出的m应为满足m2》99的最小正整数解的后一个正整数, 故输出的解析：第一次执行循环体第三次执行循环体17a= 12，n= 4;此时|a—1.414|<0.005，此时不满足判断框内的条件，输出9 •执行如图所示的程序框图a = 2，n= 2;。
高中数学人教版(A版)必修 第一册(2019)_8.1变量的相关关系及相关系数 公开课
年龄/岁
23
脂肪含量/% 9.5
年龄/岁
53
脂肪含量/% 29.6
27
39
41
45
49
50
17.8
21.2
25.9
27.5
26.3
28.2
54
56
57
58
60
61
30.2
31.4
30.8
33.5
35.2
34.6
14
参考数据:
14
14
x 48.07, y 27.26, xi yi 19403.2, xi 34181, yi 2 11051.77
30.2
31.4
30.8
33.5
35.2
34.6
脂肪含量/% 29.6
问题1：脂肪含量随着年龄的变化有什么规律吗？
答：从整体上看，脂肪含量随着年龄的增大而增大
如何分析这两
个量是否相
关？
编号
1
2
3
4
5
6
7
年龄/岁
23
27
39
41
45
49
50
17.8
21.2
25.9
27.5
26.3
28.2
脂肪含量/% 9.5
y)
2
i 1
n
i
2
i 1
n
x
i 1
i
2
i
nx
i
2
n
y
i 1
2
i
我们称r为变量x和变量y的样本线性相关系
数，
2020版一轮创新思维文数(人教版A版)课件：第十章第四节变量间的相关关系与统计案例.ppt[文字可
[例 2] (1)工人月工资 (元)依劳动产值 (千元)变化的回归直
线方程为^y＝60＋90x，下列判断正确的是 ( )
A．劳动产值为 1 000 元时，工资为 50 元
B．劳动产值提高 1 000 元时，工资提高 15．劳动产值为 1 000 元时，工资为 90 元
第四节 变量间的相关关系与统计案例
回顾教材·夯实基础 典例剖析·突破考点 真题感悟·体验考场
课时规范练
[三基自测]
1．某研究机构对高三学生的记忆力 x 和判断力 y 进行统计
分析，所得数据如下表：
x 6 8 10 12 y23 5 6 则 y 对 x 的线性回归直线方程为 ( C )
A.^y＝2.3x－0.7
第十章
考点一
第四节 变量间的相关关系与统计案例
回顾教材·夯实基础 典例剖析·突破考点 真题感悟·体验考场
考点二
考点三
相关关系的判断|方法突破
课时规范练
[例 1] (1)对四组数据进行统计，获得如图所示的散点图，
关于其相关系数的比较，正确的是( )
A．r2<r4<0<r3<r1 B．r4<r2<0<r1<r3 C．r4<r2<0<r3<r1 D．r2<r4<0<r1<r3
D．月收入的中位数是 16，x 与 y 有负线性相关关系
月收入的中位数是 15＋2 17＝16，收入增加，支出增加，故 x
与 y 有正线性相关关系．
解析 答案
第十章
考点一
第四节 变量间的相关关系与统计案例
回顾教材·夯实基础 典例剖析·突破考点 真题感悟·体验考场
考点二
2019版一轮创新思维文数(人教版A版)练习：古典概型
课时规范练 A 组基础对点练1抛掷两枚质地均匀的骰子，向上的点数之差的绝对值为 1 Ay 1 D.12解析：抛掷两枚质地均匀的骰子，向上的点数之差的绝对值为 3的情况有：1,4; 4,1；2,5;5,2; 3,6； 6,3共6种，而抛掷两枚质地均匀的骰子的情况有 36种，所以所求概率 6 1P = 366'故选B. 答案：B X ,第二次向上的点 2 •某同学先后投掷一枚质地均匀的骰子两次，第一次向上的点数记为 数记为y ，在直角坐标系xOy 中，以（x , y ）为坐标的点落在直线 2x -y = 1上的概率为（） 1 A.12 5 C.361 D.6 解析：先后投掷两次骰子的结果共有 6X 6= 36种, 而以（x , y ）为坐标的点落在直线 2x -y = 1上的结果有（1,1）, （2,3）, （3,5），共3种，故所求概 率为36=12. 答案：A3.甲、乙两人有三个不同的学习小组 A , B , C 可以参加，若每人必须参加并且仅能参加一 个学习小组，则两人参加同一个小组的概率为 （ ） 1 代32 B.3 1 C.6 5 D.6 解析：甲、乙两人参加三个不同的学习小组共有 9个基本事件，其中两人参加同一个小组有 3 1 3个基本事件，因此所求概率为 9 = 3，故选A. 答案：A 4•若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人，这五人被录用的机会均等, 则甲或乙被录用的概率为 （ ） 2 A.3 2 B.5 C.|9 D.103的概率是（ ）1 C.18解析：由题意知，从五位大学毕业生中录用三人， 所有不同的可能结果有(甲，乙，丙)，(甲, 乙丁 )，(甲，乙，戊)，(甲，丙，丁 )，(甲，丙，戊)，(甲，丁，戊)，(乙，丙，丁 )，(乙, 丙，戊)，(乙，丁，戊)，(丙，丁，戊)，共10种，其中“甲与乙均未被录用”的所有不同 的可能结果只有(丙，丁，戌)这1种，故其对立事件 “甲或乙被录用”的可能结果有9种，9所求概率P =二.答案：D 5.从 1,2,3,4中任取2个不同的数，则取出的2个数之差的绝对值为 2的概率是( )1A .21 B.3 C1 C.4 1 D.6解析：从1,2,3,4中任取2个不同的数有以下六种情况：(1,2), (1,3), (1,4), (2,3), (2,4), (3,4), 满足取出的2个数之差的绝对值为 2的有(1,3), (2,4)，故所求概率是-=16 3答案：B6•从字母a , b , c , d , e 中任取两个不同字母，则取到字母 a 的概率为 _________ .解析：总的取法有：ab ,ac , ad , ae , be , bd , be , cd , ce , de 共10种，其中含有a 的有答案：27.某校有A , B 两个文学社团，若 a , b , c 三名学生各自随机选择参加其中的一个社团, 则三人不在同一个社团的概率为 ____________________ .答案：3&设连续掷两次骰子得到的点数分别为 m , n ,令平面向量a = (m , n), b = (1, - 3).(1) 求使得事件“ a 丄b ”发生的概率； (2) 求使得事件“ |a|w |b|”发生的概率.解析：(1)由题意知，m € {1,2,3,4,5,6} , n € {1,2,3,4,5,6} , 故 (m , n)所有可能的取法共 36 种.2 1a 丄b ，即m -3n = 0，即m = 3n ,共有2种：(3,1)、(6,2)，所以事件a 丄b 的概率为36= 182 1况，其中3人同在一个文学社团中有2种情况，因此3人同在一个社团的概率为 2=：.由对8 4立事件的概率可知，三人不在同一个社团的概率为 1-134.ab , ac , ad , ae 共4种，故所求概率为4 = 210一 5.解析：a , b , c 三名学生各自随机选择参加A ,B 两个文学社团中的一个社团，共有 8种情⑵|a|w|b|,即m2+ n2< 10,共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6 种，其概率为点=；•9•某校高三学生体检后，为了解高三学生的视力情况，该校从高三六个班的 300名学生中以班为单位(每班学生50人)，每班按随机抽样方法抽取了 8名学生的视力数据.其中高三(1) 班抽取的8名学生的视力数据与人数见下表： 视力 数据 4.04.14.24.3 4.44.5 4.64.7 4.8 4.95.0 5.15.25.3人数22211(1)用上述样本数据估计高三(1)班学生视力的平均值；⑵已知其余五个班学生视力的平均值分别为4.3、4.4、4.5、4.6、48若从这六个班中任意抽取两个班学生视力的平均值作比较， 求抽取的两个班学生视力的平均值之差的绝对值不小于 0.2的概率.解析：(1)高三(1)班学生视力的平均值为4.4X 2+ 4.6 X 22+ 4.9 + 5.1 = 4.7 ,8故估计高三(1)班学生视力的平均值为4.7.(2)从这六个班中任意抽取两个班学生视力的平均值作比较，所有的取法共有 15种，而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有：(4.3,4.5), (4.3,4.6),(4.3,4.7), (4.3,4.8), (4.4,4.6), (4.4,4.7), (4.4, 4.8), (4.5,4.7), (4.5,4.8), (4.6,4.8)，共有 10 种，故抽取的两个班学生视力的平均值之差的绝对值不小于B 组能力提升练1. (2018河北三市联考)袋子中装有大小相同的5个小球，分别有 2个红球、3个白球.现从中随机抽取2个小球，则这2个小球中既有红球也有白球的概率为 ( )A 3 A .47 B.10c 4 C.5°.| 解析： 设2个红球分别为a 、b,3个白球分别为A 、B 、C ,从中随机抽取2个，则有(a , b),(a , A), (a , B), (a , C), (b , A), (b , B), (b , C), (A , B), (A , C), (B , C),共 10个基本 事件，其中既有红球也有白球的基本事件有 6个，则所求概率为 P = 6 = 3.10 5答案：D 2.在2,0,1,5这组数据中，随机取出三个不同的数，则数字 的概率为( )A.4 1 D.410 20.2的概率为p = 15= 3.2是取出的三个不同数的中位数C.^解析：分析题意可知，共有(0,1,2), (0,2,5), (1,2,5) , (0,1,5)4种取法，符合题意的取法有2种，故所求概率P= 2答案：C1 32 23. (2018商丘模拟)已知函数f(x)= 3X3+ ax2+ b2x+ 1,若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数，则该函数有两个极值点的概率为()7 Ay1 B.3C.9解析：f' (x)= x2+ 2ax+ b2,2D.3要使函数f(x)有两个极值点，则有△= (2a)2—4b2>0，即a2>b2.由题意知所有的基本事件有9 个，即(1,0), (1,1), (1,2), (2,0), (2,1), (2,2), (3,0), (3,1),(3,2)，其中第一个数表示a的取值，第二个数表示b的取值•满足a2>b2的共有6个，P=；=2—3.答案：D4•将一颗骰子投掷两次分别得到点数a, b，则直线ax—by= 0与圆(x-2)2+ y2= 2相交的概率为_________ .解析：圆心(2,0)到直线ax—by= 0的距离d =」纠2,当d< 2时，直线与圆相交，则有d\/a2+ b2=迈，得b>a，满足b>a的共有15种情况，因此直线ax —by= 0与圆(x—2)2+ y2 =2相交的概率为15=36 125答案：誇5. (2018长沙长郡中学检测)在所有的两位数10〜99中，任取一个数，则这个数能被2或3整除的概率是_________ .解析：所有两位数共有90个，其中2的倍数有45个，3的倍数有30个，6的倍数有15 个, 所以能被2或3整除的共有45+ 30 —15= 60(个)，所以所求概率是器=答案：26. 设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛.(1)求应从这三个协会中分别抽取的运动员的人数；⑵将抽取的6名运动员进行编号，编号分别为A1, A2, A3, A , A5, A6，现从这6名运动员中随机抽取2人参加双打比赛.①用所给编号列出所有可能的结果；②设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，求事件A发生的概率.解析：⑴应从甲、乙、丙三个协会中抽取的运动员人数分别为3,1,2.⑵①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为{A i, A2} , {A i, A3} , {A i, A4} , {A i ,A5} , {A i , A6} , {A2, A3} , { A2, A4} , {A2, A5} , { A2 , A6} , { A3 , A4} , {A3 , A5}, {A3 , A6}, {A4 , A5}, {A4 , A6} , {A5 , A6},共i5 种.②编号为A5和A6的两名运动员中至少有i人被抽到的所有可能结果为{A i , A5}, {A i, A6}, {A2 , A5},{A2 , A6}, {A3 , A5} , {A3 , A6} , {A4 , A5} , {A4 , A6}, {A5 , A6},共9 种.9 3因此，事件A发生的概率P(A)= “ =匚i5 57•某校夏令营有3名男同学A , B , C和3名女同学X , Y, Z ,其年级情况如下表：现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).(1) 用表中字母列举出所有可能的结果；⑵设M为事件“选出的2人来自不同年级且恰有i名男同学和i名女同学”，求事件M发生的概率.解析：⑴从6名同学中随机选出2人参加知识竞赛的所有可能结果为{A , B} , {A , C}, {A , X}, {A , Y}, {A , Z}, {B , C}, {B , X}, {B , Y} , {B , Z} , {C , X}, {C , Y} , {C , Z}, {X , Y}, {X , Z}, {Y , Z},共i5 种.(2) 选出的2人来自不同年级且恰有i名男同学和i名女同学的所有可能结果为{A , Y} , {A , Z}, {B ,X}, {B , Z}, {C , X}, {C , Y},共6 种.因此，事件M发生的概率为i；= I-。
2019版一轮创新思维文数(人教版A版)练习：第七章 第四节 空间中的平行关系
D．m∥β 且 l1∥α
解析：由 m∥l1，m⊂α，l1⊂β，得 l1∥α，同理 l2∥α，又 l1，l2 相交，所以 α∥β，反之不
成立，所以 m∥l1 且 n∥l2 是 α∥β 的一个充分不必要条件．
答案：A
3．设 α，β 是两个不同的平面，m 是直线且 m⊂α，“m∥β”是“α∥β”的( )
课时规范练
A 组 基础对点练
1．设 m，n 是不同的直线，α，β 是不同的平面，且 m，n⊂α，则“α∥β”是“m∥β 且
n∥β”的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
解析：若 m，n⊂α，α∥β，则 m∥β 且 n∥β；反之若 m，n⊂α，m∥β 且 n∥β，则 α 与 β
答案：B
4．下列命题中，错误的是( )
A．一条直线与两个平行平面中的一个相交，则必与另一个平面相交
B．平行于同一平面的两个不同平面平行
C．如果平面 α 不垂直平面 β，那么平面 α 内一定不存在直线垂直于平面 β
D．若直线 l 不平行平面 α，则在平面 α 内不存在与 l 平行的直线
解析：A 中，如果假定直线与另一个平面不相交，则有两种情形：在平面内或与平面平行，
则 SC，SB，SE 三线共面，则点 E 与点 C 重合，与题设矛盾，故①错误；因为 SA 与平面
SBC 相交，所以在平面 SBC 内不存在直线与 SA 平行，故②错误；显然，在平面 ABCE 内，
存在直线与 AE 平行，由线面平行的判定定理得平面 ABCE 内存在直线与平面 SAE 平行，
故③正确．故选 B.
是边长为 1 的菱形，∠ABC＝4，OA⊥底面 ABCD，OA＝2，M 为 OA 的中点，N 为 BC 的中点．
推荐2019版一轮创新思维文数(人教版A版)课件第十章 第三节 用样本估计总体
解析
考点二
考点一三
[方法提升]
频率、频数、样本容量的计算方法
(1)频 组率 距×组距＝频率．
频数
频数
(2)样本容量＝频率，频率＝样本容量，样本容量×频率＝频数．
考点二
考点一三
[跟踪训练]
某中学高三年级共有学生 1 000 人，将某次模拟考试的数学
成绩(满分 150 分，所有成绩均不低于 70 分)按[70,80)，
[80,90)，…，[140,150]分成 8 组，并制成如图所示的频率分
布直方图．
解析
考点二
考点一三
(1)求 x 的值； (2)用分层抽样的方法从成绩在[70,90)内的试卷中抽取 7 份， 求这 7 份试卷中成绩在[70,80)内的试卷数； (3)从(2)中抽出的 7 份试卷中任取 2 份，求成绩在[70,80)和 [80,90)内的试卷数各有 1 份的概率．
2．样本的数字特征 (1)众数、中位数、平均数
数ቤተ መጻሕፍቲ ባይዱ特征 定义与求法
众数
一组数据中重 复出现次数最 多的数
优点与缺点 通常用于描述变量的值 出现次数最多的数．但 显然它对其他数据信息 的忽视使得无法客观地 反映总体特征
数字特征 定义与求法
优点与缺点
把一组数据按 是样本数据所占频率的
中位数
_大__小__顺__序__排列，等分线，它不受少数几 处在 最中间 位 个极端值的影响，这在 置的一个数据 某些情况下是优点，但
[例 2] (1)(2018·山西四校联考)某学校组织学生参加数学测试，成
绩的频率分布直方图如图，数据的分组依次为[20,40)，[40,60)，
[60,80)，[80,100]．若低于 60 分的人数是 15，则该班的学生人数
人教A版2019高考文科数学创新思维练习(58份含答案)【DOC范文整理】
人教A版2019高考文科数学创新思维练习（58份含答案）课时规范练A组基础对点练．直线y＝bax＋3与双曲线x2a2－y2b2＝1的交点个数是A．1B．2c．1或2D．0解析：因为直线y＝bax＋3与双曲线的渐近线y＝bax 平行，所以它与双曲线只有1个交点．答案：A．抛物线y2＝4x的焦点为F，准线为l，经过F且斜率为3的直线与抛物线在x轴上方的部分相交于点A，A⊥l，垂足为，则△AF的面积是A．4B．33c．43D．8解析：∵y2＝4x，∴F，l：x＝－1，过焦点F且斜率为3的直线l1：y＝3，与y2＝4x联立，解得x＝3或x＝13，故A，∴A＝4，∴S△AF＝12×4×23＝43.故选c.答案：c．已知直线l：y＝2x＋3被椭圆c：x2a2＋y2b2＝1截得的弦长为7，则下列直线中被椭圆c截得的弦长一定为7的有①y＝2x－3；②y＝2x＋1；③y＝－2x－3；④y＝－2x＋3.A．1条B．2条c．3条D．4条解析：直线y＝2x－3与直线l关于原点对称，直线y ＝－2x－3与直线l关于x轴对称，直线y＝－2x＋3与直线l关于y轴对称，故有3条直线被椭圆c截得的弦长一定为7.答案：c．过点P作直线l与圆o：x2＋y2＝1交于A、B两点，o为坐标原点，设∠AoB＝θ，且θ∈0，π2，当△AoB的面积为34时，直线l的斜率为A.33B．±33c.3D．±3解析：∵△AoB的面积为34，∴12×1×1×sinθ＝34，∴sinθ＝32.∵θ∈0，π2，∴θ＝π3，∴圆心到直线l的距离为32.设直线l的方程为y＝，即x－y＋3＝0，∴32＝|3|1＋2，∴＝±33.答案：B．已知过定点的直线与抛物线x2＝y相交于不同的A，B 两点，则＝________.解析：设过定点的直线的方程为y＝，代入抛物线方程x2＝y得x2－x＋＝0，故x1＋x2＝，x1x2＝，因此＝x1x2－＋1＝1.答案：1．已知双曲线x2a2－y2b2＝1的焦距为2c，右顶点为A，抛物线x2＝2py的焦点为F.若双曲线截抛物线的准线所得线段长为2c，且|FA|＝c，则双曲线的渐近线方程为______________．解析：抛物线x2＝2py的准线方程为y＝－p2，与双曲线的方程联立得x2＝a2，根据已知得a2＝c2①.由|AF|＝c，得p24＋a2＝c2②.由①②可得a2＝b2，即a＝b，所以所求双曲线的渐近线方程是y＝±x.答案：y＝±x．过双曲线x2－y22＝1的右焦点作直线l交双曲线于A、B两点，若使得|AB|＝λ的直线l恰有3条，则λ＝________.解析：∵使得|AB|＝λ的直线l恰有3条．∴根据对称性，其中有一条直线与实轴垂直．此时A，B的横坐标为3，代入双曲线方程，可得y＝±2，故|AB|＝4.∵双曲线的两个顶点之间的距离是2，小于4，∴过双曲线的焦点一定有两条直线使得交点之间的距离等于4，综上可知|AB|＝4时，有三条直线满足题意．∴λ＝4.答案：4．设椭圆E的方程为x2a2＋y2b2＝1，点o为坐标原点，点A的坐标为，点B的坐标为，点在线段AB上，满足|B|＝2|A|，直线o的斜率为510.求E的离心率e；设点c的坐标为，N为线段Ac的中点，点N关于直线AB的对称点的纵坐标为72，求E的方程．解析：由题设条件知，点的坐标为23a，13b，又o＝510，从而b2a＝510，进而得a＝5b，c＝a2－b2＝2b，故e＝ca＝255.由题设条件和的计算结果可得，直线AB的方程为x5b ＋yb＝1，点N的坐标为52b，－12b.设点N关于直线AB的对称点S的坐标为x1，72，则线段NS的中点T的坐标为54b＋x12，－14b＋74.又点T在直线AB上，且NS·AB＝－1，从而有5b4＋x125b＋－14b＋74b＝1，72＋12bx1－52b ＝5，解得b＝3.所以a＝35，故椭圆E的方程为x245＋y29＝1.已知中心在坐标原点，焦点在x轴上的椭圆过点P，且它的离心率e＝12.求椭圆的标准方程；与圆2＋y2＝1相切的直线l：y＝x＋t交椭圆于，N两点，若椭圆上一点c满足o→＋oN→＝λoc→，求实数λ的取值范围．解析：设椭圆的标准方程为x2a2＋y2b2＝1，由已知得：4a2＋3b2＝1，ca＝12，c2＝a2－b2，解得a2＝8b2＝6，所以椭圆的标准方程为x28＋y26＝1.因为直线l：y＝x＋t与圆2＋y2＝1相切，所以|t＋|1＋2＝1⇒2＝1－t2t，把y＝x＋t代入x28＋y26＝1并整理得：x2＋8tx＋＝0，设，N，则有x1＋x2＝－8t3＋42，y1＋y2＝x1＋t＋x2＋t＝＋2t＝6t3＋42，因为λoc→＝，所以c－8t3＋42λ，6t3＋42λ，又因为点c在椭圆上，所以，2t23＋422λ2＋6t23＋422λ2＝1⇒λ2＝2t23＋42＝21t22＋1t2＋1，因为t2>0，所以1t22＋1t2＋1>1，所以02，又y202，所以20，∴b>－14.设，N，则x1＋x2＝－1，y1＋y22＝－x1＋x22＋b＝12＋b，由－12，12＋b在直线y＝x＋3上，即12＋b＝－12＋3，解得b＝2，联立得y＝－x＋2，y＝x2，解得x1＝－2，y1＝4，x2＝1，y2＝1.答案：，．过抛物线y2＝4x的焦点F的直线交该抛物线于A，B 两点．若|AF|＝3，则|BF|＝________.解析：抛物线y2＝4x的准线为x＝－1，焦点为F，设A，B．由抛物线的定义可知|AF|＝x1＋1＝3，所以x1＝2，所以y1＝±22，由抛物线关于x轴对称，假设A，由A，F，B三点共线可知直线AB的方程为y－0＝22，代入抛物线方程消去y得2x2－5x＋2＝0，求得x＝2或12，所以x2＝12，故|BF|＝32.答案：32．定义：在平面内，点P到曲线Γ上的点的距离的最小值称为点P到曲线Γ的距离．在平面直角坐标系xoy中，已知圆：2＋y2＝12及点A，动点P到圆的距离与到点A的距离相等，记P点的轨迹为曲线.求曲线的方程；过原点的直线l与曲线交于不同的两点c，D，点E在曲线上，且cE⊥cD，直线DE与x轴交于点F，设直线DE、cF 的斜率分别为1、2，求12.解析：由题意知：点P在圆内且不为圆心，易知|PA|＋|P|＝23>22＝|A|，所以P点的轨迹为以A、为焦点的椭圆，设椭圆方程为x2a2＋y2b2＝1，则2a＝23，2c＝22⇒a＝3，c＝2.所以b2＝1，故曲线的方程为x23＋y2＝1.设c，E，则D，则直线cD的斜率为cD＝y1x1，又cE⊥cD，所以直线cE的斜率是cE＝－x1y1，记－x1y1＝，设直线cE的方程为y＝x＋，由题意知≠0，≠0，由y＝x＋，x23＋y2＝1得x2＋6x＋32－3＝0，∴x1＋x2＝－61＋32，∴y1＋y2＝＋2＝21＋32，由题意知x1≠x2，∴1＝DE＝y2＋y1x2＋x1＝－13＝y13x1，∴直线DE的方程为y＋y1＝y13x1，令y＝0，得x＝2x1，即F．可得2＝－y1x1.∴12＝－13.．已知点A，B是抛物线y2＝4x上相异两点，且满足x1＋x2＝2.若AB的中垂线经过点P，求直线AB的方程；若AB的中垂线交x轴于点，求△AB的面积的最大值及此时直线AB的方程．解析：当AB垂直于x轴时，显然不符合题意，所以可设直线AB的方程为y＝x＋b，代入方程y2＝4x，得：2x2＋x＋b2＝0，∴x1＋x2＝4－2b2＝2，得b＝2－，∴直线AB的方程为y＝＋2，∵AB中点的横坐标为1，∴AB中点的坐标为1，2，∴AB的中垂线方程为y＝－1＋2＝－1x＋3.∵AB的中垂线经过点P，故3＝2，得＝32，∴直线AB的方程为y＝32x－16.由可知AB的中垂线方程为y＝－1x＋3，∴点的坐标为，∵直线AB的方程为2x－y＋2－2＝0，∴到直线AB的距离d＝|32＋2－2|4＋2＝22＋1||，由2x－y＋2－2＝0，y2＝4x得24y2－y＋2－2＝0，y1＋y2＝4，y1·y2＝8－422，|AB|＝1＋12|y1－y2|＝41＋22－12.∴S△AB＝41＋121－12，设1－12＝t，则0<t<1，S＝4t＝－4t3＋8t，S′＝－12t2＋8，由S′＝0，得t＝63，即＝±3时，Sax＝1669，此时直线AB的方程为3x±3y－1＝0.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课时规范练 A 组 基础对点练1．(2018·大连双基测试)已知x ，y 的取值如表所示：如果y 与x 线性相关，且线性回归方程为y ＝b x ＋132，则b 的值为( )A ．－12B.12 C ．－110D.110解析：计算得x ＝3，y ＝5，代入到y ^＝b ^x ＋132中，得b ^＝－12.故选A.答案：A2．四名同学根据各自的样本数据研究变量x ，y 之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且y ^＝2.347x －6.423；②y 与x 负相关且y ^＝－3.476x ＋5.648；③y 与x 正相关且y ^＝5.437x ＋8.493；④y 与x 正相关且y ^＝－4.326x －4.578. 其中一定不正确的结论的序号是( ) A ．①② B ．②③ C ．③④D ．①④解析：y ^＝b ^x ＋a ^，当b >0时，为正相关，b <0为负相关，故①④错误． 答案：D3．在一组样本数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )(n ≥2，x 1，x 2，…，x n 不全相等)的散点图中，若所有样本点(x i ，y i )(i ＝1,2，…，n )都在直线y ＝12x ＋1上，则这组样本数据的样本相关系数为( ) A ．－1 B ．0 C.12D ．1解析：所有点均在直线上，则样本相关系数最大即为1，故选D. 答案：D4．已知变量x 与y 正相关，且由观测数据算得样本平均数x ＝3，y ＝3.5，则由该观测数据算得的线性回归方程可能是( ) A.y ^＝0.4x ＋2.3B.y ^＝2x －2.4C.y ^＝－2x ＋9.5 D.y ^＝－0.3x ＋4.4解析：依题意知，相应的回归直线的斜率应为正，排除C 、D.且直线必过点(3,3.5)，代入A 、B 得A 正确． 答案：A5．经调查某地若干户家庭的年收入x (万元)和年饮食支出y (万元)具有线性相关关系，并得到y 关于x 的回归直线方程：y ^＝0.245x ＋0.321，由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加________万元．解析：x 变为x ＋1，y ^＝0.245(x ＋1)＋0.321＝0.245x ＋0.321＋0.245，因此家庭年收入每增加1万元，年饮食支出平均增加0.245万元． 答案：0.2456．某炼钢厂废品率x (%)与成本y (元/吨)的线性回归方程为y ^＝105.492＋42.569x .当成本控制在176.5元/吨时，可以预计生产的1 000吨钢中，约有________吨钢是废品(结果保留两位小数)．解析：因为176.5＝105.492＋42.569x ，解得x ≈1.668，即当成本控制在176.5元/吨时，废品率约为1.668%，所以生产的1 000吨钢中，约有1 000×1.668%＝16.68吨是废品． 答案：16.687．(2018·合肥模拟)某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间(x 个月)和市场占有率(y %)的几组相关对应数据：(1)(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%(精确到月)．附：b ^＝∑i ＝1nx i y i －n x ·y ∑i ＝1nx 2i －n x2，a ^＝y －b ^x .解析：(1)由题意知x ＝3，y ＝0.1，∑i ＝15x i y i ＝1.92，∑i ＝15x 2i ＝55，所以b ^＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x2＝1.92－5×3×0.155－5×32＝0.042，a ^＝y －b ^x ＝0.1－0.042×3＝－0.026， 所以线性回归方程为y ^＝0.042x －0.026.(2)由(1)中的回归方程可知，上市时间与市场占有率正相关，即上市时间每增加1个月，市场占有率约增加0.042个百分点．由y ^＝0.042x －0.026>0.5，解得x ≥13，故预计上市13个月时，该款旗舰机型市场占有率能超过0.5%.8．某校数学课外兴趣小组为研究数学成绩是否与性别有关，先统计本校高三年级每个学生一学期数学成绩的平均分(采用百分制)，剔除平均分在30分以下的学生后，共有男生300名，女生200名．现采用分层抽样的方法，从中抽取了100名学生，按性别分为两组，并将两组学生成绩分为6组，得到如下所示频数分布表.成绩与性别是否有关；(2)规定80分以上为优分(含80分)，请你根据已知条件作出2×2列联表，并判断是否有90%以上的把握认为“数学成绩与性别有关”.附表及公式K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d ).解析：(1)x 男＝45×0.05＋55×0.15＋65×0.3＋75×0.25＋85×0.1＋95×0.15＝71.5，x女＝45×0. 15＋55×0.1＋65×0.125＋75×0.25＋85×0.325＋95×0.05＝71.5，从男、女生各自的平均分来看，并不能判断数学成绩与性别有关．(2)由频数分布表可知：在抽取的100名学生中，“男生组”中的优分有15人，“女生组”中的优分有15人，据此可得2×2列联表如下：可得K 2＝100×(15×25－15×45)60×40×30×70≈1.79，因为1.79<2.706，所以没有90%以上的把握认为“数学成绩与性别有关”．B 组 能力提升练1．为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y ＝b x ＋a ，其中b ＝0.76，a ＝y －b x .据此估计，该社区一户年收入为15万元家庭的年支出为( ) A ．11.4万元 B ．11.8万元 C ．12.0万元D ．12.2万元解析：∵x ＝10.0，y ＝8.0，b ^＝0.76，∴a ^＝8－0.76×10＝0.4，∴回归方程为y ^＝0.76x ＋0.4，把x ＝15代入上式得，y ^＝0.76×15＋0.4＝11.8(万元)，故选B. 答案：B2．根据如下样本数据：得到的回归方程为y ^＝b ^x ＋a ^.若样本点的中心为(5,0.9)，则当x 每增加1个单位时，y ( ) A ．增加1.4个单位 B ．减少1.4个单位 C ．增加7.9个单位D ．减少7.9个单位解析：依题意得，y ＝a ＋b －25＝0.9，故a ＋b ＝6.5①；又样本点的中心为(5,0.9)，故0.9＝5b ＋a ②，联立①②，解得b ＝－1.4，a ＝7.9，即y ^＝－1.4x ＋7.9，可知当x 每增加1个单位时，y 减少1.4个单位，故选B. 答案：B3．(2018·岳阳模拟)某考察团对全国10个城市进行职工人均工资水平x (千元)与居民人均消费水平y (千元)统计调查，y 与x 具有相关关系，回归方程y ^＝0.66x ＋1.562.若某城市居民人均消费水平为7.675(千元)，估计该城市人均消费占人均工资收入的百分比约为________． 解析：由y ^＝0.66x ＋1.562知，当y ＝7.675时，x ＝6 113660，故所求百分比为7.675x ＝7.675×6606 113≈83%. 答案：83%4．(2018·唐山质检)为了研究某种细菌在特定环境下随时间变化的繁殖规律，得到了下表中的实验数据，计算得回归直线方程为y ^＝0.85x －0.25.由以上信息，可得表中c 的值为________.解析：x ＝3＋4＋5＋6＋75＝5，y ＝2.5＋3＋4＋4.5＋c 5＝14＋c 5，代入回归直线方程得14＋c5＝0.85×5－0.25，解得c ＝6. 答案：65．为了研究男羽毛球运动员的身高x (单位：cm)与体重y (单位：kg)的关系，通过随机抽样的方法，抽取5名运动员测得他们的身高与体重关系如下表：(1)从这5 2 kg 的概率； (2)求回归直线方程y ^＝b ^x ＋a ^.解析：(1)从这5个人中随机地抽取2个人的体重的基本事件有(74,73)，(74,76)，(74,75)，(74,77)；(73,76)，(73,75)，(73,77)；(76,75)，(76,77)；(75,77)．满足条件的有(74,76)，(74,77)，(73,76)，(73,75)，(73,77)，(75,77)6种情况，故2个人体重之差的绝对值不小于2 kg 的概率为610＝35.(2)x ＝176，y ＝75，b ^＝∑5i ＝1 (xi －x )(y i －y )∑5i ＝1(x i －x )2＝－4×(－1)＋(－2)×(－2)＋0×1＋2×0＋4×2(－4)2＋(－2)2＋02＋22＋42＝0.4，a ^＝y －b ^x ＝4.6， ∴y ^＝0.4x ＋4.6.6．(2018·郑州一中检测)为了解某地区观众对某大型综艺节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．下面是根据调查结果绘制的观众观看该节目的场数与所对应的人数的表格：10名女性． (1)根据已知条件完成如下2×2列联表，并判断我们能否有95%的把握认为是否为“歌迷”与性别有关？(2)将收看该节目所有场数2名女性，若从“超级歌迷”中任意选取2人，求至少有1名女性观众的概率． 注：K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )，n ＝a ＋b ＋c ＋d .解析：(1)由统计表可知，在抽取的100人中，“歌迷”有25人，从而完成2×2列联表如下：将2×2列联表中的数据代入公式计算得： K 2＝100×(30×10－45×15)275×25×45×55＝10033≈3.030<3.841所以我们没有95%的把握认为是否为“歌迷”与性别有关． (2)由统计表可知，“超级歌迷”有5人，其中2名女性，3名男性，设2名女性分别为a 1，a 2,3名男性分别为b 1，b 2，b 3，从中任取2人所包含的基本事件有：(a 1，a 2)，(a 1，b 1)，(a 1，b 2)，(a 1，b 3)，(a 2，b 1)，(a 2，b 2)，(a 2，b 3)，(b 1，b 2)，(b 1，b 3)，(b 2，b 3)，共10个，用A 表示“任意选取的2人中，至少有1名女性观众”这一事件， A 包含的基本事件有：(a 1，a 2)，(a 1，b 1)，(a 1，b 2)，(a 1，b 3)，(a 2，b 1)，(a 2，b 2)，(a 2，b 3)，共7个， 所以P (A )＝710.。