金属材料静态拉伸实验数据处理结果
金属材料的拉伸实验报告

材料(工程)力学实验报告学号:_ _姓名:同组人姓名:实验日期:_一、实验名称: 金属材料拉伸实验二、实验目的:1.学习全数字化电子万能材料试验机的操作方法。
2.测定低碳钢拉伸时的屈服强度σs、抗拉强度σb、断后伸长率δ、断面收缩率ψ。
3.测定铸铁的抗拉强度σb。
4.观察低碳钢、铸铁在拉伸过程中的各种现象,并比较两种材料拉伸时力学性能的特点。
三、实验设备:1.RGM-100全数字化电子万能材料试验机2.计算机、打印机3.游标卡尺四、数据记录和结果:1.原始数据2.试验后数据3.实验结果低碳钢:σs=286.41MPaσb=383.87MPaδ=25.27%ψ=60.11%铸铁:σb=279.98MPa1.拉伸曲线低碳钢铸铁五、分析讨论:1.比较低碳钢、铸铁拉伸时力学性能、断口破坏形式有何不同,并分析其破坏原因。
对于低碳钢,拉伸曲线在屈服阶段呈水平锯齿状,到达屈服点以后,变形较明显。
试件在到达最大载荷F b以前,变形是均匀的。
从最大载荷处开始,在试件局部区段,迅速伸长,并出现颈缩。
之后,由于局部部位直径减少,拉伸所需载荷也相应减小,直到断裂。
断面呈凹凸状。
铸铁试件拉伸变形极小,试件在达到最大载荷时即突然断裂,其抗拉强度远小于低碳钢的σb,断面是平整的。
(如下图,左低碳钢,右铸铁)破坏原因是因为在断面处的拉应力最大,超过材料的抗拉强度而破坏。
2. 材料相同、直径相等的长试样和短试样,其断后伸长率是否相同?试说明原因。
不相同。
断后伸长率的公式为:12=100%L L δ⨯ 虽然 相等,但是 不相等,所以断后伸长率不相同。
材料(工程)力学实验报告学号:_1002193130_姓名:云霄同组人姓名:王德隆、叶宇凡、李嘉琦实验日期:_2021-4-28一、实验名称: 金属材料压缩实验二、实验目的:1.测定低碳钢压缩时的屈服强度。
2.测定铸铁压缩时的抗压强度。
3.观察低碳钢和铸铁压缩时变形的特点和破坏现象,并进行比较。
拉伸实验报告

实验报告(一)实验名称:金属静态拉伸破坏实验实验目的:1、测定低碳钢的屈服极限S σ、强度极限b σ、延伸率δ、截面收缩率ψ。
2、测定铸铁的抗拉强度极限b σ。
3、观察低碳钢和铸铁在拉伸过程中表现的现象,绘出外力和变形间的关系曲线(L F ∆-曲线)。
4、分析和比较低碳钢和铸铁的拉伸力学性能和破坏特征。
实验设备和仪器:材料试验机、游标卡尺、试样划线器等。
拉伸试件:金属材料拉伸实验常用的试件形状如图所示。
图中工作段长度l 称为标距,试件的拉伸变形量一般由这一段的变形来测定,两端较粗部分是为了便于装入试验机的夹头内。
为了使实验测得的结果可以互相比较,试件必须按国家标准做成标准试件,即dl10=。
=或dl5对于一般板的材料拉伸实验,也应按国家标准做成矩形截面试件。
其截面面积和试件标距关系为A.5=,A为标距段l65l3.=或A11内的截面积。
实验原理:1、低碳钢低碳钢的拉伸图全面而具体的反映了整个变形过程。
观察自动绘图机绘出的拉伸图。
图1-2从图中可以看出,当载荷增加到A点时,拉伸图上OA段是直线,表明此阶段内载荷与试件的变形成比例关系,即符合虎克定律的弹性变形范围。
当载荷增加到B'点时,L-曲线变成锯齿状,这时变形F∆增加很快,载荷在小幅度内波动很慢;这说明材料产生了流动(或者叫屈服)与B'点相应的应力叫上流动极限(屈服高限),与B相应的应力叫下流动极限(屈服低限),因下流动极限比较稳定,所以材料的流动极限一般规定按下流动极限取值。
以B点相对应的载荷值F除S以试件的原始截面积A 即得到低碳钢的流动极限S σ,AF SS =σ流动阶段后,试件要承受更大的外力,才能继续发生变形若要使塑性变形加大,必须增加载荷,如图形中C 点至D 点这一段为强化阶段。
当载荷达到最大值b F (D 点)时,试件的塑性变形集中在某一截面处的小段内,此段发生截面收缩,即出现“颈缩”现象(局部变形)。
此时记下最大载荷值b F ,用b F 除以试件的原始截面积A ,就得到低碳钢的强度极限A F /b b =σ。
金属拉伸实验报告

根据国标规定,材料屈服过后,试验机得速率应使试样平行长度内得应变速 率不超过 0、008/s。在此条件下继续加载,并注意观察主动针得转动、自动绘 图得情况与相应得试验现象(强化、冷作硬化与颈缩等现象——在强化阶段得任
一位置卸载后再加载进 行冷作硬化现象得观察; 此后,待主动针再次停止 转动而缓慢回转时,材料 进入颈缩阶段,注意观察 试 样 得 颈 缩 现 象 ), 直 至 试样断裂停车。记录所加 得最大荷载 Fm(从动针最 后停留得位置)。
低碳钢得上屈服强度:
低碳钢得下屈服强度:
低碳钢得抗拉强度:
低碳钢得断后伸长率:
低碳钢得断面收缩率:
铸铁得抗拉强度:
铸铁得断后伸长率:
低碳钢得端口发生在第五格与第六格之间,符合实验要求
故实验数据处理结果如下表:
材料
上屈服强度 ReH/GPa
下屈服强度 ReL/GPa
低碳钢 铸铁
0、3636 ╱
0、3309 ╱
4、装载电子引伸计: 将电子引伸计装载在低碳钢试样上,注意电子引伸计要在比例极限处卸载。 5、进行试验: 开动试验机使之缓慢匀速加载(依据规范要求,在屈服前以 6~60 MPa/s 得 速率加载),并注意观察示力指针得转动、自动绘图得情况与相应得试验现象.当 主动针不动或倒退时说明材料开始屈服,记录上屈服点 FeH(主动针首次回转前得 最大力)与下屈服点 FeL(屈服过程中不计初始瞬时效应时得最小力或主动针首次 停止转动得恒定力),具体情况如图 2-4 所示(说明:前所给出得加载速率就是国 标中规定得测定上屈服点时应采用得速率,在测定下屈服点时,平行长度内得应 变速率应在 0、00025~0、0025∕s 之间,并应尽可能保持恒定。如果不能直接 控制这一速率,则应固定屈服开始前得应力速率直至屈服阶段完成).
静态拉伸法测弹性模量实验报告

静态拉伸法测弹性模量实验报告弹性模量(亦称杨氏模量)是固体材料的一个重要物理参数,它标志着材料对于拉伸或压缩形变的抵抗能力。
作为测定金属材料弹性模量的一个传统方法,静态拉伸法在一起合理配置、误差分析和长度的放大测量等方面有着普遍意义,但这种方法拉伸试验荷载大,加载速度慢,存在弛豫过程,对于脆性材料和不同温度条件下的测量难以实现。
实验原理及仪器胡克定律指出,对于有拉伸压缩形变的弹性形体,在弹性范围内,应力F 与应变L∆成正比,即式中比例系数E 称为材料的弹性模量,它是描写材料自身弹性的物理量.改写上式则有、(1)可见,只要测量外力F 、材料(本实验用金属丝)的长度L 和截面积S ,以及金属丝的长度变化量L ∆,就可以计算出弹性模量E 。
其中,F 、S 和L 都是比较容易测得的,唯有L ∆很小,用一般的量具不易准确测量。
本实验采用光杠杆镜尺组进行长度微小变化量的测量,这是一种非接触式的长度放大测量的方法。
本实验采用的主要实验仪器有: 弹性模量仪(如图1)、光杠杆镜尺组(如图2)、螺旋测微器、米尺、砝码等。
图1 弹性模量测量装置图2 光杠杆 图3 光杠杆放大原理仪器调节好后,金属丝未伸长前,在望远镜中可看到由平面镜反射的标尺的像,将望远镜的细叉丝对准标尺的刻度,读出读数为R 0;将砝码加在砝码托上后,金属丝被拉长,光杠杆镜面向后倾斜了α角.根据光的反射定律可知,此时在望远镜中细叉丝对准的是镜面反射后的标尺上的刻度R 1,其对应的入射光和反射光的夹角为2α。
设N=R 1-R 2,K 为光杠杆的前后足之间的垂直距离,D 为光杠杆镜面到标尺之间的距离,考虑到,角很小,所以有可得∆ (2)将式(2)代入式(1)即得拉伸法测定金属丝弹性模量的计算公式E (3)式中d 为金属丝的直径.实验步骤1.1 调整弹性模量仪① 调节三脚底座上的调节螺丝,使立柱铅直。
② 将光杠杆放在平台上,两前足放在平台前面的横槽内,后足放在夹子B 上,注意后足不要与金属丝相碰。
[理科实验报告精品]金属材料拉伸实验 实验报告
![[理科实验报告精品]金属材料拉伸实验 实验报告](https://img.taocdn.com/s3/m/f306e122cf84b9d528ea7a82.png)
材料力学实验报告(一)实验名称:金属材料拉伸实验实验地点实验日期指导教师班级小组成员报告人一、实验目的:二、实验设备及仪器试验机型号、名称:量具型号、名称:三、试件1)试件材料:试件①:低碳钢Q235,试件②:灰口铸铁2)试件形状和尺寸四、实验数据及计算结果屈服极限:0SS A F =σ 延伸率:%10001⨯-=L L L δ 强度极限:0bb A F =σ 断面收缩率:%10001⨯-=A A A ψ 五、拉伸曲线示意图1、低碳钢2、铸铁六、回答问题1)参考低碳钢拉伸图,分段回答力与变形的关系以及在实验中反映出的现象。
2)由低碳钢、铸铁的拉伸图和试件断口形状及其测试结果,回答二者机械性能有什么不同。
3)回忆本次实验过程,你从中学到了哪些知识。
材料力学实验报告(二)实验名称:金属材料压缩实验实验地点实验日期指导教师班级小组成员报告人一、实验目的:二、实验设备及仪器试验机型号、名称:量具型号、名称:三、试件1)试件材料:试件①:低碳钢Q235,试件②:灰口铸铁2)试件形状和尺寸四、数据及计算结果附:计算公式:屈服极限:0SS A =σ强度极限:0bb A =σ 五、压缩曲线示意图1、低碳钢2、铸铁六、回答问题1)为什么低碳钢压缩后成鼓形?2)为什么铸铁压缩时沿轴线大致成45°方向的斜截面破坏?材料力学实验报告(三)实验名称:测定金属材料弹性模量E 实验实验地点 实验日期 指导教师 班级小组成员报告人一、实验目的:二、实验设备及仪器试验机型号、名称: 引伸计型号、名称:三、 试件1)试件形状草图:2)试件尺寸: 标距:mm =L ,直径:mm =d ,横截面积:2mm =A3)试件材料:低碳钢(Q235)四、 实验数据记录五、实验数据整理六、实验结果计算G Pa )(=⋅∆⋅∆=Al LF E δ七、实验曲线图根据上面实验数据表格中的F 与L ∆的各对数据(表中第二行和第五行),在右边的坐标系中描出所有点,穿过以上各点画一射线,此射线即为反映材料E 值的曲线(请思考为什么此射线不过原点?)八、回答问题1)测材料的弹性模量E 为什么要掌握试件应力低于材料的比例极限?2)为什么用等量增截法进行实验?用等量截增法求出的弹性模量与一次加载到最终值求出的弹性模量是否相同?3)实验时为什么要加初载荷?材料力学实验报告(四)实验名称:简支梁弯曲正应力实验实验地点 实验日期 指导教师 班级小组成员报告人一、实验目的:二、实验设备及仪器试验机型号、名称:三、 实验装置1)装置图:2)装置尺寸数据:mm 800=L ,mm 300=a ,mm 20=h ,mm 10=b ,mm 5=c3)装置材料:铸铝,弹性模量GPa 200=E 电阻应变片灵敏度系数2=k四、实验数据记录五、实验数据整理六、计算应力值1)实验值计算:MPa 11==εσE 、MPa 22==εσE 、MPa 33==εσE MPa 44==εσE 、MPa 55==εσE 、MPa 66==εσEMPa 77==εσE2)理论值计算:MPa 71==Z,W Mσ、MPa Z26,2=⋅=I c M σ、MPa Z15,3=⋅=I c M σ2)实验值与理论值的相对误差:六、 回答问题1)为什么要进行温度补偿?2)据实验结果解释梁弯曲时横截面上正应力分布规律。
材料拉伸实验
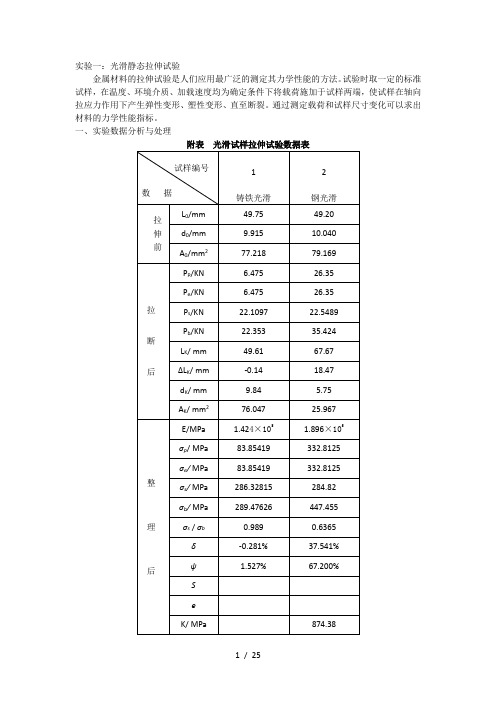
实验一:光滑静态拉伸试验金属材料的拉伸试验是人们应用最广泛的测定其力学性能的方法。
试验时取一定的标准试样,在温度、环境介质、加载速度均为确定条件下将载荷施加于试样两端,使试样在轴向拉应力作用下产生弹性变形、塑性变形、直至断裂。
通过测定载荷和试样尺寸变化可以求出材料的力学性能指标。
一、实验数据分析与处理n 0.2721S b290.6534 535.09796e B0.00406 0.17887ψeB-0.00406 -0.178871.1光滑钢1.1.1计算机数据图1—1 钢光滑拉伸试验应力~应变曲线图1—2 钢光滑拉伸试验均匀塑性变形阶段lgS~lge的线性拟合2010-4-5 15:43Linear Regression for A0709032_lgS:Y = A + B * XParameter Value Error------------------------------------------------------------A 2.9417 0.00425B 0.2721 0.00386------------------------------------------------------------R SD N P------------------------------------------------------------ 0.99321 0.00788 70 <0.0001经计算得:K=10A=102.9417=874.38MPan=B=0.27211.1.2坐标纸数据图1—3 钢光滑拉伸试验载荷~位移曲线图1—4 钢光滑拉伸试验应力~应变曲线图1—5 钢光滑拉伸试验均匀塑性变形阶段lgS~lge的线性拟合2010-4-6 20:24Linear Regression for Data1_lgs:Y = A + B * XParameter Value Error------------------------------------------------------------A 3.19016 0.05524B 0.6578 0.06625------------------------------------------------------------R SD N P------------------------------------------------------------ 0.95726 0.02645 11 <0.0001经计算得:K=10A=103.19016=1549.39MPan=B=0.65781.2光滑铸铁1.2.1计算机数据图1—6 铸铁光滑拉伸试验应力~应变曲线1.2.2坐标纸数据图1—7 铸铁光滑拉伸试验载荷~位移曲线图1—8 光滑铸铁拉伸试验应力~应变曲线(注:对于光滑铸铁,没有“均匀塑性变形阶段”,所以不能得到K,n值。
金属材料光滑静态拉伸及缺口拉伸实验

金属材料光滑静态拉伸及缺口拉伸实验学号:姓名:一.光滑静态拉伸实验2. 钢光滑拉伸应力-应变曲线(坐标纸)3. 钢光滑拉伸试验均匀塑性变形阶段logs-loge 线性拟合(坐标纸)4. 钢光滑拉伸弹性模量的测定(可求得E =208.68GPa )-1.1-1.0-0.9-0.82.622.642.662.682.702.72l o g slogeIntercept = 2.9295, Slope = 0.27614X Intercept = -10.608686. 钢光滑拉伸试验均匀塑性变形阶段logs-loge 线性拟合7. 光滑铸铁拉伸应力-应变曲线(坐标纸)应力 (N )应变 (mm)真应力 (N )真应变 (mm)l o g sloge光滑铸铁拉伸试验无均匀塑性变形阶段,故无法拟合出lgS-lge 曲线。
9. 结果讨论与分析(1)分析比较钢和铸铁σ~ɛ曲线和S~e 曲线的区别及屈强比σs / σb 、K 、 n 的大小,并根据所学知识进行解释。
答:从钢的σ~ε曲线和S~e 曲线中我们可以看出,钢的变形过程可以分为四个阶段,分别为弹性阶段、不均匀屈服塑性变形、均匀塑性变形、不均匀集中塑性变形。
在弹性变形阶段,两曲线基本重合,真实屈服应力和工程屈服应力在数值上比较接近。
这是因为试样的伸长率和截面收缩率都很小,而在塑性变形阶段,真实应力要大于工程应力,因为塑性变形阶段出现颈缩现象,此时工程应力σ=P/A0最小截面积仍按原始截面积计算,导致工程应力小于真实应力,从而表现为σ~ε曲线下降,S~e 曲线上升。
铸铁两种曲线应该是基本重合的,因为铸铁是脆性材料,只有微小的弹性变形,不发生明显的塑性变形。
铸铁屈强比σs / σb=0.981 (其中σs 用σ0.2=145.85代替)而钢的屈强比σs / σb=0.681 由此可见,铸铁的屈强比小,更容易发生脆性断裂。
钢的K=794MPa ,n=0.2理论上铸铁光滑试样在进行拉伸实验时无均匀的塑性变形阶段,故不能得到K,n 的值。
金属材料拉伸试验报告

金属材料拉伸试验报告一、实验目的。
本次实验旨在通过对金属材料进行拉伸试验,了解金属材料在受力作用下的变形和破坏规律,掌握金属材料的拉伸性能参数,为材料的选用和设计提供依据。
二、实验原理。
拉伸试验是通过在金属试样上施加拉力,使试样产生塑性变形,最终达到破坏的一种试验方法。
在拉伸试验中,通常会测定材料的抗拉强度、屈服强度、断裂伸长率等指标。
三、实验步骤。
1. 准备试样,按照标准制备金属试样,保证试样的尺寸符合要求。
2. 安装试验机,将试样安装在拉伸试验机上,并调整好试验机的参数。
3. 进行拉伸试验,开始施加拉力,记录拉力-位移曲线,直至试样发生破坏。
4. 测定参数,根据拉力-位移曲线,测定材料的抗拉强度、屈服强度、断裂伸长率等参数。
四、实验数据及结果分析。
通过拉伸试验得到的数据如下:1. 抗拉强度,XXX MPa。
2. 屈服强度,XXX MPa。
3. 断裂伸长率,XX%。
根据实验数据分析可得,材料在受拉力作用下,首先表现出线性的弹性变形,随后进入塑性变形阶段,最终发生破坏。
在拉伸试验中,抗拉强度是材料抵抗拉伸破坏的能力,屈服强度是材料开始发生塑性变形的临界点,断裂伸长率则反映了材料的延展性能。
五、实验结论。
通过本次拉伸试验,我们得出了材料的抗拉强度、屈服强度、断裂伸长率等重要参数。
这些参数对于材料的选用和工程设计具有重要意义。
在实际工程中,我们应该根据材料的拉伸性能参数,合理选择材料,并设计合适的结构,以确保工程的安全可靠。
六、实验总结。
拉伸试验是对金属材料力学性能进行评价的重要手段,通过拉伸试验可以全面了解材料在受拉力作用下的性能表现。
因此,掌握拉伸试验的原理和方法,对于材料工程师和设计人员来说是非常重要的。
在今后的工作中,我们将继续深入学习材料力学知识,不断提高对材料性能的认识,为工程实践提供更加可靠的技术支持。
七、参考文献。
1. 《金属材料拉伸试验方法》。
2. 《金属材料力学性能测试手册》。
以上就是本次金属材料拉伸试验的报告内容,希望能对大家有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金属材料静态拉伸试验
试验设施:电子拉伸材料试验机
试样
l≈10d或l=5d
1.试验结果
表1试样的原始始直径测量数据(单位:毫米)
左中右平均值
9.939.949.93
铝合金
9.927
9.919.939.92
20#钢9.9910.009.99
9.995
10.009.9910.00
铝合金
L0=66.00mm
断后的平均标距为& =72.70 mm
拉断后的断面直径平均值9.428mm
20#钢
L0=79.97 mm
断后的平均标距为4=105.01 mm
断口的直径平均值为4 =5.83mm
数据处理
1、20#钢(正火态)试样(有明显屈服平台的材料)
20#钢正火材料试样的应力应变曲线见下图。
20钢工程应力-应变曲线
读图可得Rel(屈服平台的屈服强度),Rm (抗拉强度)
2、铝合金试样(不具明显的屈服平台)
铝合金材料试样常温拉伸试验应力应变曲线如图。
600 ∏
铝工程应力-应变曲线
由于铝合金材料不具有明显的物理亏服平台,其屈服强度一般定义为“规定非 比例延长强度”此02。
即在横轴上取应变为0.2%的点(红色线条),对应的应力 即为铝合金的屈服强度。
断后伸长率:Z =
4-4
X
100% Lo
Z =务二工 100%
5。
所得结果综合如下表:
椭 S0(≡f2) S⅛f2) LO⅛m) L⅛a) [ A WRP(Mpa) RmQlPa) 20S 77.40 26.68 79.97 1105.01 65.53,31.31%
290.04 2 489.25 S 78.34 69.81 66.00 72.70 10.90% 10.15S 465.92 587.01
2、
20三钢(正火态)宏观断口示意图铝合金宏观断口图宏观断口图:
20钢:
20#钢试样在拉断之后,断口四周明显产生颈缩。
断口处可以看出有三个区域:
1.试样中心的纤维区,表面有较大的起伏,有较大的塑性变形;
2.放射区,表面较光亮平坦,有较细放射状条纹;
3.剪切唇,轴线成45。
角左右的倾斜断口
铝:
断口为和试样中轴线大约成45。
角的纤维状断口,没有颈缩,应当为为切应力达到极限,发生韧性断裂
思索题1:
提高金属材料屈服强度的方法:
影响屈服强度的内在因素有:
结合键、组织、结构、原子本性。
如将金属的屈服强度与陶瓷、高分子材料比较可看出结合键的影响是根本性的。
从组织结构的影响来看,可以有四种强化机制影响金属材料的屈服强度,这就是:
⑴固溶强化;(2)形变强化;
⑶沉淀强化和弥散强化;
(4)晶界和亚晶强化。
沉淀强化和细晶强化是工业合金中提高材料屈服强度的最常用的手段。
在这几
种强化机制中,前三种机制在提高材料强度的同时,也降低了塑性,只有细化
晶粒和亚晶,既能提高强度又能增加塑性。
影响屈服强度的外在因素有:
温度、应变速率、应力状态。
随着温度的降低与应变速率的增高,材料的屈服强度上升,尤其是体心立方金属对温度和应变速率特殊敏感,这导致了钢的低温脆化。
应力状态的影响也很重要。
思索题2:
为什么材料的塑性要以延长率和断面收缩率衡量?它们的
工程意义是什么?
答:为了确定材料的塑性变形力量以及量化比较其塑性变形力量,而且保证塑性的度量标准真正反映材料本身的塑性好坏,而不受试样的长度和几何外形的影响, 故采纳延长率和断面收缩率这两个指标来衡量。
断后延长率越大,断面收缩率越大,材料的塑性就越好,反之相反。
而且试验表明:断面收缩率和材料的缺口敏感度有肯定的关系,断面收缩率较低时,材料就对缺口比较敏感。
