k的几何意义
反比例函数K的几何意义

反比例函数K的几何意义反比例函数是一种特殊的数学函数形式,具有形如y=k/x的表达式,其中k是一个常数。
在这个函数中,x和y之间存在一种特殊的关系:当x增大时,y会减小,反之亦然。
因此,反比例函数的几何意义可以通过分析函数图像和实际例子来理解。
首先,我们可以通过绘制反比例函数的图像来揭示其几何意义。
考虑一个简单的例子:y=1/x。
对于这个函数,我们可以观察到以下几个重要的特点:1.图像总是通过第一象限的正半轴和第三象限的负半轴。
这是因为除数不能为零,所以函数在x=0时无定义。
2.图像与两条坐标轴的交点确定了函数的极值点:当x趋近于正无穷或负无穷时,y趋近于零。
这也表示当x趋近于零时,y趋近于正或负无穷。
3.图像是关于y=x和y=-x的直线对称的。
这是因为当x和y的值交换时,函数的值保持不变。
通过上述特点,我们可以揭示反比例函数的几何意义。
函数的图像形状类似于一组双曲线的分支,其中的曲线与两条坐标轴无法相交,而它们的渐近线分别与坐标轴平行。
这暗示了反比例函数的一个重要特点:随着一个变量的增加,另一个变量会减少。
例如,在y=1/x的情况下,我们可以看到当x增加时,y会减小。
1.电阻和电流:欧姆定律表明电阻与电流成反比例关系。
当电流增大时,电阻减小。
这可以解释为,当电阻较低时,电流可以更容易地通过电路,导致电流增加。
2.时间和任务完成率:假设一个人在一段时间内完成了一定数量的任务。
如果任务数量保持不变,增加时间将导致任务完成率降低。
这是因为在更长的时间内,完成的任务数量将更少。
3.运动速度和到达时间:当我们维持一定的目的地距离不变时,提高行驶速度将缩短到达目的地所需的时间。
这是因为较高的行驶速度意味着我们每单位时间所覆盖的距离更多。
这些例子揭示了反比例函数在现实生活中的广泛应用,从电路设计到时间管理,以及交通规划等等。
通过理解反比例函数的几何意义,我们可以更好地理解和应用这个数学概念。
总而言之,反比例函数是一种数学函数形式,其几何意义可以通过分析函数图像和实际例子来理解。
反比例函数中K的几何意义课件

k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中,k值决定了图 像的形状和位置。当k>0时,图像出 现在第一象限和第三象限;当k<0时 ,图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时,图像分布在第一象限和第三象限;当k<0时,图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展,反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域,如经济学、生物学等,以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念,与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系,以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小,反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用,如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解,但仍有许多未知的性质等待我们去发 现和研究。例如,反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质:当 x 增大时,y 值会减小;当 x 减小 时,y 值会增大。这是因为 xy =
k 的关系。
在图像上,反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的,且无限接近于坐标轴
。
Part
02
K的几何意义

反比例函数比例系数k 的几何意义知识梳理:如图所示,过双曲线)0(k≠=k x y 上任一点),(y x P 作x 轴、y 轴的垂线PM 、PN,垂足为M 、N ,所得矩形PMON 的面积S=PM ∙PN=|y|∙|x|.,y xk=∴||k S k xy ==,。
1.反比例函数图像上任意一点“对应的直角三角形的面积”S=12│k │2.反比例函数图像上任意一点“对应的矩形的面积”S=│k │这就说明,过双曲线上任意一点作x 轴、y 轴的垂线,所得到的矩形的面积为常数|k|。
这是系数k 几何意义,明确了k 的几何意义,会给解题带来许多方便。
典例精析专题一 K 值与面积直接应用 例1:已知如图,A 是反比例函数ky x=错误!未找到引用源。
的图象上的一点,AB 丄x 轴于点B ,且△ABO 的面积是3,则k 的值是( )A 、3B 、﹣3C 、6D 、﹣6变式练习1:如图,点P 是反比例函数6y x=错误!未找到引用源。
图象上的一点,则矩形PEOF 的面积是 .变式练习2: 如图:点A 在双曲线 y=kx 上,AB 丄x 轴于B ,且△AOB 的面积S △AOB =2,则k= .变式练习3:如图,A 是反比例函数图象上一点,过点A 作AB ⊥y 轴于点B ,点P 在x 轴上:△ABP 的面积为2,则这个反比例函数的解析式为______________.变式练习4:如图反比例函数4y x=-的图象与直线13y x =-的交点为A ,B ,过点A 作y 轴的平行线与过点B 作x 轴的平行线相交于点C ,则ABC △的面积为( )A .8B .6C .4D .2变式练习5:如图,A 、B 为双曲线x12-y =上的点,AD ⊥x 轴于D,BC ⊥y 轴于点C ,则四边形ABCD 的面积为 。
A B Px y OA OBC xyOABxy:例2:如图1所示,直线l 与双曲线)0(ky >=k x交A 、B 两点,P 是AB 上的点,试比较⊿AOC 的面积S 1,⊿BOD 的面积S 2,⊿POE 的面积S 3的大小:。
[整理版]正比例函数K的几何意义专
![[整理版]正比例函数K的几何意义专](https://uimg.taocdn.com/299fe77a82c4bb4cf7ec4afe04a1b0717fd5b32a.webp)
当k>0时,直线从左下方向右上方倾斜,倾斜角α为锐角;当k<0时,直线从左 上向右下方倾斜,倾斜角α为钝角。
直线斜率与面积关系
斜率K与三角形面积
在直角坐标系中,若直线y=kx与x轴、y轴围成一个三角形,则该三角形的面积S 与斜率k之间存在关系S=1/2*|k|。
斜率K与平行四边形面积
VS
方法二
利用相似三角形的性质,若两个三角形相 似,则它们的对应边成比例。设两个相似 三角形的对应边分别为$l_1, l_2$和$l_1', l_2'$,则有$frac{l_1}{l_1'} = frac{l_2}{l_2'}$。若这两个三角形的一条 边与x轴平行,那么这条边的长度比就等 于两三角形的斜率之比,即$frac{k}{k'} = frac{l_1}{l_1'} = frac{l_2}{l_2'}$。
工程学中效率与工作量关系
工作效率与工作量关系
在工程学中,工作效率η通常与工作量W成正比关系。高效率意味着在相同时间内可以完成更多的工 作,即η=kW,其中k为比例系数。
机器性能与工作负载关系
机器的性能表现通常与其工作负载成正比。当机器承受的负载增加时,其性能表现也会相应提升,以 保持稳定的工作效率,即P=kW,其中k为比例系数。
正比例函数与反比例函数关系
01
正比例函数和反比例函数是两种不同类型的函数,它
们之间没有直接的转化关系。
02
正比例函数的自变量和因变量之间是线性关系,而反
比例函数的自变量和因变量之间是倒数关系。
03
在平面直角坐标系中,正比例函数的图像是一条过原
点的直线,而反比例函数的图像是一条双曲线。
反比例函数中k的几何意义

【主干必备】 反比例函数中比例系数k的几何意义 设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 2
·OA·AP=
1 |m|·|n|=
2
1 |mn|=
2
1 2
|k|.
(2)过点P分别作x轴、y轴的垂线,垂足为A,B,
值为 世纪金榜导学号( D )
A.5
B.-5
C.10
D.-10
3.(2019·哈尔滨木兰期末)已知P是反比例函数y= k
x
(k≠0)图象上一点,PA⊥x轴于A,若S△AOP=4,则这个反
比例函数的解析式是 ( C )
A.y= 8
x
C.y= 8 =- 8
x
D.y= 4 或y=- 4
则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
【微点警示】 因为反比例函数y= k (k是常数,k≠0)中的k有正、负之
x
分,所以在利用解析式求矩形或三角形的面积时,都应 加上绝对值符号;已知矩形或三角形的面积求反比例函 数的解析式或k的值时,要根据函数的图象所在的象限 确定k的正负.
x
x轴于点B交反比例函数y= 2 的图象于点C,连接OA,OC,
x
则△OAC的面积为 ( B )
A.2
B.3
C.6
D.8
2.(2019·达州达川区期末)如图所示,点A是反比例函
数y= k 的图象上的一点,过点A作AB⊥x轴,垂足为B,点
x
C为y轴上的一点,连接AC,BC.若△ABC的面积为5,则k的
【核心突破】
中考数学 考点5 反比例函数中K值的几何意义(原卷版)
反比例函数中k值的几何意义的问题会以选择题、填空题或解答题的形式出现,当以选择题或填空题的形式出现时,一般会是选择题或填空题中较难的题,在解答题中也会以偏难一点的形式出现。
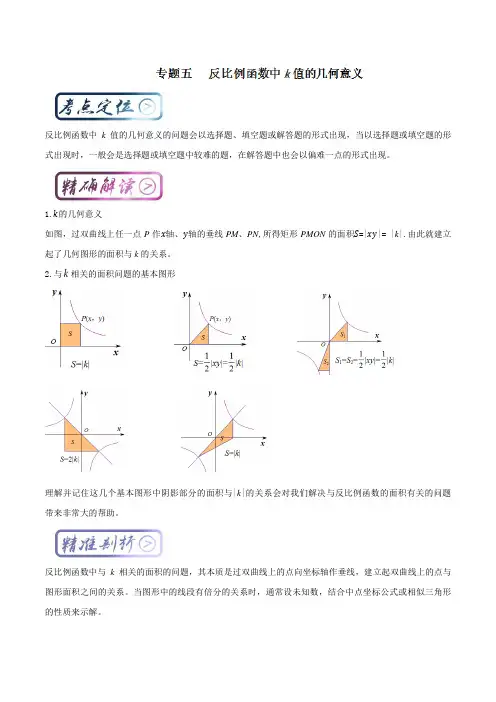
1.k的几何意义如图,过双曲线上任一点P作x轴、y轴的垂线PM、PN,所得矩形PMON的面积S=|xy|= |k|.由此就建立起了几何图形的面积与k的关系。
2.与k相关的面积问题的基本图形理解并记住这几个基本图形中阴影部分的面积与|k|的关系会对我们解决与反比例函数的面积有关的问题带来非常大的帮助。
反比例函数中与k相关的面积的问题,其本质是过双曲线上的点向坐标轴作垂线,建立起双曲线上的点与图形面积之间的关系。
当图形中的线段有倍分的关系时,通常设未知数,结合中点坐标公式或相似三角形的性质来示解。
例1.在反比例函数4 yx=的图像中,阴影部分的面积不等于4的是 ( )A B C D例2.如图,Rt AOBV的一条直角边OB在x轴上,双曲线(0)ky kx=>经过斜边OA中点C,与另一直角边交于点D,若9OCDS=V,则k的值为__________.例 3.如图,在平面直角坐标系中,Rt ABO∆的顶点O与原点重合,顶点B在x轴上,90ABO∠=︒, OA与反比例函数()0ky kx=≠的图像交于点D,且2OD AD=,过点D作x轴的垂线交x轴于点C.若ABCDS四边形=10,则k的值为___________yxOyxOyxOyxO1.如图所示,直线l 与双曲线k y x =(k >0)交于A ,B 两点,点P 在线段AB 上,试比较△AOC 的面积1S ,△BOD 的面积2S ,△POE 的面积3S 的大小关系。
2.如图,矩形ABCD 的边分别与两坐标轴平行,对角线AC 经过坐标原点,点D 在反比例函数y=k x(x >0)的图象上.若点B 的坐标为(﹣2,﹣2),则k=_____.3.如图,反比例函数()0k y x x=>的图像交Rt OAB ∆的斜边OA 于点D ,交直角边AB 于点C ,点B 在x 轴上,若OAC ∆的面积为5,:1:2AD OD =,则k 的值为1.如图所示,在平面直角坐标系中,矩形ABCD 的BC 边落在y 轴上,其它部分均在第一象限,双曲线y=k x过点A,延长对角线CA交x轴于点E,以AD、AE为边作平行四边形AEFD,若平行四边形AEFD的面积为4,则k值为()A. 2B. 4C. 8D. 122.如图,Rt△OAB的边OA在x轴上,点B在第一象限,点D是斜边OB的中点,反比例函数kyx=经过点D,若S△AOD=6,则k=________.3.如图所示,反比例函数y=kx(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值为_______.4.如图,已知第一象限内的点A在反比例函数2yx=上,第二象限的点B在反比例函数kyx=上,且OA⊥OB,sinA3,则k的值为________.5.反比例函数6yx=与3yx=在第一象限的图象如图所示,作一条平行于x轴的直线,分别交双曲线于A,B两点,连接OA,OB,求△AOB的面积。
K的几何意义
专题反比例函数中k的几何意义及应用研究函数问题要透视函数的本质特征。
反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N(如图1所示),则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。
从而有。
在解有关反比例函数的问题时,若能灵活运用反比例函数中k的几何意义,会给解题带来很多方便。
现举例说明。
应用一:比较面积大小例1、如图2,在函数(x>0)的图象上有三点A、B、C。
过这三点分别向x轴、y轴作垂线。
过每一点所作的两条垂线与x轴、y轴围成的矩形的面积分别为,则()。
A、 B、C、 D、解:根据反比例函数中k的几何意义可知。
所以。
故选D。
应用二:求面积例2、若函数与函数的图象相交于A、C两点,AB垂直x轴于B,则△ABC的面积为()。
A、1B、2C、kD、分析:如图3,若先求出A、C两点的坐标,再求△ABC的面积,则解题过程复杂烦琐。
若能利用反比例函数中k的几何意义来解,则快刀斩乱麻。
解:由反比例函数图象关于原点成中心对称知O为AC中点。
根据反比例函数中k的几何意义,有:。
又△ABO与△BOC是等底等高的三角形,∴。
故选A。
应用三:确定解析式例3、如图4,反比例函数与一次函数的图象相交于A点,过A点作AB⊥x轴于点B。
已知,直线与x轴相交于点C。
求反比例函数与一次函数的解析式。
解:由反比例函数中k的几何意义知,故。
又反比例函数图象的一支在第二象限,所以。
从而可知,两个函数的解析式分别为和。
K值的几何意义
一丶知识回顾二丶讲授新知例1.如图所示,过双曲线)0(k≠=k xy 上任一点),(y x P 作x 轴、y 轴的垂线PM 、PN,垂足为M 、N ,所得矩形PMON 的面积S=PM ∙PN=|y|∙|x|.,y xk=∴||k S k xy ==,。
总结:过双曲线上任意一点作x 轴、y 轴的垂线,所得到的矩形的面积为常数|k|。
例2.如图,A 为双曲线上一点,过A 作AC ⊥x 轴,垂足为C ,且 S AOC =2.求该反比例函数解析式;练习1.如图3中,在xy 1=的图象上有两点A 、C ,过这两点分别 向x 轴引垂线,交x 轴于B 、D 两点,连结OA 、OC ,记△ABO 、△CDO 的面积 为是S 1、S 2,则S 1与S 2的大小关系是( )A.21S S >B.21S S <C.21S S =D.不确定表达式y=kx(k ≠0) 图 象k>0k<0性 质1.图象在第一、三象限;2.每个象限内,函数y 的值随x 的增大而减小.1.图象在第二、四象限; 2.在每个象限内,函数y 值随x 的增大而增大.xyOA C 图3例3.如图所示的三个反比例函数xk y x ky x k y 321,,===在x 轴 上方的图象,则321,,k k k 的大小关系是 ( ) A .321k k k >> B .123k k k >> C .132k k k >> D .213k k k >>例 4.如图,已知双曲线ky x=(0x >)经过矩形OABC 的边AB BC ,的中点F E ,,且四边形OEBF 的面积为2,求K 的值。
思考:在上述例3中,如果E ,F 分别为BC 丶BA 的三等分点,求K 的值; 如果E ,F 分别为BC 丶BA 的三等分点,求K 的值。
xFyCB EO A。
浅谈反比例函数中的k值法解题
浅谈反比例函数中的“K ”值法解题摘 要:随着新课程标准的推进,近几年,在中考试题中关于反比例函数方面的试题出现了不少新题型。
而反比例函数的“K ”值是一个最关键的因素,可以说是反比例函数的精髓所在。
接下来,让我们一起探讨一下反比例函数中利用“K ”值法解题的问题。
关键词:反比例函数 “K ”值 象限 图像所谓“K ”值法解题,就是通过反比例函数特有的“K ”值的一些性质进行分析解题。
结合近几年中考题,“K ”值主导的反比例函数习题越来越多。
这里就反比例函数的“K ”值的意义来解决问题进行例析。
以下是利用“K ”值求解关于面积、反比例函数性质、反比例函数图像及反比例函数和正比例函数相结合等方面的解法淡析。
一、“K ”值的几何意义及利用其求相关图形面积研究函数问题要透视函数的本质特征。
所以,我们先从“K ”值的本质出发对其进行精确剖析。
下面就是反比例函数的几何意义。
反比例函数y=x k (k ≠0)中,比例系数k 有一个很重要的几何意义。
那就是:过反比例函数y=xk (k ≠0)的图像上任意一点P 作x 轴,y 轴的垂线PM 、PN ,垂足为M 、N (如图1-1所示),则矩形PMON 的面积S=PM ·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x 轴、y 轴的垂线,它们与x 轴、y 轴所围成的矩形面积为常数k 。
从而有PNO S ∆=PMO S ∆=k 21。
在解有关反比例函数的问题时,若能灵活运用反比例函数中k 的几何意义,会给解题带来很多方便。
现举例说明。
例1.已知点C 为反比例函数6y x=-上的一点,过点C 向坐标轴引垂线,垂足分别为A 、B ,那么四边形AOBC 的面积为 。
解析:因为四边形AOBC 的面积S=CA ·CB=xy x y =∙,又因为6y x=-,所以xy k =, 即S=6-=6,故四边形AOBC 的面积为6。
例2.(03年全国初中数学联赛试题)若函数kx y =(k >0)与函数1y x=的图象相交于A 、C 两点,AB 垂直x 轴于B ,则△ABC 的面积为( )。
一次函数k的几何意义
一次函数k的几何意义一次函数是数学中的一种基本函数类型,也是最简单的函数类型之一。
它的一般形式为y=kx+b,其中k和b是常数,x和y是变量。
在这个函数中,x的指数为1,因此它被称为一次函数。
一次函数在数学中有着广泛的应用,特别是在几何学中,它有着非常重要的几何意义。
一次函数的几何意义可以通过它的图像来理解。
一次函数的图像是一条直线,它的斜率k决定了这条直线的倾斜程度,而截距b则决定了这条直线与y轴的交点。
因此,一次函数的图像可以用来描述直线的性质和特征。
一次函数的斜率k表示了直线的倾斜程度。
斜率是指直线上任意两点之间的纵向距离与横向距离的比值。
在一次函数中,斜率k表示了y轴上单位长度对应的x轴上的长度。
如果k为正数,那么直线向右上方倾斜;如果k为负数,那么直线向右下方倾斜;如果k为0,那么直线是水平的。
因此,一次函数的斜率可以用来描述直线的方向和倾斜程度。
一次函数的截距b表示了直线与y轴的交点。
截距是指直线与y轴相交的点的纵坐标。
在一次函数中,截距b表示了当x=0时,直线与y轴的交点的纵坐标。
因此,一次函数的截距可以用来描述直线与y轴的位置关系。
通过斜率和截距,我们可以进一步了解一次函数的几何意义。
例如,当斜率为正数时,直线向右上方倾斜,表示y随着x的增加而增加;当斜率为负数时,直线向右下方倾斜,表示y随着x的增加而减少。
而当截距为正数时,直线与y轴的交点在y轴的正半轴上方,表示y的值始终大于0;当截距为负数时,直线与y轴的交点在y轴的负半轴上方,表示y的值始终小于0。
除了斜率和截距,一次函数还有其他的几何意义。
例如,一次函数的导数表示了直线的斜率,因此可以用来描述直线的变化率。
一次函数的积分表示了直线下方的面积,因此可以用来描述直线所代表的量的大小。
一次函数的几何意义非常重要,它可以帮助我们理解直线的性质和特征。
通过斜率和截距,我们可以描述直线的方向、倾斜程度和位置关系;通过导数和积分,我们可以描述直线的变化率和所代表的量的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的面积为2,则k的值为 2
分析:
由性质⑴知,S⊿OAC=S⊿OBD= , 由S正方形OCED= S⊿OAC+S⊿OBD+SOCED=4S⊿OBD
y2
C AE
得,k k 2 4 k ,
解得2,k2=2
2
o 图④
B Dx
探究2:如图,在x轴的正半轴上依次截
取 A反 P⊿ ⊿ 为 求于由=S⊿⊿1A32OO,1OA比OSSO,是,41PP11AA3PA3S,+P35例SPA5=7AA1214S=,241A3,A,S35A函2A+,,之+可112SS4A,1,13PS数,⊿间AA5分2233与=+O⊿S+4,2的y⊿别A,=S143S⊿P=,A2A关P34得4OAA2AA++421/P系S34,15A出PSx4S5=P,,24(52A3,A4,Sx5AP=+的A32≠分25AA,2S,S,05,值4,535别),A得的⊿。并4作=直图A设Ax2角轴象4P其A3三的A相5面,3S垂角交,2积过线形于分点12与点别AS13,分可由 S析 知13n此=: :S1nS=====可由41SSSS⊿O得⊿⊿⊿⊿性POOOO141PPPP出质AS23451AAAA5⑴:2345 15
y
0
x
y
0
x
设P(m, n)是双曲线 y k (k 0)上任意一点 x
(1)过P分别作x轴,y轴的垂线,垂足分别为A,B ,
则S矩形OAPB OA AP | m | • | n || k |(如图所示).
y
y
B
P(m,n)
oA
x
B
P(m,n)
oA
x
设P(m, n)是双曲线 y k (k 0)上任意一点 x
=4+ 1 (2 8) 3-4=15 2
y
A(1,8 )
B (4,2 ) oC D x
探究1:反比例函数 y m 与一次函数y=kx+b交于点 A(1,8 ) 和B (4,n), x
求:⑴这两个函数的解析式;⑵三角形⊿AOB的面积。
⑵解法1:设直线y=-2x+10 与x轴、y轴分别交于点C,D
EA
3 F SS11
B
SS33 SS22
oC D x
图②
3
(1)如图,A是反比例函数图象上一点,过点A作
AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则这
个反比例函数的解析式为
y4
.
xy
B A(m,n)
Po
x
点评:将△ABO通过“等 积变换”同底等高变为 △ABP
⑶ 图象如上图关③于,原A、点BO是对函称数的y任 意4x 的
60
3P…将情3如,,当形图nP,堂:4,,分检在…别反测,过比P第这n例,3些函小它点数题们作y的的=x2横轴结/x坐与(论x标y>由轴0依)的的特次垂图殊为线象推1,,上广2图有,到中点3一所P,1般构,4,成的P2,
的阴影部分的面积,从左到右依次为S1,S2,S3,…,
Sn,则S1+S2+ … + S n 的值为
3.如图,已知双曲线
y
k x
(k
0)
经过直角三角形OAB
斜边OA的中点D,且与直角边AB相交于点C.若点A的
坐标为(-6,4),则△AOC的面积为 ( B )
A.12 B.9 C.6 D.4
分析:∵A(-6,4),由D为
A
O∴A双的曲中线点的可解知析,式D为(:-y3,2) 6
x
y6 x
SOAP
1 2
OA
AP
1 2
|
m
|
•
|
n
|
1 2
|
k
|
小结:(1)反比例函数 y= k (k≠0)图象上一点 P(x,y)向 x 轴作垂线,垂足x 为A ,则构成△POA的面
S 1
积为 |k| ,即当k一定时,
2
ΔPO A也为定值。
P O Ax
y2 x
k y
S△ABC=
A
C
O
↑y
D(-3,2)
由性质1可知,S △OBC=3
C
于是有,
B
O →x
S△AOC +3=S △AOB= 12
∴ S△AOC =9
1、在 y 1 的图象中,阴影部分面积不为1的是( B ) x
想一想
若将此题改为过P点 作y轴的垂线段,其结
论成立吗?
y
P(m,n) oA x
y A P(m,n)
o
x
⑷ 你体会到哪些解题的思想和方法? 数形结合法,转化的数学思想方法
3.如图,已知双曲线
y
k x
(k
0)
经过直角三角形OБайду номын сангаасB
斜边OA的中点D,且与直角边AB相交于点C.若点A的
坐标为(-6,4),则△AOC的面积为 ( B )
A.12 B.9 C.6 D.4
分析:∵A(-6,4),由D为
A
O∴A双的曲中线点的可解知析,式D为(:-y3,2) 6
(2)过P作x轴的垂线 , 垂足为 A,则
SOAP
1 2
OA
AP
1 2
|
m
|•
|
n
|
1 2
|
k
|
以上两条性质 在课本内没有 提及,但在这 几年的中考中 都有出现,所 以在这里要把 它总结出来。
y
P(m,n)
oA
x
y P(m,n)
oA
x
⑶如图③,设P(m,n)关于原点的对称点 P′(-m,-n),过P作x轴的垂线与过P′作y轴的
垂线交于A点,则S⊿PAP′= 2 | k |
图③
如图:点A在双曲线
y
k x
上,AB⊥x轴于B,
且⊿AOB的面积S⊿AOB=2,则k= -4
分析:由性质1可知,
S⊿AOB= | k | 2 2
∴k=±4, ∵k<0, ∴k=-4
y k (k 0)
⑵如图②,点P是反比例函数
x
图象上的
通过这节课的学习,你有什么收获?
⑴ 反比例函数图象上任意一点“对应的直角三角形” 面积S1与k值有什么关系?
⑵ 反比例函数图象上任意一点“对应的矩形”面积S2 与k值有什么关系?(总结为K的几何意义)
⑶ 若反比例函数与正比例函数y=kx ( k≠0) 存在两 个交点P(x1,y1),Q(x2,y2),则点P与点Q有什么关 系?
y
(0,10 ) D A(1,8 )
则 C (5,0),D(0,10), 于是
S⊿OAB=25 - 5 -5 =15
B (4,2 )
o
C(5,0) x
探上,究且1.AB如∥图x,轴点,AC在、双D在曲x线轴上y , 若1x 四上边,形点ABB在C双D的曲面y线积 3x
为矩形,则它的面积为 2
.
y=-2x+10
的方法,叫做待定系数法。
探究1:反比例函数 y m 与一次函数y=kx+b交于点 A(1,8 ) 和B (4,2), x 求:⑴这两个函数的解析式;⑵三角形⊿AOB的面积。
⑵解法2: 如图,过A作AC⊥x轴于C,过B点 作BD⊥x轴于D 由性质(1)知:S⊿OAC=S⊿OBD=4, ∴S⊿OAB=S⊿OAC+S梯形ACDB-S⊿OBD
两点,AC∥y轴,BC ∥ x轴, ⊿ABC的面积为S,则( )
A.CS=4 B.4<S<8
C.S=8 D.S>8
y
A o
x
BC
图③
请你模仿上题,在双曲线上做出 面积为4的几何图形
探究1.如图④,已知双曲线
y k (k 0) x
经过正方形
OCED的边ED的中点B,交CE于点A,若四边形OAEB
D x
B y=-2x
y2 x
2 k y
S四边形ACBD=
A
C
O
D x
B y=-2x
y2 x
2 k y
S△ABE=
A
C
O
E
D x
B y=-2x
y2 x
4 k y S矩形AEBF=
A
C
O
E
F D
x B
y=-2x
(用n的代数式
表示)
2n
2
S1 2 2
n 1
2
S1 S 2 2 3
(1, 2 )
2
1
S1 S 2 S3 2 4
……………
2
(2, ) 2
S2
2
(3, ) 3
(4, 2)
S1 S 2 S3 Sn
S3
4
Sn
2 2 2n n1 n1
中得:m=1×8=8, 故所求函数解析式为
y
8
x
∴B(4,n)
x
将A(1,8 ) 和B (4,2)代入
y
A
B
o
x
y=kx+b
k b 8 中得:4k b 2
解得:bk
2 10
先设出函数解析式,再根据 条件确定解析式中未知的系
故所求的一次函数的解析式为:数,从而具体写出这个式子
一点,过P分别向x轴,y轴引垂线,垂足分别为A,C,阴
影部分的面积为3,则这个反比例函数的解析式是
y3 x
