追赶法
微分方程数值解追赶法

微分方程数值解追赶法追赶法,也称为三对角矩阵算法,是一种用于求解线性微分方程的数值方法。
这种方法主要基于矩阵分解和迭代的思想,能够有效地解决微分方程的数值求解问题。
在微分方程的数值解法中,追赶法通常用于求解形如 (y' = f(x, y)) 的常微分方程。
其基本思想是将微分方程转化为差分方程,然后通过迭代的方式逐步逼近微分方程的解。
具体来说,追赶法的步骤如下:矩阵分解:首先,将微分方程 (y' = f(x, y)) 转化为差分方程的形式。
然后,将差分方程中的系数矩阵进行分解,将其分解为一个下三角矩阵 (L)、一个对角矩阵 (D) 和一个上三角矩阵 (U)。
这样,差分方程可以转化为(D^{-1}Lx = D^{-1}b) 的形式。
迭代求解:接下来,使用迭代法求解 (D^{-1}Lx = D^{-1}b)。
通常,可以选择Gauss-Seidel迭代法或者SOR(Successive Over-Relaxation)迭代法等。
在每次迭代中,先求解下三角矩阵 (L) 的部分,然后求解对角矩阵(D) 的部分,最后求解上三角矩阵 (U) 的部分。
通过不断迭代,逐步逼近差分方程的解。
收敛性判断:在迭代求解的过程中,需要判断迭代的解是否收敛。
通常,可以通过比较相邻两次迭代的解的差值来判断是否收敛。
当差值小于某个预设的阈值时,认为迭代收敛。
解的输出:当迭代收敛后,可以得到微分方程的数值解。
此时,可以将解输出到控制台或者保存到文件中。
追赶法的优点在于其算法简单、易于实现,并且对于大规模的微分方程求解问题具有较高的计算效率和精度。
然而,追赶法也存在一些局限性,例如对于某些特殊类型的微分方程可能不适用,需要进行特殊处理。
追赶法

追赶法/平方根法 例2.4.1 设4阶方程组AX=B 为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------121653342231124321x x x x这就是一个三对角方程组,既系数矩阵除了对角线的“三斜线”以外的元素均为0。
用追赶法求解三对角方程组的一种做法是把系数矩阵A 写成下列形式的LU 分解(这里采用Doolittle 分解,类似地也可以采用Crout 分解):()1.4.2321111153342231124321432⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------u u u u l l l 即L 为单位上三角阵,两斜行,主对角线元素为1,其下方的斜行元素特定;U 为上三角阵,也是两斜行,主对角线元素特定,其上方斜行的元素与A 对应的斜行元素相同(直接验算可知道)。
利用矩阵乘法规则,按顺序依次考虑A 的11a ->21a ->22a ->32a ->33a ->43a ->44a ,并对比(2.4.1)式两端可得2=1u → 1u =2 -1=12u l → 2l =-1/1u =-1/23=-2l +2u →2u =3+2l =5/2-2=23u l → 3l =-2/2u =-4/5 4=-23l +3u → 3u =4+23l =12/5-3=34u l →4l =-3/3u =-5/45=-34l +4u 4u =5+3⨯(-5/4)=5/4即得分解⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------4/535/1222/51214/515/412/115334223112于是用前推过程求解下三角方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---121614/515/412/114321y y y y 得⎪⎪⎩⎪⎪⎨⎧=+==+-==+==2/54/515/65/4242/1163423121y y y y y y y再用回代过程求解上三角方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---2/55/6464/535/1222/5124321x x x x 得⎪⎪⎩⎪⎪⎨⎧=+==+==+===52/)6(4)2/5/()24(3)5/12/()35/6(2)4/5/()2/5(2132434x x x x x x x 即的方程组的解()T x 2,3,4,5=.从实例看到,三对角方程组的追赶法是三角分解发的一种特殊应用,因此,一般地,如果对三角矩阵n n R A ⨯∈非奇异,其顺序主子式)1,...,2,1(0-=≠∆n i i ,则解三对角方程组Ax=d:()2.4.2...............12112111122211⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----n n n n n nn n n d d d d x x x x b a c b a c b a c b 的追赶法可描述如下:令A=LU ,则⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----n n n nn nn n n u c u c u c u l l l b a c b a c b a c b 1122113211122211......1 (1)11.........利用矩阵乘法规则,可求L 和U 的计算公式:⎩⎨⎧=-===--)),...3,2((/1111n i c l b u u a l b u i i i i i i i (2.4.3)于是,求解LY=D 得⎩⎨⎧=-==-)),...3,2(111n i y l d y d y i i i i (2.4.4)再求解UX=Y ,得三对方程组的解⎩⎨⎧=-==+)),...3,2(/)(/1n i u x c y x u y x i i i i i n n n (2.4.5)上述3个公式便组成解三角方程组的追赶法,国外称Thomas 算法。
用追赶法解方程组步骤

用追赶法解方程组步骤方程组是数学中常见的问题之一,解方程组的方法有很多种,其中一种常用的方法是追赶法。
下面我们来详细介绍用追赶法解方程组的步骤。
步骤一:给定方程组我们需要给定一个方程组。
方程组可以由多个方程组成,每个方程中包含多个未知数和常数项。
我们的目标是求解出方程组中的未知数。
步骤二:将方程组转换为矩阵形式为了方便计算,我们将方程组转换为矩阵形式。
即将每个方程的未知数和常数项放在一个矩阵中,方程组的系数矩阵和常数矩阵分别用A和B表示。
步骤三:进行初等行变换接下来,我们需要进行初等行变换。
初等行变换包括交换两行、用非零常数乘以某一行、将某一行的倍数加到另一行上。
通过初等行变换,我们可以将方程组转化为一个三角矩阵或者行最简形。
步骤四:回代求解在经过初等行变换后,我们得到了一个三角矩阵或者行最简形。
接下来,我们可以通过回代的方式求解出未知数的值。
回代的过程就是从最后一行开始,依次代入求解出上一行的未知数,直到求解出所有的未知数。
步骤五:检验解的正确性在求解出未知数的值后,我们需要检验解的正确性。
即将求解出的未知数代入原方程组中,检查等式是否成立。
如果方程组中的每个等式都成立,则我们得到了方程组的解。
追赶法是一种有效的求解方程组的方法,它可以通过化简方程组的形式,将复杂的计算转化为简单的计算,从而节省时间和精力。
通过追赶法,我们可以快速求解出方程组中的未知数,并检验解的正确性。
在实际应用中,追赶法广泛应用于线性方程组的求解。
线性方程组是一种常见的方程组,它包含线性关系,可以用来描述很多实际问题,如电路分析、力学问题等。
追赶法的优势在于其简单易行、计算速度快的特点,使得它成为解决线性方程组的常用方法之一。
总结起来,用追赶法解方程组的步骤包括给定方程组、将方程组转换为矩阵形式、进行初等行变换、回代求解和检验解的正确性。
通过这一系列步骤,我们可以快速求解出方程组中的未知数,并验证解的正确性。
追赶法在线性方程组的求解中具有重要的应用价值,它不仅能够提高计算效率,还能够简化计算过程,使得解方程组变得更加简单和直观。
追赶法(Thomas算法)

二、解三对角线性方程组的追赶法 定理1:满足引理1条件的三对角方阵A有如下形式的 唯一的克劳特分解。
p1 a2 A= pn
p2 a3 pn 1 an
1 q1 1 q2 =PQ 1 qn 1 1
其中
p1 = b1 (i = 1,2,, n 1) qi = ci pi p = b a q (i = 2,3,, n ) i i i 1 i
解三对角线方程组Ax = f可化为求解两个三角形 方程组
Py = f
Qx = y
(1) 解 Py = f
p1 a2 ( P, f ) = p2 a3 pn 1 an f1 f2 f3 pn f n
得
{
y1 = f1 / p1
yi = ( f i ai yi 1 ) / piຫໍສະໝຸດ (i = 2,3,, n )
( 2) 解 Qx = y
1 q1 1 q2 1 qn 1 1
x1 y1 x2 = y2 x y n n
得
xn = y n
xi = yi qi xi +1
i = n 1 , , 2 ,1
作业: P50 习题11
§2-4
追赶法(Thomas算法 算法) 追赶法 算法
一、对角占优矩阵
若矩阵A = ( aij )n× n 满足
|aii |> ∑|aij |
j =1 j ≠i ≠i
n
i = 1 , 2 , , n
则称A为严格对角占优矩阵.
若矩阵A = ( aij )n× n 满足
|aii | ∑|aij | ≥
j =1 j ≠i
n
i = 1 , 2 , , n
则称A为弱对角占优矩阵.
matlab追赶法解101阶三对角方程组

在探讨MATLAB追赶法解101阶三对角方程组之前,我们首先需要了解什么是追赶法和什么是三对角方程组。
追赶法又称托马斯算法,是一种用于求解带状矩阵(即只有主对角线和两条相邻的对角线上有非零元素的矩阵)的线性方程组的方法。
而三对角矩阵就是只有主对角线和两条相邻的对角线上有非零元素的矩阵。
在实际应用中,求解带状矩阵的线性方程组是非常常见的,特别是在数值计算和科学工程领域。
现在,让我们深入探讨MATLAB追赶法解101阶三对角方程组的方法和具体步骤。
一、MATLAB追赶法解101阶三对角方程组1. 概念介绍101阶三对角方程组是一个非常大的线性方程组,通常使用传统的高斯消元法来求解会耗费大量的时间和计算资源。
而MATLAB追赶法通过利用三对角矩阵的特殊性质,可以有效地简化计算过程,并且节省大量的内存和计算资源。
2. 追赶法步骤(1)将原方程组化为追赶法所需的形式;(2)利用追赶法求解三对角线性方程组。
二、追赶法求解101阶三对角方程组的实现过程1. 将原方程组化为追赶法所需的形式对于101阶三对角方程组,我们首先需要将其化为追赶法所需的形式。
这个过程涉及到选取合适的追赶元和追赶子以及对原方程组的变形,将其化为追赶法能够直接处理的形式。
2. 利用追赶法求解线性方程组一旦将原方程组化为追赶法所需的形式,我们就可以利用追赶法对其进行求解。
追赶法的核心是通过追赶子的迭代计算,逐步求得线性方程组的解。
在MATLAB中,可以使用内置的追赶法求解函数,也可以编写自定义的追赶法算法来实现对101阶三对角方程组的求解。
三、个人观点和理解在实际工程和科学计算中,追赶法是一种非常有效的求解带状矩阵线性方程组的方法。
对于大规模的三对角方程组,特别是高阶的情况,传统的直接求解方法往往会遇到内存和计算资源的限制,而追赶法能够通过精巧的迭代计算,在保证解的精度的显著提高计算效率。
在MATLAB中,通过调用内置的追赶法函数,可以快速地求解大规模的三对角方程组,极大地方便了工程实践中的数值计算工作。
matlab追赶法

Matlab追赶法1. 简介追赶法是一种求解特殊线性方程组的数值计算方法。
在Matlab中,我们可以利用追赶法求解带有追赶矩阵的线性方程组,该方法在某些情况下比直接使用高斯消元法更加高效。
2. 追赶法原理追赶法是基于矩阵的三对角性质进行求解的。
三对角矩阵是指除主对角线外,只有上对角线和下对角线上存在非零元素的矩阵。
对于一个n阶的三对角矩阵A,我们有以下形式的线性方程组:A * x = b其中,A是一个n阶的三对角矩阵,x是未知向量,b是已知向量。
3. 算法步骤追赶法的求解过程可以分为以下步骤:3.1. 利用追赶法将矩阵化为上三角矩阵追赶法的第一步是将三对角矩阵A转化为上三角矩阵U。
这可以通过以下迭代公式实现:u[i] = a[i] (i = 1)u[i] = a[i] - c[i-1]*b[i-1]/u[i-1] (i = 2, 3, ..., n-1)3.2. 求解中间向量利用上一步得到的上三角矩阵U,我们可以通过以下迭代公式求解中间向量y:y[i] = b[i] - c[i-1]*y[i-1]/u[i-1] (i = 2, 3, ..., n)3.3. 求解未知向量最后一步是通过回代求解未知向量x。
根据回代公式,我们可以得到:x[n] = y[n]/u[n]x[i] = (y[i] - b[i]*x[i+1])/u[i] (i = n-1, n-2, ..., 1)4. Matlab代码示例以下是使用Matlab实现追赶法的示例代码:function x = tridiag_solver(a, b, c, d)n = length(d);u = zeros(n, 1);y = zeros(n, 1);x = zeros(n, 1);u(1) = a(1);for i = 2:nu(i) = a(i) - c(i-1)*b(i-1)/u(i-1);endy(1) = d(1);for i = 2:ny(i) = d(i) - c(i-1)*y(i-1)/u(i-1);endx(n) = y(n)/u(n);for i = n-1:-1:1x(i) = (y(i) - b(i)*x(i+1))/u(i);endend5. 总结追赶法是一种求解特殊线性方程组的有效方法,特别适用于三对角矩阵。
追赶法
追赶法(续)
定理:设三对角方程组系数矩阵满足下列条件: b1 c1 0 bi ai ci b a 0 n n 则它可分解为 1 u1 c1 l 1 u c 2 2 2 A LU l3 1 cn 1 ln 1 un 其中ci (i 1, 2, , n 1)为已给出的,且分解是唯一的
追赶法
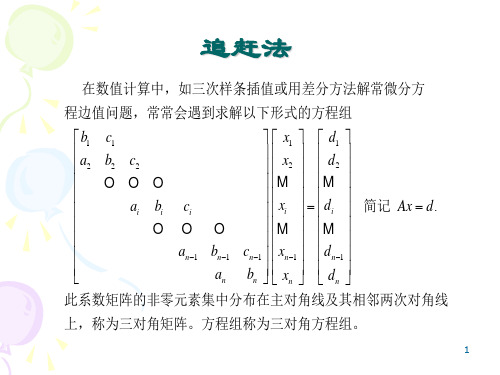
在数值计算中,如三次样条插值或用差分方法解常微分方 程边值问题,常常会遇到求解以下形式的方程组 b1 c1 x1 d1 a b c x d 2 2 2 2 2 a b c i i i xi di 简记 Ax d . an 1 bn 1 cn 1 xn 1 d n 1 x d a b n n n n 此系数矩阵的非零元素集中分布在主对角线及其相邻两次对角线 上,称为三对角矩阵。方程组称为三对角方程组。
2
ai ci 0(i 2,3, , n 1)
追赶法的计算公式
u1 b1 A LU 分解公式: li ai / ui 1 (i 2,3, , m) u b c l i i i 1 i y1 d1 解Ly d 得: yk d k lk yk 1 (k 2,3, , n) xn yn / un 再解Ux y得: xk ( yk ck xk 1 ) / uk (k n 1, n 2, ,1) 追赶法的基本思想与Gause消去法及三角分解法相同,只 是由于系数中出现了大量的零,可使计算公式简化,减少了计 算量。可证,当系数矩阵为严格对角占优时,此方法具有良好的 数值稳定性。解过程就是将系数矩阵
追赶法求解三对角方程组

追赶法求解三对角方程组追赶法,这个名字听起来就像是一种竞赛,其实它是一种解决三对角方程组的好办法,简单得让人想笑。
想象一下,你在一个热闹的市场,身边是熙熙攘攘的人群,突然你的朋友向你喊:“嘿,快来帮我算这个方程组!”你心里想,什么方程组啊,我可不想被这复杂的数学问题给吓倒。
别担心,追赶法就像你身边的超级英雄,轻松搞定这些棘手的问题。
三对角方程组的形状其实就像个台阶,每一层都有自己的高度。
我们通常会遇到的就是那种对角线上的元素大于零,旁边的元素都比较小,这样一来,整个方程组就像是在给你发出信号:“来吧,来解决我!”在这个市场里,你得学会怎么“追赶”那些神秘的数。
追赶法的核心就是把复杂的问题变得简单,想想如果你能把一个巨大的蛋糕切成小块,那你就能轻松吃掉它。
咳咳,数学也是这样!你得确定你的三对角矩阵。
这个矩阵就像是你的地图,告诉你哪里有高地,哪里有低洼。
然后,你需要开始你的追赶之旅,逐步解决每一个未知数。
听上去是不是有点像探险?这就对了!在这个过程中,你需要运用一些聪明的小技巧,比如把当前的未知数用前一个已知数来表达,仿佛在追赶一个流动的目标。
哇,数学原来可以这么有趣,仿佛在和未知数玩捉迷藏。
我们就来谈谈如何进行具体的计算。
假设你有一个三对角矩阵,分为主对角线和两条副对角线。
你得把这个矩阵转化成一个更易处理的形式。
就像你把一堆衣服整理成一个个小堆,清晰明了。
通过一些简单的运算,你可以得到一个新的方程组。
这个时候,你会发现,原本复杂的问题似乎在慢慢迎刃而解,简直就像是阳光透过云层。
然后,进入最终的“追赶”阶段。
你得逐步代入已知的值,像是在追逐那只一直跑的兔子,直到抓到为止。
这一步可能需要一些耐心,但你可以想象自己正在追逐一场美妙的冒险,哪怕有点小曲折也没关系。
在这个过程中,你会体会到一种成就感,仿佛自己是数学界的超级英雄,成功解出了一个又一个的未知数。
好啦,最后我们来总结一下追赶法的魅力。
它不仅让复杂的三对角方程组变得简单,还让整个过程充满乐趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验题目
用追赶法解线性三对角方程组:
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡322141141141124321x x x x 二、实验目的
1.熟悉掌握追赶法法的基本原理和基本方法。
2.学会用追赶法法解简单的方程组。
三、实验原理
(1)f Ly =,求y ;(2)y Ux =,求x ; 从而得到解三对角线方程组的追赶法公式。
1. 计算的递推公式:
111/b c =β
)/(1--=i i i i i a b c ββ
2. 解:f Ly =
111/b f y =
a a
b y a f y i i i i i i i )/()(11----=β
3. 解:y Ux =
n n y x =
1+-=i i i i x y x β
四、实验内容及结果
原始数据:a=[1,1,1];
b=[2,4,4,4];
c=[1,1,1];
d=[1,-2,2,-3];
追赶法解三对角方程组:
程序源代码
%machase.m
function x=machase(a,b,c,d)
%用途:追赶法解三对角方程组Ax=d
%格式:x= machase(a,b,c,d) a为次下对角线元素向量,b主对角元素
% 向量,c为次上对角线元素向量,d为右端向量,x返回解向量
n=length(a);
for k=2:n
b(k)=b(k)-a(k)/b(k-1)*c(k-1);
d(k)=d(k)-a(k)/b(k-1)*d(k-1);
end
x(n)=d(n)/b(n);
for k=n-1:-1:1
x(k)=(d(k)-c(k)*x(k+1))/b(k);
end
输入:a=[1,1,1];
b=[2,4,4,4];
c=[1,1,1];
d=[1,-2,2,-3];
machase(a,b,c,d)
结果:ans =
0.9615 -0.9231 0.7308
五、实验结果分析
追赶法为一种特殊的LU分解法。
追赶法是求解三对角矩阵的常用方法,但从整体编程角度分析,其程序编写较迭代法复杂,但通用性较好。
追赶法求解三对角矩阵不但节省存储单元,而且可以减少计算量。
