Ch1 (1.3 信号的运算)
合集下载
信号与系统-CH1
2
3 4
t
抽样信号
可以看出，（1）
Sa (t ) 为偶函数；
（2）当 （3）
t
时， S
a
(t )的振幅衰减趋近于0；
f (k ) 0 ，（k为整数，且k≠0）；
Sa (t ) 信号满足：
0
S (t )dt 2
积分）具有不连续点。 四、单位阶跃信号
1V
uc (t )
ic (t ) C 1F
1V
uc (t )
ic (t ) C 1F
_
_
_
图2
_
图1
例：RC电路如图（1）所示，C=1F，R可调，开关K在t＝0时闭合，求uc（t）， ic（t）。当R→0时， uc（t），ic（t）有何变化？
解：一阶动态电路瞬态分析可采用三要素法，有
不具有周期性的信号称为非周期信号。
例1 判断下列信号是否为周期信号，若是，确定其周期。 （1）f1(t) = sin2t + cos3t （2）f2(t) = cos2t + sinπt 解：两个周期信号x(t)，y(t)的周期分别为T1和T2，若其周期之比 T1/T2为有理数，则其和信号x(t)+y(t)仍然是周期信号，其周期为T1和 T2的最小公倍数。
同理有
f (t ) (t t0 )dt f (t0 )
δ(t) 是广义函数，不用函数“是什么”，而用函数能“干什么”来定义。
(2)乘积(加权)性质: 设f(t)为一连续函数，且在t＝0时刻有值，则有
f (t ) (t ) f (0) (t )
f (t ) (t t 0 ) f (t 0 ) (t t 0 )
CH1 信号及其表述
n1
得
x(t)
a0
n1
[
1 2
(an
jbn )e jn0t
1 2
Random Signal）
析试限工
1
第1章 信号及其描述
1.0 序（Introduction）
信号（signal）：随时间或空间变化的物理量。 信号是信息的载体，信息是信号的内容。 依靠信号实现电、光、声、力、温度、压力、流量等的传输 电信号易于变换、处理和传输，非电信号 电信号。
信号分析与处理（signal analysis and processing） 不考虑信号的具体物理性质，将其抽象为变量之间的函数关 系，从数学上加以分析研究，从中得出具有普遍意义的结论。
信号的描述（9/53）
目录 上页 下页 返退回出 29
第1章 信号及其描述 课堂习题
信号的描述（10/53）
• 求题图1-1周期三角波的频谱，并作频谱图。
x(t)
T 0T
2
2
x(t) AA2T2AAt t T
t
T t0 2
0tT 2
目录 上页 下页 返退回出 30
第1章 信号及其描述 答案
目录 上页 下页 返退回出 15
第1章 信号及其描述 思 考？
信号的分类（9/13）
某钢厂减速机上测得的振动信号波形(测点3)如图所示， 其基本波形属于何种信号？
近似的看作为周期信号
目录 上页 下页 返退回出 16
第1章 信号及其描述 (2)非确定性信号（随机信号）
信号的分类（10/13）
• 无法用明确的数学关系式表达 。其幅值、相位变化是不 可预知的，所描述的物理现象是一种随机过程。如分子热 运动，环境的噪声等，分为平稳随机信号和非平稳随机信 号。
1.3信号基本运算
f (t) = fe(t) + fo(t)
可推得： 可推得：
f (t) + f (−t) fe(t) = 2 f (t) − f (−t) fo(t) = 2
• 对离散序列： 对离散序列：
f [n] = fe[n]+ fo[n]
1 fe[n] = ( f [n]+ f [−n]) 2
1 fo[n] = ( f [n]− f [−n]) 2
f1[n]+f2[n]=
(−1 +n )
n
2 + 2n
-n
乘法： 2 乘法：
两个信号对应时刻的函数值相乘。 两个信号对应时刻的函数值相乘。例
0
t
σ >0
0
t
σ<0
0
t
σ=0
ω≠ 0
3 时移： 时移：
将原信号沿时间轴左移或右移。 将原信号沿时间轴左移或右移。 其物理意义为：表示信号的接入时间不同。 其物理意义为：表示信号的接入时间不同。
f1(t) 1 t -1
3 1
f2(t) 1 0 1 -1 2 t
0 1
f1 ( t ) + f2 ( t )
解：
-1
-1
0 1
2
3
t
例3 f1[n]=
2 n
n , n<-3 < , n≥-3 ≥
f2[n]= ；
(-1) -n 2 + n
n
, ,
n<0 n ≥0
解：
Hale Waihona Puke (−1 +2 )n
n
n<-3 < n= -3,-2,-1 n ≥0
数字信号处理课后习题Ch1
数字信号处理课后习题详解第一章1.1 试画出正弦序列sin(16πn /5)的波形，它是不是一个周期序列？若是，其周期长度是多少？解：matlab 环境下实现源代码如下： n=[0:15]; y=sin(16*pi*n/5);stem(n,y); xlabel('n'); ylabel('x(n)') 图形如下图所示。
2251685p q πππβ===，取k =p ，则周期N =p =5，即sin(16πn /5)是一个周期序列，周期长度为5；图中也可以看出这点。
1.2 判断下列序列是否是周期序列，若是，确定其周期长度。
(1) 3()cos(74x n n ππ=−解：2214337p q πππβ===∵ p ，q 是互为质数的整数，取k =q 则周期N =p =14∴周期长度为14 (2) 7cos()4sin()(nnn x ππ−=解：1284N ππ== 22147N ππ==∵N 1，N 2最小公倍数为56 ∴其周期长度为561.3 试画出如下序列的波形(1) x(n)=3δ(n+3)+2δ(n+1)-4δ(n-1)+2δ(n-2) (2)x(n)= 0.5n R 5(n)解：(1)(2)1.4 今对三个正弦信号)2cos()(1t t x a π=、)6cos()(2t t x a π−=、)10cos()(3t t x a π=进行理想采样，采样频率为π8=Ωs ，求这三个采样输出序列，比较其结果。
画出x a 1(t )、x a 2(t )、x a 3(t )的波形及采样点位置并解释频谱混叠现象。
解：matlab 环境下实现源代码如下：t=-1:0.01:1; x1=cos(2*pi*t); x2=-cos(6*pi*t); x3=cos(10*pi*t); t2=-1:0.25:1; y1=cos(2*pi* t2);y2=-cos(6*pi* t2);y3=cos(10*pi* t2);subplot(311)plot(t,x1);xlabel('t');ylabel('Xa1(t)') holdstem(t2, y1)subplot(312)plot(t,x2);xlabel('t');ylabel('Xa2(t)') holdstem(t2, y2)subplot(313)holdstem(t2, y3)plot(t,x3);xlabel('t');ylabel('Xa3(t)') 三个信号波形已知πω8=，则4182,42===πππωs T 。
1.3信号的基本运算
信号与线性系统
1.3 信号的基本运算
信号的＋、－、 ＋、－、× 一、信号的＋、－、×运算 两信号f1(·) 和f2 (·)的相+、－、×指 ) )的相+、－、× 同一时刻两信号之值对应相加减乘 两信号之值对应相加减乘。 同一时刻两信号之值对应相加减乘。
信号与线性系统
两信号相加和相乘
• 同一瞬时两信号对应值相加（相乘）。 同一瞬时两信号对应值相加（相乘）。
• 将f (t) → f (at) ，称为对信号f (t)的尺度变 换。 则波形沿横坐标压缩； • 若a >1 ，则波形沿横坐标压缩；若0< a < 1 ， 则展开。 则展开。如
信号与线性系统
• 对于离散信号，由于f (ak) 仅在ak为整数 对于离散信号， 时才有意义， 时才有意义， 进行尺度变换时可能会使部 分信号丢失。 分信号丢失。因此一般不作波形的尺度变 换。
信号与线性系统
平移、反转、 平移、反转、尺度变换相结合
三种运算的次序可任意。 进行。 三种运算的次序可任意。但一定要注意始终对时间t 进行。 例：已知f (t)，画出f (– 4 – 2t)。
信号与线性系统 已知f ，画出f 已知 (t)，画出 (– 4 – 2t)。 。
也可以先压缩、再平移、最后反转。 也可以先压缩、再平移、最后反转。
信号与线性系统
2. 平移
• 将 f ( t ) → f ( t – t 0) ， f ( k ) → f (t – k0)称为对信号f (·)的平移或移位。 ) 平移或移位。 >0， 若t0 (或k0) >0，则将f (·)右移；否则左 )右移； 移。
信号与线性系统
平移与反转相结合
• 已知f(t)如下图所示，请画出f(2-t)
1.3 信号的基本运算
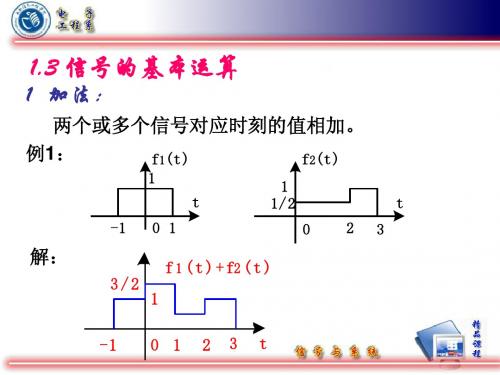
信号的＋、－、 ＋、－、× 一、信号的＋、－、×运算 两信号f1(·) 和f2 (·)的相+、－、×指 ) )的相+、－、× 同一时刻两信号之值对应相加减乘 两信号之值对应相加减乘。 同一时刻两信号之值对应相加减乘。
信号与线性系统
两信号相加和相乘
• 同一瞬时两信号对应值相加（相乘）。 同一瞬时两信号对应值相加（相乘）。
• 将f (t) → f (at) ，称为对信号f (t)的尺度变 换。 则波形沿横坐标压缩； • 若a >1 ，则波形沿横坐标压缩；若0< a < 1 ， 则展开。 则展开。如
信号与线性系统
• 对于离散信号，由于f (ak) 仅在ak为整数 对于离散信号， 时才有意义， 时才有意义， 进行尺度变换时可能会使部 分信号丢失。 分信号丢失。因此一般不作波形的尺度变 换。
信号与线性系统
平移、反转、 平移、反转、尺度变换相结合
三种运算的次序可任意。 进行。 三种运算的次序可任意。但一定要注意始终对时间t 进行。 例：已知f (t)，画出f (– 4 – 2t)。
信号与线性系统 已知f ，画出f 已知 (t)，画出 (– 4 – 2t)。 。
也可以先压缩、再平移、最后反转。 也可以先压缩、再平移、最后反转。
信号与线性系统
2. 平移
• 将 f ( t ) → f ( t – t 0) ， f ( k ) → f (t – k0)称为对信号f (·)的平移或移位。 ) 平移或移位。 >0， 若t0 (或k0) >0，则将f (·)右移；否则左 )右移； 移。
信号与线性系统
平移与反转相结合
• 已知f(t)如下图所示，请画出f(2-t)
信号与系统-ch1
差分方程求解, z 变换
• 新工具：Matlab软件
1 信号与系统的基本概念（6课时） 2 连续系统的时域分析（4课时） 3 离散系统的时域分析（4课时） 4 连续系统的频域分析（12课时） 5 6 7
连续系统的S域分析（12课时） 离散系统的Z域分析（8课时）
系统函数（4课时）
8 系统的状态变量分析（4课时）
0, 0 直流 0, 0 升指数信号 0, 0 衰减指数信号
0, 0 等幅 0, 0 增幅振荡 0, 0 衰减
在实际中不能产生复信号，引入复信号能简化运算
复指数信号的实部与虚部
离散周期信号f (n)满足:f (n) = f(n + mN)，m = 0,±1,±2,…
满足上述关系的最小T(或整数N)称为该信号的周期
连续周期信号：
f (t )
1 -3 -2 -1 0 1 -1 2 3 4 t
T=4s
离散周期信号：
2 1 ... -4 -3 -2 -1 0 1
f (n)
2 1 1 1
• 抽样信号（Sa(t) 信号）
sin t Sa(t ) t
抽样信号特点
1. 偶函数， Sa t Sa t 2. 在t 的正负两端衰减 tlim Sa(t ) 0 3. 4.
0
Sa(t )dt Sa(t ) dt
0
2
Sa(t )dt
业技术工作的重要理论基础，是后续专业课（通 信原理、数字信号处理）的基础，也是上述各类 专业硕士研究生入学考试课程。
• 课程特点：
应用数学知识较多，与电路分析关系密切，用数学 工具分析物理概念。
信号的运算和处理 (2)
详细描述
卷积运算是信号处理中非常重要的概念，它表示两个信号的结合方 式。具体来说，如果两个信号`f(t)`和`g(t)`，则它们的卷积可以表示 为`h(t) = f(t) * g(t)`。在时域中，卷积运算相当于将一个信号通过另 一个信号进行滤波。在实际应用中，卷积运算广泛应用于图像处理、 音频处理等领域。
将一个信号逐点对应地除以另一个信号。
详细描述
信号的除法运算在数学上表示为`h(t) = f(t) / g(t)`，其中`f(t)`和`g(t)`是两个信号。在信号处理中，除法运 算常用于归一化、放大等操作。同样地，除法运算也可能会引入非线性失真，因此在实际应用中需要特别 小心。
卷积
总结词
将一个信号与另一个信号进行逐点对应相乘后再求和的操作。
信号的运算和处理 (2)
目
CONTENCT
录
• 信号的数学运算 • 信号的滤波处理 • 信号的调制与解调 • 信号的变换域处理 • 信号的采样与量化
01
信号的数学运算
加法
总结词
将两个信号在时间上逐点对应相加。
详细描述
信号的加法运算是最基本的数学运算之一，它逐点对应地相加两个信号。在时域中， 如果两个信号`f(t)`和`g(t)`，则它们的和可以表示为`h(t) = f(t) + g(t)`。这种运算在 信号处理中非常常见，特别是在处理噪声和其他干扰信号时。
详细描述
在通信中，带通滤波器用于提取特定频带的信号 ，实现信号的传输和接收；在雷达中，带通滤波 器用于提取目标回波的特定频带信号；在生物医 学信号处理中，带通滤波器用于提取心电图、脑 电图等生物电信号的特定频带成分。
带阻滤波器
总结词
详细描述
总结词
卷积运算是信号处理中非常重要的概念，它表示两个信号的结合方 式。具体来说，如果两个信号`f(t)`和`g(t)`，则它们的卷积可以表示 为`h(t) = f(t) * g(t)`。在时域中，卷积运算相当于将一个信号通过另 一个信号进行滤波。在实际应用中，卷积运算广泛应用于图像处理、 音频处理等领域。
将一个信号逐点对应地除以另一个信号。
详细描述
信号的除法运算在数学上表示为`h(t) = f(t) / g(t)`，其中`f(t)`和`g(t)`是两个信号。在信号处理中，除法运 算常用于归一化、放大等操作。同样地，除法运算也可能会引入非线性失真，因此在实际应用中需要特别 小心。
卷积
总结词
将一个信号与另一个信号进行逐点对应相乘后再求和的操作。
信号的运算和处理 (2)
目
CONTENCT
录
• 信号的数学运算 • 信号的滤波处理 • 信号的调制与解调 • 信号的变换域处理 • 信号的采样与量化
01
信号的数学运算
加法
总结词
将两个信号在时间上逐点对应相加。
详细描述
信号的加法运算是最基本的数学运算之一，它逐点对应地相加两个信号。在时域中， 如果两个信号`f(t)`和`g(t)`，则它们的和可以表示为`h(t) = f(t) + g(t)`。这种运算在 信号处理中非常常见，特别是在处理噪声和其他干扰信号时。
详细描述
在通信中，带通滤波器用于提取特定频带的信号 ，实现信号的传输和接收；在雷达中，带通滤波 器用于提取目标回波的特定频带信号；在生物医 学信号处理中，带通滤波器用于提取心电图、脑 电图等生物电信号的特定频带成分。
带阻滤波器
总结词
详细描述
总结词
数字信号处理ch1_3 DTFT
j( W π )
)} / 2
例：已知x[k]的频谱如图所示，试求y[k]=x[k]cos(pk)的频谱。
X(ejW )
1
2π
π
π 2
π 2
π
2π
W
解：
2π
1
π
X(ej(W p)
π 2
π
π
2π
W
1
2π
X(e
j(W p
2
)
π
π 2
π 2 1 Y(ejW )
π 2
π
2π
3
|X (ejW )|
2 1 0
3p
2p
p
0
p
2p
3p
W
DTFT的收敛性
定义X(ejW)的部分和 X N (e jW )
若
k
k N
N
x[k ]e jW k
x[k ]
绝对可和 一致收敛
则 lim X (e jW ) X N (e jW ) 0
若
k
序列DTFT的性质
2. 对称特性
x [ k ] X ( e
DTFT
jW
)
x [ k ] X ( e jW )
DTFT
当x [k]为实奇对称序列时，由于x[k]= x*[k] ，所以
X ( e jW ) X ( e jW )
X(ejW)是W 纯虚函数, XI(ejW)为奇对称
DTFT
序列DTFT的性质
2. 对称特性
DTFT x [ k ] X ( e jW ) DTFT x [ k ] X ( e jW )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11
LOGO
2
2012/9/1
1.3 信号的运算
3. 尺度变换（横坐标展缩）
1.3 信号的运算
平移、翻转和尺度变换相结合： 已知f(t)如图所示，求 y(t)=f(-3t+6)的波形。
方法1
尺度 反转
尺度——反转——平移
平移
|a|>1表示f(t)波形在时间轴上压缩1/|a|倍 |a|<1表示f(t)波形在时间轴上扩展|a|倍
4
1.3 信号的基本运算
1.3 信号的基本运算
2、离散信号的相加和相乘
LOGO
LOGO
2012/9/1
6
1
2012/9/1
1.3 信号的运算
p22 1.移位(平移):
1.3 信号的运算
移位(平移):
t t0 f (t ) t f (t t0 )
t0 0，f(t) 右移t0， t0 0，f(t) 左移|t 0|
LOGO
7
LOGO
1.3 信号的运算
2. 反转
1.3 信号的基本运算
练习
注意：是对 t 的变换！ 思考：f[-(t+1)]与f(t+1)关于纵轴对称吗？ f(-t+1)与f(t+1)关于纵轴对称吗？
LOGO
9
LOGO
2012/9/1
10
1.3 信号的基本运算
1.3 信号的运算
LOGO
2012/9/1
17
LOGO
LOGO
3
2012/9/1
第一章
信号与系统
绪论：信号和系统的概念 信号的描述和分类
第一章 导论 主讲：赵琳娜
信号的基本运算 阶跃函数和冲激函数 系统的描述、性质和分类； LTI 系统
LOGOLOGO来自1.3 信号的基本运算
1.3 信号的基本运算
1、连续信号的相加和相乘
LOGO
2012/9/1
3
LOGO
2012/9/1
LOGO
13 14
LOGO
1.3 信号的运算
已知f(t)如图所示，求 y(t)=f(-3t+6)的波形。
方法2：
1.3 信号的运算
二、微分和积分
1、微分 1 0 1 1
df (t ) dt
平移——尺度——反转
平 移
y(t )
f (t )
df (t ) f ' (t ) f (1) (t ) dt
展 缩
3 4
t
反折
4 0 -1 1 3
t
LOGO
LOGO
16
1.3 信号的运算
2、积分 f(t)
y (t )
1
0
f ( )d f
t
t
( 1)
(t )
1 0 t 1
1
f(t)=
0
t 1
0
1
t
t
t
(0 t 1) 1d t f ( )d 0 t 1 t 1 d 1 d 0 d 1 0 1 ( 1 t ) 0 1 0