电路分析第十章习题解答
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
(完整版)电路原理课后习题答案
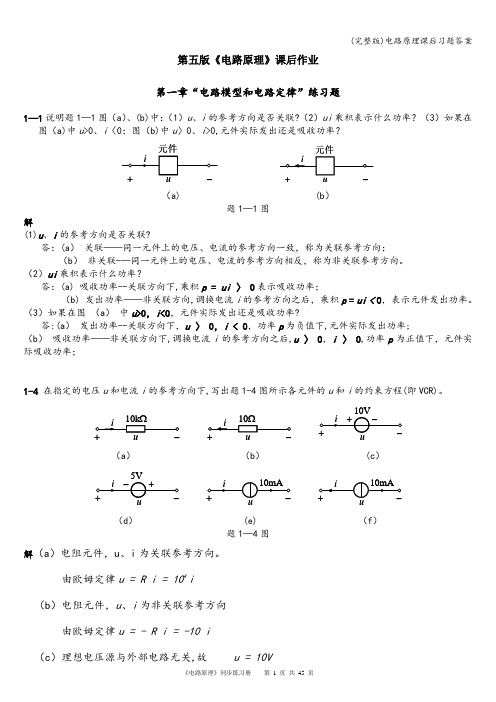
(b)非关联-—同一元件上的电压、电流的参考方向相反,称为非关联参考方向。
(2)ui乘积表示什么功率?
答:(a)吸收功率--关联方向下,乘积p=ui〉 0表示吸收功率;
(b)发出功率——非关联方向,调换电流i的参考方向之后,乘积p=ui<0,表示元件发出功率。
行列式解方程组为
所以
3-11用回路电流法求解题3—11图所示电路中电流I。
题3—11图
解由题已知,
其余两回路方程为
代人整理得
所以
3—12用回路电流法求解题3-12图所示电路中电流 及电压 .
题3—12图
3-15列出题3—15图(a)、(b)所示电路的结点电压方程。
(a)(b)
题3-15图
解:图(a)以④为参考结点,则结点电压方程为:
电压源功率 (发出30W)
(b)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1-5图(b)
故电阻功率 (吸收45W)
电流源功率 (发出30W)
电压源功率 (发出15W)
(c)由基尔霍夫电压定律和电流定律可得各元件的电压电流如解1—5图(c)
故电阻功率 (吸收45W)
电流源功率 (吸收30W)
独立的KVL方程数分别为
(1) (2)
3—7题3—7图所示电路中 , , , , , ,用支路电流法求解电流 。
题3-7图
解由题中知道 , , 独立回路数为 由KCL列方程:
对结点①
对结点②
对结点③
由KVL列方程:
对回路Ⅰ
对回路Ⅱ
对回路Ⅲ
联立求得
3—8用网孔电流法求解题3—7图中电流 。
第十章(含耦合电感的电路)习题解答

第十章(含耦合电感的电路)习题解答一、选择题1.图10—1所示电路的等效电感=eq L A 。
A.8H ; B.7H ; C.15H ; D.11H解:由图示电路可得 121 d d 2d d )63(u t i t i =++, 0d d 4d 221=+tit i d从以上两式中消去ti d d 2得t iu d d 811=,由此可见8=eq L H2.图10—2所示电路中,V )cos(18t u s ω=,则=2i B A 。
A.)cos(2t ω; B.)cos(6t ω; C.)cos(6t ω-; D.0解:图中理想变压器的副边处于短路,副边电压为0。
根据理想变压器原副边电压的关系可知原边的电压也为0,因此,有A )cos(29)cos(18 1t t i ω=ω=再由理想变压器原副边电流的关系ni i121= (注意此处电流2i 的参考方向)得A )cos(612t ni i ω==因此,该题应选B 。
3.将图10─3(a )所示电路化为图10—3(b )所示的等效去耦电路,取哪一组符号取决于 C 。
A.1L 、2L 中电流同时流入还是流出节点0;B.1L 、2L 中一个电流流入0,另一个电流流出节点0 ;C.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向无关;D.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向有关。
解:耦合电感去耦后电路中的M 前面是取“+”还是取“–”,完全取决于耦合电感的同名端是在同侧还是在异侧,而与两个电感中电流的参考方向没有任何关系。
因此,此题选C 。
4.图10—4所示电路中,=i Z B 。
A .Ω2j ; B.Ωj1; C.Ωj3; D.Ωj8解:将图10—4去耦后的等效电路如图10—4(a ),由图10—4(a )得j1 j6j6j6j6j2Ω=+⨯+-=i Z因此,该题选B。
5.在图10—5所示电路中,=i Z D 。
电路分析第十章习题解析

10-24 题图10-24所示电路中,已知电流i(t)=1cos(107t+90°)A。 求电压uR(t)、uL(t)、uC(t)、uS(t)的相量。
Im 3
400
(2)求电压与电流的相位差
u(t) 8sin(500t 50o) V i(t) 2sin(500t 140o)A
o o o
根据电流相位超前于电压90°,可确定该元件为电容 元件,其元件参数为
C Im 2 S 0.25S C 0.25S 0.25 F 5104 F 500 μF
10-1 已知正弦电压和电流为u(t)=311cos(314t-π/6)V, i(t)=0.2cos(2π×465×103t+π/3)A。(1)求正弦电压和电流的振 幅、角频率、频率和初相。(2)画出正弦电压和电流的波形
图。正弦电压和电流的波形如题图10-1所示
解:由电压和电流的瞬时值表达式得到以下结果:
Um 8
500
(3) 求电压与电流的相位差
u(t) 8cos(250t 60o) V i(t) 5sin(250t 150o)A 5cos(250t 60o)A
o o o
根据电压相位与电流同相,确定该元件为电阻元件,其元 件参数为
R Um 8 1.6 Im 5
10-23 题图10-23所示电路中,已知电压 us (t) 1.5 2 cos(105t 60o)V。 求电流iR(t)、iL(t)、iC(t)、i(t)的相量。
j2100I&m 200I&m 200 20o
求解代数方程得到电流振幅相量
I&m =
200 20o A j2100 200
200 200
20o A 1 45oA 245o
电路课程习题及答案
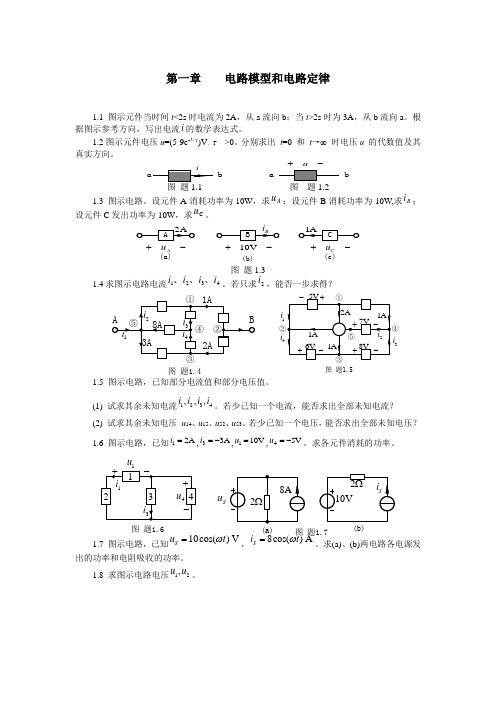
第一章 电路模型和电路定律1.1 图示元件当时间t <2s 时电流为2A ,从a 流向b ;当t >2s 时为3A ,从b 流向a 。
根据图示参考方向,写出电流i 的数学表达式。
1.2图示元件电压u =(5-9e -t /τ)V ,τ >0。
分别求出 t =0 和 t →∞ 时电压u 的代数值及其真实方向。
babu +-图 题1.21.3 图示电路。
设元件A 消耗功率为10W ,求A u ;设元件B 消耗功率为-10W,求B i ;设元件C 发出功率为-10W ,求C u 。
Au +-10V+-Cu +-(a)(b)(c)图 题1.31.4求图示电路电流4321i i i i 、、、。
若只求2i ,能否一步求得?图 题1.41i 4i 3i 图 题1.51.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流1234,,,i i i i 。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压 u 14、u 15、u 52、u 53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知A 21=i ,A 33-=i ,V 101=u ,V 54-=u 。
求各元件消耗的功率。
图 题1.61uSu (a)(b)图 题1.71.7 图示电路,已知10cos()V S u t ω=,8cos()A S i t ω=。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压12,u u 。
1u +-2u +-图 题1.830u-+图 题1.91.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N 吸收的功率和电流源发出的功率。
10V0.5A8V1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W ,求r 的值。
1V图 题1.13图 题1.141V2V1.14 求图示电路受控源和独立源各自发出的功率。
《电路原理导论》第十章习题解答

10-12图10-12所示电路中, ,非线性流控电阻的电压、电流关系为 ( 单位为A, 单位为V),设非线性电阻工作在正阻区,试用小信号分析法计算响应 。
答:
解:
非线性电阻特性
i
-3
-2
-1
0
1
2
3
u
20
10
4
2
4
10
20
Rn
-6.66
-5
-4
-∞
4
5
6.66
非线性电阻
习题10
10-1已知非线性电阻的电压、电流关系为 (式中, 的单位为V, 的单位为A),试求工作点i=1A和i=2A处的静态电阻和动态电阻。
答案: : ; :
解:i=1A: ,
10-2一非线性电感的磁链 与电流 的关系为 ,其中 ,
。试求它的静态电感Ls和动态电感Ld。
答 ,
解:Βιβλιοθήκη 1.静态2.10-3一非线性电容的电荷与电压的关系可表示为 。在此电容两端加有电压 。求电容中的电流 ,并把它表为其中所含谐波之和的形式。若给定 , , ,算出电流 。
答:正阻区: A, V;负阻区: A, V
解:戴维南定理化简
I-3
-2
-1
1
2
3
4
5
U
8
3
-1
0
3
8
15
10-11含有理想二极管VD的一段并联电路如图10-11所示,试画出该段电路关于 口的等效CV特性曲线 ,并指出相应等效元件的性质。
解:等效电路如图
当U>0二极管反向截止
当U=2I=0
当U=0I=-1A
《数字电路-分析与设计》1--10章习题及解答(部分)_北京理工大学出版社

6-17先分别将‘290接为8421和5421计数器,再分别用M-1=6(QDQCQBQA=0110)8421和(QAQDQCQB=1001)5421置位即可,应特别注意高低位的顺序。波形图和状态图略。
低电平噪声容限:
甲的关门电平大,所以甲在输入低电平时的
抗干扰能力强。
3-6 试说明下列各种门电路中哪些可以将输出端并联使用(输入端的状态不一定相同)。
⑴ 具有推拉式输出级的TTL电路;
⑵ TTL电路的OCபைடு நூலகம்;
⑶ TTL电路的TS门;
⑷ 普通的CMOS门;
⑸ 漏极开路输出的CMOS门;
⑹ CMOS电路的TS门。
6-24应从RCO引出,此时不管分频比为多少,分频关系都是正确的。
6-25画出状态顺序表或状态图即可。
对于图(a),只要注意QB=0时预置,并且DCBA=QD110即可。
由状态图知,这是模6计数器。
对于图(b),只要注意QC=0时预置,并且DCBA=QD100即可。
由状态图知,这是模10计数器。
该电路设计巧妙,QD均为占空比为50%的方波。
3-5 有两个相同型号的TTL“与非”门,对它们进行测试的结果如下:
⑴ 甲的开门电平为1.4V,乙的开门电平为1.5V;
⑵ 甲的关门电平为1.0V,乙的关门电平为0.9V。
试问在输入相同高电平时,哪个抗干扰能力强?在输入相同的低电平时,哪个抗干扰能力强?
解:高电平噪声容限:
甲的开门电平小,所以甲在输入高电平时的抗干扰能力强;
(新)正弦波振荡器基本习题解答(PDF 7页)

第10章 正弦波振荡器——基本习题解答10.1试用瞬时极性法判别题10.1图各电路能否满足自激振荡的相位条件?假设电路的幅值条件均满足,各电路能否起振? 解:用瞬时极性法判别如下题 10.1图10.2由集成运算放大器和RC 并联谐振电路组成的振荡器如题10.2图所示,已知R=160k Ω,C=0.01µF 。
试问:(1)若R 1=3k Ω,求满足振荡幅值条件的f R 值; 为了使电路可靠起振, 起振时f R 应比计算值大一些还是小一些?为什么?•fU(2)估算振荡频率0f 。
R题10.2图解:(1)A f =33111=+=⎟⎟⎠⎞⎜⎜⎝⎛+f f R R R 则Ω=k R f 6 31=F & 要可靠起振1>F A f && 起振时fR >6k Ω (2) Hz Hz RC f 1005.991001.0101602121630≈=××××==−ππ10.3设计一个振荡频率为125Hz 的正弦波振荡电路(电容用0.047µF ,并用一个正温度系数10k Ω的热敏电阻作为稳幅元件)。
试画出电路,并标出各电阻阻值。
解:画出电路如题10.3图所示:RR 1:正温度系数的热敏电阻 125210==RCf π即 1.272710312510047.0216Ω=Ω=⇒=××−k R Rπ取Ω=k R f 20 起振时:f R >20k Ω10.4用下列元器件能否构成正弦波振荡电路?(1)16k Ω电阻三只,27k Ω的负温度系数的热敏电阻一只,集成运放一只, 10k Ω电位器一只,0.01µF 电容器两只。
(2)1k Ω、5.1k Ω、15k Ω的电阻各一只, 0.1µF 的电容器两只, 300pF 的电容器一只,变压器一只, 三极管一只。
解:(1)可以,其构成电路如下图所示:16k 0.01 (2) 可以,其构成电路如下图所示:10.5试标出题10.5图中各电路变压器的同名端,使之满足正弦振荡的相位条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Nm
=
0.3 × 1− (2×π
1 × 25 ×103 )2 × 50 ×10−3
× 0.2 ×10−6
≈ 1.22mV
信噪比 = U 2m = 0.39 ×103 = 319
Nm
1.22
6.图题 10-2 所示 RC 高通滤波器,若要求其截止频率为 200Hz,且 R=5kΩ,计算合适的电
容值,并计算当频率为 200Hz 时电路的相移(输出信号与输入信号相位差)。
解:
Q ω0 =
1 LC
∴
L
=
1
ω
2 0
C
=
(2π
1 ×106 )2 × 200 ×10−12
= 127μH
Q
Q = ω0C = R G
C = 25 L
200 ×10−12 127 ×10−6
= 31.4 ×10−3
17.一个 GCL 并联谐振电路的谐振角频率为 107 rad/s,通频带宽为 105 rad/s,已知 R=100 k Ω,求:(1)电感、电容和 Q 的值;(2) 上、下截止频率。 解: GCL 并联谐振电路
0.5μF
+
+
4kΩ
u1
0.2μF u2
-
-
解:该电路的相量模型为
图题 10-9
−
j
2π
1 × 50 × 0.5×10−6
Ω
+
+
U&1
4 kΩ
−
j
2π
1 × 50 × 0.2×10−6
Ω
U& 2
−
−
U& 2 U& 1
=
−
−
j
2π
1 × 10 −5
j
2π
1 × 10 −5
+
4000
×
(−
j
5π
1 × 10 −5
− 1 ) × 500 ×103 2 × 25
= 490kHz
14.一个 RLC 串联电路的谐振频率为 876Hz,通频带为 750Hz 到 1kHz,已知 L=0.32H,求 R、 C 及 Q,并求谐振时电感及电容电压的有效值。
解:
Q
谐振频率
f0
=
2π
1 LC
∴
C=
1
f
2 0
×
4π
2
×
L
=
1
8762 × 4 × 3.142 × 0.32
解:图 10-2 电路的截止频率为
ωc
=
1 RC
BW = ω − ∞
=
1.5 ×103
1 ×10 ×10−6
−∞
= 66.67 rad s
9.在电子仪器中,经过放大后的电压如在相位上比原来的电压超前而引起误差,可以加一 个滞后网络进行补偿。图题 10-9 所示为一个滞后网络,求当 f =50Hz 时,输出对输入的相 移是多少?
= 0.103μF
BW = 1000 − 750 = 250Hz
Q BW = ω0 = 2π × f0 QQ
∴ Q = 2π × 876 = 3.5 2π × 250
Q Q = ω0L R
∴ R = ω0 L = 2π × 876 × 0.32 = 503Ω
Q
3.5
谐振时: U& L0 = jQU& S
第十章
1.已知转移函数 H ( jω) = jω + 1 ,求ω=1 rad/s 及ω=10 rad/s 时的函数值。 jω + 10
解:ω = 1rad s 时
H ( j) = ( j + 1) ( j + 10) = (1 + j)(10 − j) = 10 + 1 + 9 j = 11 + 9 j
+
+
−j 1
ωc
U&1
R
U& 2
−
−
Au
(
jω )
=
U& 2 U& 1
=
R
(R
−
j
1 ωC
)
=1 1− j 1 ωRC
= jωRC 1 + jRωC
Au 1 0.707
Au ( jω) =
1 1+( 1
)2
ωRC
ϕ(ω) = arctan 1 ωRC
当 ω= 1 时 RC
Au ( jω) =
1 2
(1)
BW
= ω0 Q
=
G rad Cs
∴
Q = ω0 BW
= 107 105
= 100
C= G =
102 + 1
101
101
ω = 10 rad s 时
H ( j) = ( 11 )2 + ( 9 )2 = 0.1407 101 101
H ( j10) = (10 j + 1) (10 j + 10) = (1 + 10 j)(10 −10 j) 102 + 102
= 10 + 100 + 90 j = 11 + 9 j
−
j
1 ωC
= 1 + jR2ωC 1 + j(R1 + R2 )ωC
4.一低通 RC 滤波器,C=100μF,R=100Ω,对(a)10Hz 的输入频率,(b)250Hz 的输入频 率,求电路的衰减。 解:低通滤波器的频率相响应为
Au
(
jω)
=
U& 2 U& 1
= 1+
1 jωRC
Au ( jω) =
1 1 + (ωRC)2
(1) f = 10Hz 时 衰减 =
1
1 + (10 ×100 ×100 ×10−6 × 2 × 3.14)2
=1 1 + 0.394
= 0.85
(2) f = 250Hz 时 衰减 =
1
1 + (250 × 2 × 3.14 ×100 ×100 ×10−6 )2
=1 1 + 246.5
谐振角频率 ω0 =
1= LC
1
= 5000
400 ×10−3 C
∴
C
=
5000 2
×
1 4000 ×10−3
= 0.1μF
谐振时 电路中电流 I = U = 1 = 0.2A R5
i(t) = 0.2 2 cos 5000t A
谐振时 U& L0 = jω0 LI&0 = j5000 × 400 ×10−3 × 0.2
= 400∠90o
uL0 (t) = 400
2 cos(5000t + π ) 2
U& C0 = −U& L0
= −400∠90o
= 400∠ − 90o
uC (t) = 400
2 cos(5000t − π ) 2
12.一个 RLC 串联电路:R=25Ω,L=100μH,C =1000pF。求谐振频率和品质因数。
C L
解:
图题 10-7
−j 1
U&1
ωC jωL
U& 2
电路
Au
(
jω )
=
U& 2 U& 1
= jωL jωL − j 1 ωC
=1 1− 1 ω 2 LC
∴
U 2m = U1m ⋅ 1−
1 1
ω 2 LC
= 2×
1
1
−
(2
×
3.14
×
5
×103
1 )2 ×
0.47
× 10 −3
× 10 −6
20kHz
⎡ ωC1 = ⎢
⎣
1+ 1 4Q 2
+
1 2Q
⎤ ⎥ω ⎦
0
=
(
1+ 1 4 × 252
− 1 ) × 2π × 500 ×103 2 × 25
= 2π × 510k rad s
fC1 = 510kHz
⎡ fC2 = ⎢
⎣
1+ 1 4Q 2
−
1⎤
2Q
⎥ ⎦
f0
=
(
1+ 1 4 × 252
1 + 0.6282
ϕ = − arctan 4000 × 2π ×10−5 0.16 + 1 + 0.6282
= −0.16o
10.求图题 10-10 所示电路的转移电压比 Au ( jω) = U& 2 U&1 。当 R1C1=R2C2 时,此网络函数有何
特性。
R1
+
U&1
-
1 jωC1
1 jωC2
+
jωL
+
U&1
−j 1 ωC
U& 2
−
−
电路的频率响应为
−j 1
Au ( jω) =
ωC jωL − j 1
=
1 1 − ω 2 LC
=
U& 2 U& 1
ωC
U 2m
=
U 1m
⋅
1
−
1 ω2
LC
=
1×
1
−
(2
×π
×
3
×103
)2
1 × 50
× 10 −3
×
0.2
× 10 −6
