2018年北京市中学生数学竞赛初二试题(含答案)
2018年北京市中学生数学竞赛高一年级初赛参考答案

二、填空题 1.已知实数 a, b, c, d 满足 5a=4,4b=3,3c=2,2d=5,则(abcd)2018=______. 答:1. 解:化 5a=4,4b=3,3c=2,2d=5 为对数,有 ln 4 ln 3 ln 2 ln 5 , a log5 4 , b , c , d ln 5 ln 4 ln 3 ln 2 所以
2018 年北京市中学生数学竞赛高中一年级初赛参考解答 第 2页 共6页
6 . 设 f (x) 是 定 义 在 R 上 的 函 数 , 若 存 在 两 不 等 实 数 x1, x2 R , 使 得 x +x f ( x1 ) f ( x2 ) ,则称函数 f (x)具有性质 P.那么以下函数: f( 1 2) 2 2
2018 年北京市中学生数学竞赛高中一年级初赛参考解答 第 4页 共6页
6. 在 3×3 的“九宫格”中填数, 使每行、 每列及两条对角线上 的三数之和都相等,有 3 个方格已经填的数分别为 4, 7, 2018,如右 图,则“九宫格”中其余 6 个方格所填数之和为______. 答:−11042.5. 解: 将其余 6 个格子标上字母, 如右下图, 由 a+2018+b=4+7+b
1 ( x 0) ① f ( x) x ; 0 ( x 0)
② f ( x) x 2 ;
③ f ( x) x 2 1 ;
④ f ( x) x3
中,不具有性质 P 的函数为 (A)①. 答:B. 解:具有性质 P 的函数的特点是:存在一条直线与函数图象有三个交点,且其中 一个是另外两个交点的中点. 画图可知①、③、④都是具有性质 P 的函数,②不具备有 三个交点,②是不具有性质 P 的函数 (B)②. (C)③. (D)④.
八年级数学竞赛专题训练13 三角形的基本知识(附答案)

八年级数学竞赛专题训练13 三角形的基本知识阅读与思考三角形是最基本的几何图形,是研究复杂几何图形的基础,许多几何问题都可转化为三角形的问题来解.三角形基本知识主要包括三角形基本概念、三角形三边关系定理及推论、三角形内角和定理及推论等,它们在线段和角度的计算、图形的计数等方面有广泛的应用.解与三角形的基本知识相关的问题时,常用到数形结合及分类讨论法,即用代数方法解几何计算题及简单的证明题,对三角形按边或按角进行恰当分类.应熟悉以下基本图形:图4图3图2图1CDBAD CBADCBA DCOBA例题与求解【例1】 在△ABC 中,∠A =50°,高BE ,CF 交于O ,则∠BOC =________.(“东方航空杯”——上海市竞赛试题)解题思路:因三角形的高不一定在三角形内部,故应注意符合题设条件的图形多样性.【例2】 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形底边的长为( )A .17cmB .5cmC .5cm 或17cmD .无法确定(北京市竞赛试题)解题思路:中线所分两部分不等的原因在于等腰三角形的腰与底的不等,应分情况讨论.【例3】 如图,BE 是∠ABD 的平分线,CF 是∠ACD 的平分线,BE 与CF 交于G ,若∠BDC =140°,∠BGC =110°,求∠A 的大小.(“希望杯”邀请赛试题)解题思路:运用凹四边形的性质计算.GC DBEF A【例4】 在△ABC 中,三个内角的度数均为正数,且∠A <∠B <∠C ,4∠C =7∠A ,求∠B 的度数.(北京市竞赛试题)解题思路:把∠A ,∠C 用∠B 的代数式表示,建立关于∠B 的不等式组,这是解本题的突破口.【例5】 (1)周长为30,各边长互不相等且都是整数的三角形共有多少个?(2)现有长为150cm 的铁丝,要截成)2(>n n 小段,每段的长不小于1cm 的整数,如果其中任意3小段都不能拼成三角形,试求n 的最大值.此时有几种方法将该铁丝截成满足条件的n 段.(江苏省竞赛试题)解题思路:对于(1),不妨设三角形三边为a ,b ,c ,且c b a <<,由条件及三角形三边关系定理可确定c 的取值范围,从而可以确定整数c 的值. 对于(2),因n 段之和为定值150cm ,故欲使n 尽可能的大,必须使每段的长度尽可能的小.这样依题意可构造一个数列.【例6】 在三角形纸片内有2 008个点,连同三角形纸片的3个顶点,共有2 011个点,在这些点中,没有三点在一条直线上.问:以这2 011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形?(天津市竞赛试题)解题思路:本题的解题关键是找到规律:三角形内角每增加1个内点,就增加了2个三角形和3条边.能力训练A 级1.设a ,b ,c 是△ABC 的三边,化简c b a c b a --+++=____________.2.三角形的三边分别为3,a 21-,8,则a 的取值范围是__________.3.已知一个三角形三个外角度数比为2:3:4,这个三角形是_______(按角分类)三角形.4.如图,∠A +∠B +∠C +∠D +∠E 的度数为____________. (“缙云杯“试题)EDCBAHDCMG BAEC BA(第4题) (第5题) (第6题)5.如图,已知AB ∥CD ,GM ,HM 分别是∠AGH ,∠CHG 的角平分线,那么∠GMH =_________.T ED GHCBA F21AC EDB(第7题) (第9题) 6.如图,△ABC 中,两外角平分线交于点E ,则∠BEC 等于( )A .)90(21A ∠-︒ B .A ∠+︒2190 C .)180(21A ∠-︒ D .A ∠-︒21180 7.如图,在△ABC 中,BD ,BE 分别是高和角平分线,点F 在CA 的延长线上,FH ⊥BE 交BD 于G ,交BC 于H .下列结论:①∠DBE =∠F ;②2∠BEF =∠BAF +∠C ;③∠F =21(∠BAC -∠C );④∠BGH =∠ABE +∠C . 其中正确的是( )A .①②③B .①③④C .①②③D .①②③④8.已知三角形的每条边长的数值都是2 001的质因数,那么这样的不同的三角形共有( ) A .6个 B .7个 C .8个 D .9个 9.如图,将纸片△ABC 沿着DE 折叠压平,则( ) A .∠A =∠1+∠2 B .∠A =21(∠1+∠2)C .∠A =31(∠1+∠2) D .∠A =41(∠1+∠2)(北京市竞赛试题)10.一个三角形的周长是偶数,其中的两条边分别是4和1 997,则满足上述条件的三角形的个数是( ) A .1个 B .3个 C .5个 D .7个(北京市竞赛试题)11.如图,已知∠3=∠1+∠2,求证:∠A +∠B +∠C +∠D =180°.(河南省竞赛试题)321EG FDCBA12.平面内,四条线段AB ,BC ,CD ,DA 首尾顺次连接,∠ABC =24°,∠ADC =42°. (1)∠BAD 和∠BCD 的角平分线交于点M (如图1),求∠AMC 的大小.(2)点E 在BA 的延长线上,∠DAE 的平分线和∠BCD 平分线交于点N (如图2),求∠ANC .CDBAEND CBA图1 图213.三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在下图中,E 位于线段CA 上,D 位于线段BE 上.(1)证明:AB +AE >DB +DE ; (2)证明:AB +AC >DB +DC ;(3)AB +BC +CA 与2(DA +DB +DC )哪一个更大?证明你的结论; (4)AB +BC +CA 与DA +DB +DC 哪一个更大?证明你的结论.(加拿大埃蒙德顿市竞赛试题)E DCBAB 级1.已知三角形的三条边长均为整数,其中有一条边长是4,但不是最短边,这样的三角形的 个数有_______个.(“祖冲之杯”邀请赛试题)2.以三角形的3个顶点和它内部的9个点共12个点为顶点能把原三角形分割成______个没有公共部分的小三角形.3.△ABC 中,∠A 是最小角,∠B 是最大角,且有2∠B =5∠A ,若∠B 的最大值是m ,最小值是n ,则=+n m ___________.(上海市竞赛试题)4.如图,若∠CGE =α,则∠A +∠B +∠C +∠D +∠E +∠F =_______.(山东省竞赛试题)αGFEDCBADA 2A 1CBA(第4题) (第5题)5.如图,在△ABC 中,∠A =96°,延长BC 到D ,∠ABC 与∠ACD 的平分线相交于1A 点,BC A 1∠与CD A 1∠的平分线相交于2A 点,依此类推,BC A 4∠与CD A 4∠的平分线相交于5A 点,则5A ∠的大小是( )A .3°B .5°C .8°D .19.2°6.四边形ABCD 两组对边AD ,BC 与AB ,DC 延长线分别交于点E ,F ,∠AEB ,∠AFD 的平分线交于点P .∠A =64°,∠BCD =136°,则下列结论中正确的是( )①∠EPF =100°; ②∠ADC +∠ABC =160°; ③∠PEB +∠PFC +∠EPF =136°; ④∠PEB +∠PFC =136°.A .①②③B .②③④C .①③④D .①②③④FEDPCBA7.三角形的三角内角分别为α,β,γ,且γβα≥≥,βα2=,则β的取值范围是( ) A .4536≤≤β B .6045≤≤β C .9060≤≤β D .3245≤≤β(重庆市竞赛试题)8.已知周长小于15的三角形三边的长都是质数,且其中一边的长为3,这样的三角形有( ) A .4个 B .5个 C .6个 D .7个(山东省竞赛试题)9.不等边△ABC 的两条高的长度分别为4和12,若第三条高的长也是整数,试求它的长.(第三十二届美国邀请赛试题)10.设m ,n ,p 均为自然数,满足p n m ≤≤且15=++p n m ,试问以m ,n ,p 为三边长的三角形有多少个?11.锐角三角形用度数来表示时,所有角的度数为正整数,最小角的度数是最大角的度数的41,求满足此条件的所有锐角三角形的度数.(汉城国际数学邀请赛试题)12.如图1,A 为x 轴负半轴上一点,B 为x 轴正半轴上一点,C (0,-2),D (-2,-2). (1)求△BCD 的面积;(2)如图2,若∠BCO =∠BAC ,作AQ 平分∠BAC 交y 轴于P ,交BC 于Q .求证:∠CPQ =∠CQP ;(3)如图3,若∠ADC =∠DAC ,点B 在x 轴正半轴上运动,∠ACB 的平分线交直线AD 于E ,DF ∥AC交y 轴于F ,FM 平分∠DFC 交DE 于M ,EDMFBCF ∠∠-∠2的值是否发生变化?证明你的结论.x图313.如图1,),0(m A ,)0,(n B .且m ,n 满足0)42(32≤-+-n m.图1 图2(1)求A ,B 的坐标;(2)C 为y 轴正半轴上一动点,D 为△BCO 中∠BCO 的外角平分线与∠COB 的平分线的交点,问是否存在点C ,使∠D =41∠COB .若存在,求C 点坐标; (3)如图2,C 为y 轴正半轴上A 的上方一动点,P 为线段AB 上一动点,连CP 延长交x 轴于E ,∠CAB 和∠CEB 平分线交于F ,点C 在运动过程中FECOABO ∠∠+∠的值是否发生变化?若不变求其值;若变化,求其范围.专题13 三角形的基本知识例1130°或50°例2 B 例380°提示:∠A=2∠BGC-∠BDC例4设∠C=x°,则∠A=(47 x)°,∠B=180°-∠C-∠A=180°-117x°由∠A<∠B<∠C,得47x<180-117x<x.解得70<x<84.∵47x是整数,∴x=77.故∠C=77°,则∠A=44°,∠B=180°-77°-44°=59°.例5(1)不妨设a<b<c,则由30a b ca b c+=-⎧⎨+>⎩,得10<c<15.∵c是整数,∴c=11,12,13,14.当c=11时,b=10,a=9.当c=12时,b=11,a=7;b=10,a=8.当c=13时,b=12,a=5;b=11,a=6;b=10,a=7;b=19,a=8.当c=14时,b=13,a=3;b=12,a=4;b=11,a=5;b=10,a=6;b=9,a=7.(2)这些小段的长度只可能分别是1,1,2,3,5,8,13,21,34,55,89…但1+1+2+5+8+13+21+34+55=143<150,1+1+2+3+5+8+13+21+34+55+89>150,故n的最大值为10.共有以下7种方式:(1,1,2,3,5,8,13,21,34,62);(1,1,2,3,5,8,13,21,35,61);(1,1,2,3,5,8,13,21,36,60);(1,1,2,3,5,8,13,21,37,59);(1,1,2,3,5,8,13,22,35,60);(1,1,2,3,5,8,13,22,36,59);(1,1,2,3,5,8,14,22,36,58).例6 解法1一个小三角形内,它与该三角形的三个顶点可得到三个小三角形,从而增加了两个小三角形,于是可以推出,当三角形内有2008个点是,连线可得到小三角形的个数为:3+2×(2008-1)=4017(个).解法2 整体核算法设连线后把原三角形分割成n个小三角形,则它们的内角和为180°·n,又因为原三角形内每一个点为小三角形顶点时,能为小三角形提供360°的内角,2008个点共提供内角2008×360°,于是得方程180n=360×2008+180,解得n=4017,即这2008个点能将原三角形纸片分割成4017个小三角形.A 级1. 2(b +c )2. -5<a <-23. 钝角4. 180°5. 90°6. C7. D8. B9. B 10. B 11. 提示:过G 作GH ∥EB ,可推得BE ∥CF . 12. (1)∠AMC =12(∠ABC +∠ADC )=12×(24°+42°)=33° (2)∵AN 、CN 分别平分∠DAE ,∠BCD ,∴可设∠EAN =∠DAB =x ,∠BCN =∠DCN =y ,∴∠BAN =180°-x ,设BC 与AN 交于S ,∴∠BSA =∠CSN ,∴180°-x +∠B =y +∠ANC ,① 同理:180°-2x +∠B =2y +∠D ,②由①×2-②得:2∠ANC =180°+∠B +∠D . ∴∠ANC =12(180°+24°+42°)=123°. 13. (1)(2)略 提示:(3)DA +DB >AB ,DB +DC >DC ,DC +DA >CA ,将三个不等式相加,得2(DA +DB +DC )>AB +CB +CA .(4)由(2)知AB +AC >DB +DC ,同理BC +BA >DC +DA ,CA +CB >DA +DB , 故AB +BC +CA >DA +DB +DCB 级1. 82. 193. 175 提示:设∠A =(2x )°,∠B =(5x )°,则∠C =180°-(7x )°,由∠A ≤∠C ≤∠B 得15≤x ≤204. 2a5. A6. D7. D8. B9. 提示:设长度为4和12的高分别是边a ,b 上的,边c 上的高为h ,△ABC 的面积为S , 则24S a =,212S b =,2S c h =,由22222412412S S S S S h -<<+得36h <<,故5h =. 10. 711. 设锐角三角形最小角的度数为x ,最大角的度数为4x ,另一角为y ,则41804490x x y x y xx ++=︒⎧⎪⎨⎪<︒⎩,解得20≤x ≤22.5,故x =20或21或22. 所有锐角三角形的度数为:(20°,80°,80°),(21°,75°,84°),(22°,70°,88°). 12. (1)S △BCD =2 (2)略(3)设∠ABC =x ,则∠BCF =90°+x ,可证:∠E =12x ,∠DMF =45°. ∴2(90)245212BCF DMF x E x ∠-∠︒+-⨯︒==∠。
八年级数学(竞赛)因式分解

第一讲 分解方法的延拓——换元法与主元法因式分解是针对多项式的一种恒等变形,提公因式法、公式法,分组分解法是因式分解的基本方法,通常根据多项式的项数来选择分解的方法.一些复杂的因式分解问题.常用到换元法和主元法.所谓换元,即对结构比较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),则能使复杂的问题简单化、明朗化,在减少多项式项数,降低多项式结构复杂程度等方面有独到作用.所谓主元,即在解多变元问题时,选择其中某个变元为主要元素,视其他变元为常量,将原式重新整理成关于这个字母的按降幂排列的多项式,则能排除字母间的干扰,简化问题的结构.例题求解【例1】分解因式:10)3)(4(2424+++-+x x x x = .(第12届“五羊杯”竞赛题)思路点拨 视24x x +为一个整体.用一个新字母代替,从而能简化式子的结构.【例2】 多项式xyz y z x y z x x z z y y x 2222222-++-+-因式分解后的结果是( ).A .(y -z)(x+y)(x -z)B .(y -z)(x -y)(x +z)C . (y+z)(x 一y)(x+z)D .(y 十z)(x+y)(x 一z) (上海市竞赛题)思路点拨 原式是一个复杂的三元三次多项式,直接分解有一定困难,把原式整理成关于某个字母按降幂排列的多项式,改变其结构,寻找分解的突破口.【例3】把下列各式分解因式:(1)(x+1)(x +2)(x+3)(x+6)+ x 2; (天津市竞赛题)(2)1999x 2一(19992一1)x 一1999; (重庆市竞赛题)(3)(x+y -2xy)(x+y -2)+(xy -1)2; (“希望杯”邀请赛试题)(4)(2x -3y)3十(3x -2y)3-125(x -y)3. (第13届“五羊杯”竞赛题)思路点拔 (1)是形如abcd+e 型的多项式,分解这类多项式时,可适当把4个因式两两分组,使得分组相乘后所得的有相同的部分;(2)式中系数较大,不妨把数用字母表示;(3)式中x+y ;xy 多次出现,可引入两个新字母,突出式子特点;(4)式前两项与后一项有密切联系.【例4】把下列各式分解因式:(1)a 2(b 一c)+b 2(c -a)+c 2 (a 一b); (2)x 2+xy -2y 2-x+7y -6.思路点拨 (1)式字母多次数高,可尝试用主元法;(2)式是形如ax 2+bxy+cy 2+dx+ey+f 的二元二次多项式,解题思路宽,用主元法或分组分解法或用待定系数法分解.【例5】证明:对任何整数 x 和y ,下式的值都不会等于33.x 5+3x 4y -5x 3y 2一15x 2y 3+4xy 4+12y 5.(莫斯科奥林匹克八年级试题)思路点拨 33不可能分解为四个以上不同因数的积,于是将问题转化为只需证明原式可分解为四个以上因式的乘积即可.注:分组分解法是因式分解的量本方法,体现了化整体为局部、又统揽全局的思想.如何恰当分组是解题的关键,常见的分组方法有:(1)按字母分组;(2)按次数分组; (3)按系数分组.为了能迅速解决一些与代教式恒等变形相关的问题,读者因熟悉如下多项式分解因式后的结果:(1)))((2233b ab a b a b a +±=± ;(2)))((3222333ac bc ab c b a c b a abc c b a ---++++=-++学历训练1.分解因式:(x 2+3x)2-2(x 2+3x)-8= .2.分解因式:(x 2+x+1)(x 2+x+2)-12= .3.分解因式:x 2-xy -2y 2-x -y= .4.已知二次三项式82--mx x 在整数范围内可以分解为两个一次因式的积,则整数m 的可能取值为 .5.下列各式分解因式后,可表示为一次因式乘积的是( ).A .2727923-+-x x xB .272723-+-x x xC .272734-+-x x xD .279323-+-x x x (第13届“希望杯”邀请赛试题)6.若51-=+b a ,13=+b a ,则53912322+++b ab a 的值为( ). A .92 B .32 C .54 D .0 7.分解因式:(1)(x 2+4x+8)2+3x(x 2+4x+8)+2x 2; (2)(2x 2-3x+1)2一22x 2+33x -1;(3)x 4+2001x 2+2000x+2001; (4)(6x -1)(2 x -1)(3 x -1)( x -1)+x 2;(5)bc ac ab c b a 54332222+++++; (6)613622-++-+y x y xy x .8.分解因式:22635y y x xy x ++++= .9.分解因式:333)()2()2(y x y x -----= .10.613223+-+x x x 的因式是( )A .12-xB .2+xC .3-xD .12+xE .12+x11.已知c b a >>,M=a c c b b a 222++,N=222ca bc ab ++,则M 与N 的大小关系是( )A .M<NB .M> NC .M =ND .不能确定12.把下列各式分解因式:(1)22212)16)(1(a a a a a ++-++; (2)91)72)(9)(52(2---+a a a ; (黄冈市竞赛题)(3)2)1()21(2)3()1(-+-++-+++y x y x xy xy xy ; (天津市竞赛题)(4)4242410)13)(14(x x x x x ++++-;(第13届“五羊杯”竞赛题)(5)z y xy xyz y x z x x 222232242-++--. (天津市竞赛题)17.已知乘法公式:))((43223455b ab b a b a a b a b a +-+-+=+; ))((43223455b ab b a b a a b a b a ++++-=-. 利用或者不利用上述公式,分解因式:12468++++x x x x (“祖冲之杯”邀请赛试题)18.已知在ΔABC 中,010616222=++--bc ab c b a (a 、b 、c 是三角形三边的长).求证:b c a 2=+第二讲 分解方法的延拓——配方法与待定系数法在数学课外活动中,配方法与待定系数法也是分解因式的重要方法。
2018年北京市中学生数学竞赛初二试题(含答案)

2018年北京市中学生数学竞赛初二试题(含答案)2,3,4,5,6,7,8,9中的一个,且这些自然数的和为2018.请问这个学生写出的这17个自然数中,最小的数是多少?(请给出详细解题过程)解:设这17个自然数分别为a1,a2,…,a17,则有:a1+a2+…+a17=2018由于每个自然数的个位数码只能是1,2,3,4,5,6,7,8,9中的一个,所以每个自然数的个位数字之和一定是45,即这17个自然数的个位数字之和为765.设b1,b2,…,b17分别为这17个自然数的十位数字,则有:b1+b2+…+b17=765由于每个自然数的十位数字也只能是1,2,3,4,5,6,7,8,9中的一个,所以每个自然数的十位数字之和一定是45,即这17个自然数的十位数字之和为765.设c1,c2,…,c17分别为这17个自然数的百位数字,则有:c1+c2+…+c17=765由于每个自然数的百位数字也只能是1,2,3,4,5,6,7,8,9中的一个,所以每个自然数的百位数字之和一定是45,即这17个自然数的百位数字之和为765.由此可得,这17个自然数中最小的数为100+10+1=111.一、1.A在1到100这100个自然数中,有25个质数,分别是2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97.因此,质数在这100个自然数中所占的百分比是25%。
2.C将10分拆成三个正整数之和,共有8种情况:1+1+8、1+2+7、1+3+6、1+4+5、2+2+6、2+3+5、2+4+4、3+3+4.根据“三角形两边之和大于第三边”的原则,只有(2,4,4)和(3,3,4)两组可以构成三角形。
由于等腰三角形的两个底角都是锐角,因此以2、4、4为边的等边三角形中,最小边2对的顶角也是锐角。
以3、3、4为边的等腰三角形中,由3的平方加3的平方大于4的平方可知顶角也是锐角。
八年级数学竞赛例题专题讲解22:关于中点的联想 含答案

专题 22 关于中点的联想阅读与思考线段的中点把线段分成相等的两部分,图形中出现中点,可以引起我们丰富的联想:首先它和三角形的中线紧密联系;若中点是在直角三角形的斜边上,又可以引用“斜边上的中线等于斜边的一半”结论;其次,中点又与中位线息息相关;另外,中点还可以与中心对称相连.解答中点问题的关键是恰当地添加辅助线,如作中线倍长、作直角三角形的斜边上的中线、构造三角形、梯形中位线、构造中心对称图形等,如图所示:例题与求解【例1】如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP ⊥AD,M为BC的中点,则PM的值为___________.(安徽省竞赛试题)例2题图例1题图F解题思路:∠A的平分线与BP边上的垂线互相重合,通过作辅助线,点P可变为某线段的中点,利用三角形中位线定理解题.【例2】如图,边长为1的正方形EFGH在边长为3的正方形ABCD所在的平面上移动,始终保持EF ∥AB,线段CF,DH的中点分别为M,N,则线段MN的长度为( ) (北京市竞赛试题)A.102B.172C.173D.2103解题思路:连接CG,取CG的中点T,构造三角形中位线、梯形中位线.【例3】如图,在△ABC 中,AB =AC ,延长AB 到D ,使BD =AB ,E 为AB 中点,连接CE ,CD , 求证:CD =2EC . (宁波市竞赛试题)解题思路:图形中有两个中点E ,B ,联想到与中点相关的丰富知识,将线段倍分关系的证明转化为线段相等关系的证明,关键是恰当添加辅助线.【例4】如图1,P 是线段AB 上一点,在AB 的同侧作△APC 和△BPD ,使∠APC =∠BPD ,PC =P A ,PD =PB ,连接CD ,点E ,F ,G ,H 分别是AC ,AB ,BD ,CD 的中点,顺次连接E ,F ,G ,H .(1) 猜想四边形EFGH 的形状,直接回答,不必说明理由;(2) 当点P 在线段AB 的上方时,如图2,在△APB 的外部作△APC 和△BPD ,其他条件不变,(1)中的结论还成立吗?说明理由;(3) 如果(2)中,∠APC =∠BPD =90°,其他条件不变,先补全图3,再判断四边形EFGH 的形状,并说明理由. (营口市中考试题)BAPAFP BG D H CE HGF E PABC D图① 图② 图③解题思路:结论随着条件的改变也许发生变化,但解决问题的方法是一致的,即通过连线,为三角形中位线定理的应用创造条件.例3图CA D【例5】如图,以△ABC 的AB ,AC 边为斜边向形外作直角三角形ABD 和ACE ,且使∠ABD =∠ACE ,M 是BC 的中点,求证:DM =EM . (“祖冲之杯”邀请赛试题)解题思路:显然△DBM 不全等于△ECM ,必须通过作辅助线,构造全等三角形证明DM =EM .【例6】如图,已知△ABC 中,∠ACB =90°,AB 边上的高CH 与△ABC 的两条内角平分线AM ,BN 分别交于P ,Q 两点,PM ,QN 的中点分别为E ,F ,求证:EF ∥AB . (全国初中数学联赛题)解题思路:从图形的形成过程,逐步探索相应结论.将原问题分解为多个小问题.○能 ○力 ○训 ○练 A 级1.如图,若E ,F ,G ,H 分别是四边形ABCD 各边的中点,则四边形EFGH 是____________.(1)如果把条件中的四边形ABCD 依次改为矩形、菱形、正方形或等腰梯形,其他条件不变,那么所得的四边形EFGH 分别为_______________________;(2)如果把结论中的平行四边形EFGH 依次改为矩形、菱形、正方形,那么原四边形ABCD 应具备的条件是_______________________. (湖北省黄冈市中考试题)例5图 EDMABC例6图CB D2.如图,已知AG ⊥BD ,AF ⊥CE ,BD ,CE 分别是∠ABC 和∠ACB 的角平分线,若BF =2,ED =3,GC =4,则△ABC 的周长为_______________. (重庆市竞赛试题)3.如图,在△ABC 中,AB =AC ,AD ⊥BC 于点D ,E 是AC 的中点,若BC =16,DE =5,则AD =______________. (南京市中考试题)4.如图,在△ABC 中,AB =AC ,M ,N 分别是AB ,AC 的中点,D ,E 为BC 上的点,连接DN ,EM ,若AB =13cm ,BC =10cm ,DE =5cm ,则图中阴影部分的面积为________________. (北京市中考试题)5.A ′,B ′,C ′,D ′顺次为四边形ABCD 的各边的中点,下面条件中使四边形A ′B ′C ′D ′为正方形的条件是( )A .四边形ABCD 是矩形B .四边形ABCD 是菱形C .四边形ABCD 是等腰梯形 D .四边形ABCD 中,AC ⊥BD 且AC =BD 6.若等腰梯形的两条对角线互相垂直,中位线长为8cm ,则该等腰梯形的面积为( ) A .16cm 2 B .32cm 2 C .64cm 2 D .112cm 27.如图,梯形ABCD 中,AD ∥BC ,E ,F 分别是BD ,AC 的中点,若AD =6cm ,BC =18cm ,则EF 的长为( )A .8cmB .7cmC .6cmD .5cm8.如图,在梯形ABCD 中,AD ∥EF ∥GH ∥BC ,AE =EG =GB ,AD =18,BC =32,则EF +GH =( )A .40B .48C .50D .56 (泰州市中考试题)第4题图第1题图第2题图C第3题图A第7题图B第8题图 第9题图9.如图,在△ABC 中,∠B =2∠C ,AD ⊥BC 于点D ,M 是BC 的中点,求证:DM =12AB .10. 如图,在△ABC 中,BD =CE ,BE ,CD 的中点分别是M ,N ,直线MN 分别交AB ,AC 于点P ,Q ,求证:AP =AQ .11.在图1至图3中,点B 是线段AC 的中点,点D 是线段CE 的中点.四边形BCGF 和CDHN 都是正方形.AE 的中点是M .(1)如图1,点E 在AC 的延长线上,点N 与点G 重合时,点M 与点C 重合,求证:FM = MH ,FM ⊥MH ; (2)将图1中的CE 绕点C 顺时针旋转一个锐角,得到图2,求证:△FMH 是等腰直角三角形; (3)将图2中的CE 缩短到图3的情况,△FMH 还是等腰直角三角形吗?(不必说明理由) (2009年河北省中考试题)第10题图图1AHC (M )DEBFG (N )G图2 AHC DEBFNMAHCDE图3BFG MN12.在六边形ABCDEF 中,AB ∥DE ,BC ∥EF ,CD ∥F A ,AB +DE =BC +EF ,A 1,B 1,D 1,E 1分别是边AB ,BC ,DE ,EF 的中点,A 1D 1=B 1E 1.求证:∠CDE =∠AFE .B 级1.如图,正方形ABCD 两条对角线相交于点E ,∠CAD 的平分线AF 交DE 于点G ,交DC 于点F ,若GE =24,则FC =_________________.2.如图,四边形ABCD 的对角线AC ,BD 相交于点F ,M ,N 分别是AB ,CD 的中点,MN 分别交BD ,AC 于点P ,Q ,且∠FPQ =∠FQP ,BD =10,则AC =_________. (重庆市竞赛试题)3.如图,在△ABC 中,∠BAC =120°,以AB ,AC 为边分别向形外作正三角形ABD 和正三角形ACE ,M 为AD 的中点,N 为AE 的中点,P 为BC 的中点,则∠MPN =_________. (北京市竞赛试题) 4.如图,已知A 为DE 的中点,设△DBC ,△ABC ,△EBC 的面积分别为S 1,S 2,S 3,则S 1,S 2,S 3之间的关系是( )A .S 2=32(S 1+S 3)B .S 2=12(S 3―S 1)C .S 2=12(S 1+S 3)D .S 2=32(S 3―S 1)5.如图,在图形ABCD 中,AB ∥DC ,M 为DC 的中点,N 为AB 的中点,则 ( ) A .MN >12(AD +BC ) B .MN <12(AD +BC )C .MN =12(AD +BC ) D .无法确定MN 与12(AD +BC )的关系第2题图C第12题图FEF第1题图F第3题图6.如图,凸四边形ABCD 的面积是a ,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,那么图中的阴影部分的面积为( )A .18aB .16aC .14aD .12a(江苏省竞赛试题)7.如图,在△ABC 中,D 为AB 的中点,分别延长CA ,CB 到点E ,F ,使DE =DF ,过E ,F 分别作CA ,CB 的垂线,相交于点P .求证:∠P AE =∠PBF . (全国初中数学联赛试题)8.如图,锐角△ABC 中,作高BD 和CE ,过顶点B ,C 分别作DE 的垂线BF 和CG ,求证:EF =DG .(全俄奥林匹克数学竞赛试题)9. 如图,在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN =90°,如果BM 2+CN 2=DM 2+DN 2.求证:AD 2=14(AB 2+AC 2). (北京市竞赛试题)第8题图BG 第5题图DC M第4题图D第6题图ABE第7题图EPF90°,如果BM 2+CN 2=DM 2+DN 2.求证:AD 2=14(AB 2+AC 2). (北京市竞赛试题)10.已知:△ABD 和△ACE 都是直角三角形,且∠ABD =∠ACE =90°.如图1,连接DE ,设M 为DE 的中点.(1)求证:MB =MC ;(2)设∠BAD =∠CAE ,固定△ABD ,让Rt △ACE 绕顶点A 在平面内旋转到图2的位置,试问:MB =MC 是否还成立?请说明理由. (江苏省竞赛试题)图2图111.已知△OAB ,△OCD 都是等腰直角三角形,∠AOB =∠COD =90°. (1) 如图1,点C 在OA 边上,点D 在OB 边上,连接AD ,BC ,M 为线段AD 的中点,求证:OM ⊥BC . (2) 如图2,在图1的基础上,将△OCD 绕点O 逆时针旋转α(α为锐角),M 为线段AD 的中点.①求证:OM =12BC ;②OM ⊥BC 是否还成立?若成立,请证明;若不成立,请说明理由.第9题图ABCD图1图2BBODC12.如图1,在△ABC 中,点P 为BC 边的中点,直线a 绕顶点A 旋转,若点B ,P 在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接PM ,PN .(1)延长MP 交CN 于点E (如图2). ①求证:△BPM ≌△CPE ; ②求证:PM =PN .(2)若直线a 绕点A 旋转到如图3的位置时,点B ,P 在直线a 的同侧,其他条件不变,此时PM =PN 还成立吗?若成立,请证明;若不成立,请说明理由.(3) )若直线a 绕点A 旋转到与BC 边平行的位置时,其他条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 是否成立.不必说明理由. (沈阳市中考试题)图3图2图1BB。
2018年北京市中学生数学竞赛初二年级获奖名单

2018年北京市中学生数学竞赛初二年级获奖名单一等奖(94名)姓名学校年级姓名学校年级唐锦琪人大附中初一樊骏一人大附中初一袁浩然人大附中初二杨丽鸿清华附中初二陈竞帆人大附中初二段睿思清华附中初二关乃粼人大附中早六宋知轩清华附中初一张世奇人大附中初二沈芸伍清华附中初二张世潇北师大实验中学初一许易清华附中初二赵亦阳十一学校初二张一锐清华附中初二王浩霖人大附中初一潘宇锐北京一零一中初二廖昱博人大附中初一陈昕宇北京一零一中初二李永一人大附中初一李昊轩人大附中初一王原北大附中初二苗硕人大附中初二邹听雨十一学校初一黄安辀人大附中初一张书豪十一学校初二梁恒睿人大附中分校初一黄亦骐人大附中早六王俣涵北大附中初二宋嘉玺人大附中初二武正坤人大附中初一胡殊闻人大附中早六卢远人大附中初一王誉墨北师大实验中学初二谢昊霖人大附中初一贾博暄人大附中初二黄鹤鸣人大附中初一黄子萌北师大实验中学初二曲兆轩牛栏山一中实验学校初二张涵之人大附中初二阮宗泽人大附中初一陈嘉雪人大附中初二王慕涵人大附中初二徐健十一学校初一许睿泽北师大实验中学初二徐文昕人大附中初一许远航北京一零一中初二周亚琪清华附中初二刘若易北师大实验中学初二肖子健清华附中初一李海峰清华附中初一孙胤博人大附中初一许子涵人大附中初一王小龙人大附中早六朱祎然北京二中分校初二陈吉轲人大附中初二张元之清华附中初二李思学北大附中初二郭逸远北京一零一中初一廖原北京五中分校初二吴迪北师大实验中学初二王默涵清华附中初一钟沐阳人大附中初二刘星彤清华附中初二陈宇轩人大附中早六张皓翔北京一零一中初一蓝漩十一学校初二张章北京一零一中初二邓宇晨人大附中初一修时雨人大附中初二邓怡馨人大附中初一游天宇人大附中初一刘馨阳人大附中初一孙晓森清华附中初二吕博涵清华附中初二刘睿韬清华附中初一高子昂清华附中初一邹岳桐人大附中初二虞明达清华附中初一何翰韬十一学校初一李祖豫人大附中早六徐烨堃十一学校初二王中天人大附中初二张翔宇人大附中初二左泽成北师大实验中学初二张皓天北师大实验中学初一吴紫菱北师大实验中学初二张远洋人大附中初一罗天择人大附中初二高梓博人大附中初二卢天戈北大附中初二陈坤宁人大附中初二范唯楚清华附中初一张庭语人大附中初一付紫成人大附中初一二等奖(144名)姓名学校年级姓名学校年级范天舒人大附中初二齐锴人大附中初一张家铭人大附中初二李安之北京二中分校初二蔡振浩人大附中初二肖翊宸人大附中初一王凤怡人大附中初二袁籁人大附中初一孟博彰人大附中初一张泰然人大附中初一晁一沣人大附中初二彦昕人大附中初一王培阳清华附中初一孙嘉鸿人大附中初一毛嘉琛人大附中初一郭尉含章人大附中初二刘一铭清华附中初一栗选丞人大附中早六陈胤彤清华附中初二葛皓天人大附中初一李汝诚清华附中初二董亦麟人大附中初二曾广宇清华附中初二查益清华附中初二曹硕清华附中六年顾芸萌北师大实验中学初二张邵博清华附中初一丛诗雨北京一零一中初二张智清人大附中初二于天润北京一零一中初二王梓畅人大附中初一王梓翔人大附中初一杨昊源北京一零一中初二刘俊宏人大附中初一李宗润北师大实验中学初二洪维清华附中初一张一博北师大实验中学初二蒋辰昊人大附中初一刘以诺清华附中初二高慈欣北京一零一中初二吴梦晗清华附中初二董昀翱人大附中初一刘嫁新清华附中初二张天意北师大实验中学初二孙嘉阳清华附中初一翟凌飞人大附中早六夏海闻北师大实验中学初一朱泽睿人大附中初二陈宇奇人大附中初一周以端十一学校初二董天诺人大附中初二张煦恒人大附中初一吴飞扬人大附中初二李易铭人大附中初一段文博人大附中初二李飞跃十一学校初二郑元彬人大附中初二王羽健十一学校初二夏一桐人大附中初一斯文人大附中初二苗可明人大附中初一吴奕涵人大附中初一钱海天人大附中初一赵宸宇北京二中分校初二陆雪松人大附中初二李佳俊清华附中初二肖旭磊十一学校初一陈彦旭清华附中初二李春进人大附中早六王子兮清华附中初二乔铎北京亦庄实验中学初二李子豪清华附中初一郭俊游人大附中早六常三思人大附中初一黄俊维人大附中早六吕逍依人大附中初一王雨晗十一学校初二王镜廷人大附中早六龙韬智十一学校初二祝世博十一学校初二吴青阳人大附中初二陆洲锋北京二中分校初二龚云锋牛栏山一中实验学校初二黄兆屹人大附中分校初二方郑琦牛栏山一中实验学校初二张广源清华附中初一徐定坤人大附中初二刘一晨北京一零一中初二周蔚然人大附中初二张致远北京二中分校初二崔焱扬北京二中分校初二陈炫东北大附中初二张逸轩北大附中初一赵泽昕人大附中分校初二陈灵钧北京五中分校初二肖惠文清华附中六年黎丹宇北大附中初二张殊赫北京一零一中初二申君皓清华附中初二李依桐北京一零一中初二赵培源清华附中初二汪远北京一零一中初二韩羽霄清华附中初二姚亦嵩北京一零一中初二关清元人大附中初一李思颖北京一零一中初二余凌越清华附中初二李奕含北师大实验中学初二卞皓晨北师大实验中学初二吕彦荣北师大实验中学初二陈霁芸人大附中早六田昊霖人大附中初一耳昶玮人大附中初二孟晙阳北京二中分校初二王子初北京二中分校初二刘语玹人大附中初二刘任达北京四中初二郭晟毓十一学校初二申奕坤人大附中初二徐皓天人大附中初二马迹昀十一学校初一胡晓君人大附中初二阮家琪人大附中初一张子睿人大附中分校初一王子鸣人大附中初一徐金人大附中初二吴雨轩人大附中初二王子涵人大附中早六李铭泽清华附中初一陈智谦人大附中初二徐启鑫清华附中初一董雪瑞北大附中初二郑睿阳清华附中初二杨子谦北京五中分校初二杨舒涵清华附中初二付浩辰十一学校初二刘语涵清华附中初一赵柯人大附中初一荆明健清华附中初二蒋穆清人大附中初一李浩明北师大实验中学初一许景粟人大附中初一张涵钰清华附中初一郑睿阳清华附中初二三等奖(123名)姓名学校年级姓名学校年级刘相卿清华附中初二赵天珺十一学校-初二杜胤臻清华附中初二杨成科人大附中初一钱铭阳清华附中初二李卓言北京五中分校初二张文健清华附中初二李天圣北大附中初一陈楚瑜清华附中初二陈桢懿北大附中初二董予人大附中初一陈灿首师大附中初二赵一辰北师大实验中学初二张逸扬北京二中分校初二陈誉霄人大附中初二蔡泊屹北大附中初一周子昂人大附中初二马昊宇十一学校初二张雪桢北京二中分校初二苗瀚文人大附中初一王帅烨人大附中早六鲍俊辰清华附中初二张冰喆人大附中初一张宁远清华附中初二王泽尘人大附中初二张天翼清华附中初二田笑冰北京五中分校初二贺家琦北师大实验中学初一李昀濠清华附中初一张雨桐北京一零一中初二李金宸清华附中初一余瑶北师大实验中学初二孙一文清华附中初一张杰辰北京一零一中初二陆宜行十一学校初二杨谨毓北京一零一中初一周雪阳清华附中初一梁毓北师大实验中学初二孙家瑞人大附中初二杨博涵北师大实验中学初二李一申北京五中分校初二诸晨岳清华附中初二韩沛瑾人大附中初一郭馨锴清华附中初二康恺文牛栏山实验中学初二王一飞清华附中初二梁宸菲牛栏山实验中学初二关澜清华附中初二张喆人大附中初二宋清岳清华附中初二李诗均北大附中初一许赫男清华附中初一杜恒奕北京二中分校初二杨凡楷清华附中初二卢思翰人大附中早六吕桉驰清华附中初二杨紫雄人大附中初二汪佳萱北师大实验中学初二朱炯亦首师大附中初一李子闻北师大实验中学初一匡天一北京二中分校初二杨润欣北师大实验中学初一王彦翔北京四中初二刘孟歆北师大实验中学初一石家霖人大附中初二徐鼎新人大附中分校初一徐隽镕人大附中早六姬奕晨北京一零一中初二罗嘉祺北京一零一中初二高飞人大附中初二张亦鑫人大附中初一张沁月北大附中初二汪宁北京二中分校初二贾天歌人大附中初一王雨桉北京四中初二吴道宁人大附中初一张童开首师大附中初二李思海人大附中初一丁牧云北京市第十二中学初二魏梦萱人大附中初一刘涵柞人大附中初二邢琬瑜人大附中早六高欢瑜人大附中早六方大容人大附中初一何思远清华附中初二陈瑞泽首师大附中初一任墨也人大附中初二郑文博首师大附中初二王禹腾清华附中初二里正阳北京四中初二陈禹铭清华附中初二何阳松人大附中初二侯博文十一学校初一许昊翔人大附中早六东紫昭十一学校初二丁天岚人大附中初一王润山十一学校初一王泽芃北京四中初二隋远昊十一学校初一陈子璐北京一零一中初二史洪毓人大附中初一高江山清华附中初二杨佳营北京五中分校初二纪明悦清华附中初二迟嘉会北京五中分校初二李熙民北师大实验中学初二张语轩人大附中初二战治成师达中学初二王众一人大附中初二张斗和人大附中初二温雪岭人大附中初二王心睿人大附中初二刘羿镝人大附中初二孟繁钰人大附中初二张皓翔人大附中初二张婧婷十一学校初一刘俊扬人大附中初一闫岳霖牛栏山一中实验学校初二张戈飞人大附中早六张天艺牛栏山一中实验学校初二侯梓超人大附中初二杨卓然首师大附中初二陈含哲北京一零一中初二。
北京市初二数学竞赛学生版
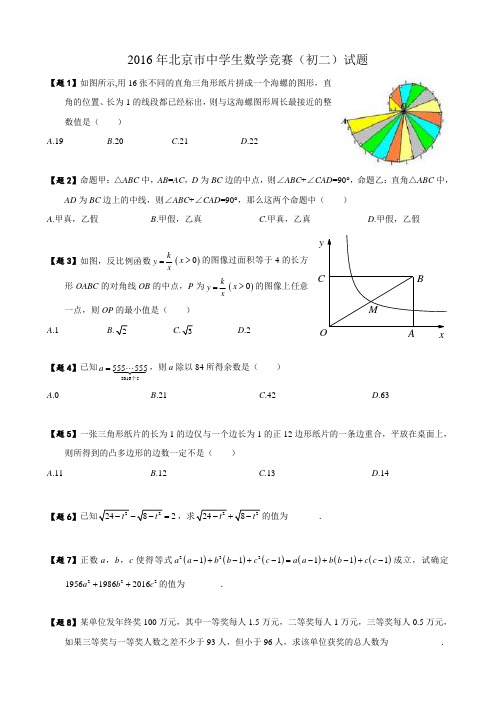
【题 9】△ABC 中,∠BAC=45°,∠ABC=60°,高线 AD 与 BE 相交于 H,若 AB=1,求四边形 CDHE 的面 积_________.
x
一点,则 OP 的最小值是( )
A.1
B. 2
C. 3
D.2
O
B M
Ax
【题 4】已知 a 555555 ,则 a 除以 84 所得余数是( )
2016个5
A.0
B.21
C.42
D.63
【题 5】一张三角形纸片的长为 1 的边仅与一个边长为 1 的正 12 边形纸片的一条边重合,平放在桌面上, 则所得到的凸多边形的边数一定不是( )
A.11
B.12
C.13
D.14
【题 6】已知 24 t2 8 t2 2 ,求 24 t2 8 t2 的值为_______.
【题 7】正数 a,b,c 使得等式 a2 a 1 b2 b 1 c2 c 1 a a 1 bb 1 c c 1 成立,试确定
1956a2 1986b2 2016c2 的值为________.
A C1 C2
B2 B1
B A1 A2 C
【题 13】一个自然数 n 若能表示为若干个正整数的和,且这些正整数的倒数和也恰等于 1,则称 n 为“金 猴数”,比如 2 4 8 8 22 且 1 1 1 1 1 ,22 就是一个“金猴数” 2488
(1)证明:11 与 28 是两个“金猴数”; (2)证明:如果 n 是“金猴数”,则 2n 2 、 2n 9 也是“金猴数”; (3)请你判定:2016 也是“金猴数”.
北京市中学生数学竞赛初二年级获奖名单

2018年北京市中学生数学竞赛初二年级获奖名单一等奖(94名)姓名学校年级姓名学校年级唐锦琪人大附中初一樊骏一人大附中初一袁浩然人大附中初二杨丽鸿清华附中初二陈竞帆人大附中初二段睿思清华附中初二关乃粼人大附中早六宋知轩清华附中初一张世奇人大附中初二沈芸伍清华附中初二张世潇北师大实验中学初一许易清华附中初二赵亦阳十一学校初二张一锐清华附中初二王浩霖人大附中初一潘宇锐北京一零一中初二廖昱博人大附中初一陈昕宇北京一零一中初二李永一人大附中初一李昊轩人大附中初一王原北大附中初二苗硕人大附中初二邹听雨十一学校初一黄安辀人大附中初一张书豪十一学校初二梁恒睿人大附中分校初一黄亦骐人大附中早六王俣涵北大附中初二宋嘉玺人大附中初二武正坤人大附中初一胡殊闻人大附中早六卢远人大附中初一王誉墨北师大实验中学初二谢昊霖人大附中初一贾博暄人大附中初二黄鹤鸣人大附中初一黄子萌北师大实验中学初二曲兆轩牛栏山一中实验学校初二张涵之人大附中初二阮宗泽人大附中初一陈嘉雪人大附中初二王慕涵人大附中初二徐健十一学校初一许睿泽北师大实验中学初二徐文昕人大附中初一许远航北京一零一中初二周亚琪清华附中初二刘若易北师大实验中学初二肖子健清华附中初一李海峰清华附中初一孙胤博人大附中初一许子涵人大附中初一王小龙人大附中早六朱祎然北京二中分校初二陈吉轲人大附中初二张元之清华附中初二李思学北大附中初二郭逸远北京一零一中初一廖原北京五中分校初二吴迪北师大实验中学初二王默涵清华附中初一钟沐阳人大附中初二刘星彤清华附中初二陈宇轩人大附中早六张皓翔北京一零一中初一蓝漩十一学校初二张章北京一零一中初二邓宇晨人大附中初一修时雨人大附中初二邓怡馨人大附中初一游天宇人大附中初一刘馨阳人大附中初一孙晓森清华附中初二吕博涵清华附中初二刘睿韬清华附中初一高子昂清华附中初一邹岳桐人大附中初二虞明达清华附中初一何翰韬十一学校初一李祖豫人大附中早六徐烨堃十一学校初二王中天人大附中初二张翔宇人大附中初二左泽成北师大实验中学初二张皓天北师大实验中学初一吴紫菱北师大实验中学初二张远洋人大附中初一罗天择人大附中初二高梓博人大附中初二卢天戈北大附中初二陈坤宁人大附中初二范唯楚清华附中初一张庭语人大附中初一付紫成人大附中初一二等奖(144名)姓名学校年级姓名学校年级范天舒人大附中初二齐锴人大附中初一张家铭人大附中初二李安之北京二中分校初二蔡振浩人大附中初二肖翊宸人大附中初一王凤怡人大附中初二袁籁人大附中初一孟博彰人大附中初一张泰然人大附中初一晁一沣人大附中初二彦昕人大附中初一王培阳清华附中初一孙嘉鸿人大附中初一毛嘉琛人大附中初一郭尉含章人大附中初二刘一铭清华附中初一栗选丞人大附中早六陈胤彤清华附中初二葛皓天人大附中初一李汝诚清华附中初二董亦麟人大附中初二曾广宇清华附中初二查益清华附中初二曹硕清华附中六年顾芸萌北师大实验中学初二张邵博清华附中初一丛诗雨北京一零一中初二张智清人大附中初二于天润北京一零一中初二王梓畅人大附中初一王梓翔人大附中初一杨昊源北京一零一中初二刘俊宏人大附中初一李宗润北师大实验中学初二洪维清华附中初一张一博北师大实验中学初二蒋辰昊人大附中初一刘以诺清华附中初二高慈欣北京一零一中初二吴梦晗清华附中初二董昀翱人大附中初一刘嫁新清华附中初二张天意北师大实验中学初二孙嘉阳清华附中初一翟凌飞人大附中早六夏海闻北师大实验中学初一朱泽睿人大附中初二陈宇奇人大附中初一周以端十一学校初二董天诺人大附中初二张煦恒人大附中初一吴飞扬人大附中初二李易铭人大附中初一段文博人大附中初二李飞跃十一学校初二郑元彬人大附中初二王羽健十一学校初二夏一桐人大附中初一斯文人大附中初二苗可明人大附中初一吴奕涵人大附中初一钱海天人大附中初一赵宸宇北京二中分校初二陆雪松人大附中初二李佳俊清华附中初二肖旭磊十一学校初一陈彦旭清华附中初二李春进人大附中早六王子兮清华附中初二乔铎北京亦庄实验中学初二李子豪清华附中初一郭俊游人大附中早六常三思人大附中初一黄俊维人大附中早六吕逍依人大附中初一王雨晗十一学校初二王镜廷人大附中早六龙韬智十一学校初二祝世博十一学校初二吴青阳人大附中初二陆洲锋北京二中分校初二龚云锋牛栏山一中实验学校初二黄兆屹人大附中分校初二方郑琦牛栏山一中实验学校初二张广源清华附中初一徐定坤人大附中初二刘一晨北京一零一中初二周蔚然人大附中初二张致远北京二中分校初二崔焱扬北京二中分校初二陈炫东北大附中初二张逸轩北大附中初一赵泽昕人大附中分校初二陈灵钧北京五中分校初二肖惠文清华附中六年黎丹宇北大附中初二张殊赫北京一零一中初二申君皓清华附中初二李依桐北京一零一中初二赵培源清华附中初二汪远北京一零一中初二韩羽霄清华附中初二姚亦嵩北京一零一中初二关清元人大附中初一李思颖北京一零一中初二余凌越清华附中初二李奕含北师大实验中学初二卞皓晨北师大实验中学初二吕彦荣北师大实验中学初二陈霁芸人大附中早六田昊霖人大附中初一耳昶玮人大附中初二孟晙阳北京二中分校初二王子初北京二中分校初二刘语玹人大附中初二刘任达北京四中初二郭晟毓十一学校初二申奕坤人大附中初二徐皓天人大附中初二马迹昀十一学校初一胡晓君人大附中初二阮家琪人大附中初一张子睿人大附中分校初一王子鸣人大附中初一徐金人大附中初二吴雨轩人大附中初二王子涵人大附中早六李铭泽清华附中初一陈智谦人大附中初二徐启鑫清华附中初一董雪瑞北大附中初二郑睿阳清华附中初二杨子谦北京五中分校初二杨舒涵清华附中初二付浩辰十一学校初二刘语涵清华附中初一赵柯人大附中初一荆明健清华附中初二蒋穆清人大附中初一李浩明北师大实验中学初一许景粟人大附中初一张涵钰清华附中初一郑睿阳清华附中初二三等奖(123名)姓名学校年级姓名学校年级刘相卿清华附中初二赵天珺十一学校-初二杜胤臻清华附中初二杨成科人大附中初一钱铭阳清华附中初二李卓言北京五中分校初二张文健清华附中初二李天圣北大附中初一陈楚瑜清华附中初二陈桢懿北大附中初二董予人大附中初一陈灿首师大附中初二赵一辰北师大实验中学初二张逸扬北京二中分校初二陈誉霄人大附中初二蔡泊屹北大附中初一周子昂人大附中初二马昊宇十一学校初二张雪桢北京二中分校初二苗瀚文人大附中初一王帅烨人大附中早六鲍俊辰清华附中初二张冰喆人大附中初一张宁远清华附中初二王泽尘人大附中初二张天翼清华附中初二田笑冰北京五中分校初二贺家琦北师大实验中学初一李昀濠清华附中初一张雨桐北京一零一中初二李金宸清华附中初一余瑶北师大实验中学初二孙一文清华附中初一张杰辰北京一零一中初二陆宜行十一学校初二杨谨毓北京一零一中初一周雪阳清华附中初一梁毓北师大实验中学初二孙家瑞人大附中初二杨博涵北师大实验中学初二李一申北京五中分校初二诸晨岳清华附中初二韩沛瑾人大附中初一郭馨锴清华附中初二康恺文牛栏山实验中学初二王一飞清华附中初二梁宸菲牛栏山实验中学初二关澜清华附中初二张喆人大附中初二宋清岳清华附中初二李诗均北大附中初一许赫男清华附中初一杜恒奕北京二中分校初二杨凡楷清华附中初二卢思翰人大附中早六吕桉驰清华附中初二杨紫雄人大附中初二汪佳萱北师大实验中学初二朱炯亦首师大附中初一李子闻北师大实验中学初一匡天一北京二中分校初二杨润欣北师大实验中学初一王彦翔北京四中初二刘孟歆北师大实验中学初一石家霖人大附中初二徐鼎新人大附中分校初一徐隽镕人大附中早六姬奕晨北京一零一中初二罗嘉祺北京一零一中初二高飞人大附中初二张亦鑫人大附中初一张沁月北大附中初二汪宁北京二中分校初二贾天歌人大附中初一王雨桉北京四中初二吴道宁人大附中初一张童开首师大附中初二李思海人大附中初一丁牧云北京市第十二中学初二魏梦萱人大附中初一刘涵柞人大附中初二邢琬瑜人大附中早六高欢瑜人大附中早六方大容人大附中初一何思远清华附中初二陈瑞泽首师大附中初一任墨也人大附中初二郑文博首师大附中初二王禹腾清华附中初二里正阳北京四中初二陈禹铭清华附中初二何阳松人大附中初二侯博文十一学校初一许昊翔人大附中早六东紫昭十一学校初二丁天岚人大附中初一王润山十一学校初一王泽芃北京四中初二隋远昊十一学校初一陈子璐北京一零一中初二史洪毓人大附中初一高江山清华附中初二杨佳营北京五中分校初二纪明悦清华附中初二迟嘉会北京五中分校初二李熙民北师大实验中学初二张语轩人大附中初二战治成师达中学初二王众一人大附中初二张斗和人大附中初二温雪岭人大附中初二王心睿人大附中初二刘羿镝人大附中初二孟繁钰人大附中初二张皓翔人大附中初二张婧婷十一学校初一刘俊扬人大附中初一闫岳霖牛栏山一中实验学校初二张戈飞人大附中早六张天艺牛栏山一中实验学校初二侯梓超人大附中初二杨卓然首师大附中初二陈含哲北京一零一中初二。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年北京市中学生数学竞赛初二试题一、选择题(每小题5分,共25分)1.在1~100这100个自然数中,质数所占的百分比是().(A)25% (B)24% (C)23% (D)22%2.一个三角形的三边长都是整数,它的周长等于10,则这个三角形是().(A)直角三角形(B)钝角三角形(C)恰有两边相等的三角形(D)恰有一个内角为60°的三角形3.已知n为正整数,S=1+2+…+n.则S的个位数字不能取到的数字是().(A)0,1,2,3 (B)3,4,5,6(C)3,5,6,8 (D)2,4,7,94.如图1,四边形ABCD的对角线AC、BD相交于点O.S△AOB=4,S△COD=9.则S四边形的最小值是().ABCD(A)22 (B)25 (C)28 (D)32(1)(2) (3)5.如果│a-b│=1,│b+c│=1,│a+c│=2,则│a+b+2c│等于().(A)3 (B)2 (C)1 (D)0二、填空题(每小题7分,共35分)1.如图2,大圆的两条直线AC、BC垂直相交于点O,分别以边AB、BC、CD、DA为直径向大圆外侧作四个半圆,图中四个“月形”阴影的总面积是2cm2.•则大圆的半径等于_______cm.2.2 005被两位的自然数去除,可能得到的最大余数是_______.3.已知a2+bc=14,b2-2bc=-6.则3a2+4b2-5bc=_________.4.如图3,在凸六边形ABCDEF中,AD、BE、CF三线共点于O,•每相邻三个顶点所组成的三角形的面积都等于1,则S六边形ABCDEF=_______.5.有6个被12除所得余数都相同的自然数,它们的连乘积为971 425.则这6•个自然数之和的最小值是________.三、(15分)已知非零实数a、b、c满足a+b+c=0.求证:(1)a3+b3+c3=3abc;(2)(a bc-+b ca-+c ab-)(ca b-+ab c-+bc a-)=9.四、(15分)如图,在△ABC中,∠BAC=∠BCA=44°,M为△ABC形内一点,•使得∠MCA=30°,∠MAC=16°,求∠BMC的度数.五、(10分)某学生在黑板上写出了17个自然数,•每个自然数的个位数码只能是0,1,2,3,4这5个数字中的一个.证明:从这17个数中可以选出5个数,•它们的和能被5整除.参考答案一、1.A在1~100这100个自然数中,有质数2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97共25个,所以,其中质数所占的百分比是25%.2.C将10分拆成三个正整数之和,有10=1+1+8=1+2+7=1+3+6=1+4+5=2+2+6=2+3+5=2+4+4=3+3+4共八种情况.由“三角形两边之和大于第三边”可知,只有(2,4,4),(3,3,4)两组可构成三角形.由于等腰三角形两个底角都是锐角,于是,以2、4、4为边的等边三角形中,最小边2对的顶角也是锐角.以3、3、4为边的等腰三角形中,由32+32>42,•知顶角也是锐角.所以,以2、4、4为边的等腰三角形以及以3、3、4为边的等腰三角形都是锐角三角形,排除选项(A)、(B)•.•又由于等腰三角形中恰有一个内角为60°时变为等边三角形,与边为(2,4,4)、(3,3,4)的条件矛盾,排除选项(D).由(2,4,4)、(3,3,4)为边的三角形是恰有两边相等的三角形.3.D.由S=(1)2n n+,又n、n+1是两个连续的自然数,知n(n+1)的个位数字只能取0,2,6.•所以,S的个位数字只能是0,1,3,5,6,8这六个数字.因此,S的个位数字不能取到的是2,4,7,9.4.B如图1,设S△AOD=x,S△BOC=y,则S四边形ABCD=4+9+x+y≥13+2xy.由49xy=,有xy=36.所以,S四边形ABCD≥13+2xy=13+12=25.故S四边形ABCD的最小值是25.此时,AB∥DC,即四边形ABCD是梯形.5.A.由│a-b│=1,知a-b=1或a-b=-1;由│b+c│=1,知b+c=1或b+c=-1;由│a+c│=2,知a+c=2或a+c=-2.这样,可以得到23=8个三元一次方程组:(1)a-b=1,b+c=1,a+c=2;(2)a-b=1,b+c=1,a+c=-2;(3)a-b=1,b+c=-1,a+c=2;(4)a-b=1,b+c=-1,a+c=-2;(5)a-b=-1,b+c=1,a+c=2;(6)a-b=-1,b+c=1,a+c=-2;(7)a-b=-1,b+c=-1,a+c=2;(8)a-b=-1,b+c=-1,a+c=-2.对于(2)~(7),将前两个方程相加得到的a+c的值与后一个方程不同,所以,不会出现这六种情况.对于(1),有a=2-c,b=1-c,所以,a+b+2c=3.对于(8),有a=-2-c,b=-1-c,所以,a+b+2c=-3.故│a+b+2c│=3.二、1.1.由勾股定理知AD2+CD2=AC2.所以,上面半个大圆的面积等于以AD、CD为直径的两个半圆的面积.同理,下面半个大圆的面积等于以AB、BC为直径的两个半圆的面积.•因此,正方形ABCD的面积等于四个“月形”的总面积.容易计算,大圆的半径OD是1cm.2.85.由2 005依次被99,98,97,…去除,观察所得余数的值变化得2 005=99×20+25=98×20+45=97×20+65=96×20+85=95×21+10=94×21+31=93×21+52=92×21+73=91×22+3=90×22+25=89×22+47=88×22+69=87×23+4=86×23+27=85×23+50.以下的余数不会大于84,故可能得到的最大余数是85.3.18.3a2+4b2-5bc=3(a2+bc)+4(b2-2bc)=3×14+4×(-6)=18.4.6.如图5,连结BD、CE.因为S△BCD=S△ECD=1,所以,BE∥CD.因为S△BAF=S△EAF,所以,BE∥AF.因此,BE∥AF∥CD.同理,CF∥DE∥BA,AD∥FE∥BC.由AD、BE、CF三线共点于O,可知四边形OCDE、四边形OEFA、四边形OABC 都是平行四边形,易知,每个平行四边形的面积都等于2.5.150.因为971 425被12除余1,而971 425=5×5×7×7×13×61,其中被12除余5、余7、余1的质因数各都是两个,由于两个被12除余5(余7)的数的乘积被12除余1,而971 425与若干个1的积仍为971 425,被12除余1,所以,•只能是6个被12除余1的数的乘积为971 425.计算得知:971 425=1×1×1×1×1×971 425,这6个因数之和为1+1+1+1+1+971 425=971 430;971 425=1×1×1×1×13×74 725,这6个因数之和为1+1+1+1+13+74 725=74 742;971 425=1×1×1×13×25×2 989,这6个因数之和为1+1+1+13+25+2 989=3 030.事实上,设a、b都是被12除余1的大于1的自然数,且a≥b,则a≥b>2,易知ab>a×2=a+a>a+b.①根据式①得971 425=13×74 725>13+74 725=13+25×2 989>13+25+2 989=13+25+49×61>13+25+49+61.因为971 425=52×72×13×61=1×1×13×25×49×61,所以,971 425表为6•个被12除余1的自然数,它们和的最小值等于1+1+13+25+49+61=150.三、(1)由a+b+c=0,得a+b=-c,因此,(a+b)3=-c3.于是,有a3+3a2b+3ab2+b3=-c3.故a3+b3+c3=-3ab(a+b)=-3ab(-c)=3abc.(2).(a bc-+b ca-+c ab-)·ca b-=1+(b ca-+c ab-)·ca b-=1+22cab.同理,(a bc-+b ca-+c ab-)·ab c-=1+22abc.(a bc-+b ca-+c ab-)·bc a-=1+22bac故(a bc-+b ca-+c ab-)(ca b-+ab c-+bc a-)=1+22cab+1+22abc+1+22bac=3+3332()a b cabc++=3+23abcabc⨯=9.四、在△ABC中,由∠BAC=∠BCA=44°,得AB=BC,∠ABC=92°.如图6,作BD⊥AC于点D,延长CM交BD于点O,连结OA,则有∠OAC=∠MCA=30°,∠BAO=∠BAC-∠OAC=44°-30°=14°.∠OAM=∠OAC-∠MAC=30°-16°=14°.所以,∠BAO=∠MAO.又∠AOD=90°-∠OAD=90°-30°=60°=∠COD,所以,∠AOM=120°=∠AOB.又AO=AO,因此,△ABO≌△AMO.故OB=OM.由于∠BOM=120°,从而,∠OMB=∠OBM=1802BOM︒-∠=30°.所以,∠BMC=180°-∠OMB=150°.五、如果17个数的末位数字0,1,2,3,4每个都有,可选出5•个数的末位数字恰分别为0,1,2,3,4,则这5个数之和的末位数字为0,其和被5整除.如果17个数的末位数字不是0,1,2,3,4每个都有,则最多只有4•种不同的末位数字.这时,根据轴屉原理,这17个数中至少有5个数的末位数字一样.于是,这5•个数之和被5整除.。
