初中数学几个常用模型
初中数学66个常考几何模型50个应用题答题公式

初中数学常考的几何模型和应用题答题公式是学习和备考数学的关键内容。
不过,
请注意,我无法列出具体的66个常考几何模型或50个应用题答题公式,因为这
取决于不同地区、不同版本的教材和考试要求。
但我可以为你提供一些常见的几何模型和应用题答题思路或公式。
几何模型示例:
1.等边三角形模型:等边三角形的三条边相等,三个内角都是60°。
2.等腰三角形模型:等腰三角形有两条边相等,且对应的两个底角也相等。
3.直角三角形模型:直角三角形有一个90°的角,满足勾股定理(a² + b² = c²)。
4.平行四边形模型:平行四边形的对边平行且相等,对角相等。
5.梯形模型:梯形有一组对边平行,常考察其面积计算(上底加下底,乘以高,再除
以2)。
应用题答题公式或思路示例:
1.速度、时间、距离关系:速度= 距离/ 时间,距离= 速度×时间,时间= 距
离/ 速度。
2.工作问题:工作效率= 工作总量/ 工作时间,常用于比较不同人或机器的工作效
率。
3.百分比问题:部分= 总量×百分比,总量= 部分/ 百分比,百分比= 部分/
总量× 100%。
4.利息问题:简单利息= 本金×利率×时间,复利则考虑本金和利息的共同增
长。
5.浓度问题:浓度= 溶质质量/ 溶液质量× 100%,常用于解决混合溶液的浓度问
题。
初中三年常用的数学模型大汇总
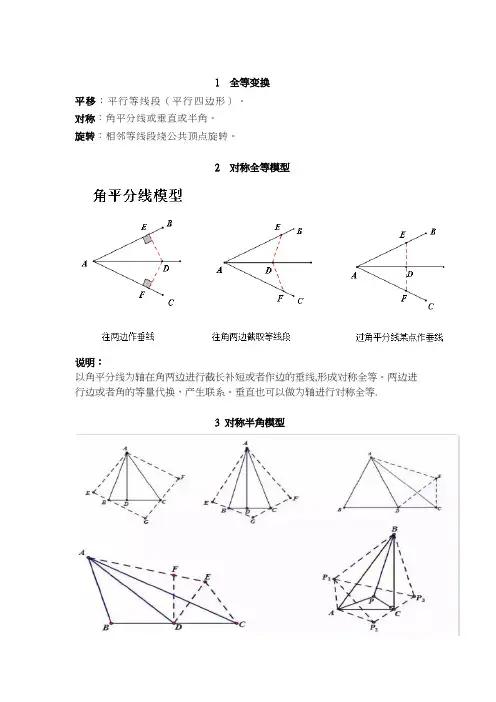
1 全等变换平移:平行等线段(平行四边形)。
对称:角平分线或垂直或半角。
旋转:相邻等线段绕公共顶点旋转。
2 对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等.3 对称半角模型说明:上图依次是45°、30°、22。
5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
4 旋转全等模型半角:有一个角含1/2角及相邻线段。
自旋转:有一对相邻等线段,需要构造旋转全等.共旋转:有两对相邻等线段,直接寻找旋转全等。
中点旋转:倍长中点相关线段转换成旋转全等问题。
5 旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等.6 自旋转变换构造方法:遇60度旋60度,造等边三角形;遇90度旋90度,造等腰直角;遇等腰旋顶点,造旋转全等;遇中点旋180度,造中心对称。
7 共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
8 模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用.当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
9 中点旋转模型说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
10 几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离.旋转最值(共线有最值)说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
初中几何48种数学模型系统讲解

初中几何48种数学模型系统讲解初中几何是数学中非常重要的一个分支,涉及到许多基础知识和技能。
在初中几何学习中,数学模型是非常重要的一环,它能够帮助学生更好地理解和掌握几何知识,并提高解题的能力。
下面我们就来介绍一下初中几何中常见的48种数学模型系统。
1. 平面几何模型:平面几何模型是研究平面上的图形和变换的数学模型,例如平移、旋转、对称等。
2. 立体几何模型:立体几何模型是研究空间中的图形和变换的数学模型,例如立体的投影、旋转、平移等。
3. 直线模型:直线模型是用来表示直线的数学模型,例如在平面几何中,可以使用坐标系来表示一条直线。
4. 线段模型:线段模型是用来表示线段的数学模型,例如在平面几何中,可以使用坐标系来表示一条线段。
5. 角度模型:角度模型是用来表示角度的数学模型,例如在平面几何中,可以使用角度制和弧度制来表示角度。
6. 相交模型:相交模型是用来表示图形相交的数学模型,例如在平面几何中,可以使用交点来表示两条直线相交的情况。
7. 平行模型:平行模型是用来表示平行线的数学模型,例如在平面几何中,可以使用平行线的定义来表示两条直线平行的情况。
8. 垂直模型:垂直模型是用来表示垂直线的数学模型,例如在平面几何中,可以使用垂直线的定义来表示两条直线垂直的情况。
9. 对称模型:对称模型是用来表示对称图形的数学模型,例如在平面几何中,可以使用对称轴来表示对称图形的情况。
10. 相似模型:相似模型是用来表示相似图形的数学模型,例如在平面几何中,可以使用相似比例来表示两个相似图形之间的关系。
11. 等比模型:等比模型是用来表示等比数列的数学模型,例如在几何中,可以使用等比数列来表示一些几何问题。
12. 等分模型:等分模型是用来表示等分线段的数学模型,例如在几何中,可以使用等分线段来表示将一个线段分成若干等分的情况。
13. 圆模型:圆模型是用来表示圆形的数学模型,例如在平面几何中,可以使用圆心、半径来表示一个圆。
初中48个数学模型

初中48个数学模型
1. 直线方程模型
2. 一次函数模型
3. 二次函数模型
4. 指数函数模型
5. 对数函数模型
6. 三角函数模型
7. 幂函数模型
8. 反比例函数模型
9. 绝对值函数模型
10. 分段函数模型
11. 等差数列模型
12. 等比数列模型
13. 等差数列求和模型
14. 等差数列通项求值模型
15. 等差数列前n项和求值模型
16. 等差数列前n项平均值模型
17. 等比数列求和模型
18. 等比数列通项求值模型
19. 等比数列前n项和求值模型
20. 等差数列与等差数列之和关系模型
21. 平方根模型
22. 平方根与二次方程关系模型
23. 正方形面积模型
24. 三角形面积模型
25. 平行四边形面积模型
26. 斜率模型
27. 切线斜率模型
28. 余弦定理模型
29. 正弦定理模型
30. 几何相似模型
31. 三角形相似模型
32. 平行线与平行线之间的角关系模型
33. 同位角与内错角模型
34. 相交弦定理模型
35. 角平分线定理模型
36. 体积模型
37. 圆锥体积模型
38. 圆柱体积模型
39. 球体积模型
40. 柱台体积模型
41. 三维图形表面积模型
42. 立体图形展开模型
43. 均值不等式模型
44. 不等式求解模型
45. 组合数学模型
46. 排列数学模型
47. 方程求解模型
48. 实际问题建模模型
以上是初中数学常见的48个数学模型,希望对你有所帮助!。
初中数学九大几何模型
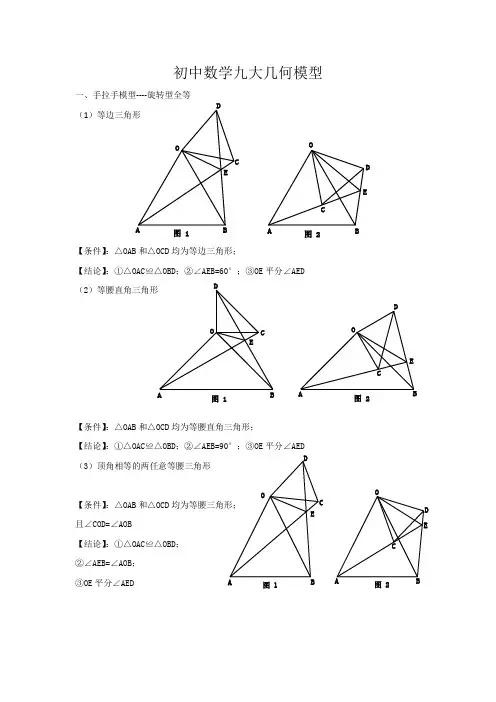
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学196个模型

初中数学196个模型篇一:初中数学是学生学习数学知识的重要阶段,也是培养他们数学思维能力和解决问题能力的关键时期。
在初中数学学习中,掌握数学模型是非常重要的,因为它能帮助学生将抽象的数学概念与现实生活中的问题相联系,使数学知识更加具体和实用。
在初中数学学习中,有许多重要的数学模型,下面将介绍其中的一些。
1. 几何模型:几何模型是初中数学中最基本的模型之一,它涉及到点、线、面、体等几何图形的性质和关系。
学生通过学习几何模型,可以掌握几何图形的特点,如直线的特性、平行线的性质、三角形的分类等,并能够运用几何模型解决实际问题。
2. 等式模型:等式模型是初中代数学习中的核心模型之一,它包括一元一次方程、一元一次不等式、二元一次方程等。
学生通过学习等式模型,可以掌握代数运算的基本规律,如加减乘除的计算,以及解方程、解不等式的方法,从而能够解决与等式相关的实际问题。
3. 概率模型:概率模型是初中数学学习中的一个重要模型,它涉及到随机事件的发生概率和统计推断等内容。
学生通过学习概率模型,可以了解事件发生的可能性,并能够运用概率模型解决与概率相关的实际问题,如掷硬币、抽卡片等。
4. 数列模型:数列模型是初中数学学习中的一个重要模型,它涉及到数列的概念、性质和应用等内容。
学生通过学习数列模型,可以了解数列的规律和特点,如等差数列、等比数列等,并能够运用数列模型解决与数列相关的实际问题,如找规律、预测未知数等。
5. 图形模型:图形模型是初中数学学习中的一个重要模型,它涉及到平面图形的性质和关系等内容。
学生通过学习图形模型,可以了解平面图形的分类、性质和变换等,并能够运用图形模型解决与图形相关的实际问题,如面积计算、图形的相似性等。
总之,初中数学学习中有许多重要的数学模型,通过学习这些模型,学生不仅可以增加对数学知识的理解和掌握,还可以培养数学思维能力和解决问题能力,为将来的学习和生活打下坚实的数学基础。
篇二:初中数学是学习和掌握数学基础知识的重要阶段。
初中数学几个常用模型
(1:3)
④(2005年浙江绍兴T18.)(以下两小题选做一题,第(1)小题满分5分,第(2)小题
满分为3分。若两小题都做,以第(1)小题计分)
选做第________小题,答案为________
(1)将一副三角板如图叠放,则左右阴影部分面积S1:S2之比等于________
222
⑵三对相似三角形:⊿ACD∽⊿CBD∽⊿ABC, AC =AD·AB BC =BD·AB CD=BD·AD⑶边之比的推广
⑷面积:AC·BC=AB·CD
⑸勾股定理
⑹AB是ABC外接圆的直径
①
②③④⑤
∽
模型5增长率
①②③④⑤⑧增长率与百分数问题
i
ii某商品降价20%后出售,一段时间后恢复原价,则应在售价的基础上提高的百分数是
截面如图所示,如果油面宽
AB=8m,那么油的最
大深度是______m.
模型7
配方法
用配方法解关于
x2+px+q=0时,此方程可变为(
A)
( x
p2p2
4q
( x
p
24q p2
(x
p
2p2
4q
p
2
4q p2
)
4
)
4
)
4
(x
)
A.
2
B.
2
C.
2
D.
2
4
模型8
三个非负量
初中阶段学过三个非负量:平方数
,绝对值
交于点N,分别过点M、N作直线AB的垂线,垂足为G、H。
(1)当α=30°时(如图②),求证:AG=DH;
初中几何46种模型大全
初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
初中数学|23种模型汇总
初中数学|23种模型汇总初中数学中,有许多不同的模型方法可以帮助学生理解和解决问题。
这些模型方法以图形、物体和实际情境等形式呈现,通过具象化和抽象化的方式引导学生建立数学概念和解题能力。
以下是初中数学中常用的23种模型汇总:1.长方形模型:将实际问题或数学关系转化为长方形的长度和宽度,以便解决各种问题。
2.正方形模型:通过将关系表达为正方形的边长和面积来解决问题。
3.圆形模型:将实际问题或数学关系转换为圆的直径、半径、周长和面积,以解决相应的问题。
4.三角形模型:通过将问题转化为三角形的底边、高和面积来解决问题。
5.平行四边形模型:通过将问题转化为平行四边形的底边、高和面积来解决问题。
6.梯形模型:将问题转化为梯形的上底、下底、高和面积,以解决相应的问题。
7.直角三角形模型:通过将问题转化为直角三角形的直角边、斜边和面积来解决问题。
8.立体模型:通过制作模型或利用图形来解决与立体图形相关的问题,如长方体、正方体、圆柱体、圆锥体、球体等。
9.比例模型:通过将问题转化为比例关系来解决问题,如平均速度、单位价格等。
10.百分比模型:将问题转化为百分比的概念和计算来解决问题,如打折、涨价等。
11.质量守恒模型:通过将问题转化为质量守恒的原理来解决问题。
12.可视化模型:通过绘制图形、示意图或使用图表来解决问题,以帮助学生更好地理解和分析问题。
13.数轴模型:通过在数轴上表示数值和位置来解决问题,如正数、负数、小数、分数等。
14.曲线图模型:通过绘制曲线图或利用曲线图来解决问题,如成长曲线、销售曲线等。
15.关系图模型:通过绘制关系图或利用关系图来解决问题,如家族关系、人际关系等。
16.流程图模型:通过绘制流程图或利用流程图来解决问题,如计算、制作工艺等。
17.条形图模型:通过绘制条形图或利用条形图来解决问题,如统计数据、比较等。
18.平面几何模型:通过绘制图形和利用几何关系来解决问题,如平行线、垂直线、对称等。
(完整版)初中数学九大几何模型
初中数学九大几何模型OD ECABAED DOECBABOC ECAEDD图2图 2、手拉手模型 - 旋转型全等D E③OE 平分∠ AED图 2图 1 OABD OAO ②∠ AEB=∠AOB ; 且∠ COD=∠AOB1)等边三角形3)顶角相等的两任意等腰三角形 2)等腰直角三角形图 1图 1C结论】:①△ OAC ≌△ OBD ;C条件】:△ OAB 和△ OCD 均为等边三角形条件】:△ OAB 和△ OCD 均为等腰直角三角形条件】:△ OAB 和△ OCD 均为等腰三角形 结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 平分∠ 结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 平分∠、模型二:手拉手模型 -- 旋转型相似(1)一般情况 【条件】:CD ∥AB , 将△ OCD 旋转至右图的位置 O OD EA A结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA2)特殊情况 条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ; ③ A BD C O O C D O O A B tan ∠OCD ;④BD ⊥AC ; ⑤连接 AD 、BC ,必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1)全等型 -90 ° 条件】:①∠ AOB=∠ DCE=90°;② OC 平分∠ AOB结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCE CD ;⑥S△BCD证明提示: ①作垂直,如图 2,证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC , 如图 3,证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4): S△OCDS以上三个结论:① CD=CE ;② OE-OD= 2 OC ; ③ S △ OCE S △ OCD2)全等型 -120 °条件】:①∠ AOB=2∠ DCE=120°;② OC 平分∠ AOB32 结论】:① CD=CE ;② OD+OE=O ;C ③ S △DCES △OCDS △OCEOC 2 4证明提示:①可参考“全等型 -90 °”证法一;②如右下图:在 OB 上取一点 F ,使 OF=OC ,证明△ OCF 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初 中 数 学 几 个 数 学 模 型模型1、l:r=3600:n 0①圆锥母线长5cm ,底面半径长3cm ,那么它的侧面展开图的圆心角是 216 。
②劳技课上,王芳制作了一个圆锥形纸帽,其尺寸如图.则将这个纸帽展开成扇形时的圆心角等于( C ) A .45° B.60° C .90° D.120°③要制作一个圆锥形的模型,要求底面半径为2cm ,母线长为4cm ,在一个边长为8cm 的正方形纸板上,能否裁剪制作一个这种模型(侧面和底面要完整,不能拼凑)( C ) (A)一个也不能做 (B)能做一个 (C)可做二个 (D)可做二个以上 4、(2004河北T7)在正方形铁皮上剪下个圆形和扇形,使之恰好围成如图所示的圆锥模型.设圆的半径为r,扇形的半径为R,则圆半径与扇形半径之间的关系是 (D )A 、2r=R B 、R r =49C 、R r =3D 、R r =4模型2、角平分线+平行=等腰三角形如图,∆ABC 中BD 、CD 平分∠ABC 、∠ACB ,过D 作直线平行于BC ,交AB 、AC 于E 、F ,当∠A 的位置及大小变化时,线段EF 和BE+CF 的大小关系( B ).(A )EF>BE+CF (B )EF=BE+CF (C )EF<BE+CF (D )不能确定 模型3、一副三角板①在△ABC 中,a=1,b=3,∠A=300,则∠B=___60___度。
②两个全等的含300, 600角的三角板ADE 和三角板ABC 如图所示放置,E,A,C 三点在一条直线上,连结BD ,取BD 的中点M ,连结ME ,MC .试判断△EMC 的形状,并说明理由.(等腰直角三角形)③(2006邵阳T8. ) 将一副三角板按图(一)叠放,则△AOB 与△DOC 的面积之比等于(1:3 )④(2005年浙江绍兴T18.)(以下两小题选做一题,第(1)小题满分5分,第(2)小题满分为3分。
若两小题都做,以第(1)小题计分) 选做第________小题,答案为________(1) 将一副三角板如图叠放,则左右阴影部分面积1S :2S 之比等于________ (2) 将一副三角板如图放置,则上下两块三角板面积1A :2A 之比等于________⑤(2006年武汉市T24.10分)已知:将一副三角板(Rt △ABC 和Rt △DEF )如图①摆放,点E 、A 、D 、B 在一条直线上,且D 是AB 的中点。
将Rt △DEF 绕点D 顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE 、AC 相交于点M ,直线DF 、BC 相交于点N ,分别过点M 、N 作直线AB 的垂线,垂足为G 、H 。
(1)当α=30°时(如图②),求证:AG =DH ;(2)当α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由;(3)当0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由。
⑥一副三角板由一个等腰直角三角形和一个含300的直角三角形组成,利用这副三角板构成一个含有150角的方法较多,请你画出其中两种不同构成的示意图,并在图上标出必要的标注,不写作法.A GD H MEF C BN第24题图图③ EF M N D A BGH 图④ C 45° 60°A E DBC F A GD H ME FC B (N )第24题图 图① 图②⑦将一副三角尺如图摆放一起,连接AD, 则∠ADB 的余切值为 .⑧如图,ABC ∆中,︒=∠90ACB ,︒=∠30B ,1=AC ,过点C 作AB CD ⊥1于1D ,过1D 作BC D D ⊥21于2D ,过2D 作AB D D ⊥32于3D ,这样继续作下去,……,线段1+n n D D 能等于(n 为正整数)(A) n⎪⎭⎫ ⎝⎛23 (B) 123+⎪⎭⎫⎝⎛n (C)n ⎪⎪⎭⎫ ⎝⎛23 (D)123+⎪⎪⎭⎫⎝⎛n⑨已知∠AOB=90°,OM 是∠AOB 的平分线,按以下要求解答问题:(1)将三角板的直角顶点P 在射线OM 上移动,两直角边分别与边OA ,OB 交于点C ,D..①在图甲中,证明:PC=PD ;②在图乙中,点G 是CD 与OP 的交点,且PG=23PD ,求△POD 与△PDG 的面积之比.(2)将三角板的直角顶点P 在射线OM 上移动,一直角边与边OB 交于点D ,OD=1,另一直角边与直线OA ,直线OB 分别交于点C ,E ,使以P ,D ,E 为顶点的三角形与△OCD 相似,在图丙中作出图形,试求OP 的长.⑩如图,客轮沿折线A -B -C 从A 出发经B 再到C 匀速航行,货轮从AC 的中点D 出发沿某一方向匀速直线航行,将一批物品送达客轮。
两船同时起航,并同时到达折线A -B -C 的某点E 处,已知AB =BC =200海里,∠ABC =90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E 点( )。
A 、在线段AB 上 B 、在线段BC 上 C 、可以在线段AB 上,也可以在线段BC 上 (2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
AB O M 图丙 A B CO P M D 图乙 图甲 D M P O C B A (第⑧题图)CA B 1D 2D4D6D5D3DDA⒒将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的另一边始终经过点B ,另一边与射线DC 相交于点Q 。
设A 、P 两点间的距离为x ,(1)当点Q 在CD 上时,线段PQ 、PB 之间有怎样的大小关系?试证明你观察到的结论。
(2)当点Q 在CD 上时,求四边形PBCQ 的面积y 与x 的函数解析式,并求出X 的取值范围;(3)当点P 在线段AC 上滑动时,三角形PCQ 是否能为等腰三角形?如果可能,指出所有可能使三角形PCQ 成为等腰三角形的点Q 的位置,并求出相应的X 的值;如果不能说明理由(以下三个图的形状,大小相同,以供操与解题时备用) 解:(1)PQ=PB证明:连接BD 交AC 于点O ,连接PD ,如图(1) 四边形ABCD 是正方形∴ AC 垂直平分BD ,045=∠=∠OCD ODC ∴ PB=PD ,0904=∠+∠∴ 21∠=∠ 图 (1)PQPB PQ PD PQD PDQ OCD PQD ODC PDQ PD PB =∴=∴∠=∠∴+∠=∠+∠=∠+∠=∠+∠=∠∠=∠∴∠=∠∴=∠+∠∴⊥0004533452232319043 ……………………………..4分(2)连接BD 交AC 于点O ,作QE AC ⊥于点E (如图2)AO 143BCP QO APQE)21(121)2)(2(21)(212290,,20<≤+-=∴-+=+=+=∴-=-==∴∆≅∆∴=∠=∠∠=∠=∆∆x x y x x QE BO PC S S S x AP OA OP QE QEP POB QEP POB QPE PBO PQ PB PCQ PBC PBCQ………………………………………………4分 (3)可能当P 与A 重合时,Q 与D 重合,有PQ=QC ,X=0 当PC=CQ 时,且Q 在DC 的延长线上时,(图形3),连接BD 交AC 于点O ,连接BQ ,则CQ=PC=2222)2(1,2x CQ BC BQ x -+=+=-由(1)证得,PB=PQ ,[]222)2(121)22(x BQ PB -+==∴由[]1)22()22()2(121222222=∴-+=-=∴+=x x x OP BO PB …………….3分12.如图,操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与边DC 或射线DC 相交于点Q 。
当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到的结论;② 当点Q 在边CD 运动上时,设四边形PBCQ 的面积为S 时,试用含有x 的代数式表示S :③ 当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由。
①过点P 作PE AB ⊥ 交AB 于E, 过点P 作PF CD ⊥交BC 于F -----1分 PE=AE,BE=1-AE,PF=1-PE=1-AE ∴BE=PF ------2分90EPB FPQ ∠+∠=090EPB EBP ∠+∠=∴EBP FPQ ∠=∠------3分 ∴ PEB PFQ ∆≅∆ ------4分 ∴PB=PQ --------5分 设PM=x,BM=1-x, QC=1-x-x=1-2xOBAC DQP21122111(21)22PBC PCQS S SBC PM CQ PF x x x x ∆=+=⨯⨯+⨯=⨯⨯+-=-----------8分③有可能成为等腰三角形,求出x 值-------11分13.(12分)用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB ,AC 重合.将三角尺绕点A 按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC ,CD 相交于点E ,F 时,(如图13—1),通过观察或测量BE ,CF 的长度,你能得出什么结论?并证明你的结论; (2)当三角尺的两边分别与菱形的两边BC ,CD 的延长线相交于点E ,F 时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.(1)BE=CF. ……2分证明:在△ABE 和△ACF 中, ∵∠BAE+∠EAC=∠CAF+∠EAC=60°, ∴∠BAE=∠CAF.∵AB=AC ,∠B=∠ACF=60°,∴△ABE ≌△ACF (ASA ). ……4分∴BE=CF. ……6分 (2)BE=CF 仍然成立. 根据三角形全等的判定公理,同样可以证明△ABE 和△ACF 全等,BE 和CF 是它们的对应边.所以BE=CF 仍然成立.………………………………10分 27.(8分)等腰△ABC ,AB=AC=8,∠BAC=120°,P 为BC 的中点,小慧拿着含 30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转.(1)如图1,当三角板的两边分别交AB 、AC 于点E 、F 时.问△BPE 与△CFP 是否相似;(2)操作:将三角板绕点P 旋转到图2情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F .① 探究1:△BPE 与△CFP 还相似吗?(只需写出结论)② 探究2:连结EF ,△BPE 与△PFE 是否相似?请说明理由; ③ 设EF=m ,△EPF 的面积为S ,试用m 的代数式表示S .(1)如图,由题意得∠FPC+∠BPE=150, ∠BEP+∠BPE=150∴∠BEP=∠FPC 又∵∠B=∠C=30∴△BPE~△CFP…………………2分(2)①△BPE与△CFP还相似……………………………………3分②△BPE与△PFE相似,……………………………………4分由△BPE与△CFP相似,得FPPECPBE=,又∵BP=CP∴FPPEBPBE=,即FPBPPEBE=,又∵∠B=∠EPF=30 ∴△BPE~△PFE ……………6分③如图,∵△BPE~△PFE ,∴∠PEB=∠PEF作PH⊥BE于点H,PG⊥EG于点G,则PH=PG ………7分在Rt△BPH中, PBHBPPH∠⋅=sin=32∴S=m3………………8分模型4知二求四在上图中隐含有以下重要性质:⑴两对相等的锐角;∠A= ∠BCD ,∠B= ∠ACD⑵三对相似三角形:⊿ACD∽⊿CBD∽⊿ABC, AC2=AD·AB BC2=BD·AB CD2=BD·AD⑶边之比的推广(1)PFECBA(2)AB CEFPGHPFECBA(2)⑷面积:AC ·BC=AB ·CD ⑸勾股定理⑹AB 是ΔABC 外接圆的直径 ①②③④⑤ ∽模型5增长率①②③④⑤⑧增长率与百分数问题 iii 某商品降价20%后出售,一段时间后恢复原价,则应在售价的基础上提高的百分数是 ( )A 、20% B 、25% C 、30% D 、35%某商品经过两次降价,由每件100元降至81元,则平均每次降价的百分率为( ) A 、8.5% B 、9% C 、9.5% D 、10% iii模型6垂径定理①如图:一个残破的圆钢轮,为了再铸做一个同样大小的圆轮,请用圆规、直尺作出它的圆心(不用写作法,保留作图痕迹)。
