最新-平行四边形知识点汇总资料
平行四边形及特殊平行四边形知识点总结

平行四边形及特殊平行四边形知识点总结平行四边形、矩形、菱形、正方形的共同性质是:对边平行且相等,对角线相等。
其中,矩形还有一个特殊性质是有一个角为直角,菱形还有一个特殊性质是四条边相等,正方形则同时满足矩形和菱形的特殊性质。
2.判定方法小结:1)判定平行四边形的方法:①两组对边分别平行;②两组对边分别相等;③两组对角分别相等;④对角线互相平分;⑤一组对边平行且相等。
2)判定矩形的方法:①有一个角是直角;②对角线相等;③有三个角是直角;④对角线相等且互相平分。
3)判定菱形的方法:①有一组邻边相等;②对角线互相垂直;③四边都相等;④对角线互相垂直平分。
4)判定正方形的方法:①有一组邻边相等且有一个角是直角;②对角线互相垂直且相等;③对角线互相垂直平分且相等。
3.基础达标训练:1)两条对角线的四边形是平行四边形;2)两条对角线的四边形是矩形;3)两条对角线的四边形是菱形;4)两条对角线的四边形是正方形;5)两条对角线的平行四边形是矩形;6)两条对角线的平行四边形是菱形;7)两条对角线的平行四边形是正方形;8)两条对角线的矩形是正方形;9)两条对角线的菱形是正方形。
1.以不在同一直线上的三个点为顶点作平行四边形,最多能作1个。
2.若平行四边形的一边长为10cm,则它的两条对角线的长度可以是8cm和12cm。
3.在平行四边形ABCD中,直线通过两对角线交点O,分别与BC和AD相交于点E和F。
已知BC=7,CD=5,OE=2,则四边形ABEF的周长为多少?答案:C。
16解析:根据平行四边形的性质,AE=CD=5,BF=BC=7.由于OE=2,因此EF=BC-OE=5.所以ABEF是一个边长分别为5和7的矩形,周长为2(5+7)=16.4.如图,在矩形ABCD中,对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为多少?答案:B。
6解析:由于CE∥BD,DE∥AC,因此三角形AOD和BOC相似,三角形COE和DOE相似。
《平行四边形和梯形》垂线和平行线-知识点整理

垂线和平行线1、垂直与平行:(1)在同一平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
如下图一:“直线A和直线B是平行线;直线A的平行线是直线B”(2)如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
如下图二:“直线A和直线B相互垂直;直线A 是直线B的垂线;点C是垂足。
”2、画垂线:(1)过直线上一点画这条直线的垂线方法?把三角尺的一条直角边靠近直线,三角尺上的直角顶点靠近直线上的点,然后用笔沿另一条直角边画出直线就可以了。
(2)过直线外一点画这条直线的垂线方法?把三角尺的一条直角边靠近直线,三角尺上的另一条边靠近直线外的点,然后用笔沿这条边画直线就可以了。
(3)把直线外一点A与直线上任意一点连接,所画线段哪个最短?小结:从直线外一点到这条直线所画的垂直线段最短,它的长度叫做这点到直线的距离。
即“点A到直线所画的垂直线段最短;点A到这条直线的距离是10厘米”3、画平行线:(1):怎样画平行线?可以用直尺和三角尺来画平行线,先把三角尺的一条直角边紧靠直线,再把直尺紧靠三角尺的另一条直角边,这时沿直尺平移三角尺,再画一条直线就可以了。
(2):在两条平行线之间画几条与平行线垂直的线段,这些线段的长度特点?小结:两条平行线之间的距离是相等的。
下图中,直线AB和直线CD平行,123三条线段垂直于AB,CD,则123条线段相等。
经验之谈:记住两个非常重要的结论,一、直线外一点到直线的线段中垂线段最短;二、两条平行线之间的距离是相等的。
平行四边形和梯形1、平行四边形:两组对边都平行的四边形叫平行四边形从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
垂足所在的边叫做平行四边形的底。
特征:(1)对边平行(2)对边相等(3)对角相等(4)邻角和为180度(5)容易变形,它不具有稳定性。
2、梯形:(1)梯形:一组对边平行而另一组对边不平行的四边形叫梯形梯形有上底和下底,从上底到下底的垂线叫梯形的高,两边叫梯形的腰。
平行四边形的面积计算知识点总结

平行四边形的面积计算知识点总结平行四边形是几何学中的一种基本图形,它具有许多有趣的性质和应用。
本文将对平行四边形的面积计算知识点进行总结,并介绍一些相关的公式和方法。
无影响阅读体验的情况下,我会适当增加字数以满足1500字的要求。
1. 平行四边形的定义平行四边形是指有两对对边分别平行的四边形。
它的特点是对边相等且对角线互相平分。
2. 平行四边形的面积计算公式平行四边形的面积可以使用以下公式进行计算:面积 = 底边长度 ×高3. 平行四边形的特殊情况当平行四边形的高度垂直于底边时,我们可以使用以下公式计算面积:面积 = 底边长度 ×高4. 平行四边形的计算方法在实际计算中,我们可以根据实际情况选择不同的方法来计算平行四边形的面积。
4.1 底边和高的已知情况当底边的长度和高度已知时,可以直接使用公式面积 = 底边长度 ×高进行计算。
4.2 边长和夹角的已知情况当平行四边形的两条边长和夹角的大小已知时,可以使用以下公式计算面积:面积 = 一条边长 ×另一条边长 × sin(夹角)4.3 对角线和夹角的已知情况当平行四边形的对角线的长度和夹角的大小已知时,可以使用以下公式计算面积:面积 = 一条对角线长度 ×另一条对角线长度 × sin(夹角)5. 平行四边形面积计算的例题解析为了更好地理解和应用上述计算方法,我们来看一个具体的例题:【例题】已知平行四边形的底边长为12 cm,高度为6 cm,求其面积。
解:根据公式面积 = 底边长度 ×高,可直接计算得到:面积 = 12 cm × 6 cm = 72 cm²6. 平行四边形的相关知识点在学习和计算平行四边形的面积过程中,还有一些相关的知识点需要了解。
6.1 平行四边形的性质平行四边形有以下几个重要的性质:- 对边相等:平行四边形的对边长度相等。
- 互补角:相邻的内角互补(和为180°)。
四年级数学平行四边形和梯形知识点大全

四年级数学平行四边形和梯形知识点大全四年级数学平行四边形和梯形知识点一垂直与平行1认识平行和垂直①同一平面内的两条直线的位置关系只有两种:相交和不相交。
相交又有成直角的和不成直角的两种情况。
_“同一平面”是确定两条直线平行关系的前提,如果不在同一平面内,即便不相交,也不能称为互相平行。
②平行线:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
平行的表示方法:a//b,读作a平行于b。
生活中平行的例子:窗户相对的框,黑板相对的两条边,公路上的斑马线......③垂直:如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
垂直的表示方法:ab生活中垂直的例子:三角尺上的两条直角边互相垂直......④三条直线的特殊关系:a//b,b//c,那么a//c:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线互相平行ab,bc,那么a//c:在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线互相平行。
2垂线的画法和性质①过直线上和直线外一点怎样画这条直线的垂线:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使三角尺的顶点和直线上的已知点重合;从直角的顶点起,沿着另一条直角边画出一条直线,这条直线就是已知直线的垂线。
②过直线外一点怎样画这条直线的垂线:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使三角尺的另一条直角边与直线外的一点重合;沿着三角尺的另一条直角边画一条直线③垂线的性质:从直线外一点到这条直线所画的垂直线段最短,它的长度叫做这点到直线的距离。
3平行线的画法及运用①平行线的画法:固定三角尺,沿一条直角边先画一条直线;用直尺紧靠三角尺的另一条直角边,固定直尺,然后平移三角尺;再沿第一步中的直角边画出另一条直线。
②检验两条直线是否平行的方法:把三角尺的一条直角边与其中的一条直线重合;用直尺紧靠三角尺的另一条直角边,固定直尺,然后平移三角尺;如果第一步的三角尺的直角边与另一条直线完全重合,这两条直线就互相平行,如果不完全重合,这两条直线就不平行。
平行四边形知识点总结

角菱形的对角相等
菱形的邻角互补
对角线菱形的两条对角线互相平分且互相垂直,并且每一条对角线平分一组对角
判定:
边有一组邻边相等的平行四边形是菱形
四条边都相等的四边形是菱形
对角线对角线互相垂直的平行四边形是菱形
菱形是轴对称图形,两条对角线为它的对称轴。
正方形
定义:四条边都相等,四个角都是直角的四边形叫做正方形
角两组对角分别相等的四边形是平行四边形对角线对角线互相平分四边形是平行四边形矩形
定义:有一个角是直角的平行四边形叫做矩形
性质:
边矩形的对边平行且相等
角矩形的四个角都是直角
对角线矩形的对角线互相平分且相等
判定:
角有一个角是直角的平行四边形是矩形
有三个角是直角的四边形是矩形
对角线对角线相等是平行四边形是矩形
提示:判断一个四边形是正方形,关键是先判定这个四边形是平行四边形,再判定这个四边形是菱形(或矩形),最后判定这个平行四边形还是矩形(或菱形)。但由于判定平行四边形、矩形、菱形的方法各异,所给出的条件不尽相同,所以判定一个四边形的具体过程方法也得视情况而定。
矩形是轴对称图形,有两条对称轴。
相关性质
平行线段:两条平行线之间的任何两条平行线段都相等
两条平行线之间的距离相等
连接三角形两边中点的线段叫做三角形的中位线
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
直角三角形斜边上的中线等于斜边的一半。
菱形
定义:有一组邻边相等的平行四边形叫做菱形
性质:
边菱形的对边互相平行
平行四边形知识点总结
平行四边形
定义:两组对边分别平行的四边形叫做平行四边形
性质:
平行四边形初中知识点

平行四边形初中知识点
一、平行四边形的定义。
1. 两组对边分别平行的四边形叫做平行四边形。
- 用符号“▱”表示平行四边形,例如平行四边形ABCD记作“▱ABCD”。
二、平行四边形的性质。
1. 边的性质。
- 平行四边形的对边平行且相等。
- 即若▱ABCD,则AB = CD,AD = BC;AB∥CD,AD∥BC。
2. 角的性质。
- 平行四边形的对角相等,邻角互补。
- 在▱ABCD中,∠A = ∠C,∠B = ∠D;∠A+∠B = 180°,∠B + ∠C=180°等。
3. 对角线的性质。
- 平行四边形的对角线互相平分。
- 若▱ABCD,对角线AC、BD相交于点O,则AO = CO,BO = DO。
三、平行四边形的判定。
1. 边的判定。
- 两组对边分别平行的四边形是平行四边形(定义判定)。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
2. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
3. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
四、平行四边形的面积。
1. 平行四边形的面积等于底乘以高。
- 若平行四边形的底为a,这条底边上的高为h,则面积S = ah。
- 同底(等底)等高的平行四边形面积相等。
平行四边形知识点
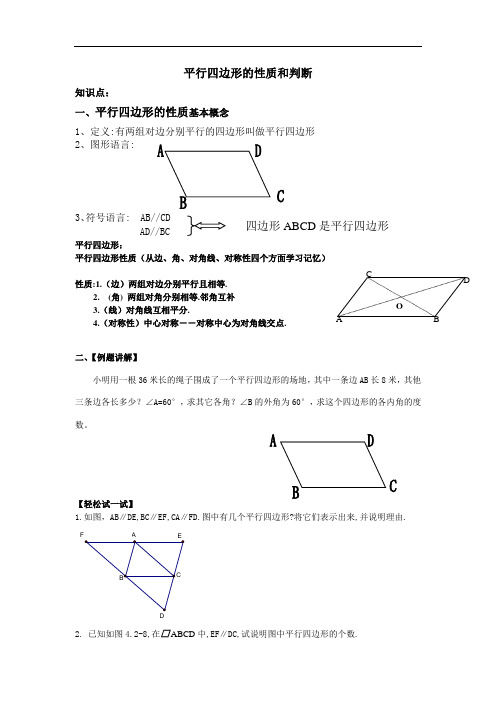
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
平行四边形知识点

平行四边形知识点一、平行四边形1,平行四边形的定义及性质定义:两组对边分别平行的四边形叫做平行四边形。
①平行四边形的对边相等。
性质②平行四边形的对角相等。
③平行四边形的对角线互相平分。
2,平行四边形的判定①两组对边平行的四边形是平行四边形;从边看:②两组对边分别相等的四边形是平行四边形;③一组对边平行且相等的四边形是平行四边形。
从角看:两组对角分别相等的四边形是平行四边形。
从对角线看:对角线互相平分的四边形是平行四边形。
、3,三角形的中位线连接三角形两边中点的线段叫做三角形的中位线。
点拨:①三角形的中位线共有三条。
②三角形的中位线与中线的区别:主要是型短的端点不同。
中位线是中点与中点的连线,中线是顶点与对边中点的连线。
4,三角形中位线定理三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
知识点二:特殊的平行四边形1,矩形(1)定义:有一个角是直角的平行四边形叫做矩形。
①矩形的四个角都是直角,(2)性质②矩形的对角线相等。
③矩形性质的推论;直角三角形斜边上的中线等于斜边的一半。
①有一个角是直角的平行四边形是矩形。
(3)判定定理:②对角线相等的平行四边形是矩形。
③有三个角是直角的四边形是矩形。
2,菱形(1)定义:有一组邻边相等的平行四边形叫做菱形。
(2)性质:①菱形的四边形都相等。
②菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
①一组邻边相等的平行四边形是菱形。
②对角线互相垂直的平行四边形是菱形。
(3)判定定理③对角线互相垂直平分的四边形是菱形。
④四边形相等的四边形是菱形。
点拨:(1)菱形是轴对称图形,它的对角线所在的直线就是它的对称轴。
(2)菱形的面积:菱形被它的两条对角线分成四个全等的直角三角形,它们的底和高都分别是两条对角线的一半。
利用三角形的面积公式可推得,菱形的面积等于它对角线之积的一半。
3、正方形(1)定义:四边形都相等,四个角都是直角的四边形是正方形。
所以,正方形既是矩形,又是菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的知识点汇总平行四边形定义:两组对边分别平行的四边形叫做平行四边形。
平行四边形是中心对称图形,对称中心是两条对角线的交点。
平行四边形性质1:平行四边形的两组对边分别相等。
平行四边形性质2:平行四边形的两组对角分别相等。
平行四边形性质3:平行四边形的两条对角线互相平分。
平行四边形判定1:两组对边分别平行的四边形是平行四边形。
平行四边形判定2:两组对边分别相等的四边形是平行四边形。
平行四边形判定3:两组对角分别相等的四边形是平行四边形。
平行四边形判定4:两条对角线互相平分的四边形是平行四边形。
平行四边形判定5:一组对边平行且相等的四边形是平行四边形。
平行线之间的距离及特征平行线之间的距离定义:若两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
平行线之间的距离特征1:平行线之间的距离处处相等。
平行线之间的距离特征2:夹在两条平行线之间的平行线段相等。
矩形矩形定义1:有一个角是直角的平行四边形叫做矩形矩形定义2:有三个角是直角的四边形叫做矩形矩形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线。
矩形性质1:矩形的四个角都是直角。
矩形性质2:矩形的对角线相等且互相平分。
(注意:矩形具有平行四边形的一切性质)直角三角形的性质:直角三角形斜边上的中线等于斜边的一半矩形判定1:有一个角是直角的平行四边形是矩形。
矩形判定2:有三个角是直角的四边形是矩形。
矩形判定3:对角线相等的平行四边形是矩形。
菱形菱形定义1:有一组邻边相等的平行四边形叫做菱形.菱形定义2:四条边都相等的四边形叫做菱形。
菱形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是对角线所在的直线。
菱形性质1:菱形的四条边都相等。
菱形性质2:菱形的对角线互相垂直平分。
菱形性质3:菱形的每一条对角线平分一组对角。
菱形的面积:菱形的面积等于对角线乘积的一半。
推广:对角线互相垂直的四边形面积等于对角线乘积的一半。
菱形判定1:有一组邻边相等的平行四边形是菱形。
菱形判定2:四条边都相等的四边形是菱形。
菱形判定3:对角线互相垂直的平行四边形是菱形。
菱形判定4:每条对角线平分一组对角的四边形是菱形。
(注意:菱形具有平行四边形的一切性质)正方形正方形定义1:有一组邻边相等的矩形叫做正方形。
正方形定义2:有一个角是直角的菱形叫做正方形。
正方形定义3:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
正方形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线和对角线所在的直线。
正方形性质1:正方形的四个角都是直角。
正方形性质2:正方形的四条边都相等。
正方形性质3:正方形的两条对角线互相垂直平分且相等。
正方形判定1:有一组邻边相等的矩形是正方形。
正方形判定2:有一个角是直角的菱形是正方形。
正方形判定3:有一组邻边相等并且有一个角是直角的平行四边形是正方形。
正方形判定4:对角线垂直平分且相等的四边形是正方形。
(注意:正方形具有平行四边形、矩形、菱形的一切性质)四边形的典型题目精编1,如图1,在平行四边形ABCD 中,下列各式不一定正确的是( ) A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180°2,如图2,在□ABCD 中,EF //AB ,GH //AD ,EF 与GH 交于点O ,则该图中的平行四边形的个数共有( )A.7 个B.8个C.9个D.11个 E F BC D H D OF E C 4D 231A3,如图3,在平行四边形ABCD 中,∠B =110°,延长AD 至F ,延长CD 至E ,连接EF ,则∠E +∠F =( )A. 110° B .30° C.50° D.70° 4,对角线互相垂直平分且相等的四边形一定是( ) A .正方形 B .菱形 C .矩形 D .等腰梯形5,下列说法中,正确的是( ) A. 正方形是轴对称图形且有四条对称轴 B.正方形的对角线是正方形的对称轴 C.矩形是轴对称图形且有四条对称轴 D.菱形的对角线相等6,菱形、矩形、正方形都具有的性质是( )A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角线平分一组对角7,已知:如图4,菱形ABCD 中,对角线AC 与BD 相交于点O ,OE ∥DC 交BC 于点E ,AD =6cm ,则OE 的长为( )A.6 cmB.4 cmC.3 cmD.2 cm8,在学习“四边形”一章时,小明的书上有一图因不小心被滴上墨水(如图5),看不清所印的字,请问被墨迹遮盖了的文字应是( )A .等边三角形B .四边形C .等腰梯形D .菱形9,如图6,在宽为20m ,长为30m 的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中数据,计算耕地的面积为( )A .600m 2B .551m 2C .550 m 2D .500m 210,如图7,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 的面积比是 ( )BA.3∶4B.5∶8C.9∶16D.1∶2 二、填空题(每题3分,共24分)11,如图8,AB ∥DC ,AD ∥BC ,如果∠B =50°,那么∠D =___度.12,已知梯形ABCD 中,AD ∥BC ,∠ABC =60°,BD =,AE 是梯形的高,且BE =1,则AD =___.A C 图7 图6 A EBC DFCHD AE BF G图8 图1D C B A S 4S 3S 2S 1DC BA 图9ED CBA13,一个平行四边形被分成面积为S1、S2、S3、S4的四个小平行四边形(如图9),当CD 沿AB自左向右在平行四边形内平行滑动时, S1·S4与S2·S3与的大小关系是___.14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.15015,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D 重合,折痕为EF,则DE=___cm.16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD =___cm.17,如图12,矩形ABCD的相邻两边的长分别是3cm和4cm,顺次连接矩形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于___cm,四边形EFGH的面积等于___cm2.18,在直线l上依次摆放着七个正方形(如图13所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=___.三、解答题(共40分)19,如图14,等腰梯形ABCD中,AD∥BC,AD=3,AB=4,BC=7.求∠B的度数.20,如图15,四边形ABCD是平行四边形,对角线AC、BD交于点O,过点O画直线EF分别交AD、BC于点E、F.求证:OE=OF.21,如图17,在□ABCD中,∠ABC=5∠A,过点B作BE⊥DC交AD的延长线于点E,O是垂足,且DE=DA=4cm,求:(1)□ABCD的周长;(2)四边形BDEC的周长和面积(结果可保留根号).22,如图18,□ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.23,如图20,正方形ABCD中,P是CD边上一点,DF⊥AP,BE⊥AP.求证:AE=DF.24,如图19,在矩形ABCD中,P是形内一点,且PA=PD.求证:PB=PC.图18图13l321S4S3S2S1图19图17A BCDOE图16E DCOBFA图21图14ACDB25,如图,在梯形ABCD 中,AD BC ∥,AB DC AD ==,60C ∠=°,AE BD ⊥于点E ,F 是CD 的中点,DG 是梯形ABCD 的高. (1)求证:四边形AEFD 是平行四边形;(2)设AE x =,四边形DEGF 的面积为y ,求y 关于x 的函数关系式.参考答案:一、1,D ;2,C ;3,D ;4,A ;5,A ;6,C ;7,C ;8,D ;9,B ;10,B .二、11,50;12,2;13,S 1·S 4=S 2·S 3;14,150;1516,9;17,10、6;18,4.三、19,过A 点作AE ∥CD ,有□AECD ,则△ABE 为等边三角形. 即∠B=60°;20,因为四边形ABCD 是平行四边形,所以AD ∥BC ,AO =CO ,即∠EAO =∠FCO ,又∠AOE =∠COF ,则△AOE ≌△COF ,故OE =OF ;21,在□ABCD 中,因为∠ABC =5∠A ,又∠A+∠B =180°,所以∠A =30°,而AB ∥DC ,BE ⊥DC ,所以BE ⊥AB ,在Rt △ABE 中,∠ABE =90°,AE =2AD =8cm ,∠A =30°,所以BE =12AE =4cm ,由勾股定理,得AB=cm ),所以□ABCD 的周长=(+8)cm ;(2)因为BC ∥AD ,BC =AD ,而AD =DE ,所以DE =BC 且DE ∥BC ,即四边形BDEC 是平行四边形,又BE ⊥DC ,所以□BDEC 是菱形,所以四边形BDEC 的周长=4DE =16(cm ),面积=12DC ·BE =cm 2);22,易证△AOE ≌△COF ,所以OE =OF ,所以四边形AFCE 是平行四边形,又AC ⊥EF ,所以四边形AFCE 是菱形;23,证△ABE ≌△DAF 即得;24,证△PBA ≌△PCD 即得; 25,【答案】:(1) 证明: ∵AB DC =,∴梯形ABCD 为等腰梯形.∵∠C=60°,图20∴120BAD ADC ∠=∠=,又∵AB AD =,∴30ABD ADB ∠=∠=.∴30DBC ADB ∠=∠=.∴90BDC ∠=. 由已知AE BD ⊥,∴AE∥DC. 又∵AE 为等腰三角形ABD 的高, ∴E 是BD 的中点,∵F 是DC 的中点, ∴EF∥BC. ∴EF∥AD.∴四边形AEFD 是平行四边形.(2)解:在Rt△AED 中, 30ADB ∠=,∵AE x =,∴2AD x =.在Rt△DGC 中 ∠C=60°,并且2DC AD x ==,∴DG =.由(1)知: 在平行四边形AEFD 中2EF AD x ==,又∵DG BC ⊥,∴DG EF ⊥,∴四边形DEGF 的面积12EF DG =, ∴ 212332y x x x =⨯=(0)x >.。
