普通逻辑重言式和真值表
真值表逻辑等价永真蕴涵

(10)(P→Q)∧(Q→R) ⇒ P→R
(11)(P∨Q)∧(P→R)∧(Q→R) ⇒ R (12)(P→Q)∧(R→S) ⇒ (P∧R)→(Q∧S ) (13)(PQ) ∧(QR) ⇒ (P R)
33
永真蕴含的性质
• 设A、B、C是命题公式 (1)若A⇔B,则A⇒B,B⇒A; (2)若A⇒B, 则 PA⇒PB; PA⇒PB;(补充) PA⇒PB;(补充) (注意: AP⇒BP;AP⇒BP; PA⇒PB 或PA⇒PB 都不一定成立。)
证明: 因为P→Q ⇔ ┐P∨Q, 利用代换规则得 P∧(P→Q) ⇔ P∧(┐P∨Q) ⇔ (P∧ ┐P)∨(P∧Q) ⇔ 0∨(P∧Q) ⇔ P∧Q
17
命题的演算
• 利用代换规则从一个命题得到另一 个逻辑等价的命题称为命题的演算。
18
证明逻辑等价、永真(假) 式的方法(1)
• 方法一:真值表法
永真蕴含式例1(2)
• 证明P∧Q⇒P 方法三:证明P∧Q→P为永真式等 价于证明当P∧Q为真时,P必为真。 若P∧Q为真,则P为真且Q为真, 因此P必为真。
30
永真蕴含式例2
• 证明 (P→Q)∧(Q→R) ⇒ P→R 证明:等价于证明:当(P→Q)∧(Q→R)为T时,P→R必为T。 若(P→Q)∧(Q→R)为T时,有: (P→Q)为T且(Q→R)为T。 下面根据R的取值分两种情况讨论P→R 的取值: (1)当R取值为T时,显然, P→R为T。 (2)当R取值为F时,由(Q→R)为T可知:Q必为F,进而,由 (P→Q)为T可知:P必为F。 因此, 当R为F时,P→R必为T 综上所证,当(P→Q)∧(Q→R)为T时, P→R必为T 所以(P→Q)∧(Q→R) ⇒ (P→R)
《离散数学》双语教学 第一章 真值表,逻辑和证明

《离散数学》双语教学第一章真值表,逻辑和证明《离散数学》双语教学第一章真值表,逻辑和证明CHAPTER 1TRUTH TABLES, LOGIC, AND PROOFSGlossarystatement, proposition:命题 logical connective:命题联结词compound statement:复合命题 propositional variable:命题变元negation:否定(式)truth table:真值表conjunction:合取 disjunction:析取 propositional function:命题公式fallacy: 谬误syllogism:三段论universal quantification:全称量词化 existential quantification:存在量词化 hypothesis(premise): 假设~前提~前件 conditional statement, implication:条件式~蕴涵式 consequent, conclusion:结论~后件 converse:逆命题contrapositive:逆否命题biconditional, equivalence:双条件式~等价(逻辑)等价的 logically equivalent:contingency:可满足式tautology:永真式(重言式)contradiction, absurdity:永假(矛盾)式 logically follow:是…的逻辑结论 argument:论证axioms:公理第 1 页共 47 页 2010-12-27《离散数学》双语教学第一章真值表,逻辑和证明 postulate:公设rules of reference:推理规则modus ponens:肯定律 modus tollens:否定律reductio ad absurdum:归谬律proof by contradiction:反证法counterexample:反例 minterm:极小项disjunctive normal form:主析取范式maxterm:极大项conjunctive normal form:主合取范式第 2 页共 47 页 2010-12-27《离散数学》双语教学第一章真值表,逻辑和证明本章内容及教学要点:1.1 Statements and Connectives教学内容:statements(propositions)~compound statement~connectives:negation~conjunction~disjunction~truth tables 1.2 Conditional Statements教学内容:implications(conditional statements)~biconditional~equivalent~and quantifications1.3 Equivalent Statements教学内容:logical equivalence~converse~inverse~contrapositive~tautology~contradiction(absurdity)~contingency~properties of logical connectives1.4 Axiomatic Systems: Arguments and Proofs教学内容:rules of reference~augument~valid argument~hypotheses~premises~law of detachment(modus ponens)~syllogism~modus tollens~addition~proof by contradiction 1.5 Normal Forms教学内容:minterm~disjunctive normal form~maxterm~conjunctive normal form定理证明及例题解答第 3 页共 47 页 2010-12-27《离散数学》双语教学第一章真值表,逻辑和证明Logic, developed by Aristotle, has been used through the centuries in the development of many areas of learning including theology, philosophy, and mathematics. It is the foundation on which the whole structure of mathematics is built. Basically it is the science of reasoning, which may allow us to determine statements about mathematics whether are true or false based on a set of basic assumptions called axioms. Logic is also used in computer science to construct computer programs and to show that programs do what they are designed to do.逻辑学是研究人的思维形式的科学. 而数理逻辑是逻辑学的一个重要分支~是用数学形式化的方法研究思维规律的一门学科. 由于它使用了一套符号来简洁地表达出各种推理的逻辑关系~故它又称符号逻辑.数理逻辑用数学方法研究推理、利用符号体系研究推理过程中前提和结论之间的关系. 数理逻辑的主要内容:逻辑演算(L和L)、公理化集合论、模型论、S p构造主义与证明论. 数理逻辑在电子线路、机器证明、自动化系统、编译理论、算法设计方法方面有广泛的应用.The rules of logic specify the meaning of mathematicalstatements. Logic is the basis of all mathematical reasoning, and it has practical applications to the design of computing machines, to system specifications, to artificial intelligence(AI), to computer programming, to programming languages, and to other areas of computer science, as well as to many other fields of study.第 4 页共 47 页 2010-12-27《离散数学》双语教学第一章真值表,逻辑和证明1.1 Statements and Connectivess(命题和联结词)命题逻辑研究的对象是命题及命题之间的逻辑关系.Propositions are the basic building blocks of logic. Many mathematical statements are constructed by combining one or more propositions.定义1.1.1 A proposition is a statement or declarative sentence that is either true or false, but not both,命题是一个非真即假的陈述句,.因此不能判断真假的陈述句、疑问句、祈使句和感叹句都不是命题.,1, The true or false value assigned to a statement is called its truth value; (一个命题的真或假称为命题的真值. 真用T或1表示~假用F或0表示),2, 一个陈述句有真值与是否知道它的真假是两回事.例1.1.1 判断下列语句是不是命题,若是~给出命题的真值: (1) 陕西师大不是一座工厂.(2) 你喜欢唱歌吗,(3) 给我一块钱吧:(4) 我不是陕西师大的学生.(5) 我正在说谎.Logical connectives(命题联结词)数理逻辑的特点是并不关心具体某个命题的真假~而是将逻辑推理变成类似数学演算的形式化过程, 关心的是命题之间的关联性. 因此需要进行命题符号化.命题联结词的作用是为了将简单命题组合成复合命题.We will now introduce the logical connectives that are used to form new propositions from existing propositions. And once truth values have been assigned to simple propositions, we can progress to more complicated compound statements.A statement that contains no connectives is called a simple第 5 页共 47 页 2010-12-27《离散数学》双语教学第一章真值表,逻辑和证明statement. We will use p,q,r…to represent simple statements(简单命题就是简单陈述句~用字母p,q,r…(或带下标)表示),Sometimes, the letters p,q,r,s,…are used to denote propositional variables that can be replacedby statements(命题变元:可以用命题代替的变元).A statement that contains logical connectives(命题联结词) is called compound statements(复合命题). In general, a compound statement may have many component parts, each of which is itself a statement, represented by some propositional variable. The truth of a compound proposition is determined by the truth or falsity of the component parts.propositional constant(命题常元):T(1)或F(0)~或者表示一个确定的命题,propositional variable(命题变元):可用一个特定的命题取代。
逻辑符号及真值表

逻辑符号及真值表
这些逻辑符号可以用于构建命题逻辑中复杂命题的逻辑结构,从而方便我们进行推理和论证。
在使用逻辑符号时,通常会用到真值表来验证命题的逻辑结构。
真值表是一种用来列出命题不同取值组合的表格。
在真值表中,每一行代表一种取值组合,每一列代表一个命题变量或逻辑符号。
通过对每个命题变量进行相应的逻辑运算,可以得出最终命题的真值(T 或F)。
例如,在合取命题p ∧ q中,p和q为命题变量,∧为逻辑符号。
我们可以列出如下的真值表:
p | q | p ∧ q
--|---|------
T | T | T
T | F | F
F | T | F
F | F | F
从表中可以看出,在p为真、q为真的情况下,p ∧ q的真值为真(T)。
而在其他情况下,其真值为假(F)。
通过使用逻辑符号和真值表,我们可以更加清晰地理解和分析命题逻辑中的复杂结构,从而更加准确地进行推理和论证。
- 1 -。
逻辑式与真值表

等值逻辑式
如果对于逻辑变量的任何一组取值,两个逻辑式 的值都相等,这样的两个逻辑式叫做等值逻辑式。 等值逻辑式可用“=”连接,并称为等式,需要 注意的是,这种相等是状态的相同。
三、例题与练习
例4 如图所示,开关电路中的灯D的状态,能否用 开关A,B,C的逻辑运算来表示?试给出结果. 分析 这个电路
用真值表验证下列等式是否成立:
A (B C) ( A B) ( A C)
A 0 0 0 0 1 1 1 1
A (B C) ( A B) ( A C)
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
BC
A (B C)
A B A C ( A B) ( A C)
可以看出对于逻辑变量的任何一组值, A B与 AB的值都相等 所以 A B AB .
用真值表验证下列等式是否成立:
AB AB ( A B)( A B)
三、例题与练习
A 0 0 1 1 B 0 1 0 1
AB
0 0 1 0
AB
0 1 0 0
A B
1 1 1 0
AB AB
A A 0
A A
A 0 1
A
1 0
A A
1 1
A A 1
用真值表验证下列等式是否成立:
AB BA
A 0 0 1 1
B 0 1 0 1
A B B A
A B B A
0 0 0 1
0 0 0 1
用真值表验证下列等式是否成立:
AB B A
A 0 0 1 1
A 1 1 0 0
B 1 0 1 0
逻辑学真值表
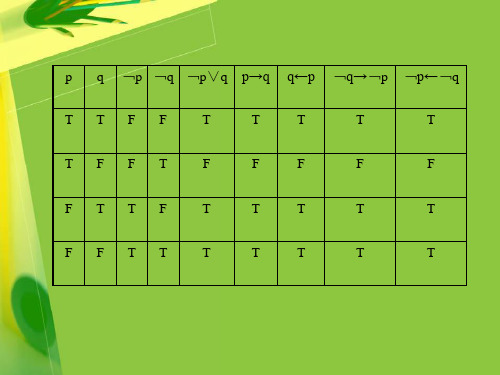
例如:用真值表法判定下列推理是否 有效。 1.如果乔丹是美国总统,那么他是美国 领导人。乔丹不是美国总统,所以, 他不是美国领导人。 (p:乔丹是美国总统;q:乔丹是美国 领导人) 推理形式:((p→q)∧﹁p)→ ﹁q
p T T F F
q T F T F
﹁p ﹁q F F T T F T F T
p T T F F
q T F T F
﹁p ﹁q p→q F F T T F T F T T F T T
﹁q→﹁p (p→q)→(﹁q → ﹁p) T F T T T T T T
p→q T F T T
(p→q)∧﹁p ((p→q)∧﹁p)→﹁q F F T T T T F T
2.如果美国绕开联合国向伊拉克改动战 争,联合国的权威就会受到破坏。所 以,要想联合国的权威不会受到破坏, 美国就不绕开联合国向伊拉克改动战 争。 (p:美国绕开联合国向伊拉克改动战争; q:联合国的权威就会受到破坏) 推理形式:(p→q)→(﹁q → ﹁p)
p T T F F
q T F T F
﹁p ﹁q ﹁p∨q F F T T F T F T←p T F T T
﹁q→﹁p T F T T
﹁p←﹁q T F T T
真值表方法: 1.用符号表达出命题形式。 2.列出命题形式中的命题变元。 3.根据括号和联结词的用法确定命题形式内部的次序。 4.画出真值表。 5.依照确定的表达式次序检验真值。 6.根据最后一步即主联结词一栏的真值情况对该表达式做 出判定。 (1)如果主联结词一栏都为真,则该命题为重言式,相 应的推理有效。 (2)如果主联结词一栏都为假,则该命题为矛盾式,相 应的推理无效。 (3)如果主联结词一栏有真有假,则该命题为可真公式, 相应的推理无效。
4.重言式

课堂练习: 课, R))∧ Q)的真值为 的真值为T
则R的真值为:( 的真值为:( ) )种指派下真值为T. 种指派下真值为T.
2 命题公式(P → Q) ∨ (Q →P)在( 命题公式(P P)在
答案: 答案:1:F 2:4
重言公式的代入规则:重言式 的某个子公式 的某个子公式B出现的 重言公式的代入规则:重言式A的某个子公式 出现的 每一处均用同一命题公式C置换,所得命题公式 每一处均用同一命题公式 置换,所得命题公式A‵公 置换 式仍然是一个重言式。 式仍然是一个重言式。
两类特殊的重言式: 两类特殊的重言式: 等价重言式和蕴涵重言式。 等价重言式和蕴涵重言式。 等价重言式, 定义:如果等价式 为永真式, 定义:如果等价式P Q为永真式,则称为等价重言式,并记 为永真式 则称为等价重言式 相等, 为P Q,它们也可称为 与Q相等,记为 ,它们也可称为P与 相等 记为P=Q。 。 此式子亦可叫P与 的等式 逻辑等式) 的等式( 此式子亦可叫 与Q的等式(逻辑等式) 定义:如果蕴涵式 为永真, 蕴涵重言式, 定义:如果蕴涵式P→Q为永真,则称为蕴涵重言式,并记为: 为永真 则称为蕴涵重言式 并记为: P Q
p F F T T q F T F T T T F F T F T F
┒p∨ ┒q ∨
┒(p∧q)
T T T F
T T T F
重言蕴含式可用真值表证明,也可用以下办法证明: 重言蕴含式可用真值表证明,也可用以下办法证明: (1) 假定前件是真 若能推出后件是真 则此蕴含式是真。 假定前件是真,若能推出后件是真 则此蕴含式是真。 若能推出后件是真,则此蕴含式是真 (2) 假定后件是假,若能推出前件是假 则此蕴含式是真。 假定后件是假 若能推出前件是假,则此蕴含式是真。 若能推出前件是假 则此蕴含式是真
重言式和真值表
用真值表判定重言式
真值表判定任一命题形式是否是重言式。 例1、((p∨q)∧¬p)→q
p q ¬p p∨q
(p∨q) ∧¬p F F T F
((p∨q)∧¬p) →q T T T T
T T F T F F F T T F F T
T T T F
例2、((p∨q)∧p)→
¬q
p q ¬q p∨q (p∨q)∧ p T T F T F T F T F F F T T T T F T T F F
((p∨q)∧p) →¬q F T T T
真值表判定任意两个复合命题之间 是否具有等值关系
例1、¬(p ∧ q) ¬p∨ ¬q
p q ¬p ¬q (p∧q) T T F T F F F T T F F T F T F T T F F F
¬(p∧q) F T T T
¬p∨¬q F T T T
以下,必须分情况进行讨论。
( p T
∨
T
在第一种情况下,子公式p ∨ q→r既为T又为F。
q → r ) → ( p → r ) ∧ ( q → r ) T F T F F F F F q → r ) → ( p → r ) ∧ ( q → r ) T T F F F F T F F
( p
∨
T
p ∨ ¬p (p → p)
矛盾式:
p ∧ ¬p ¬(p → p)
常见重言式
¬(p ∧ q)↔ ¬p ∨ ¬ q ¬(p ∨ q)↔ ¬p ∧ ¬ q ¬(p → q)↔ p ∧ ¬ q ¬ ¬p ↔ p
常见重言式
(p (p (p (p
→ q)↔ ¬p ∨ q → q)↔ ¬(p ∧ ¬ q) ∨ q) ↔ (¬ p → q) ∧ q) ↔ ¬(p → ¬ q)
自考普通逻辑学知识点及公式
作者◆一剑钻神一、判断(一)1.SAP是指所有的S是P; SEP是指所有的S不是P;SIP是指有的S是P; SOP是指有的S不是P。
2.A与E是反对关系(不能同真,可以同假);I与O时下反对关系(不能同假,可以同真);A与O和E与I是矛盾关系(不能同假,已不能同真);A与I和E与O是差等关系逻辑方阵全同真包含于真包含交叉全异A 1 1 0 0 0E 0 0 0 0 1I 1 1 1 1 0O 0 0 1 1 1A、E、I、O四种判断的真假情况列表注:1代表“真”;0代表“假”(下同)。
4.普通逻辑是研究思维的逻辑形式及其基本规律和简单逻辑方法的科学。
任何一种逻辑形式都是由逻辑常项和逻辑变项两部分组成。
普通逻辑所研究的思维是指抽象思维中的知性思维。
现代形式逻辑主要是指数理逻辑。
知觉是感觉的综合。
感性认识的基本特征是直接感受性。
人们平常提到逻辑学时,通常指的是形式逻辑。
在感性认识阶段,人们对客观事物的认识的三种存在形式人别是感觉、知觉、表象。
在理性认识阶段,人们对事物的认识的三种存在形式人别是概念、判断、推理。
5.概念是反映对象特有属性或本质属性的思维形式,概念有两个逻辑特征,他们是内涵和外延。
概念的内涵是指反映到概念中的对象中的特有属性或本质属性。
具有概念所反映的特有属性或本质属性的对象,称为概念的外延。
从逻辑的角度讲,所谓明确概念,指的就是要明确概念的内涵和外延。
普通逻辑不去研究概念在具体内容上的关系,而是把概念作为思维形式,从内涵或外延方面来研究概念间的关系。
根据概念的外延大小,概念分为单独概念和普通概念。
根据概念反映的对象是否为集合体,概念分为集合概念和非集合概念。
根据概念所反映对象是否具有某种性质,概念分为正概念和负概念。
6.定义的规则?(1)定义项的外延和被定义项的外延应是相同的(违反这条规则,就会犯“定义过宽”或“定义过窄”的逻辑错误)。
(2)定义项中不能直接或间接地包括被定义项(违反这条规则,就会犯“同语反复”或“循环定义”的逻辑错误)。
3、利用真值表判断公式(())是否为重言式-世.解答
3、利用真值表判断公式((P Q)(Q R))(P R)是否为重言式。
解:P Q R P R P Q Q R P R(P R)(P Q)( Q R)((P Q)(Q R))(P R)0 0 0 1 1 1 1 1 0 1 00 0 1 1 0 1 1 0 1 1 10 1 0 1 1 1 0 1 0 0 10 1 1 1 0 1 1 0 1 1 11 0 0 0 1 0 1 1 0 0 11 0 1 0 0 0 1 1 0 0 11 1 0 0 1 1 0 1 0 0 11 1 1 0 0 1 1 1 0 1 0 由真值表得:((P Q)(Q R))(P R)在它的各种赋值下取值不全为真。
故((P Q)(Q R))(P R)不是重言式。
6、构造下列推理的证明:只要A曾到过受害者房间并且11点以前没离开,A就犯了谋杀罪。
A曾到过受害者房间,如果在11点以前离开,看门人会看见他。
看门人没看见他,所以A犯了谋杀罪。
解:令P:A曾到过受害者房间;Q:11点以前离开;R :看门人看见了A ;S :A 犯了谋杀罪;前提:PR QS QP ,,结论:RS证明:(1)P前提引入(2)PQS前提引入(3)Q S (1)(2)析取三段论(4)Q 附加前提引入(5)S (3)(4)析取三段论(6)RS(5)附加7、构造下列推理的证明:如果小张和小明,去看电影,则小李也去看电影。
小赵不去看电影或小张去看电影,小王去看电影。
所以,当小赵去看电影时,小李也去。
解:令P :小张去看电影;Q :小王去看电影;R :小李去看电影;S :小赵去看电影;前提:P Q R ,S P ,Q结论:SR证明:(1)Q前提引入(2)P Q R前提引入(3)PR(1)(2)析取三段论(4)S P前提引入(5)S R (3)(4)假言三段论。
逻辑式与真值表
05 实际应用案例分 析
数字电路设计与分析中应用
逻辑门电路的设计
利用逻辑式描述门电路输入与输出之间的关系,进而实现门电路 的设计。
电路分析与故障检测
通过真值表验证电路逻辑功能的正确性,帮助分析电路故障。
组合逻辑电路优化
利用逻辑式化简方法,简化组合逻辑电路的结构,提高电路性能 。
计算机程序设计中应用
THANKS
感谢观看
配项法
在逻辑式中添加冗余项,使得逻辑式 更加规整,便于化简。
不同化简方法比较与选择
卡诺图化简法与代数法比较
卡诺图化简法直观易懂,适用于变量较少的情况;代数法适 用于变量较多的情况,可以灵活运用各种公式进行化简。
选择依据
根据逻辑式的复杂程度和化简需求选择合适的化简方法。对 于简单的逻辑式,可以直接观察并手动化简;对于复杂的逻 辑式,可以采用卡诺图或代数法进行化简。同时,也可以结 合两种方法的优点进行综合化简。
语言学与自然语言处理
在语言学和自然语言处理中,利用逻辑式描述语句的语义关系,实 现自然语言的理解和生成。
06 总结与展望
课程重点内容回顾
逻辑式基本概念
逻辑式是描述事物之间逻辑关系的一种数学表达式,包括命题逻辑和 谓词逻辑两种形式。
真值表及其作用
真值表是用来表示逻辑式真值情况的一种表格,可以直观地展示逻辑 式的真假情况,方便进行逻辑分析和推理。
04
根据真值表画出卡诺图。
05
将相邻的1或0圈起来,并尽量使圈内的元素最多。
06
根据圈的组合写出最简逻辑表达式。
代数法化简复杂逻辑式方法
并项法
利用公式AB+AB’=A将两项合并为 一项,消去其中的B与B’。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
归谬赋值法
根据→的意义,可知原公式的前件¬ p ∨ q 为真, 后件p → q为假。 在¬ p ∨ q的主联接词下方标T,在p → q的 主联接词下方标F,以表明上述推断:
(¬ p ∨ q) → (p → q) TFF
归谬赋值法
继续上一过程,直至…… ( ¬ p ∨ q )→ ( p → q) TFF TF TF F F
以上推导表明,假设存在p、q的一种取值使得原公 式为假,那么在p、q的这种取值下, ¬ p∨q 既为T 又为F,但这是不可能的。故不存在p、q的取值使原 公式为假,因而原公式必是重言式。
归谬赋值法
例 判定( p ∨ q)→ (p→ q)是否为重言式。
证:
(1)( p ∨ q )→ ( p → q ) TTF F TFF
三者有何关系?
02
真值表法
真值表法
真值表的定义:真值表是显示一个真值形式都在其变项的各种真值组合下的逻辑值图表
例1用真值表方法判断((p ∨ q)∧¬ p)→q)真值形式。 解:列出这一真值形式的真值表:
p q ¬p p ∨ q
TT
F
T
TF
F
T
FT
T
T
FF
T
F
(p ∨ q)∧¬ p F F T F
(1)命题中上式没有赋值矛盾,因而不是重言 式。
Thank you
((p ∨ q)∧¬ p)→q) T T T T
上述真值表中可以看出, ((p ∨ q)∧¬ p)→q)的真值都为真,因此该式是重言式值法
真值表判定法是直接去“看”公式在命题变元的各种取值 情况下,原公式的真值是否都为真。
赋值归谬法是通过对一个真值形式进行变项赋值,来确 定是否会出现前件真而后件假,从而判断该真值形式是否为 重言式。
01
重言式及其判断
Tautology and its judgment
02
重言式及其判断
01. 真值形式
- 真值形式的定义 - 真值形式的分类
02. 真值表法
- 真值表的含义 - 真值表判断法
03. 赋值归谬法
- 归谬赋值法的含义和原理 - 归谬赋值法的方法
01
真值形式
真值形式及其分类
真值形式的定义:真值形式就是真值联结词和命题变项所构成的形式结构
真值形式的分类
1 重言式(永真式)重言式是无论命题变项取什么值, 逻辑值总为真的真值形式。如p∨¬ p ,p → p
2 矛盾式(永假式)矛盾式是无论命题变项取什么值, 逻辑值总为假的真值形式。如p∧¬ p ,¬ (p → p) 3 可满足式(协调式)可满足式是在命题变项的各种 取值下,至少有一组逻辑值为真的真值形式。 如 p∨p
反其道而行, 我们可以去寻找命题变元的某种取值,使得原公式在这种 取值情况下为假: 若实际找到命题变元的这种取值,则原公式不是重言式。 若能证明命题变元的这种取值不存在,则原公式是重言式。 这就是归谬赋值法的思想
归谬赋值法
以(¬ p ∨ q)→(p → q)的判定为例子 假定(¬ p ∨ q)→(p → q)为假,在这个公式的主联接 词下标F以表明这一点:
