北京市第四中学2017届中考数学冲刺复习 实数03 实数(无答案)
北京市第四中学2017届中考数学冲刺复习第1章有理数010有理数的加减无答案201708092172

有理数的加减一.基本概念1、有理数加法的运算法则(1)同号两数相加,取相同的符号,并把相加;(2)绝对值不相等的异号两数相加,取绝对值较大的的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得。
(3)一个数同0相加,仍得。
例1.计算下列各题(1)(+2)+(+7)(2) (-4)+(+7)(3) 5+02.注意事项:(1)有理数加法法则是进行有理数加法的根本依据,它也是人为规定的。
不过这个规定不仅符合实际,回答了过去用算术计算方法不能解决的某些问题,而且这个规定(有理数加法法则)与算术里的加法法则不矛盾。
(2)由于任何一个有理数都是由它的符号和绝对值两部分组成的,因此有理数加法法则的叙述中,都是强调先确定和的符号,再计算和的绝对值。
这样在进行加法运算时,必须先判断两个加数的符号,是同号?是异号?或是有一个加数为零,从而来确定用哪一条法则进行计算。
(3)在算式中一定要分清表示数的正、负的性质符号和表示加法运算的运算符号,并用括号分开。
如 (-2)+(+5) 、(+2)+(-5)、(-2)+(-5)等。
(4)可以证明,加法的交换律,加法的结合律在有理数范围内仍然成立,因此,利用有理数加法的运算律,有时可使计算简化。
例2.计算下列各题。
(1) -721+1061; (2) (-21)+(-7.3);(3) 411+(312-); (4) 517+(-3.8)+(-7.2)例3.计算(1)(-2.4)+(-4.2)+(-3.8)+(+3.1)+(+0.8)+(-0.7)(2) )324(83)65()851(432-++-+-+例4.已知:|a|=2,|b|=3,求a+b 的值。
例5.某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某 天自A 地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2, -8,+13,-2,+12,+8,+5。
(1)问收工时距A 地多远?(2)若每千米路程耗油0.2升,问从A 地出发到收工时共耗油多少升?二、有理数的减法1.已知两个有理数的和及其中一个加数,求另一个加数的运算叫做。
北京四中中考数学专练总复习 实数(提高)巩固练习

实数(提高)巩固练习【巩固练习】一.选择题1.代数式21a +,|y |,2(1)a -中,一定是正数的有( ).A .4个B .3个C .2个D .1个2. 三个数π-,-3, ).A .3π-<-<.3π-<-<C .3π<-<-D .3π-<<-3. 3k =-,k 的取值范围是( ).A .k ≤3B .k ≥3C .0≤k ≤3D .一切实数4. ).A .7和8之间B .6和7之间C .3和4之间D .2和3之间5. 若0a ≠,a 、b 互为相反数,则下列各对数中互为相反数的一对是( )与()33b - 6. 实数x 、y 、z 在数轴上对应点的位置如图所示,则下列关系正确的是( )A .x y z ++>0B .x y z ++<0C .xy yz <D .xy xz <二.填空题 7.227,3.33……,2π,22- ,8±, 554544554445.0,3271,90.0- ,中,无理数的个数是 个.8. m <0时,化简||m m =________.9. 计算:1||3+-=__________.10.已知,a b 互为相反数,,c d 互为倒数,21,2x y ==,则21999)(y cd x b a --++的值 .11. 若2|()03x y +-=,求2010()xy 的值. 12. 当x 时,243x --有最大值,最大值是 ________.三.解答题13.已知实数a 、b 在数轴上的位置,如图所示..14.已知实数x 、y 、z 满足21|441|()02x y z -+-=,求2()y z x +的值;15. 已知n m m n A -+-=3是3n m -+的算术平方根,322n m B n m +=+-是2m n +的立方根,求B -A 的平方根.【答案与解析】一.选择题1. 【答案】D ;【解析】仅21a +>0,其余可以为0还可为负数.2. 【答案】B ;33ππ<<⇒>->-.3. 【答案】D ;【解析】本题主要考查立方根的性质,即a =3k =-,所以k 可取一切实数.4. 【答案】D ;【解析】5 5.5<<,2.53<<,所以选D. 5. 【答案】C ;【解析】a +b =0,a =-b ==,所以=0.6. 【答案】B ;【解析】从数轴上可以看出-3<x <-2,-2<y <-1,0<z <1,所以很明显x y z ++<0.二.填空题7. 【答案】4;【解析】2π,22- ,8±, 554544554445.0为无理数. 8. 【答案】0;【解析】∵ 0m <,∴ ||0m m m m m m =--++=.9.【答案】4-+【解析】||1||3134+-=-=-+ 10.【答案】-4;【解析】原式=()()()0199921124±+--±=-. 11.【答案】1;【解析】3,,3x y =-= ∴1xy =-,∴2010()1xy =. 12.【答案】±2;3;0=时,243x --有最大值3.三.解答题13.【解析】解:由图所示可得0a b <<,且||||a b <.∴ 原式=|a |+|b |-|a -b |-|a +b |=-a +b +(a -b )-(a +b )=-a -b .14.【解析】解:∵ |441|0xy -+≥0≥,2102z ⎛⎫-≥ ⎪⎝⎭. 由题意,得方程组 441020102x y y z z ⎧⎪-+=⎪+=⎨⎪⎪-=⎩, 解得121412x y z ⎧=-⎪⎪⎪=-⎨⎪⎪=⎪⎩. ∴2()y z x +=21111114224416⎛⎫⎛⎫-+⋅=⨯= ⎪ ⎪⎝⎭⎝⎭. 15.【解析】解:∵n m m n A -+-=3是3n m -+的算术平方根,322n m B n m +=+-是2m n +的立方根,∴2m n -=,233m n -+=解得4,2m n ==∴A =1,B =2,B -A =1∴B -A 的平方根=±1.。
北京市第四中2017年中考数学冲刺复习专题训几何综合问题(无答案

几何综合问题以几何为主的综合题常研究以下几个方面的问题: ① 证明线段、角的数量关系(包括相等、和、差、倍、分关系及比例关系等);② 证明图形的位置关系(如点与线、线与线、线与圆、圆与圆等);③ 几何计算问题;④ 动态几何问题.在解几何综合题时,常常需要画图并分解其中的基本图形,挖掘其中隐含的等量关系.另外,也要注意使用数形结合、方程、分类讨论、转化等数学思想方法来解决问题.有时借助变换的观点也能帮助我们更有效地找到解决问题的思路.例1.如图,直角三角形纸片ABC 中,∠ACB=90°,AC=8,BC=6.折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别为D 、E.(1) DE 的长为 ;(2) 将折叠后的图形沿直线AE 剪开,原纸片被剪成三块,其中最小一块的面积等于 .例2.已知:在如图1所示的锐角三角形ABC 中,CH⊥AB 于点H ,点B 关于直线CH 的对称点为D ,AC 边上一点E 满足∠EDA =∠A,直线DE 交直线CH 于点F .(1) 求证:BF ∥AC ;(2) 若AC 边的中点为M ,求证:2DF EM ; (3) 当AB=BC 时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE相等的线段,并证明你的结论.图 1图2例3.已知:如图,N、M是以O为圆心,1为半径的圆上的两点,B是MN上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.(1)四边形EPGQ (填“是”或者“不是”)平行四边形;(2)若四边形EPG Q是矩形,求OA的值.。
中考试题北京市第四中学总复习:实数--巩固练习(提高).docx

中考总复习:实数—巩固练习 (提高)【巩固练习】一、选择题1. 在实数π、13、2、sin30°,无理数的个数为( ) A.1 B.2 C.3 D.42. 对于实数a 、b ,给出以下三个判断:①若b a =,则 b a =.②若b a <,则 b a <. ③若b a -=,则 22)(b a =-.其中正确的判断的个数是( )A .3B .2C .1D .03.根据第六次全国人口普查的统计,截止到2010年11月1日零时,我国总人口约为1 370 000 000人,将1 370 000 000用科学记数法表示应为( )A. 100.13710⨯B. 91.3710⨯C. 813.710⨯D. 713710⨯4.如图,矩形OABC 的边OA 长为2 ,边AB 长为1,OA 在数轴上,以原点O 为圆心,对角线OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )A .2.5B .2 2C . 3D . 55.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m 的值是( )A .38B .52C .66D .746. 若a 、b 两数满足567a ⨯3=103,a ÷103=b ,则b a ⨯之值为( )A .9656710B .9356710C .6356710D .56710二、填空题7.(1)先找规律,再填数:1111111111111111,,,,122342125633078456............111+_______.2011201220112012+-=+-=+-=+-=-=⨯则(2)对实数a 、b ,定义运算★如下:a ★b=(,0)(,0)b b a a b a a a b a -⎧>≠⎪⎨≤≠⎪⎩, 例如2★3=2-3=18.计算[2★(﹣4)]×[(﹣4)★(﹣2)]= . 8.已知:,,观察前面的计算过程,寻找计算规律计算27A = (直接写出计算结果),并比较59A 310A (填“>”或“<”或“=”)9.右图为手的示意图,在各个手指间标记字母A ,B ,C ,D .请你按图中箭头所指方向(即A →B →C →D →C →B →A →B →C →…的方式)从A 开始数连续的正整数1,2,3,4,…,当数到12时,对应的字母是 ;当字母C 第201次出现时,恰好数到的数是 ;当字母C 第2n +1次出现时(n 为正整数),恰好数到的数是 (用含n 的代数式表示).10.根据如图所示的程序计算,若输入x 的值为1,则输出y 的值为___________.11.已知,当n=1时,a 1=0;当n=2时,a 2=2;当n=3时,a 3=0;… 则a 1+a 2+a 3+a 4+a 5+a 6 的值为___________. 12.在五环图案内,分别填写五个数a ,b ,c ,d ,e ,如图,,其中a ,b ,c 是三个连续偶数(a<b),d ,e 是两个连续奇数(d<e),且满足a+b+c=d+e ,例如.请你在0到20之间选择另一组符合条件的数填入下图:.三、解答题13.对于任何实数,我们规定符号c a db 的意义是:c ad b =bc ad -.按照这个规定请你计算: 当0132=+-x x 时,21-+x x 13-x x 的值.14. 若[]x 表示不超过x 的最大整数(如[]3322,3-=⎥⎦⎤⎢⎣⎡-=π等), 求111212323201320122013⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥-⨯-⨯-⨯⎣⎦⎣⎦⎣⎦的值.15.根据以下10个乘积,回答问题:11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;(2)将以上10个乘积按照从小到大的顺序排列起来;(3)试由(1)、(2)猜想一个一般性的结论.(不要求证明)16.已知等边△OAB 的边长为a ,以AB 边上的高OA 1为边,按逆时针方向作等边△OA 1B 1,A 1B 1与OB 相交于点A 2.(1)求线段OA 2的长;(2)若再以OA 2为边按逆时针方向作等边△OA 2B 2,A 2B 2与OB 1相交于点A 3,按此作法进行下去,得到 △OA 3B 3,△OA 4B 4,…,△OA n B n (如图).求△OA 6B 6的周长.【答案与解析】一、选择题1. 【答案】B ;【解析】π、2是无理数.2.【答案】C ;【解析】通过举反例说明①②是不对的,只有③是正确的.3.【答案】B ; 【解析】根据科学记数法的定义,科学记数法的表示形式为1010n a a <⨯≤,其中1,n 为整数,表示时关键要正确确定a 的值以及n 的值,故选B.4.【答案】D ;【解析】用勾股定理求得OB= 5 即可.5.【答案】D ;【解析】先分析出阴影方格的数,如图,找出规律:m=左下角方格的数的平方加上右上角方格的数.6.【答案】C ;二、填空题7.【答案】(1)11006;(2)1; 【解析】(1)规律为:111111(1)2n n n n n +-=+++(n 为正整数). (2) [2★(﹣4)]×[(﹣4)★(﹣2)]=2-4×(-4)2=1.8.【答案】42;>.【解析】27A =7×6=42;∵59A =9×8×7×6×5,310A =10×9×8,∴59A >310A .9.【答案】B ;603;6n +3;【解析】字母C 第“奇数”次出现时,恰好数到的数是这个“奇数”的3倍。
北京市第四中学2017届中考数学冲刺复习 实数02 立方根、实数(无答案)

立方根、实数
知识要点:
一、立方根的定义
如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.
即如果3x a=,那么x叫做a的立方根。
求一个数的立方根的运算,叫做开立方.
一个数a的立方根,用a是被开方数,
3是根指数.开立方和立方互为逆运算.
二、立方根的特征
立方根的特征:正数的立方根是正数,
负数的立方根是负数,0的立方根是0.
说明:任何数都有立方根,一个数的立方根有且只有一个,并且它的符号与这个非零数的符号相同.两个互为相反数的数的立方根也互为相反数.
三、实数
有理数和无理数统称为实数.
1.实数的分类
按定义分:
按与0的大小关系分:
2.实数与数轴上的点一一对应.
数轴上的任何一个点都对应一个实数,反之任何一个实数都能在数轴上找到一个点与之对应.
四、实数大小的比较
对于数轴上的任意两个点,右边的点所表示的实数总是比左边的点表示的实数大.正实数大于0,负实数小于0,两个负数,绝对值大的反而小.
开立方例题分析
1、下列结论正确的是()
A.64的立方根是±4B.1
2-是
1
6-的立方根。
四中中考数学专练总复习 实数全章复习与巩固(基础)知识讲解
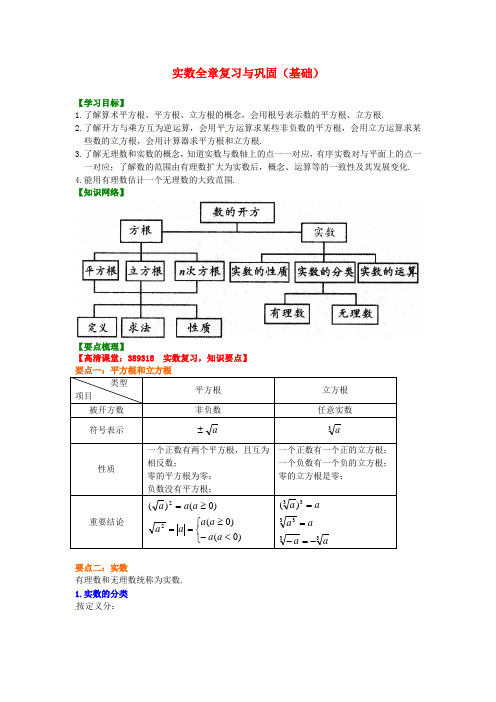
实数全章复习与巩固(基础)【学习目标】1.了解算术平方根、平方根、立方根的概念,会用根号表示数的平方根、立方根.2.了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用计算器求平方根和立方根.3.了解无理数和实数的概念,知道实数与数轴上的点一一对应,有序实数对与平面上的点一一对应;了解数的范围由有理数扩大为实数后,概念、运算等的一致性及其发展变化.4.能用有理数估计一个无理数的大致范围.【知识网络】【要点梳理】【高清课堂:389318 实数复习,知识要点】要点二:实数有理数和无理数统称为实数.1.实数的分类按定义分:实数⎧⎨⎩有理数:有限小数或无限循环小数无理数:无限不循环小数按与0的大小关系分:实数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正有理数正数正无理数负有理数负数负无理数要点诠释:(1)所有的实数分成三类:有限小数,无限循环小数,无限不循环小数.其中有限小数和无限循环小数统称有理数,无限不循环小数叫做无理数.(2②有特殊意义的数,如π;③有特定结构的数,如0.1010010001…(3)凡能写成无限不循环小数的数都是无理数,并且无理数不能写成分数形式.(4)实数和数轴上点是一一对应的.2.实数与数轴上的点一 一对应.数轴上的任何一个点都对应一个实数,反之任何一个实数都能在数轴上找到一个点与之对应.3.实数的三个非负性及性质:在实数范围内,正数和零统称为非负数。
我们已经学习过的非负数有如下三种形式: (1)任何一个实数a 的绝对值是非负数,即|a |≥0; (2)任何一个实数a 的平方是非负数,即2a ≥0;(30≥ (0a ≥).非负数具有以下性质: (1)非负数有最小值零;(2)有限个非负数之和仍是非负数;(3)几个非负数之和等于0,则每个非负数都等于0. 4.实数的运算:数a 的相反数是-a ;一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0.有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序:先乘方、开方、再乘除,最后算加减.同级运算按从左到右顺序进行,有括号先算括号里. 5.实数的大小的比较:有理数大小的比较法则在实数范围内仍然成立.法则1. 实数和数轴上的点一一对应,在数轴上表示的两个数,右边的数总比左边的数大;法则2.正数大于0,0大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小;法则3. 两个数比较大小常见的方法有:求差法,求商法,倒数法,估算法,平方法. 【典型例题】类型一、有关方根的问题1、下列命题:①负数没有立方根;②一个实数的算术平方根一定是正数;③一个正数或负数的立方根与这个数同号;④如果一个数的算术平方根是这个数本身,那么这个数是1或0;⑤如果一个数的立方根是这个数本身,那么这个数是1或0 ,其中错误的有( ) A.2个 B.3 个 C.4 个 D.5个 【答案】B ;【解析】①负数有立方根;②0的算术平方根是0;⑤立方根是本身的数有0,±1. 【总结升华】把握平方根和立方根的定义是解题关键. 举一反三:【变式】下列运算正确的是( )A 2=±B =2=- D .|2|2--=【答案】C ;210.1== 若7160.03670.03=,542.1670.33=,则_____________3673= 【答案】±1.01;7.16;【解析】102.01向左移动2位变成1.0201,它的平方根向左移动1位,变成1.01,注意符号;0.3670向右移动3位变成367,它的立方根向右移动1位,变成7.16【总结升华】一个数向左移动2位,它的平方根向左移动1位;一个数向右移动3位,它的立方根向右移动1位.类型二、与实数有关的问题3、把下列各数填入相应的集合: -1、3、π、-3.14、9、26-、22-、7.0 . (1)有理数集合{ }; (2)无理数集合{ }; (3)正实数集合{ }; (4)负实数集合{ }.【思路点拨】首先把能化简的数都化简,然后对照概念填到对应的括号里. 【答案与解析】(1)有理数集合{-1、-3.14、9、7.0 };(2)无理数集合{ 3、π、26-、22-};(3)正实数集合{ 3、π、9、26-、7.0 };(4)负实数集合{ -1、-3.14、22-}. 【总结升华】有理数是有限小数和无限循环小数,无理数是无限不循环小数.总结常见的无理数形式. 举一反三:π227,0.3,其中无理数有( ) A .1个 B .2个 C .3个 D .4个【答案】B ;π.4、计算(1)233)32(1000216-++ (2)23)451(12726-+-(3)32)131)(951()31(--+【思路点拨】先逐个化简后,再按照计算法则进行计算.【答案与解析】解:(1)233)32(1000216-++=226101633++=(2)23)451(12726-+-1113412=-+=-(3)32)131)(951()31(--+=1112133333++=-=-.【总结升华】根据开立方和立方,开平方和平方互逆运算的关系,可以通过立方、平方的方法去求一个数的立方根、平方根. 举一反三: 【变式】计算(1) 333000216.0008.012726---- (2) ()223323)3()21()4()4(2--⨯-+-⨯-【答案】 解:(1) 333000216.0008.012726----()0.20.06=-- 29150=-(2) ()223323)3()21()4()4(2--⨯-+-⨯-()184434=-⨯+-⨯- 321336=---=-.5、若0,0<<ab a ,化简334+----a b b a【思路点拨】由0,0<<ab a 判断b >0,再判断绝对值里的数的正负,由绝对值的定义去掉绝对值.【答案与解析】解:∵0,0<<ab a ,∴b >0,∴0,0a b b a --->∴a b b a ---((a b b a =-----a b b a =-+++=【总结升华】含绝对值号的代数式的化简是重点也是难点.分类的标准应按正实数,负实数,零分类考虑.掌握好分类标准,不断加强分类讨论的意识. 举一反三:【变式1】实数a 、b 在数轴上所对应的点的位置如图所示:化简2a +∣a -b ∣=.【答案】解:∵a <0<b ,∴a -b <0∴2a +∣a -b ∣=-a -(a -b )=b -2a . 【高清课堂:389318 实数复习,例5】 【变式2】实数a 在数轴上的位置如图所示,则2,1,,a aa a -的大小关系是: ; -1a【答案】21a a a a<<<-; 类型三、实数综合应用6、现有一面积为150平方米的正方形鱼池,为了增加养鱼量,欲把鱼池的边长增加6米,那么扩建鱼池的面积为多少(最后结果保留4个有效数字)?【答案与解析】解:因为原正方形鱼池的面积为150平方米,根据面积公式,12.247≈ (米).由题意可得扩建后的正方形鱼池的边长为(12.247+6)米, 所以扩建后鱼池的面积为218.247≈333.0(平方米).答:扩建后的鱼池的面积约为333.0(平方米).【总结升华】要求扩建后的鱼池的面积,应先求出其边长,而原鱼池的面积为150平方米,由此可得原鱼池的边长,再加上增加的6米,故新鱼池面积可求. 举一反三:【变式】一个底为正方形的水池的容积是4863m ,池深1.5m ,求这个水池的底边长. 【答案】解:设水池的底边长为x ,由题意得2 1.5486x ⨯= 2324x = 18x =答:这个水池的底边长为18m .。
北京市第四中学2017届中考数学冲刺复习 第1章 有理数05 有理数的乘方及混合运算(无答案)
有理数的乘方及混合运算一、 概念1. 有理数乘方的概念n 个相同的因数a 相乘,即⋅⋅⋅a a a n 个,记作na ; 求几个相同因数的积的运算,叫做 ; 叫做幂;单独一个数a 也可看成是指数为1的幂,即1a a =。
当n 为正整数时,n a 表示的意义是,(1),(2)=⎧⎪=⎨⨯⨯⨯⨯≥⎪⎩n a n a a a a a n在na 中,a 叫作 ,n 叫做指数,n a 读作 , n a 看作是a 的n 次方的结果时,也可读作a 的n 次幂.2.乘方的性质:正数的任何次幂都是 数;负数的奇次幂是 数,负数的偶次幂 是 数;0的任何非零次幂都是 。
任何一个数的偶数次幂都是 。
3.有理数的混合运算(1)先算乘方,再算乘除,最后算 ;(2)同级运算,按照 的顺序进行;(加法和减法叫做第一级运算;乘法和除法叫做第二级运算;乘方和今后将会学到的开方叫做第三 级运算)(3)如果有括号,先算 里的,再算中括号里的,最后算大括号里的。
(4)可以应用运算律,适当改变运算顺序,使运算简便设a 、b 为有理数,现对a b *运算作定义如下:a b a b a b *=⨯++,对b a ∆运算作定义如下: b a b a 32+=∆.(1)试说明“∆”这种运算是否满足交换律?(2)试说明“∆”运算对“*”运算是否满足分配律?典型例题:例1:计算(1)()⎡⎤⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭⎣⎦211-1-0.5××2--33 (2)()⎡⎤⎣⎦341-1-×2--36 (3)3201111(1+-2.75)×(-24)+(-1)--238(4)33211-+|-2-3|(-0.1)(-0.2)例2:选择(1)下列说法中,正确的个数为( ).①对于任何有理数m ,都有m 2>0;②对于任何有理数m ,都有m 2=(-m )2;③对于任何有理数m 、n (m ≠n ),都有(m -n )2>0;④对于任何有理数m ,都有m 3=(-m )3.(A )1 (B )2 (C )3 (D )0 (2)(-2)2003+(-2)2004=( )(A )-2 (B )(-2)4007(C )22003 (D )-22003例3:观察下面三行数:-3 -1 1 3 5 7 …1 3 5 7 9 11 …2 8 32 128 512 2048 …(1) 第一行数是按什么规律排列的?(2) 第二、三行数与第一行数有什么关系?(3) 计算第三行中的第八个数是多少?例4:观察下列等式:221=,422=,823=,1624=,3225=,6426=,12827=,82256=,……,通过观察,用你所发现的规律2的个位数字是什么,并说明理由.确定2011。
北京市第四中学2017年中考数学冲刺复习 专题训练 7 数形结合问题(无答案)
数形结合问题 数形结合问题,也可以看作代数几何综合问题.从内容上来说,是把代数中的数与式、方程与不等式、函数,几何中的三角形、四边形、圆等图形的性质,以及解直角三角形的方法、图形的变换、相似等内容有机地结合在一起,同时也会融入开放性、探究性等问题.经常考查的题目类型主要有坐标系中的几何问题(简称坐标几何问题),以及图形运动过程中求函数解析式的问题等.解决这类问题,第一,需要认真审题,分析、挖掘题目的隐含条件,翻译并转化为显性条件;第二,要善于将复杂问题分解为基本问题;第三,要善于联系与转化,进一步得到新的结论.尤其要注意的是,恰当地使用综合分析法及方程与函数的思想、转化思想、数形结合思想、分类与整合思想等数学思想方法,能更有效地解决问题.例1. 如图, 在平面直角坐标系xOy 中,抛物线x x my 222-=与x 轴负半轴交于点A, 顶点为B, 且对称轴与x 轴交于点C.(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式;(3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐标.例2.在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M,直线2 2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B.⑴直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3)已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值.。
北京市第四中学2017届中考数学冲刺复习 第1章 有理数07 有理数复习与提高(无答案)
有理数的复习与提高一、知识结构二、复习要点:1. 有理数的概念2. 数轴定义,数轴上的点与有理数的关系3. 相反数的定义,互为相反数的两个数的特征4. 一个数的绝对值的定义及求法,有理数的绝对值的性质5. 比较两个有理数的大小的方法6. 有理数的加法、减法、乘法、除法的运算法则7. 乘方的意义和运算法则8. 正确进行有理数的混合运算(分笔算和用计算器算)9. 近似数和有效数字的概念, 用科学记数法表示数10. 有理数在实际应用中的实例11.有理数集有哪些性质?三、复习例题:例1.下列说法是否正确?并将不正确的说法修改为正确的说法(1)正数、负数和零都是有理数(2)任何一个有理数都有相反数和倒数.(3)任何一个有理数的平方都是正数.(4)若x2=25, 则x=5.(5)若|x|<5,则x<5.(6)-a表示负数.例2.选择题(1)已知四种说法:①|a|=a时,a>0; |a|=-a时,a<0.②|a|就是a与-a中较大的数.③|a|就是数轴上表示a的点到原点的距离.④对于任意有理数,-|a|≤a≤|a|.其中说法正确的个数是()A、1B、2C、3D、4(2)有四个说法:①有最小的有理数2 ②有绝对值最小的有理数③有最小的正有理数④没有最大的负有理数上述说法正确的是( )A 、①②B 、③④C 、②④D 、①②(3)已知(-ab)3>0,则( )A 、ab<0B 、ab>0C 、D 、(4)若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是( )A 、120B 、-15C 、0D 、-120(5)下列各对算式中,结果相等的是( )A 、-a6与(-a)6B 、-a3与|-a|3C 、[(-a)2]3与(-a3)2D 、(ab)3与ab3例3.已知有理数a ,b ,c 在数轴上对应的点的位置如图所示:化简:|3a-c|+|2a+b|-|c-b|例4.为体现社会对教师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师。
北京市第四中学2017届中考数学冲刺复习 第1章 有理数05 有理数的乘方及混合运算
有理数的乘方及混合运算一、 概念1. 有理数乘方的概念n 个相同的因数a 相乘,即⋅⋅⋅ a a a n 个,记作na ; 求几个相同因数的积的运算,叫做 ; 叫做幂;单独一个数a 也可看成是指数为1的幂,即1a a =。
当n 为正整数时,na 表示的意义是,(1),(2)=⎧⎪=⎨⨯⨯⨯⨯≥⎪⎩ n a n a a a a a n 在n a 中,a 叫作 ,n 叫做指数,na 读作 , n a 看作是a 的n 次方的结果时,也可读作a 的n 次幂.2.乘方的性质:正数的任何次幂都是 数;负数的奇次幂是 数,负数的偶次幂 是 数;0的任何非零次幂都是 。
任何一个数的偶数次幂都是 。
3.有理数的混合运算(1)先算乘方,再算乘除,最后算 ;(2)同级运算,按照 的顺序进行;(加法和减法叫做第一级运算;乘法和除法叫做第二级运算;乘方和今后将会学到的开方叫做第三 级运算)(3)如果有括号,先算 里的,再算中括号里的,最后算大括号里的。
(4)可以应用运算律,适当改变运算顺序,使运算简便设a 、b 为有理数,现对a b *运算作定义如下:a b a b a b *=⨯++,对b a ∆运算作定义如下: b a b a 32+=∆.(1)试说明“∆”这种运算是否满足交换律?(2)试说明“∆”运算对“*”运算是否满足分配律?典型例题:例1:计算(1)()⎡⎤⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭⎣⎦211-1-0.5××2--33 (2)()⎡⎤⎣⎦341-1-×2--36 (3)3201111(1+-2.75)×(-24)+(-1)--238(4)33211-+|-2-3|(-0.1)(-0.2)例2:选择(1)下列说法中,正确的个数为( ).①对于任何有理数m ,都有m 2>0;②对于任何有理数m ,都有m 2=(-m )2;③对于任何有理数m 、n (m ≠n ),都有(m -n )2>0;④对于任何有理数m ,都有m 3=(-m )3.(A )1 (B )2 (C )3 (D )0 (2)(-2)2003+(-2)2004=( )(A )-2 (B )(-2)4007(C )22003 (D )-22003例3:观察下面三行数:-3 -1 1 3 5 7 …1 3 5 7 9 11 …2 8 32 128 512 2048 …(1) 第一行数是按什么规律排列的?(2) 第二、三行数与第一行数有什么关系?(3) 计算第三行中的第八个数是多少?例4:观察下列等式:221=,422=,823=,1624=,3225=,6426=,12827=,82256=,……,通过观察,用你所发现的规律2的个位数字是什么,并说明理由.确定2011。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实数
知识要点:
一。
平方根和立方根
二.实数
有理数和无理数统称为实数.
1.实数的分类
按定义分:
按与0的大小关系分:
2.实数与数轴上的点一一对应.
数轴上的任何一个点都对应一个实数,反之任何一个实数都能在数轴上找到一个点与之对应.
三、实数大小的比较
对于数轴上的任意两个点,右边的点所表示的实数总是比左边的点表示的实数大.正实数大于0,负实数小于0,两个负数,绝对值大的反而小. 四.实数的运算:
数a的相反数是-a;一个正实数的绝对值是它本身;
一个负实数的绝对值是它的相反数;0的绝对值是0.
有理数的运算法则和运算律在实数范围内仍然成立.
实数混合运算的运算顺序:先乘方、开方、再乘除,最后算加减.同级运算按从左到右顺序进行,有括号先算括号里.
五.实数的大小的比较:
有理数大小的比较法则在实数范围内仍然成立。
法则1. 实数和数轴上的点一一对应,在数轴上表示的两个数,右边的数总比左边的数大;
法则2.正数大于0,0大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小;
法则3. 两个数比较大小常见的方法有:求差法,求商法,倒数法,估算法,平方法。
例题分析
2、已知M是满足不等式
a a的和,N是满足不等式
的最大整数.
求M+N的平方根.
4、阅读理解,回答问题.
在解决数学问题的过程中,有时会遇到比较两数大小的问题,解决这类问
题的关键是根据命题的题设和结论特征,采用相应办法,其中巧用“作差
2
法”是解决此类问题的一种行之有效的方法:
若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a<b.
例如:在比较m2+1与m2的大小时,小东同学的作法是:
请你参考小东同学的作法,比较大小:
5、已知a、b满足
解关于 x的方程
练习:设a、b、c都是实数,且满足,
求代数式的值。
6、阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
似值.
小明的方法:
问题:(1)请你依照小明的方法,估算
巩固练习
1.已知a、b是实数,下列命题结论正确的是()
4 A .若a >b ,则22a b > B .若a >|b |,则22a b >
C .若|a |>b ,则22a b >
D .若33a b >,则22a b >
2.下列式子表示算术平方根的是 ( ).
3. 下列说法错误的有( )
①无限小数一定是无理数; ②无理数一定是无限小数;③带根号的数一 定是无理数; ④不带根号的数一定是有理数.
A ①②③
B ②③④
C ①③④
D ①②④
4. 下列语句、式子中
① 4是16
的算术平方根,即4=
②4是16的算术平方根,即
4=
③-7是49的算术平方根,即
7=
④7是(-7)²的算术平方根,即
7=
其中正确的是( )
A. ①③
B. ②③
C. ②④
D. ①④
6.下列运算中正确的是( )。
