流体力学 第七章习题及答案2 - 2
流体力学课后习题及答案

第二章2-2解:由P gh ρ=得h 水 =Pg ρ水=3350101109.8⨯⨯⨯=5.1m 335010=3.21.6109.8Ph m gρ⨯==⨯⨯四氯化碳四氯化碳 335010=0.37513.6109.8Ph m g ρ⨯==⨯⨯水银水银2-3 解:(1)体积弹性模量 /dpEv d ρρ=+在重力场中流体的压强形式为:dpg dzρ=- d dp gdz Evρρρ∴=-=两边积分,带入边界条件:00,0,z p ρρ===0lnEvp Ev Ev ghρ∴=- 11222212.5*160N F *40000NF L L s F s ==⎛⎫=== ⎪⎝⎭题解:有杠杆原理知:F 所以: 6、如题2-6图所示,封闭容器中盛有ρ=800kg/3m的油,1300h mm =,油下面为水,2500h mm =,测压管中水银液位读数400hmm =,求封闭容器中油面上的压强p 的大小。
解:12g 0p h gh gh ρρρ++-=油水水银12g p gh h gh ρρρ=--水银油水333313.6109.840010109.8500100.8--=⨯⨯⨯⨯-⨯⨯⨯-⨯=44.6110pa ⨯2-7:解:(1)、2224F gh s 10009.81001010101098Nρ--==⨯⨯⨯⨯⨯=2)m 121216G [s h h s h ]1000199109.81.95g Nρ-=⨯⨯=⨯⨯⨯=(-)+02h(3)因为在21h h -处谁对容器有向上的压力2-8,解:由同一液面压强相等可列:(0)()gh sin /6p(0)1239.21/^3p p h l kn m θθπ===∴=液2-9 解:设A 点距左U 形管测压计水银页面高度为H 则B 点距右U 型管测压计水银高度为H+hB A B h gh g H h gh gh gh m ag ρρρρρρA P -P -+P P -P =-=-⨯⨯P 水水水水则(+)=则()=(13600-1000)9.80.3=370442.10,解:选取右侧U 形管汞柱高作为等压面,有:1132()m B P g h h gh gh gh p ρρρρ++-+=+酒汞汞水B p 42.7410pa =-⨯2-11解:左边液面压强与右边液面压强相等知,.66g .66.89g .82g .8211g ⨯+-⨯=⨯+-⨯未知水未知水)()(ρρρρ解得333102.31m kg 103.85⨯=⋅⨯=-未知ρ3m kg -⋅2-12 解:设左支管液面到另一液体分界面的距离为1h ,右支管为2h ,则有:1112222P gh P gh gh ρρρ+=++或121122121221()()P P g h h ghP P gh gh ghρρρρρρ-=--+-=-+=-得 1221()P P h gρρ-=-2-13解:gh P gh ρρ+=水水银P=gh gh ρρ∴-水银水127400.07891.8F PS N∴==⨯=2-14解:以闸门与液面交点为O 点,沿闸门向下方向建立坐标S ,取微元ds ,在面积bds 内,液体压力对链轴取矩()()0.2sin600.2dM ghbds s g s sdsρρ=-+=-+ 所以)0sin 600.2Mgb s sds ρ=-+Q对链轴取矩)cos600.2Q M Q =由力矩平衡得 0Q M M +=化简)1.*1.9320.302Q -=得 26778Q N=()()D 33352.151y y *1132***2*4121232,8832**10*10*12*89.6*10xcC c xc cD c I y sI b a y s d y F g h s ρ=+==========题解:依题意知又即:*16、一个很长的铅垂壁面吧海水和淡水隔开,海水深7m ;试确定淡水多深时壁面所受液体作用力合力为零。
《工程流体力学》习题1~7章参考答案

等
学
校
教
材
过程装备与控制工程专业核心课程教材
工程流体力学
习题参考答案
主讲:陈庆光
化学工业出版社教材出版中心
黄卫星, 陈文梅主编. 工程流体力学, 北京:化学工业出版社教材出版中心,2001.8
习题 1-1 如图 1-9 所示,一个边长 200mm 重量为 1kN 的滑块在 20 斜面的油膜上滑动,油膜 厚度 0.005m,油的粘度 µ = 7 × 10−2 Pa ⋅ s 。设油膜内速度为线性分布,试求滑块的平衡速度。
V= 1000 3 1000 (因为是正方形容器,厚度为 3m) 。 m 的油,使左侧容器中的油的高度增加了 ρ油 g 3ρ油 g
假设此时右侧容器的水位在原来的基础上升高了 ym,则根据左右容器的尺寸关系,左侧的油 柱将下降 2ym。再根据等压面(等压面下降了 2ym 的高度)的性质有: 1000 1000 + ρ油 g h ( y + 2 y ) + (3 − 2) ⇒ y = 9 ρ g ≈ 0.01134m = 11.34mm 3ρ g = ρ水 g 水 油 习题 3-2 在海中一艘满载货物的船,其形态如图 3-10 所示。船底长度 12m,舱体宽度(垂直 于纸面)上下均为 6m,船长两端梯度均为 45 ,并近似取海水的密度为 1000 kg m3 。求船加 上货物的总质量。
参考答案 3
∂v ∂v y ∂vx ∂vz ∂v y ∂vx − − Ω = ∇×v = z − i + j+ ∂y ∂z ∂z ∂x ∂x ∂y ∂v ∂v cz cy j− k = x j+ x k = ∂z ∂y y2 + z2 y2 + z2
流体力学答案第七章习题及答案2 2.doc

习题及答案7 —9薄壁孔口出流,直径d=2mm,水箱水位恒定H=2m,试求: (1)孔口流量。
;⑵此孔口外接圆柱形管嘴的流量Q;(3) 管嘴收缩断面的真空。
解:(1 ) @=心顷~ j2gx2=1.22 n?/s(2) Q n = ^,A^H = 0.82^2gx2 =1.61 m3/s(3) 4 = 0.75//=0.75x2 = 1.5 mPg7 —10水箱用隔板分为A、B两室,隔板上开一孔口,其直径d 户4cm,在B室底部装有圆柱形外管嘴,其直径d2=3cm0 已知H=3m, h3=0. 5m,试求:(1) »、h2; (2)流出水箱的流量Q。
解:(1) & ="专7^ =「冬山(丑—4)=00.62 x 郴•。
町皿 = 0.82x得hi=1.07m h2=H- hFl.43m(2) Q=/Z^7^=0.62X"°:4)j2gxl.O7 =3.57 Vs7-12游泳池长25m,宽10m,水深1.5m,池底设有直径10cm 的放水孔直通排水地沟,试求放尽池水所需的时间。
V =25x10x1.5 = 375m31Qmax = M X/2^O = O^x-7rd2d2gH o =2.64xl0-2m3 解: 42Vt =——= 7.89/iQmax7-14虹吸管将A池中的水输入B池,已知长度/F3m, Z2=5m, 直径d=75mm,两池水面高差H=2m,最大超高h=1.8m,沿程阻力系数入二0.02,局部阻力系数:进口J = 0.5,转弯支=0. 2,出口J = 1。
试求流量及管道最大超高断面的真空度。
80.075 、2 2— = 3.83—2g2g 19.6x23.20 m/s3.83 (0.075)2 Q = D * = 3.20X —~ -------------- =14.13 41/s列上游水池和最大超高处的伯诺里方程 〃噫+。
3噫g +如 (I> 决如十讦+检斗l ・5H 1+-^- + 0 = H 2+0 + 0 + /Z Z Pg(d\卜勺+£+£+与+易 1 2x98000 仁 l+ --------------- =5+16.4— 9800 2g解:( 10 0.025x —— 2g I 0.025 i} i}^0.5+4+3x03+1 —=16.4—2g 2g(i +i 宙《解:列上下游水池的伯诺里方程丑+0 + 0 = ° + 0 + 0 + "『罗斋= 3.E7-16水从密闭容器A,沿直径d=25mm,长Z=10m 的管道流 入容器B,已知容器A 水面的相对压强pF2at,水面高HFlm, Hi =1 m, H2=5m,沿程阻力系数入=0.025,局部阻力系数:阀 门C a=4. 0,弯头£b=0.3,试求流量。
工程流体力学 禹华谦 习题答案 第7章

7.1 水以来流速度v 0=0.2m/s 顺流绕过一块平板。
已知水的运动粘度s /m 10145.126-⨯=ν,试求距平板前缘5m 处的边界层厚度。
【解】计算x=5m 处的雷诺数50x 107.8/x v Re ⨯=ν=该处的边界层属湍流m 12.0)107.8(537.0Re x 37.051551x=⨯==δ7.2 流体以速度v 0=0.8m/s 绕一块长 L=2m 的平板流动,如果流体分别是水(s /m 10261-=ν)和油(s /m 108252-⨯=ν),试求平板末端的边界层厚度。
【解】先判断边界层属层流还是湍流水:610L 106.1/L v Re ⨯=ν= 油:520L 102/L v Re ⨯=ν=油边界层属层流m 077.08.02108477.5v L 477.5502=⨯⨯=ν=δ-水边界层属湍流m 042.0)106.1(237.0Re L 37.051651L=⨯==δ7.3 空气以速度v 0=30m/s 吹向一块平板,空气的运动粘度s /m 101526-⨯=ν,边界层的转捩临界雷诺数6xcr 10Re =,试求距离平板前缘x=0.4m 及x=1.2m 的边界层厚度。
空气密度3m /kg 2.1=ρ。
【解】(1)x=0.4m ,xcr 60x Re 108.0/x v Re <⨯=ν=,为层流边界层m 0024.0304.01015477.5v x 477.560=⨯⨯=ν=δ- (2)x=1.2m ,xcr 60x Re 104.2/x v Re >⨯=ν=,为湍流边界层m 023.0)104.2(2.137.0Re x 37.051651x=⨯==δ7.4 边长为1m 的正方形平板放在速度v 0=1m/s 的水流中,求边界层的最大厚度及双面摩擦阻力,分别按全板都是层流或者都是湍流两种情况进行计算,水的运动粘度s /m 1026-=ν。
【解】b=1m, L=1m, 60L 10/L v Re =ν=层流: m 005.01110477.5v L 477.560=⨯=ν=δ- 3Lf 1046.1Re 46.1C -⨯==N 46.1bL 2C v 21F f 20D =ρ=湍流: m 023.0)101(137.0Re L 37.051651L =⨯==δ 32.0L f 105.4)(Re 072.0C -⨯==N 5.4bL 2C v 21F f 20D =ρ=7.5 水渠底面是一块长L=30m ,宽b=3m 的平板,水流速度v 0=6m/s ,水的运动粘度s /m 1026-=ν,试求:(1)平板前面x=3m 一段板面的摩擦阻力;(2)长L=30m 的板面的摩擦阻力【解】设边界层转捩临界雷诺数5xcr 105Re ⨯=,因为5cr 0105/x v ⨯=ν,所以 m 083.0x cr =(1) x=3m ,平板边界层为混合边界层60x 1018/x v Re ⨯=ν=0025.01805)002.00053.0(0026.0Re Re )Re 46.1Re 074.0(Re 074.0C xxcr xcr 5xcr5xfm =--=--=N 406bL v 21C F 20fmD =ρ= (2) L=30m ,平板边界层为混合边界层60L 10180/L v Re ⨯=ν=00159.018005)002.00053.0(0016.0Re Re )Re 46.1Re 074.0(Re 074.0C Lxcr xcr 5xcr5Lfm =--=--=N 2577bL v 21C F 20fm D =ρ=7.6 一块面积为m 8m 2⨯的矩形平板放在速度s /m 3v 0=的水流中,水的运动粘度s /m 1026-=ν,平板放置的方法有两种:以长边顺着流速方向,摩擦阻力为F 1;以短边顺着流速方向,摩擦阻力为F 2。
流体力学第七章习题答案
第七章习题答案选择题(单选题)7.1比较在正常工作条件下,作用水头H ,直径d 相等时,小孔口的流量Q 和圆柱形外管嘴的流量n Q :(b )(a )Q >n Q ;(b )Q <n Q ;(c )Q =n Q ;(d )不定。
7.2圆柱形外管嘴的正常工作条件是:(b )(a )l =(3~4)d ,0H >9m ;(b )l =(3~4)d ,0H <9m ;(c )l >(3~4)d ,0H >9m ;(d )l <(3~4)d ,0H <9m 。
7.3图示两根完全相同的长管道,只是安装高度不同,两管的流量关系是:(c )(a )1Q <2Q ;(b )1Q >2Q ;(c )1Q =2Q ;(d )不定。
7.4并联管道1、2,两管的直径相同,沿程阻力系数相同,长度2l =31l ,通过的流量为:(c )2(a )1Q =2Q ;(b )1Q =1.52Q ;(c )1Q =1.732Q ;(d )1Q =32Q 。
7.5并联管道1、2、3、A 、B 之间的水头损失是:(d )1(a )fAB h =1f h +2f h +3f h ;(b )fAB h =1f h +2f h ;(c )fAB h =2f h +3f h ;(d )fAB h =1f h =2f h =3f h 。
7.6长管并联管道各并联管段的:(c )(a )水头损失相等;(b )水里坡度相等;(c )总能量损失相等;(d )通过的流量相等。
7.7并联管道阀门为K 全开时各段流量为1Q 、2Q 、3Q ,现关小阀门K ,其他条件不变,流量的变化为:(c )(a )1Q 、2Q 、3Q 都减小;(b )1Q 减小,2Q 不变,3Q 减小;(c )1Q 减小,2Q 增加,3Q 减小;(d )1Q 不变,2Q 增加,3Q 减小。
7.8 有一薄壁圆形孔口,直径d 为10mm ,水头H 为2m。
《流体力学》 第七章 不可压缩粘性流体的流动

应力与应变的关系--------本构关系
du
dy
对照牛顿实验
pyx
斯托克斯假设
(1). 应力与变形速率之间为线性关系(小变 形(各向同性假设) (3). 趋于零时, 应力状态退化为理想流体 的应力状态(当流体处于静止状态时,符合 静止流体的应力特征)
pyz pzy
pzx pxz
pyx
p y x y
dy 2
pyy
p y y y
dy 2
pxx
pxx x
dx 2
pxy
pxy x
dx 2
y x
pxx
pxx x
dx 2
pxy
pxy x
dx 2
pyx
p y x y
dy 2
pyy
p y y y
dy 2
p y x y
pzx z
)
将pxx pyx pzx 的表达式代入, 设不可压, 则有
同理有
ax
fx
1
p x
(
2u x 2
2u y 2
2u z 2
)
ay
fy
1
p y
(
2v x 2
2v y 2
2v z 2 )
az
fz
1
p z
pzz
p
2
w z
相 加
1 3
(
pxx
pyy
《工程流体力学》第七章 粘性流体动力学
x方向 : 1)表面力:作用在左右两面上力的合力:
作用在上下两面上力的合力:
作用在前后两面上力的合力:
作用在整个六面体上表面力沿x轴方向的合力:
2) x方向质量力 : 单位质量流体受到的质量力分量:X;
六面体受到的质量力: Xrdxdydz
牛顿第二定律:
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式:
应力:各向同性
运动粘性流体:存在法向、切向表面力 应力:各向异性
流体中:任一点c :绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz:定义c上的应力
需要2个下标表示:9个应力分量
第1个下标i:应力作用方向 第2个下标j:作用面方向
第七章 粘性流体动力学
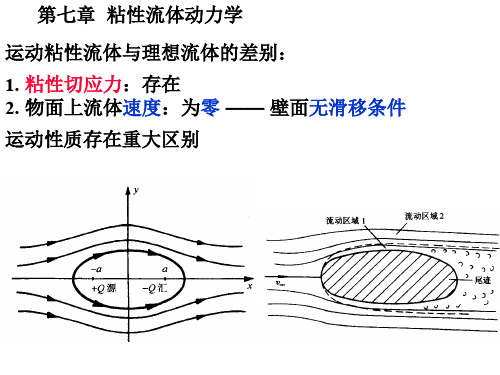
运动粘性流体与理想流体的差别: 1. 粘性切应力:存在 2. 物面上流体速度:为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力: 1.质量力:与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法:和理想流体相同
2. 表面力: 静止和运动理想流体:仅存在指向作用面法向表面力
由于外部无粘流:受到分离流的排挤 明显改变:其中压强分布 实际计算:用实测物面压力分布计算分离点前附面层流动 附面层分离:使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生:是工程上一个重要问 题
边界层分离后:形成尾涡区 尾涡区压强:基本上等于分离点压强 压强:上下对称 若将压强在圆柱面上积分:则得压差阻力
流体在y+l层时均速度:
流体力学习题及答案-第七章(DOC)

第七章 粘性流体动力学7-1 油在水平圆管内做定常层流运动,已知75=d (mm ),7=Q (litres/s ),800=ρ (kg/m 3),壁面上480=τ(N/m 2),求油的粘性系数ν。
答:根据圆管内定常层流流动的速度分布可得出2081m u λρτ=; 其中:λ是阻力系数,并且Re64=λ; m u 是平均速度,585.1075.014.325.010741232=⨯⨯⨯==-d Qu m π(m/s )。
由于阻力系数208m u ρτλ=,因此0202886464Re τρτρλmm u u ===; 即:28τρνmm u du =;所以油的粘性系数为401055.3585.18008075.0488-⨯=⨯⨯⨯==m u d ρτν(m 2/s )。
7-2 Prandtl 混合长度理论的基本思路是什么?答:把湍流中流体微团的脉动与气体分子的运动相比拟。
7-3无限大倾斜平板上有厚度为h 的一层粘性流体,在重力g 的作用下做定常层流运动,自由液面上的压力为大气压Pa ,且剪切应力为0,流体密度为ρ,运动粘性系数为ν,平板倾斜角为θ。
试求垂直于x 轴的截面上的速度分布和压力分布。
答:首先建立如图所示坐标系。
二维定常N-S 方程为:⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y u x u x pf y u v x u u x νρ ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y v x v y pf y v v x v u y νρ 对于如图所示的流动,易知()y u u =,()y p p =,0=v ,θsing f x =,θcos g f y -=;即x 方向速度u 和压力p 仅是y 的函数,y 方向速度分量0=v 。
因此上式可改写为:⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+=∂∂2222y u x u f x uu x ν ypf y ∂∂=ρ1 由不可压缩流体的连续方程0=∂∂+∂∂y v x u 可知,由于0=v ,0=∂∂yv,则0=∂∂x u ; 则上式可进一步简化为:022=∂∂+yuf x ν (1)ypf y ∂∂=ρ1 (2) 对于(1)式,将θsin g f x =代入,则有:θνsin 122g y u -=∂∂ 两端同时积分,得到:1sin 1C y g y u +-=∂∂θν由于当h y =时,0=∂∂=yuμτ,即0=∂∂y u ,代入上式有:h g C θνsin 11=因此:y g h g y u θνθνsin 1sin 1-=∂∂ 两端再次同时积分,得到:()22sin 21sin 1C y g hy g y u +-=θνθν由于0=y 时,()00=u ,代入上式,知02=C ;则有:()⎪⎭⎫ ⎝⎛-=221sin 1y hy g y u θν 若将ρμν=代入,则上式成为: ()⎪⎭⎫ ⎝⎛-=221sin y hy g y u θμρ 该式即为流动的速度分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题及答案
7-9薄壁孔口出流,直径d=2mm,水箱水位恒定H=2m ,试求:(1)孔口流量Q ;(2)此孔口外接圆柱形管嘴的流量Q n ;(3)管嘴收缩断面的真空。
解: (1)
2
3
=0.62 1.22 m /s
Q μ=⨯
=
(2)
2
3
0.82 1.61 m /s
n
n Q μ==⨯
=
(3)
v
0.750.752 1.5 m
p H g
ρ==⨯=
7-10 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径d 1=4cm ,在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知H=3m,h 3=0.5m ,试求:(1)h 1、h 2;(2)流出水箱的流量Q 。
解:(
1)
n
n Q Q μ
μ===
()
()
()12
12
24
03.082.024
04.062.0h H g gh -⨯
=⨯
ππ
得 h 1=1.07m h 2=H- h 1=1.43m
(2)
2
0.62 3.57 l/s
Q
μ
==⨯
=
7-12 游泳池长25m ,宽10m ,水深1.5m ,
池底设有直径10cm 的放水孔直通排水地沟,试求放尽池水所需的时间。
解:
3
2
2
3
m ax m ax
10 1.537510.62 2.6410
4
27.89m
Q d
m
V t h
Q μπ-⨯⨯===⨯=⨯=
=V =25
7-14 虹吸管将A 池中的水输入B 池,已知长度l 1=3m, l 2=5m,直径d=75mm ,两池水面高差H=2m ,最大超高h=1.8m ,沿程阻力系数λ=0.02,局部阻力系数:进口ζa =0.5,转弯ζb =0.2,出口ζc =1。
试求流量及管道最大超高断面的真空度。
解:列上下游水池的伯诺里方程00000l H h ++=+++
2
2
2
1280.020.50.21 3.83
20.07522l a b c l l h d g g g υυ
υλζζζ+⎛⎫⎛⎫=+++=⨯+++= ⎪ ⎪⎝
⎭⎝⎭
()
2
3.20m
0.0753.2014.13 l/s
4
Q A υπυ=
=
=⨯==⨯
=
列上游水池和最大超高处的伯诺里方程
()2
2
1 1 1
2
2
v
0 1.5 2.5223.20
1 1.5 1.8 2.5 3.11m
219.6
a
c
l l a b a c
p p l H h h h g
g g
d g P P P h g g
g
υ
υλζζρρυ
ρρ⎛⎫
++=+
+
+=++=+⨯
⎪⎝⎭
-=
=+
+=+⨯
=
7-16 水从密闭容器A ,沿直径d=25mm ,长l =10m 的管道流入容器B ,已知容器A 水面的相对压强p 1=2at ,水面高H 1=1m, H 1=1m, H 2=5m,沿程阻力系数λ=0.025,局部阻力系数:阀门ζa=4.0,弯头ζb =0.3,试求流量。
解: 1
12000l p H H h g
ρ+
+=+++
2
2
2
v 2
1030.0250.5430.3116.4
20.025222980001516.4
9800
24.373 m s 2.15 l l e b d h l g g g g
Q A υυ
υλζζζζυ
υυ⎛⎫⎛⎫=++++=⨯+++⨯+= ⎪ ⎪⎝⎭⎝⎭⨯+=+⇒=
===出
7-18 自密闭容器经两段串连管道输水,已知压力表读值p m =1at ,水头H=2m ,管长l 1=10m ,l 2=20m ,直径d 1=100mm, d 2=200mm ,沿程阻力系数λ1=λ2=0.03,试求流量并绘总水头线和测压管水头线。
解: 2
2
12
000 42M
l p H h g g
υυυρ++=+++=
2
22
2
2
2
2
211222122
2
1212151 0.5117222222f m l l d h h d g d g g g d g g υυυυυυλλ⎡⎤⎛⎫⎢⎥
=+==+-= ⎪⎢⎥⎝⎭⎣⎦
2
222269
12 1.846m s 58 l 2Q A g
υυυ=⇒===
7-21 在长为2 l ,直径为d 的管道上,并联一根直径相同,长为l 的支管(图中虚线),若水头H 不变,不计局部损失,试求并联支管前后的流量比。
解:并联前2
12alQ H =
并联后2
2
2
22
2452alQ Q al alQ H =⎪⎭
⎫ ⎝⎛+=
水头相等 22
2
2
4
52alQ
alQ =
26
.1581
2==
Q Q。
