2009秋博士线性系统
线性系统的时域分析法二阶系统

04
二阶系统的稳定性分析稳定性定义平衡状态
线性系统在平衡状态下的输出称为平衡状态输出。
稳定性
如果一个系统的平衡状态输出对于所有初始条件和输入都是稳定的,则称该系统是稳定 的。
稳定性判据
劳斯-赫尔维茨判据
数值法
数值法是通过数值计算来求解二阶系 统的方法。它通过将时间轴离散化, 将微分方程转化为差分方程,然后使 用迭代或直接计算的方法求解。
数值法具有简单易行和适用性广的优 点,适用于各种类型的二阶系统。但 是,对于某些特殊类型的系统,数值 法可能存在精度和稳定性问题。
实验法
实验法是通过实际实验来测试二阶系统的方法。它通过在系统中输入激励信号,然后测量系统的输出 响应,从而得到系统的性能参数。
线性系统的时域分析 法二阶系统
目录
CONTENTS
• 线性系统的时域分析法概述 • 二阶系统的基本概念 • 二阶系统的时域分析方法 • 二阶系统的稳定性分析 • 二阶系统的性能指标分析 • 二阶系统的应用实例
01
线性系统的时域分
析法概述
定义与特点
定义
时域分析法是一种通过在时间域 内对系统进行直接分析的方法, 用于研究系统的动态性能和响应 特性。
通过计算系统特征方程的根来判断系统 的稳定性。如果所有根都位于复平面的 左半部分,则系统稳定;如果有根位于 右半部分,则系统不稳定。
VS
Nyquist稳定判据
通过绘制系统的开环传递函数的Nyquist 曲线,判断曲线是否不穿越复平面的右半 部分,从而判断系统的稳定性。
稳定性分析方法
直接法
自动控制原理实验教程

Ui(S )
TS
(3) 阶跃响应: Uo(t) = K + 1 t
T
(t ≥ 0)
(4) 模拟电路图:如图 1.1-6 所示。
其中 K = R1 / R0 ; T = R0C
4
自动控制原理
第 1 章 线性系统的时域分析
比例积分环节
R1
C
Ui
R0
_
10K
信号输入端
反相器
10K _
R0 = R1 = 200K; C = 1uF 或 2uF
Ui(S)
1
Uo(S)
TS
(2) 传递函数: Uo(S) = 1
Ui(S) TS
(3) 阶跃响应: Uo(t) = 1 t (t ≥ 0)
T
(4) 模拟电路图:如图 1.1-4 所示。
图 1.1-3
其中 T = R0C
Ui
R0
信号输入端
积分环节 C
_
反相器
10K
10K
_
Uo
输出测量端
R0 = 200K; C = 1uF 或 2uF
图 1.1-4 3
自动控制原理
(5) 理想与实际阶跃响应曲线对照: ① 取 R0 = 200K;C = 1uF。
理想阶跃响应曲线
Uo 无穷
Uo(t)
1 Ui(t)
0 0.2s
t
② 取 R0 = 200K;C = 2uF。
第 1 章 线性系统的时域分析
实测阶跃响应曲线
Uo
10V
Uo(t)
1 Ui(t)
(5) 理想与实际阶跃响应曲线对照: ① 取 R0 = R1 = 200K;C = 1uF。
图 1.1-6
实验3 信号通过线性系统的特性分析

信号通过线性系统的特性分析一、 实验原理通过频谱分析可以看出,在一般情况下线性系统的响应波形与激励波形是不同的,即:信号在通过线性系统传输的过程中产生了失真。
线性系统引起的信号失真是由两方面的因素造成的,一是系统对信号中各频率分量的幅度产生不同程度的衰减,使响应各频率分量的相对幅度产生变化,造成幅度失真;一是系统对各频率分量产生的相移不与频率成正比,使响应各频率分量在时间轴上的相对位置产生变化,造成相位失真。
线性系统的幅度失真与相位失真都不产生新的频率分量。
对于非线性系统,由于其非线性特性,对于传输信号产生非线性失真,非线性失真可能产生新的频率分量。
如果信号在传输过程中不失真,则响应)(t r 与激励)(t e 波形相同,只是幅度大小或出现的时间不同。
激励与响应的关系可表示为)()(0t t ke t r -=为了实现信号无失真传输,线性系统应该满足什么条件?由式(3-1)得0)()(t j e j kE j R ωωω-=设)(t e 与)(t r 的傅里叶变换分别是)(ωj E 和)(ωj R ,则)()()(ωωωj E j H j R =比较式(3-2)与式(3-3),在信号无失真传输时,系统函数应为0)()()(t j j ke e j H j H ωωφωω-==因此,为了实现任意信号通过线性系统不产生波形失真,该系统应满足以下两个理想条件,如图3-1。
⎩⎨⎧-==0)()(t kj H ωωφω图3.1理想线性传输系统的系统函数的频率特性很显然,在传输有限频宽的信号时,上述的理想条件可以放宽,只要在信号占有频带范围内系统满足上述理想条件即可。
ω二、实验内容1.在Multism上实现低通滤波器的输入、输出频谱的测量及分析(1)绘制测量电路并做输入、输出信号的参数仿真(2)无失真传输线性输入、输出信号幅度频谱的仿真测量虚拟电压信号源设置参数为周期矩形信号,其中周期T=100μs,脉冲宽度τ=60μs,脉冲幅度Vp=5V;采用虚拟示波器测量滤波器输入、输出信号的时域波形,波特仪测量线性系统传输特性的频谱图,并记录输出波形。
桥梁博士 教程

• 如果拉索安装时没有张拉力,则拉索的重量按照等效节点荷 载原理施加到拉索的两端;
• 如果安装时有初张拉力,则自重只等效到非张拉端,而张拉 端的索力为初始张拉力。
• 优化计算和施工计算的拉索初始力都是指张拉端的索力,仅 由张拉设备控制,没有重力的效应。在非张拉端则根据张拉 端的内力考虑重力对索力的影响后计算得到。所以,对于拉 索单元,左端张拉与右端张拉得到的最终索力将是不同的。
单位约定
坐标系
平面杆系
❖总体坐标系:系统默认的坐标系,节点坐标、节 点位移以及反力均按总体坐标系输出。
X:水平向右为正 Y:垂直X轴向上为正 ❖单元局部坐标系:单元内力和应力均按单元局部 坐标系输出。 X:沿构件的纵轴线方向, 以左节点到右节点方 向为正 Y:垂直X轴向上为正
荷载方向
水平力:沿整体坐标的x方向向右为正; 竖直力:沿整体坐标的y方向向上为正; 弯 矩:依右手螺旋法则,垂直于整体坐标系向 外(向用户方向)为正
❖ 预应力混凝土:截面由混凝土、普通钢筋和预应力钢筋组成。
按和钢材组成。按全断面计算应力。 ❖ 钢构件:截面只由钢材组成。按全断面计算应力。 ❖ 拉索:截面只由钢筋或钢材组成。只有当构件需要调整其轴力
时,才有必要将其置为拉索单元。拉索单元只提供拉力,而不 会产生其它性质的内力。
• 结构重要性系数:在《公桥规》2004版中,根据结构的 重要性确定的内力扩大系数。
规范
• 用户选择计算适用的规范。由于《桥梁博士》3.0可以 按照多个规范进行验算,在输入单元材料、单元钢筋、 预应力材料等信息时,必须使之与适用的规范相对应
输入单元信息
• 用户可以使用右键菜单或“数据”下拉式菜单,切换到单元 输入窗口:
• 调束阶段号:用户填入需要产生调束信息的施工阶段号, 不填默认为全部阶段。在选中“生成调束信息”时有效。
信号与线性系统 白恩健书答案

第1章基本概念K第1章习题k1.1解:(1)x(t)为周期信号,周期为T=10。
(2)x(t)为非周期信号。
(3)x[n]为非周期信号。
(4)x[n]为周期信号,周期为N=2。
(5)x(t)为非周期信号。
(6)x[n]为周期信号,周期为N=2。
1.2解:(1)x(t)为功率信号。
(2)x(t)既不是能量信号也不是功率信号。
(3)x[n]为能量信号。
(4)x(t)为能量信号。
(5)x(t)为能量信号。
(6)x[n]为能量信号。
1.3略。
1.4略。
1.5(原题有误)一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统,即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解:提示:可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解:(1)因果、无记忆、非线性、时不变、BIBO稳定系统。
(2)因果、无记忆、线性、时变和BIBO稳定系统。
(3)因果、无记忆、线性、时变和非稳定系统。
(4)因果、记忆、线性、时不变和BIBO稳定系统。
(5)因果、无记忆、线性、时变和BIBO稳定系统。
(6)因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念(7)因果、无记忆、线性、时不变和BIBO稳定系统。
(8)非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解:(1)x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
(2)x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
(3)x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示:根据微积分的极限定义证明。
1.10解:(1)x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
(2)x(t)的响应为[2(t+e−t)−2]u(t)。
华东师范大学系统分析与集成博士研究生课程

华东师范大学系统分析与集成博士研究生课程专业名称:系统分析与集成课程编号:B0112010711003 课程名称:非线性控制系统理论与应用课程英文名称:Nonlinear Control-System Theory and Application学分: 3 周学时总学时:54课程性质:博士学位专业课适用专业:系统理论、系统分析与集成教学内容及基本要求:教学内容:1. 反馈系统分析(包括绝对稳定性,小增益定理,描写函数方法)2. 反馈线性化(包括输入-状态线性化,输入-输出线性化,状态反馈控制)、3. 微分几何方法(包括微分几何工具,输入-输出线性化,输入-状态线性化4. Lyapunov设计方法5. Backstepping方法6. 滑模控制7. 自适应控制。
基本要求:要求掌握解决问题的思想方法和技巧。
考核方式及要求:笔试。
学习本课程的前期课程要求:线性系统教材及主要参考书目、文献与资料:1. Hassan K. Khalil:《Nonlinear System (Second edition)》。
填写人:陈树中教授审核人:顾国庆教授课程编号:B0112010711004 课程名称:分布计算与分布式系统课程英文名称:Systems and Architecture of Distributed Databases学分: 3 周学时总学时:54课程性质:博士学位专业课适用专业:系统理论、系统分析与集成教学内容及基本要求:教学内容:本课程主要讨论分布式数据库系统的原理,技术和系统结构。
在第一部分,介绍DBMS的主要成分。
第二部分介绍经典的分布数据库系统理论和系统。
第三部分主要讨论Internet/Intranet时代的分布数据库理论和系统。
基本要求:学生在理解讲课内容的基础上,阅读大量相关论文,从而对基本知识有深入理解和对前沿技术有全面的了解。
考核方式及要求:考试。
学习本课程的前期课程要求:数据库系统基础,计算机网络基础教材及主要参考书目、文献与资料:1.周龙骧等:《分布式数据库管理系统实现技术》,科学出版社,1998。
重庆市2009年度优秀博士、硕士学位论文评选结果
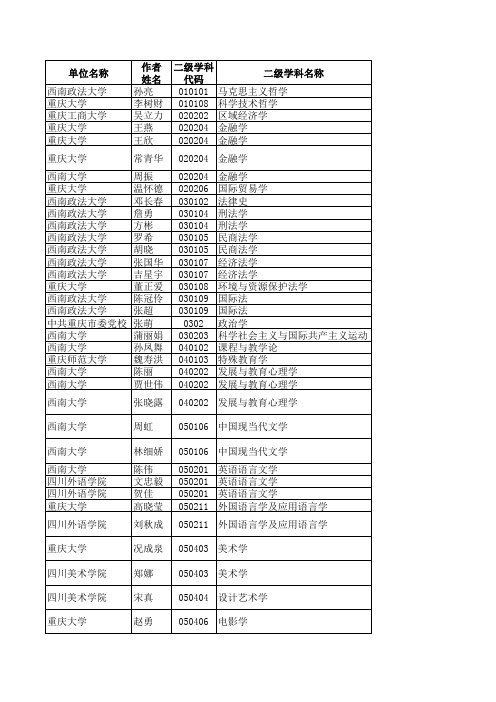
作者 二级学科 二级学科名称 姓名 代码 孙亮 010101 马克思主义哲学 李树财 010108 科学技术哲学 吴立力 020202 区域经济学 王燕 020204 金融学 王欣 020204 金融学 常青华 周振 温怀德 邓长春 詹勇 方彬 罗希 胡晓 张国华 吉星宇 董正爱 陈冠伶 张超 张萌 蒲丽娟 孙凤舞 魏寿洪 陈丽 贾世伟 张晓露 周虹 林细娇 陈伟 文忠毅 贺佳 高晓莹 刘秋成 况成泉 郑娜 宋真 赵勇 020204 金融学 020204 020206 030102 030104 030104 030105 030105 030107 030107 030108 030109 030109 0302 030203 040102 040103 040202 040202 金融学 国际贸易学 法律史 刑法学 刑法学 民商法学 民商法学 经济法学 经济法学 环境与资源保护法学 国际法 国际法 政治学 科学社会主义与国际共产主义运动 课程与教学论 特殊教育学 发展与教育心理学 发展与教育心理学
张明富 刘贤宁 杨新民 吴正茂 胡陈果 魏子栋 黄承志 傅瓦利 苏维词 郭跃 赵元莙 殷幼平 廖志华 鲁成 肖月华 严波 温志渝 魏彪 赵明富 温良英 王广军 邓兆祥 李辉 孙才新 周林 潘武 陈前斌 马大玮 胡中豫 王琳 冯辉宗 段其昌 周尚波 朱征宇 王国胤 郭平
人脸表情识别中的跟踪与识别方法研究 用于基因芯片和质谱数据分析的混合模型研究 重庆直辖十年主城住区建设研究系列之城市居住 空间分异研究 深埋洞室围岩分区破裂化机理及应用 岩体强度准则的可靠度分析 高庙子膨润土GMZ001胀缩变形与三向膨胀力研究 纤维模型中考虑剪切效应的RC结构非线性特征研 究 垃圾渗滤液中DOM特性分析及去除性能研究 多功能高层建筑火灾烟流运动特性预测研究 基于监控量测与数值分析的隧道围岩稳定性判定 方法研究 CFST拱桥稳定计算及相关参数分析 水沙数学模型在西江航道整治中的应用研究 碳纳米管为载体的燃料电池催化剂研究 循环载荷作用下岩石损伤演化规律研究 可扁平软管抽回油技术研究 滑坡灾变过程时空预测理论模型及应用 高液限土地区公路路堤修筑技术研究 基于虚拟试验技术的山区高等级公路危险路段 仿真识别研究 重庆主城区大气汞时空分布特征及人为排放研究 两步浸提法提取花椒籽皮油、仁油工艺研究 陡脉冲电场诱导肿瘤细胞凋亡及机理的研究 用于药物靶向释放的一种新型温度敏感纳米粒的 研究 添加膳食纤维对面团特性及面包品质的影响 柑橘属及其近缘植物基于AFLP分子标记的分类与 进化研究 家蚕30K蛋白LP7的分离纯化及功能初探 大鼠大脑皮质及皮质内有髓神经纤维的体视学研 究 PARP抑制对小鼠结肠癌CT26细胞侵袭影响及其机 制探讨 胶质瘤干细胞(GSCs)的分离与鉴定及GSCs基因组 甲基化状态的测定 APE1在线粒体DNA损伤修复中的作用及其线粒体定 位机制的研究 中国人群2型糖尿病与脂联素基因单核苷酸多态性 关系研究的Meta分析 组蛋白乙酰化酶亚型在小鼠心脏发育中的时空表 达 支气管动脉64层螺旋CT血管成像的临床应用研究 脑静脉系统64层螺旋CT血管成像及临床应用研究 LAVA整合ASSET在磁共振肝门脉成像的应用价值研 究
线性系统论文(三)最终修订版

摘要本文基于11阶天线伺服系统模型,并对其进行降阶。
用平衡实现方法降至3阶的模型,对降阶后的模型分别设计PID、超前-滞后控制器,并分析控制器参数对闭环系统的影响。
运用极点配置、LQR以及方法设计状态反馈控制器和运用LQR方法设计输出反馈控制器,然后结合内膜原理,使设计后的闭环系统能够在有参数扰动或者常数扰动下,能够实现对阶跃信号无静差地跟踪,基于3阶模型的闭环系统的阶跃响应的过渡时间在4s以内,并给出了相应的对应仿真结果。
然后用设计好的控制系统去控制11阶模型,使要求基于11阶模型的闭环系统其阶跃响应的过渡过程的时间在6s以内。
关键词:天线伺服系统 PID 超前-滞后极点配置 LQR H内膜原理∞第一章 基于平衡实现的系统降阶1.1平衡实现的原理一个模型的实现有无穷多种,其中阶次最小的实现被称为最小实现。
定理:实现是最小实现的充要条件是该实现是能控能观的。
定理:所有的传递函数()g s 的所有最小实现均代数等价。
定理:若{,,}{,,}A B C A B C 是同一个传递函数的两个能控能观实现。
,,,C O C O W W W W 分别为上述实现的能控Gramian 矩阵和能观Gramian 矩阵,则C O C O W W W W 与相似并且所有特征根均为正数。
定理: 若{,,}A B C 为一任意一最小实现,其Hankel 奇异值为22212,,,n σσσ,则存在一个实现{,,}A B C 满足12{,,,}C O n W W diag σσσ==∑=,该实现称为平衡实现。
1.2平衡实现的系统降阶过程由上平衡实现的Hankel 奇异值,若12k σσσ≥≥≥ 并且121,,,,,k k n σσσσσ+012(,)C W W diag ==∑∑ 且对应的平衡实现为: []111121111222122222x A A x b x u y c c x A A x b x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 则我们可以把系统降阶为:1111111x A x b u y c x =+=本次设计六十五米大口径天线伺服系统的模型如下:由于Matlab里有求平衡实现的函数balreal,故可以直接调用,求出平衡实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共3页
2)试判断能否通过有限个输出序列 观测状态 ?能否仅通过 观测状态 ?能否仅通过 观测状态 ?(5分)
8.(10分)试证明: 能控,则 为系统 的一个镇定律,其中 , 为一适当的正数。
10
10
10
100分
1.(15分)给定二维线性定常系统
若对两个不同初始状态的响应分别为
1)、 时,
2)、 时,
试据此确定系统矩阵 。
2.(15分)如果 是能观测的, 为半正定阵, 满足 ,那么 是否能观测?若是,试证明之,若不是,试举例说明。
3.(15分)设有渐近稳定的SISO线性定常系统
其中 ,P为如下Lyapunov方程
3)试证明,如果这两个实现都是能观的,那么,系统1位于前向通道和系统2位于反馈通道组成的反馈结构能观的充要条件是 和 互质。(3分)
6.(10分)已知线性系统
试设计全维观测器,使观测器的极点位于 。
7.(10分)设有一离散系统
1)能否找到一个控制序列 ,使该系统在有限时间内从任意初始状态到达原点?若不能,试阐述理由;若能,试求出控制序列 (5分)
的对称正定解阵。试证:
第2页
共3页
4.(15分)证明:若线性定常系统
是内部稳定的,则必是外部稳定的。
5.(10分)设 是传递函数 的 阶实现, 的阶数也等于 。
1)试证明,如果这两个实现都是能控的,那么,系统1后接系统2的串联组合能控的充要条件是 和 互质;(4分)
2)试证明,如果这两个实现都是能观的,那么,系统1和系统2的并联组合能观的充要条件是 和 互质;(3分)
第1页
共3页
哈尔滨工业大学
二OO九年博士研究生考试试题
考试科目:____线性系统理论______考试科目代码:[ 2041 ]
报考专业:____控制科学与工程_____是否允许使用计算器:[是]
考生注意:答案务必写在答题纸上,并标明题号。答在试题上无效。
题号
1
2
3
4
5
6
7
8总分Βιβλιοθήκη 分数1515
15
15
10
