1高中必修一分数指数幂知识点+例题全面

合集下载

指数及指数函数知识点总结及经典例题

高中数学必修1知识点总结—指数及指数函数1、根式na （一般的，如果n x a =，那么x 叫做a 的n 次方根，其中*1,n n N >∈且.）35325325n n n ⎧=⎪⎨-=-⎪⎩正数的次方根是正数如当是奇数时，负数的次方根是负数如20,n a n an ⎧>±⎪⎨⎪⎩正数的次方根有个，且互为相反数如：则次方根为当是偶数时，负数没有偶次方根0的任何次方根都是0，记作0n2、nna的讨论 n nn a a =当是奇数时，；,0,0n n a a n a a a a ≥⎧==⎨-≤⎩当是偶数时，（2）分数指数幂的概念）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mnmna a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：11()()(0,,,m mmnnnaa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义．义．注意口诀：底数取倒数，指数取相反数．底数取倒数，指数取相反数．（3）分数指数幂的运算性质）分数指数幂的运算性质①(0,,)rsr saa aa r s R +⋅=>∈ ②()(0,,)r s rsa a a r s R =>∈③()(0,0,)rr rab a b a b r R =>>∈一、指数计算公式：()Q s r a ∈>,,0_____=⋅s r a a ________=sraa _____)(=s r a ______)(=r ab )1,,0_______(>∈>=*n N n m a anm，________=n na 练习计算下列各式的值：计算下列各式的值：（1）)4()3)((636131212132b a b a b a ÷- （2）()322175.003129721687064.0+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛---（3）421033)21(25.0)21()4(--⨯+-- （4）33)3(625π-+-2．已知31=+-x x ，则=+-22x x 已知23=a,513=b，则=-ba 23＝____________. 3. 若21025x x =，则10x x-等于_________________【2.1.2】指数函数及其性质（4）指数函数）指数函数函数名称函数名称指数函数指数函数定义定义函数(0x y a a =>且1)a ≠叫做指数函数叫做指数函数图象图象1a >01a <<定义域定义域 R 值域值域(0,)+∞过定点过定点图象过定点(0,1)，即当0x=时，1y =．奇偶性奇偶性非奇非偶非奇非偶单调性单调性在R 上是增函数上是增函数在R 上是减函数上是减函数函数值的函数值的变化情况变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对变化对图象的影响图象的影响在第一象限内，a 越大图象越高；在第二象限内，a 越大图象越低．越大图象越低．题型1、求函数经过的点 1、2)(f 1-=+x a x )10(≠>a a 且过定点______________2、函数y=4+a x -1的图象恒过定点P 的坐标是________________3.已知指数函数图像经过点)3,1(-p ，则=)3(f题型2、图像问题1.下列说法中：下列说法中：①任取x ∈R 都有3x >2x ； ②当a >1时，任取x ∈R 都有a x >a －x ；③函数y =(3)－x 是增函数；④函数y =2|x |的最小值为1 ；⑤在同一坐标系中，y =2x 与y =2－x 的图象对称于y 轴。

高中数学必修一指数运算性质及指数函数

第8课时指数运算性质及指数函数知识点一分数指数幂给定正实数a ，对于任意给定的整数m ，n (m ，n 互素)，存在唯一的正实数b ，使得b n ＝a m，我们把b 叫作a 的mn次幂，记作b ＝mn a .指数运算性质一般地，在研究实数指数幂的运算性质时，约定底数为大于零的实数.当a >0，b >0时，有： (1)a m ·a n ＝；(2)(a m )n ＝；(3)(ab )n ＝，其中m ，n ∈R . 例1 计算下列各式(式中字母都是正数).(1)10.5233277(0.027)21259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭；2)211511336622(2)(6)(3)a b a b a b ÷－－；2152.530.064-0⎡⎤-π.⎢⎥⎣⎦（）知识点二指数函数一般地，函数叫作指数函数，其中x 是自变量，函数的定义域是R .注意①底数是大于0且不等于1的常数；②指数函数的自变量必须位于指数的位置上；③a x 的系数必须为1；④指数函数等号右边不会是多项式，如y ＝2x ＋1不是指数函数. 知识点三指数函数的图像和性质例2 (1)下列函数中是指数函数的是________.(填序号) ①y ＝2·(2)x ；②y ＝2x －1；③y ＝⎝⎛⎭⎫π2x；④y ＝13x-；⑤y ＝13x . (2)若函数y ＝(a 2－3a ＋3)·a x 是指数函数，则实数a ＝________. (3)若函数y ＝(2a －3)x 是指数函数，则实数a 的取值范围是________. 例3 (1)函数y ＝a x －1a(a >0，且a ≠1)的图像可能是( )(2)函数f (x )＝1＋a x －2(a >0，且a ≠1)恒过定点________.(3)已知函数y ＝3x 的图像，怎样变换得到y ＝⎝⎛⎭⎫13x ＋1＋2的图像？并画出相应图像.跟踪训练3 (1)已知函数f (x )＝4＋a x ＋1(a >0，且a ≠1)的图像经过定点P ，则点P 的坐标是( ) A.(－1,5) B.(－1,4) C.(0,4) D.(4,0) 例4 比较下列各题中两个值的大小. (1)1.7－2.5，1.7－3；(2)1.70.3，1.50.3；(3)1.70.3，0.83.1.跟踪训练4 比较下列各题中的两个值的大小.(1)0.8－0.1，1.250.2；(2)⎝⎛⎭⎫1π－π，1；(3)0.2－3，(－3)0.2.例5 (1)不等式4x <42－3x的解集是________.(2)解关于x 的不等式：a 2x ＋1≤a x －5(a >0，且a ≠1).例6 判断f (x )＝2213x x⎛⎫ ⎪⎝⎭－的单调性，并求其值域.反思感悟研究y ＝a f (x )型单调区间时，要注意a >1还是0<a <1.当a >1时，y ＝a f (x )与f (x )的单调性相同.当0<a <1时，y ＝a f (x )与f (x )的单调性相反.跟踪训练6 求函数y ＝223x x a ＋－的单调区间.课后作业1.化简238的值为( ) A.2 B.4 C.6 D.82.下列根式与分数指数幂的互化正确的是( ) A.－x ＝12()x －(x >0) B.1263=y y (y <0) C.33441=xx ⎛⎫⎪⎝⎭－(x >0) D.133=x x －(x ≠0) 3.式子a 2a ·3a 2(a >0)经过计算可得到( ) A.a B.1a6 C.5a 6 D.6a 5 4.计算124－⎝⎛⎭⎫12－1＝________.5.下列各函数中，是指数函数的是( ) A.y ＝(－3)x B.y ＝－3x C.y ＝3x －1D.y ＝⎝⎛⎭⎫13x6.若函数y ＝(2a －1)x (x 是自变量)是指数函数，则a 的取值范围是( ) A.a >0，且a ≠1 B.a ≥0，且a ≠1 C.a >12，且a ≠1 D.a ≥127.函数f (x )＝a x －b的图像如图所示，其中a ，b 均为常数，则下列结论正确的是( )A.a >1，b <0B.a >1，b >0C.0<a <1，b >0D.0<a <1，b <08.函数y ＝a x －3＋3(a >0，且a ≠1)的图像恒过定点_________________________________. 9.函数f (x )＝1－2x ＋1x ＋3的定义域为________. 10.下列各式中成立的是( )A.⎝⎛⎭⎫m n 7＝177n m B.12(－3)4＝3－3 C.4x 3＋y 3＝34()x y + D.39＝3311.下列大小关系正确的是( )A.0.43<30.4<π0B.0.43<π0<30.4C.30.4<0.43<π0D.π0<30.4<0.43 12.方程42x －1＝16的解是( )A.x ＝－32B.x ＝32 C.x ＝1 D.x ＝213.函数f (x )＝2112x ⎛⎫⎪⎝⎭－的递增区间为( )A.(－∞，0]B.[0，＋∞)C.(－1，＋∞)D.(－∞，－1) 14.函数y ＝⎝⎛⎭⎫12x，y ＝2x ，y ＝3x的图像(如图)分别是________.(用序号作答)15.设0<a <1，则关于x 的不等式22232223x x x x aa －＋＋－＞的解集为________.16.已知a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系是( ) A.a >b >c B.b >a >c C.c >b >a D.c >a >b 17.已知函数f (x )＝3x －⎝⎛⎭⎫13x ，则f (x )( ) A.是奇函数，且在R 上是增函数 B.是偶函数，且在R 上是增函数 C.是奇函数，且在R 上是减函数 D.是偶函数，且在R 上是减函数18.计算：⎝⎛⎭⎫2590.5－⎝⎛⎭⎫27813-－⎝⎛⎭⎫－780＋160.25＝__________________________________.19.已知函数f (x )＝2|x －a |(a 为常数)，若f (x )在区间[1，＋∞)上是增函数，则a 的取值范围是________. 20.已知函数f (x )＝4x －14x ＋1.(1)解不等式f (x )<13；(2)求函数f (x )的值域.能力提升已知定义在R 上的函数f (x )＝a ＋14x ＋1是奇函数.(1)求a 的值；(2)判断f (x )的单调性(不需要写出理由)；(3)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求实数k 的取值范围.。

苏教版高中数学必修一知识讲解_分数指数幂_提高

分数指数幂：：【学习目标】理解分数指数的含义，了解实数指数幂的意义，理解n 次方根，n 次根式的概念，熟练掌握用根式与分数指数幂表示一个正实数的算术根；能运用有理指数幂的运算性质进行运算和化简，会进行根式与分数指数幂的相互转化。

【要点梳理】要点一、整数指数幂 1．整数指数幂的概念()()),0(1010*Z*n a a a a a Z n a a a a nn an n ∈≠=≠=∈⋅⋅⋅=-个2．运算法则（1）nm nma a a +=⋅；（2）()mn nma a =；（3）()0≠>=-a n m a aa nm n m ，；（4）()mm mb a ab =.要点二、根式 1．n 次方根的定义：若x n=y(n ∈N *，n>1，y ∈R)，则x 称为y 的n 次方根.n 为奇数时，正数y 的奇次方根有一个，是正数，记为n y ；负数y 的奇次方根有一个，是负数，记为ny ；零的奇次方根为零，记为00=n ；n 为偶数时，正数y的偶次方根有两个，记为；负数没有偶次方根；零的偶次方根为零，记为0=.2．两个等式（1）当1n >且*n N ∈时，na =；（2）⎩⎨⎧=)(||)(,为偶数为奇数n a n a a n n要点诠释：①要注意上述等式在形式上的联系与区别；②计算根式的结果关键取决于根指数的取值，尤其当根指数取偶数时，开方后的结果必为非负数，可先写成||a 的形式，这样能避免出现错误．要点三、分数指数幂为避免讨论，我们约定a>0，n ，m ∈N *，且mn为既约分数，分数指数幂可如下定义： 1na =m m na ==-1m nm naa=要点四、有理数指数幂 1．有理数指数幂的运算性质()Q b a ∈>>βα,00，，(1);a a aαβαβ+⋅=(2)();a a αβαβ= (3)();ab a b ααα=当a>0，p 为无理数时，a p是一个确定的实数，上述有理数指数幂的运算性质仍适用. 要点诠释：(1)根式问题常利用指数幂的意义与运算性质，将根式转化为分数指数幂运算；(2)根式运算中常出现乘方与开方并存，要注意两者的顺序何时可以交换、何时不能交换.如2442)4()4(-≠-；(3)幂指数不能随便约分.如2142)4()4(-≠-. 2.指数幂的一般运算步骤有括号先算括号里的；无括号先做指数运算．负指数幂化为正指数幂的倒数．底数是负数，先确定符号，底数是小数，先要化成分数，底数是带分数，先要化成假分数，然后要尽可能用幂的形式表示，便于用指数运算性质．在化简运算中，也要注意公式：a2－b2＝（a－b）（a＋b），（a±b）2＝a2±2ab＋b2，（a ±b）3＝a3±3a2b＋3ab2±b3，a3－b3＝（a－b）（a2＋ab＋b2），a3＋b3＝（a＋b）（a2－ab＋b2）的运用，能够简化运算.【典型例题】类型一、根式例1.计算：（1+.（2【答案】【解析】对于（1）需把各项被开方数变为完全平方形式，然后再利用根式运算性质求解.对于（2），则应分子、分母同乘以分母的有理化因式.（12|-|22-（2）（211=【点评】对于多重根式的化简，一般是设法将被开方数化成完全n次方，再解答，或者用整体思想来解题.化简分母含有根式的式子时，将分子、分母同乘以分母的有理化因式即可，如本例（2）的分子、分母中同乘以1).举一反三：【变式1】化简：（1；（2|3) x<【答案】（11；（2）22(31),4(13).x xx---<<⎧⎨-≤<⎩。

高一数学指数与指数幂的计算题及答案解析

高一数学知识点幂函数
定义：
形如y=x^a(a为常数)的函数，即以底数为自变量幂为因变量，指数为常量的函数称为幂函数。定义域和值域：
当a为不同的数值时，幂函数的定义域的不同情况如下：如果a为任意实数，则函数的定义域为大于 0的所有实数;如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根[据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;如果同时q为奇数，则函数的定义域为不等于0的所有实数。当x为不同的数值时，幂函数的值域的不同情况如下：在x大于0时，函数的值域总是大于0的实数。在x小于0时，则只有同时q为奇数，函数的值域为非零的实数。而只有a为正数，0才进入函数的值域
定义
一般地，对于函数f(x) (1)如果对于函数定义域内的任意一个x，都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数。 (2)如果对于函数定义域内的任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。 (3)如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。
高一数学指数与指数幂的计算题（一） 1.将532写为根式，则正确的是( ) A.352 B.35 C.532 D.53 解析：选D.532=53. 2.根式 1a1a(式中a>0)的分数指数幂形式为( ) A.a-43 B.a43 C.a-34 D.a34 解析：选C.1a1a= a-1• a-1 12= a-32=(a-32)12=a-34. 3. a-b 2+5 a-b 5的值是( ) A.0 B.2(a-b) C.0或2(a-b) D.a-b 解析：选C.当a-b≥0时，原式=a-b+a-b=2(a-b); 当a-b<0时，原式=b-a+a-b=0. 4.计算：(π)0+2-2×(214)12=________. 解析：(π)0+2-2×(214)12=1+122×(94)12=1+14×32=118. 答案：118

人教版高一数学必修1第16课时分数指数幂与幂的运算(含解析)

解析：设4x＝6y＝1442＝t，则4＝t ，6＝t ，144＝t ，∴36＝t .又144＝4×36，∴t ＝t ·t ，即＝＋，选D.
6．已知0<x<1，x2－3x＋1＝0，则x －x 的值为()
A．1 B．－1
C．1或－1 D．－
答案：B
解析：∵x2－3x＋1＝0，∴x2＋1＝3x，∵0<x<1，∴两边除以x，得x＋x－1＝3，∴(x －x )2＝x＋x－1－2＝3－2＝1.又0<x<1，∴x －x ＝－＝ <0，∴x －x ＝－1.故选B.
∵ ＝(x3＋y3) ≠(x＋y) ，∴C错；
∵ ＝＝3 ，∴D正确，故选D.
4．式子 (a>0)经过计算可得()
A．aB．－
C. D.
答案：D
解析：原式＝＝a ＝a ＝ .
5．设x，y，z∈R，xyz≠0，且4x＝6y＝144z，则()
A. ＝＋ B. ＝＋
C. ＝＋ D. ＝＋
答案：D
＝2－4× ＋10(2＋ )－10
＝21.
(3)(7＋4 ) －81 ＋32 －2× ＋ × －1
＝[(2＋ )2] －(34) ＋(25) －2×(2－3) ＋2 ×(22)
＝2＋－＋8－8＋2
＝4.
11．(13分)已知x ＋x ＝3，计算：
(1)x－x－1；
(2) .
解：(1)将x ＋x ＝3两边平方，得x＋x－1＋2＝32，即x＋x－1＝7，
解析：原式＝2 · · · ·…· ＝2 ·…· ＝2 ＝2－ .
13．(15分)设的整数部分为x，小数部分为y，求x2＋ xy＋的值．
解：因为＝＝＝2＋，

高一数学上册指数函数知识点及练习题含答案

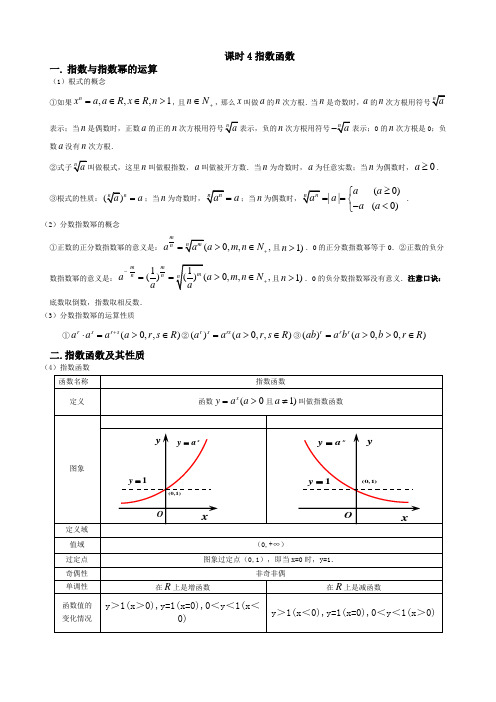
课时4指数函数一. 指数与指数幂的运算（1）根式的概念 ①如果,,,1nxa a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n表示；当n 是偶数时，正数a 的正的nn次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当na =；当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m naa m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质（4）指数函数a 变化对图象影响在第一象限内，a 越大图象越高，越靠近y 轴；在第二象限内，a 越大图象越低，越靠近x 轴．在第一象限内，a 越小图象越高，越靠近y 轴；在第二象限内，a 越小图象越低，越靠近x 轴．三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析：A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析：当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=［f(x)］n D.f ［(xy)n ］=［f(x)］n ［f(y)］n (n ∈N *) 解析：易知A 、B 、C 都正确. 对于D,f ［(xy)n］=a(xy)n,而［f(x)］n·［f(y)］n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析：a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析：令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析：因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明：∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.［1,+∞)C.(0,+∞)D.(-∞,+∞)解析：当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1］;当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析：可利用函数图象的对称性来判断两图象的关系.10.当x ∈［-1,1］时,函数f(x)=3x -2的值域为_______［-35,1］___________. 解析：f(x)在［-1,1］上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析：(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩［2,+∞］=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈［-3,2］的最大值和最小值. 解：设2-x =t,由x ∈［-3,2］得t ∈［41,8］,于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解：∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.［1,2］B.［2,3］C.(-∞,2]D.［2,+∞)解析：因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈［2,+∞)上递增,故所求的递增区间为［2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.［-1,+∞)B.［-1,63) C.［0,+∞)D.(0,63］解析：由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=［f(x)-1］2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈［1,9］. ∴所求值域为［-1,63］.2.1指数函数练习1．下列各式中成立的一项（）A ．7177)(m n mn= B ．31243)3(-=-C ．43433)(y x y x +=+D ．3339=2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 6B ．a -C ．a 9-D ．29a3．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确的是（） A ．f (x +y )=f(x )·f (y ) B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)(+∈=N n y f x f xy f n n n4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数x a y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于（）A ．251+B ．251+- C ．251± D ．215± 6．当a ≠0时，函数y ax b =+和y b ax =的图象只可能是（）7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围（）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．函数22)21(++-=x x y 得单调递增区间是（）A ．]21,1[-B ．]1,(--∞C ．),2[+∞D ．]2,21[10．已知2)(xx e e x f --=，则下列正确的是（）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 11．已知函数f (x )的定义域是（1，2），则函数)2(x f 的定义域是. 12．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点. 三、解答题：13．求函数y x x =--1511的定义域.14．若a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）证明f (x )在(－∞，+∞)上是增函数.16．函数f(x)＝a x(a>0，且a ≠1)在区间[1,2]上的最大值比最小值大，求a 的值．参考答案一、DCDDDAADDA二、11．(0,1)；12．(2，－2)；三、13．解：要使函数有意义必须：∴定义域为：{}x x R x x ∈≠≠且01,14．解：rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+，其中10,10<<<<cbc a . 当r ＞1时，1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr，所以a r +b r ＜c r；当r ＜1时，1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ，所以a r +b r ＞c r . 15．解：(1)是奇函数.(2)设x 1＜x 2，则1111)()(221121+--+-=-x x x x a a a a x f x f 。

高中数学必修一《指数幂与运算》精选练习(含详细解析)

高中数学必修一《指数幂与运算》精选练习（含详细解析）一、选择题1.若(1-2x有意义,则x的取值范围是( )A.x∈RB.x≠0.5C.x>0.5D.x<0.52化简[的结果为( )A.5B.C.-D.-53.+(-1)-1÷0.75-2+= ( )A. B. C.- D.-4.化简()4·()4的结果是( )A.a16B.a8C.a4D.a25设-=m,则= ( )A.m2-2B.2-m2C.m2+2D.m2二、填空题6.化简= .7已知a>0,化简-= .三、解答题8.(10分)将下列根式化为分数指数幂的形式.(1)(a>0).(2).(3)((b>0).9.(10分)已知+=3,求下列各式的值:(1)a+a-1. (2)a2+a-2.参考答案与解析1选D.将分数指数幂化为根式,可知需满足1-2x>0,解得x<0.5.2选B.[=(===.3选A.原式=-1÷+=-1÷+=-+=.4选C.原式=()4·()4=()4·()4=a2·a2=a4.5选 C.将-=m平方得(-)2=m2,即a-2+a-1=m2,所以a+a-1=m2+2,即a+=m2+2⇒=m2+2.6【解析】==a+b.答案:a+b7【解题指南】利用完全平方公式展开后合并同类项计算.【解析】因为a>0,所以-=-=4.答案:48【解析】(1)原式====.(2)原式======.(3)原式=[(==.9【解析】(1)因为+=3,所以(+)2=a+a-1+2=9,所以a+a-1=7.(2)因为a+a-1=7,所以(a+a-1)2=a2+a-2+2=49,所以a2+a-2=47.。

人教A版必修1指数与指数幂的运算知识点总结与典例讲解

指数与指数幂的运算知识点总结与例题讲解本节知识点（1）整数指数幂; （2）根式; （3）分数指数幂; （4）有理数指数幂; （5）无理数指数幂. 知识点一整数指数幂1.正整数指数幂的定义:an na a a a 个⋅⋅=,其中∈n N*. 2.正整数指数幂的运算法则: （1）nm nmaa a +=⋅(∈n m ,N*);（2）nm nma a a -=÷（,,0n m a >≠且∈n m ,N*）;（3）()mn nma a=(∈n m ,N*);（4）()mm mb a ab =(∈m N*);（5）m m mb a b a =⎪⎭⎫ ⎝⎛（,0≠b ∈m N*）.3.两个规定（1）任何不等于零的数的零次幂都等于1.即()010≠=a a .零的零次幂没有意义.（2）任何不等于零的数的n -（n 为正整数）次幂,等于这个数的n 次幂的倒数.即:()01≠=-a a a nn . 零的负整指数幂没有意义. 知识点二根式的概念及其性质 1.n 次方根（1）定义一般地,如果a x n=（1>n 且∈n N*）,那么x 叫做a 的n 次方根. （2）性质:①当n 为奇数时,正数的n 次方根是一个正数,负数的n 次方根是一个负数,这时,a 的n 次方根用na 表示;②当n 为偶数时,正数的n 次方根有两个,这两个数互为相反数,表示为na ±.负数没有偶次方根;③0的任何次方根都是0,记作00=n.2.根式的定义形如na （1>n 且∈n N*）的式子叫做根式,其中n 叫做根指数,a 叫做被开方数.对根式na 的理解,要注意以下几点: （1）1>n 且∈n N*; （2）当n 为奇数时,∈a R ; （3）当n 为偶数时,a ≥0.根式na （1>n 且∈n N*）的符号的确定:由n 的奇偶性和被开方数a 的符号共同确定. （1）当n 为奇数时,na 的符号与a 的符号相同; （2）当n 为偶数时,a ≥0,na 为非负数. 3.根式的性质: （1）()a a nn=;（2）对于n na ,当n 为奇数时,a a nn=;当n 为偶数时,()()⎩⎨⎧≤-≥==00a a a a a a nn . ()nna 与nn a 的联系与区别:（1）对于()nna ,当n 为奇数时,∈a R ;当n 为偶数时,a ≥0.而对于nn a ,是一个恒有意义的式子,不受n 的奇偶性的限制,但式子的值受到n 的奇偶性的限制. （2）当n 为奇数时,()=nna a a nn =.知识点三分数指数幂1. 规定正数的正分数指数幂的意义是nm nm a a =（0>a ,∈n m ,N*,且1>n ）于是在条件0>a ,∈n m ,N*,且1>n 下,根式都可以写成分数指数幂的形式.2. 正数的负分数指数幂的意义与负整数指数幂的意义相仿,规定nmnm nm aaa11==-（0>a ,∈n m ,N*,且1>n ）3. 0的正分数指数幂等于0,0的负分数指数幂没有意义. 对分数指数幂的理解:（1）分数指数幂nm a 不能理解为nm个a 相乘,它是根式的一种新的写法; （2）分数指数nm不能随意约分. 如()()214233-≠-,事实上,()()424233-=-,式子是有意义的;而()3321-=-在实数范围内是没有意义的.（3）在保证相应的根式有意义的前提下,负数也存在分数指数幂.如上面提到的()()424233-=-,但()()434355-=-没有意义.所以对于分数指数幂nm a ,当a ≤0时,有时有意义,有时无意义.因此,在规定分数指数幂的意义时,要求0>a . 知识点四有理数指数幂规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数. 整数指数幂的运算性质对于有理数指数幂同样适用: （1）sr s r a a a +=⋅（,0>a s r ,∈Q ）;（2）()rs sra a=（,0>a s r ,∈Q ）;（3）()rr rb a ab =（0,0>>b a r ∈Q ）.有理数指数幂的运算还有如下性质: （4）sr sraa a -=÷（,0>a s r ,∈Q ）;（5）r r r b a b a =⎪⎭⎫ ⎝⎛（0,0>>b a r ∈Q ）.常用结论:（1）当0>a 时,0>ba ; （2）若,0≠a 则10=a ;（3）若sr a a =（0>a ,且1≠a ）,则s r =;（4）乘法公式适用于分数指数幂.如b a b a b a b a -=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+22122121212121（0,0>>b a ）.知识点五无理数指数幂一般地,无理数指数幂αa （0>a ,α是无理数）是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.知识点六运用公式进行指数幂的运算（条件求值）常用公式:（1）平方差公式 ()()b a b a b a -+=-22.（2）完全平方公式 ()()2222222,2b ab a b a b ab a b a +-=-++=+.（3）立方和公式 ()()2233bab a b a b a +-+=+. （4）立方差公式 ()()2233bab a b a b a ++-=-.（5）完全立方和公式 ()3223333b ab b a a b a +++=+.（6）完全立方差公式 ()3223333b ab b a a b a -+-=-.常用公式变形:（1）()ab b a b a 2222-+=+,()ab b a b a 2222+-=+.（2）211222-⎪⎭⎫ ⎝⎛+=+x x x x ,211222+⎪⎭⎫⎝⎛-=+x x x x .或者写成()22122-+=+--x x x x ,()22122+-=+--x x x x .（3）⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+b b a a b a b a b a 212121213213212323;⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-b b a a b a b a b a 212121213213212323.例题讲解例1. 已知32121=+-x x ,求32222323++++--x x x x 的值.分析:采用整体思想方法,对所求式子进行合理变形,然后把条件整体代入求值.本题用到的公式和结论有:()22122-+=+--x x x x ;()()1112121121213213212323-+⎪⎭⎫ ⎝⎛+=+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+------x x x x x x x x x x xx . 解:∵32121=+-xx∴92122121=++=⎪⎭⎫ ⎝⎛+--x x x x ,∴71=+-x x . ∴()4727222122=-=-+=+--x x x x .()()181731121213213212323=-⨯=+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+----x x x x x x xx ∴52502034721832222323==++=++++--x x x x .例2. 已知22121=+-a a ,求下列各式的值:（1）1-+a a ; （2）22-+a a ; （3）22--a a .分析:在求22--a a 的值时,直接入手比较困难,我们可以先求出()222--a a 的值,然后在进行开平方运算. 解:（1）∵22121=+-aa∴42122121=++=⎪⎭⎫ ⎝⎛+--a a a a ,∴21=+-a a ; （2）()222222122=-=-+=+--a a a a ;（3）∵()()04242222222=-=-+=---a a a a∴022=--a a .例3. 已知41=+-x x ,其中10<<x ,求xx x x 122+--的值.分析:要学会根式与分数指数幂的相互转化,在转化时要注意:根指数是分数指数的分母,被开方数（或式）的指数是分数指数的分子.解:∵41=+-x x∴4222121=-⎪⎭⎫ ⎝⎛+-x x ,∴622121=⎪⎭⎫ ⎝⎛+-x x ,∴62121=+-x x . ()1424222122=-=-+=+--x x x x∴()()19241442222222=-=-+=---x x x x∵10<<x ,∴22-<x x ,∴3819222-=-=--x x .∴24638121212222-=-=+-=+----x x x x x x x x . 例4. （1）已知42121=+-aa ,求21212323----aa a a 的值;（2）已知9,12==+xy y x ,且y x <,求21212121yx y x +-的值;解:（1）∵42121=+-aa∴212212142=++=⎪⎭⎫ ⎝⎛+--a a a a ,∴142161=-=+-a a . ∴()15114111212112121212132132121212323=+=++=-++⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=----------a a a a a a a a a a a a aa a a ; （2）∵9,12==+xy y x∴()()3192129212222221212212122121221212121=+-=++-+=++-+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛+-xy y x xy y x xy y x xy y x y x y x y x y x∵y x <,∴2121y x <,∴021212121<+-yx y x∴333121212121-=-=+-yx y x . 例5. 已知3232+=a ,求31311--++aa a a 的值.分析:借助于分式的性质. 解:∵3232+=a ∴3232113232-=+==-a a,()34732223234+=+=⎪⎭⎫⎝⎛=a a .∴()132323431313113131311++=⎪⎭⎫⎝⎛++=++-----a aa a a a a a a aa aa ()3333333333913232347=++=++=++-++=.解法二:∵3232+=a∴113232313132323131313133133131311-+=+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++--------a a a a a a a a a a a a aa a a 313232132132113232=--++=-+++=-+=aa .例6. （1）当22,22-=+=y x 时,求⎪⎭⎫ ⎝⎛++⋅⎪⎭⎫ ⎝⎛----323132343132y y x x y x 的值;（2）若122-=xa,求xx xx aa a a --++33的值. 分析: 结论对于二次根式C B A ±,若C B A 22-是完全平方数,则C B A ±也是完全平方数. 本题中,22+=x ,被开方数22+不是完全平方数,所以x 不能化简,当确有()222222+=+=x .解:（1）∵22,22-=+=y x∴12331332323132343132------=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++⋅⎪⎭⎫ ⎝⎛-y x y x y y x x y x ()22122222221222+=+-+=--+=; （2）∵122-=x a∴()()()()1122223333-+=++-+=++=++--------xx xx x x x x x x x x x xx x a a aa a a a a a a a a a a a a 1121121122--+-=-+=xx a a 12211212-=-++-=. 另解:解例5的解法一.题型一整数指数幂的运算例7. 已知a x x =+-22（a 为常数,且∈x Z ）,求x x -+88的值.分析:因为()()()()x x x x x x x x x x 22333321222222288-----+-+=+=+=+,所以先由条件a x x =+-22求出x x 2222-+的值.完全立方和公式 ()3223333b ab b a a b a +++=+.解法一:∵a x x =+-22∴()2222222222-=-+=+--a x x x x∴()()()()x x x x x x x x x x 22333321222222288-----+-+=+=+=+()()a a a a a a 3312322-=-=--=.解法二:（完全立方和公式） ∵a x x =+-22∴()3322a x x =+-,展开得:()()()()3322322232232a x x x x x x =+⨯⨯+⨯⨯+---.整理得:()382238a x x x x =+++--,∴3838a a x x =++-. ∴a a x x 3883-=+-.例8. 已知3101=+-x x ,则=--22x x _________. 解:∵3101=+-x x ∴()9822310222122=-⎪⎭⎫ ⎝⎛=-+=+--x x xx ∴()()816400498242222222=-⎪⎭⎫ ⎝⎛=-+=---x x xx ∴98081640022±=±=--x x . 解法二分析:使用平方差公式得()()1122----+=-x x x x x x . 解法二:∵3101=+-x x ∴()()9644310422121=-⎪⎭⎫ ⎝⎛=-+=---x x xx ∴389641±=±=--x x . ∴()()980383101122±=⎪⎭⎫ ⎝⎛±⨯=-+=----x x x x x x . 例9. 若31=+-x x ,求2323-+x x 的值. 解:∵31=+-x x （这里0>x ）∴3222121=-⎪⎭⎫ ⎝⎛+-x x ,∴522121=⎪⎭⎫ ⎝⎛+-x x . ∵02121>+-x x ,∴52121=+-xx .∴()1212132132123231----+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+x x x x x x xx ()52135=-⨯=.解法二:∵31=+-x x∴()723222122=-=-+=+--x x x x∴()()()202173122213322323=+-⨯=+-+=++=⎪⎭⎫ ⎝⎛+----x x x x x x x x ∴52202323==+-xx .例10. 已知41=+-x x ,则=+-2121x x【】（A ）2 （B ）2或2- （C ）6 （D ）6或6- 分析:题目的隐含条件为0>x . 解:∵41=+-x x∴42221211=-⎪⎭⎫ ⎝⎛+=+--x x x x ,∴622121=⎪⎭⎫ ⎝⎛+-x x ∵02121>+-x x∴62121=+-x x.选择【 C 】.例11. 已知212121++=⎪⎭⎫ ⎝⎛+--x x x x f ,则()=+1x f 【】（A ）42-x （B ）()21+x（C ）()()2111-+++-x x （D ）322-+x x解:（换元法）设t xx =+-2121,则有∴222221211-=-⎪⎭⎫ ⎝⎛+=+--t x x x x∴()2222t t t f =+-=,∴()2x x f =. ∴()()211+=+x x f .选择【 B 】.解法二（凑整法）:∵212121++=⎪⎭⎫ ⎝⎛+--x x x x f∴2212122121212122⎪⎭⎫ ⎝⎛+=+-⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+---x x x x x x f ,∴()2x x f =.∴()()211+=+x x f .题型二根式的化简在进行根式的化简时,主要用到的是根式的性质: （1）()a a nn=;（2）对于nna ,当n 为奇数时,a a nn=;当n 为偶数时,()()⎩⎨⎧≤-≥==00a a a a a a nn.注意对于()nna ,当n 为奇数时,∈a R ;当n 为偶数时,a ≥0.而对于nn a ,是一个恒有意义的式子,不受n 的奇偶性的限制,但式子的值受到n 的奇偶性的限制.例12. 化简下列各式: （1）()()222535-+-;（2）()()2231x x -+-（x ≥1）.解:（1）原式125532535=-+-=-+-=;（2）()()x x x x -+-=-+-313122.∵x ≥1∴当1≤x ≤3时,原式231=-+-=x x ; 当3>x 时,原式4231-=-+-=x x x . 例13. 化简: （1）()nnx π-; （2）62144+-a a （a ≤21）.分析:对于（1）,要对n 的奇偶性进行分类讨论. 解:（1）当n 为奇数时,()ππ-=-x x nn ;当n 为偶数时,()()()⎩⎨⎧<-≥-=-=-ππππππx x x x x x nn; （2）()()()33162626221212112144a a a a a a -=-=-=-=+-.注意:当底数为正数时,其分数指数可以约分.例14. 求下列各式的值: （1）223223-++;（2）347246625-+--+.分析: 结论对于二次根式C B A ±,若C B A 22-是完全平方数,则C B A ±也是完全平方数.根据此结论,可知625+,246-,347-均可以化为完全平方的形式. 解:（1）原式()()221212*********2=-++=-++=-++=;（2）原式()()()222322232-+--+=22322232322232=-++-+=-+--+=.总结形如n m 2±（0,0>>n m ）的双重二次根式的化简,一般是将其化为()2ba ±的形式,然后再化简.由()ab b a ba n m 222±+=±=±得:⎩⎨⎧==+nab mb a 所以b a ,是一元二次方程02=+-n mx x 的两个实数根.例15. 化简32-. 解:()()226213213222132324322-=-=-=-=-=-. 例16. 计算:()()4123323-+-.解:原式()[]()58323233443=+-=-+-=-+-=.注意在利用根式的性质进行nna 的化简时,一定要注意当n 为偶数时,底数a 的符号.例17. 化简下列各式: （1）()()665544b a b a a -+++（0<<b a ）;（2）1212----+x x x x （21<<x ）. 解:（1）∵0<<b a∴原式()a b a b b a a b a b a a -=-+++-=-+++=2; （2）∵21<<x ,∴110<-<x ∴原式()()1111111122---+-=---+-=x x x x()1211111111-=-+-+-=---+-=x x x x x .例18. 求值=-++335252_________. 解:令y x =-=+3352,52,则有4525233=-++=+y x ,1-=xy .∴()()422=+-+y xy x y x ,∴()()[]432=-++xy y x y x设t y x =+,则0>t ,有()432=+t t ,∴0433=-+t t ,01333=--+t t∴()()0412=++-t t t∵042>++t t ,∴01=-t ,∴1=t . ∴1525233=-++. 解法二:设=x 335252-++,则有()x x 3452523333-=-++=,∴0432=-+x x∴()()03313=-+-x x ,()()0412=++-x x x ∵042>++x x ,∴01=-x ,∴1=x ∴1525233=-++. 例19. 根据已知条件求值: （1）已知32,21==y x ,求yx y x yx y x +---+的值;（2）已知b a ,是方程0462=+-x x 的两根,且0>>b a ,求ba b a +-的值.解:（1）∵32,21==y x ∴原式()()()()()()yx yx yx yx yx yx -+--+-+=22yx xyy x y x xy y x --+--++=22383221322144-=-⨯⨯=-=yx xy; （2）∵b a ,是方程0462=+-x x 的两根 ∴4,6==+ab b a∴()()204464222=⨯-=-+=-ab b a b a∵0>>b a ,∴0>-b a ∴5220==-b a . ∴()()()55515242622==-=--+=-+-=+-b a ab b a ba ba ba ba b a .（2）解法二:∵b a ,是方程0462=+-x x 的两根,∴4,6==+ab b a∴()()5110242642622222==+-=++-+=+-=⎪⎪⎭⎫⎝⎛+-abb a ab b a b a b a b a b a . ∵0>>b a ,∴b a >,∴0>+-ba b a∴5551==+-ba b a . 例20. 已知⎪⎭⎫ ⎝⎛-=-n n x 115521,∈n N*,求()n x x 21++的值.解:∵⎪⎭⎫ ⎝⎛-=-n nx 115521∴n n n n n n x 222221125215525411552111---++=⎪⎭⎫ ⎝⎛+-+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=+2115541⎪⎭⎫ ⎝⎛+=-n n.∴⎪⎭⎫ ⎝⎛+=+-n nx 11255211∴()55552155211111112=⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=++--nn n nn n n nx x .例21. 已知函数()53131--=x x x f ,()53131-+=x x x g .（1）证明:()x f 在()+∞,0上是增函数（已知31x y =在R 上是增函数）;（2）分别计算()()()2254g f f -和()()()3359g f f -的值,由此概括出函数()x f 和()x g 对所有不等于0的实数x 都成立的一个等式,并加以证明.（1）证明:任取()+∞∈,0,21x x ,且21x x <∴()()55531131231231131231231131121⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=---=-----x x x x x x x x x f x f ∵()+∞∈,0,21x x ,且21x x <,31x y =在R 上是增函数 ∴312311312311,--><x x x x∴()()021<-x f x f ,∴()()21x f x f < ∴()x f 在()+∞,0上是增函数; （2）解:()()()2254g f f -0522522552222554432323232313131313131=---=⨯⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⨯--=-----.同样求得()()()03359=-g f f . 猜想:()()()052=-x g x f x f . 证明: ()()()x g x f x f 52-055555532323232313131313232=---=⨯⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⨯--=-----x x x x x x x x xx .例22. 当0,0>>y x ,且()()y x y y x x 53+⋅=+时,求yxy x y xy x -+++32的值.解:∵0,0>>y x ,且()()y x y y x x53+⋅=+∴y xy xy x 153+=+,0152=--y xy x ∴()()053=-+y x yx∴05=-y x ,y x y x 25,5==. ∴22958525355032==-+++=-+++yyy y y y y y yxy x y xy x .题型三根式与分数指数幂的互化在进行根式与分数指数幂的互化时要注意两个对应: （1）根指数对应分数指数的分母;（2）被开方数（或式）的指数对应分数指数的分子. 当出现多重根号时,应从里向外化简.例23. 用根式或分数指数幂表示下列各式:51a ,()043>a a ,36a ,()013>a a;()0>a a a .解:551a a =;()43430a a a =>;23636a a a ==;()23233101-==>a aa a;()4323210a a a a a a a ==⋅=>.例24. 将根式53-a 化为分数指数幂是【】（A ）53-a （B ）53a （C ）53a - （D ）35a - 解:选择【 A 】. 例25. 化简:()()=⋅÷⋅109532a a a a _________.（用分数指数幂表示）解:由题意可知:0>a .∴原式561012101451310921532a a a a a a a a ==÷=⎪⎭⎫⎝⎛⋅÷⎪⎭⎫ ⎝⎛⋅=.例26. 设0>a ,化简:434334aa a a -.解:∵0>a∴611616653163254343234434334---===⋅⋅=aaa aa a a aa aa aa.例27. 下列根式与分数指数幂的互化中,正确的是【】（A ）()()0414>-=-x x x （B ）()0551≠-=-x x x（C ）()0,4343≠⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛-y x x y y x （D ）4182y y = 解:（A ）()0414>-=-x x x ,故（A ）错;（B ）()0155151≠==--x xx x,故（B ）错; （D ）4182y y =,故（D ）错. 选择【 C 】. 例28. 下列各式正确的是【】（A ）35531aa=-; （B ）2332x x =（C ）⎪⎭⎫ ⎝⎛-⨯⨯-=814121814121aaa a （D ）x x x x 412212323131-=⎪⎭⎫ ⎝⎛---解:（A ）53535311aaa ==-,故（A ）错;（B ）3232x x =,故（B ）错; （C ）85814121814121a aaa a ==⎪⎭⎫ ⎝⎛-++-,故（C ）错. 选择【 D 】.题型四根式和分数指数幂有意义的条件1.对于n 次根式na ,当n 为奇数时,∈a R ;当n 为偶数时,a ≥0. 2.0的0次幂和负实数幂都没有意义.例29. 若()4321--x 有意义,则x 的取值范围是__________.解:∵()()()43434321121121x x x -=-=--∴021>-x ,解之得:21<x . 即x 的取值范围是⎪⎭⎫ ⎝⎛∞-21,.例30. 函数()()2125--+-=x x y 的定义域是【】（A ）{}2,5≠≠x x x （B ）{}2>x x（C ）{}5>x x （D ）{}552><<x x x 或解:∵()()()()()215215250210210-+-=-+-=-+-=-x x x x x x y∴⎩⎨⎧>-≠-0205x x ,解之得:2>x 且5≠x .∴该函数的定义域为()()+∞,55,2 .选择【 D 】.题型五幂的运算目前,当底数大于0时,指数已经由整数指数推广到了实数指数,整数指数幂的运算性质适用于实数指数幂的运算.运算的结果可以化成根式形式或者保留分数指数幂的形式,但不能既有根式又有分数指数幂,也不能同时含有分母和负指数幂.（1）s r s r a a a +=⋅（∈>s r a ,,0R ）; （2）()rs sr a a =（∈>s r a ,,0R ）;（3）()r r rb a ab =（∈>>r b a ,0,0R ）.例31. 计算下列各式（式中的字母均为正数）: （1）()()()c b a b a b a 24132124-----÷-⋅;（2）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--+----------212121211122b a b a b a b a . 解:（1）原式()ca ac cb a b a 33112412423-=-=÷-=-----;（2）原式()()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+---=--------21212121112121b a b a b a b a ()()()bb b a b a b a ba b a b a221111111111111==+-+=----+=------------- 例32. 化简下列各式: （1）212121211111aaa a a++------;（2）111113131313132---+++++-x xx x x x x x .解:（1）原式()()011112121212121211=-=+⎪⎭⎫ ⎝⎛+---=-----a a a a a a a a a ; （2）原式11111131323131333131323331-⎪⎭⎫ ⎝⎛--++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛=x x x x x x x x 31323132313131313131313231313231323111111111111xx x x x x x x x x x x x x x x x x --+-+-=-⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-= 31x -=.例33. 化简:()()()()()1421443333211--------++-++-+aa a a a a a a a a a a. 解:原式()()()()()()1221442212212111---------+-+-++++-+-+=a a a a a a a a a a a a a aa a()[]()[]()()1214412222111--------++++++-+=aa a a a a a a a a a a()()aa a a a aa a a a a a a 21111144144=-++=-++++++=------ 例34. 化简下列各式:（1）436532yx xy⋅; （2）1111212331++-+++a a a a a .解:（1）原式1212143653231--==yx yx y x ;（2）原式111111111121212131313231213321313331++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=++-⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛=a a a a a a a a a a a a a a 21313221313211aa a a a a +-=-++-=例35. ()=-⎪⎭⎫⎝⎛⨯+⎪⎭⎫ ⎝⎛--21212001.04122532【】（A ）1516 （B ）30173 （C ）658- （D ）0 解:()21212001.04122532-⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛--1516101324111001491411=-⨯+=-⨯+=.选择【 A 】.例36. 化简:=⎪⎪⎭⎫⎝⎛÷⋅⋅----321132132a b b a bab a _________.解:原式656161673223236167322121131212132--------=÷=⎪⎭⎫⎝⎛÷=⎪⎪⎪⎭⎫ ⎝⎛÷=b a ab b a b a b a ba ba b a b a .例37.=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛---442102324953121_________.解:原式22322322232491112=-++=-++-+=. 例38. 已知3,2==n m ,则32432332⎪⎪⎭⎫⎝⎛÷⋅----m n nm m n n m 的值是_________. 解:∵3,2==n m∴原式32325343322534312322332⎪⎭⎫ ⎝⎛÷=⎪⎭⎫ ⎝⎛÷=⎪⎪⎪⎭⎫ ⎝⎛÷=--------mn n m n m n m n m mn n m n m 27232333131=⨯==⎪⎭⎫⎝⎛=---mn n m . 例39. 已知函数()()⎪⎩⎪⎨⎧≥--<=1,351,312x x x x x f ,则=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--4321353f f _________.解:⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛---4343213533353f f f f 33939335353331243=+-=+⎪⎭⎫⎝⎛-+-⨯=-. 题型六解含幂的方程例40. 解下列方程:（1）2291381+⎪⎭⎫ ⎝⎛=⨯x x; （2）0123222=-⨯++x x .解:（1）()2224333+-=⨯x x ,424233--+=x x ∴4242--=+x x ,解之得:2-=x ;（2）()0123242=-⨯+⨯x x ,设t x =2,则0>t∴01342=-+t t ,()()0114=+-t t 解之得:1,241221-===-t t （舍去）. ∴222-=x ,∴2-=x .结论若sr a a =（0>a ,且1≠a ）,则s r =题型七指数幂等式的证明设参数法例41. 设c b a ,,都是正数,且c b a 643==,求证:ba c 122+=. 证明:设t cba===643,则有cbat t t 12116,2,3===. ∵236⨯= ∴ba bacttt t 2112111+=⋅=,∴ba c 2111+= 等式两边同时乘以2得:b ac 122+=. 例42. 设m b a ==52,且211=+b a ,则=m _________.分析:这是指数幂的连等式,参数已经给出. 解:∵m ba==52,∴bam m 115,2==. ∵211=+ba ∴2111152m m m m ba ba==⋅=⨯+,∴102=m ,10±=m .∵0>m ,∴10=m . 例43. 已知333cz by ax ==,且1111=++zy x . 求证:()31313131222c b a czby ax ++=++.证明:设t cz by ax ===333,则zt cz y t by x t ax ===222,,. ∴⎪⎭⎫⎝⎛++=++z y x t cz by ax 111222.∵1111=++z y x ,∴t z y x t =⎪⎭⎫ ⎝⎛++111 ∴t cz by ax =++222,()3131222t czby ax =++∵3131313313313313131111t z y x t z t y t x t c b a =⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++∴()31313131222c b a czby ax ++=++.例44. 对于正整数c b a ,,（a ≤b ≤c ）和非零实数ω,,,z y x ,若ω70===z y x c b a ,zy x 1111++=ω,求c b a ,,的值. 解:设k c b a zyx====ω70,则有ω111170,,,k k c k b k a zyx====.∴zy x k abc 111++=∵zy x 1111++=ω,∴70=abc . ∵c b a ,,为正整数,且a ≤b ≤c ∴752107170⨯⨯=⨯⨯==abc ∴10,7,1===c b a 或7,5,2===c b a当10,7,1===c b a 时,0===ωz y ,不符合题意,舍去. ∴7,5,2===c b a .本节易错题例45. 计算()()=-++44332121_________.分析对于对于nna ,当n 为奇数时,a a nn=;当n 为偶数时,()()⎩⎨⎧≤-≥==00a a a a a a nn.解:原式2212212121=-++=-++=.例46. 化简()()=-⋅-43111a a _________. 分析:题目的隐含条件为1>a . 解:原式()()()()()()()414343431111111--=-⋅--=-⋅-=-⋅-=---a a a a a a a .例47. 已知1,0><<n b a ,∈n N*,化简()()nn nnb a b a ++-.解:当n 为奇数时,原式a b a b a 2=++-=; 当n 为偶数时,原式b a b a ++-=. ∵0<<b a ,∴原式a b a a b 2-=---=.其它例48. 已知函数()⎪⎩⎪⎨⎧≤⎪⎭⎫ ⎝⎛>=0,210,21x x x x f x ,则()=-)4(f f _________. 解:∵()1621121444=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=--f ∴()()4161616)4(21====-f f f .例49. 已知集合{}4,,2a a A -=,⎭⎬⎫⎩⎨⎧-=b a aa B 2,,33,且B A =,则=+b a _______.解:{}{}4,,4,,2a a a a A -=-=根据集合元素的互异性,a a -≠,∴0>a∴{}b b a a a a B 2,1,2,,33-=⎭⎬⎫⎩⎨⎧-=∴⎩⎨⎧==421b a ,解之得:⎩⎨⎧==21b a .∴=+b a 3.例50. 设()244+=x xx f ,若10<<x ,则=⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛10011000100131001210011f f f f _________. 解:∵()244+=x xx f∴()()=+++=+++=+++=-+--24224444444244244244111x x x xx x xx xx xx f x f 12424=++x x ∴⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛10011000100131001210011f f f f500111100150110015001001100010011=++=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛= f f f f .。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学科教师辅导教案―分数指数幂
(n a
a a a
a 个
2、分数指数幂
观察：(25)2=210
51022= 2
1010
22
=
(1)正数的正分数指数幂的意义是：n
m a ＝n
a m (a >0，m 、n ∈N *，且n>1)； (2)正数的负分数指数幂的意义是：n
m a
-＝
n
m a
1 (a >0，m 、n ∈N *，且n>1)；
(3)0的正分数指数幂等于0，0的负分数指数幂没有意义．
注意：不要轻易对n
m 进行约分，否则有时会改变a 的取值范围导致出错，若.0,;,41
48
2≥=∈a a a R a a
[例1]求下列各式的值：
（1）2
1
25-
（2）5)2
1(- （3）43)8116(- （4）0
421
)127(-+
[巩固]计算求值：（1） 0212
3
1)1627()2
1(8---+++
（2）21
4)4
25()15(4)21(25.0----÷--⨯
[例2] 将下列分数指数幂化为根式（1）_______53
4=（2）_______22
1=-（3）_______2
3=a （4）_______2
5=-
a
[巩固] 用分数指数幂表示下列各式：
（1）_____2=（2）_____)0(32=>a a （3）_____)(57
=-b a （4）_____)()(224322=≥-b a b a
3、有理数指数幂的运算性质
(1)a t a s ＝a t ＋
s (a >0，t 、s ∈Q )； (2)(a t )s ＝a ts (a >0，t 、s ∈Q )； (3)(ab )t ＝a t b t (a >0，b >0，t ∈Q )．
[例1]化简
精典例题透析
精典例题透析。