初中一年级数学几何证明题答案
(完整版)初中几何证明题五大经典(含答案)
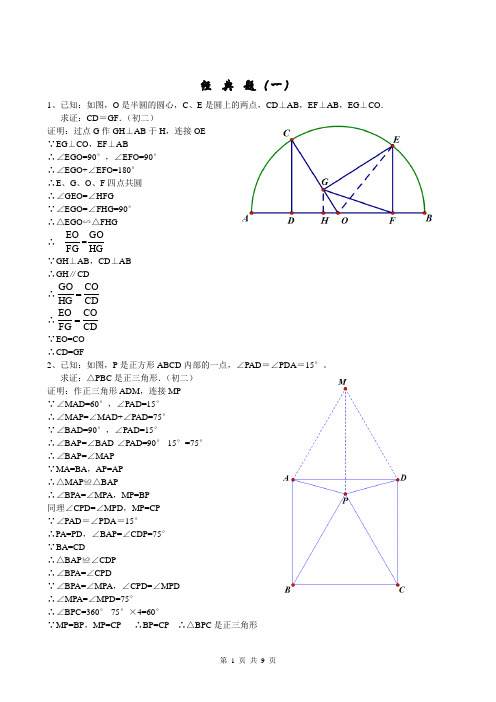
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中数学几何证明题及参考答案

初中数学几何证明题及参考答案初中数学几何证明题及参考答案几何证明题是初中学生在学习数学时需要掌握的重点知识。
为了帮助初中生学会几何证明题,下面就是店铺给大家整理的初中数学几何证明题及参考答案,希望大家喜欢。
初中数学几何证明题及参考答案1己知M是△ABC边BC上的中点,,D,E分别为AB,AC上的点,且DM⊥EM。
求证:BD+CE≥DE。
延长EM至F,使MF=EM,连BF.∵BM=CM,∠BMF=∠CME,∴△BFM≌△CEM(SAS),∴BF=CE,又DM⊥EM,MF=EM,∴DE=DF而∠DBF=∠ABC+∠MBF=∠ABC+∠ACB<180°,∴BD+BF>DF,∴BD+CE>DE。
初中数学几何证明题及参考答案2己知M是△ABC边BC上的中点,,D,E分别为AB,AC上的点,且DM⊥EM。
求证:BD+CE≥DE过点C作AB的'平行线,交DM的延长线于点F;连接EF因为CF//AB所以,∠B=∠FCM已知M为BC中点,所以BM=CM又,∠BMD=∠CMF所以,△BMD≌△CMF(ASA)所以,BD=CF那么,BD+CE=CF+CE (1)且,DM=FM而,EM⊥DM所以,EM为线段DF的中垂线所以,DE=EF在△CEF中,很明显有CE+CF>EF (2)所以,BD+CE>DE当点D与点B重合,或者点E与点C重合时,仍然采用上述方法,可以得到BD+CE=DE综上就有:BD+CE≥DE。
初中数学几何证明题及参考答案3证明因为∠DME=90°,∠BMD<90°,过M作∠BMD=∠FMD,则∠CME=∠FME。
截取BF=BC/2=BM=CM。
连结DF,EF。
易证△BMD≌△FMD,△CME≌△FME所以BD=DF,CE=EF。
在△DFE中,DF+EF≥DE,即BD+CE≥DE。
当F点落在DE时取等号。
另证延长EM到F使MF=ME,连结DF,BF。
初中经典几何证明练习题(含问题详解)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中数学几何证明题含答案
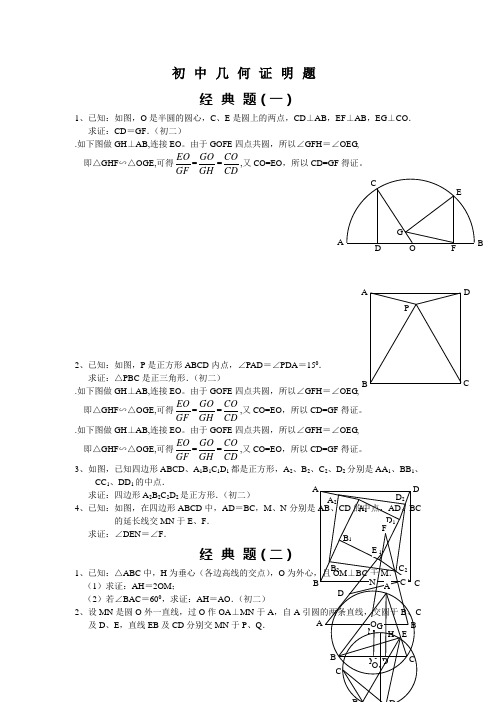
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
.如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N的延长线交MN 于E 、F .求证:∠DEN =∠F . 经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . APCDBAFGCEBOD求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN求证:AP=AQ.4、如图,分别以△ABC的ACCBFG,点P是EF的中点.求证:点P到边AB1、如图,四边形ABCD求证:CE=CF.(初二)2、如图,四边形ABCD求证:AE=AF.(初二)3、设P是正方形ABCD一边求证:PA=PF.(初二)4、如图,PC切圆O于C,ACB、D.求证:AB=DC,BC1、已知:△ABC是正三角形,P求:∠APB的度数.(初二)2、设P是平行四边形ABCD求证:∠PAB=∠PCB.3、设ABCD4、平行四边形ABCD中,设EAE=CF.求证:∠DPA=∠1、设P是边长为1的正△ABC求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC ∠EBA =200,求∠BED 的度数. 经典题(一)1.如下图做GH ⊥AB,连接EO 。
初一下数学证明例题及答案

如图,已知D是△A B C内一点,试说明A B+A C>B D+C D 证明:延长BD交AC于E在△ABC中,AB+AE>BE,即AB+AE>BD+DE……①在△DEC中,DE+EC>DC……②①+②,得AB+AE+DE+EC>BD+DE+CD即AB+AE+EC+DE>BD+DE+CD即AB+AC+DE>BD+DE+CD∴AB+AC>BD+CD如图,△ABC中,D是BC的中点,求证:1AB+AC>2AD2若AB=5,AC=3,求AD的范围;1延长AD到点G,使DG=AD.连接BG在△CDA和△BDE中AD=GD,∠ADC=∠GDB∵D是BC的中点∴CD=BD∴△CDA≌△BDG.∴BG=AC在△ABG中,AB+BG=AB+BCAG=2AD因为三角形两边和大于第三边,所以AB+BE>AG ∴AB+BC>2ADDC BAEAB CDG2AB-AC <2AD <AB+AC2<2AD <8 1<AD <4如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F 为DE 的中点,求证:BC=2AF. 延长AF 到点G,使AF=DF.连接GD 在△AFE 和△DFG 中 AF=GF,∠AFE=∠DFG ∵点F 为DE 的中点 ∴DF=EF所以△AFE ≌△DFG. SAS GD=AE=AC;∠G=∠FAE.∴DG ∥AE.内错角相等,两直线平行则∠GDA+∠DAE=180°.两直线平行,同旁内角互补 又∵∠BAC+∠DAE=180°. ∴∠GDA=∠BAC.同角的补角相等. 又∵AD=AB. ∴⊿ADG ≌⊿BACSAS ∴AG=BC,即2AF=BC. ∴BC=2AF.如图,AD 是△ABC 的中线,点E 在BC 的延长线上,CE=AB, ∠BAC=∠BCA 求证:AE=2AD证明:在AD 的延长线上取点F,使AD =FD,连接CFCECDBA∵AD是中线∴BD=CD,AD=FD,∠ADB=∠FDC∴△ABD≌△FCD SAS∴CF=AB,∠B=∠FCD∵∠ACF=∠BCA+∠BCE,∠ACE=∠BAC+∠B,∠BAC=∠BCA∴∠ACF=∠ACE∵CE=AB∴CE=CF∴△ACE≌△ACF SAS∴AE=AF∵AF=AD+FD=2AD∴AE=2AD如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F;1求证:EF=DF Array 2求证:S△ABC=S△DCE证明:①作EG⊥BF,交BF延长线于G则∠CGE=∠ABC=90°∵∠ACE=90°∴∠ACB+∠ECG=90°∵∠ACB+∠BAC=90°∴∠ECG=∠BAC又∵AC=EC∴△ABC≌△CGEAAS∴BC=EG∵BC=CD∴EG=CD∵∠BCD=90°∴∠DCF=90°=∠EGF又∵∠CFD=∠GFE对顶角相等,CD=EG∴△CFD≌△GFEAAS∴EF=DF②∵△CFD≌△GFE∴S△CFD=S△GFE∴S△CFD+S△CFE=S△GFE+S△CFE即S△DCE=S△CGE∵△ABC≌△CGE∴S△ABC=S△CGE∴S△ABC=S△DCE如图,在△ABC,△DEF中,AM,DN分别是两三角形中线,AB=DE,AC=DF,AM=DN.求证:△ABC≌△DEFD证明:如图,延长AM至A′,使A′M=AM延长DN至D′,使D′N=DNEFN连接A′C、D′F ∵AM 是△ABC 的中线 ∴BM=MC在△ABM 和△A′CM 中BM =MC ∠AMB =∠A′MCAM=A′M ∴△ABM ≌△A′CMSAS ∴AB=A′C ,同理可得DE=D′F ∵AB=DE,∴A′C=D′F ∵AM=DN,AA′=2AM ,DD′=2DN∴AA′=DD′,在△AA′C 和△DD′F 中,AC =DFAA′=DD′A′C=D′F ∴△AA′C≌△DD′FSSS∴∠A′=∠D′,在△A′MC 和△D′NF 中,A′M=D′N∠A′=∠D′A′C=D′F∴△A′MC≌△D′NFSAS ,∴MC=NF∵AM 、DN 分别是两三角形中线 ∴BC=2MC,EF=2NF∴BC=EF,在△ABC 和DEF 中,AB =DEAC =DFBC =EF ∴△ABC ≌DEFSSS .BAMCA ′。
初一数学几何证明题答案

初一典型几何证明题1、已知: AB=4,AC=2,D是 BC中点, AD是整数,求 AD解:延长 AD到 E, 使 AD=DE∵D是 BC中点∴ BD=DC在△ ACD和△ BDE中AAD=DE∠BDE=∠ADC BD=DC∴△ ACD≌△ BDE ∴AC=BE=2∵在△ ABE中AB-BE<AE< AB+BE ∵AB=4即4-2 <2AD< 4+2 1<AD<3∴AD=2B CD2、已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A12B EC F D证明:连接 BF 和 EF∵BC=ED,CF=DF,∠ BCF=∠EDF∴△ BCF≌△ EDF (S.A.S)∴BF=EF,∠ CBF=∠ DEF连接 BE在△ BEF中 ,BF=EF∴ ∠ EBF=∠ BEF。
∵ ∠ ABC=∠ AED。
∴ ∠ ABE=∠ AEB。
∴AB=AE。
在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠AEB+∠BEF=∠AEF∴△ ABF≌△ AEF。
∴ ∠ BAF=∠ EAF ( ∠1=∠ 2) 。
3、已知:∠ 1=∠2,CD=DE, EF//AB,求证: EF=ACA12FCDEB过C 作 CG∥EF 交 AD的延长线于点G CG∥EF,可得,∠ EFD= CGDDE=DC∠FDE=∠ GDC(对顶角)∴△ EFD≌△ CGDEF=CG∠CGD=∠ EFD又, EF∥AB∴,∠ EFD=∠1∠1=∠2∴∠ CGD=∠2∴△ AGC为等腰三角形,AC=CG又EF=CG∴EF=AC4、已知: AD平分∠ BAC,AC=AB+BD,求证:∠ B=2∠C证明:延长 AB取点 E,使 AE=AC,连接 DE∵AD平分∠ BAC∴∠ EAD=∠ CAD∵AE=AC,AD= AD∴△ AED≌△ ACD (SAS)∴∠ E=∠ C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠ BDE=∠ E∵∠ ABC=∠ E+∠BDE∴∠ ABC=2∠E∴∠ ABC=2∠C5、已知: AC平分∠ BAD,CE⊥ AB,∠ B+∠D=180°,求证: AE=AD+BE证明:在AE上取 F,使 EF=EB,连接 CF∵CE⊥AB∴∠ CEB=∠ CEF=90°∵EB=EF,CE= CE,∴△ CEB≌△ CEF∴∠ B=∠ CFE∵∠ B+∠ D=180°,∠ CFE+∠ CFA=180°∴∠ D=∠ CFA∵AC平分∠ BAD∴∠ DAC=∠ FAC∵AC=AC∴△ ADC≌△ AFC(SAS)∴AD=AF∴AE=AF+FE= AD+BE6、如图,四边形 ABCD中, AB∥DC,BE、CE分别平分∠ ABC、∠BCD,且点 E 在 AD上。
初一数学几何证明题答案

初一典型几何证明题1、已知: AB=4,AC=2,D是BC中点, AD是整数,求AD解:延长A D到 E,使AD=DE∵D是 BC中点A ∴BD=DC在△ ACD和△ BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ACD≌△ BDE∴AC=BE=2∵在△ ABE中AB-BE<AE<AB+BE∵AB=4即 4-2<2AD<4+21<AD<3∴AD=22、已知: BC=DE,∠B=∠E,∠ C=∠D,F 是 CD中点,求证:∠1=∠2A21B EC F D证明:连接BF和 EF∵BC=ED,CF=DF∠, BCF=∠EDF∴△BCF≌△ EDF 第1页共22 页∴BF=EF,∠CBF=∠DEFB E连接在△ BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△ AEF。
∴∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=D,E EF证明:连接EF ∵AB∥CD共22 页第9页∴∠B=∠C∴△BEM≌△CFM( SAS)∵M是 BC中点∴CF=BE∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM7. 已知:如图所示,AB=AD,BC=DC,E、F 分别是DC、BC的中点,求证:AE=AF。
证:连接AC DE=BF∵在△ ADC和△ABC中∴△ADE≌△ ABF(SAS)AD=AB ∴AE=AFDC=BCAC=AC∴△ADC≌△ ABC(SSS)D∴∠B=∠ DE∵E、F 分别是DC、BC的中点AC又∵ BC=DCF∴DE=BFB∵在△ ADE和△ABF中AD=AB∠D=∠B8. 如图,在四边形ABCD中, E是AC上的一点,∠1=∠2,∠3=∠4,求证 : ∠5=∠6.证明:∵在△ADC和△ ABC中∴△DEC≌△ BEC(SAS)∠BAC=∠DAC ∴∠DEC=∠BEC∠BCA=∠DCAAC=AC∴△ADC≌△ ABC(AAS)D∵AB=AD,BC=CD在△ DEC与△ BEC中A12E5634CCE=CEB∠BCA=∠DCABC=CD9. 如图,在△ABC中, AD为∠ BAC的平分线,DE⊥AB于 E,DF⊥AC于 F。
(完整版)初中数学几何证明经典试题(含答案)
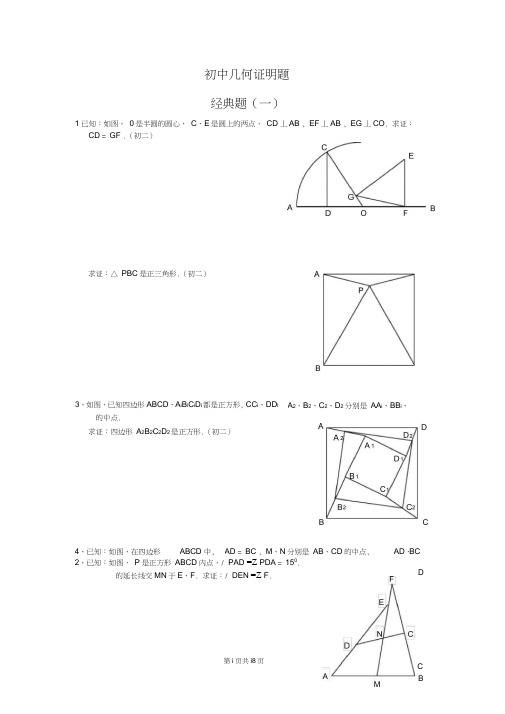
初中几何证明题 经典题(一)1 已知:如图, 0是半圆的圆心, C 、E 是圆上的两点, CD 丄AB , EF 丄AB , EG 丄CO . 求证:CD = GF .(初二)2、已知:如图, P 是正方形 ABCD 内点,/ PAD =Z PDA = 150.的延长线交MN 于E 、F . 求证:/ DEN =Z F .求证:△ PBC 是正三角形.(初二)3、如图,已知四边形 ABCD 、A i B i C i D i 都是正方形, CC i 、DD i的中点.求证:四边形 A 2B 2C 2D 2是正方形.(初二)A 2、B 2、C 2、D 2 分别是 AA i 、BB i 、4、已知:如图,在四边形 ABCD 中, AD = BC , M 、N 分别是 AB 、CD 的中点, AD 、BCD经典题(二)及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二) 3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆0的弦,过MN 的中点A 任作两弦BC 、DE , 于 P 、Q .求证:AP = AQ .(初二)4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于1已知:△ ABC 中,H 为垂心(各边高线的交点)(1) 求证:AH = 2OM ;(2) 若/ BAC = 600,求证:AH = AO .(初二),O 为外心,且0M 丄BC 于M .2、设MN 是圆0外一直线,过0作0A 丄MN 于A ,自A 引圆的两条直线,交圆于AB 的一半.(初二)HEBCM DG N BF经典题(二)1 如图,四边形 ABCD 为正方形,DE // AC , AE = AC , AE 与CD 相交于F .求证:CE = CF .(初二)4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB = DC , BC = AD .(初三)F .E2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于 求证:AE = AF .(初二)3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)经典题(四)1已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)C经典难题(五)1、设P是边长为1的正△ ABC内任一点,求证:一:<L V 2.B C2、已知:P是边长为1的正方形ABCD内的一点,求PA + PB + PC的最小值.3、P为正方形ABCD内的一点,并且PA= a, PB= 2a, PC= 3a,求正方形的边长.4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数.经典题(一)1•如下图做GH丄AB,连接E0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一典型几何证明题1、已知: AB=4,AC=2,D是BC中点, AD是整数,求AD解:延长A D到 E,使AD=DE∵D是 BC中点A ∴BD=DC在△ ACD和△ BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ ACD≌△ BDE∴AC=BE=2∵在△ ABE中AB-BE<AE<AB+BE∵AB=4即 4-2<2AD<4+21<AD<3∴AD=22、已知: BC=DE,∠B=∠E,∠ C=∠D,F 是 CD中点,求证:∠1=∠2A21B EC F D证明:连接BF和 EF∵BC=ED,CF=DF∠, BCF=∠EDF∴△ BCF≌△ EDF (S.A.S)第1页共22 页∴BF=EF,∠CBF=∠DEFB E连接在△ BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ ABF≌△ AEF。
∴∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=D,E EF//AB,求证: EF=ACA21FCDEB点GC作 CG∥EF交 AD的延长线于过CG∥EF,可得,∠ EFD= CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠ EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC4、已知: AD平分∠ BAC,AC=AB+B,D求证:∠B=2∠CA共22 页第2页证明:延D E长AB取点E,使AE=AC,连接∵AD平分∠ BAC∴∠ EAD=∠ CAD∵AE=AC,AD=AD∴△ AED≌△ ACD (SAS)∴∠ E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠ BDE=∠ E∵∠ ABC=∠ E+∠BDE∴∠ ABC=2∠E∴∠ ABC=2∠C5、已知: AC平分∠ BAD,CE⊥AB,∠ B+∠D=180°,求证: AE=AD+BE证明:C F在 AE上取F,使EF=EB,连接∵CE⊥AB∴∠ CEB=∠ CEF=90°∵EB=EF,CE=CE,共22 页第3页∴△ CEB≌△ CEF∴∠ B=∠CFE∵∠ B+∠D=180°,∠ CFE+∠ CFA=180°∴∠ D=∠CFA∵AC平分∠ BAD∴∠ DAC=∠ FAC∵AC=AC∴△ ADC≌△ AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求B C=AB+D。
C 又∵∠ DCE=∠FCE证:E F CE 平分∠ BCD在 BC上截取BF=AB,连接∵BE平分∠ ABC CE=CE∴∠ ABE=∠FBE ∴⊿DCE≌⊿ FCE(AAS)又∵ BE=BE ∴CD=CF∴⊿ ABE≌⊿ FBE(SAS)∴BC=BF+CF=AB+CD∴∠ A=∠BFE∵AB//CD∴∠ A+∠D=180o∵∠ BFE+∠CFE=180o∴∠ D=∠CFE7. P 是∠ BAC平分线A D上一点, AC>AB,求证:P C-PB<AC-AB在 AC上取点E,∴PC<( AC-AE)+PB使 AE=AB。
∴PC-PB<AC-AB。
∵AE=ABCAP =AP∠EAP=∠BAE,∴△EAP≌△BAPAP D∴PE=PB。
PC<EC+PEB共22 页第4页8.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE证明:∴点E 一定在直线 BD上,在AC上取一点 D,使得角 DBC=角C 在等腰三角形ABD中,AB=AD,AE垂直 BD ∵∠ABC=3∠C∴点E 也是BD的中点∴∠ABD=∠ABC- ∠DBC=∠3C- ∠C=2∠C;∴BD=2BE∵∠ADB=∠C+∠DBC=∠2C; ∵BD=CD=AC-AB∴AB=AD ∴AC-AB=2BE∴AC –AB =AC-AD=CD=BD在等腰三角形ABD中,AE是角 BAD的角平分线,∴AE垂直 BD∵BE⊥AE9.如图,在△ ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.解:延长 AD至BC于点 E,∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC是等腰三角形∴AB=AC在△ABD和△A CD中AB=AC∠1=∠2BD=DC∴△ABD和△ACD是全等三角形(边角边)∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC10.如图,OM平分∠POQ,MA⊥OP, MB⊥OQ,A、B为垂足,AB交 OM于点 N.求证:∠O A B=∠OBA证明:∵OM平分∠POQ∴∠POM=∠QOM∵MA⊥OP,MB⊥OQ第 5 页共22 页∴∠MAO=∠ MBO=90∵OM=OM∴△AOM≌△ BOM (AAS)∴OA=OB∵ON=ON∴△AON≌△ BON (SAS)∴∠OAB=∠OBA,∠ ONA=∠ONB∵∠ONA+∠ONB=180∴∠ONA=∠ ONB=90∴OM⊥AB11.如图,已知A D∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:A D+B C=A B.PC证明:EE F在 AB上取F,使AF=AD,连接D∵AE平分∠ DAB∴∠ DAE=∠FAEA B在⊿ ADE和⊿ AFE中AD=AF∠DAE=∠FAEAE = AE∴⊿ ADE≌⊿ AFE(SAS)∴∠ ADE=∠AFE∵AB//CD∴∠ ADE+∠C=180o∵∠ AFE+∠BFE=180o∴∠ C=∠BFE∵BE 平分∠ ABC∠CBE=∠FBE在⊿ BFE和⊿ BCE中∠C=∠BFE∠CBE=∠FBECE=CE∴⊿ BFE≌⊿ BCE(AAS)∴CB=BF∴AB=AF+FB=AD+BC共22 页第6页12.如图①,E、F 分别为线段A C上的两个动点,且DE⊥AC于E,BF⊥AC于 F,若AB=CD,AF=CE,BD交 AC于点M.(1)求证: MB=MD,ME=MF若成(2)当E、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?由.立请给予证明;若不成立请说明理(1) 证:∵ DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在 Rt△DEC和 Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA( HL)∴DE=BF.在△DEM和△BFM中∠D E M=∠BFM∠D M E=∠B MFDE=BF∴△D E M≌△BFM(AAS)∴MB=M,D ME=MF(2) 证:∵ DE⊥AC于E,BF⊥A C于F,∴∠DEC=∠BFA=90°,DE∥BF,在 Rt△DEC和 Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA( HL)∴DE=BF.在△DEM和△BFM中∠D E M=∠BFM∠D M E=∠B MFDE=BF∴△D E M≌△BFM(AAS)∴MB=M,D ME=MF13 如图,△ ABC中,∠BAC=90度,AB=AC,BD是∠ ABC的平分线, BD的延长线垂直于过C共22 页第7页点的直线于E,直线CE交 BA的延长线于F.求证: BD=2CE.F证:∵∠ CEB=∠CAB=9°0∠ADB=∠CDEA在△ ABD中,∠ ABD =°- ∠CAB-∠ADBE 在△ CED中,∠ DCE =°- ∠CEB-∠CDED∴∠ ABD =∠DCEB C 在△ ABD和△ ACF中∠DAB=∠CAFAB=AC∠ABD =∠DCF∴△ ABD≌△ ACF(ASA)∴BD=CF∵BD是∠ ABC的平分线∴∠ FBE =∠CBE在△ FBE和△ CBE中∠FBE =∠CBEBE=BE∠BEF =∠BEC∴△ FBE≌△ CBE(ASA)∴CE=FE CF=2CE∴BD=2CE13.如图: DF=CE,AD=BC,∠D=∠C。
求证:△ AED≌△ BFC。
证明:∵ DF=CE,∴DF-EF=CE-EF,即 DE=C,FE FD C在△AED和△BFC中,∵ AD=BC,∠D=∠C ,DE=CF∴△AED≌△BFC( SAS)A B14.如图: AE、BC交于点M,F 点在AM上, BE∥CF,BE=CF。
求证: AM是△ ABC的中线。
证明:∵ BE‖CF ∵BE=CF∴∠ E=∠CFM,∠EBM=∠FCM ∴△BEM≌△ CFM共22 页第8页∴BM=CMA∴AM是△ ABC的中线FBC ME15.AB=AC,DB=D,C F是AD的延长线上的一点。
求证:BF=CF证:在△ ABD与△ACD中AB=AC ∴△FBD≌△ FCD(SAS)BD=DC ∴BF=FCAD=ADA∴△ ABD≌△ ACD(SSS)∴∠ ADB=∠ADCD∴∠ BDF=∠FDC在△ BDF与△ FDC中B CBD=DC∠BDF=∠FDCFDF=DF16.如图: AB=CD,AE=DF,CE=FB。
求证: AF=DE。
证:∵ CF=CE+EF AB=CDEB=EF+FB ∠ABF =∠DCE又∵ CE=FB BF=CE∴CF=EB ∴△ABF≌△ CDE (SAS)在△ CDF与△ ABE中∴AF=EDAB=CDABAE=DFFBE=CF∴△ CDF≌△ ABE(SSS)∴∠ DCB=∠ABFE在△ ABF与△ CDE中CD17.公园里有一条“Z”字形道路ABCD,如图所示,其中AB∥CD,在 AB,CD,BC三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试说明三只石凳E,F,M恰好在一条直线上 .证明:连接EF ∵AB∥CD共22 页第9页∴∠B=∠C∴△BEM≌△CFM( SAS)∵M是 BC中点∴CF=BE∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM18.已知:如图所示,AB=AD,BC=DC,E、F 分别是DC、BC的中点,求证:AE=AF。
证:连接AC DE=BF∵在△ ADC和△ABC中∴△ADE≌△ ABF(SAS)AD=AB ∴AE=AFDC=BCAC=AC∴△ ADC≌△ ABC(SSS)D∴∠B=∠ DE∵E、F 分别是DC、BC的中点AC又∵ BC=DCF∴DE=BFB∵在△ ADE和△ABF中AD=AB∠D=∠B19.如图,在四边形ABCD中, E是AC上的一点,∠1=∠2,∠3=∠4,求证 : ∠5=∠6.证明:∵在△ADC和△ ABC中∴△DEC≌△ BEC(SAS)∠BAC=∠DAC ∴∠DEC=∠BEC∠BCA=∠DCAAC=AC∴△ ADC≌△ ABC(AAS)D∵AB=AD,BC=CD在△ DEC与△ BEC中A12 E5634CCE=CEB∠BCA=∠DCABC=CD20.如图,在△ABC中, AD为∠ BAC的平分线,DE⊥AB于 E,DF⊥AC于 F。
