自动控制原理 邢春芳 第3章习题参考答案
自动控制原理第三章课后习题答案(最新)汇总

3-1设系统的微分方程式如下:(1)0.2c(t) 2r(t)单位脉冲响应:C(s) 10/s g(t) 103t3 3tc(t) 1 e cos4t e si n4t413-2 温度计的传递函数为 —,用其测量容器内的水温,1min 才能显示出该温度的Ts 198%的数值。
若加热容器使水温按 10(C/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数由一阶系统阶跃响应特性可知: c(4T) 98 o o ,因此有 4T 1 min ,得出T 0.25 min 。
视温度计为单位反馈系统,则开环传递函数为(s)1K 1TG(s)—1(s) Tsv 1用静态误差系数法,当r(t) 10t 时,e ss10 10T 2.5 C oK(2) 0.04c(t)0.24c(t) c(t)r(t)试求系统闭环传递函数① 部初始条件为零。
解:(s),以及系统的单位脉冲响应 g(t)和单位阶跃响应 c(t)。
已知全(1)因为 0.2sC(s)2R(s) 闭环传递函数(s)C(s) 10R(s) s单位阶跃响应c(t) C(s) 10/s 2c(t) 10t t 0(2) (0.04s 20.24s 1)C(s) R(s)C (s )闭环传递函数(s)C(s) R(s)120.04s0.24s 1单位脉冲响应:C(s)120.04s 2 0.24s 1g(t)25 e 33tsi n4t单位阶跃响应h(t) C(s)25 s[(s 3)216]1 s 6 s (s 3)216(s)1 Ts 1解法二依题意,系统误差疋义为e(t) r(t) c(t),应有e(s)E(s)1 C(s)R(s)11 TsR(s) Ts 1 Ts 13-3 已知二阶系统的单位阶跃响应为c(t) 10 12.5e 1.2t sin(1.6t 53.1o)试求系统的超调量c%、峰值时间t p和调节时间t'si n( 1n t )t p Jl- 1.96(s■1 2n1.63.5 3.5t s 2.92(s)n 1.2或:先根据c(t)求出系统传函,再得到特征参数,带入公式求解指标。
自动控制原理第3章 习题及解析

自动控制原理(上)习 题3-1 设系统的结构如图3-51所示,试分析参数b 对单位阶跃响应过渡过程的影响。
考察一阶系统未知参数对系统动态响应的影响。
解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式:111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时,系统响应速度变慢;当/0T K b -<<时,系统响应速度变快。
3-2 设用11Ts +描述温度计特性。
现用温度计测量盛在容器内的水温,发现1min 可指示96%的实际水温值。
如果容器水温以0.1/min C ︒的速度呈线性变化,试计算温度计的稳态指示误差。
考察一阶系统的稳态性能分析(I 型系统的,斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数,进一步得到时间响应函数为:()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温,由题意得到:600.961Te-=-推出18.64T =,此时求输入为()0.1r t t =⋅时的稳态误差。
由一阶系统时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差为:lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10,并保证总的放大倍数不变,试选择H K 和0K 的值。
解 一阶系统的调节时间s t 与时间常数成正比,则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++)比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-)试求系统的超调量%σ,峰值时间p t ,上升时间r t 和调节时间s t 。
自控第三章答案

K
p
不稳定
稳定
0
K
d
不稳定
不稳定
临界阻尼轨迹: D ( s ) s 4 K d s 4 K
2 p
0 出现重根时
p
临界阻尼条件为: 即: K
2 d
4 K
2
2 d
4 4K
0 线。
K p , 以纵轴为对称轴的抛物 K K
2 d 2 d
过阻尼区: 欠阻尼区: K
B3.15 分析图B3.15所示的两个系统,引入与不引入反馈时 系统的稳定性 。
解 不引入反馈 显然不稳定。 引入反馈 D ( s ) s ( s 1 )( s 5 ) 10 ( s 1 ) 0 闭环稳定。 (s ) 10 ( s 1 ) s ( s 1 )( s 5 )
3
赫尔维茨判据: 9 100 D2 20 1 100 9 80 0
1 20 4 100
2
1
0
故系统是稳定的。
(3)s4+4s3+13s2+36s+K=0
解
(1 ) 劳思判据: s s s s s
4
1 4 4 36 K K
13 36 K K
K 0
3
2
1
0
若系统稳定,则
36 K 0 0 K 36 K 0
( 2 )由
G (s )
7(s 1) s ( s 4 )( s 2 s 2 )
2
0 . 875 ( s 1 ) s ( 0 . 25 s 1 )( 0 . 5 s s 1 )
2
可知系统为
1
型的,于是
自动控制第三章习题答案

一、主要内容• 系统时域分析(性能指标的定义、二阶欠阻尼系统计算) • 稳定性(概念、充要条件、劳斯判据) •稳态误差(概念、求解、与系统型别关系)二、基本概念1) 典型输入信号2) 动态过程和稳态过程在典型输入信号作用下,任何一个控制系统的时间响应可以分成动态过程和稳态过程两部分。
1.动态过程动态过程又称过渡过程或瞬态过程,指系统在典型输入倍导作用下,系统输出量从初始状态到最终状态的响应过程。
表现为衰减、发放或等幅振荡形式。
用动态性能描述动态过程的时域性能指标。
2.稳态过程稳态过程又称为稳态响应。
系统在典型输入情号作用下,当时间t 趋于无穷时,系统输出量的表现方式。
反映系统输出量最终复现输入量的程度。
用稳态性能描述稳态过程的时域性能指标。
3) 动态性能指标通常以阶跃响应来定义动态过程的时域性能指标• 延迟时间T d (delay time):响应曲线第一次达到其终值A(m)的一半所需的时间;• 上升时间T r (rise time):响应从终值的10%上升到终值的90%所需的时间,对于有振荡的系统,亦可定义为响应从零第一次上升到终值所需的时间;• 峰值时间T p (peak time):响应超过其终值到达第一个峰值所需的时间;• 调节时间T s (settle time):响应到达并保持在终值的5%之内所需的最短时间; •超调量σ%:4) 稳定性• 平衡位置:• 稳定性:指系统和扰动消失后,由初始偏差状态恢复到原平衡状态的性能。
•线性控制系统的稳定性:在初始扰动的影响下,其动态过程随时间的推移逐渐衰减并趋于零(原平衡点),则称系统浙近稳定。
5) 稳态性能——稳态误差通常用在阶跃函数、斜坡面数或加速度函数作用下系统的稳态误差来报述。
用于衡量系统的控制精度和抗干扰能力。
•误差的基本定义– 在系统输入端定义的误差: – 在系统输出端定义的误差: • 稳态误差:•系统型别:为开环系统在s 平面坐标原点上的极点重数。
自动控制原理第三章答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t 25.1e 0125.0)t (k -=,试求系统闭环传递函数)s (Φ。
解 [])25.1s /(0125.0)t (k L )s (+==Φ3-2 一阶系统结构如图所示。
要求单位阶跃输入时调节时间4.0t s ≤s (误差带为5%),稳态输出为2,试确定参数21k ,k 的值。
解 由结构图写出闭环系统传递函数 1k k s k 1k k s k sk k 1s k )s (212211211+=+=+=Φ 闭环增益2k 1k 2==Φ, 得:5.0k 2= 令调节时间4.0k k 3T 3t 21s ≤==,得:15k 1≥。
3-3 给定典型二阶系统的设计指标:超调量0<%32.4%≤σ,调节时间 s 5.0t s <,峰值时间s 1t p <,试确定系统极点配置的区域,以获得预期的响应特性。
解 依题 %32.4%≤σ, )45(707.0︒≤≥⇒βξ;5.05.3t ns <ωξ=, 7n >ωξ⇒; n p t ωξπ21-=1<, 14.312>-⇒n ωξ综合以上条件可画出满足要求的特征根区域如图所示。
3-4 电子心脏起博器心律控制系统结构如图所示,其中模仿心脏的传递函数相当于一纯积分环节。
解 依题,系统传递函数为2n n 22n 2s 2s 05.0K s 05.01s 05.0K)s (ω+ξω+ω=++=Φ ⎪⎪⎩⎪⎪⎨⎧ω⨯=ξ=ωn n 205.0105.0K 令 5.0=ξ可解出 ⎩⎨⎧=ω=2020K n将 s 1t =代入二阶系统阶跃响应公式 ()β+ωξ-ξ--=ξω-t 1sin 1e 1)t (h n 22tn 可得 min 00145.60s 000024.1)1(h 次次==5.0=ξ时,系统超调量 %3.16%=σ,最大心速为min 78.69163.1163.01t (h p 次次)==+=3-5 机器人控制系统结构如图所示, 试确定参数21k ,k 值,使系统阶跃响应的峰值时间5.0t p =s ,超调量%2%=σ。
自动控制原理第三章课后习题 答案(最新)要点

3-1(1) )(2)(2.0t r t c= (2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4s i n 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T s Ts Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 23-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ%、峰值时间tp 和调节时间ts 。
自动控制原理第三章课后习题 答案(最新)

3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c =&(2) )()()(24.0)(04.0t r t c t c t c =++&&&试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC = 闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
自动控制原理 第3章习题解答
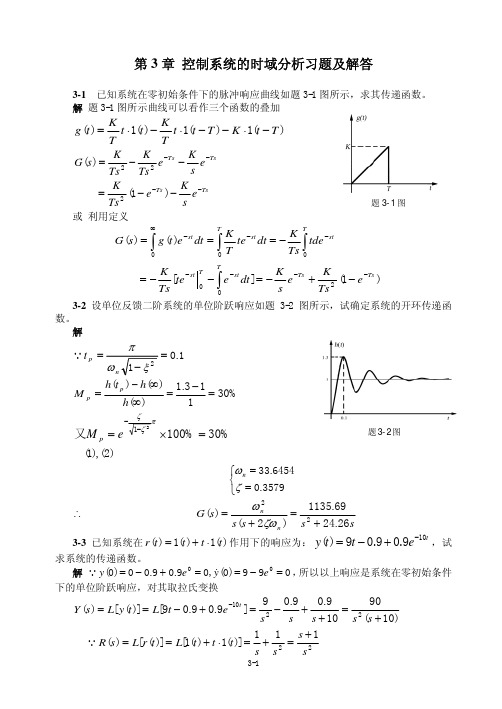
1−ζ 2 = π
ζ
3
2π
tr
=
π −β ωd
=
3 3
=
23 9
π
;t p
=π ωd
=
π 3
=
3π 3
−ζ π
M p = e 1−ζ 2 ×100% = 16.3% ;
t
5% s
=3 ζω n
=
3s,
t
2% s
=4 ζω n
= 4s
3-6 系统结构图如题 3-6 图所示,试求当τ = 0 时,
系统的ζ 和ωn 之值,如要求ζ =0.7,试确定参数τ 。
s2
0.8
1+ K
s1 0.8(2 + K ) − (1 + K ) 0
0.8
s0 1+ K
Q 系统临界稳定
∴ 0.8(2 + K ) − (1 + K ) = 0
即K = 3 即系统的临界增益K = 3
由s 2行构成辅助多项式:0.8s 2 + (1 + K ) = 0
即0.8s 2 + 4 = 0 ∴ s1,2 = ± j 5 = ± j2.24 ∴系统的振荡频率为ωn = 2.24rad / s
= 150.5°
h(t) = 1 − 0.06e−5.76t + 1.07e−0.37t cos(1.27t + 150.5°)
3-4
已知根据主导极点 s1,2 确定的调整时间为 10.82s,考察这一时刻系统单位阶跃响应中
的指数项值 − 0.06e−5.76t |t=10.82 = −5.15 ×10−29 ,可见指数项值在 ts = 10.82 时已经衰减到 微不足道的程度。事实上,在峰值时间 t p = 2.48s ,指数项的值为 − 3.7 ×10−8 ,可见对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参考答案3-1. 设温度计需要在一分钟内指示出响应值的98%,并且假设温度计为一阶系统,求时间常数T 。
如果将温度计放在澡盆内,澡盆的温度以10/min C ︒的速度线性变化,求温度计的误差。
解:()()98%c t c =∞⨯,41min t T ==,0.25T =;()10r t t =,()10()t Tc t t T e-=-+,()()()10()tTe t r t c t T e-=-=-,lim ()10 2.5ss t e e t T →∞===3-2.已知单位负反馈系统的开环传递函数为4()5G s s =+ 求系统的单位阶跃响应。
解:24()54s s s φ=++,1()R s s=, 21444133()()()(54)(4)(1)41C s s R s s s s s s s s s s φ=⋅===+-++++++; 414()133t t c t e e --=+-3-3. 已知单位负反馈系统的开环传递函数为1()(1)G s s s =+ 求系统的上升时间r t 、峰值时间p t 、超调量%σ和调整时间s t 。
解:2()1()1G s R s s s =++,2121n n ωωξ⎧=⎪⎨=⎪⎩,10.5n ωξ=⎧⎨=⎩,0.866d ω=,arccos 60βξ︒== 2.42r d t πβω-==s , 3.63p dt πω==s,%100%16%eσ=⨯=,48s nt ξω==s3-4. 已知系统的单位阶跃响应:为6010()10.2 1.2t t c t e e --=+-,试求:(1)系统的闭环传递函数;(2)系统的阻尼比ξ和无阻尼自然振荡频率n ω。
解:10.2 1.2600()6010(60)(10)C s s s s s s s =+-=++++,1()R s s =, 2()600()70600C s R s s s =++,2600270n nωωξ⎧=⎪⎨=⎪⎩,24.51.43n ωξ=⎧⎨=⎩3-5. 已知单位负反馈系统的开环传递函数为:()(1)KG s s Ts =+当()()r t t ε=时,系统的动态性能指标%30%σ=,0.3(5%)s t s ≤∆=,求系统K 、T 值以满足动态指标。
解:22()1()KC s K T KR s Ts s K s s T T ==++++, 30.3s nt ξω=≤,12n Tξω=,10n ξω≥,0.05T ≤%0.3eσ=≤,0.35ξ≥,28.6n ω≥,2817.96n KTω==,40.9K ≥3-6.闭环系统的特征方程如下,试用老四判据判断系统的稳定性。
(1)322091000s s s +++= (2)4328181650s s s s ++++= 解:(1)322091000s s s +++= 列劳斯表如下: 321019201004100s s s s系统稳定(2)4328181650s s s s ++++= 列劳斯表如下: 43211185816165216165s s s s s系统稳定 3-7.已知单位负反馈系统的开环传递函数为()(4)(10)KG s s s s =++ (1)试确定系统稳定时的K 值范围;(2)确定使闭环极点的实部不大于-1的K 值范围。
解:(1)系统的闭环传递函数为32()1440Ks s s s Kφ=+++特征方程为:3214400s s s K +++= 列劳斯表如下:3211401456014s s KK s s K-若使系统稳定,则有5600,014KK ->>,所以0560K <<。
(2)令'1s s =-,代入()(4)(10)KG s s s s =++得:(')('1)('3)('9)KG s s s s =-++闭环传递函数为:32(')'11'15'27Ks s s s Kφ=++-+特征方程为: 32'11'15'270s s s K ++-+= 列劳斯表如下: 32111511271921127s s KKs s K-+--+ 若使系统稳定,则有1920,(27)011KK ->-+>,所以27192K <<。
3-8.已知系统的结构如题图3.1所示,试问τ取值多少,系统才能稳定?题图3.1解:22110(1)10(1)()10(10)s s G s s s s s s s s ττ++==++++32210(1)()101010s s s s s s φτ+=++++ 列劳斯表如下:321310110(110)1010s s s b s τ+若使系统稳定,3110(110)100110b ττ+-=>+,即0τ>。
3-9.已知单位反馈控制系统的开环传递函数如下。
试求各系统的静态位置误差系数p K 、速度误差系数v K 和加速度误差系数a K ,并确定当输入信号为()()r t t ε=,2t ,2t 和212t t ++时系统的稳态误差ss e 。
(1)20()(0.11)(0.21)G s s s =++;(2)200()(2)(10)G s s s s =++;(3)2210(21)()(410)s G s s s s +=++;(4)2()(4200)KG s s s s =++ 解:(1)20()(0.11)(0.21)G s s s =++010202301lim ()()201210,lim ()()0lim ()()0ss p s v ss s ss a s R e K G s H s K K sG s H s e e K s G s H s ν→→→⎧====+⎪⎪====∞⎨⎪=∞==⎪⎩,所以ss e =∞ (2)2002()(2)(10)(0.51)(0.11)G s s s s s s s ==++++ 100202300lim ()()1,lim ()()100.2lim ()()0ss p s v ss s a ss s e K G s H s vK sG s H s e K K s G s H s e ν→→→=⎧==∞⎪⎪=====⎨⎪===∞⎪⎩,所以ss e =∞(3)222210(21)(21)()(410)(0.10.41)s s G s s s s s s s ++==++++ 01202030lim ()()02,lim ()()0lim ()()12p s ss v ss s a ss s aK G s H s e K sG s H s e aK s G s H s e K ν→→→⎧==∞=⎪⎪===∞=⎨⎪==⎪==⎩,所以2ss e = (4)2()(4200)KG s s s s =++ 闭环传递函数为:32()4200Ks s s s Kφ=+++特征方程为:3242000s s s K +++= 列劳斯表如下: 321120048004s s KK s s K-系统稳定的条件为:0800K <<22200()(4200)(0.0050.021)KK G s s s s s s s ==++++ 01020230lim ()()04002,lim ()()200lim ()()0p s ss v ss s a a ss s K G s H s e v K K sG s H s e K K K s G s H s e ν→→→==∞⎧=⎪⎪=====⎨⎪==⎪=∞⎩,所以ss e =∞ 3-10.已知系统的结构图如题图3.2所示,若使系统满足阻尼比0.7ξ=和单位斜坡函数输入时稳态误差ss e =0.25,试确定参数K 和τ的取值。
题图3.2解:22()12(1)2KK K G s s s K s s s K τττ+==++++,所以2()(2)K s s K s K φτ=+++ 222n nK K ωωξτ⎧=⎪⎨=+⎪⎩又因为20.25ss K e K τ+== 解之得:31.6,0.186K τ==3-11.已知系统的结构图如题图3.3所示,其中()()r t t ε=,1()()d t t ε=,2()()d t t ε=。
试求:(1)在()r t 作用下系统的稳态误差;(2)在1()d t 和2()d t 同时作用下系统的稳态误差; (3)在1()d t 作用下,且()p K G s K s =+和1()F s Js=时,系统的稳态误差。
题图3.3解:(1)在()r t 作用下系统的稳态误差011lim 1()()1(0)(0)ssrs s e s G s F s G F →=⋅=++(2)212()()()()1()()()d G s H s E d D s G s G s H s -=⋅+0()11[1()]lim 1()()1()()1(0)(0)ssd s F s F s e s G s F s G s F s s G F →⎡⎤---+=⋅+⋅=⎢⎥+++⎣⎦(3)1(),()p K G s K F s s Js=+= 001()11lim lim 011()()1()ssds s pF s Js e s s KG s F s s sK s Js→→--=⋅⋅=⋅⋅=+++⋅。
