七年级新思维26-图形面积的计算
几何图形的面积计算

几何图形的面积计算几何图形的面积计算是数学中非常重要的一部分,它涉及到了诸多的几何知识和计算方法。
在几何学中,面积是用来描述平面图形所占的空间大小的一个指标。
不同的几何图形有不同的面积计算公式,下面将会一一介绍各个常见几何图形的面积计算方法。
一、矩形的面积计算矩形是最简单的几何图形之一,它的面积计算公式是:面积 = 长 ×宽。
例如,一个矩形的长为5cm,宽为3cm,那么它的面积 = 5cm ×3cm = 15cm²。
二、三角形的面积计算三角形也是常见的几何图形,它的面积计算公式是:面积 = 1/2 ×底边长 ×高。
例如,一个三角形的底边长为4m,高为6m,那么它的面积 = 1/2 ×4m × 6m = 12m²。
三、圆形的面积计算圆形是一种特殊的几何图形,其面积计算公式是:面积= π × 半径²。
其中,π是一个无理数,约等于3.14159。
半径是圆的半径长度。
例如,一个圆的半径为5cm,那么它的面积 = 3.14159 × 5cm × 5cm= 78.54cm²。
四、正方形的面积计算正方形是边长相等的矩形,因此它的面积计算公式与矩形相同,即:面积 = 边长 ×边长。
例如,一个正方形的边长为7cm,那么它的面积 = 7cm × 7cm =49cm²。
五、梯形的面积计算梯形也是一种常见的几何图形,它的面积计算公式是:面积 = 1/2 ×(上底 + 下底) ×高。
例如,一个梯形的上底为4cm,下底为8cm,高为5cm,那么它的面积 = 1/2 × (4cm + 8cm) × 5cm = 30cm²。
六、圆环的面积计算圆环是由两个同心圆围成的区域,它的面积计算公式是:面积= π× (外圆半径² - 内圆半径²)。
初一几何图形的面积计算

初一几何图形的面积计算几何图形是数学中的重要概念,通过计算几何图形的面积可以帮助我们更好地理解和应用几何知识。
在初一阶段,我们学习了一些基本的几何图形,比如正方形、矩形、三角形和圆形,下面将介绍这些图形的面积计算方法。
正方形正方形是边长相等的四边形,所有内角都是直角。
计算正方形的面积非常简单,只需要将正方形的边长乘以边长即可得到面积。
假设正方形的边长为a,则正方形的面积S为:S = a * a矩形矩形是边长不等的四边形,所有内角都是直角。
计算矩形的面积也很简单,只需要将矩形的长乘以宽即可得到面积。
假设矩形的长为a,宽为b,则矩形的面积S为:S = a * b三角形三角形是由三条边和三个内角组成的图形。
计算三角形的面积需要根据已知条件使用不同的公式。
以下介绍几种常见的计算方法。
1. 已知底和高假设三角形的底为b,高为h,则三角形的面积S为:S = (1/2) * b * h2. 已知两边和夹角假设三角形的两边分别为a和b,夹角为θ,则三角形的面积S为:S = (1/2) * a * b * sin(θ)3. 海伦公式当已知三角形的三边长分别为a、b、c时,可以使用海伦公式来计算三角形的面积。
假设半周长为s,则三角形的面积S为:S = √(s * (s - a) * (s - b) * (s - c))其中,s = (a + b + c) / 2圆形圆形是由一个半径为r的圆心和无数个等距离圆心的点组成的图形。
计算圆形的面积需要使用圆周率π。
假设圆形的半径为r,则圆形的面积S为:S = π * r * r综上所述,初一阶段几何图形的面积计算方法包括正方形的边长乘以边长、矩形的长乘以宽、直角三角形的底乘以高除以2、一般三角形的两边乘以夹角的正弦比除以2以及圆形的半径乘以半径再乘以π。
通过掌握这些计算方法,我们可以准确地计算各种几何图形的面积,进一步提升数学学习的能力和应用能力。
利用图形的面积计算

利用图形的面积计算图形的面积计算是数学中重要的一部分,通过计算图形的面积可以帮助我们解决实际问题,例如计算土地面积、房间面积、庭院面积等等。
本文将介绍几种常见图形的面积计算方法,包括正方形、矩形、三角形和圆形。
正方形的面积计算方法:正方形的边长相等,因此可以通过一个边长的平方来计算面积。
假设正方形的边长为a,则正方形的面积S = a * a。
矩形的面积计算方法:矩形的两个相邻边相等,可以通过两个相邻边的乘积来计算面积。
假设矩形的两个相邻边分别为a和b,则矩形的面积S = a * b。
三角形的面积计算方法:对于普通三角形,可以使用海伦公式或直角三角形的面积公式来计算面积。
海伦公式:海伦公式适用于已知三角形的三条边长,假设三角形的三条边长分别为a、b和c,半周长(即三边之和的一半)为p,则三角形的面积S = √(p * (p - a) * (p - b) * (p - c))。
直角三角形的面积公式:对于直角三角形,假设直角边的长度分别为a和b,则直角三角形的面积S = (a * b) / 2。
圆形的面积计算方法:圆形的面积计算方法与半径相关,假设圆的半径为r,则圆的面积S = π * r²,其中π是一个常数,约等于3.14159。
需要注意的是,面积的单位需要与图形的尺寸单位保持一致。
例如,若图形的尺寸单位为米,则计算出的面积单位为平方米。
除了上述介绍的几种常见图形的面积计算方法,还有其他复杂图形的面积计算方法,如梯形、扇形等。
这些复杂图形的面积计算方法需要根据具体的图形特征来确定。
在实际应用中,可以通过将复杂图形分解为简单图形的组合,然后计算各部分的面积并相加,来计算整个图形的面积。
总结:图形的面积计算可以帮助我们解决实际问题。
本文介绍了常见图形(正方形、矩形、三角形和圆形)的面积计算方法,对于复杂图形,可以分解为简单的图形进行计算。
通过正确运用面积计算方法,我们可以更好地应用数学知识解决实际问题。
图形的面积计算方法

图形的面积计算方法面积是图形的一个重要属性,它描述了图形所占有的平面区域的大小。
计算图形的面积是数学中一个基本的问题,而不同类型的图形有不同的面积计算方法。
本文将为您介绍几种常见图形的面积计算方法。
一、长方形的面积计算方法长方形是一种矩形,它的两边长度不同,但相邻两边分别相等。
长方形的面积计算方法非常简单,只需要将长方形的长度与宽度相乘即可计算得出。
设长方形的长度为l,宽度为w,则其面积S可以表示为:S = l × w。
二、正方形的面积计算方法正方形是一种特殊的长方形,它的四条边长度都相等。
正方形的面积计算方法与长方形类似,也是将正方形的边长平方即可。
设正方形的边长为a,则其面积S可以表示为:S = a × a = a²。
三、三角形的面积计算方法三角形是由三条边所围成的图形,它没有平行边。
计算三角形的面积需要使用三角形的底和高的长度。
设三角形的底为b,高为h,则其面积S可以表示为:S = 1/2 × b × h。
四、圆形的面积计算方法圆形是一个完全由曲线所围成的图形,其特点是任意两点到圆心的距离都相等。
计算圆形的面积需要使用圆的半径。
设圆的半径为r,则其面积S可以表示为:S = π × r²,其中π是一个常数,近似取值为3.14159。
五、梯形的面积计算方法梯形是一个由两条平行边和两条非平行边所围成的图形。
计算梯形的面积需要使用梯形的上底、下底及高的长度。
设梯形的上底为a,下底为b,高为h,则其面积S可以表示为:S = 1/2 × (a + b) × h。
六、其他图形的面积计算方法除了上述几种常见图形外,还有许多其他类型的图形,如圆环、扇形、多边形等。
这些图形的面积计算方法不在本文的讨论范围内,但是它们的面积计算方法一般都可以通过将图形划分为若干个已知面积的基本图形来计算。
综上所述,计算图形的面积需要根据图形的类型选择相应的面积计算方法。
初一数学求面积知识点总结

初一数学求面积知识点总结一、简单图形的面积求解1. 长方形的面积求解长方形的面积就是长乘以宽,公式为:S = 长 * 宽。
2. 正方形的面积求解正方形的面积就是边长的平方,公式为:S = 边长 * 边长。
3. 三角形的面积求解三角形的面积为底边乘以高再除以2,公式为:S = 底 * 高 / 2。
4. 平行四边形的面积求解平行四边形的面积为底边乘以高,公式为:S = 底 * 高。
二、复杂图形的面积求解1. 梯形的面积求解梯形的面积为上底加下底乘以高再除以2,公式为:S = (上底 + 下底) * 高 / 2。
2. 圆的面积求解圆的面积公式为:S = π * r²,其中π为圆周率,r为半径。
3. 扇形的面积求解扇形的面积为圆的面积乘以弧度再除以360,公式为:S = π * r² * (θ/360),其中r为半径,θ为扇形的弧度。
三、多边形的面积求解1. 正多边形的面积求解正n边形的面积为:S = 1/4 * n * a² * cot(π/n)。
2. 不规则多边形的面积求解不规则多边形的面积可以通过分割成简单图形后分别求解,然后累加得出整个多边形的面积。
四、特殊图形的面积求解1. 等腰梯形的面积求解等腰梯形的面积为上底加下底乘以高再除以2,公式为:S = (上底 + 下底) * 高 / 2。
2. 菱形的面积求解菱形的面积为对角线相乘再除以2,公式为:S = d1 * d2 / 2,其中d1和d2为菱形的对角线。
五、面积求解的实际应用1. 园艺设计中的面积求解在园艺设计中,需要求解花坛或草坪的面积,以确定种植花卉或进行铺装的材料数量。
2. 建筑工程中的面积求解在建筑工程中,需要求解墙面、地面或天花板的面积,以确定需要购买的施工材料数量。
3. 地理测量中的面积求解在地理测量中,需要求解地块或地形的面积,以确定土地的地理位置或资源利用价值。
六、常见错误及解决方法1. 面积单位错误面积单位通常为平方厘米(cm²)、平方米(m²)或平方公里(km²),在求解面积时需要注意使用相应的单位,避免引起计算错误。
初中数学面积问题总结归纳

初中数学面积问题总结归纳
在初中数学中,面积问题主要涉及到平面图形的面积计算。
以下是在初中数学中常见的面积问题总结归纳:
1. 矩形的面积计算:矩形的面积可以通过长度和宽度的乘积来计算,即面积 = 长 ×宽。
2. 正方形的面积计算:正方形的边长相等,所以正方形的面积可以通过边长的平方来计算,即面积 = 边长 ×边长。
3. 三角形的面积计算:三角形的面积可以通过底边长和高的乘积再除以2来计算,即面积 = 底边长度 ×高 ÷ 2。
4. 平行四边形的面积计算:平行四边形的面积可以通过底边长和高的乘积来计算,即面积 = 底边长度 ×高。
5. 梯形的面积计算:梯形的面积可以通过上底与下底之和的一半再乘以高来计算,即面积 = (上底 + 下底) ×高 ÷ 2。
6. 圆的面积计算:圆的面积可以通过半径的平方再乘以π(pi)来计算,即面积 = 半径 ×半径× π。
在解决这些面积问题时,需要注意图形的参数,如边长、底边长、高、半径等,并且对于复杂图形,可能需要将其分解为多个基本图形来计算面积。
此外,也要注意单位的转换和精确计算的问题。
初一数学培优之图形面积的计算
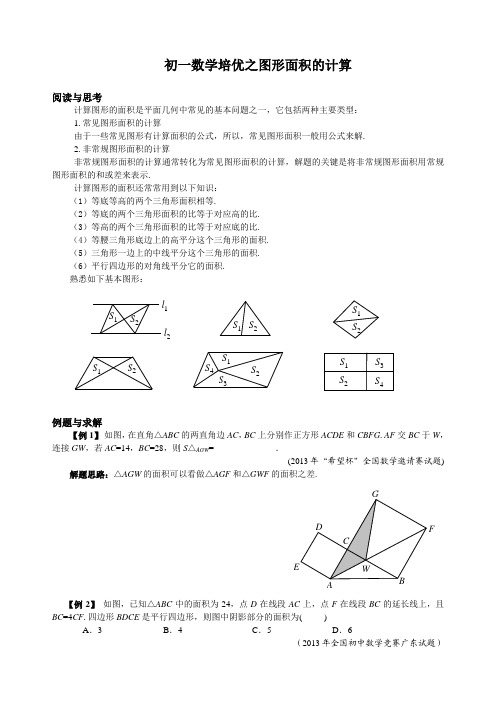
初一数学培优之图形面积的计算阅读与思考计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常规图形面积的和或差来表示.计算图形的面积还常常用到以下知识:(1)等底等高的两个三角形面积相等.(2)等底的两个三角形面积的比等于对应高的比. (3)等高的两个三角形面积的比等于对应底的比. (4)等腰三角形底边上的高平分这个三角形的面积. (5)三角形一边上的中线平分这个三角形的面积. (6)平行四边形的对角线平分它的面积. 熟悉如下基本图形:S 3S 4S 3S 4S 1S 2S 1S 2S 1S 2S 1S 2S 1S 2S 2S 1l 2l 1例题与求解【例1】 如图,在直角△ABC 的两直角边AC ,BC 上分别作正方形ACDE 和CBFG .AF 交BC 于W ,连接GW ,若AC =14,BC =28,则S △AGW =______________.(2013年“希望杯”全国数学邀请赛试题)解题思路:△AGW 的面积可以看做△AGF 和△GWF 的面积之差.F【例2】 如图,已知△ABC 中的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF .四边形BDCE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .5D .6(2013年全国初中数学竞赛广东试题)解题思路:设△ABC 底边BC 上的高为h .本例关键是通过适当变形找出h 和DE 之间的关系.FC B【例3】 如图,平行四边形ABCD 的面积为30cm 2,E 为AD 边延长线上的一点,EB 与DC 交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9cm 2,AD =5cm ,求DE 长.(北京市“迎春杯”竞赛试题)解题思路:由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其它线段表示.BACFDE【例4】 如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形,已知BE =80 cm ,CE =60 cm ,DE =40 cm ,AE =30 cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗庚杯”竞赛决赛试题)解题思路:甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.丁乙丙甲E BCDA【例5】 如图,△ABC 的面积为1,D ,E 为BC 的三等分点,F ,G 为CA 的三等分点,求四边形PECF 的面积.解题思路:连CP ,设S △PFC =x ,S △PEC =y ,建立x ,y 的二元一次方程组.Q P FG ED CBA【例6】如图,E,F分别是四边形ABCD的边AB,BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC.求梯形APCQ的面积与平行四边形ABCD的面积的比值.(2013年”希望杯“数学邀请赛试题)解题思路:连接EF,DF,AC,PB,设S□ABCD=a,求得△APQ和△CPQ的面积.F DB能力训练A 级1.如图,边长为1的正方形ABCD的对角线相交于点O.过点O的直线分别交AD,BC于E,F,则阴影部分面积是______.F CB(海南省竞赛试题)2.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是_____________平方厘米.EFDCBA(“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB ,BC ,CD ,DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是____________.C(安徽省中考试题)4.如图,已知AB ,CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是_________平方厘米.C(“祖冲之杯”邀请赛试题)5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF =BC 31,则长方形ABCD的面积是阴影部分面积的( )倍.A .2B . 3C . 4D .5F CBE6.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ).A .c b a ab )(+-B . c b a ab )(--C .))((c b c a --D .))((c b c a +-7.如图,线段AB =CD =10cm ,»BC和»DA 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心、DC 为半径的圆面积的41,则阴影部分的面积是( ). A .25π B . 100 C .50π D .200CD(“五羊杯”竞赛试题)8.如图,一个大长方形被两条线段AB 、CD 中分成四个小长方形,如果其中图形Ⅰ,Ⅱ,Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ). A .29 B .27 C .310 D .815BDA9.如图,长方形ABCD 中,E ,F 分别为AD ,BC 边上的任一点,△ABG ,△DCH 的面积分别为15和20,求阴影部分的面积.CF B(五城市联赛试题)10.如图,正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的边长为4,求△DEK 的面积.KEB AD(广西壮族自治区省南宁市中考试题)B 级1.如果图中4个圆的半径都为a ,那么阴影部分的面积为_____________.(江苏省竞赛试题)2.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是_________cm 2.DCFE BA(北京市“迎春杯”邀请赛试题)3.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为___________________.(“希望杯”邀请赛试题)4.如图,若正方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是_____.CMNDQB A(“五羊杯”竞赛试题)5.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次“生长”,在得到的多边上类似“生长”,一共“生长”三次后,得到的多边形的边数=________,面积是原三角形面积的______倍.第2次生长第1次生长原图(“五羊杯”竞赛试题)6.如图,在长方形ABCD 中,AE =BG =BF =21AD =31AB =2,E ,H ,G 在同一条直线上,则阴影部分的面积等于( ).A .8B .12C .16D .20F BGCDA7.如图,边长分别为8cm 和6cm 的两个正方形,ABCD 与BEFG 并排放在一起,连接EG 并延长交AC 于K ,则△AKE 的面积是( ).A .48cm 2B .49cm 2C .50cm 2D .51cm 2FEB A(2013年“希望杯”邀请赛试题)8.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆外部分的面积之和记为S 2,则21S S 的整数部分是( ).A .0B .1C .2D .3(全国初中数学联赛试题)9.如图,△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是( ).A .25B .30C .35D .40GFE CBDA10.已知O (0,0),A (2,2),B (1,a ),求a 为何值时,S △ABO =5?11.如图,已知正方形ABCD 的面积为1,M 为AB 的中点,求图中阴影部分的面积.CAD(湖北省武汉市竞赛试题)12.如图,△ABC中,21===FAFBECEADBDC.求的面积△的面积△ABCGHI的值.GIHEDCBFA(“华罗庚金杯”邀请赛试题)。
【初一方法归纳专题】平面直角坐标系中图形面积的求法

【初⼀⽅法归纳专题】平⾯直⾓坐标系中图形⾯积的求法Hello,各位⽼铁周末愉快应部分⽼铁的要求今天分享平⾯直⾓坐标系中⾯积的求法好了话不多说~~上货~~回顾篇——知识链接1.⾯积公式:(1)三⾓形的⾯积:S三⾓形=1/2×底×⾼(2)梯形的⾯积:S梯形=1/2×(上底+下底)×⾼2.两点间的距离:(1)当两点横坐标相同时,两点间的距离为这两点纵坐标差的绝对值(2)当两点纵坐标相同时,两点间的距离为这两点横坐标差的绝对值基础篇——三⾓形⾯积的求法题型1 三⾓形有⼀边在坐标轴上【例1】如图,平⾯直⾓坐标系中,已知三⾓形ABC的三个顶点的坐标分别是A(2,3),B(-4,0),C(4,0),求三⾓形ABC的⾯积.温馨提⽰:【思路及解答】请观看视频【⽅法归纳】当三⾓边有⼀边在坐标轴上时,将此边作为底边,那么⾼便垂直于坐标轴,底和⾼就能通过两点间的距离很快求出.题型2 三⾓形有⼀边与坐标轴平⾏【例2】如图,平⾯直⾓坐标系中,已知三⾓形ABC的三个顶点的坐标分别是A(-1,-4),B(2,0),C(-4,-4),求三⾓形ABC的⾯积.温馨提⽰:【思路及解答】请观看视频【⽅法归纳】当三⾓边有⼀边与坐标轴平⾏时,将此边作为底边,那么⾼便垂直于坐标轴,底和⾼就能通过两点间的距离很快求出.根据图形特殊,我们通常把平⾏于坐标轴的⼀边作为底边.题型3 三⾓形三边均不与坐标轴平⾏【例3】在如图所⽰的正⽅形⽹格中,每个⼩正⽅形的单位长度均为1,三⾓形ABC的三个顶点恰好是正⽅形⽹格的格点.(1)写出图中所⽰各顶点的坐标;(2)求三⾓形ABC的⾯积.温馨提⽰:【思路及解答】请观看视频【⽅法归纳】当三⾓边的三边均不与坐标轴平⾏时:(1)将原三⾓形围在⼀个梯形或长⽅形中,⽤长⽅形或梯形的⾯积,减去长⽅形或梯形边缘的直⾓三⾓形的⾯积,即可求得原三⾓形的⾯积,这种⽅法叫做补形法;(2)若三⾓形内⼀割线长度已知,并且它平⾏于坐标轴,那么可将其作为底边,把原三⾓形拆分为两个三⾓形,则两⾼的长度可得,⾯积即可求得,这种⽅法叫做分割法.以上两种⽅法就是数学⼏何图形运算中常⽤的割补法.例题讲授视频三⾓形⾯积的求法同学们,例题看明⽩了吗?⽅法掌握了吧!快来试试下⾯的变式训练吧!变式训练【变式训练1】如图,在平⾯直⾓坐标系中,三⾓形ABC的顶点坐标分别为A(-3,0),B(0,3),C(0,-1),则三⾓形ABC的⾯积为.答案6【变式训练2】如图,三⾓形ABC三个顶点的坐标分别为A(4,2),B(4,6),C(-1,3),三⾓形ABC的⾯积为.答案10【变式训练3】如图,在平⾯直⾓坐标系中,已知点A(-3,-1),B(1,3),C(2,-3),你能求出三⾓形ABC的⾯积吗?答案提升篇——四边形⾯积的求法【例4】如图,在平⾯直⾓坐标系中,四边形ADCB各顶点的坐标分别是A(-3,4),D(2,3),C(2,0),B(-4,-2),且AB与x轴交点E的坐标为(,0),求这个四边形的⾯积.【变式训练4】在如图所⽰的平⾯直⾓坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(-4,10),B(-12,8),C(-14,0),求四边形OABC的⾯积.答案总结篇——割补法求⾯积我们将不能直接求解的图形的⾯积转化为可直接求解的⾯积,常⽤的⽅法是“分割”和“补形”.1.利⽤“补形法”求图形的⾯积:2.利⽤“分割法”求图形的⾯积:好记性不如烂笔头快快整理到笔记本上吧!找题⽬练练哦题⽬都给同学们准备好啦!专题⼩练1.已知点A(-2,3),B(4,3),C(-1,-3).(1)在平⾯直⾓坐标系中标出点A,B,C的位置;(2)线段AB的长为_______;(3)点C到x轴的距离为_______,点C到AB的距离为_______;(4)三⾓形ABC的⾯积为_______.2.(1)在平⾯直⾓坐标系中,描出下列3个点:A(﹣1,0),B(3,﹣1),C(4,3);(2)顺次连接A,B,C,组成△ABC,求△ABC的⾯积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26.图形面积的计算问题解决 例1 (“五羊杯”邀请赛试题)如图,梯形ABCD 被对角线分为4个小三角形,已知△AOB 和△BOC 的面积分别为225cm 和235cm ,那么梯形的面积是_______cm 2.【答案】144 AOD S =△235(cm )BOC S =,△ AOD DOCABO BOCS S DO S BO S ==,△△△△得249(cm )DOC S =△. 例2 (江苏省竞赛题)如图,正方形ABCD 和CEFG 的边长分别为m n 、,那么△AEG 的面积的值( ). A .只与m 的大小有关 B .只与n 的大小有关 C .与m n 、的大小都有关 D .与m n 、的大小都无关【答案】B 连AC AC ,∥GE ,212AGE GCE S S n ==△△.例 3 如图,三角形ABC 内的线段BD CE 、相交于点O ,已知2OB OD OC OE ==,.设三角形BOE 、三角形BOC 、三角形COD 和四边形AEOD 的面积分别为1234S S S S 、、、.(1)求1S ∶3S 的值; (2)如果22S =,求4S 的值.【答案】(1)23212S S S S ==,,得1S ∶31S =∶2.(2)由22S =,得1312S S ==,,连接OA ,设AOE S x =,△则1AOD AOB S S x ==+,△△ 因2AOC AOE S S =△△.故122x x ++=,解得314x x =+=,,所以4347S =+=.例4 如图,△ABC 的面积为1,D E 、为AC 的三等分点,F G 、为BC 的三等分点. 求:(1)四边形PECF 的面积; (2)四边形PFCN 的面积.【答案】(1)133133x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩①②①+②,得16x y +=,即16PECF S =四形边.AOBDCAB CD EF GABCD EON M Q GFE D CBA P(2)连NC ND ,,设NGB NCE S a S b ==,,△△则22NCG NEAS a S b ==,,△△则1332233a b a b ⎧+=⎪⎪⎨⎪+=⎪⎩解得121421a b ⎧=⎪⎪⎨⎪=⎪⎩,故1115321642BEC BNG PFGN PECF S S S S =--=--=四形四形△△边边.例5 (武汉市竞赛题)如图①,已知正方形ABCD 的面积为1,M 为AB 的中点.求图中阴影部分的面积.解法1 如图①,14AMD AMC AMG S S S ==,△△△为公共部分,所以AGD MCG S S =,△△因为AMG AMD 与△△的高相等(以A 为顶点作高),MCG MCD 与△△的高相等(以C 为顶点作高),所以AMG MCGAMD MCDS S MG S S MD==,△△△△即141142MCHMCG S S -=,△△解得1112663MCG S S ==⨯=影,△阴.M CM CB图①图②图③解法2 如图②,连接GB ,由正方形的对称性得ABG AGD S S =△△,又1122AMG ABG AGD S S S ==,△△△所以221122212343AGD AMD S S S ==⨯=⨯⨯=+影△△阴. 解法3 如图③,连接BD BG 、,设BD AC 、交于点O ,AMG S x =△,因为14AMD AOD ABCD S S S ==,△△所以GOD AOD AGD AMD AGD AMG S S S S S S x =-=-==△△△△△△. 又BOG GOD BMG AMG S S x S S x ====,,△△△△ 因为AOB AGM GOB BMG S S S S =++△△△△,即14x x x =++,所以112x =. 所以12().3AGD MCG AMD AMG S S S S S =+=-=影△△△△阴皮克公式例6 (江苏省常州市中考题)用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S ,它各边上格点的个数和为x .(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出与x 之间的关系式.答:_______.(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2个格点.此时所画的各个多边形的面积S 与它各边上格点的个数和x 之间的关系式是:S =_______.(3)请你继续探索,当格点多边形内部有且只有n 个格点时,猜想S 与x 有怎样的关系? 【答案】(1)111;(2)1;(3)1222S x S x S x n ==+=+-. 数学冲浪知识技能广场1.(江苏省竞赛题)如图,一个大正方形被2条线段分割成2个小正方形和2个长方形,如果175S =cm 2,2215cm S =,那么大正方形的面积S =_______cm 2.【答案】108 2.(《时代学习报》数学文化节试题)图中最大正方形的边长是10cm ,阴影部分的总面积是_______cm 2 【答案】25(第1题)ABCDEFG (第3题)(第2题)S 4S 3S 2S 13.(2012年“希望杯”邀请赛试题)如图,边长为4cm 的等边△ABC 沿边BC 向右平移2cm 得△DEF ,DE 与AC 交于点G ,则ABC ABFD S S =四形△边∶_______.【答案】2∶1 ABC ADFC S S =四形△边4.(河北省中考题)把三张大小相同的正方形卡片A B C ,,叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图①摆放时,阴影部分的面积为1S ;若按图②摆放时,阴影部分的面积为2S ,则1S _______2S (填“>”、“<”或“=”). 【答案】=图①图②(第6题)(第5题)(第4题)5.(“希望杯”邀请赛试题)如图,在直角扇形ABC 中,分别以AB AC 、为直径作半圆,两条半圆弧相交于点D ,整个图形被分成1234S S S S 、、、四部分,则2S 与4S 的大小关系是( ).A .24S S <B .24S S =C .24S S >D .无法确定的【答案】B 6.(黑龙江省中考题)已知在正方形网格中,每个小方形都是边长为1的正方形,A B 、两点的小方格的顶点上,位置如图所示,点C 也在小方格的顶点上,且以A B C 、、为顶点的三角形的面积为1个平方单位,则点C 的个数为( ). A .3个 B .4个 C .5个 D .6个 【答案】D 7.(“希望杯”邀请赛试题)如图,在长方形ABCD 中,11223AE BG BF AD AB =====,E H G 、、在同一条直线上,则阴影部分的面积等于( ). A .8 B .12 C .16 D .20【答案】B 8.(“希望杯”邀请赛试题)如图,凸四边形ABCD 中,对角线AC BD 、相交于O 点,若三角形AOD 的面积是2,三角形COD 的面积是1,三角形COB 的面积是4,则四边形ABCD 的面积是( ). A .16 B .15 C .14 D .13 【答案】B(第7题)CDF GOABC(第8题)DFGKABCDE(第9题)(第10题)9.(南宁市中考题)如图,正方形ABCD 、正方形BEFG 和正方形PKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的长边为4,求△DEK 的面积. 【答案】16DEK BEFG S S ==四形△边10.(江苏省竞赛题)如图,ABC △的边30cm AB =,25cm AC =,点D F 、在AC 上,点E G 、在AB 上,12345ADE DEF EFG GBC S S S S =△△△△∶∶∶∶∶∶∶,求AD 和GE 的长.【答案】设cm AD x =,则2cm DF x =,3cm AF x =,由(122)432AFG FGC S S =++=△△∶∶∶,得2cm FC x =,3225AC x x =+=,故5x =,即5cm AD =,同理2AE EC AG BG ==,, 20cm 10cm AG EG ==,.思维方法天地 11.(“五羊杯”邀请赛试题)如图,若长方形APHM BNHP CQHN 、、的面积分别为746、、,则阴影部分的面积是_______. 【答案】8.5 连HDQ B CDM NABCD EPABCD P Q(第11题)(第12题)(第13题)12.(江苏省竞赛题)如图,三角形ABC 的面积为1,BD ∶DC =2∶1,E 是AC 的中点,AD 与BE 相交于点P ,那么四边形PDCE 的面积为_______. 【答案】73013.(《时代学习报》数学文化节试题)如图,长方形ABCD ,60cm 45cm AD AB ==,,Q 为CD 的中点,在BC 上取一点P ,使APQ △的面积等于9002cm ,则BP =_______.【答案】40cm 设cm BP x =,则(60)cm PC x =-,由1451604560222APQ S =⨯-⨯⨯-⨯△145(60)2x x --×45900402x ==,得.14.(2012年四川省竞赛题)如图,若P 为平行四边形ABCD 内的一点,且52PAB PAD S S ==,,△△则PAC S △ =_______.【答案】3 设PAH PCH S m S n ==,,△△则1252BHC BHC ABCDS n m S S++=-+=△△.(第16题)A BCDH P ABCDEF(第15题)(第14题)15.(“希望杯”邀请赛试题)如图,ABCD 平行四边形,E 在AB 上,F 在AD 上,1214BCE CDF S S S ==⋅=平行四形,△△边则CEF S =△_______. 【答案】74 连AC DE ,,则11422BCE CDF ABCD S S S AB EB E ====平行四形,,,,△△边为AB 中点,344AD FD AF AD ==,,3344AEF ADE CEF CDF ABCD S S S S S ===--平行四形,△△△△边 13741244AEF BCE BCE S S S --=---=△△△. 16.(世界数学团体锦标赛试题)如图,大圆有4个面积相等的小圆,已知小圆半径为5cm ,大圆半径等于小圆直径,则空白部分的面积是_______cm 2(π取3).【答案】150 如图,因为1与2、3与4、5与6、7与8、9与10、11与12部分的面积相等,所以空白部分的面积为半个大圆的面积,即20.5π1050π=150⨯⨯=(平方厘米).(第16题)17.(“希望杯”邀请赛试题)如图,三角形ABC 的面积为1,E 是AC 的中点,O 是BE 的中点,连接AO 并延长交BC 于D ,连接CO 并延长交AB 于F .求四边形BDOF 的面积. 【答案】16设BOF BOD S x S y ==,,△△ 则14AOE COE AOB COBS S S S ====,△△△△ (第17题)D CABE FO131444AOF ACF BCF S x S x S x =-=-=+,,△△△. 由AOF ACFBOF BCFS S AF S BF S ==,△△△△得134414x x x x --=+,即2213164x x x -=-,解得112x =. 同理有131444COD ACD ABD S y S y S y =-=-=+,,,△△△由 BOD ABD CODBCD S S BD S CD S ==,△△△△得112y =. 故11112126BDOF S x y =+=+=四形边. 18.(“华罗庚杯”邀请赛试题)如图,△ABC 中,12DC EA FB DB EC FA ===,求GHI ABC 的面的面△积△积的值. 【答案】17 连BG ,设ABC DCG BGF S S S x S y ===,,,△△△则1332233x y S x y S ⎧+=⎪⎪⎨⎪+=⎪⎩,解得121421x S y S⎧=⎪⎪⎨⎪=⎪⎩,同理可得121EAH ABC S S S ==,△△又13ADC BEA S S S ==,△△得12532121GCEH HAFI S S S S ⎛⎫==-= ⎪⎝⎭四形四形,边边这样21011321217GHI S S S ⎛⎫=--= ⎪⎝⎭,△即17GHI ABC S S =△△. 应用探究乐园 19.(河北省中考题)在如图①至图③中,ABC △的面积为a . 探索(1)如图①,延长ABC △的边BC 到点D ,使CD BC =,连接DA .若△ACD 的面积为1S ,则1S =_______(用含a 的代表式表示);(2)如图②,延长ABC △的边BC 到点D ,延长CA 到点E ,使CD BC AE CA ==,,连接DE .若△DEC 的面积为2S ,则2S =_______(用含a 的代数式表示),并写出理由;(第18题)G HI FEBA CD(第19题)B图④图①图②图③C DHFDB CDMG(3)在图②的基础上延长AB到点F,使BF AB=,连接FD FE、,得到DEF△(如图③).若阴影部分的面积为3S,则3S=_______(用含a的代数式表示).发现像上面那样,将ABC△各边均顺次延长一倍,连接所得端点,得到DEF△(如图③),此时,我们称ABC△向外扩展了一次,可以发现,扩展一次后得到的DEF△的面积是原来ABC△面积的_______倍.应用去年在面积为10m2的ABC△空地上栽种了某种花卉.今年准备扩大种植规模,把ABC△向外进行两次扩展,第一次由ABC△扩展成DEF△,第二次由DEF△扩展成MGH△(如图④).求这两次扩展的区域(即阴影部分)面积共为多少m2?【答案】探索:(1)a;(2)2a;理由:连接AD CD BC AE CA==,,,22;(3)6;DAC DAE ABCS S S a S a a∴===∴=,△△△发现:7应用:拓展区域的面积:22(71)10480(m)-⨯=.20.(“五羊杯”竞赛题)如图,红黄绿三块一样大的正方形纸片放在一个正方形盒内,它们之间互相重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10,求正方形盒子的面积.【答案】51.2 移动黄块到左边缘,在移动的过程中,黄块露出的部分减少多少,绿块块露出的部分就增加多少,即“黄+绿”=14+10=24不变.当黄块移动到靠左边缘时,由于红块是正方形,大盒也是正方形,可得这时“黄”=“绿”=24÷2=12,易知此时“左上”ד右下”=“右上”ד左下”,可得“右上”=12×12÷20=7.2,所以“大盒”的面积.绿红黄(第20题)。
