直方图的做法与工程能力的计算方法
直方图的绘制及其解读

直方图的绘制及其解读直方图是一种常用的统计图表,用于展示数据的分布情况。
通过直方图,我们可以直观地了解数据的分布规律,找出数据的特点和规律。
本文将介绍直方图的绘制方法以及如何解读直方图。
一、直方图的绘制方法1. 收集数据:首先需要收集需要展示的数据,确保数据的准确性和完整性。
2. 分组数据:将数据按照一定的区间进行分组,通常将数据分成若干个组,每个组的数据范围相等。
3. 绘制坐标轴:在纵轴上标注频数或频率,在横轴上标注数据的分组区间。
4. 绘制矩形条:根据每个数据组的频数或频率,在相应的区间上绘制矩形条,矩形条的高度表示数据的频数或频率。
5. 添加标题和标签:在图表上方添加标题,标明数据的主题,同时在坐标轴上添加标签,说明数据的含义。
6. 美化图表:可以根据需要添加网格线、颜色填充等,使图表更加美观和易于理解。
二、直方图的解读方法1. 数据分布:通过直方图可以直观地看出数据的分布情况,了解数据的集中程度和离散程度。
2. 数据趋势:观察直方图的形状可以发现数据的趋势,如是否存在峰值、对称性等。
3. 数据比较:可以通过直方图比较不同数据集之间的分布情况,找出数据之间的差异和联系。
4. 异常值:直方图可以帮助我们找出数据中的异常值,即与其他数据差异较大的数值。
5. 预测趋势:通过直方图可以预测未来数据的趋势,帮助我们做出合理的决策和规划。
三、直方图的应用领域1. 经济学:直方图可以用来展示不同地区的经济发展水平,帮助政府制定相关政策。
2. 医学:直方图可以用来展示不同年龄段人群的健康状况,帮助医生进行诊断和治疗。
3. 环境科学:直方图可以用来展示不同地区的环境污染情况,帮助环保部门采取相应措施。
4. 教育学:直方图可以用来展示学生的学习成绩分布情况,帮助老师进行个性化教学。
5. 市场营销:直方图可以用来展示不同产品的销售情况,帮助企业调整营销策略。
通过以上介绍,相信大家对直方图的绘制方法和解读技巧有了更深入的了解。
QC七大手法教材(直方图)7

11
QC 七大手法教材—直方图 直
2-12必要时与规格标准范围比较,如下图: 必要时与规格标准范围比 必要时与规 如下图
SL
XU
Su
# # # # # # # # # # $ $ $ $ $ $ $ $ $
12
QC 七大手法教材—直方图 直
或正符號 或正符號 或正符號 或正符號 或正符號 或正符號 或正符號 或正符號 或正符號 或正符號
QC 七大手法教材—直方图 直
2-8划出1条横轴,并且依据「次数分配表栏內」的各組組界 划 条横轴, 且依据 分配表栏 条横轴 出刻度,如下图 值标示划出刻度,如下图:
2-9标出各組組界值,如下图: 标出各組組界值 如下图
(1)中间长棒最高,往左右高低交錯降低 (1)最高点往某一边呈自然的下降。但 (2)从中间往左右,呈某种因素的影响。 另一边如同断崖峭壁般。 (2)如美国大峽谷的形狀。 (3)如桂林山水形狀。 (3)代表从某一点以外的数据被取走。 (4)代表数据的读取有偏好。(如图a) (如图b.)
a.桂林山型
b.峭壁型
5
QC 七大手法教材—直方图 直
2-4算出组界值: 算出组 算出 首左組界= 首左組界 最小值-数据末數最小單位的1/2 首右組界=首左組界+組距 首右組界
組 界
首左組界 ~ 首右組界 首右組界 ~ 首右組界+組距 首右組界 組距 右組界+組距 第 2 組右組界 ~ 右組界 組距 右組界+組距 第 3 組右組界 ~ 右組界 組距 第 4 組右組界 ~ 右組界+組距 右組界 組距 右組界+組距 第 5 組右組界 ~ 右組界 組距 右組界+組距 第 6 組右組界 ~ 右組界 組距 右組界+組距 第 7 組右組界 ~ 右組界 組距 右組界+組距 第 8 組右組界 ~ 右組界 組距 右組界+組距 第 9 組右組界 ~ 右組界 組距
2.直方图

频数分布表
频数统计
____年____月____日
fi
1 3 6 14 19
0.5~5.5 5.5~15.5 15.5~20.5 20.5~25.5 25.5~30.5
6
7 8 9 10
30.5~35.5
35.5~40.5 40.5~45.5 45.5~50.5 50.5~55.5 合计
28
33 38 43 48
Page‹#›
五.直方图的应用
1. 2. 3. 4. 5. 6. 7. 8. 9. 测试制程能力, 作为制程改善的依据。 计算产品不良率。 调查是否有混入两个以上不同群体。 测知是否有假数据。 测知分布型态。 藉以订定规格界限。 所设计的管制界限可否用于管制制程。 与规格或标准相比较。 改善前后的比较。
第二组下限值:等于第一组上限值,即5.5;
第二组上限值:第二组下限值+组距,即5.5+5=10.5; 第三组以后,依此类推出各组的界限值: 15.5 , 20.5 , 25.5 , 30.5,35.5,40.5,45.5,50.5。
Page‹#›
5. 编制频数分布表。
数据记录No _____________ 组 号 1 2 3 4 5 组界 小 大 组 中 值 3 8 13 18 23 / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /
• 9. 改善前后的比较
(1) 改善前
个数
6 5 4 3 2 1
SL SU
(2) 改善后
个数
6 5 4 3 2 1
SL SU
3
4
直方图的做法

A
B
C
D
E
F
G
H
I
J
1 33.2 41.7 45.0 48.1 49.2 50.9 53.1 56.1 59.0 65.2
2 34.5 42.0 45.5 48.3 49.3 51.3 53.9 56.2 59.5 66.2
3 36.6 42.4 46.0 48.5 49.8 51.6 54.1 56.7 60.1 67.0
频数
30
25
n=100
20
x = 52.2
15
s=9.01
10
5
0
中心值 35.35 39.75 44.15 48.55 52.95 57.35 61.75 66.15 70.55 74.95
拉伸强度kg/cm2
图 7-1 某金属拉伸强度直方图 作图人:李 力 日期 1998.3.12.
步骤 9 当有规格要求时,应把规格要求的上下限画在图上。通常根据规格要求要计算 工程能力指数。假设规格要求是 33.5~77.0,则:
多种数据混在一起,或者是在生产过程中由于某种缓慢因素的作用是分布中心缓慢向一侧移 动。
除此之外,其他类型还有常见的反映数据分布分散程度的所谓胖型、瘦型分布形态。
a
b
c
d
e
a
图 7-2 直方图几种分布形态
上述计算方法,如不用计算机,可按表 7-4 进行手工计算。这种计算方法称为等距分组 连乘法,计算步骤是:
去除率的原因,大家对下述几方面原因进行了仔细分析,经统计,主要有以下几个方面: DO 低 发生频数 62 次
SS 波动 发生频数 12 次
COD 波动 发生频数 33 次 CN 高 发生频数 5 次
SPC基础知识-工程能力分析与控制
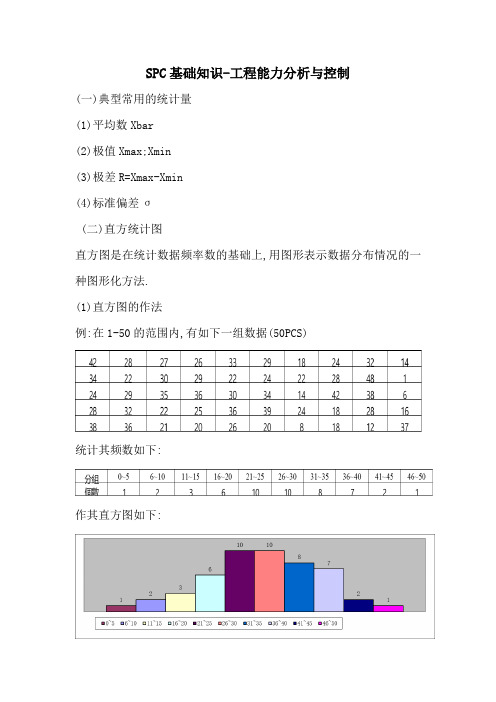
作其直方图如下:
(二).直方图的观察与分析
(1)对图形形状的分析:常见的直方图有以下几种
2)孤岛型:说明在短时间内有异常因素在作用,如原材料发生变化,有不熟练工人替班等.
3)偏向型:说明加工中心发生了偏移
4)双峰型:是由产品混批造成的
5)造成这种情况不是生产上的问题,往往是由于测量误差或分组不当造成的.
因此在兼顾工序能力满足技术要求的程度和工序加工的经济两个方面,用6σ来表示工序能力.
(二)工序能力指数
以6σ定义的工序能力只表示工序所固有的实际加工能力,并不说明这一能力能否满足产质量量要求.为了反映工序能力满足产品质量要求的程度,引入工序能力指数的概念.
工序能力指数,是指产品质量标准(或技朮要求)与工序能力的比值.一般采用符号CP(ProcessCapability)表示,即CP=T/6σ,T为质量标准的范围,即公差.
从定量的角度看,工序能力是工序本身所固有的一种可以度量的特性.如果工序能力高,所加工产品质量指针的波动就小,说明工序质量好.
我们可以用产品质量的实际波动来定量描述工序能力的大小,定义:B=6σ,为什么用6σ来刻划工序能力呢?因为当工序处于稳定状态时,产品的质量指针服从政态分布,此时,在μ±3σ的范围内包括了99.73%的产品,如果取μ±4σ或μ±5σ,相应的产品范围会增大至99.994%和99.9994%,分别增加了0.264%和0.26994%,而同时要求提供的各种保证更多,精力花费更大,经济上是不合理的.
质量数据的统计分布规律
(一)正态分布(nomaldistribution)
在计量值数据中,应用最广的一类连续形概率分布为正态分布.
(二)正态分布的解释与应用
正态分布函数中的μ与σ是互相独立的两个分布函数,μ决定正态曲线的位置,σ决定它的形状.
初中数学 什么是直方图 如何绘制直方图

初中数学什么是直方图如何绘制直方图直方图是一种用于展示数据分布情况的图表,常用于初中数学中处理和分析数据。
它将数据按照一定的范围或类别进行分类,并以矩形的高度表示每个范围或类别中数据的频数或频率。
本文将介绍直方图的概念,并详细说明如何绘制直方图。
直方图的绘制步骤如下:1. 确定数据的范围或类别。
根据数据的特点和分布情况,选择合适的范围或类别进行分类。
范围可以是数值范围,类别可以是某种特定属性或特征。
2. 统计每个范围或类别中的数据频数或频率。
遍历整个数据集,统计每个范围或类别中数据出现的次数或计算频率。
3. 绘制坐标轴。
在纸上或计算机屏幕上,绘制水平和垂直的坐标轴。
水平轴表示数据的范围或类别,垂直轴表示频数或频率。
4. 绘制矩形。
根据统计的频数或频率,在每个范围或类别的水平轴上,绘制相应高度的矩形。
矩形的宽度可以根据范围或类别的宽度进行调整。
5. 添加标签和标题。
给坐标轴和图表添加相应的标签和标题,以便读者理解和解释图表。
例如,假设有一个班级的学生身高数据集,要绘制身高的直方图,可以选择范围为150-160cm、161-170cm、171-180cm等,然后统计每个范围中身高出现的次数或计算频率。
在图表中,将每个范围表示为水平轴上的刻度,并根据统计结果绘制相应高度的矩形。
在绘制直方图时,我们需要注意以下几点:1. 分类标准的合理性:选择合适的范围或类别进行分类,以便更好地分析和解释数据。
2. 矩形的宽度和间距:矩形的宽度可以根据范围或类别的宽度进行调整,矩形之间的间距可以根据实际情况进行调整,以保持图表的美观和易读性。
3. 坐标轴的刻度和标签:确保坐标轴的刻度和标签清晰可读,方便观察和分析。
4. 图表的标题和标签:给图表添加相应的标题和标签,以便读者理解和解释图表。
综上所述,直方图是一种用于展示数据分布情况的图表。
绘制直方图的步骤包括确定数据的范围或类别、统计每个范围或类别的频数或频率、绘制坐标轴和矩形,并添加标签和标题。
直方图的制作详细步骤讲解

直方图(Histogram)一、前言现场工作人员经常都要面对许多的数据,这些数据均来自于生产过程中抽样或检查所得的某项产品的质量特性。
如果我们应用统计绘图的方法,将这些数据加以整理,则生产过程中的质量散布的情形及问题点所在及过程、能力等,均可呈现在我们的眼前;我们即可利用这些信息来掌握问题点以采取改善对策。
通常在生产现场最常利用的图表即为直方图。
二、直方图的定义⒈什么是直方图:即使诸如长度、重量、硬度、时间等计量值的数值分配情形能容易地看出的图形。
直方图是将所收集的测定值特性值或结果值,分为几个相等的区间作为横轴,并将各区间内所测定值依所出现的次数累积而成的面积,用柱子排起来的图形。
因此,也叫做柱状图。
⒉使用直方图的目的:⑴了解分配的形态。
⑵研究制程能力或计算制程能力。
⑶过程分析与控制。
⑷观察数据的真伪。
⑸计算产品的不合格率。
⑹求分配的平均值与标准差。
⑺用以制定规格界限。
⑻与规格或标准值比较。
⑼调查是否混入两个以上的不同群体。
⑽了解设计控制是否合乎过程控制。
116 品管七大手法3.解释名词:⑴次数分配将许多的复杂数据按其差异的大小分成若干组,在各组内填入测定值的出现次数,即为次数分配。
⑵相对次数在各组出现的次数除以全部的次数,即为相对次数。
⑶累积次数(f)自次数分配的测定值较小的一端将其次数累积计算,即为累积次数。
⑷极差(R)在所有数据中最大值和最小值的差,即为极差。
⑸组距(h)极差/组数=组距 ⑹算数平均数(X)数据的总和除以数据总数,通常一X (X-bar )表示。
⑺中位数(X)将数据由大至小按顺序排列,居于中央的数据为中位数。
若遇偶位数时,则取中间两数据的平均值。
⑻各组中点的简化值(μ)⑼众数(M)次数分配中出现次数最多组的值。
例:次数最多为24,不合格数是9,故众数为9。
⑽组中点(m)一组数据中最大值与最小值的平均值, (上组界+下组界)÷ 2=组中点第八章 直方图 117 X= X 1+X 2+ …… +X n n X= ∑μf nX 0+h ~ μ= , X i - X 0 组距(h) X 0=次数最多一组的组中点 X i =各组组中点 n Xi ni ∑=1=⑾标准差(σ)⑿样本标准差(S)三、直方图的制作⒈直方图的制作方法步骤1:收集数据并记录收集数据时,对于抽样分布必须特别注意,不可取部分样品,应全部均匀地加以随机抽样。
工程质量统计 分析方法

本模块学习内容: 直方图法
直方图法
1. 直方图与直方图法
(1)直方图—横坐标表示质量特性值,纵坐标表 示频数或频率值,各组频数或频率的大小用直方 形(矩形条)高度表示的图形。
依纵坐标不同,分频数分布 直方图和频率分布直方图。
(2)直方图法—将收集到 的质量数据进行分组整理, 绘制成频数分布直方图,用以描述质量分布状态 的一种分析方法,又称为质量分布图法。
4. 直方图应用之二:判断实际生产过程能力
通过直方图显示的实际质量分布范围B与质量标 准中公差带T的比较,以及质量分布中心与公差 中心是否重合或偏离的程度,可以判断实际生产 过程能力。
(a)图情形:基本正 态分布,质量中心与公 差中心大致重合,分布 在公差范围内,且两侧 还有一定余地。
生产过程处于正常的稳定状态,工序能力足够, 生产出来的产品全部都是合格品。
37.1
39.7
34.0
38.0
46.2
31.8
4
39.9
36.4
34.3
38.3
33.2
43.4
40.4
38.2
41.2
38.0
43.4
33.2
5
39.2
44.4
35.4
42.0
34.4
37.9Βιβλιοθήκη 38.138.440.3
39.5
44.4
34.4
【解】强度单位N/mm2,xmax=46.2, xmin=31.5
第三组下限=第二组上限,第三组上限=其下限+h。 ……
(4)编制数据统计频数表 对于刚好位于组限上的数据 ,可采用就低不就高(或就 高不就低)的办法处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入数据
接收数 据
注:接收 数据的最 小值与最 大值,以 及其刻度 尺寸是根 据输入数 据决定
4.97 4.95 4.90 4.93
(由输入 数据决 定)
4.80 4.85 4.90 4.95
极差 (mm)
0.10 0.20 0.24 0.13 0.27 0.29 0.30 0.33 0.37 0.37 0.10 0.29 0.23 0.43 0.19 0.23 0.27 0.26 0.56 0.33 0.20 0.30 0.25 0.55 0.15
点击"插 入"工具 栏,选择" 函数",选 择 "STDEVP" ,点击确 认,选取 25组一共 100件子 数据并点 击确认, 输出结果 2.求出分 布容量T 及偏差K 由图纸可 知,尺寸 分布界限 为5± 0.7mm.由 USLLSL=T=0. 7-(0.7)=1.4 K=︱(Xμ)*2/T ︱=︱ (4.955)*2/1.4 ︱=0.07; 6*σ =6*0.137 =0.822
表一
厚度值 (mm) 第四次
4.98 4.89 5.02 4.94 5.08 4.86 5.19 5.01 4.87 4.81 4.99 5.09 4.92 5.11 4.97 4.90 4.70 4.85 5.12 4.95 4.98 5.06 5.25 4.81 4.94
一. 直方 图分
析
对于上表 中的平均
二. 工程 能力 分析
SPC统计 过程控制 主要分为 两部分, 一部分是 利用控制 图对缺陷 进行预防 和及时发 现,另一 部分就是 计算工程 能力 控制图主 要由零部 件供应商 在生产过 程中采 用,我们 主机厂应 用到的主 要是工程 能力的相 关知识. 常用的工 程能力计 算公式 为:
关于双侧 公差的计 算方法
平均值(mm)
4.97 4.95 4.90 4.93 4.94 5.05 5.04 4.93 4.95 5.00 4.93 4.96 4.92 4.97 4.90 4.89 4.82 4.86 4.95 4.98 4.99 4.94 5.10 5.15 4.87
R=0.28 X=4.95
具体知识 请参见 "QC七手 法之直方 图详解"
CPU,CPL
}
CP=(USLLSL)/6σ
注:计算 CP以及 CPK时σ 的标准情 况必须用 公式σ =R/d2求 得,但实 际我们在 使用的时 候常用计 算PPK的 σ计算公 式来代替 (关于CPK 及PPK的 区别及应 用请见 SPC手册)
计算过 程: 1.求出σ 表一中的 σ =0.13721
CPK=(1K)*CP "CP"指 的是无 偏移的 工程能 力指 数."CPK "指的是 修偏后 的工程 能力指 数
EXCEL中的直方图做法与工程能力计算方法
以LLC水管厚度分析为例
序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
厚度值 (mm) 第一次
5.00 4.88 4.80 4.98 4.81 5.10 5.01 4.94 4.97 5.18 4.94 4.97 4.83 5.07 4.96 5.00 4.81 4.91 4.59 4.95 5.08 5.06 5.00 5.25 4.92
CP=T/6σ =1.4/0.8 22=1.703 CPK=CP(1 K)=1.703 *(10.07)=1. 584
因为CPK >1.33, 所以该水 管厚度的 工程能力 比较优 秀,可满 足需要.
另:关于 单侧公差 的计算方 法
CPU=(USL -μ)/3 σ; CPL=(μLSL)/3σ
CP=MIN{
接收 频率
4.80
0
4.85
14.90 4.95Fra bibliotek5.00 5.05 5.10
3
12
11
10 8
频率
6
6 4
2
2 0
1
5.15
0
5.20
1
其他
0
此处呈现孤岛 分布形态
直方图 频率
接收
可见该数据为 孤岛形分布 导致此情况的 原因可能是加 工时出现了特 殊情况 或者测量值有 所偏差,需要进 行相关分析改 进.
4.94 5.05 5.04
5.00
5.05 5.10
4.93
4.95 5.00
5.15 5.20
4.93
4.96
4.92 4.97 4.90 4.89 4.82 4.86 4.95 4.98 4.99 4.94 5.10
5.15
4.87
表二
EXCEL制 作直方图 的操作步 骤:
1.选择" 工具"栏. 点击"数 据分析" 选项(若" 工具"栏 内没有" 数据分析 选项,可 以 通过"加 载宏"功 能添加) 2.点击" 直方图" 选项,并 点击"确 认" 3.分别插 入左表二 中的"输 入区域" 及"输出 区域" 4.形成直 方图(如 下所示)
LLC水管 厚度数据 (图纸要 求为5± 0.7mm) 厚度值 厚度值 (mm) (mm) 第二次 第三次
4.90 5.00 4.94 5.08 5.01 4.78 4.93 4.85 5.01 4.85 5.08 5.15 4.89 5.08 5.05 4.72 4.79 5.16 5.12 4.89 4.89 4.91 4.80 4.96 5.06 4.88 5.00 4.68 4.90 4.78 4.88 4.77 4.78 4.97 4.97 4.71 5.15 4.93 5.18 4.85 4.88 5.01 4.86 4.76 5.06 5.08 5.19 5.36 4.81 4.79
