初中数学较难题目
初一最难的数学题目包括答案

初一最难的数学题目包括答案初一最难的数学题目包括答案如下:1. 若干学生住若干间房间,如果每间住4人,则有20人没有地方住,如果每间房住8人,则有一间只有4人住,问共有多少个学生?解答:设有x间宿舍每间住4人,则有20人无法安排所以有4x+20人每间住8人,则最后一间不空也不满所以x-1间住8人,最后一间大于小于8所以0<(4x+20)-8(x-1)<80<-4x+28<8 乘以-1,不等号改向-8<4x-28<0加上28 20<4x<28 除以4 5<x<7x是整数所以x=6 4x+20=44所以有6间宿舍,44人2.甲对乙说:“你给我100元,我的钱将比你多1倍。
”乙对甲说:“你只要给我10元,我的钱将比你多5倍。
”问甲乙两人各有多少元钱?解答:设甲原有x元,乙原有y元.x+100=2*(y-100) 6*(x-10)=y+10 x=40 y=1703.小王和小李从AB两地,相向而行,80分钟后相遇,小王先出发60分钟后小李在出发,40分钟后相遇,问小李和小王单独走完这段距离需要多长时间?解:设小王的速度为x,小李的速度为y根据:路程=路程,可列出方程:80(x+y)=60x+40(x+y)解得y=1\2x 设路程为单位1,则:80(1\2x+x)=1 解得x=1\120 所以y=1\240所以小王单独用的时间:1*1\120=120(分)小李单独用的时间:1*1\240=240(分)4.一天,猫发现前面20米的地方有只老鼠,立即去追,同时,老鼠也发现了猫,马上就跑。
猫每秒跑7米,用了10秒追上老鼠。
老鼠每秒跑多少米?解:设老鼠每秒跑X米7*10=10X+20 10X=70-20 X=5 答:老鼠每秒跑5米。
5.一项工程,甲单独做10天完成,乙单独做6天完成。
先由甲先做2天,然后甲乙合作,问:甲乙合作还需要多少天完成工作?解答:设甲乙合作一起还需要x天完成总工程为 1 甲先做了2天他完成了总工程的2*1/10=1/5 那么此时还剩下为1-1/5=4/5那么就有了(1/10+1/6)*x=4/5 解得x=3即一起工作3天完成整个工作思路:主要是看每个完成的工作量跟整个的相对关系的。
初中的数学经典几何的题目(难)及问题详解分析报告
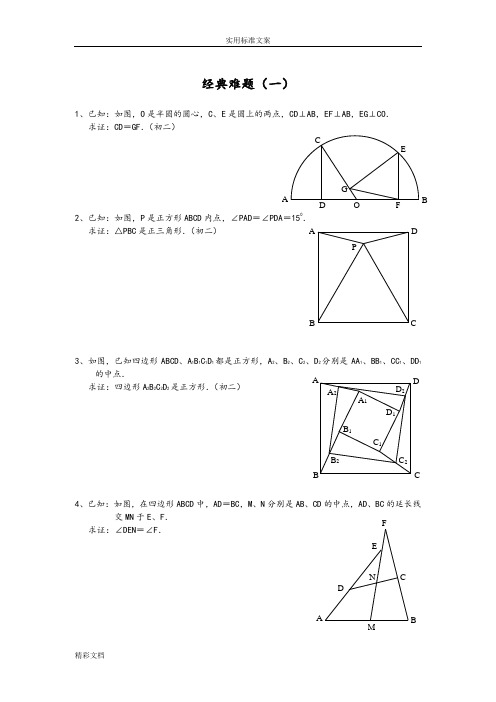
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBPCG FBQADE 经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DE C N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)AP CB P A DCB CBDAFPDE CBA1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA=200,求∠BED 的度数.经典难题(一)APCB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。
苏教版七年级下册期末数学重点初中题目(比较难)

苏教版七年级下册期末数学重点初中题目(比较难)一、选择题1.下列计算正确的是( )A .(a 5)2=a 10B .x 16÷x 4=x 4C .2a 2+3a 2=6a 4D .(ab )2 =ab 2 答案:A解析:A【分析】根据幂的乘方、同底数幂的除法、合并同类项法则及积的乘方运算法则即可求解.【详解】A 、(a 5)2=a 10,正确,该选项符合题意;B 、x 16÷x 4=x 12,错误,该选项不符合题意;C 、2a 2+3a 2=5a 2,错误,该选项不符合题意;D 、(ab )2=a 2b 2,错误,该选项不符合题意;故选:A .【点睛】此题主要考查幂的乘方、同底数幂的除法、合并同类项法则及积的乘方运算法则,解题的关键是熟知其运算法则及公式.2.如图,1∠和2∠不是同旁内角的是( )A .B .C .D . 答案:B解析:B【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.根据同旁内角的概念可得答案.【详解】解:选项A 、C 、D 中,∠1与∠2在两直线的之间,并且在第三条直线(截线)的同旁,是同旁内角;选项B 中,∠1与∠2的两条边都不在同一条直线上,不是同旁内角.故选:B .【点睛】此题主要考查了同旁内角,关键是掌握同旁内角的边构成“U ”形.3.关于x 的不等式()a b x b a ->-的解集为1x <-,则a 与b 的大小关系为( ) A .a b > B .a b = C .a b < D .无法确定 答案:C解析:C【分析】根据不等式的性质可得a -b <0,进而可得答案.【详解】解:∵不等式(a -b )x >b -a 的解集是x <-1,∴a -b <0,∴a <b ,则a 与b 的大小关系是a <b .故选:C .【点睛】本题主要考查了不等式的解集,在解题时要注意注意不等式两边同时乘以同一个负数时,不等号的方向改变.4.已知230a a +-=,那么2(4)a a +的值是( )A .9B .12-C .18-D .15-答案:A解析:A【分析】由a 2+a -3=0,变形得到a 2=-(a -3),a 2+a =3,先把a 2=-(a -3)代入整式得到a 2(a +4)=-(a -3)(a +4),利用乘法得到原式=-(a 2+a -12),再把a 2+a =3代入计算即可.【详解】解:∵a 2+a -3=0,∴a 2=-(a -3),a 2+a =3,a 2(a +4)=-(a -3)(a +4)=-(a 2+a -12)=-(3-12)=9.故选:A .【点睛】本题考查了整式的混和运算及其化简求值:先把已知条件变形,用底次代数式表示高次式,然后整体代入整式进行降次,进行整式运算求值.5.如果关于x 的不等式组0,312(1)x m x x -<⎧⎨->-⎩无解,那么m 的取值范围为( ) A .1m ≤- B .1m <- C .10m -<≤ D .10m -≤< 答案:A解析:A【分析】分别求出每一个不等式的解集,根据不等式组无解,依据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了可得答案.【详解】解:解不等式0x m -<,得:x m <,解不等式312(1)x x ->-,得:1x >-,不等式组无解,1m ∴≤-,故选:A .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.6.给出下列4个命题:①对顶角相等;②等角的补角相等;③同旁内角相等,两直线平行;④同位角的平分线平行.其中真命题为 ()A .①④B .①②C .①③④D .①②④ 答案:B解析:B【分析】根据对顶角,平行线等性质进行分析即可.【详解】解:∵对顶角相等,故①正确;∵等角的补角相等,故②正确;∵同旁内角互补,两直线平行,故③错误.∵同位角的平分线不一定平行,故④错误.∴其中正确的有①②,其中正确的个数是2个.故选B .【点睛】考核知识点:真命题.理解相关定理是关键.7.(阅读理解)计算:2511275⨯=,1311143⨯=,4811528⨯=,7411814⨯=,观察算式,我们发现两位数乘11的速算方法:头尾一拉,中间相加,满十进一.(拓展应用)已知一个两位数,十位上的数字是a ,个位上的数字是b ,这个两位数乘11,计算结果中十位上的数字可表示为( )A .a 或1a +B .a b +或abC .10a b +-D .a b +或10a b +- 答案:D解析:D【分析】根据题目中的速算法可以解答本题.【详解】由题意可得,某一个两位数十位数字是a ,个位数字是b ,将这个两位数乘11,得到一个三位数,则根据上述的方法可得:当a +b < 10时,该三位数百位数字是a ,十位数字是a + b ,个位数字是b ,当a +b ≥10时,结果的百位数字是a + 1,十位数字是a +b - 10,个位数字是b .所以计算结果中十位上的数字可表示为:a +b 或a +b −10.故选D.本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.8.如图,AD 是△ABC 的中线,DE 是△ADC 的高线,AB=3,AC=5,DE=2,点D 到AB 的距离是( )A .2B .53C .65D .103答案:D解析:D【详解】分析:作DF ⊥AB 于点F ,先由AD 是△ABC 的中线可得S △ABD =S △ACD ,然后根据面积法即可求出DF 的长,详解:作DF ⊥AB 于点F ,∵AD 是△ABC 的中线,∴S △ABD =S △ACD ,∴1122AB DF AC DE ⋅=⋅, ∴3DF =5×2,∴DF =103. 故选D.作点睛:本题考查了三角形中线的性质和面积法求线段的长,由中线的性质得出S △ABD =S △ACD 是解答本题的关键.二、填空题9.计算:23x xy ⋅=____________.解析:26x y【解析】【分析】根据单项式与单项式的乘法法则计算即可.23x xy ⋅=26x y .故答案为26x y .【点睛】本题考查了单项式的乘法,单项式与单项式的乘法法则是,把它们的系数相乘,字母部分的同底数的幂分别相乘,对于只在一个单项式里含有的字母,连同它的指数作为积的一个因式.10.能使命题“若a b >,则2ab b >”为假命题的b 所有可能值组成的范围为____. 解析:0b ≤【分析】根据不等式的性质和命题的真假判断即可;【详解】当b=0时,得2ab b =,此命题是假命题;当0b <时,得2ab b <,此命题是接命题;故b 的取值范围为0b ≤.【点睛】本题主要考查了命题与定理的考查,结合不等式的性质判断是关键.11.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为______. 解析:100°【分析】利用三角形的外角性质列方程计算,再根据三角形内角与外角的关系得到它的最大内角度数.【详解】解:设三角形三个外角的度数分别为2x ,3x ,4x .根据多边形的外角和是360度,列方程得:2x +3x +4x =360°,解得:x =40°,则最小外角为2×40°=80°,则最大内角为:180°−80°=100°.故答案为:100°.【点睛】由多边形的外角和是360°,可求得最大内角的相邻外角是80°.12.若ab =2,a -b =3,则代数式ab 2-a 2b =_________.解析:6【分析】用提公因式法将ab 2-a 2b 分解为含有ab ,a -b 的形式,代入即可.【详解】解:∵ab =2,a -b =3,∴ab 2-a 2b =-ab (a -b )=2×3=6,故答案为:6.本题考查了用提公因式法因式分解,解题的关键是将ab 2-a 2b 分解为含有ab ,a -b 的形式,用整体代入即可.13.已知方程组32231x y k x y k +=⎧⎨+=+⎩满足3x y +=,则k 的值为___________. 解析:7【分析】利用整体思想,将两个方程相加,再整体代入3x y +=解题即可.【详解】32231x y k x y k +=⎧⎨+=+⎩①② ①+②,552+1x y k +=3x y +=5515x y ∴+=即2115k +=∴k=7故答案为:7.【点睛】本题考查二元一次方程组,是重要考点,难度较易,掌握相关知识是解题关键. 14.一块长为25cm ,宽为15cm 的长方形木板中间有一条裂缝(如图甲).若把裂缝右边的一块向右平移2cm (如图乙),则产生的裂缝的面积是__________2cm .解析:30【分析】利用新长方形的面积减去原长方形的面积得到产生的裂缝的面积.【详解】解:产生的裂缝的面积为:(25+2)×15-25×15=(27-2)×15=30(cm 2).故答案为:30.【点睛】本题主要考查了生活中的平移现象,利用利用两个长方形形的面积差得出裂缝的面积是解题关键.15.在ABC中,AB=6,AC=9,则第三边BC的值可以是_________ .答案:10(答案不唯一)【分析】先根据三角形的三边关系定理求出第三边的取值范围,再选一个合适的值即可.【详解】由三角形的三边关系定理得:,即则第三边BC的值可以是10故答案为:10(答案不解析:10(答案不唯一)【分析】先根据三角形的三边关系定理求出第三边的取值范围,再选一个合适的值即可.【详解】-<<+由三角形的三边关系定理得:AC AB BC AC AB==AB AC6,9<<BC9696∴-<<+,即315BC则第三边BC的值可以是10故答案为:10(答案不唯一).【点睛】本题考查了三角形的三边关系定理,熟记三角形的三边关系定理是解题关键.16.如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,第n次操作后,得到△A n B n Cn,要使△A n B n Cn的面积超过2020,则至少需要操作__________次.答案:4【分析】根据题意分析可得:每次操作后,△CC1B1、△A1B1B、△AA1C1边长变为△ABC边长的2倍,故△A1B1C1面积变大为△ABC面积的7倍;即第n次操作后,面积变为7n;故要使得到解析:4【分析】根据题意分析可得:每次操作后,△CC 1B 1、△A 1B 1B 、△AA 1C 1边长变为△ABC 边长的2倍,故△A 1B 1C 1面积变大为△ABC 面积的7倍;即第n 次操作后,面积变为7n ;故要使得到的三角形的面积超过2020,最少经过4次操作.【详解】解:每次操作后,△CC 1B 1、△A 1B 1B 、△AA 1C 1边长变为△ABC 边长的2倍,故△A 1B 1C 1面积变大为△ABC 面积的7倍,可得规律第n 次操作后,面积变为7n ,∵37343=,472401=,则7n ≥2020,解得n 最小为4.故最少经过4次操作,故答案为:4;【点睛】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.17.计算:(1)()()1020201π312-⎛⎫-+-+ ⎪⎝⎭ (2)()()322x x x -÷--答案:(1)4;(2)【分析】(1)根据零指数幂,有理数的乘方,负整指数幂进行计算即可;(2)根据立方以及平方运算,单项式的除法以及单项式的加减运算即可;【详解】(1)(2)【点睛】本题考解析:(1)4;(2)29x -【分析】(1)根据零指数幂,有理数的乘方,负整指数幂进行计算即可;(2)根据立方以及平方运算,单项式的除法以及单项式的加减运算即可;【详解】(1)()()1020201π312-⎛⎫-+-+ ⎪⎝⎭1124= (2)()()322x x x -÷--328x x x =-÷-29x =-【点睛】本题考查了零指数幂,有理数的乘方,负整指数幂,单项式的除法以及单项式的加减运算,掌握以上运算法则是解题的关键.18.因式分解(1)m2n﹣9n;(2)x2﹣2x﹣8.答案:(1)n(m+3)(m-3);(2)(x-4)(x+2)【分析】(1)先提公因式n,再利用平方差公式进行因式分解即可;(2)利用十字相乘法进行因式分解即可.【详解】解:(1)m2n-9n解析:(1)n(m+3)(m-3);(2)(x-4)(x+2)【分析】(1)先提公因式n,再利用平方差公式进行因式分解即可;(2)利用十字相乘法进行因式分解即可.【详解】解:(1)m2n-9n=n(m2-9)=n(m+3)(m-3);(2)x2-2x-8=(x-4)(x+2).【点睛】本题考查提公因式法、公式法、十字相乘法分解因式,掌握平方差公式的结构特征以及十字相乘法适用二次三项式的特点是正确应用的前提.19.解方程组(1)20 328 x yx y-=⎧⎨+=⎩(2)1 2333(1)1 x yx y⎧-=⎪⎨⎪-=+⎩答案:(1);(2)【分析】(1)根据加减消元法,即可求解;(2)先化简二元一次方程组,再利用加减消元法,即可求解.【详解】解:(1),①+②得:4x=8,解得:x=2,把x=2代入①得:2解析:(1)21x y =⎧⎨=⎩;(2)22x y =⎧⎨=⎩ 【分析】(1)根据加减消元法,即可求解;(2)先化简二元一次方程组,再利用加减消元法,即可求解.【详解】解:(1)20328x y x y -=⎧⎨+=⎩①②, ①+②得:4x =8,解得:x =2,把x =2代入①得:2-2y =0,解得:y =1,∴方程组的解为:21x y =⎧⎨=⎩; (2)12333(1)1x y x y ⎧-=⎪⎨⎪-=+⎩, 化简得:32234x y x y -=⎧⎨-=⎩①②, ①-②得:-y =-2,解得:y =2,把y =2代入②得:3x -2=4,解得:x =2,∴方程组的解为:22x y =⎧⎨=⎩. 【点睛】本题主要考查解二元一次方程组,熟练掌握加减消元法是解题的关键.20.解不等式组()217122x x x x ⎧+>⎪⎨+-≥⎪⎩并把它的解集在数轴上表示出来.答案:,数轴见解析【分析】先分别求出两个不等式的解集,可得到不等式组的解集,然后再数轴上表示出来即可.【详解】解:解不等式①得:.解不等式②得:.所以,不等式组的解集是:.在数轴上表示不等解析:21x -<≤-,数轴见解析【分析】先分别求出两个不等式的解集,可得到不等式组的解集,然后再数轴上表示出来即可.【详解】解:()217122x x x x ⎧+>⎪⎨+-≥⎪⎩①② 解不等式①得:2x >-.解不等式②得:1x ≤-.所以,不等式组的解集是:21x -<≤-.在数轴上表示不等式组的解集为【点睛】本题主要考查了解一元一次不等式组,熟练掌握解不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.三、解答题21.如图,已知//AB CD ,直线EB 与AB 相交于点B ,1:2:31:2:3∠∠∠=. (1)求1∠,2∠的度数;(2)求证:BA 平分EBF ∠.答案:(1)36°,72°; (2)证明见解析.【分析】(1)根据平行线的性质与角度的比值求得∠2的度数,再求得∠1的度数即可;(2)根据∠EBA 与互补求得∠EBA 的度数即可得证.【详解】解:解析:(1)36°,72°;(2)证明见解析.【分析】(1)根据平行线的性质与角度的比值求得∠2的度数,再求得∠1的度数即可;(2)根据∠EBA与1+2∠∠互补求得∠EBA的度数即可得证.【详解】AB CD,解:(1)∵//∴∠2+∠3=180°,∵∠2:∠3=2:3,∴∠2= 2180⨯︒=72°.5∵∠1:∠2=1:2,∴∠1= 12∠=36°;2∠︒∠︒(2)证明:∵2=72,1=36,∴∠EBA=180°-∠2-∠1=180°-72°-36°=72°,∴∠EBA=∠2,即BA平分∠EBF.【点睛】本题主要考查平行线的性质,角平分线的定义,解此题的关键在于熟练掌握其知识点并能灵活运用逻辑推理进行证明.22.实验中学开学初到商场购买A、B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元.(1)求A、B两种品牌的足球单价各是多少元.(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A、B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买方案有且只有三种方案,则这次学校购买B品牌足球至少多少个?(3)请你求出学校在第二次购买活动中最少需要多少资金?答案:(1)A、B两品牌足球每个分别为50元、80元;(2)这次购买B品牌足球至少23个;(3)最少需资金3114元【分析】(1)设A、B两品牌足球每个分别为元,元,根据“总费用=买A种足球费用+买B解析:(1)A、B两品牌足球每个分别为50元、80元;(2)这次购买B品牌足球至少23个;(3)最少需资金3114元【分析】(1)设A、B两品牌足球每个分别为x元,y元,根据“总费用=买A种足球费用+买B种足球费用,以及B 种足球单价比A 种足球贵30元”可得出关于x 、y 的二元一次方程组,解方程组即可得出结论;(2)设购买B 品牌足球m 个,则购买A 品牌足球()50m -个,根据“学校此次购买A ,B 两种品牌足球的总费用不超过第一次花费的70%”可得出关于m 的一元一次不等式,解不等式可得出m 的取值范围,由此即可得出结论;(3)根据(2)的结论分别求出三种方案所花费用即可.【详解】(1)解:设A 、B 两品牌足球每个分别为x 元,y 元,依题意得5025450030x y y x +=⎧⎨-=⎩,解得5080x y =⎧⎨=⎩, 答:A 、B 两品牌足球每个分别为50元、80元;(2)设购买B 品牌足球m 个,则购买A 品牌足球()50m -个,由题意得()()95045080450070%10m m +-+⨯≤⨯,解得25m ≤, ∵这次学校有三种购买方案,∴2325m ≤≤,答:这次购买B 品牌足球至少23个.(3)方案一: 275423723114⨯+⨯=元,方案二:265424723132⨯+⨯=元,方案三:255425723150⨯+⨯=元,∴最少需资金3114元.【点睛】本题考查了二元一次方程组的应用,以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)由两种品牌足球单价间的关系,找出最省钱的购买方案.23.阅读下列文字,请仔细体会其中的数学思想.(1)解方程组321327x y x y -=-⎧⎨+=⎩,我们利用加减消元法,很快可以求得此方程组的解为 ;(2)如何解方程组()()()()3523135237m n m n ⎧+-+=-⎪⎨+++=⎪⎩呢?我们可以把m +5,n +3看成一个整体,设m +5=x ,n +3=y ,很快可以求出原方程组的解为 ;(3)由此请你解决下列问题:若关于m ,n 的方程组722am bn m bn +=⎧⎨-=-⎩与351m n am bn +=⎧⎨-=-⎩有相同的解,求a 、b 的值. 答案:(1);(2);(3)a =3,b =2.【分析】(1)利用加减消元法,可以求得;(2)利用换元法,设m+5=x ,n+3=y ,则方程组化为(1)中的方程组,可求得x ,y 的值进一步可求出原方程组的解解析:(1)12x y =⎧⎨=⎩;(2)41m n =-⎧⎨=-⎩;(3)a =3,b =2. 【分析】(1)利用加减消元法,可以求得;(2)利用换元法,设m+5=x ,n+3=y ,则方程组化为(1)中的方程组,可求得x ,y 的值进一步可求出原方程组的解;(3)把am 和bn 当成一个整体利用已知条件可求出am 和bn ,再把bn 代入2m-bn=-2中求出m 的值,然后把m 的值代入3m+n=5可求出n 的值,继而可求出a 、b 的值.【详解】解:(1)两个方程相加得66x =,∴1x =,把1x =代入321x y -=-得2y =,∴方程组的解为:12x y =⎧⎨=⎩; 故答案是:12x y =⎧⎨=⎩; (2)设m +5=x ,n +3=y ,则原方程组可化为321327x y x y -=-⎧⎨+=⎩, 由(1)可得:12x y =⎧⎨=⎩, ∴m+5=1,n+3=2,∴m =-4,n =-1,∴41m n =-⎧⎨=-⎩, 故答案是:41m n =-⎧⎨=-⎩; (3)由方程组722am bn m bn +=⎧⎨-=-⎩与351m n am bn +=⎧⎨-=-⎩有相同的解可得方程组71am bn am bn +=⎧⎨-=-⎩, 解得34am bn =⎧⎨=⎩, 把bn =4代入方程2m ﹣bn =﹣2得2m =2,解得m =1,再把m =1代入3m +n =5得3+n =5,解得n =2,把m=1代入am=3得:a=3,把n=2代入bn=4得:b=2,所以a=3,b=2.【点睛】本题主要考查二元一次方程组的解法,重点是考查整体思想及换元法的应用,解题的关键是理解好整体思想.24.【问题探究】如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;【问题迁移】如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.(1)当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.(2)如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC 与α、β之间的数量关系,并说明理由.(图1)(图2)答案:∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析. 【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C解析:∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)化成图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【问题探究】解:∠DPC=α+β如图,过P作PH∥DF∵DF∥CE,∴∠PCE=∠1=α,∠PDF=∠2∵∠DPC=∠2+∠1=α+β【问题迁移】(1)70(图1)(图2)(2) 如图1,∠DPC=β -α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1-∠FDP=∠1-α.∴∠DPC=β -α如图2,∠DPC= α -β∵DF∥CE,∴∠PDF=∠1=α∵∠DPC=∠1-∠ACE=∠1-β.∴∠DPC=α - βAB CD,点O在直线CD上,点P在直线AB和CD之间,25.如图,//∠.ABP PDQα∠=∠=,PD平分BPQ(1)求BPD ∠的度数(用含α的式子表示);(2)过点D 作//DE PQ 交PB 的延长线于点E ,作DEP ∠的平分线EF 交PD 于点F ,请在备用图中补全图形,猜想EF 与PD 的位置关系,并证明;(3)将(2)中的“作DEP ∠的平分线EF 交PD 于点F ”改为“作射线EF 将DEP ∠分为1:3两个部分,交PD 于点F ”,其余条件不变,连接EQ ,若EQ 恰好平分PQD ∠,请直接写出FEQ ∠=__________(用含α的式子表示).答案:(1);(2)画图见解析,,证明见解析;(3)或【分析】(1)根据平行线的传递性推出,再利用平行线的性质进行求解;(2)猜测,根据平分,推导出,再根据、平分,通过等量代换求解; (3)分两种情解析:(1)2BPD α∠=;(2)画图见解析,EF PD ⊥,证明见解析;(3)452α︒-或3452α︒- 【分析】(1)根据平行线的传递性推出////PG AB CD ,再利用平行线的性质进行求解; (2)猜测EF PD ⊥,根据PD 平分,2BPQ BPD α∠∠=,推导出2BPD DPQ α∠=∠=,再根据//DE PQ 、EF 平分DEP ∠,通过等量代换求解;(3)分两种情况进行讨论,即当:1:3PEF DEF ∠∠=与:1:3DEF PEF ∠∠=,充分利用平行线的性质、角平分线的性质、等量代换的思想进行求解.【详解】(1)过点P 作//PG AB ,//,//AB CD PG AB ,////PG AB CD ∴,,BPG ABP DPG PDQ αα∴∠=∠=∠=∠=,2BPD BPG DPG α∴∠=∠+∠=.(2)根据题意,补全图形如下:猜测EF PD ⊥,由(1)可知:2BPD α∠=, PD 平分,2BPQ BPD α∠∠=,2BPD DPQ α∴∠=∠=,//DE PQ ,2EDP DPQ α∴∠=∠=,1801804DEP BPD EDP α∴∠=︒-∠-∠=︒-,又EF 平分DEP ∠,19022PEF DEP α∠=∠=︒-, 18090EFD PEF BPD ∴∠=︒-∠-∠=︒,EF PD ∴⊥.(3)①如图1,:1:3PEF DEF ∠∠=,由(2)可知:2,1804EPD DPQ EDP DEP αα∠=∠=∠=∠=︒-,:1:3PEF DEF ∠∠=, 1454PEF DEP α∴∠=∠=︒-, 313534DEF DEP α∠=∠=︒-, //DE PQ ,DEQ PQE ∴∠=∠,180EDQ PQD ∠+∠=︒,2,EDP PDQ αα∠=∠=, 3EDQ EDP PDQ α∴∠=∠+∠=,1801803PQD EDQ α∠=︒-∠=︒-,又EQ 平分PQD ∠,139022PQE DQE DEQ PQD α∴∠=∠=∠=∠=︒-, 331353(90)4522FEQ DEF DEQ ααα∴∠=∠-∠=︒--︒-=︒-; ②如图2,1804DEP α∠=︒-,1803PQD α∠=︒-(同①);若:1:3DEF PEF ∠∠=,则有11(1804)4544DEF DEP αα∠=∠=⨯︒-=︒-, 又113(1803)90222PQE DQE PQD αα∠=∠=∠=⨯︒-=︒-,//DE PQ ,3902DEQ PQE α∴∠=∠=︒-, 1452FEQ DEQ DEF α∴∠=∠-∠=︒-, 综上所述:3452FEQ α∠=︒-或452α︒-, 故答案是:452α︒-或3452α︒-. 【点睛】 本题考查了平行线的性质、角平分线、三角形内角和定理、垂直等相关知识点,解题的关键是掌握相关知识点,作出适当的辅助线,通过分类讨论及等量代换进行求解.。
初中数学中考常见重难点题大全

以下是初中数学中考常见的重难点题目:
1. 初一下数学:
- 平方差公式的运用;
- 两点间距离公式的运用;
- 正比例、反比例的运用;
- 简单统计:平均数、中位数、众数、极差等。
2. 初一上数学:
- 一元一次方程式的解法:解方程、解不等式问题;
- 合并同类项、开平方问题以及它们的运算;
- 面积知识:基本平面图形面积以及环的面积;
- 相交线与平行线性质问题。
3. 初一下数学:
- 二元一次方程组与不等式组的求解;
- 三角形(等腰三角形、直角三角形、角平分线问题)面积计算;
- 勾股定理的运用;
- 正方体的表面积、体积计算。
4. 初二上数学:
- 一元二次方程式的求解:解方程组、解不等式问题;
- 计算容斥、组合、排列;
- 立体图形的表面积、体积计算;
- 二次函数的解析式、图像以及相关变换问题。
5. 初二下数学:
- 斜率、二直线问题;
- 数列等差、等比问题及求和问题;
- 概率与统计相关问题;
- 初中三角题基本应用。
以上是初中数学中考常见的重难点题目,建议在复习中注重以上重点题目的练习和掌握,同时也应注意整体的知识综合及应用能力的培养。
初中一年级上册数学难题

初中一年级上册数学难题
当然,我可以提供一些初中一年级上册数学难题供您参考。
请注意,这些题目可能对一些学生来说具有挑战性,因此请根据学生的实际情况来选择适合的题目。
1. 题目:若$a$、$b$、$c$为整数,且$a - b + c - a + b - c = 2$,则$a + b + c =$____
2. 题目:若$a$、$b$、$c$为整数,且$a - b + c - a + b - (a + c) = 4$,则$2a + b + c =$____
3. 题目:已知$x - 3 + x - 5 + x + 3 + x + 5 = 14$,如果对任意实数$x$,上面的等式都成立,那么满足条件的实数$x$的个数是()
A.$1$个
B.$2$个
C.$3$个
D.$4$个
4. 题目:已知点A($- 2a + 1$,$a - 4$)在$x$轴上,则点A的坐标为()
A.($- 3$,$0$)
B.($1$,$0$)
C.($- \frac{5}{3}$,$0$)
D.
($\frac{5}{3}$,$0$)
5. 题目:已知点A($- 2a + 1$,$a - 4$)在第三象限,则字母a的取值
范围是()
A.$1 < a < \frac{5}{2}$
B.$1 \leq a \leq \frac{5}{2}$
C.$a <
\frac{5}{2}$ D.$a > 1$
这些题目考察了绝对值、代数式的性质和一元一次不等式的解法等知识点。
解答这些题目需要学生具备扎实的基础知识和灵活的解题技巧。
初二数学最难练习题

初二数学最难练习题数学是一门需要不断练习的学科,而初中数学中也存在着一些难题,让学生们感到头疼和困惑。
本文将介绍初二数学中最难的练习题,并提供解题思路,希望能帮助同学们更好地应对这些挑战。
一、挑战一:几何难题在初二数学中,几何题通常被认为是相对较难的。
其中一道经典的几何难题是关于平行线与角度的题目。
题目描述:已知折线ABCD如图所示,AB // CD,角α = 30°,角β = 75°,求角γ的度数。
解题思路:首先,我们可以观察到三个角度之和必然为180°。
根据已知条件,我们可以得出以下等式:α+ β + γ = 180°。
代入已知数值,即可得到γ的度数。
计算过程:α + β + γ = 180°30° + 75° + γ = 180°105° + γ = 180°γ = 180° - 105°γ = 75°因此,角γ的度数为75°。
二、挑战二:代数难题代数题在初二数学中同样具有一定的难度,尤其是涉及到方程的解的问题。
下面是一道典型的代数难题。
题目描述:已知方程3x - 2 = 4(x + 1),求x的值。
解题思路:我们可以通过移项和合并同类项的方法来解方程。
由于方程两边都包含x,因此我们需要将x的项集中在一起。
计算过程:3x - 2 = 4(x + 1)3x - 2 = 4x + 4-2 - 4 = 4x - 3x-6 = x因此,方程的解为x = -6。
三、挑战三:概率与统计难题另一个比较困难的数学领域是概率与统计。
下面是一个涉及到概率的难题。
题目描述:甲乙丙丁四人从1到20中随机取数,取出的数不能重复,甲取数后乙取数,丙取数,丁取数。
求甲乙丙丁四人顺序取数后,乙取到数1的概率。
解题思路:根据题目描述,甲取数后,乙共有19个数可以选择,其中只有一个数是1。
初二比较难的数学练习题

初二比较难的数学练习题在初二的数学学习中,遇到一些难题是很常见的。
这些题目需要我们掌握一定的数学知识和解题技巧才能顺利解答。
下面,我将为大家列举一些初二比较难的数学练习题。
一、立体几何题1. 某矩形纸片的长是宽的四倍,将该矩形剪成两个正方形,剪下的两个正方形面积之和是矩形面积的81%,求矩形的长和宽分别是多少?2. 下面的解析几何图形中,点A、B、C、D、E、F六点不在同一平面中,求ADE面与BCF面的夹角。
3. 设一条直线通过坐标轴上的点A(a, 0)和B(0, b),且直线与y轴交于点C(0, c),若三点A、B、C共线,求a、b、c之间的关系。
二、初中代数题4. 已知方程组:2x + 3y = 114x + ky = 15求k的值,使得方程组有唯一解。
5. 某数学题库有机试题100道,其中单选题每个题目的正确答案有4个选项,多选题每个题目的正确答案有5个选项,则这100道题中的选择题正确答案选项总数为多少?三、数列题6. 在等差数列{an}中,已知a1 = 3,a2 = 7,a4 = 17,则an的通项公式是什么?7. 若等比数列{bn}满足b1 = 2,b2 = 6,b4 = 90,则bn的通项公式是什么?四、概率题8. 一件商品的质量服从正态分布,已知其平均值为μ,标准差为σ。
若70%的商品质量在80kg到100kg之间,求μ和σ的值。
9. 一枚正六面体骰子有6个面,分别刻有1、2、3、4、5、6这6个数字。
现随机扔一枚骰子,连续扔5次,且每次都得到数字4的概率是多少?五、面积和体积题10. 在长方体中,一条对角线为18,长和宽的比为3:2,求长方体的体积和表面积。
以上是初二比较难的数学练习题,希望通过解题过程,能帮助大家加深对数学知识的理解和运用。
在解答这些题目时,我们要掌握相应的数学概念,并善于运用所学的数学方法和技巧进行推导和计算。
祝愿大家在数学学习中取得优异的成绩!。
七年级上册数学难题100题

一、填空题.(每小题3分,共24分)1.已知4x2n-5+5=0是关于x的一元一次方程,则n=_______.2.若x=-1是方程2x-3a=7的解,则a=_______.3.当x=______时,代数式x-1和的值互为相反数.4.已知x的与x的3倍的和比x的2倍少6,列出方程为________.5.在方程4x+3y=1中,用x的代数式表示y,则y=________.6.某商品的进价为300元,按标价的六折销售时,利润率为5%,则商品的标价为____元.7.已知三个连续的偶数的和为60,则这三个数是________.8.一件工作,甲单独做需6天完成,乙单独做需12天完成,若甲、乙一起做,•则需________天完成.二、选择题.(每小题3分,共30分)9.方程2m+x=1和3x-1=2x+1有相同的解,则m的值为().A.0 B.1 C.-2 D.-10.方程│3x│=18的解的情况是().A.有一个解是6 B.有两个解,是±6C.无解D.有无数个解11.若方程2ax-3=5x+b无解,则a,b应满足().A.a≠ ,b≠3B.a= ,b=-3C.a≠ ,b=-3 D.a= ,b≠-312.把方程的分母化为整数后的方程是().13.在800米跑道上有两人练中长跑,甲每分钟跑300米,乙每分钟跑260米,•两人同地、同时、同向起跑,t分钟后第一次相遇,t等于().A.10分B.15分C.20分D.30分14.某商场在统计今年第一季度的销售额时发现,二月份比一月份增加了10%,三月份比二月份减少了10%,则三月份的销售额比一月份的销售额().A.增加10% B.减少10% C.不增也不减D.减少1%15.在梯形面积公式S= (a+b)h中,已知h=6厘米,a=3厘米,S=24平方厘米,则b=(•)厘米.A.1 B.5 C.3 D.416.已知甲组有28人,乙组有20人,则下列调配方法中,能使一组人数为另一组人数的一半的是().A.从甲组调12人去乙组B.从乙组调4人去甲组C.从乙组调12人去甲组D.从甲组调12人去乙组,或从乙组调4人去甲组17.足球比赛的规则为胜一场得3分,平一场得1分,负一场是0分,•一个队打了14场比赛,负了5场,共得19分,那么这个队胜了()场.A.3 B.4 C.5 D.618.如图所示,在甲图中的左盘上将2个物品取下一个,则在乙图中右盘上取下几个砝码才能使天平仍然平衡?()A.3个B.4个C.5个D.6个三、解答题.(19,20题每题6分,21,22题每题7分,23,24题每题10分,共46分)19.解方程:-9.5.20.解方程:(x-1)- (3x+2)= - (x-1).21.如图所示,在一块展示牌上整齐地贴着许多资料卡片,•这些卡片的大小相同,卡片之间露出了三块正方形的空白,在图中用斜线标明.•已知卡片的短边长度为10厘米,想要配三张图片来填补空白,需要配多大尺寸的图片.22.一个三位数,百位上的数字比十位上的数大1,个位上的数字比十位上数字的3倍少2.若将三个数字顺序颠倒后,所得的三位数与原三位数的和是1171,求这个三位数.23.据了解,火车票价按“ ”的方法来确定.已知A站至H站总里程数为1500千米,全程参考价为180元.下表是沿途各站至H站的里程数:车站名 A B C D E F G H各站至H站里程数(米)1500 1130 910 622 402 219 72 0例如:要确定从B站至E站火车票价,其票价为=87.36≈87(元).(1)求A站至F站的火车票价(结果精确到1元).(2)旅客王大妈乘火车去女儿家,上车过两站后拿着车票问乘务员: “我快到站了吗?”乘务员看到王大妈手中的票价是66元,马上说下一站就到了.请问王大妈是在哪一站下的车(要求写出解答过程).24.某公园的门票价格规定如下表:购票人数1~50人51~100人100人以上票价5元 4.5元4元某校初一甲、乙两班共103人(其中甲班人数多于乙班人数)去游该公园,如果两班都以班为单位分别购票,则一共需付486元.(1)如果两班联合起来,作为一个团体购票,则可以节约多少钱?(2)两班各有多少名学生?(提示:本题应分情况讨论)答案:一、1.32.-3 (点拨:将x=-1代入方程2x-3a=7,得-2-3a=7,得a=-3)3.(点拨:解方程x-1=- ,得x= )4.x+3x=2x-6 5.y= - x6.525 (点拨:设标价为x元,则=5%,解得x=525元)7.18,20,228.4 [点拨:设需x天完成,则x(+ )=1,解得x=4]二、9.D10.B (点拨:用分类讨论法:当x≥0时,3x=18,∴x=6当x<0时,-3=18,∴x=-6故本题应选B)11.D (点拨:由2ax-3=5x+b,得(2a-5)x=b+3,欲使方程无解,必须使2a-5=0,a= ,b+3≠0,b≠-3,故本题应选D.)12.B (点拨;在变形的过程中,利用分式的性质将分式的分子、•分母同时扩大或缩小相同的倍数,将小数方程变为整数方程)13.C (点拨:当甲、乙两人再次相遇时,甲比乙多跑了800•米,•列方程得260t+800=300t,解得t=20)14.D15.B (点拨:由公式S= (a+b)h,得b= -3=5厘米)16.D 17.C18.A (点拨:根据等式的性质2)三、19.解:原方程变形为200(2-3y)-4.5= -9.5∴400-600y-4.5=1-100y-9.5500y=404∴y=20.解:去分母,得15(x-1)-8(3x+2)=2-30(x-1)∴21x=63∴x=321.解:设卡片的长度为x厘米,根据图意和题意,得5x=3(x+10),解得x=15所以需配正方形图片的边长为15-10=5(厘米)答:需要配边长为5厘米的正方形图片.22.解:设十位上的数字为x,则个位上的数字为3x-2,百位上的数字为x+1,故100(x+1)+10x+(3x-2)+100(3x-2)+10x+(x+1)=1171解得x=3答:原三位数是437.23.解:(1)由已知可得=0.12A站至H站的实际里程数为1500-219=1281(千米)所以A站至F站的火车票价为0.12×1281=153.72≈154(元)(2)设王大妈实际乘车里程数为x千米,根据题意,得=66解得x=550,对照表格可知,D站与G站距离为550千米,所以王大妈是在D站或G•站下的车.24.解:(1)∵103>100∴每张门票按4元收费的总票额为103×4=412(元)可节省486-412=74(元)(2)∵甲、乙两班共103人,甲班人数>乙班人数∴甲班多于50人,乙班有两种情形:①若乙班少于或等于50人,设乙班有x人,则甲班有(103-x)人,依题意,得5x+4.5(103-x)=486解得x=45,∴103-45=58(人)即甲班有58人,乙班有45人.②若乙班超过50人,设乙班x人,则甲班有(103-x)人,根据题意,得4.5x+4.5(103-x)=486∵此等式不成立,∴这种情况不存在.故甲班为58人,乙班为45人.====================================================== ================3.2 解一元一次方程(一)——合并同类项与移项【知能点分类训练】知能点1 合并与移项1.下面解一元一次方程的变形对不对?如果不对,指出错在哪里,并改正.(1)从3x-8=2,得到3x=2-8; (2)从3x=x-6,得到3x-x=6.2.下列变形中:①由方程=2去分母,得x-12=10;②由方程x= 两边同除以,得x=1;③由方程6x-4=x+4移项,得7x=0;④由方程2- 两边同乘以6,得12-x-5=3(x+3).错误变形的个数是()个.A.4 B.3 C.2 D.13.若式子5x-7与4x+9的值相等,则x的值等于().A.2 B.16 C.D.4.合并下列式子,把结果写在横线上.(1)x-2x+4x=__________; (2)5y+3y-4y=_________;(3)4y-2.5y-3.5y=__________.5.解下列方程.(1)6x=3x-7 (2)5=7+2x(3)y- = y-2 (4)7y+6=4y-36.根据下列条件求x的值:(1)25与x的差是-8.(2)x的与8的和是2.7.如果方程3x+4=0与方程3x+4k=8是同解方程,则k=________.8.如果关于y的方程3y+4=4a和y-5=a有相同解,则a的值是________.知能点2 用一元一次方程分析和解决实际问题9.一桶色拉油毛重8千克,从桶中取出一半油后,毛重4.5千克,•桶中原有油多少千克?10.如图所示,天平的两个盘内分别盛有50克,45克盐,问应该从盘A内拿出多少盐放到盘B内,才能使两盘内所盛盐的质量相等.11.小明每天早上7:50从家出发,到距家1000米的学校上学,•每天的行走速度为80米/分.一天小明从家出发5分后,爸爸以180米/分的速度去追小明,•并且在途中追上了他.(1)爸爸追上小明用了多长时间?(2)追上小明时距离学校有多远?【综合应用提高】12.已知y1=2x+8,y2=6-2x.(1)当x取何值时,y1=y2? (2)当x取何值时,y1比y2小5?13.已知关于x的方程x=-2的根比关于x的方程5x-2a=0的根大2,求关于x的方程-15=0的解.【开放探索创新】14.编写一道应用题,使它满足下列要求:(1)题意适合一元一次方程;(2)所编应用题完整,题目清楚,且符合实际生活.【中考真题实战】15.(江西)如图3-2是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为相应两点间的路程(单位:千米).一学生从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为0.5小时.(1)当他沿路线A—D—C—E—A游览回到A处时,共用了3小时,求CE的长.(2)若此学生打算从A处出发,步行速度与各景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,•并说明这样设计的理由(不考虑其他因素).答案:1.(1)题不对,-8从等号的左边移到右边应该改变符号,应改为3x=2+8.(2)题不对,-6在等号右边没有移项,不应该改变符号,应改为3x-x=-6.2.B [点拨:方程x= ,两边同除以,得x= )3.B [点拨:由题意可列方程5x-7=4x+9,解得x=16)4.(1)3x (2)4y (3)-2y5.(1)6x=3x-7,移项,得6x-3x=-7,合并,得3x=-7,系数化为1,得x=- .(2)5=7+2x,即7+2x=5,移项,合并,得2x=-2,系数化为1,得x=-1.(3)y- = y-2,移项,得y- y=-2+ ,合并,得y=- ,系数化为1,得y=-3.(4)7y+6=4y-3,移项,得7y-4y=-3-6,合并同类项,得3y=-9,系数化为1,得y=-3.6.(1)根据题意可得方程:25-x=-8,移项,得25+8=x,合并,得x=33.(2)根据题意可得方程:x+8=2,移项,得x=2-8,合并,得x=-6,系数化为1,得x=-10.7.k=3 [点拨:解方程3x+4=0,得x=- ,把它代入3x+4k=8,得-4+4k=8,解得k=3] 8.19 [点拨:∵3y+4=4a,y-5=a是同解方程,∴y= =5+a,解得a=19]9.解:设桶中原有油x千克,那么取掉一半油后,余下部分色拉油的毛重为(8-0.5x)千克,由已知条件知,余下的色拉油的毛重为4.5千克,因为余下的色拉油的毛重是一个定值,所以可列方程8-0.5x=4.5.解这个方程,得x=7.答:桶中原有油7千克.[点拨:还有其他列法]10.解:设应该从盘A内拿出盐x克,可列出表格:盘A 盘B原有盐(克)50 45现有盐(克)50-x 45+x设应从盘A内拿出盐x克放在盘B内,则根据题意,得50-x=45+x.解这个方程,得x=2.5,经检验,符合题意.答:应从盘A内拿出盐2.5克放入到盘B内.11.解:(1)设爸爸追上小明时,用了x分,由题意,得180x=80x+80×5,移项,得100x=400.系数化为1,得x=4.所以爸爸追上小明用时4分钟.(2)180×4=720(米),1000-720=280(米).所以追上小明时,距离学校还有280米.12.(1)x=-[点拨:由题意可列方程2x+8=6-2x,解得x=- ](2)x=-[点拨:由题意可列方程6-2x-(2x+8)=5,解得x=- ]13.解:∵x=-2,∴x=-4.∵方程x=-2的根比方程5x-2a=0的根大2,∴方程5x-2a=0的根为-6.∴5×(-6)-2a=0,∴a=-15.∴-15=0.∴x=-225.14.本题开放,答案不唯一.15.解:(1)设CE的长为x千米,依据题意得1.6+1+x+1=2(3-2×0.5)解得x=0.4,即CE的长为0.4千米.(2)若步行路线为A—D—C—B—E—A(或A—E—B—C—D—A),则所用时间为(•1.6+1+1.2+0.4+1)+3×0.5=4.1(小时);若步行路线为A—D—C—E—B—E—A(或A—E—B—E—C—D—A),则所用时间为(1.6+1+0.4+0.4×2+1)+3×0.5=3.9(小时).故步行路线应为A—D—C—E—B—E—A(或A—E—B—E—C—D—A)。
