运筹学模型与算法2008
运筹学-第1章-1-线性规划问题及其数学模型资料

2 x1
x2 x3 x1
8
x1 x2 4x3 9
x1, x2 , x3 0
19
第十九页,共28页。
线性规划的标准形式
-目标函数为极大化, -约束条件全部为等号约束 -决策变量全部是非负
maxZ=c1x1+c2x2+……+cnxn s.t. a11x1+a12x2+……+a1nxn =b1
• 运筹学与控制论专业(数学一级学科)
–20世纪50年代,钱学森、许国志等将运筹学引入中国, 华罗庚推广统筹法和优选法
• 管理科学与工程(管理科学与工程一级学科)
–管理运筹学
5
第五页,共28页。
• 运筹学 operational research(operations research,O.R)
• 运筹学是在第二次世界大战中诞生和发展起 来的。由于战争的需要,英国和美国招募了 一批年轻的科学家和工程师,在军队将军的 领导下研究战争中的问题,例如大规模轰炸 的效果、搜索和攻击敌军潜水艇的策略、兵 力和军需物质的调运等等。这些研究在战争 中取得了很好的效果。
最少?
解:将1m的钢分别切成A,B,C三种钢的可能方案如下:
方案 1
A
2
B
0
C
1
剩料 0
2
3
4
5
6
7
8
1
1
1
0
0
0
0
2
1
0
3
2
1
0
0
1
3
0
2
3
5
0 0.1 0 0.1 0 0.1 0
17
第十七页,共28页。
运筹学 参考书

参考书1.《运筹学》(科学版精品课程立体化教材·管理学系列)(第2版),张伯生等编著,科学出版社,2012年;2.《数据、模型与决策》(第13版),戴维·R·安德森/丹尼斯·J·斯威尼编著,于淼译,机械出版社,2012年;3、《运筹学》(新体系经济管理系列教材),李成标,刘新卫主编,清华大学出版社,2012年;4.《运筹学——优化模型与算法》,(美)拉丁(Rardin,R.L.) 著,电子工业出版社,2007年5.《Introduction to Operations Research》(第6 版)(外原版经典教材), F. S. Hillier and G. J. Lieberman 著,McGraw-Hill 出版社;6. 《运筹学》,党耀国,李帮义等编著,科学出版社,2009年;7. 《物流运筹学》,刘蓉主编,电子工业出版社,2012年;8. 《运筹学导论》(第9版)(美国麦格劳-希尔教育出版公司工商管理最新教材(英文版)),(美)希利尔,(美)利伯曼著,清华大学出版社,2010年;9. 《运筹学》(第4版)(面向21世纪课程教材(信息管理与信息系统专业教材系列),《运筹学》教材编写组编,清华大学出版社,2012年;10.《运筹学:应用与解决方法》(第4版)(美国商学院原版教材精选系列),(美)温斯顿著,清华大学出版社,2011年;11.《管理运筹学》(高等学校经济与工商管理系列教材),茹少峰,申卯兴编著,清华大学出版社,2008年;12.《运筹学》(第3版),刁在筠等编,高等教育出版社,2007年;13.《实用运筹学:模型、方法与计算》,韩中庚主编,清华大学出版社,2007年;14.《运筹学》(现代信息管理与信息系统系列教材),李红艳,范君晖主编,清华大学出版社,2012 年;15.《管理运筹学:管理科学方法》(21世纪管理科学与工程系列教材),谢家平著,中国人民大学出版社,2010年;16.《运筹学与实验》,薛毅,耿美英编著,电子工业出版社,2008年;17.《实用运筹学——上机实验指导及习题解答》,叶向编,中国人民大学出版社,2007年;18.《应用运筹学》(第二版),曹勇,周晓光,李宗元编著,经济管理出版社,2008年;19.《运筹学导论》(第8版),(美)希利尔(Hillier,F.S.),(美)利伯曼(Lieberman,G.J.)著,胡运权等译,清华大学出版社,2007年;20.《经济管理运筹学习题集》,王玉梅,孙在东,张志耀编著,中国标准出版社,2012年;21.《运筹学习题集》(第4版),胡运权主编,清华大学出版社,2010年;22.《运筹学解题指导》,周华任主编,清华大学出版社,2006年;23.《运筹学概率模型应用范例与解法》(第4版),(美)温斯顿(Winston,W.L.)著,李乃文等译,清华大学出版社,2006年;24.《运筹学学习辅导与习题解析》(第3版),戎晓霞,宿洁,刘桂真编,高等教育出版社,2009年;25.《管理运筹学习题集》(普通高等学校管理科学与工程类学科核心课程教材辅助教材),韩伯棠,艾凤义主编,高等教育出版社,2010年;26.《运筹学学习指导及习题集》(普通高等教育经济管理类专业规划教材,第2版),吴祈宗主编,机械工业出版社,2013年。
数据、模型与决策(运筹学)课后习题和案例答案008

CHAPTER 8 PERT/CPM MODELS FOR PROJECT MANAGEMENTReview Questions8.1-1 The bid is for $5.4 million with a penalty of $300,000 if the deadline of 47 weeks is notmet. In addition, a bonus of $150,000 will be paid if the plant is completed within 40 weeks.8.1-2 He has decided to focus on meeting the deadline of 47 weeks.8.1-3 An immediate predecessor is an activity that must be completed just prior to startingthe given activity. Given the immediate predecessors of an activity, this activity then becomes the immediate successor of each of these immediate predecessors.8.1-4 (1) the activities of the project; (2) the immediate predecessors of the activities; and (3)the estimated duration of the activities8.2-1 (1) activity information; (2) precedence relationships; and (3) time information(duration)8.2-2 In an AOA network, each activity is represented by an arc, while in an AON network,each activity is represented by a node. AON networks are being used here.8.2-3 The bars in a Gantt chart show the scheduled start and finish times for activities in aproject.8.3-1 (a) A path through a project network is one of the routes following the arrows (arcs)from the start node to the finish node; (b) the length of a path is the sum of the estimated durations of the activities on the path; (c) the longest path is called the critical path.8.3-2 (1) The actual duration of each activity must be the same as its estimated duration;and (2) each activity must begin as soon as all its immediate predecessors are finished.8.3-3 The earliest start time of an activity is equal to the largest of the earliest finish times ofits immediate predecessors.8.3-4 A forward pass is the process of starting with the initial activities and working forwardin time toward the final activities.8.3-5 It is a last chance schedule because anything later will delay the completion of theproject.8.3-6 The latest finish time of an activity is equal to the smallest of the latest start times ofits immediate successors.8.3-7 A backward pass starts with the final activities and works backward in time toward theinitial activities instead of starting with the initial activities.8.3-8 Any delay along the critical path will delay project completion.8.3-9 (1) Identify the longest path through the project network; and (2) identify the activitieswith zero slack—they are on the critical path.8.4-1 The three estimates are the most likely estimate, optimistic estimate, and pessimisticestimate.8.4-2 The optimistic and pessimistic estimates are meant to lie at the extremes of what ispossible, whereas the most likely estimate provides the highest point of the probability distribution.8.4-3 It is assumed that the mean critical path will turn out to be the longest path throughthe project network.8.4-4 It is assumed that the durations of the activities on the mean critical path arestatistically independent.8.4-5 μp=sum of the means of the durations for the activities on the mean critical path.8.4-6 σp2=sum of the variances of the durations for the activities on the mean critical path.8.4-7 It is assumed that the form of the probability distribution of project duration is thenormal distribution.8.4-8 It is usually higher than the true probability.8.5-1 Using overtime, hiring additional labor, and using special materials or equipment areall ways of crashing an activity.8.5-2 The two key points are labeled normal and crash. The normal point shows the timeand cost of the activity when it is performed in the normal way. The crash point shows the time and cost when the activity is fully crashed.8.5-3 No, only crashing activities on the critical path will reduce the duration of the project.8.5-4 Crash costs per week saved are being examined.8.5-5 The decisions to be made are the start time of each activity, the reduction in theduration of each activity due to crashing, and the finish time of the project.8.5-6 An activity cannot start until its immediate predecessor starts and then completes itsduration.8.5-7 Because of uncertainty, the plan for crashing the project only provides a 50% chanceof actually finishing within 40 weeks, so the extra cost of the plan is not justified.8.6-1 PERT/Cost is a systematic procedure to help the manager plan, schedule, and controlproject costs.8.6-2 It begins by developing an estimate of the cost of each activity when it is performedin the planned way.8.6-3 A common assumption is that the costs of performing an activity are incurred at aconstant rate throughout its duration.8.6-4 A work package is a group of related activities.8.6-5 PERT/Cost uses earliest start time and latest start time schedules as a basis fordeveloping cost schedules.8.6-6 A PERT/Cost schedule of costs shows the weekly project cost and cumulative projectcost for each time period.8.6-7 A PERT/Cost report shows the budgeted value of the work completed of each activityand the cost overruns to date.8.6-8 Since deviations from the planned work schedule may occur, a PERT/Cost report isneeded to evaluate the cost performance of individual activities.8.7-1 Planning, scheduling, dealing with uncertainty, time-cost trade-offs, and controllingcosts are addressed by PERT/CPM.8.7-2 Computer implementation has allowed for application to larger projects, fasterrevisions in project plans and effortless updates and changes in schedules.8.7-3 The accuracy and reliability of end-point estimates are not as good for points that arenot at the extremes of the probability distribution.8.7-4 The technique of computer simulation to approximate the probability that the projectwill meet its deadline is an alternative for improving on PERT/CPM.8.7-5 The Precedence Diagramming Method has been developed as an extension ofPERT/CPM to deal with overlapping activities.8.7-6 PERT/CPM assumes that each activity has available all the resources needed toperform the activity in a normal way.8.7-7 It encourages effective interaction between the project manager and subordinatesthat leads to setting mutual goals for the project.8.7-8 New improvements and extensions are still being developed but have not beenincorporated much into practice yet.Problems8.1 a)3b) Start → A → C → Finish Length = 4 weeksStart → A → D → E → Finish Length = 7 weeksStart → B → C → Finish Length = 5 weeksStart → B → D → E → Finish Length = 8 weeks *critical pathc)Critical Path: Start → B → D → E → Finishd) No, this will not shorten the length of the project because the activity is not on thecritical path.8.2 a)4b) Start → A → D → Finish Length = 4 weeksStart → A → E → Finish Length = 5 weeks Start → A → F → K → Finis Length = 8 weeks *critical path Start → A → G → H → I →J → Finish Length = 8 weeks *critical path Start → B → D → Finish Length = 3 weeks Start → B → C → E → Finish Length = 6 weeks Start → B → C → H → I →J → Finish Length = 8 weeks *critical path Start → B → C → K → Finish Length = 7 weeksc)Critical Paths: Start → A → F →K →Finish Start → A →G →H →I →J →FinishStart → B → C → H → I →J → Finishd) No, this will not shorten the length of the project because A is not on all of thecritical paths.8.3 a)25b, c, & d)Critical Paths: Start →A →B →C →F →H →I →J →L →N →Finish Start → A → B → D → G → I → J → L → N → Finish8.4 a)b) Start → A → B → J → L → Finish Length = 75 minutes *critical pathStart → C → D → J → L → Finish Length = 45 minutesStart → E → F → J → L → Finish Length = 72 minutesStart → G → H → I → J → L → Finish Length = 67 minutesStart → K → L → Finish Length = 45 minutesc, d & e)Critical Path: Start → A → B → J → L → Finishf) Dinner will be delayed 3 minutes because of the phone call. If the food processoris used then dinner will not be delayed because there was 3 minutes of slack and 5minutes of cutting time saved and the call only used 6 minutes of the 8 total.8.5 a) Start → A → D → H → M → Finish Length = 19 weeksStart → B → E → J → M → Finish Length = 20 weeks *critical pathStart → C → F → K → N → Finish Length = 16 weeksStart → A → I → M → Finish Length = 17 weeksStart → C → G → L →N → Finish Length = 20 weeks *critical pathb)Ken will be able to meet his deadline if no delays occur.c) Critical Paths: Start → B → E →J →M →FinishStart → C →G →L →N →FinishFocus attention on activities with 0 slack (those in the critical paths).d) If activity I takes 2 extra weeks there will be no delay because its slack is 3. Ifactivity H takes 2 extra weeks then there will be a delay of 1 week because its slack is 1. If activity J takes 2 extra weeks there will be a delay of 2 weeks because it has no slack.8.6 a)2b)Critical Path: Start → A → E → F → FinishLength = 14 monthsc) 6 months8.7Critical Path: Start → A → B → C → D →G →H →M →Finish Total duration = 70 weeks8.8Critical Path: Start → A → B → C → E → F →J →K →N→Finish Total duration = 26 weeks8.9Critical Paths: Start → A → B → C → E → F →J →K →N→Finish Start → A → B → C → E → F →J →L →N→Finish Total duration = 28 weeks8.10 μ= (o+ 4m+ p) / 6 = [30 + (4)(36) + 48] / 6 = 37σ2 = [(p–o) / 6]2 = [(48 – 30) / 6]2 = 98.11 a) Start → A → E → I → Finish Length = 17 monthsStart → A → C → F → I → Finish Length = 17 monthsStart → B → D → G → J → Finish Length = 17 monthsStart → B → H → J → Finish Length = 18 months *critical pathb) d-μpσp2=22-1831=0.72By Table 8.7, P(T≤ 22 months) is just less than 0.77.c) Start → A → E →I →Finishd-μpσp2=22-1725=1By Table 8.7, P(T≤ 22 months) = 0.84. Start → A → C → F →I →Finishd-μpσp2=22-1727=0.96By Table 8.7, P(T≤ 22 months) is just less than 0.84. Start → B → D →G →J →Finishd-μpσp2=22-1728=0.95By Table 8.7, P(T≤ 22 months) is just less than 0.84.d) There is somewhat less than a 77% chance that the drug will be ready in 22 weeks.8.12Then, based on these spreadsheets, the answers to (a), (b), (c), and (d) would bea) Start → A → E → I → Finish Length = 17.08 monthsStart → A → C → F → I → Finish Length = 17.58 monthsStart → B → D → G → J → Finish Length = 17.83 monthsStart → B → H → J → Finish Length = 18.42 months *critical pathb) P(Start → B → H → J →Finish ≤ 22 months) = 0.7394c) P(Start → A → E →I →Finish ≤ 22) = 0.8356P(Start → A → C → F →I →Finish ≤ 22) = 0.8007P(Start → B → D → G → J →Finish ≤ 22) = 0.7843d) There is approximately a 73% chance that the drug will be ready in 22 weeks.8.13 a)b)c) Start → A → B → C → Finish Length = 10.83 weeks *critical pathStart → A → B → E → Finish Length = 9.17 weeks Start → A → D → E → Finish Length = 10.17 weeksd) d-μpσp2=11-10.830.361=0.03. Then, by Appendix A, P(T≤ 11 weeks) = 0.512, or by Table 8.7, P(T≤ 11 weeks) = slightly more than 0.5.e) It is a borderline call. By the PERT analysis, there is barely more than a 50% chanceof meeting the deadline, but PERT tends to provide optimistic estimates.8.14 a)b) Start → A → C → E → F → Finish Length = 51 days *critical pathStart → B → D → Finish Length =50 daysc) d-μpσp2=57-519=2. By Appendix A, P(T≤ 57 days) = 0.9772. By Table 8.7, P(T≤ 57 days) = 0.997.d) d-μpσp2=57-5025=1.4. By Appendix A, P(T≤ 57 days) = 0.9192. By Table 8.7, P(T≤ 57 days) is between 0.89 and 0.933.e) (0.9772)(0.9192)=0.8982.This answer tells us that the procedure used in part (c) overestimates theprobability of completing within 57 days.8.15 a)b) Start → A → C → J → Finish Length = 85.7 weeksStart → B → F → J → Finish Length =99.1 weeks *critical pathStart → B → E → H → Finish Length = 80 weeksStart → B → E → I → Finish Length =93.7 weeksStart → B → D → G → H → Finish Length = 80.7 weeksStart → B → D → G → I → Finish Length =94.4 weeksc) d-μpσp2=100-99.143.89=0.136.By Appendix A, P(T≤ 100 weeks) = 0.5557. By Table 8.7, P(T≤ 100 weeks) is between 0.5 and 0.6.d) Higher8.16 a) False. The optimistic estimate is the duration under the most favorable conditions.Therefore activity durations are assumed to be no smaller than the optimisticestimate. Similarly, activity durations are assumed to be no larger than thepessimistic estimate. (Pg. 340)b) False. PERT also assumes that the form of the probability distribution is a betadistribution. (Pg. 340)c) False. It is assumed that the mean critical path will turn out to be the longest paththrough the project network. (Pg. 343)8.178.18 a) Let A= reduction in A due to crashingC= reduction in C due to crashing Minimize Crashing Cost = $5,000A+ $4,000Csubject to A≤ 3 monthsC≤ 2 monthsA+ C≥ 2 months and A≥ 0, C≥ 0.Optimal solution: (x1, x2) = (A, C) = (0, 2) and Crashing Cost = $8,000.b) Let B= reduction in B due to crashingD= reduction in D due to crashing Minimize Crashing Cost = $5,000B+ $6,000D subject to B≤ 2 months D≤ 3 monthsB+ D≥ 4 months and B≥ 0, D≥ 0.Optimal solution: (x1, x2) = (B, D) = (2, 2) and Crashing Cost = $22,000.c) Let A= reduction in A due to crashingB= reduction in B due to crashingC= reduction in C due to crashingD= reduction in D due to crashing Minimize Crashing Cost = $5,000A+ $5,000B+ $4,000C+ $6,000D subject to A≤ 3 months B≤ 2 monthsC≤ 2 monthsD≤ 3 monthsA+ C≥ 2 monthsB+ D≥ 4 months and A≥ 0, B≥ 0, C≥ 0, D≥ 0.Optimal solution (A, B, C, D) = (0, 2, 2, 2) and Crashing Cost = $30,000.d)e)8.19 a)b)c)8.20 a)Critical Path: Start → A → C → E →FinishTotal duration = 12 weeksb)New Plan:$7,834 is saved by this crashing schedule.c)Extra Direct Cost = ($309,167 –$297,000) = $12,167Indirect Costs Saved = 4($5,000) = $20,000Net Savings = $20,000 – $12,167 = 7,834.8.218.228.23 a)Total duration = 8 weeksb)c)d)e)Michael should concentrate his efforts on activity C since it is not yet completed.8.24 a)The earliest finish time for the project is 20 weeks.b)c)d)C u m u l a t i v e P r o j e c t C o s tWeeke)The project manager should focus attention on activity D since it is not yet finished and is running over budget.8.25 a)b)c)C u m u l a t i v e P r o j e c t C o s tWeekd)The project manager should investigate activities D, E and I since they are not yet finished and running over budget.Cases8.1a) Adiagramoftheprojectnetwork appears below.Select a syndicate of underw rite rsN egotiate the commitmen t o f each memb er of the s y ndicateN ego tiate the spre ad for each memb er of the s y ndicatePre pa re the reg is tra tio n s tatem entSubmit th e r egi stra tion stateme nt to the SECMak e prese ntati ons toins tituti ona l investor s an d de velop the inter est o f po te nti al bu yersD istribute the re d herr ingC alculate the issue priceR eceive d eficiencym emorandu m from th e SECA mend statement and r esubmit to the S ECR eceive r egistrati o n c onfi r mati on fro m the SECC on firm that the new issu e c omplies w i th ñb l u e s ky î la w sA ppo int a registrarA ppo int atran sfer age ntIssue fi n al p ro spectu sPh on e interested buyer sSTARTFINISHEv aluate the pr estig e of ea ch p otential un de rw rite r31.52351635312133.54.54ABCDEFGHIJKLMNOPQTo determine the project schedule and which activities are critical, we calculate the early start, late start, early finish, late finish, and slack below.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21A B C D E F G H ITime SlackActivity Description(w eeks)E S E F LS LF(w eeks)Critical?A E valuate prestige30=E S+Tim e=LF-Tim e=M IN(F4)=LF-E F=IF(Slack=0,"Yes","No")B Select syndicate 1.5=M AX(E3)=E S+Tim e=LF-Tim e=M IN(F5,F6)=LF-E F=IF(Slack=0,"Yes","No")C Negotiate com m itm ent2=M AX(E4)=E S+Tim e=LF-Tim e=M IN(F7)=LF-E F=IF(Slack=0,"Yes","No")D Negotiate spread3=M AX(E4)=E S+Tim e=LF-Tim e=M IN(F7)=LF-E F=IF(Slack=0,"Yes","No")E P repare registration5=M AX(E5,E6)=E S+Tim e=LF-Tim e=M IN(F8)=LF-E F=IF(Slack=0,"Yes","No")F Subm it registration1=M AX(E7)=E S+Tim e=LF-Tim e=M IN(F9,F10,F11,F12)=LF-E F=IF(Slack=0,"Yes","No")G P resent6=M AX(E8)=E S+Tim e=LF-Tim e=M IN(F15)=LF-E F=IF(Slack=0,"Yes","No")H Distribute red herring3=M AX(E8)=E S+Tim e=LF-Tim e=M IN(F15)=LF-E F=IF(Slack=0,"Yes","No")I Calculate price5=M AX(E8)=E S+Tim e=LF-Tim e=M IN(F15)=LF-E F=IF(Slack=0,"Yes","No") J Receive deficiency3=M AX(E8)=E S+Tim e=LF-Tim e=M IN(F13)=LF-E F=IF(Slack=0,"Yes","No") K Am end statem ent1=M AX(E12)=E S+Tim e=LF-Tim e=M IN(F14)=LF-E F=IF(Slack=0,"Yes","No") L Receive registration2=M AX(E13)=E S+Tim e=LF-Tim e=M IN(F15,F16,F17)=LF-E F=IF(Slack=0,"Yes","No") M Confirm blue sky1=M AX(E9,E10,E11,E14)=E S+Tim e=LF-Tim e=M IN(F18,F19)=LF-E F=IF(Slack=0,"Yes","No") N Appoint registrar3=M AX(E14)=E S+Tim e=LF-Tim e=M IN(F18,F19)=LF-E F=IF(Slack=0,"Yes","No") O Appoint transfer 3.5=M AX(E14)=E S+Tim e=LF-Tim e=M IN(F18,F19)=LF-E F=IF(Slack=0,"Yes","No") P Issue prospectus 4.5=M AX(E15,E16,E17)=E S+Tim e=LF-Tim e=P rojectDuration=LF-E F=IF(Slack=0,"Yes","No") Q P hone buyers4=M AX(E15,E16,E17)=E S+Tim e=LF-Tim e=P rojectDuration=LF-E F=IF(Slack=0,"Yes","No")Project Duration=M AX(E F)WeekThe initial public offering process is 27.5 weeks long. The critical path is: START → A → B → D → E → F → J → K → L → O → P → FINISHb) We explore each change independently.i) Negotiating the commitment (step C) is performed parallel to negotiating thespread (step D). In part (a) above, negotiating the spread is on the critical path since it takes three days to complete while negotiating the commitment takes only two days to complete. We now increase the time to negotiate the commitment from two days to three days, and negotiating the commitment now takes as much time as negotiating the spread. Thus, there are now two critical paths through the network:START → A → B → C → E → F →J →K →L →O →P →FINISH START → A → B → D → E → F →J →K →L →O →P →FINISHThe project duration is still 27.5 weeks.ii) In part (a) above, calculating the issue price is not on the critical path. Thus, decreasing the time to calculate the price does not change the solution found in part (a). The critical path remains the same, and the project duration is still27.5 weeks.iii) In part (a) above, the step to amend the statement and resubmit it to the SEC (step K) is on the critical path. Therefore, increasing the time for the step increases the project duration. The project duration increases to 29 weeks, and the critical path remains the same.iv) In part (a) above, the step to confirm that the new issue complies with “blue sky” laws (step M) occurs in parallel to appointin g a registrar (step N) and to appointing a transfer agent (step O). Step M is not on the critical path since it only takes one week while step O takes 3.5 weeks. When we increase the time to complete step M from one week to four weeks, we change the critical path since step M now takes longer than step O. We also change the project duration. The project duration is now 28 weeks. Two new critical paths appear:START → A → B → D → E → F →G →M →P →FINISH START → A → B → D → E → F → J → K → L → M → P → FINISHc)1234567891011121314151617181920G H I J KMaximum Crash Cost Start Tim e Finish Tim e Reductionper Week Saved Tim e Reduction Tim e (w eeks)($thousand)(w eek)(w eeks)(w eek)=Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 0 1.5=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 1.51=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e 030=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e 020=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 50=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e 0100=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 110=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 140=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 120=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e 0110=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 140.5=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e 014.50=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 170=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 16.5 1.5=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 16.52=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e =(CrashCost-Norm alCost)/MaxTimeReduction 180.5=StartTim e+N ormalTime-TimeReduction =Norm alTim e-CrashTim e=(CrashCost-Norm alCost)/MaxTimeReduction180=StartTim e+N ormalTime-TimeReduction25H ITotal Cost=SUM(NormalCost)+SUMPRODUCT(CrashCostPerWeekSaved,TimeReduction)The constraints in the linear programming spreadsheet model were as follows: TimeReduction ≤ MaxTimeReduction ProjectFinishTime ≤ MaxTime BStart ≥ AFinish CStart ≥ BFinish DStart ≥ BFinish EStart ≥ CFinish EStart ≥ DFinis h FStart ≥ EFinish GStart ≥ FFinish HStart ≥ FFinish IStart ≥ FFinish JStart ≥ FFinish KStart ≥ JFinish LStart ≥ KFinish MStart ≥ GFinish MStart ≥ HFinish MStart ≥ IFinish MStart ≥ LFinish NStart ≥ LFinish OStart ≥ LFinish PStart ≥ MFinish P Start ≥ NFinish PStart ≥ OFinish QStart ≥ MFinish QStart ≥ NFinish QStart ≥ OFinish ProjectFinishTime ≥ PFinish ProjectFinishTime ≥ QFinishJanet and Gilbert should reduce the time for step A (evaluating the prestige of each potential underwriter) by 1.5 weeks, the time for step B (selecting a syndicate of underwriters) by 1 week, the time for step K (amending statement and resubmitting it to the SEC) by 0.5 weeks, the time for step N (appointing a registrar) by 1.5 weeks, the time for step O (appointing a transfer agent) by two weeks, and the time for step P (issuing final prospectus) by 0.5 weeks. Janet and Gilbert can now meet the new deadline of 22 weeks at a total cost of $260,800.d) We use the same model formulation that was used in part (c). We change oneconstraint, however. The project duration now has to be less-than-or-equal to 24 weeks instead of 22 weeks. We obtain the following solution.Janet and Gilbert should reduce the time for step A (evaluating the prestige of each potential underwriter) by 1.5 weeks, the time for step B (selecting a syndicate of underwriters) by 1 week, the time for step K (amending statement and resubmitting it to the SEC) by 0.5 weeks, and the time for step O (appointing a transfer agent) by 0.5 weeks. Janet and Gilbert can now meet the new deadline of24 weeks at a total cost of $236,000.8.2 a) The project networkappears below.STARTRegister online orientation resume InternetAttend companysessionsAttend mock FINISH2571025A EGTo determine the project schedule and which activities are critical, we calculate the early start, late start, early finish, late finish, and slack below.1234567891011121314151617181920212223ABC DE F GH ITim e SlackActivity Description (days)E SE F LS LF(days)Critical?A Register online 20=E S+Tim e =LF-Tim e =M IN(F8,F9,F10)=LF-E F =IF(Slack=0,"Yes","No")B Attend orientation 50=E S+Tim e =LF-Tim e =M IN(F8,F9,F10)=LF-E F =IF(Slack=0,"Yes","No")C Write initial resum e 70=E S+Tim e =LF-Tim e =M IN(F9,F10)=LF-E F =IF(Slack=0,"Yes","No")D Search internet100=E S+Tim e =LF-Tim e =M IN(F15)=LF-E F =IF(Slack=0,"Yes","No")E Attend com pany sessions 250=E S+Tim e =LF-Tim e =M IN(F17)=LF-E F =IF(Slack=0,"Yes","No")F Review industry, etc.7=M AX(E 3,E 4)=E S+Tim e =LF-Tim e =M IN(F14)=LF-E F =IF(Slack=0,"Yes","No")G Attend m ock interview 4=M AX(E 3,E 4,E 5)=E S+Tim e =LF-Tim e =P rojectDuration =LF-E F =IF(Slack=0,"Yes","No")H Subm it initial resum e 2=M AX(E 3,E 4,E 5)=E S+Tim e =LF-Tim e =M IN(F11)=LF-E F =IF(Slack=0,"Yes","No")I M eet resum e expert 1=M AX(E 10)=E S+Tim e =LF-Tim e =M IN(F12)=LF-E F =IF(Slack=0,"Yes","No")J Revise resum e 4=M AX(E 11)=E S+Tim e =LF-Tim e =M IN(F13)=LF-E F =IF(Slack=0,"Yes","No")K Attend career fair 1=M AX(E 12)=E S+Tim e =LF-Tim e =M IN(F15)=LF-E F =IF(Slack=0,"Yes","No")L Search jobs 5=M AX(E 8)=E S+Tim e =LF-Tim e =M IN(F15)=LF-E F =IF(Slack=0,"Yes","No")M Decide jobs 3=M AX(E 6,E 13,E 14)=E S+Tim e =LF-Tim e =M IN(F16,F17)=LF-E F =IF(Slack=0,"Yes","No")N Bid3=M AX(E 15)=E S+Tim e =LF-Tim e =P rojectDuration =LF-E F =IF(Slack=0,"Yes","No")O Write cover letters 10=M AX(E 7,E 15)=E S+Tim e =LF-Tim e =M IN(F18)=LF-E F =IF(Slack=0,"Yes","No")P Subm it cover letters 4=M AX(E 17)=E S+Tim e =LF-Tim e =M IN(F19)=LF-E F =IF(Slack=0,"Yes","No")Q Revise cover letters 4=M AX(E 18)=E S+Tim e =LF-Tim e =M IN(F20,F21)=LF-E F =IF(Slack=0,"Yes","No")R M ail 6=M AX(E 19)=E S+Tim e =LF-Tim e =P rojectDuration =LF-E F =IF(Slack=0,"Yes","No")SDrop2=M AX(E 19)=E S+Tim e=LF-Tim e=P rojectDuration=LF-E F=IF(Slack=0,"Yes","No")P roject Duration (days)=M AX(E F)WeekBrent can start the interviews in 49 days. The critical steps in the process are:START → E → O → P → Q → R → FINISHb) We substitute first the pessimistic and then the optimistic estimates for the timevalues used in the part (a) spreadsheet.The spreadsheet showing the project schedule with the pessimistic time estimates appears below.begin interviewing. The critical path changes to:START → B → F →L →M →O →P →Q →R →FINISHThe spreadsheet showing the project schedule with the optimistic time estimates appears below.Under the best-case scenario, Brent will require 32 days before he is ready to begin interviewing. The critical path remains the same as that in part (START → E → O → P → Q → R → FINISH).c) The mean critical path is the path through the project network that would be thecritical path if the duration of each activity equals its mean. We therefore first need to determine the mean duration of each activity given the optimistic, most likely, and pessimistic length estimates. To calculate the mean duration of each activity, we use the PERT template.。
(典型例题)《运筹学》运输问题

xj0,yij0,zij0,(i=1,┈,4;j=1,┈,5)
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型:
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量;yij—第i天送第j天使用快洗 餐巾的数量;zij—第i天送第j天使用慢洗餐巾的数量;
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天:x1=1000
需 第二天:x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销>产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
01《运筹学》(第四版)线性规划模型

x x , x
其中 x 0 , 。 x 0
实际含义:
如果变量 x 代表某产品当年计划数与上一年计划数之差,
则 x 的取值可能是正也可能是负。
水电与数字化工程学院
莫 莉
1.2 型式转换
3.实例
将下面线性规划模型化为标准形式:
m in z x1 2 x 2 3 x 3
线性规划模型 三要素
决策变量
需决策的量,即待求 的未知数
约束条件 目标函数
需优化的量,即欲达 的目标,用决策变量 的表达式表示
为实现优化目标需受到 的限制,用决策变量的 等式或不等式表示
水电与数字化工程学院
莫 莉
资源单耗 甲 乙 资源限量
A 2 2
B 1 2
C 4 0 16kg
D 0 4 12kg
水电与数字化工程学院
莫 莉
线性规划的几种表示形式
1)一般形式
1.1 线性规划模型
m a x (或 m in ) Z c 1 x 1 c 2 x 2 c n x n
a 11 x 1 a 12 x 2 a 1n x n a x a x a x 21 1 22 2 2n n a x a x a x m2 2 mn n m1 1 x1, x2 , , xn 0
莫 莉
上节课内容回顾
莫 莉
第一章 线性规划
1 2 3 4 5 6
水电与数字化工程学院
线性规划模型 线性规划解★ 单纯形法 对偶问题 对偶理论
算法复杂性
莫 莉
前节回顾
温
型式转换
故
求解
知
清华大学运筹学-1.1线性规划数学模型
, ci 为
8
例3、合理下料问题 、 2.9m 钢筋架子100 钢筋架子 2.1m 1.5m Ⅰ 2.9m 2.1m 1.5m 合计 料头 1 0 3 7.4 0 Ⅱ 2 0 1 7.3 0.1 Ⅲ 0 2 2 7.2 0.2 Ⅳ 1 2 0 7.1 0.3 Ⅴ 0 1 3 6.6 0.8
9
各1,原料长 ,原料长7.4m
方案 2.9m 2.1m 1.5m 合计 1 2 0 1 2 1 2 0 3 1 1 1 4 1 0 3 5 0 3 0 6 0 2 2 7 0 1 3 8 0 0 4 6.0 1.4
12
7.3 7.1 6.5 7.4 6.3 7.2 6.6 1.1 0.2 0.8
剩余料头 0.1 0.3 0.9 0
2
例2
原料 1 2 3 4
每单位添 加剂中维生 素最低含量
A 4 6 1 2
B 1 1 7 5
C 每单位成本 0 2 1 3 2 5 6 8
12
14
8
求:最低成本的原料混合方案
3
的用量为x 解:设每单位添加剂中原料i的用量为 i(i =1,2,3,4) 设每单位添加剂中原料 的用量为 minZ= 2x1 + 5x2 +6x3+8x4 4x1 + 6x2 + x3+2x4 ≥12 x1 + x2 +7x3+5x4 ≥14 2x2 + x3+3x4 ≥ 8 xi ≥ 0 (i =1,…,4)
4
线性规划模型特点
• 决策变量:向量(x1… xn)T 决策人要考 决策变量:向量 虑和控制的因素, 虑和控制的因素,非负 • 约束条件:线性等式或不等式 约束条件: • 目标函数:Z=ƒ(x1 … xn) 线性式,求Z极 目标函数: 线性式, 极 大或极小
运筹学2008
中国石油大学(北京)2007--2008学年第二学期《运筹学》期末考试试卷A (闭卷考试)班级: 姓名: 学号:一、单向选择题(30分)1. 下列最终单纯表中有无穷多最优解的为 ( ) :2. 已知线性规划问题:213x x MaxZ += 531=+x x 102421=++x x x 452=+x x 0,,51≥x x 下列解中哪个是基可行解?( )A. 025*******=====x x x x xB. 40501054321==-===x x x x xC. 4720354321=====x x x x xD. 265254321=====x x x x x3. 某公司计划制造Ⅰ、Ⅱ、Ⅲ三种家电产品。
已知各制造一件时分别占用的设备A,B 和工艺C,D 的台时如表1所示,用线性规划模型解决这一问题,得到的最终单纯型表如表2所示,则该公司设备B 单位台时的影子价格为:( ) 表1表2A. 8.48B. 10.61C. 0.91D. 04. 某企业全年需要某种材料1000吨,单价为500元/吨,每吨年保管费用为50元,每次订货手续费为170元,则每次订货的经济批量为( )吨,最优订货周期为( )天。
A. 87B. 82C. 83D.85E. 30F.34 G .28 G .325. 判断下列调运方案中哪个不能作为表上作业法求解时的初始解。
( )6. 已知线性规划原问题及其对偶问题如下:CX MaxZ = Yb MinW = b AX ≤ C YA ≥ 0≥X 0≥Y若X Y 分别为原问题和对偶问题的可行解,*X *Y 分别为最优解,则下列说法错误的是( )A. 当对偶问题无可行解时,原问题一定具有无界解B. b Y CX **=C. 当原问题有无界解时,对偶问题一定无可行解D. b Y X C ≤ 7.关于网络图的下列说法正确的是( )A. 网络图中任何一个节点都表示前一工序的结束和后一工序的开始。
山东科技大学运筹学2004--2008,2010--2016,2018--2020年考研初试真题
六.已知4个城市间往返路距离如下表所示,求从V1城出发,经其余城市一次且仅一
次最后返回V1城的最短路径与距离。(20分)
距 Vj
V1
V2
V3
V4
Vi离
V1
0
8
5
6
V2
6
0
8
5
V3
7
9
0
5
V4
9
7
8
0
七.已知某工程资料如下表,按要求求解下列问题(25分)
工序
紧前工序
a
g,m
b
h
c
-
d
l
e
c
f
a,e
g
b,c
M inf(x) x1 x2 2x12 2x1x2 x22 给定初始点 x(1) (0,0)T 满足精度 f (x(k) ) 0.3 时的解。(20分)
三.已知下列线性规划问题(矩阵形式)(25分) MinZ CX AX b X 0
《运筹学》全套课件清华大学
运输问题
通过线性规划求解运输问题中 的最优运输方案,使得总运费 最小化。
投资组合
通过线性规划确定最优的投资 组合,使得风险最小化或收益
最大化。
03
整数规划
整数规划问题的数学模型
整数规划问题的定义和分类
介绍整数规划问题的基本概念、分类以及与其 他优化问题的关系。
03
Bellman-Ford算法
适用于存在负权边的图,通过不断松弛边的方式求解最短路。
网络最大流问题
网络最大流问题的定义
给定一个有向带权图,找到从源点到汇点的最大流 量。
增广路算法
通过不断寻找增广路来增加流量,直到没有增广路 为止。
Edmonds-Karp算法
对增广路算法进行优化,使用广度优先搜索寻找增 广路。
整数规划问题的应用
生产计划问题
阐述整数规划在生产计划问题中的应用,如 生产批量计划、生产排程等。
金融投资问题
分析整数规划在金融投资问题中的应用,如 投资组合优化、风险管理等。
物流配送问题
探讨整数规划在物流配送问题中的应用,如 车辆路径问题、设施选址问题等。
其他应用领域
介绍整数规划在其他领域的应用,如计算机 科学、生物医学工程等。
运筹学的应用领域
工业工程
在生产计划、物流管理、设施规划等领域 ,运筹学可以帮助企业提高生产效率、降 低成本、优化资源配置。
其他领域
如金融工程、医疗健康、环境保护等领域 ,运筹学也发挥着重要作用,为各种实际 问题提供有效的解决方法。
交通运输
在交通规划、交通控制、航空运输等领域 ,运筹学可以优化交通网络设计、提高运 输效率、减少交通拥堵等问题。
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第5章 线性目标规划
清华大学出版社
第1节 目标规划的数学模型
目标规划的一般数学模型为
目标函数: min z Pl (lk d k lk dk ) l 1 k 1 L K
(4 1) (4 2) (4 3) (4 4) (4 5)
n c x d d g k , k 1, , K kj j k k j 1 n a x (, )b , i 1, , m 满足约束条件: ij j i j 1 x j 0, j 1, , n d k , d k 0, k 1, , K
16
清华大学出版社
第2节 解目标规划的图解法
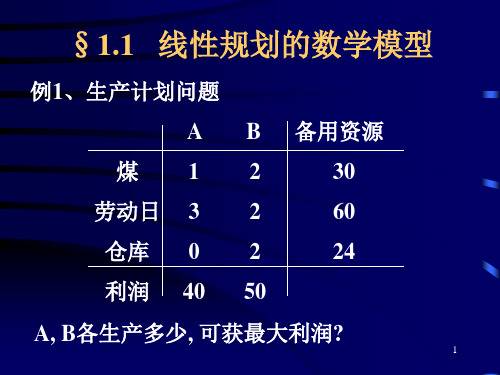
解:设x1,x2分别表示黑白和彩色电视机的产量,本问题的 目标规划模型为:
目标函数: min z P d P d P ( 2 d d 1 1 3 3 4) 2 2
x1 x2 d1 d1 40 d2 50 x1 x2 d 2 满足约束条件: x1 d3 d3 24 x d d 2 4 4 30 x , x , d , d 0, i 1,2,3,4 1 2 i i
14
清华大学出版社
第2节 解目标规划的图解法
注意:求解目标规划问题时,把绝对约束作为最高优先 级考虑。在本例中,能依先后次序都满足d1+=0, d2++d2−=0,d3−=0,因而z*=0。但在大多数问题中并非如 此,会出现某些约束得不到满足,故将目标规划问题的 最优解称为满意解。
15
清华大学出版社
c j z j akj Pk j 1,2,, n; k 1,2,, K
