小学数学图形计算例题大汇总.
平行四边形,三角形,梯形面积计算练习
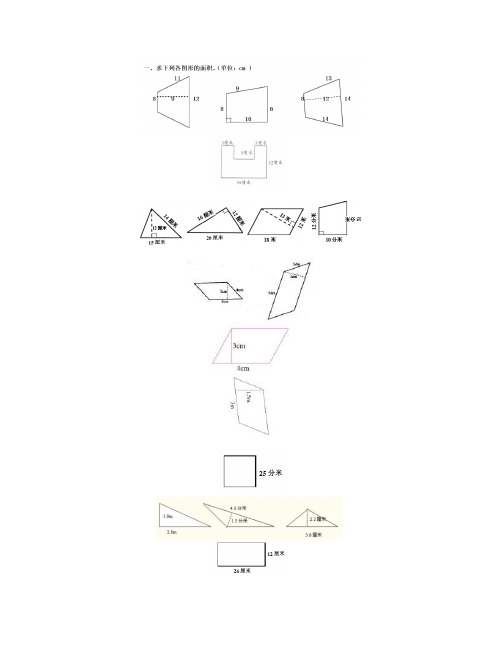
二、1、用65米长的篱笆沿墙边围一个直角梯形的鸡舍,梯形的直角边是15米,你能计算出围成的鸡舍的面积吗?8、用篱笆围成一个梯形养鸡场(如下图所示),其中一边利用房屋墙壁,已知篱笆的长是80米,求养鸡场的面积。
2、一条新挖的渠道,横截面是梯形(如图),渠道口宽3.2 m,渠底宽2.2 m,渠深1.8 m,它的横截面的面积是多少平方米?3、一块梯形的铁皮,上、下底的和是25厘米,高是22厘米,这块铁皮的面积是多少平方厘米?4、一块梯形土地的上底是60米,比下底短80米,高150米,这块土地的面积是多少平方米?5、一块梯形土地上底是160米,下底是90米,高是120米,如果平均每棵果树占地10平方米,这块土地共可种多少棵果树?6、一堆水泥电杆,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水泥电杆共有多少根?7、一条新挖的渠道,横截面是梯形。
(如图)渠口宽2.8米,渠底宽1.4米,渠深1.2米。
它的横截面的面积是多少平方米?9、直角梯形上下底之和是12米,求阴影部分的面积。
10、已知右图的上底是20厘米,下底是34厘米,其中阴影部分的面积是340平方厘米。
这个梯形的面积是多少?11、已知下图梯形的面积是252平方米,空白部分为平行四边形,求阴影部分的面积。
(单位:米)12、在一个底为6分米,高为15分米的直角三角形右侧对接上一个梯形(阴影部分)拼成了一个平行四边形,求这个梯形的面积。
13、一块直角梯形的地,它的下底是40米,如果上底增加38米,这块地就变成了正方形,原来梯形的面积是多少?14、如下图,一个平行四边形被分成甲、乙两部分,甲的面积比乙大32平方米,甲的上底是多少米?三、判断题1、平行四边形的面积大于梯形面积。
()2、两个形状相同的三角形可以拼成一个平行四边形。
()3、三角形面积等于平行四边形面积的一半。
()4、三角形的底越长,面积就越大。
()(5)三角形的底扩大2倍,高扩大3倍,面积就扩大6倍。
长方形正方形的周长面积计算(图题50题)

长方形正方形的周长面积计算(图题50题) 1.填写下表:图形。
| 长。
| 宽。
| 面积。
|长方形。
| 16厘米。
| 11厘米。
| 612平方厘米 |长方形。
| 36厘米。
| 18厘米。
| 900平方厘米 |长方形。
| 27分米。
| 20分米。
| 648平方分米 |长方形。
| 未给出 | 未给出 | 未给出。
|2.填写下表:图形。
| 边长。
| 面积。
|正方形 | 13厘米。
| 169平方厘米 |正方形 | 16厘米。
| 256平方厘米 |正方形 | 20分米。
| 4平方分米。
|正方形 | 28米。
| 784平方米。
|3.填写下表:图形。
| 长宽。
| 周长。
| 面积。
|长方形 | 19米 * 16米 | 90分米。
| 304平方米。
| 正方形 | 12厘米。
| 24分米。
| 144平方厘米 |未给出 | 14厘米。
| 56厘米。
| 196平方厘米 | 4.下列图形的周长:图形。
| 周长 |未给出。
| 25.|长方形。
| 10.|未给出。
| 2515 |正方形。
| 4.|未给出。
| 100.|长方形。
| 18.|5.用54米长的篱笆围成一个长方形的养鸡场,其中两条边利用屋墙壁,如图,这个养鸡场的占地面积是多少?该养鸡场的长为 27 米,宽为 12 米,因此占地面积为 27 * 12 = 324 平方米。
6.有一个正方形花圃,一面靠墙(如图),在这个花圃四周围上竹篱笆,竹篱笆长27米,这个花圃占地多少平方米?如果这块地的三分之二用来种杜鹃花,杜鹃花占地多少平方米?正方形花圃的周长为 4 * 27 / 4 = 27 米,因此边长为 27 / 4 = 6.75 米,面积为 6.75 * 6.75 = 45.56 平方米。
三分之二的面积为 45.56 * 2 / 3 = 30.37 平方米。
7.下面图形的面积和周长各是多少?(单位:米)图形。
| 面积 | 周长 |未给出。
| 15.| 8.|正方形。
| 4.| 16.|正方形。
图形加减法运算练习题(打印版)

图形加减法运算练习题(打印版)### 图形加减法运算练习题#### 一、基础加减法1. 题目:小明有3个苹果,又得到了2个苹果,请问小明现在有几个苹果?- 答案:\[ 3 + 2 = 5 \]2. 题目:小华有5个橙子,吃掉了1个,还剩下几个?- 答案:\[ 5 - 1 = 4 \]3. 题目:小刚有4个梨,又买了3个,现在他有多少个梨?- 答案:\[ 4 + 3 = 7 \]4. 题目:小红有6个草莓,送给朋友2个,还剩几个?- 答案:\[ 6 - 2 = 4 \]5. 题目:小亮有7个香蕉,吃掉了3个,还剩下几个?- 答案:\[ 7 - 3 = 4 \]#### 二、进阶加减法1. 题目:小丽有10个气球,又买了5个,然后放飞了3个,现在她有多少个气球?- 答案:\[ 10 + 5 - 3 = 12 \]2. 题目:小强有8个足球,借给朋友3个,又收回了2个,现在他有多少个足球?- 答案:\[ 8 - 3 + 2 = 7 \]3. 题目:小芳有12个乒乓球,送给同学4个,又买了6个,现在她有多少个乒乓球?- 答案:\[ 12 - 4 + 6 = 14 \]4. 题目:小刚有15个篮球,借给同学5个,又收回了3个,现在他有多少个篮球?- 答案:\[ 15 - 5 + 3 = 13 \]5. 题目:小红有20个羽毛球,送给朋友6个,又买了4个,现在她有多少个羽毛球?- 答案:\[ 20 - 6 + 4 = 18 \]#### 三、混合加减法1. 题目:小华有20个玩具,送给弟弟5个,又从朋友那里得到了8个,现在他有多少个玩具?- 答案:\[ 20 - 5 + 8 = 23 \]2. 题目:小亮有18个积木,送给妹妹3个,又从同学那里得到了5个,现在他有多少个积木?- 答案:\[ 18 - 3 + 5 = 20 \]3. 题目:小芳有25个橡皮,送给同学7个,又从老师那里得到了10个,现在她有多少个橡皮?- 答案:\[ 25 - 7 + 10 = 28 \]4. 题目:小刚有30个彩笔,送给朋友9个,又从亲戚那里得到了6个,现在他有多少个彩笔?- 答案:\[ 30 - 9 + 6 = 27 \]5. 题目:小红有35个贴纸,送给朋友11个,又从同学那里得到了4个,现在她有多少个贴纸?- 答案:\[ 35 - 11 + 4 = 28 \]#### 四、应用题1. 题目:小明和小华一共有20个苹果,小明有8个,小华有几个? - 答案:\[ 20 - 8 = 12 \]2. 题目:小刚和小芳一共有30个梨,小刚有15个,小芳有几个? - 答案:\[ 30 - 15 = 15 \]3. 题目:小亮和小刚一共有40个香蕉,小亮有20个,小刚有几个? - 答案:\[ 40 - 20 = 20 \]4. 题目:小红和小芳一共有50个草莓,小红有25个,小芳有几个? - 答案:\[ 50 - 25 = 25 \]5. 题目:小华和小亮一共有60个橙子,小华有30个,小亮有几个? - 答案:\[ 60 - 30 = 30 \]请同学们认真完成以上练习题,加强加减法的运算能力。
二年级数学几何图形计算题目

B. 长方形
C. 圆形
D. 三角形
7. 一个梯形的上底是5厘米,下底是7厘米,高是4厘米,它的面积是____。
A. 24平方厘米
B. 30平方厘米
C. 36平方厘米
D. 40平方厘米
8. 在几何图形中,有四个角都是直角的四边形叫做____。
A. 正方形
B. 长方形
C. 平行四边形
D. 梯形
2. 根据给定的信息,画出一个底为3厘米,高为4厘米的三角形。
## 七、案例分析题(共5分)
某学校操场是一个长方形,长为100米,宽为50米。请计算操场的面积,并说明如果将操场扩大为原来的两倍,即长为200米,宽为100米,新的操场面积将是多少?
# 其余试题
## 八、案例设计题(共5分)
某房间的一面墙是一个矩形,长为8米,宽为6米。如果要在这面墙上挂一幅宽度为3米的画,请设计画在墙上的位置,使得画的中间位置与墙的中间位置对齐。
## 四、简答题(每题2分,共10分)
1. 请解释什么是圆周率π?
2. 请说明如何计算一个三角形的面积。
3. 请描述什么是立方体,并给出它的体积计算公式。
4. 请解释什么是平行四边形,并说明如何计算它的面积。
5. 请说明如何计算一个圆锥的体积。
## 五、计算题(每题2分,共10分)
1. 一个圆的直径是14厘米,求它的周长和面积。
## 九、应用题(每题2分,共10分)
1. 一个菜园是一个长方形,长为20米,宽为10米。如果每平方米可以种植2株蔬菜,那么这个菜园最多可以种植多少株蔬菜?
2. 一个书架是一个长方形,长为1.2米,宽为0.8米。如果每本书的尺寸为0.3米×0.2米,那么这个书架最多可以放置多少本书?
07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版)(含答案).doc

(期末真题精选)07-图形计算100题(提高)2023年四年级下册数学期末高频易错题(人教版)试卷说明:本试卷试题精选自广东省广州市各区县2020-2022近三年的四年级期末真题试卷,难易度均衡,适合广东省广州市各区县和使用人教版教材的四年级学生期末复习备考使用!一、图形计算1.求出下图的周长。
2.下面是一张纸折起来以后形成的图形,已知∠1=50°,你能求出∠2的度数吗?3.一张直角三角形纸片,剪去直角后得到一个四边形(如下图),求12∠+∠的度数。
4.算出下面未知角的度数。
5.算一算。
在一个三角形中∠2=65°,∠3=73°,求∠1。
6.求出下面未知角的度数。
7.如图,已知∠1=72°,∠2=32°,∠3=45°,求∠5。
8.已知∠1=105°,求∠2的度数。
9.算出下面各个未知角的度数。
10.求下面各未知角的度数。
(1)(2)(3)11.求出图中未知角的度数。
(1)(2)12.求出下面∠1的度数。
13.已知∠1=75°,求∠2的度数。
14.计算下面图形的周长。
(单位:厘米)(1)(2)15.列式计算角的度数。
16.下图中每个正方形的边长是4cm,求阴影部分的面积。
17.小兔家的屋顶是一个等腰三角形(如图),请你算出顶角的度数。
18.算一算。
在三角形中∠1=72°,∠2=90°,求∠3。
19.算一算角的度数。
①②20.求出下面三角形各个角的度数。
21.求出下面三角形各个角的度数。
(1)(2)(3)22.求出下图中∠1的度数。
23.计算如图图形的周长。
(单位:厘米)24.计算下面图形中阴影部分的面积。
(图中每个小方格的面积是1cm2)25.求图中∠1的度数.26.求阴影部分的面积。
(单位:cm)27.算出下面各个未知角的度数(写出计算过程)。
28.计算下面图形的周长和面积。
29.计算下面未知角的度数。
数学六上易错易混图形计算题50题精粹

1、求涂色部分的面积(单位:厘米)。
【答案】27.44平方厘米【分析】观察图示可知,涂色部分面积等于长10厘米宽4厘米的长方形面积减去半径为4里面圆面积的14,根据长方形面积公式和圆面积公式,代入数据求解即可。
【详解】10×4-14×3.14×42=40-12.56=27.44(平方厘米)答:涂色部分的面积是27.44平方厘米。
【点睛】运用转化的思想,将我们学过的一般图形,通过割补求得不规则图形的面积,是一种重要数学思想和常用方法。
2、下图是一个长方体展开图,求它的体积和表面积.【答案】720cm³;538cm²【详解】略3、求下面图形的表面积.(单位:厘米)【答案】(2×6+2×2+6×2)×2=56(平方厘米)【详解】略4、求右图的表面积和体积.【答案】表面积62平方厘米;体积30立方厘米【详解】略5、计算下面图形的周长。
【答案】50.24cm【分析】根据C=πd=2πr,分别求出直径是8cm的圆的周长和半径为8cm的圆周长的一半,相加即可。
【详解】3.14×8+3.14×8×2÷2=3.14×8+3.14×8=3.14×8×2=50.24(cm)6、一个粮仓如右图,计算它的体积.【答案】6.594m3【分析】观察图可知,粮仓的体积=圆柱的体积+圆锥的体积,根据圆柱的体积V=πr2h,圆锥的体积V=13πr2h,据此列式解答.【详解】3.14×(22)2×(2+0.3×13)=6.594m37、计算下列图形的表面积和体积。
(单位:cm)(1)(2)【答案】(1)正方体表面积:294cm2;正方体体积:343cm3;(2)长方体的表面积:236cm2;长方体体积:240cm3【分析】(1)根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,将棱长=7cm带入计算即可;(2)根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,将长=8cm、宽=6cm、高=5cm带入计算即可。
图形题加减法练习题(打印版)

图形题加减法练习题(打印版)### 图形题加减法练习题(打印版)一、基础加法练习1. 苹果树上有3个苹果,又来了2个苹果,现在有多少个苹果? - 答案:______2. 小明有5支铅笔,又买了3支,现在他有多少支铅笔?- 答案:______3. 动物园里有4只猴子,又来了3只,现在有多少只猴子?- 答案:______4. 书架上原本有7本书,又增加了4本,现在书架上有多少本书? - 答案:______5. 花园里有6朵花,又种了5朵,现在花园里有多少朵花?- 答案:______二、基础减法练习1. 小红有10个气球,放飞了3个,现在还剩下多少个气球?- 答案:______2. 学校里有20个学生,放学后走了6个,现在还剩下多少个学生?- 答案:______3. 鱼缸里有8条鱼,死了2条,现在还剩下多少条鱼?- 答案:______4. 班级里有15个同学,今天有4个同学请假,现在还剩下多少个同学?- 答案:______5. 桌子上有12个橙子,吃掉了5个,现在还剩下多少个橙子?- 答案:______三、综合加减法练习1. 小华有8个苹果,又买了5个,然后送给朋友3个,现在还剩下多少个苹果?- 答案:______2. 班级里有18个同学,今天有3个同学请假,又有2个新同学加入,现在班级里有多少个同学?- 答案:______3. 小明有12支铅笔,借给同学4支,又买了6支,现在还剩下多少支铅笔?- 答案:______4. 动物园里有15只猴子,又来了5只,然后有3只逃跑了,现在有多少只猴子?- 答案:______5. 花园里有10朵花,又种了8朵,然后有5朵凋谢了,现在花园里有多少朵花?- 答案:______四、图形题应用1. 请画出一个有5个方块的图形,再画出增加3个方块后的图形。
- 答案:[图形]2. 画一个有7个圆圈的图形,然后减去2个圆圈,画出结果图形。
- 答案:[图形]3. 用图形表示一个班级有10个同学,再表示又有5个新同学加入班级。
(完整)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题求下列图形的面积:(单位:cm )435254367886101:一个等腰直角三角形,最长的边是10厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
2: 求右面平行四边形的周长。
8612【巩固练习2】:求右面三角形的AB 上的高。
典型例题3:求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)【巩固练习3】:求四边形ABCD 的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?【巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
410CBA543【巩固练习5】:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?DC BA 610DC BA20m墙【典型例题】【例1】已知平行四边表的面积是28平方厘米,求阴影部分的面积。
【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)【例2】下图中甲和乙都是正方形,求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲不规则图形面积的计算(一)我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
解:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
又因为S甲+S乙=12×12+10×10=244,所以阴影部分面积=244-(50+132+12)=50(平方厘米)。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.解:因为△ABE、△ADF与四边形AECF的面积彼此相等,所以四边形AECF的面积与△ABE、△ADF的面积都等于正方形ABCD在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
解:在等腰直角三角形ABC中∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影部分面积=S△ABG-S△BEF=25-8=17(平方厘米)。
例4 如右图,A为△CDE的DE边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米.求△ABD及△ACE的面积.解:取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,所以它们的面积相等,都等于5平方厘米.所以△ACD的面积等于15平方厘米,△ABD的面积等于10平方厘米。
又由于△ACE与△ACD等底、等高,所以△ACE的面积是15平方厘米。
例5 如下页右上图,在正方形ABCD中,三角形ABE的面积是8平方厘解:过E作BC的垂线交AD于F。
在矩形ABEF中AE是对角线,所以S△ABE=S△AEF=8.在矩形CDFE中DE是对角线,所以S△ECD=S△EDF。
例6 如右图,已知:S△ABC=1,解:连结DF。
∵AE=ED,∴S△AEF=S△DEF;S△ABE=S△BED,例7 如下页右上图,正方形ABCD的边长是4厘米,CG=3厘米,矩形DEFG的长DG为5厘米,求它的宽DE等于多少厘米?解:连结AG,自A作AH垂直于DG于H,在△ADG中,AD=4,DC=4(AD上的高).∴S△AGD=4×4÷2=8,又DG=5,∴S△AGD=AH×DG÷2,∴AH=8×2÷5=3.2(厘米),∴DE=3.2(厘米)。
例8 如右图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.解:∵梯形面积=(上底+下底)×高÷2即45=(AD+BC)×6÷2,45=(AD+10)×6÷2,∴AD=45×2÷6-10=5米。
∴△ADE的高是2米。
△EBC的高等于梯形的高减去△ADE的高,即6-2=4米,例9 如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等.证明:连结CE,ABCD的面积等于△CDE面积的2倍,而DEFG的面积也是△CDE 面积的2倍。
∴ABCD的面积与DEFG的面积相等。
习题一一、填空题(求下列各图中阴影部分的面积):二、解答题:1.如右图,ABCD为长方形,AB=10厘米,BC=6厘米,E、F分别为AB、AD中点,且FG=2GE.求阴影部分面积。
2.如右图,正方形ABCD与正方形DEFG的边长分别为12厘米和6厘米.求四边形CMGN(阴影部分)的面积.3.如右图,正方形ABCD的边长为5厘米,△CEF的面积比△ADF的面积大5平方厘米.求CE的长。
4.如右图,已知CF=2DF,DE=EA,三角形BCF的面积为2,四边形BEDF的面积为4.求三角形ABE的面积.5.如右图,直角梯形ABCD的上底BC=10厘米,下底AD=14厘米,高CD=5厘米.又三角形ABF、三角形BCE和四边形BEDF的面积相等。
求三角形DEF的面积.6.如右图,四个一样大的长方形和一个小的正方形拼成一个大正方形,其中大、小正方形的面积分别是64平方米和9平方米.求长方形的长、宽各是多少?7.如右图,有一三角形纸片沿虚线折叠得到右下图,它的面积与原三角形面积之比为2:3,已知阴影部分的面积为5平方厘米.求原三角形面积.8.如右图,ABCD的边长BC=10,直角三角形BCE的直角边EC长8,已知阴影部分的面积比△EFG的面积大10.求CF的长.习题一解答一、填空题:二、解答题:3.CE=7厘米.可求出BE=12.所以CE=BE-5=7厘米.4.3.提示:加辅助线BD∴CE=4,DE=CD-CE=5-4=1。
同理AF=8,DF=AD-AF=14-8=6,6.如右图,大正方形边长等于长方形的长与宽的和.中间小正方形的边长等于长方形的长与宽的差.而大、小正方形的边长分别是8米和3米,所以长方形的宽为(8-3)÷2=2.5(米),长方形的长为8-2.5=5.5(米).7.15平方厘米.解:如右图,设折叠后重合部分的面积为x平方厘米,x=5.所以原三角形的面积为2×5+5=15平方厘米.∴阴影部分面积是:10x-40+S△GEF由题意:S△GEF+10=阴影部分面积,∴10x-40=10,x=5(厘米).第五讲同余的概念和性质你会解答下面的问题吗?问题1:今天是星期日,再过15天就是“六·一”儿童节了,问“六·一”儿童节是星期几?这个问题并不难答.因为,一个星期有7天,而15÷7=2…1,即15=7×2+1,所以“六·一”儿童节是星期一。
问题2:1993年的元旦是星期五,1994年的元旦是星期几?这个问题也难不倒我们.因为,1993年有365天,而365=7×52+1,所以1994年的元旦应该是星期六。
问题1、2的实质是求用7去除某一总的天数后所得的余数.在日常生活中,时常要注意两个整数用某一固定的自然数去除,所得的余数问题.这样就产生了“同余”的概念.如问题1、2中的15与365除以7后,余数都是1,那么我们就说15与365对于模7同余。
同余定义:若两个整数a、b被自然数m除有相同的余数,那么称a、b对于模m同余,用式子表示为:a≡b(modm). (*)上式可读作:a同余于b,模m。
同余式(*)意味着(我们假设a≥b):a-b=mk,k是整数,即m|(a-b).例如:①15≡365(mod7),因为365-15=350=7×50。
②56≡20(mod9),因为56-20=36=9×4。
③90≡0(mod10),因为90-0=90=10×9。
由例③我们得到启发,a可被m整除,可用同余式表示为:a≡0(modm)。
例如,表示a是一个偶数,可以写a≡0(mod 2)表示b是一个奇数,可以写b≡1(mod 2)补充定义:若m(a-b),就说a、b对模m不同余,用式子表示是:a b(modm)我们书写同余式的方式,使我们想起等式,而事实上,同余式与等式在其性质上相似.同余式有如下一些性质(其中a、b、c、d是整数,而m是自然数)。
性质1:a≡a(mod m),(反身性)这个性质很显然.因为a-a=0=m·0。
性质2:若a≡b(mod m),那么b≡a(mod m),(对称性)。
性质3:若a≡b(mod m),b≡c(mod m),那么a≡c(mod m),(传递性)。
性质4:若a≡b(mod m),c≡d(mod m),那么a±c≡b±d(mod m),(可加减性)。
性质5:若a≡b(mod m),c≡d(mod m),那么ac≡bd(mod m)(可乘性)。
性质6:若a≡b(mod m),那么a n≡b n(mod m),(其中n为自然数)。
性质7:若ac≡bc(mod m),(c,m)=1,那么a≡b(mod m),(记号(c,m)表示c与m的最大公约数)。
注意同余式性质7的条件(c,m)=1,否则像普通等式一样,两边约去,就是错的。
例如6≡10(mod 4),而35(mod 4),因为(2,4)≠1。
请你自己举些例子验证上面的性质。
同余是研究自然数的性质的基本概念,是可除性的符号语言。
例1 判定288和214对于模37是否同余,74与20呢?解:∵288-214=74=37×2。
∴288≡214(mod37)。
∵74-20=54,而3754,∴7420(mod37)。
例2 求乘积418×814×1616除以13所得的余数。
分析若先求乘积,再求余数,计算量太大.利用同余的性质可以使“大数化小”,减少计算量。
解:∵418≡2(mod13),814≡8(mod13),1616≡4(mod13),∴根据同余的性质5可得:418×814×1616≡2×8×4≡64≡12(mod13)。
答:乘积418×814×1616除以13余数是12。
例3 求14389除以7的余数。
分析同余的性质能使“大数化小”,凡求大数的余数问题首先考虑用同余的性质化大为小.这道题先把底数在同余意义下变小,然后从低次幂入手,重复平方,找找有什么规律。
解法1:∵143≡3(mod7)∴14389≡389(mod 7)∵89=64+16+8+1而32≡2(mod 7),34≡4(mod7),38≡16≡2(mod 7),316≡4(mod 7),332≡16≡2(mod 7),364≡4(mod 7)。
∵389≡364·316·38·3≡4×4×2×3≡5(mod 7),∴14389≡5(mod 7)。
答:14389除以7的余数是5。
解法2:证得14389≡389(mod 7)后,36≡32×34≡2×4≡1(mod 7),∴384≡(36)14≡1(mod 7)。
