《立体几何中的角度与距离问题》
立体几何中夹角与距离的计算(绝对精品)

第三节 立体几何中夹角与距离的计算一、求距离:1、点到平面的距离:①直接法:平面外一点P 在该平面上的射影为P ′,则线段PP ′的长度就是点到平面的距离, “一找二证三计算”;②等体积法:三棱锥换顶点等体积法。
2、直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;3、平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离。
点到平面的距离平面到平面的距离直线到平面的距离⇒⎩⎨⎧ 二、求夹角1、两条异面直线所成的角:求法:先通过其中一条直线或者两条直线的平移,找出这两条异面直线所成的角,然后通过解三角形去求得;2、直线和平面所成的角:“一找二证三求”,三步都必须要清楚地写出来。
除特殊位置外,主要是指平面的斜线与它在平面内的射影之间的夹角;3、二面角:通常的作法有:①定义法:在二面角的棱上任取一点O (常指特殊点),过点O 分别在两个半平面内作垂直于棱的射线OA 和OB ,则∠AOB 即为所求二面角的平面角;②三垂线定理或逆定理:过一个半平面内一点P 向另一个半平面作垂线PA ,过点A 向棱作垂线AB ,连接PB ,则∠PAB 即为所求二面角的平面角;③自空间一点作棱垂直的垂面,截二面角得两条射线所成的角,俗称垂面法.④射影面积法解之,cos θ=SS ',其中S 为斜面面积,S ′为射影面积,θ为斜面与射影面所成的二面角题型一:异面直线的夹角及二面角例1、如图,在五面体ABCDEF 中,FA ⊥平面ABCD, AD//BC//FE ,AB ⊥AD ,M 为EC 的中点,AF=AB=BC=FE=12A(I) 求异面直线BF 与DE 所成的角的大小; (II) 证明平面AMD ⊥平面CDE ; (III )求二面角A-CD-E 的余弦值题型二:点面距离例2、如题(19)图,在四棱锥S ABCD -中,ADBC 且AD CD ⊥;平面CSD ⊥平面ABCD ,,22CS DS CS AD ⊥==;E 为BS 的中点,2,3CE AS ==.求:(Ⅰ)点A 到平面BCS 的距离; (Ⅱ)二面角E CD A --的大小.题型三:线面距离例3、如题(18)图,在五面体ABCDEF 中,AB ∥DC ,2BAD π∠=,2CD AD ==,四边形ABFE 为平行四边形,FA ⊥平面ABCD ,3,7FC ED ==(Ⅰ)直线AB 到平面EFCD 的距离; (Ⅱ)二面角F AD E --的平面角的正切值.题型四:线面夹角例4、如图3,在正三棱柱111ABC A B C -中,AB =4, 17AA =点D 是BC 的中点,点E 在AC 上,且DE ⊥1A E.(Ⅰ)证明:平面1A DE ⊥平面11ACC A (Ⅱ)求直线AD 和平面1A DE 所成角的正弦值题型五:点到面的距离例5、在长方体ABCD—A1B1C1D1中,AB=4,BC=3,CC1=2,如图:(1)求证:平面A1BC1∥平面ACD1;(2)求(1)中两个平行平面间的距离;(3)求点B1到平面A1BC1的距离。
立体几何2-角与距离
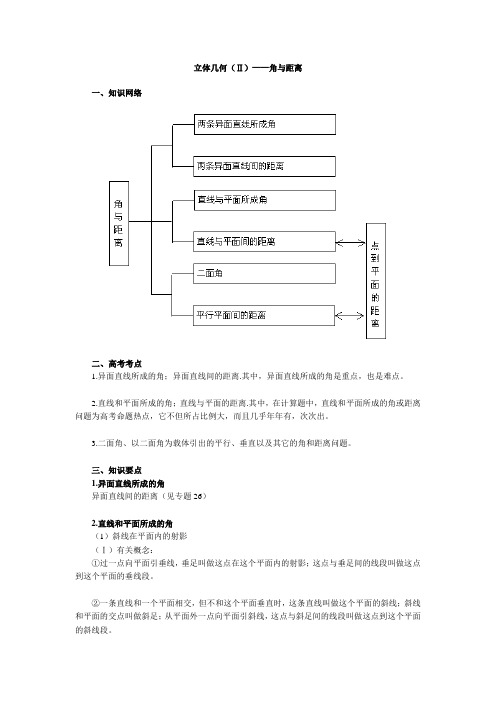
立体几何(Ⅱ)——角与距离一、知识网络二、高考考点1.异面直线所成的角;异面直线间的距离.其中,异面直线所成的角是重点,也是难点。
2.直线和平面所成的角;直线与平面的距离.其中,在计算题中,直线和平面所成的角或距离问题为高考命题热点,它不但所占比例大,而且几乎年年有,次次出。
3.二面角、以二面角为载体引出的平行、垂直以及其它的角和距离问题。
三、知识要点1.异面直线所成的角异面直线间的距离(见专题26)2.直线和平面所成的角(1)斜线在平面内的射影(Ⅰ)有关概念:①过一点向平面引垂线,垂足叫做这点在这个平面内的射影;这点与垂足间的线段叫做这点到这个平面的垂线段。
②一条直线和一个平面相交,但不和这个平面垂直时,这条直线叫做这个平面的斜线;斜线和平面的交点叫做斜足;从平面外一点向平面引斜线,这点与斜足间的线段叫做这点到这个平面的斜线段。
③从斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影,垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影。
(Ⅱ)定理:从平面外一点向平面所引的垂线段和斜线段中①射影等长斜线段等长;②射影较长斜线段较长;③斜线段长大于垂线段。
(2)直线和平面所成的角(Ⅰ)定义与命题①定义:平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角。
特例:若直线与平面垂直,则说直线和平面所成的角是直角;若直线与平面平行或在平面内,则说直线与平面所成角是0°的角。
认知:设斜线l与平面所成角为θ,则θ∈(0°,90°);设直线l与平面所成角为θ,则θ∈[0°,90°]。
②命题(最小角定理):斜线和平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角。
(3)三垂线定理及其逆定理三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
立体几何中的角度与距离问题

立体几何中的角度与距离问题【基础知识】一.空间角度问题(一)理解空间中各种角的定义及其取值范围1.异面直线所成的角、直线与平面所成的角及二面角的概念。
2.各种角的取值范围:(1)异面直线所成的角的取值范围是:0°< θ ≤90°;(2)直线于平面所成的角的取值范围是: 0°≤ θ ≤90°;(3)二面角的大小可以用它的平面角来度量,通常认为二面角平面角的取值范围是: 0°< θ ≤180° (二)空间中的角的计算1、用直接法求角的一般步骤是:(1)找出或做出有关角的图形;(2)证明它符合定义(3)计算(一般通过解三角形)2、异面直线所成的角:用平移转化的方法使它成为相交直线所成的角。
当异面直线垂直时,运用直线垂直平面的定义或三垂线定理(或逆定理)判定所成角是90°.3. 斜线和平面所成的角是一个直角三角形所成的锐角,它的三条边分别是平面的垂线段/斜线段及斜线段在平面内的射影。
4. 二面角要转化为其平面角,掌握以下三种基本做法:(1)直接利用定义;(2)利用三垂线定理及其逆定理(3)作棱的垂面另外,还要特别注意观察图形本身是否已含有所求的平面角注意:1.空间各种角的计算方法都是转化为平面角来计算的,应熟练掌握这种转化。
2.计算题必须有推理过程。
二.空间距离问题1.立体几何中的各种距离有:(1)点到直线的距离(2)点到平面的距离(3)平行直线间的距离(4)异面直线间的距离(5)直线与平面的距离(6)两个平面间的距离(7)球面上两点间距离2.空间七种距离求法,通常是转化为平面上两点间的距离:(1)找出或作出有关距离的图形;(2)证明它们就是所求的距离;(3)利用平面几何和解三角形的知识在平面内计算α βAOP A BOP αβ (1)(2)(3)3. 求异面直线距离(1)定义:关键确定公垂线段(2)转化为直线和平面间距离(过a 而与b 平行的平面)(3)转化为平面间距离(4)极值法4. 求点面距离其法有二:(1)直接法,确定垂足的位置(2)等体积法,同一个三棱锥,从不同的角度选择底和高计算体积并加以比较即可。
浅谈立体几何中空间角和距离问题

yzNB CC 11B 11A A 11 Mx浅谈空间角、距离--向量解法随着高考对立体几何考查力度的加大,立体几何中空间向量的运用,已成为解答立体几何问题的通性、通法.利用空间向量来解答问题,能将空间抽象思维转化为坐标运算问题,从而降低了对空间想象能力的要求.以多面体为载体,以空间向量为工具,来论证和求解空间角、距离、线线关系以及线面关系相关问题,是不少立体几何题的主要特征。
用空间向量解立体几何问题,较为程序化,思路自然且较少添加辅助线,更易于被学生接受。
1.空间中夹角的向量求法在立体几何中,空间的角有:异面直线所成的角,直线和平面所成的角,平面和平面所成的角即二面角。
俗称线线角,线面角、面面角。
我们经常遇到求角的问题,这个问题一般都是转化为直线与直线的角来计算,总是先定位,后算其值。
但有时定位非常麻烦,难点在于不知道所求的角在哪儿?辅助线怎么作?灵活运用向量法,这些问题就迎刃而解,下面通过几个例子来说明向量在求角中的应用。
1.1. 异面直线夹角的向量求法异面直线之间夹角的计算可以转化为异面直线间方向向量的夹角的计算,设异面直线n m ,所成的角为θ,则θ等于n m ,的方向向量b a ,所成的角或其补角的大小,则||||||cos b a b a ∙∙=θ。
例1(2000年高考新课程卷试题)如图,直三棱柱ABC —A 1B 1C 1的底面三角形ABC 中,CA=CB=1,∠BCA=900,棱AA 1=2,M 、N 分别是A 1B 1、A 1A 的中点。
(1)求BN 的长;(2)求><11,cos CB BA 的值。
解:以C 为原点建立如图空间直角坐标系, (1)B (0,1,0),N (1,0,1), ∴3)01()10()01(||222=-+-+-=BN (2))2,1,0(),0,0,0(),2,0,1(11B C A∴5||,6||11==CB BA , 且3)2,1,0()2,0,1(11=⋅=⋅CB BA , ∴1030||||111111,cos =>=<⋅⋅CB BA CB BA CB BA1.2. 直线与平面所成的角直线l 与平面α成角θ,a 是直线l 的方向向量,b 是平面α的一个法向量, 则|||||||,cos |sin b a b a b a ∙∙=><=θ。
立体几何中的角度、体积、距离问题

第02讲 玩转立体几何中的角度、体积、距离问题【学习目标】1.掌握各种角的定义,弄清异面直线所成的角与两直线所成的角,二面角与二面角的平面角,直线与平面所成的角和斜线与平面所成的角,二面角与两平面所成的角的联系与区别,弄清他们各自的取值范围。
2.细心体会求空间角的转化和数形结合思想。
3.掌握各种距离和距离的求解方法.【基础知识】知识点1.求点线、点面、线面距离的方法(1)若P 是平面α外一点,a 是平面α内的一条直线,过P 作平面α的垂线PO ,O 为垂足,过O 作OA ⊥a ,连接P A ,则以P A ⊥a .则线段P A 的长即为P 点到直线a 的距离(如图所示).(2)一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离叫直线与平面的距离.(3)求点面距离的常用方法:①直接过点作面的垂线,求垂线段的长,通常要借助于某个直角三角形来求解.②转移法:借助线面平行将点转移到直线上某一特殊点到平面的距离来求解.③体积法:利用三棱锥的特征转换位置来求解.知识点2.异面直线所成角的常用方法求异面直线所成角的一般步骤:(1)找(或作出)异面直线所成的角——用平移法,若题设中有中点,常考虑中位线.(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.(3)结论——设(2)所求角大小为θ.若090θ︒<≤︒,则θ即为所求;若90180θ︒<<︒,则180θ︒-即为所求.知识点3.直线与平面所成角的常用方法求平面的斜线与平面所成的角的一般步骤(1)确定斜线与平面的交点(斜足);(2)通过斜线上除斜足以外的某一点作平面的垂线,连接垂足和斜足即为斜线在平面上的射影,则斜线和射影所成的锐角即为所求的角;(3)求解由斜线、垂线、射影构成的直角三角形.知识点4.作二面角的三种常用方法(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图①,则∠AOB 为二面角α-l -β的平面角.(2)垂直法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如图②,∠AOB 为二面角α-l -β的平面角.(3)垂线法:过二面角的一个面内异于棱上的一点A 向另一个平面作垂线,垂足为B ,由点B 向二面角的棱作垂线,垂足为O ,连接AO ,则AOB ∠为二面角的平面角或其补角.如图③,AOB ∠为二面角l αβ--的平面角.知识点5.求体积的常用方法选择合适的底面,再利用体积公式求解.【考点剖析】考点一:异面直线所成的角例1.在空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,若2==AC BD ,且AC 与BD 所成的角为60°,则EG 的长为()A .1或2B .2或3C .1或3D .12或32考点二:线面角例2.如图,在三棱柱ABC A B C '''-中,底面ABC 是正三角形,AA '⊥底面ABC ,且1AB =,2AA '=,则直线BC '与平面ABB A ''所成角的正弦值为______.考点三:二面角例3.在四棱锥P ABCD -中,底面ABCD 是菱形,60ABC ∠=︒,PA ⊥平面ABCD ,2PA AB ==.(1)求证:PC BD ⊥;(2)求二面角P CD A --的正弦值.考点四:距离问题例4.如图,在直三棱柱111ABC A B C -中,1,,22AB BC AA AC AB BC ⊥===,E ,F 分别是11,AC AB 的中点.(1)证明:AE ∥平面11B C F .(2)求点C 到平面11B C F 的距离.考点五:体积问题例5.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 为正方形,点F 为线段PC 上的点,过A ,D ,F 三点的平面与PB 交于点E .(1)证明://EF 平面ABCD ;(2)若E 为PB 中点,且2AB PA ==,求四棱锥P AEFD -的体积.【真题演练】1.在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π62.如图,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是( ) A .AC ⊥SBB .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角D .AB 与SC 所成的角等于DC 与SA 所成的角1.线面平行垂直的判定;2.线面角,异面直线所成角3.已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S AB C --的平面角为3θ,则A .123θθθ≤≤B .321θθθ≤≤C .132θθθ≤≤D .231θθθ≤≤4.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A 235D 7 5.已知正方体1111ABCD ABCD -中,E 、F 分别为11、BB CC 的中点,那么异面直线AE 与1D F 所成角的余弦值为____________.6.如下图,在四棱锥S ABCD -中,底面ABCD 是正方形,平面SAD ⊥平面ABCD ,2SA SD ==,3AB =. (1)求SA 与BC 所成角的余弦值;(2)求证:AB SD ⊥.7.如图,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =. (1)证明:C//B 平面D P A ;(2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.8.如图,在圆锥PO 中,已知2PO O 的直径2AB =,点C 在AB 上,且30CAB ∠=,D 为AC 的中点.(I )证明:AC ⊥平面POD ;(II )求直线OC 和平面PAC 所成角的正弦值.9.如图,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O .(Ⅰ)证明PA ⊥BF ;(Ⅰ)求面APB 与面DPB 所成二面角的大小的余弦值.10.在四棱锥P ABCD -中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD ∥平面MAC ,PA PD =.(1)判断M 点在PB 的位置并说明理由;(2)记直线DM 与平面P AC 的交点为K ,求DK KM的值;(3)若异面直线CM 与AP M CD A --的平面角的正切值. 11.如图,在长方体1111ABCD A B C D -中,AD =1,12AB AA ==,H ,F 分别是棱11C D ,1BB 的中点.(1)判断直线HF 与平面11A BCD 的位置关系,并证明你的结论;(2)求直线HF 与平面ABCD 所成角的正弦值;(3)在线段HF 上是否存在一点Q ,使得点Q 到平面11A BCD ,若存在,求出HQ HF的值;若不存在,说明理由. 【过关检测】1.在长方体1111ABCD A B C D -中,12AB AA ==,3AD =,点E 、F 分别是棱AB 、1AA 的中点,E 、F 、1C ∈平面α,直线11A D 平面P α=,则直线BP 与直线1CD 所成角的余弦值为()A C 2.在正方体1111ABCD ABCD -中,E ,F 分别为棱AD ,11A B 的中点,则异面直线EF 与1CD 夹角的余弦值为()A D3.如图所示,三棱锥P ABC -的底面ABC 是等腰直角三角形,90ACB ∠=,且2PA PB AB ===,=PC 则PC 与平面P AB 所成角的余弦值等于()A B 4.在空间四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,若2==AC BD ,且AC 与BD 所成的角为60°,则EG 的长为()A.1.1.125.在棱长为1的正方体1111ABCD A B C D -中,O 为正方形1111D C B A 的中心,则下列结论错误的是() A .BO AC ⊥B .BO ∥平面1ACDC .点B 到平面1ACD D .直线BO 与直线1AD 的夹角为3π 6.在正方体1111ABCD A B C D -中,,,E F G 分别为11,,BC CC BB 的中点,则下列结论中正确的是() A .1D D AF ⊥B .二面角F AEC --的正切值为2C .异面直线1A G 与EFD .点G 到平面AEF 的距离是点C 到平面AEF 的距离的2倍7.如图,AB 是半球的直径,O 为球心,4,,AB M N =依次是半圆AB 上的两个三等分点,P 是半球面上一点,且PN MB ⊥,(1)证明:平面PBM ⊥平面PON ;(2)若点P 在底面圆内的射影恰在BM 上,求二面角--A PB N 的余弦值.8.已知平面四边形ABCD ,2AB AD ==,60BAD ∠=︒,30BCD ∠=︒,现将ABD △沿BD 边折起,使得平面ABD ⊥平面BCD ,此时AD CD ⊥,点P 为线段AD 的中点.(1)求证:BP ⊥平面ACD ;(2)若M 为CD 的中点,求MP 与平面BPC 所成角的正弦值;(3)在(2)的条件下,求二面角P BM D --的平面角的余弦值.9.已知四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)当1PD =,BD =PB 与AD 所成角的余弦值;10.已知四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)已知1PD =,(Ⅰ)当BD PB 与AD 所成角的余弦值;(Ⅰ)当直线PB 与平面ABCD 所成的角为45︒时,求四棱锥P ABCD -的体积.11.在直三棱柱111ABC A B C -中,90ABC ∠=︒,1AB BC ==,12BB =.(1)求异面直线11B C 与1A C 所成角正切值的大小;(2)求点1B 与平面1A BC 的距离.第02讲 玩转立体几何中的角度、体积、距离问题【学习目标】1.掌握各种角的定义,弄清异面直线所成的角与两直线所成的角,二面角与二面角的平面角,直线与平面所成的角和斜线与平面所成的角,二面角与两平面所成的角的联系与区别,弄清他们各自的取值范围。
立体几何中角度与距离求法

立体几何中角度距离的求法空间向量及其运算1 .空间向量的坐标表示及应用(1)数量积的坐标运算 _____________________________________________________ 设 a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),则 a ·b = _____________________________________ (2)共线与垂直的坐标表示设 a =(a 1,a 2,a 3), b =(b 1,b 2,b 3),则 a ∥b ? ________a ⊥b ? _________ ? _______________________ ( a ,b 均为非零向量 ). (3)模、夹角和距离公式 设 a = (a 1, a 2, a3), b = (b 1,b 2,b3),设 A (a 1,b 1,c 1),B (a 2, b 2,c 2), 则 d AB =|A →B|= ____2.空间向量的数量积及运算律 (1)数量积及相关概念① 两向量的夹角, 已知两个非零向量 a ,b ,在空间任取一点 O ,作O →A =a ,O →B =b ,则∠AOB叫做向量 a 与 b 的夹角,记作 ___________ ,其范围是 __________ ,若〈 a ,b 〉= 2π,则 称 a 与 b _________,记作 a ⊥ b .② ___________________________________________________ 两向量的数量积, 已知空间两个非零向量 a ,b ,则 _____________________________________ 叫做向量 a ,b 的数量积, 记作 ________ ,即 __________________ .(2)空间向量数量积的运算律①结合律: (λa ) ·b = _____ ; ②交换律:a ·b = _________③ ________________________分配律: a ·(b + c )= .2.共线向量、共面向量定理和空间向量基本定理(1)共线向量定理对空间任意两个向量 a ,b (b ≠0) ,a ∥b 的充要条件是推论, 如图所示,点 P 在 l 上的充要条件是: O →P =O →A + t a ①其中 a 叫直线 l 的方向向量, t ∈R ,在 l 上取 A →B =a , 则①可化为 O →P = ______________________ 或O →P =(1-t )O →A + tO →B.(2)共面向量定理的向量表达p = __________ ,其中 x ,y ∈R ,a ,b 为不共线向量,M →→→→→→yO →A +z O →B , 其中 x + y + z = .(3)空间向量基本定理,如果三个向量 a ,b ,c 不共面,那么对空间任一向量 p ,存在有序实数组 { x ,y , z} ,使得 p = ________ ,把 { a , b , c }叫做空间的一个基底 .则 |a |= a ·a =cos 〈a , b 〉a ·b|a||b|用向量的方法求角度(一)知识清单1.直线的方向向量与平面的法向量的确定(1) 直线的方向向量:在直线上任取一非零向量作为它的方向向量.(2) 平面的法向量可利用方程组求出:设a,b是平面α内两不共线向量,n 为平面α的法向n·a=0量,则求法向量的方程组为.n·b=02.空间向量与空间角的关系(1) ____________________________________________________________________________ 设异面直线l 1,l2的方向向量分别为m1,m2,则l1与l2所成的角θ满足cos θ=__________ .(2) 设直线l 的方向向量和平面α的法向量分别为m,n,则直线l 与平面α所成角θ满足sin θ= ________ .(3) 求二面角的大小1°如图①,AB、CD 是二面角α—l—β的两个面内与棱l 垂直的直线,则二面角的大小2°如图②③,n1,n2分别是二面角α—l—β的两个半平面α,β的法向量,则二面角的大小θ 满足cos θ= __________________________________ .(二) 题型题型一求异面直线所成的角例 1 如图所示,在长方体ABCD —A1B1C1D1中,已知AB=4,AD=3AA1=2.E、F 分别是线段AB、BC 上的点,且EB=BF=1. 求直线EC1 与FD1所成的角的余弦值.解方法一以 A 为原点,A→B、A→D、A→A1分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有 D 1(0,3,2) ,E(3,0,0),F(4,1,0),C1(4,3,2),于是E→C1=(1,3,2),F→D1=(-4,2,2),设EC1 与FD1所|EC1·FD 1| =1× -4 +3×2+2×2|E →C1| |·F→D1|12+32+22× -4 2+22+22∴直线EC1与FD1所成的角的余弦值为21.14方法二延长BA 至点E1,使AE1=1,连接E1F、DE1、D1E1、有D1C1∥E1E,D1C1=E1E,则四边形 D 1E1 EC1 是平行四边形=21,=14,成的角为β,则:cos β=则E1D 1∥EC 1.于是∠ E1D 1F(或补角)为直线EC1与FD1所成的角.在Rt△BE1F中,E1F=E1B2+BF 2=52+12=26.在 Rt △ D 1DE 1中, D 1E 1= DE 12+DD 21= AE 12+AD 2+DD 12= 12+32+22= 14. 在 Rt △D 1DF 中,FD 1= FD 2+DD 12= CF 2+CD 2+ DD 12= 22+42+22= 24.练习 1 如图,在四棱锥 O —ABCD 中,底面 ABCD 是边长为 1 的菱形, π∠ABC =4.OA ⊥底面 ABCD ,OA =2,M 为 OA 的中点, N 为 BC 的中点 . (1)证明:直线 MN ∥平面 OCD ;(2) 求异面直线 AB 与 MD 所成角的大小 .(1)证明作 AP ⊥CD 于点 P.如图,分别以 AB ,AP ,AO 所在直线为 x , y ,z轴建立直角坐标系 .A(0,0,0),B(1,0,0),P 0, 22, 0 ,D - 22, 22, 0 ,题型二 求直线与平面所成的角例 2 如图所示,直三棱柱 ABC —A 1B 1C 1 中,底面是等腰直角三角形, ∠ACB =90°,侧棱 AA 1=2,D 、E 分别是 CC 1、A 1B 的中点,点 E 在平面 ABD 上的射影是△ ABD 的重心 G. 求 A 1B 与平面 ABD 所成角的正弦值 .解建立空间直角坐标系,坐标原点为 C ,设 CA = 2a ,则 A(2a,0,0),B(0,2a,0)在△E 1FD 1 中,由余弦定理得: cos ∠ E1D 1F = D 1E 12+FD 21- E 1 F 2 2×D1E 1×FD 1 21. 14 .∴直线 EC 1 与 FD 1所成的角的余弦值为21. 14 .D(0,0,1), A 1(2a,0,2), E(a ,a,1),G ,23a , 31 ,E →G = - BD =(0, -2a,1),·B →D =32a 2-23=0,∴a =1,E →G = -31,- 13, a ,3,O(0,0,2),M(0,0,1), N 1- 42, 42, 0 . M →N =OD =2, 2,22,-2 .设平面 OCD 的法向量为 n = (x , y ,z), 则 n ·O →P = 0, 22y -2z =0,n ·O →D =0.即- 22x + 22y -2z = 0.取 z = 2,解得 n = (0,4, 2).∵M →N ·n = 1- 2,24,4,- 1 ·(0,4, 2)=0,∴MN ∥平面 OCD.(2)解设 AB 与 MD 所成角为 θ, ∵A →B =(1,0,0),M →D = - 2, 222∴ cos θ= |AB ·MD | |A →B||·M →D |ππ∴θ=3.∴直线 AB 与 MD 所成的角为 3.22,- 2 ,2, 2,- 11- 4 , 4 ,-112, θ∈于是 cos 〈 n ,A →D 〉n·AD = - 3 7 |n | |·A →D| 4× 2 3题型三 求二面角 例 3 如图,四边形 ABCD 为正方形, (1)证明:平面 PQC ⊥平面 DCQ ; (2)求二面角 Q — BP — C 的余弦值 .(1)证明如图,以 D 为坐标原点,线段以 AD 、DP 、DC 所在直线为 x 轴、y 轴、 z 轴建立空间直角坐标系 Dxyz. 依题意有 Q(1,1,0),C(0,0,1),P(0,2,0),则 D →Q =(1,1,0) ,D →C = (0,0,1) ,P →Q =(1,- 1,0). 所以P →Q ·D →Q =0,P →Q ·D →C =0,即 PQ ⊥DQ ,PQ ⊥DC.又 DQ ∩DC =D ,所以 PQ ⊥平面 DCQ. 又 PQ? 平面 PQC ,所以平面 PQC ⊥平面 DCQ.(2)解依题意有 B(1,0,1),C →B =(1,0,0),B →P =(-1,2,- 1).A 1B =(-2,2,- 2).∵EG 为平面 ABD 的一个法向量, 且 cos 〈A →1B ,E →G 〉= A →1B ·E →G = 32,∴A 1B 与平面 ABD 所成角的正弦值是 32. |A →1B||E →G| 3 3 练习 2 如图所示,在正三棱柱 ABC —A 1B 1C 1中, AB =4,AA 1= 7, 点 D 是 BC 的中点,点 E 在 AC 上,且 DE ⊥A 1E. (1)证明:平面 A 1DE ⊥平面 ACC 1A 1; (2) 求直线 AD 和平面 A 1DE 所成角的正弦值 . (1)证明由正三棱柱 ABC —A 1B 1C 1的性质知,AA 1⊥平面 ABC.又DE? 平面 ABC ,所以DE ⊥AA 1.又 DE ⊥A 1E ,AA 1∩ A 1E = A 1, 所以 DE ⊥平面 ACC 1A 1 .又 DE? 平面 A 1DE , 故平面 A 1DE ⊥平面 ACC 1A 1. (2)解 如图所示,设 O 是 AC 的中点,以 O 为原点建立空间直角坐标 系,则相关各点的坐标分别是 A(2,0,0), A 1(2,0, 7), D(- 1, 3,0),E(-1,0,0).易知 A →1D =(-3, 3,- 7), D →E =(0,- 3,0),A →D = (-3, 3,0).设 n =(x , y ,z)是平面 A 1DE 的一个法向量,则 n ·D →→E =- 3y =0, n ·A →1D =- 3x + 3y -7z = 0. 解得 x =- 37z ,y =0. 故可取 n =( 7,0,- 3).故直线 AD 和平面 A 1DE 所成角的正弦值为21 8218 PD ⊥平面 ABCD ,PD ∥QA , QA =AB =12PD.2 DA 的长为单位长,即 n设 n = (x , y , z)是平面 PBC 的法向量,同理,设 m 是平面 PBQ 的法向量,故二面角 Q —BP —C 的余弦值为- 515.B →D =(-2 3, 2,0). ∴B →D ·A →P =0,B →D ·A →C =0. ∴BD ⊥ AP ,BD ⊥AC.又∵ PA ∩ AC = A ,∴ BD ⊥面PAC.(2)解 设平面 ABD 的法向量为 m = (0,0,1),设平面 PBD 的法向量为 n = (x , y , z), 则 n ·B →D = 0,n ·B →P = 0.∵B →P = ( -2 3,0,3),二距离的求法 ②等体积法,转化为求三棱锥的高③等价转移法; 则 B 到平面 α的距离 d④法向量法 .如图,设 AB 为平面 α的一条斜线段, n 为平面 α的法向量,2 题型则n ·C →B = 0,n ·B →P = 0,m ·BP =0,则 可取 m = (1,1,1).所以 cos 〈 m , n 〉 m ·P →Q =0,15 5(2)求二面角 P —BD —A 的大小 .(1)证明 如图,建立坐标系,则 A(0,0,0), B(2 3,0,0),C(2 3, 6,0), y = 3x ,解得2 3 z = 3 x. 令 x = 3, 则 n = ( 3,3,2),面角 P —BD — A 的大小为 60°.1.点面距的求法 ①垂面法:借助面面垂直的性质来作垂线,其中过已知点确定已知面的垂面是关键题型一 用向量法求空间距离x =0,-x +2y -z =0. 因此可取 n =(0,- 1,- 2).练习 3 如图,在底面为直角梯形的四棱锥 P —ABCD 中, AD ∥BC , ∠ABC =90°, PA ⊥平面 ABCD ,PA =3,AD =2,AB =2 3,BC =6.(1)求证: BD ⊥平面 PAC ;D(0,2,0),P(0,0,3),∴A →P = (0,0,3),A →C =(2 3,6,0),- 2 3x + 2y =0, -2 3x + 3z = 0 ∴cos 〈m ,n 〉=|m m ·||nn |=21.例 1 在三棱锥 S —ABC 中,△ ABC 是边长为 4 的正三角形,平面 SAC ⊥平面 ABC ,SA =SC =2 3,M 、N 分别为 AB 、 SB 的中点,如图所示 . 求点 B 到平面 CMN 的距离 .说明 :点到平面的距离,利用向量法求解比较简单,它的理论基础仍出于几何法 .如本题,事 实上,作 BH ⊥平面 CMN 于 H.由B →H =B →M +M →H 及B →H ·n =n ·B →M , ∴|B →H ·n |=|n ·B →M|=|B →H| |·n |, ∴|B →H|=|n ·|n B |M|,即 d =|n ·|n B |M|.解 取 AC 的中点 O ,连接 OS 、 OB.∵SA =SC ,AB =BC , ∴AC ⊥SO ,AC ⊥ BO. ∵平面SAC ⊥平面 ABC ,平面 SAC ∩平面 ABC =AC ,∴ SO ⊥平面 ABC ,又∵ BO? 平面 ABC ,∴SO ⊥BO.如图所示,建立空间直角坐标系 Oxyz ,则 B (0,2 3, 0),C (-2,0,0),S (0,0,2 2),M (1, 3,0),N (0, 3, 2). ∴C →M = (3, 3, 0), M →N = ( - 1,0, 2), M →B = (- 1, 3,0). 设n =(x ,y ,z )为平面 CMN 的一个法向量, ,取 z =1,则 x =2,y =- 6,∴ n =( 2,- 6,1).∴点 B 到平面 CMN 的距离 d =|n ·MB|=432. 3练习 1 如图,△ BCD 与△MCD 都是边长为 2 的正三角形,平面MCD ⊥平面 BCD ,AB ⊥平面 BCD , AB =2 3 .求点 A 到平面 MBC的距离 .解 取 CD 中点 O ,连接 OB ,OM ,则 OB ⊥CD ,OM ⊥CD. 又平面 则MO ⊥平面 BCD .取O 为原点,直线 OC 、BO 、OM 为 x 轴、y 轴、z 轴, 建立空间直角坐标系如图 .OB =OM = 3,则各点坐标分别为 C (1,0,0), M (0,0, 3),B (0,- 3,0),A (0,- 3,2 3).设 n =(x ,y ,z )是 平面 MBC 的法向量,则 B →C = (1, 3,0),B →M =(0, 3, 3), 由 n ⊥B →C 得 x + 3y =0; 由n ⊥B →M 得 3y +3z =0.取 n =( 3,-1,1),B →A =(0,0,2 3), 则点 A 到平面 MBC 的距离|B →A ·n | 2 3 2 15 d =|n | =5 =5 . 题型二 用等体积法求距离 例2 已知直二面角 D AB E 中,四边形ABCD 是边长为 2 的正方形, AE=EB,F 为 CEC →M ·n =3x + 3y =0则→M →N ·n =- x + 2z =|n |上的点,且 BF 平面 ACE(1) 求证 AE 平面 BCE , (2) 求二面角 B AC E 的大小, (3) 求点 D 到平面 ACE 的距离练习 2、如图,已知正三棱柱 ABC — A 1B 1C 1的底面边长是 2, D 是侧棱 CC 1的中点,直 线 AD 与侧面 BB 1C 1C 所成的角为 45 .AFE 为二面角 A BD C 的平面角 在 Rt BEF 中,BE 1,sin EBF CD 2 3, EFBD 22( 2)23Ⅱ) Ⅲ) 解: 求此正三棱柱的侧棱长; 求二面角 A BD C 的大小; 求点 C 到平面 ABD 的距离. Ⅰ)设正三棱柱BEABC— A 1B 1C 1的侧棱长为 x . C取 BC 中点 E ,连 AE . ABC 是正三角形, AE BC .又底面 ABC 侧面 BB 1C 1C , 且交线为 BC . AE侧面BB 1C 1C .连 ED ,则直线 AD 与侧面 BB 1C 1C 所成的角为AEADE 45 . 在 Rt AED 中, tan45 ED3,解得 x 2 2 此正三棱1 x 42柱的侧棱长为 2 2 . 注:也可用向量法求侧棱长. Ⅱ)解法 1:过 E 作 EF BD 于 F ,连 AF ,AE侧面 BB 1C 1C, AF BD .EF BEsin EBF ,又33. 又AE 3,A 1AB1DC 1在 Rt AEF 中, tan AFE EF 3,故二面角 A BD C 的大小为 arctan3. 解法 2 :(向量法,)Ⅲ)解法 1 :由(Ⅱ)可知, BD 平面 AEF , 平面 AEF 平面 ABD ,且交线为 AF , 过 E 作 EG AF 于G ,则 EG 平面 ABD解法 2 :取 AB 中点 H ,连 CH 和 DH ,由 CA CB, DA DB ,易得平面 ABD 平面CHD ,且交线为 DH .过点 C 作CI DH 于 I ,则CI 的长为点 C 到平面 ABD 的距离. 解法 3:等体积变换 :由 V C ABD V A BCD 可求.解法 4 :(向量法,见后)题(Ⅱ) 、(Ⅲ)的向量解法:取 n 1 ( 6, 3,1). 又平面 BCD 的一个法向量 n 2 (0,0,1).结合图形可知,二面角 A BD C 的大小为 arccos 10 . 10 Ⅲ)解法 4 :由(Ⅱ)解法 2 , n 1 ( 6, 3,1), CA (0, 1, 3)(0, 1, 3) ( 6, 3,1) 2 30( 6)2 ( 3) 2 12 10在 Rt AEF 中, EGAE EF AF3 33( 3) 2 ( 33)230 10E 为 BC 中点, 点C 到平面 ABD 的距离为 2EG2 30 10Ⅱ)解法 2:如图,建立空间直角坐标系 o xyz . z A 则 A(0,0, 3), B(0, 1,0), C(0,1,0), D ( 2,1,0) .设n 1(x, y, z )为平面 ABD 的法向量. n 1n 2 AB 0,得AD 02 x y 3z 0n 1 n 2cos n 1 ,n 2n 1 n 210( 6, 3,1) (0,0,1) 2 2 210点 C 到平面 CA n 1n 1B1BC 1DCyABD 的距离 d5.设 A (2,3,1),B (4,1,2),C (6,3,7),D (-5,-4,8),则 D 到平面 ABC的距离为6 在空间直角坐标系 O —xyz 中,平面 OAB 的一个法向量为 n =(2,-2,1),已知点 P (-1,3,2), 则点 P 到平面 OAB 的距离 d 等于( B ) A. 4 B. 2 C .3 D .1练习题1.如图所示,在空间直角坐标系中,有一棱长为 a 的正方体 ABCO —A ′B ′C ′D ′,A ′C 的中点 E 与 AB 的中点 F 的距离为22a2 在长方体 ABCD —A 1B 1C 1D 1中, AA 1=5,AB =12,那么直线 B 1C 1和平面 A 1BCD 1 的距离是 ___61033.正方体 ABCD —A 1B 1C 1D 1的棱长为 1,E 、F 分别为 BB 1、CD 的中点,则点 F 到平面 A 1D 1E的距离为 __3105 _____ .4.在四面体 PABC 中, PA ,PB ,PC 两两垂直,设 PA = PB = PC =a ,则点 P 到平面 ABC 的距离为___33a49 17__________ . 17______ .7 已知在矩形 ABCD 中, AB =4,AD = 3,沿对角线 AC 折叠,使面 ABC 与面 ADC 垂直,求 B 、 D 间的 距离. 解方法一 如图,过 D 、B 分别作 DE ⊥AC 于点 E ,BF ⊥AC 于点 F ,则由已知条件得 AC =5, 2 AD ·DC 12 AB ·BC 12 AD 2 9 7 ∴DE = = ,BF = = . ∴AE = = =CF. ∴EF =AC -2AE = . AC 5 AC 5 ∴ = AC 5 5 → → → → → 2 → → → 2 ∵DB =DE +EF +FB , ∴|DB|2=|DE + EF +FB|2 → → → → → → → → → =DE 2+EF 2+FB 2+2DE ·EF +2DE ·FB +2EF ·FB. ∵面 ADC ⊥面 ABC ,而 DE ⊥AC , ∴DE ⊥面 ABC ,∴ DE ⊥ BF.(8 分) ∴|D →B |2=D →E 2+E →F 2+F →B 2=144+49+144=337. 25 25 25 25 ∴|D →B |= 337,故 B 、D 间的距离为 337 55 方法二 过E 作 FB 的平行线交 AB 于 P 点,以E 为坐标原点, EC 、ED 所在直线分别为 x 、y 、z 轴建立空间直角坐标系,EF = 57.(4 分) x 12 由方法一知 DE =FB = ∴D 0,0, 152 ,B ∴|D →B|= 5 ,7 ,5 + 7 2 ++ 5 + 0. 12 2 337 5=5。
立体几何中的夹角、距离、向量归纳

D BA C α一、空间中各种角包括:异面直线所成的角、直线与平面所成的角以及二面角 1、异面直线所成的角(1)异面直线所成的角的范围是]2,0(π。
(2)求两条异面直线所成的角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决(3)具体步骤如下:①利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选择在特殊的位置上;②证明作出的角即为所求的角; ③利用三角形来求角 2、直线与平面所成的角(1)直线与平面所成的角的范围是]2,0[π。
(2)求直线和平面所成的角用的是射影转化法。
(3)具体步骤如下:①找过斜线上一点与平面垂直的直线;②连结垂足和斜足,得出斜线在平面的射影,确定出所求的角;③把该角置于三角形中计算。
3、二面角(1)二面角的范围在课本中没有给出,一般是指],0(π,解题时要注意图形的位置和题目的要求。
(2)作二面角的平面角常有三种方法图一 图二 图三 ①棱上一点双垂线法:在棱上任取一点,过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角; 如图一示②面上一点三垂线法:自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角; 如图二示③空间一点垂面法:自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角 如图三示1、点到直线的距离:点P到直线a 的距离为点P到直线a 的垂线段的长,常先找或作直线a 所在平面的垂线,得垂足为A,过A作a 的垂线,垂足为B连PB,则由三垂线定理可得线段PB即为点P到直线a 的距离。
在直角三角形PAB中求出PB的长即可。
例1、在△ABC 中,AB=2,BC=3,AC=4,求点A 到BC 的距离。
解:作BC AD ⊥,垂足为D ,又 AB=2,BC=3,AC=4, 874322432cos 222222=⨯⨯-+=⋅-+=∴BC AC AB BC AC C815)87(1sin 2=-=∴C41538154321sin 4321=⨯⨯⨯=⨯⨯=∴∆C S ABC AD BC S ABC ⋅=∆21又 2153415322=⨯==∴∆BCS AD ABC∴点A 到BC 的距离为2152、点到平面的距离:点P到平面α的距离为点P到平面α的垂线段的长.常用求法①作出点P到平面的垂线后求出垂线段的长;②转移法,如果平面α的斜线上两点A,B到斜足C的距离AB,AC的比为n m :,则点A,B到平面α的距离之比也为n m :.特别地,AB=AC时,点A,B到平面α的距离相等;③体积法例2、如图,在长方体1111D C B A ABCD -中,,22,2,51===AA BC AB E 在AD 上,且AE=1,F 在AB 上,且AF=3,(1)求点1C 到直线EF 的距离;(2)求点C 到平面EF C 1的距离。
立体几何第六课用空间向量求距离和角度

立体几何第六课 §用空间向量求距离和角度一、知识点向量的常用方法 ①点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α的距离为②.异面直线间的距离 :d =(12,l l 是两异面直线,其公垂向量为n ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).③.直线AB 与平面所成角:sin||||AB marc AB m β⋅=(m 为平面α的法向量).④.求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n n 反方,则为其夹角).二面角l αβ--的平面角cos||||m n arc m n θ⋅=或cos ||||m narc m n π⋅-(m ,n 为平面α,β的法向量).二、例题1.如图,已知正三棱柱111ABC A B C -的侧棱长和底面边长为1,M 是底面BC 边上的中点,N 是侧棱1CC 上的点,且12CN C N =。
(Ⅰ)求二面角1B AM N --的平面角的余弦值;(Ⅱ)求点1B 到平面AMN 的距离。
2.如图,在四棱锥S ABCD -中,平面SAD ⊥平面ABCD .底面ABCD 为矩形,,AD AB =,SA SD a ==.(Ⅰ)求证:CD SA ⊥;(Ⅱ)求二面角C SA D --的大小. 3.如图,在三棱柱ABC —A 1B 1C 1中,AA 1⊥平面A 1B 1C 1,∠B 1A 1C 1=90°,D 、E 分别为CC 1和A 1B 1的中点,且A 1A=AC=2AB=2. (I)求证:C 1E∥平面A 1BD ; (Ⅱ)求点C 1到平面A 1BD 的距离.4.如图,在四棱锥ABCD P -中,底面ABCD 是菱形,060BAD =∠,2AB =,1PA =,⊥PA 平面ABCD ,E 是PC 的中点,F 是AB 的中点. (Ⅰ) 求证:BE ∥平面PDF ;(Ⅱ)求证:平面PDF ⊥平面PAB ;(Ⅲ)求平面PAB 与平面PCD 所成的锐二面角的大小.5.已知四边形ABCD 满足AD ∥BC ,12BA AD DC BC a ====,E 是BC 的中点,将BAE ∆沿着AE翻折成1B AE ∆,使面1B AE ⊥面AECD ,F 为1B D 的中点. (Ⅰ)求四棱1B AECD -的体积;(Ⅱ)证明:1B E ∥面ACF ;(Ⅲ)求面1ADB 与面1ECB 所成二面角的余弦值.6.如图,在四棱锥S —ABCD 中,SD ⊥底面ABCD ,底面ABCD是矩形,且SD AD ==,E 是SA 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二年级下学期小学期末检测
数学试卷
(考试时间:60分钟,满分100分)
题号一二三四五六总分
得分
一、我会算。
(12分)
35÷7=900-700=73-(13+27)=9×9÷9=
280+300=1000-600=56-(90-60)= 37+8÷8=
860-260= 60-27÷3= 4×(78-70)= (40-8)÷4=
二、我会填。
(22分)
1、有一个四位数,最高位上是5,十位上是3,其余各位上是0,这个数是(),读作()。
2、□÷7=3……□,余数最大是(),当余数最大时,被除数是()。
3、找规律填数。
537,437,(),237,();150,200,(),300,()。
4、605是()位数,最高位上的数字是(),这里的5表示()个()。
5、()×7<50,括号里最大能填()。
6、在()里填上合适的单位名称:
教室的门高2();铅笔长14();数学书厚4();课桌高8()。
7、在○里填上“>”、“<”、“=”。
5千米○5000米30mm○3dm纯角○锐角
8、最大的两位数是(),与它相邻的两个数分别是()和()。
三、我是小判官。
(对的画“√”,错的画“×”)(12分)
1、50÷7=6……8。
…………………………………………………………………()
2、“333”里的“3”表示的意思一样。
…………………………………………()
3、正方形和长方形都有4条边,4个直角。
………………………………………()
4、角的大小与边的长短有关系。
…………………………………………………()
5、2+10÷2=12÷2=6。
…………………………………………………………()
6、左图中共有6个角。
………………………………………………()
四、我是计算能手。
(14分)
1、用竖式计算并验算。
(6分)
284+357923-657
2、脱式计算。
(8分)
614-596+172 800-(304+199)
五、我真棒,看图完成(10分) 北 1、游乐场在小林家( )面, 在文化馆的( )面。
2、从小林家到文化馆,有几条路? 哪条路近?(涂上颜色),近 ( )米。
六、我真聪明,解决问题。
(4+7+7+12=30分)
1、有66个苹果平均放在9个盘子里,每盘放几个?还剩几个?
2、妈妈给小强买上衣用去69元,买裤用去58元,付给售货员200元,应找回多少元?
3、一根绳子长180米,第一次用去49米,第二次用去58米,这根绳子短了多少?
4、某班爱好水果情况如下,请你根据
表中的数据完成统计图,并回答问题。
水果
人数 26 10 18 8
(1)爱好( )的人最多,爱好( )的人最少的。
(2)爱好苹果的比爱好梨的多多少?□○□=□(人)
(3)一共有多少人爱好水果? □○□○□○□=□(人)
(4)你还能提出哪些数学问题?并试着解答。
游乐场 文化馆 小林家 小明家。
