抽水试验换算公式
抽水试验含砂率计算公式

抽水试验含砂率计算公式引言。
在土力学和岩土工程中,含砂率是一个重要的参数,用于描述土壤或岩石中砂的含量。
含砂率的准确计算对于工程设计和施工具有重要意义。
抽水试验是一种常用的方法,用于测定土壤或岩石中的含砂率。
本文将介绍抽水试验含砂率计算公式,并讨论其应用。
抽水试验原理。
抽水试验是一种通过抽水来测定土壤或岩石中的含砂率的方法。
在抽水试验中,首先需要在试验区域内设置一个抽水井,然后通过抽水井抽取地下水,将地下水中的土壤或岩石颗粒一同抽出。
随着抽水的进行,地下水位下降,土壤或岩石中的含砂率也会逐渐增加。
通过监测抽水井中的地下水位下降速度和含砂率的变化,可以计算出土壤或岩石中的含砂率。
抽水试验含砂率计算公式。
抽水试验含砂率计算公式是根据地下水位下降速度和含砂率的变化来计算的。
一般来说,含砂率可以通过以下公式来计算:含砂率 = (Qs / Q) 100%。
其中,含砂率表示土壤或岩石中的含砂率,Qs表示抽水井中的地下水位下降速度,Q表示抽水井中的地下水位下降速度。
通过监测抽水井中的地下水位下降速度和含砂率的变化,可以利用上述公式来计算土壤或岩石中的含砂率。
应用与意义。
抽水试验含砂率计算公式是一种简单而有效的方法,用于测定土壤或岩石中的含砂率。
通过抽水试验,可以快速准确地测定土壤或岩石中的含砂率,为工程设计和施工提供重要的参考数据。
含砂率的准确计算对于地基工程、土方工程、岩土工程等领域具有重要意义。
因此,抽水试验含砂率计算公式的应用具有广泛的实际意义。
总结。
抽水试验含砂率计算公式是一种简单而有效的方法,用于测定土壤或岩石中的含砂率。
通过抽水试验,可以快速准确地测定土壤或岩石中的含砂率,为工程设计和施工提供重要的参考数据。
含砂率的准确计算对于地基工程、土方工程、岩土工程等领域具有重要意义。
因此,抽水试验含砂率计算公式的应用具有广泛的实际意义。
希望本文对抽水试验含砂率计算公式的理解和应用有所帮助。
铁路抽水水自动计算(N多种公式,自己编制)

巴布什金公式)
2m 4m r 0.756 36.29 16.61 432.6 0.053 20.5 216.3 0 98.6 325 25.6 - A)- log 4m R
}
m3 ←涌水量(m3/d) ←抽水时水位降深(m) ←过滤器有效渗透部分的长度(m)即抽水过程稳定水位以下过滤器有效长度 ←试验段钻孔半径(m) ←影响半径(m) ← 过滤器中部以下有效带厚度(m)(一般可计算为1/2L) ←系数(根据a=L/m确定,查图表得)
影响半径R的计算 R= 2S(HK) R=
-2
27.13315636 (m)
H= K= S=
K=( K=
R )2 2S 0.000847752 (m/d)
÷
H
注: 只需输入红色 条件: 1,抽水稳定
潜水完整井抽水试验K值计算公式 试验井深 降深稳定水位 30分钟的稳定流量 R Q= r H= S= h= R= r= 试验段¢91有效长度= 试验段¢110有效长度= 试验段¢130有效长度=
注:只需输入红色部
潜水不完整井抽水试验渗透系数K的计算(巴布什金公式)
0.732Q K= S*
{
R r =
L+S log R r + m 2L
2m
*(2log
计算: ① ② ③ ④ ⑤
L+S log m 2L 2log
=
0.25
4m r 4m log = R 渗透系数K= 0.00148512
30分钟的稳定流量 173.9 其中: Q= S= L= r= R= A= 8.4177548 m= A= 1.625 试验段¢91有效长度= 试验段¢110有效长度= (m/d) 试验段¢130有效长度=
抽水试验规范方法及计算公式

抽水试验规范方法及计算公式第四章抽水试验抽水试验是确定含水层参数,了解水文地质条件的主要方法。
采用主孔抽水、带有多个观测孔的群孔抽水试验,包括非稳定流和稳定流抽水实验,要求观测抽水期间和水位恢复期间的水位、流量、水温、气温等内容。
要求了解试验基地及其所在地区的水文气象、地质地貌及水文地质条件,了解并掌握抽水试验的目的意义、工作程序、现场记录的主要内容、数据采集与处理方法,掌握相关资料的整理、编录方法和要求,了解对抽水试验工作质量进行评价的一般原则,能够利用学过的理论及方法进行水文地质参数计算,并对参数的合理性和精确性进行分析和检验。
§4.1 基本要求掌握抽水试验的目的、分类、方法及抽水试验准备工作。
4.1.1 抽水试验的目的(1) 确定含水层及越流层的水文地质参数:渗透系数K、导水系数T、给水度、弹性释水系数?、导压系数a、弱透水层渗透系数K'、越流系数 b、越流因素 B、影响半径 R等。
(2) 通过测定井孔涌水量及其与水位下降(降深)之间的关系,分析确定含水层的富水程度、评价井孔的出水能力。
(3) 为取水工程设计提供所需的水文地质数据,如影响半径、单井出水量、单位出水量、井间干扰出水量、干扰系数等,依据降深和流量选择适宜的水泵型号。
(4) 确定水位下降漏斗的形状、大小及其随时间的增长速度;直接评价水源地的可开采量。
(5) 查明某些手段难以查明的水文地质条件,如确定各含水层间以及与地表水之间的水力联系、边界的性质及简单边界的位置、地下水补给通道、强径流带位置等。
4.1.2 抽水试验分类抽水试验主要分为单孔抽水、多孔抽水、群孔干扰抽水和试验性开采抽水。
(1)单孔抽水试验:仅在一个试验孔中抽水,用以确定涌水量与水位降深的关系,概略取得含水层渗透系数。
(2)多孔抽水试验:在一个主孔内抽水,在其周围设置若干个观测孔观测地下水位。
通过多孔抽水试验可以求得较为确切的水文地质参数和含水层不同方向的渗透性能及边界条件等。
抽水水自动计算各种公式

潜水非完整井抽水试验(工程地质手册
K= K= 0.366Q(㏒R-㏒r) Hs 9.4562238 (m/d)
Ry的结果= 29.31141777 (m) 公式Ry= 2S(HK)-2
WG08
潜水非完整井抽水试验(工程地质手册
K= K= 0.366Q(㏒R-㏒r) Hs 11.0553898 (m/d)
K= 0.366Q(㏒R-㏒r) Hs
K=
10.7995516
(m/d)
Ry的结果= 78.97987735 (m) 公式Ry= 2S(HK)-2
3.4 2.9 3.2 3.8
15.6 14.2 13.6 14.8
4.588235 4.896552 4.25 3.894737
试验(工程地质手册第四版)
30分钟的稳定流量→ Q→ (H)自然状况下潜水含水层厚度→ Ry→ 7.4 355.2 10 78.9 (m3/30min) (m3/d) (m) (m) 14.8
r→ (s)水位降升→
0.055 3.8
(m) (m) 4.111111
只需输入红色部分
试验(工程地质手册第四版)
30分钟的稳定流量→ Q→ (H)自然状况下潜水含水层厚度→ Ry→ r→ (s)水位降升→ 6.8 326.4 10 68.8 0.055 3.2 (m3/30min) (m3/d) (m) (m) (m) (m) 3.777778 只需输入红色部分 13.6
试验(工程地质手册第四版)
Ry的结果= 66.80448914 (m) 公式Ry= 2S(HK)-2
WG10
潜水非完整井抽水试验(工程地质手册
K= K= 0.366Q(㏒R-㏒r) Hs 11.5625632 (m/d)
抽水试验规范方法及计算公式

可编辑第四章抽水试验抽水试验是确定含水层参数,了解水文地质条件的主要方法。
采用主孔抽水、带有多个观测孔的群孔抽水试验,包括非稳定流和稳定流抽水实验,要求观测抽水期间和水位恢复期间的水位、流量、水温、气温等内容。
要求了解试验基地及其所在地区的水文气象、地质地貌及水文地质条件,了解并掌握抽水试验的目的意义、工作程序、现场记录的主要内容、数据采集与处理方法,掌握相关资料的整理、编录方法和要求,了解对抽水试验工作质量进行评价的一般原则,能够利用学过的理论及方法进行水文地质参数计算,并对参数的合理性和精确性进行分析和检验。
§4.1 基本要求掌握抽水试验的目的、分类、方法及抽水试验准备工作。
4.1.1 抽水试验的目的(1) 确定含水层及越流层的水文地质参数:渗透系数 K、导水系数 T、给水度、弹性释水系数∗、导压系数 a、弱透水层渗透系数 K'、越流系数 b、越流因素 B、影响半径 R等。
(2) 通过测定井孔涌水量及其与水位下降(降深)之间的关系,分析确定含水层的富水程度、评价井孔的出水能力。
(3) 为取水工程设计提供所需的水文地质数据,如影响半径、单井出水量、单位出水量、井间干扰出水量、干扰系数等,依据降深和流量选择适宜的水泵型号。
(4) 确定水位下降漏斗的形状、大小及其随时间的增长速度;直接评价水源地的可开采量。
(5) 查明某些手段难以查明的水文地质条件,如确定各含水层间以及与地表水之间的水力联系、边界的性质及简单边界的位置、地下水补给通道、强径流带位置等。
4.1.2 抽水试验分类抽水试验主要分为单孔抽水、多孔抽水、群孔干扰抽水和试验性开采抽水。
(1)单孔抽水试验:仅在一个试验孔中抽水,用以确定涌水量与水位降深的关系,概略取得含水层渗透系数。
(2)多孔抽水试验:在一个主孔内抽水,在其周围设置若干个观测孔观测地下水位。
通过多孔抽水试验可以求得较为确切的水文地质参数和含水层不同方向的渗透性能及边界条件等。
抽水试验公式计算

(1)采用承压转无压完整式大 井涌水量解析法公式计算,即:K[(2H M)M ho]inR o式中:Q —大井涌水量,m 3/d ;K —含水层渗透系数,m/d ;H —抽水前大井的水柱高度(从含水层底板到初始静止水位)(m )M —承压含水层厚度,(m )h o —抽水稳定后大井中的水柱高度(从含水层底板到动水位)(m )r o —大井的引用半径(基坑的等效半径),(m ); R o —引用影响半径,R o =R+r ,其中R —为用抽水试验资料或者经验公式计算出的影响半径,(m ):(1)基坑等效半径的确定r o 引用半径为基坑的假想等效半径,当基坑为矩形或者长条形时,基坑的等效半径可可按下式计算:式中,a――基坑长度;b --- 基坑宽度(m);(3)对于潜水,当降深一定时,可采用下面的经验公式来计算大井的影响半径:R 2s 「KH(4)n 为概化系数,n 值取值见下表:(基坑工程手册)表1 系数n 与b/a 关系表本次降水基坑长度为98m ,宽度为3m ,这样计算出的r 为:r 0=1.15 X 98+43 ) /4=40.54m (2)大井法引用影响半径的确定对承压水,当降深一定时,可采用承压水影响半径的经验公式吉 哈尔特公式近似计算大井的影响半径:R 10sJkR --- 影响半径,m ; s --- 大井中的水位降深,m ; K --- 渗透系数其中,H ――含水层厚度,m ;若采用承压水计算影响半径的公式,贝卅算出的影响半径为:R 10s虑10 5.0 J75.17 =433.5m若采用潜水计算影响半径的公式,则计算出的影响半径为:R 2s、KH 2 5.0、75.17 6 212.37m由于本次基坑的降水过称为承压转无压,所以既不能采用承压水的经验公式,也不能采用潜水的经验公式来计算大井的影响半径。
而应该根据实际情况和以往经验综合判定。
结合以往的降水经验,本次采用二者的平均值,即323m。
抽水试验线型及经验公式
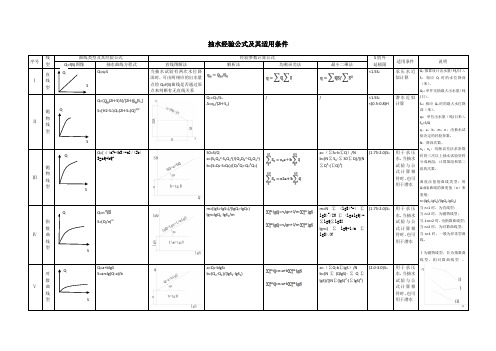
抽水经验公式及其适用条件序号线型曲线类型及其经验公式经验参数计算公式S值外延极限适用条件说明Q=f(S)图像抽水曲线方程式直线图解法解析法均衡误差法最小二乘法Ⅰ直线型Q=q n S 当抽水试验有两次水位降深时,可由两相应的出水量点绘Q=f(S)曲线是否通过原点来判断有无直线关系<1.5S n承压水近似计算Q:推算设计出水量(吨/日)。
S:相应Q时的水位降深(米)。
Q n:单井实抽最大出水量(吨/日)。
S n:相应Q n时的最大水位降深(米)。
q n:单位出水量(吨/日米)。
S0=S/Qq、a、b、m、n:由抽水试验决定的经验参数。
N:降深次数。
n1、n2:均衡误差法求参数时将三次以上抽水试验资料分成两组,计算第组和第二组的次数。
曲度法鉴别曲线类型:用Q=f(S)曲线的曲度值(n)来鉴别:n=(lgS2-lgS1)/(lgQ2-lgQ1)当n=1时,为直线型;当n=2时,为抛物线型;当1<n<2时,为指数曲线型;当n>2时,为对数曲线型;当n<1时,一般为异常型曲线。
Ⅰ为抛物线型,Ⅱ为指数曲线型,Ⅲ对数曲线型。
Ⅱ抛物线型Q={(2H-S)S}/[2H-]S n]S=[H2-S n\Q n(2H-S n)Q]1\2Q n=Q n/S nA=q n/(2H-S n)/ / <1.5S n<(0.5-0.8)H潜水近似计算Ⅲ抛物线型Q=[√(a2+4bS)-a]/(2b)S=aQ+bQ2S0=S/Qa=(S1Q22-S2Q12)/(Q1Q22-Q2Q12)b=(S1Q2-S2Q1)/(Q12Q2-Q22Q1)a=(∑S0-b∑Q)/Nb=(N∑S0-∑S0∑Q)/[(N∑Q2-(∑Q)2)(1.75-2.0)S n用于承压水,当抽水试验与公式计算相符时,也可用于潜水Ⅳ指数曲线型Q=nS=(Q/n)mm=(lgS2-lgS1)/(lgQ2-lgQ1)lgn=lgQ1-lgS1/m=n1lgn+1/m=n2lgn+1/mm=N∑(lgS)2-(∑lgS)2/[N∑(lgslgQ)-∑lgQ∑lgS]lgn=(∑lgQ-1/m∑lgS)/N(1.75-2.0)S n用于承压水,当抽水试验与公式计算相符时,也可用于潜水Ⅴ对数曲线型Q=a+blgSS=arclg(Q-a)/ba=Q1-blgS1b=(Q2-Q1)/(lgS2-lgS1)=n1a+b=n2a+ba=(∑Q-b∑lgS)/Nb=(N∑(QlgS)-∑Q∑lgS)/[(N∑(lgS)2-(∑lgS)2)(2.0-3.0)S n用于承压水,当抽水试验与公式计算相符时,也可用于潜水QSQSQSQSQS。
数学二抽水做功公式

数学二抽水做功公式
数学二抽水做功公式(Bernoulli’sequationforhydraulicpower)是用来描述从一个高位到一个低位抽水的重要物理公式。
数学二抽水做功公式由荷兰数学家贝尔努里(DanielBernoulli)于1738年提出,在其著作《动力学论》中有详细阐述。
贝尔努里曾指出,当从一个高位到一个低位抽水时,由于水流经过毛细管,水面会受到一定的压力,从而产生气压力差,最终导致抽水效果。
首先,数学二抽水做功公式的基本结构大致如下:
P +gH + 0.5ρV2 = C
其中,P为有效压强,ρ为水的密度,g为重力加速度,H为水
的高度,V为水的流速,C为一个常数,通常取值为2.
其次,数学二抽水做功公式的使用方法有两种:
第一种为一次性计算,即用已知的参数对数学二抽水做功公式进行求解。
由于数学二抽水做功公式有一个常数C,因此我们可以用已知的参数计算C的值,然后给定其他变量,求出P,ρ,g,H,V的值。
第二种是分步求解,这种方法可以详细描述抽水的过程,更符合实际情况。
首先我们要计算高位和低位的压强和水面高度,然后假设流体在管道内运动时是无摩擦的,计算出流速。
最后,将这些参数代入数学二抽水做功公式,求出水流给定传输功所需的有效压强。
最后,要说明的是,数学二抽水做功公式不仅仅适用于抽水,同样也可以用于描述流体在一个渠道中的运动,例如河流,水泵等等。
在工程学中,它也有广泛的应用,如液压机械,水力发电,液压动力系统等。
总之,数学二抽水做功公式是一个功能强大而又有广泛应用的公式,它在从高位到低位抽水的情况下,可以精确计算出水的压强和水的流速,从而达到抽水的最佳效果。
