动点到两定点的距离最值上课讲义
动点问题中的最值、最短路径问题解析版
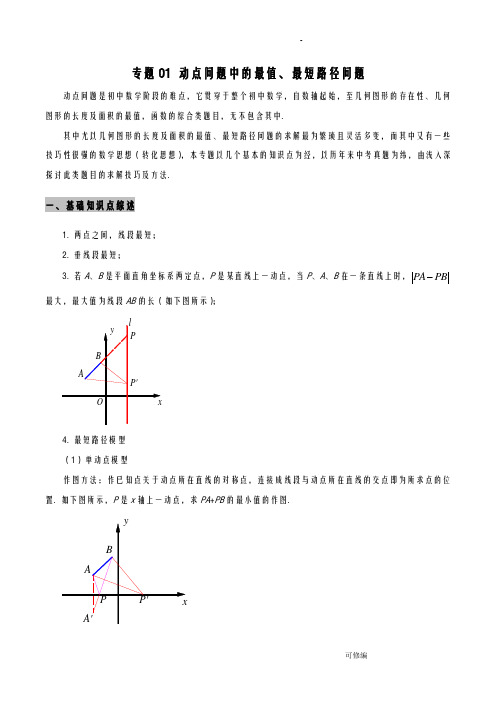
专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点,它贯穿于整个初中数学,自数轴起始,至几何图形的存在性、几何图形的长度及面积的最值,函数的综合类题目,无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变,而其中又有一些技巧性很强的数学思想(转化思想),本专题以几个基本的知识点为经,以历年来中考真题为纬,由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间,线段最短;2. 垂线段最短;3. 若A 、B 是平面直角坐标系两定点,P 是某直线上一动点,当P 、A 、B 在一条直线上时,PA PB 最大,最大值为线段AB 的长(如下图所示);(1)单动点模型作图方法:作已知点关于动点所在直线的对称点,连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示,P 是x 轴上一动点,求PA +PB 的最小值的作图.(2)双动点模型P是∠AOB一点,M、N分别是边OA、OB上动点,求作△PMN周长最小值.作图方法:作已知点P关于动点所在直线OA、OB的对称点P’、P’’,连接P’P’’与动点所在直线的交点M、N即为所求.OBPP'P''MN5. 二次函数的最大(小)值()2y a x h k=-+,当a>0时,y有最小值k;当a<0时,y有最大值k.二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. (详见精品例题解析)三、精品例题解析例1. (2019·凉山州)如图,正方形ABCD中,AB=12,AE=3,点P在BC上运动(不与B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为例2.(2019·凉山州)如图,已知A、B两点的坐标分别为(8,0),(0,8). 点C、F分别是直线x=-5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取最小值时,tan∠BAD=()x y A B C F D EO x=-5A .817B . 717C . 49D . 59例3.(2019·)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,AB =24,BC =5,给出结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;②△OAB 的面积的最大值为144;③当OD 最大时,点D 的坐标为)2626125,262625(,其中正确的结论是(填写序号).例4.(2019·XX )已知抛物线2y x bx c =-+(b 、c 为常数,b >0)经过点A (-1,0),点M (m ,0)是x 轴正半轴上的动点,若点Q (1,2Q b y +22AM QM +332时,求b 的值.例5. (2019·)如图,一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上,边AC 与EF 重合,12AC cm .当点E 从点A 出发沿AC 方向滑动时,点F 同时从点C 出发沿射线BC 方向滑动.当点E 从点A 滑动到点C 时,点D 运动的路径长为cm ;连接BD ,则△ABD 的面积最大值为2cm .例6. (2019·)如图,在菱形ABCD 中,连接BD 、AC 交于点O ,过点O 作OH ⊥BC 于点H ,以O 为圆心,OH 为半径的半圆交AC 于点M .(1)求证:DC 是圆O 的切线;(2)若AC =4MC ,且AC =8,求图中阴影部分面积;(3)在(2)的前提下,P 是线段BD 上的一动点,当PD 为何值时,PH +PM 的值最小,并求出最小值. ABC DH O M N专题01 动点问题中的最值、最短路径问题(解析)例1. (2019·凉山州)如图,正方形ABCD中,AB=12,AE=3,点P在BC上运动(不与B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为【答案】4.【解析】解:∵PQ⊥EP,∴∠EPQ=90°,即∠EPB+∠QPC=90°,∵四边形ABCD是正方形,∴∠B=∠C=90°,∠EPB+∠BEP=90°,∴∠BEP=∠QPC,∴△BEP∽△CPQ,∴BE BP CP CQ=,∵AB=12,AE=3,∴BE=9,设CQ=y,BP=x,CP=12-x,(0<x<12)∴912xx y=-,即()()21216499x xy x-==--+,∴当x=6时,y有最大值为4,即CQ的最大值为4.【点睛】此题为“一线三直角模型”,解题方法为相似三角形性质求解,综合利用二次函数的性质求解最值问题.例2.(2019·)如图,已知A、B两点的坐标分别为(8,0),(0,8). 点C、F分别是直线x=-5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取最小值时,tan∠BAD=()A . 817B . 717C . 49D . 59【答案】B .【解析】解:S △ABE =142BE OA BE ⨯⨯=,当BE 取最小值时,△ABE 面积为最小值.设x =-5与x 轴交于点G ,连接DG ,因为D 为CF 中点,△CFG 为直角三角形,所以DG =152CD =,∴D 点的运动轨迹为以G 为圆心,以5半径的圆上,如图所示 xyABD E O x=-5G由图可知:当AD 与圆G 相切时,BE 的长度最小,如下图,xyABD E O x=-5G H过点E 作EH ⊥AB 于H ,∵OG =5,OA =8,DG =5,在Rt △ADG 中,由勾股定理得:AD =12,△AOE ∽△ADG , ∴AO AD OE DG =, 求得:OE =103, 由OB =OA=8,得:BE =143,∠B =45°,AB =82 ∴EH =BH =27223BE =,AH =AB -BH =1723, ∴tan ∠BAD =727317172EH AH ==, 故答案为B .【点睛】此题解题的关键是找到△ABE 面积最小时即是AD 与D 的远动轨迹圆相切的时刻. 进而构造以∠BAD 为角的直角三角形,利用勾股定理求出边长,代入三角函数定义求解.例3.(2019·)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,AB =24,BC =5,给出结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;②△OAB 的面积的最大值为144;③当OD 最大时,点D 的坐标为)2626125,262625(,其中正确的结论是(填写序号).【答案】②③.【解析】解:根据题意可知:OE =12AB =12,即E 的轨迹为以O 为圆心以12为半径的四分之一圆(第一象限的部分),根据弧长公式,得点E 的路径长为:9012180π⨯⨯=6π,故①错误; 因为AB =24,当斜边AB 上的高取最大值时,△OAB 的面积取最大值,点O 在以AB 为直径的圆上(圆心为E ),当OE ⊥AB 时,斜边AB 上的高最大, 所以△OAB 的面积取最大值为:124122⨯⨯=144,故②正确;连接OE 、DE ,得:OD ≤OE +DE ,当O 、E 、D 三点共线时取等号,即OD 的最大值为25,如图,过点D 作DF ⊥y 轴于F ,过点E 作EG ⊥y 轴于G ,25DF OD 即:1225EG DF =,512AF AD EG AE ==, 即:51125AF EG DF ==,设DF =x ,在Rt △ADF 中,由勾股定理得:221255x x ⎛⎫+= ⎪⎝⎭,解得:x =26,在Rt △ODF 中,由勾股定理得:OF =26,即点D 的坐标为)2626125,262625(,故③正确.综上所述,答案为:②③. 例4.(2019·XX )已知抛物线2y x bx c =-+(b 、c 为常数,b >0)经过点A (-1,0),点M (m ,0)是x 轴正半轴上的动点.若点Q (1,2Q b y +)在抛物线上,当22AM QM +的最小值为3324时,求b 的值. 【答案】见解析. 【解析】解:∵2y x bx c =-+经过点A (-1,0),∴1+b +c =0,即21y x bx b =--- ∵点Q (1,2Q b y +)在抛物线2y x bx c =-+上, ∴324Q b y =--, 即13,224b Q b ⎛⎫+-- ⎪⎝⎭, ∵b >0,∴Q 点在第四象限,2222AM QM AM QM ⎛⎫+=+ ⎪⎝⎭所以只要构造出22AM QM ⎛⎫+ ⎪⎝⎭即可得到22AM QM +的最小值取N (1,0),连接AN ,过M 作MG ⊥AN 于G ,连接QM ,如图所示,△AGM 为等腰直角三角形,GM =22AM ,即当G 、M 、Q 三点共线时,GM +MQ 22QM +取最小值, 此时△MQH 为等腰直角三角形,∴QM=2QH=3224b⎛⎫+⎪⎝⎭,GM=22AM=()212m+∴()223332222=21222244bAM QM AM QM m⎛⎫⎡⎤⎛⎫+=++++=⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦①∵QH=MH,∴324b+=12b m+-,解得:m=124b-②联立①②得:m=74,b=4.即当22AM QM+的最小值为3324时,b=4.【点睛】此题需要利用等腰直角三角形将22AM QM+转化为222AM QM⎛⎫+⎪⎝⎭,进而根据两点之间线段最短及等腰三角形性质求解.例5. (2019·)如图,一副含30°和45°角的三角板ABC和EDF拼合在个平面上,边AC与EF重合,12AC cm=.当点E从点A出发沿AC方向滑动时,点F同时从点C出发沿射线BC方向滑动.当点E从点A滑动到点C时,点D运动的路径长为cm;连接BD,则△ABD的面积最大值为2cm.【答案】24-1223623126;【解析】解:如图1所示,当E运动至E’,F滑动到F’时,DD'E'G图1过D ’作D ’G ⊥AC 于G ,D ’H ⊥BC 交BC 延长线于点H ,可得∠E ’D ’G =∠F ’D ’H ,D ’E ’=D ’F ’,∴Rt △E ’D ’G ≌Rt △F ’D ’H ,∴D ’G =G ’H ,∴D ’在∠ACH 的角平分线上,即C ,D ,D ’三点共线.通过分析可知,当D ’E ’⊥AC 时,DD ’的长度最大,随后返回初始D 点,如图2所示,D 点的运动路径为D →D ’→D ,行走路线长度为2DD ’;BD'图2∵∠BAC =30°,AC =12,DE =CD∴BC =CD =DE=由图知:四边形E ’CF ’D ’为正方形,CD ’=EF =12,∴DD ’=CD ’-CD =12-D 点运动路程为2DD ’=24-D'图3如图3所示,当点D 运动至D ’时,△ABD ’的面积最大,最大面积为:'''''''ABC AE D BD F E CF D S S S S ++-△△△正方形=(((211112222⨯+⨯--⨯+⨯=【点睛】准确利用全等、角平分线判定得到D 点的运动轨迹是关键,利用三角函数及勾股定理求解,计算较为繁琐,尤其是利用割补法求解三角形的面积时对学生计算能力要求较高,此题难度较大,新颖不失难度.例6. (2019·)如图,在菱形ABCD 中,连接BD 、AC 交于点O ,过点O 作OH ⊥BC 于点H ,以O 为圆心,OH 为半径的半圆交AC 于点M .(1)求证:DC 是圆O 的切线;(2)若AC =4MC ,且AC =8,求图中阴影部分面积;(3)在(2)的前提下,P 是线段BD 上的一动点,当PD 为何值时,PH +PM 的值最小,并求出最小值.BD【答案】见解析.【解析】(1)证明:过点O 作ON ⊥CD 于N , AC 是菱形ABCD 的对角线,∴AC 平分∠BCD ,∵OH ⊥BC ,ON ⊥CD ,∴OH =ON ,又OH 为圆O 的半径,∴ON 为圆O 的半径,即CD 是圆O 的切线.(2)由题意知:OC =2MC =4,MC =OM =2,即OH =2,在Rt △OHC 中,OC =2OH ,可得:∠OCH =30°,∠COH =60°,由勾股定理得:CH==23OCH OMHS S S π-=-△阴影扇形(3)作点M 关于直线BD 的对称点M ’,连接M ’H 交BD 于点P , 可知:PM =PM ’即PH +PM =PH +PM ’=HM ’,由两点之间线段最短,知此时PH +PM 最小, ∵OM ’=OM =OH ,∠MOH =60°,∴∠MM ’H =30°=∠HCM ,∴HM ’=HC=即PH +PM的最小值为在Rt △M ’PO 及Rt △COD 中,OP =OM ’ tan 30°=3,OD =OCtan 30°=3, 即PD =OP +OD=B D。
圆周一动点到两定点的最短距离

圆周一动点到两定点的最短距离圆周一动点到两定点的最短距离是一个经典的几何问题,涉及到圆的性质与直线的关系。
在本文中,我们将从不同的角度探讨这个问题,展示出它的深度和魅力。
首先,我们来了解一下这个问题的背景。
假设有一个圆,圆心为O,半径为r;另外有两个定点A和B,我们需要找到一个动点P,使得P到A和B的距离之和最小。
为了解决这个问题,我们可以运用几何分析的方法。
首先,我们将P点与A、B两点分别连线,得到线段PA和PB。
我们可以观察到,P 到A和B的距离之和等于线段PA和线段PB的长度之和。
接下来,我们观察到一个重要的性质:当线段PA和线段PB的长度相等时,P到A和B的距离之和达到最小值。
这是因为,当PA和PB 的长度相等时,P点正好位于线段AB的中垂线上,此时P到A和B 的距离之和等于2倍的线段PA(或PB)的长度。
根据这个性质,我们可以得出结论:圆周上与线段AB的中垂线相交的点P,即为P到A和B的距离之和最小的点。
这个点P的位置并不唯一,因为圆周上有无数个与线段AB的中垂线相交的点,它们的P到A和B的距离之和都是最小的。
这个结论可以通过几何推导得到,但也可以用数学方法进行证明。
我们可以设圆的方程为(x-a)²+(y-b)²=r²,定点A的坐标为(x₁,y₁),定点B的坐标为(x₂,y₂)。
根据求解最短距离的条件,可以列出以下方程组:√((x-x₁)²+(y-y₁)²)+√((x-x₂)²+(y-y₂)²)=k其中,k为常数。
通过求解这个方程组,我们可以得到圆周与线段AB的中垂线相交的点P的坐标。
除了几何和数学的方法,还有其他方法可以求解这个问题。
例如,我们可以利用优化算法来找到P到A和B的距离之和最小的点。
通过将问题转化为一个优化问题,我们可以建立一个目标函数,使得这个函数的取值在P点附近达到最小值。
通过迭代求解,我们可以找到使得目标函数取值最小的P点。
动点到两定点的距离最值

一动点到两定点得距离最值熊明军在学习三角形时,我们知道了三角形得三边之间有一个不等关系:“三角形得两边之与大于第三边”;“三角形得两边之差小于第三边”。
借助这个三角不等式,再结合典型例题,我们可以得到一个动点到两个定点距离最值问题得研究方法与相关结论。
一、典型例题得回顾E、两个村庄,如【例题】已知有一段河岸AB相互平行得一条河,在河岸得一侧有F下图。
现在政府为了让两个村庄用上自来水,决定出资在河岸边建一个自来水厂,并在村庄与水厂之间铺设输水管道输水,为了降低成本,就必须使铺设得管道总长度最短,那么自来水厂应该建在河岸得什么位置,用尺规作图在图中标出。
E、就是两个固定得点,此题得意思【解析】假设靠近村庄得河岸为线段AB,村庄F就就是问:在线段AB上有一个动点P,求P在线段AB上移动到什么位置才能使PE+最短。
PF结论:①直线上一动点P到两个定点距离之与最小问题,要根据点对称将两个定点转化到直线得两侧;②直线上一动点P到两个定点距离之差最大问题,要根据点对称将两个定点转化到直线得同侧。
二、研究问题得理论A、得距离之与有最小值,当且仅当P在线段法则一:平面上一动点P到两个定点BAB之间时取最小值。
A、得距离之差有最大值,当且仅当P在线段法则二:平面上一动点P到两个定点BAB得延长线上时取最大值。
*注意①:一动点P到两定点BA、距离最值得取得都就是使动点与定点转化到一条直线上;如若不在一条直线上,就必须借助题中得条件与相关结论转化之。
*注意②:平面上一动点P到两个定点BA、得距离之与有最小值;距离之差有最大值。
A、得距离之与有最大值;距离之差有最小值,就必须使之如若出现动点P到两个定点B转化为法则中得情况,即:距离之与⇔最小值;距离之差⇔最大值。
【证明】(法则一)已知平面上两个动点B A 、,P 就是平面上任意一个动点,如下图:①当动点P 与定点B A 、不共线时,根据三角形三边关系“两边之与大于第三边”可知AB PB PA >+; ②当动点P 与定点B A 、共线,且在线段AB 得延长线上时,显然有AB PB PA >+; ③当动点P 与定点B A 、共线,且在线段AB 之间时,显然有AB PB PA =+; 综上所述,AB PB PA ≥+,当且仅当动点P 在线段AB 之间时取最小值AB 。
第十一周第一课时关于定直线上的动点到两定点间距离和(差)的极值问题一历城三中尹健

关于定直线上的动点到两定点间距离和(差)的极值问题专题学习目标:1、领会和最小与差的绝对值最大问题的内涵,能正确求解二次函数综合问题中的相关问题;2、能够正确的分析问题、转化问题,合理利用条件解决问题。
学情分析:关于在一条直线上的动点到两定点间距离的和(或差)的极值问题,学生的得分率不高,大约为50﹪左右。
本着数学归类、归纳的理念,在这里把同一类问题作一整理、归纳、延展。
重点:能够正确的分析和最小与差的绝对值最大问题、转化问题 难点:理解和最小与差的绝对值最大问题的内涵 一、问题引入:问题1:大家记得这样一个常识吗?“牵牛从点A 出发,到河边l 喝水,再到点B 处吃草,走哪条路径最短?”即在l 上找一点P ,使得PA+PB 和最小。
(1)A ,B 两点在直线异侧时(2)A ,B 两点在直线同侧时方法是:小结1:在直线l 上找一点P 使PA+PB 和最小,常把两点转化到直线的 ,即作B 点关于 (也可以作A点关于l 的对称点A′),连接AB′交l 于点P,即为所要找的P点。
(3)变式讨论:在l 上找一P 点,使得△PAB 周长最小问题2:在l 上找一点P ,使得∣PA -P B ∣最大 (1)A ,B 两点在直线同侧时l A · B · l A · B · l A · B ·l B · A ·(2)A ,B 两点在直线异侧时小结2:在直线l 上找一点P 使∣PA -P B ∣最大,常把两点转化到直线的 ,即作A 点关于 (也可以作B 点关于l 的对称点B ′),连接A ′B 交l 于点P,即为所要找的P点。
基础知识梳理:分清题目类型,若是和最小,则把两点转化到直线的异侧;若是差的绝对值最大,则把两点转化到直线的同侧;可以简记为“ ”。
二、例题讲解 和的最小值问题例1、在直角坐标系中,点A 、B 的坐标分别为(-4,-1)和(-2,-5);点P 是y 轴上的一个动点,求点P 在何处时,PA +PB 的和为最小?并求最小值。
动点最值问题归纳及解法

在直线两侧找一点,使得到两定点的距离之和最短
作对称点,连接对称点与另一定点,与直线的交点即为所求
构造平行四边形
利用平移构造平行四边形,求最小或最大值
过一点作平行线,构造平行四边形,利用平行四边形的性质求解
相似三角形
利用相似三角形求解最值问题
根据题目条件,构造相似三角形,利用相似比求解
三角函数
利用三角函数求解最值问题
根据题目条件,构造直角三角形,利用三角函数求解
定圆到定圆
圆圆之间连心线截距最短(长)
连接两圆心,求两圆的位置关系(相交、相切、相离),再计算截距
动点路径待确定
动点路径不明确,需先确定路径
根据题目条件,利用几何性质或代数方法确定动点路径
动线(定点)位置需变换
动线或定点位置需通过变换求解
利用翻折、平移、相似、三角等变换方法,将问题转化为基本图形求解
最值问题归纳及解法
问题类型
归纳描述
解法
定点到定点
两点之间线段最短
直接连接两点求线段长度
定点到定线
点线之间垂线段最短
过点作线的垂线,求垂线段长度
ቤተ መጻሕፍቲ ባይዱ定点到定圆
点圆之间点心线截距最短(长)
连接圆心与点,利用勾股定理或相似三角形求解
定线到定圆
线圆之间心垂线截距最短
过圆心作线的垂线,求垂线段与圆的交点,再计算截距
中考数学例析直线上动点与两定点的距离和的最值问题
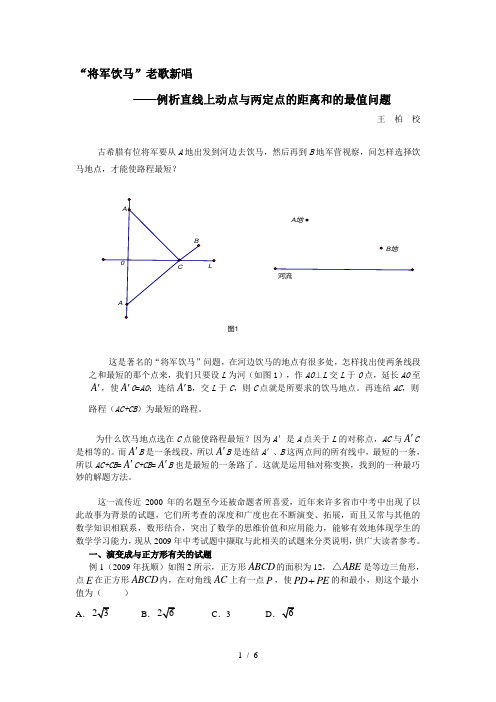
“将军饮马”老歌新唱——例析直线上动点与两定点的距离和的最值问题王柏校古希腊有位将军要从A地出发到河边去饮马,然后再到B地军营视察,问怎样选择饮马地点,才能使路程最短?图1A地B地这是著名的“将军饮马”问题,在河边饮马的地点有很多处,怎样找出使两条线段之和最短的那个点来,我们只要设L为河(如图1),作AO⊥L交L于O点,延长AO至A',使A'O=AO;连结A'B,交L于C,则C点就是所要求的饮马地点。
再连结AC,则路程(AC+CB)为最短的路程。
为什么饮马地点选在C点能使路程最短?因为A'是A点关于L的对称点,AC与A'C 是相等的。
而A'B是一条线段,所以A'B是连结A'、B这两点间的所有线中,最短的一条,所以AC+CB=A'C+CB=A'B也是最短的一条路了。
这就是运用轴对称变换,找到的一种最巧妙的解题方法。
这一流传近2000年的名题至今还被命题者所喜爱,近年来许多省市中考中出现了以此故事为背景的试题,它们所考查的深度和广度也在不断演变、拓展,而且又常与其他的数学知识相联系,数形结合,突出了数学的思维价值和应用能力,能够有效地体现学生的数学学习能力,现从2009年中考试题中撷取与此相关的试题来分类说明,供广大读者参考。
一、演变成与正方形有关的试题例1(2009年抚顺)如图2所示,正方形ABCD的面积为12,ABE△是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD PE+的和最小,则这个最小值为()A.B.C.3 D分析与解:正方形ABCD是轴对称图形,对角线AC所在直线是它的一条对称轴,相对的两个顶点B、D关于对角线AC对称,在这个问题中D和E是定点,P是动点。
我们可以找到一个定点D的轴对称点B,连结BE,与对角线AC交点处P就是使距离和最小的点(如图3),而使PD+PE的和的最小值恰好等于BE,因为正方形ABCD的面积为12,所以它的边长为23,即PD+PE的最小值为23。
中考数学几何动点运动轨迹及最值专题讲义

2020春中考数学几何动点运动轨迹及最值专题讲义一、动点运动轨迹——直线型(动点轨迹为一条直线,利用“垂线段最短”)Ⅰ.当一个点的坐标以某个字母的代数式表示,若可化为一次函数,则点的轨迹是直线;1.在平面直角坐标系中,点P的坐标为(0,2),点M的坐标为39(1,)44m m−−−(其中m为实数),当PM 的长最小时,m的值为__________.2.如图,在平面直角坐标系中,A(1,4),B(3,2),C(m,-4m+20),若OC恰好平分四边形...OACB....的面积,求点C的坐标.Ⅱ.当某一动点到某条直线的距离不变时,该动点的轨迹为直线;3.如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为_________.【变式1】如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB运动到点B停止.过点E作EF⊥PE交边BC或CD于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为___________.ABDCEFPMABDCEFPMyxBAO【变式2】如图,在矩形ABCD 中,点P 在AD 上,AB =2,AP =1,E 是AB 上的一个动点,连接PE ,过点P 作PE 的垂线,交BC 于点F ,连接EF ,设EF 的中点为G ,当点E 从点B 运动到点A 时,点G 移动的路径的长是_________.【变式3】在矩形ABCD 中,AB =4,AD =6,P 是AD 边的中点,点E 在AB 边上,EP 的延长线交射线CD于F 点,过点P 作PQ ⊥EF ,与射线BC 相交于点Q .(1)如图1,当点Q 在点C 时,试求AE 的长; (2)如图2,点G 为FQ 的中点,连结PG . ①当AE =1时,求PG 的长;②当点E 从点A 运动到点B 时,试直接写出线段PG 扫过的面积. 变式3图14.如图,C 、D 是线段AB 上两点,且AC =BD =16AB =1,点P 是线段CD 上一个动点,在AB 同侧分别作等边△P AE 和等边△PBF ,M 为线段EF 的中点。
动点到两定点的距离最值

浅析动点到两个定点的距离之和(差)的最值一、直线上的动点到直线外两个定点的距离之和(差)的最值.例1(1)已知点A(1,1),点B(3,-2),P是x轴上任意一点,则PA+PB的最小值为,此时点P的坐标为;(2)已知点A(1,1),点B(3,2),P是x轴上任意一点,则PB-PA的最大值为,此时点P的坐标为.解析:(1)如图1,当点P在x轴上运动时,PA+PB AB(当且仅当A,P,B三点共线时等号成立)(PA+PB)min =AB=此时,点P的坐标为(2)如图2,当点P在x轴上运动时,PB- PA AB(当且仅当A,P,B三点共线时等号成立)(PB-PA)max =AB=此时,点P的坐标为变题:(1)已知点A(1,1),点B(3,2),P是x轴上任意一点,则PA+PB的最小值为,此时点P的坐标为;解析:(1)如图3,作点B关于x轴的对称点Bˊ(3,-2),则有PB=PBˊ当点P在x轴上运动时,PA+PB=PA+PBˊ=ABˊ(当且仅当A,P,Bˊ三点共线时等号成立)(PA+PB)min =AB=此时,点P的坐标为(2)已知点A(1,1),点B(3,-2),P是x轴上任意一点,则PB-PA的最大值为,此时点P的坐标为.解析:(2)如图4,作点B关于x轴的对称点Bˊ,则有PB=PBˊ当点P在x轴上运动时,PB- PA= PBˊ-PA ﹦ABˊ(当且仅当A,P,Bˊ三点共线时等号成立)(PB-PA)max =ABˊ=此时,点P的坐标为归纳:①当两定点位于直线的异侧时可求得动点到两定点的距离之和的最小值;②当两定点位于直线的同侧时可求得动点到两定点的距离之和的绝对值的最大值.若不满足①②时,可利用对称性将两定点变换到直线的同(异)侧,再进行求解.如变题的方法.例2函数的值域为.解析:将函数进行化简得:即为动点P(x,0)到两定点A(1,1)、B(3,-2)的距离之和.由例1可知:该值域为二、圆锥曲线上的动点到两个定点的距离之和(差)的最值.(一)直接求解或利用椭圆(或双曲线)的定义进行适当转化后求解.例3(1)已知A(4,0)和B(2,2),M是椭圆上的动点,则MA-MB的范围是;解析:(1)如图5,在MAB中有MA-MB<AB,当M,A,B三点共线且MB>MA即点M位于M2处时,有MA-MB=AB,所以MA-MB AB;同理在MAB中有MB-MA AB,即MB-MA-AB(当点M位于M1处时等号成立)综上所述:-AB≦MA-MB≦AB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动点到两定点的距离
最值
一动点到两定点的距离最值
熊明军
在学习三角形时,我们知道了三角形的三边之间有一个不等关系:“三角形的两边之和大于第三边”;“三角形的两边之差小于第三边”。
借助这个三角不等式,再结合典型例题,我们可以得到一个动点到两个定点距离最值问题的研究方法与相关结论。
一、典型例题的回顾
E、两个村庄,
【例题】已知有一段河岸AB相互平行的一条河,在河岸的一侧有F
如下图。
现在政府为了让两个村庄用上自来水,决定出资在河岸边建一个自来水厂,并在村庄与水厂之间铺设输水管道输水,为了降低成本,就必须使铺设的管道总长度最短,那么自来水厂应该建在河岸的什么位置,用尺规作图在图中标出。
E、是两个固定的点,此题的意思
【解析】假设靠近村庄的河岸为线段AB,村庄F
就是问:在线段AB上有一个动点P,求P在线段AB上移动到什么位置才能使
PE 最短。
PF
结论:
①直线上一动点P到两个定点距离之和最小问题,要根据点对称将两个定点转化到直线的两侧;
②直线上一动点P到两个定点距离之差最大问题,要根据点对称将两个定点转化到直线的同侧。
二、研究问题的理论
A、的距离之和有最小值,当且仅当P在线段
法则一:平面上一动点P到两个定点B
AB之间时取最小值。
法则二:平面上一动点P 到两个定点B A 、的距离之差有最大值,当且仅当P 在线段AB 的延长线上时取最大值。
*注意①:一动点P 到两定点B A 、距离最值的取得都是使动点与定点转化到一条直线上;如若不在一条直线上,就必须借助题中的条件与相关结论转化之。
*注意②:平面上一动点P 到两个定点B A 、的距离之和有最小值;距离之差有最大值。
如若出现动点P 到两个定点B A 、的距离之和有最大值;距离之差有最小值,就必须使之转化为法则中的情况,即:距离之和⇔最小值;距离之差⇔最大值。
【证明】(法则一)已知平面上两个动点B A 、,P 是平面上任意一个动点,如下图:
①当动点P 与定点B A 、不共线时,根据三角形三边关系“两边之和大于第三边”可知AB PB PA >+; ②当动点P 与定点B A 、共线,且在线段AB 的延长线上时,显然有AB PB PA >+;
③当动点P 与定点B A 、共线,且在线段AB 之间时,显然有AB PB PA =+; 综上所述,AB PB PA ≥+,当且仅当动点P 在线段AB 之间时取最小值AB 。
【证明】(法则二)已知平面上两个动点B A 、,P 是平面上任意一个动点,如下图:
①当动点P 与定点B A 、不共线时,根据三角形三边关系“两边之差小于第三边”可知AB PB PA <-;
②当动点P 与定点B A 、共线,且在线段AB 之间时,显然有AB PB PA <-; ③当动点P 与定点B A 、共线,且在线段AB 的延长线上时,显然有
AB PB PA =-;
综上所述,AB PB PA ≤-,当且仅当动点P 在线段AB 的延长线上时取最大值AB 。
三、典型例题的讲解
①动点在直线上
【例一】已知点()()()2,32,11,1C B A ,,-,点P 是直线x y l =:上的动点,求PB PA +的最小值及PC PA -的最大值。
【解析】在平面直角坐标系中做出题中所给的直线图象与相应的点,如上右图所示: ①如右图可知()()2,11,1B A ,-在直线l 同侧,要取PB PA +的最小值,根据法则一可知,必须使动点P 在线段AB 之间,显然这是不可能的。
所以必须把两定点B A 、中的一个对称到直线另一侧(本题解法采用作B 的对称点得'B ),连结'AB ,这样就很好的满足了法则一:只要动点P 在线段'AB 之间就有最小值。
因此,如左图所示,直线上的点P 就是使PB PA +有最小值的点,计算得()3''min ==+=+AB PB PA PB PA 。
②如右图可知()()2,31,1C A ,-在直线l 两侧,要取PC PA -的最大值,根据法则二可知,必须使动点P 在线段AC 的延长线上,显然这是不可能的。
所以必须把两定点
C A 、中的一个对称到直线另一侧(本题解法采用作C 的对称点得'C ),连结'AC ,这样就很好的满足了法则二:只要动点P 在线段'AC 的延长线上就有最大值。
即如左图所示直线上的点'P 就是使PC PA -有最大值的点,计算得
()13''max ==-=-AC PC PA PC PA 。
②动点在圆上
【例二】已知点()1,1-A 和圆07014102
2=+--+y x y x C :,一束光线从点A 发出,经过x 轴反射到圆C 的圆周上,求光线从A 点发出到圆周上走过的最短路程。
【解析】在平面直角坐标系中做出题中所给圆的图象与相应的点,如上右图所示。
本题看似有两个动点,P 与'P ,但是由于圆的特殊性,到圆周上的点距离可以转化为到圆心的距离,如此,本题题意就是在直线0=y 的同侧有两个定点O A 、,找该直线上一动点P ,使PO PA +有最小值。
()1,1-A Θ,圆()()()2,7,54752
2=⇒=-+-r O y x O :,作点A 关于直线0=y 的对称点得()1,1'--A ,利用法则一,可得PO PA +的最小值为点P 在线段'OA 之间时取得;
∴()10''min ==+=+OA PO PA PO PA ;
∴光线从A 点发出到圆周上走过的最短路程为821010=-=-r 。
③动点在圆锥曲线上
【例三】(动点在椭圆上)设21F F ,分别是椭圆116252
2=+y x 的左、右焦点,P 是椭圆上任一动点,已知点()4,6M ,求1PF PM +的最大值。
【解析】显然1F M 、为两定点,P 为动点,由法则一可知1PF PM +只能求最小值,没有最大值;但题中偏偏让我们求最大值,这就意味着我们得利用题中的条件把1PF PM +转化为动点P 到两定点的差的形式,这样方能求解。
(
)2121211010102PF PM PF PM PF PF a PF PF -+=+⇒-=⇒==+Θ ∴利用椭圆的定义把求1PF PM +的最大值转化成了求2PF PM -的最大值,利用法则二可知,当动点P 在线段2MF 延长线上时,如上右图所示,2PF PM -有最大值。
即
()()1551010''101022max 2max 1=+=+=-+=-+=+MF F P M P PF PM PF PM 。
【例四】(动点在双曲线上)设21F F ,分别是双曲线116922=-y x 的左、右焦点,P 是双曲线右支上任一动点,已知点()4,2M ,求1PF PM -的最小值。
【解析】显然1F M 、为两定点,P 为动点,由法则二可知1PF PM -没有最小值;但题中让我们求最小值,同例三,只要利用条件把1PF PM -转化为动点P 到两定点的和的形式就能求解。
()2121216662PF PM PF PM PF PF a PF PF ++=+⇒+=⇒==-Θ ∴利用双曲线的定义把求1PF PM -的最小值转化成了求2PF PM +的最小值,利用法则二可知,当动点P 在线段2MF 上时,如上右图所示,2PF PM +有最小值。
即 ()
()11
566''6622min 2min 1=+=+=++=++=-MF F P M P PF PM PF PM 。
【例五】(动点在抛物线上)设F 是抛物线的焦点,P 是抛物线x y 42=上的任一动
点,已知点()1,2M ,求PF PM +的最小值。
【解析】F M 、为两定点,P 为动点,由法则一可知点P 若能在线段MF 之间,可立即得到PF PM +的最小值,在平面直角坐标中做出抛物线及相应的点,如上左图所示。
在抛物线中,由定义可得动点到焦点的距离等于动点到准线的距离,即
()l P d PF ,=,所以()l P d PM PF PM ,+=+。
显然,当动点P 运动到如上右图所示的位置时,点P 在线段()l P d ,之间,即
()()()3,,''min ==+=+l M d l P d M P PF PM 。
【练习】已知P 为抛物线x y 42=上任一动点,Q 为圆()1422=-+y x 上任一动点,
求点P 到点Q 的距离与点P 到抛物线准线的距离之和的最小值。
简单中蕴含着复杂,复杂中蕴含着简单,数学并不孤傲,是我们思考和解决问题的强有力的工具。
