19年10月稼轩初级中学初三上学期月考数学
2019~2020学年12月山东济南历城区济南稼轩初级中学初三上学期月考数学试卷
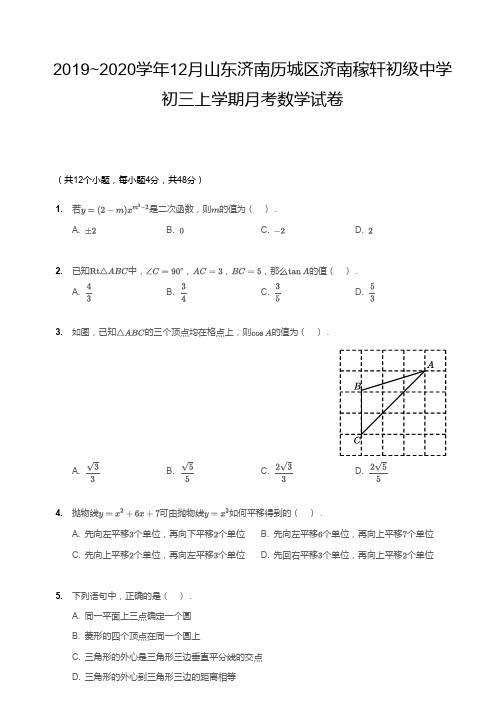
与抛物线交于 , 两点( 在 的左
侧),当以点 , 和( )中第二象限的点 为顶点的三角形是直角三角形时,求 的
值.
/
单位长度为半径作⊙ ,当⊙ 与直线 相切时,点 的坐标是
.
18. 已知函数 点,则 的取值范围为
的图象如图所示,若直线 .
与该图象恰有三个不同的交
三、解答题
(共7个题,共78分) 19. 计算:
/
(1) (2)
20. 如图,在
中,
为线段 上一点,且
. .
,以 为直径的半圆交 于点 , 是该半圆所在圆的圆心, .
的图象经过
、
、
,则 、 、 的大小关系是( ).
A.
B.
C.
、
、
D.
10. 如图,一个扇形纸片的圆心角为 ,半径为 ,将这张扇形纸片折叠,使点 与点 恰好重合, 折痕为 ,图中阴影为重合部分,则阴影部分的面积为( ).
/
A.
B.
C.
D.
11. 如图,二次函数
①
;②
;④若方程
确的有( ).
的图象过点
,对称轴为直线
;③若
,
是抛物线上的两点,当
的两根为 , ,且
,则
,有以下结论: 时,
,其中结论正
y
x
O
A. 个
B. 个
C. 个
D. 个
12. 如图,在
中,
,
,
,点 是 的三等分点,半圆 与 相
切, , 分别是 与半圆弧上的动点,则 的最小值和最大值之和是( ).
A.
B.
C.
D.
二、填空题
(共6个小题,每小题4分,共24分)
陕西省2019年九年级上学期10月月考数学试题C卷

陕西省2019年九年级上学期10月月考数学试题C卷姓名:________ 班级:________ 成绩:________一、单选题1 . 若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2016﹣a﹣b的值是()A.2018B.2011C.2014D.20212 . 在下列方程中,一元二次方程的个数是()①3x2+7=0;②ax2+bx+c=0;③(x﹣2)(x+5)=x2﹣1;④3x2﹣=0.A.1个B.2个C.3个D.4个3 . 如图,矩形ABCD为⊙O的内接四边形,AB=2,BC=3,点E为BC上一点,且BE=1,延长AE交⊙O于点F,则线段AF的长为()A.B.5C.+1D.4 . 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E、F,若CE=1,则BF的长为()A.B.C.D.5 . 如图,菱形ABCD中,∠A=60°,AB=6,⊙A,⊙B的半径分别为4和2,P,E,F分别是线段CD,⊙A,⊙B上的动点,则PE+PF的最大值为()A.B.C.D.66 . 下列说法正确的是()A.垂直于弦的直线平分弦所对的两条弧B.平分弦的直径垂直于弦C.垂直于直径平分这条直径D.弦的垂直平分线经过圆心二、填空题7 . 关于x的一元二次方程kx2﹣4x﹣1=0有两个实根,则k的取值范围是_____.8 . 如图,把一个圆分成三个扇形,则圆心角∠AOB=______度.9 . 在中,,,在外有一点,且,则的度数是__________.10 . 若,是方程的两个实数根,则______.11 . 如图,在平面直角坐标系xOy中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ取最小值时,Q点的坐标为_____.12 . 当________时,方程是一元二次方程.13 . 如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点A.则图中阴影部分的面积为__.14 . 已知的半径为,圆心到直线的距离为,则直线与的位置关系是________.15 . 如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连结CD,若AD=3,AC=2,则cosB的值为________.16 . 如图,点A、B在半径为3的⊙O上,以OA、AB为邻边作平行四边形OCBA,作点B关于OA的对称点D,连接CD,则CD的最大值为________.三、解答题17 . 若是一元二次方程的根,,,试比较A、B的大小。
济南市稼轩中学九年级上册压轴题数学模拟试卷含详细答案

济南市稼轩中学九年级上册压轴题数学模拟试卷含详细答案一、压轴题1.⊙O 是四边形ABCD 的外接圆,OB AC ⊥,OB 与AC 相交于点H ,21012BC AC CD ===,.(1)求⊙O 的半径; (2)求AD 的长;(3)若E 为弦CD 上的一个动点,过点E 作EF//AC ,EG//AD . EF 与AD 相交于点F ,EG 与AC 相交于点G .试问四边形AGEF 的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由. 2.如图,抛物线214y x bx c =-++经过点()6,0C ,顶点为B ,对称轴2x =与x 轴相交于点A ,D 为线段BC 的中点.(1)求抛物线的解析式;(2)P 为线段BC 上任意一点,M 为x 轴上一动点,连接MP ,以点M 为中心,将MPC 逆时针旋转90︒,记点P 的对应点为E ,点C 的对应点为F .当直线EF 与抛物线214y x bx c =-++只有一个交点时,求点M 的坐标. (3)MPC 在(2)的旋转变换下,若2PC =①求证:EA ED =.②当点E 在(1)所求的抛物线上时,求线段CM 的长. 3.如图,在平面直角坐标系中,抛物线21322y x bx =-++与x 轴正半轴交于点A ,且点A 的坐标为()3,0,过点A 作垂直于x 轴的直线l .P 是该抛物线上的任意一点,其横坐标为m ,过点P 作PQ l ⊥于点Q ;M 是直线l 上的一点,其纵坐标为32m -+,以PQ ,QM 为边作矩形PQMN .(1)求b 的值.(2)当点Q 与点M 重合时,求m 的值.(3)当矩形PQMN 是正方形,且抛物线的顶点在该正方形内部时,求m 的值. (4)当抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小时,直接写出m 的取值范围.4.已知抛物线2y ax bx c =++经过原点,与x 轴相交于点F ,直线132y x =+与抛物线交于()()2266A B -,,,两点,与x 轴交于点C ,与y 轴交于点D ,点E 是线段OC 上的一个动点(不与端点重合),过点E 作//EG BC 交BF 于点C ,连接DE DG ,.(1)求抛物线的解析式及点F 的坐标; (2)当DEG ∆的面积最大时,求线段EF 的长;(3)在(2)的条件下,若在抛物线上有一点()4H n ,和点P ,使EHP ∆为直角三角形,请直接写出点P 的坐标.5.在平面直角坐标系中,O 是坐标原点,抛物线2115:L y x bx a a=+-的顶点D 在第四象限,且经过(1,)A m n +,(1,)(0,0)B m n m n ->>两点直线AB 与y 轴交于点C ,与抛物线的1L 对称轴交于点E ,8AC BC ⋅=,点E 的纵坐标为1. (1)求抛物线1L 所对应的函数表达式;(2)若将直线AB 绕着点E 旋转,直线AB 与抛物线1L 有一个交点Q 在第三象限,另一个交点记为P ,抛物线2L 与抛物线1L 关于点P 成中心对称,抛物线2L 的顶点记为1D . ①若点Q 的横坐标为-1,抛物线1L 与抛物线2L 所对应的两个函数y 的值都随着x 的增大而增大,求相应的x 的取值范围;②若直线PQ 与抛物线2L 的另一个交点记为Q ,连接1PD ,11Q D ,试间:在旋转的过程中,1PDQ ∠的度数会不会发生变化?请说明理由. 6.如图1,在平面直角坐标系中,抛物线212y x bx c =-++与x 轴交于A ,B 两点,A 点坐标为(2,0)-,与y 轴交于点(0,4)C ,直线12y x m =-+与抛物线交于B ,D 两点.(1)求抛物线的函数表达式; (2)求m 的值和D 点坐标;(3)点P 是直线BD 上方抛物线上的动点,过点P 作x 轴的垂线,垂足为H ,交直线BD 于点F ,过点D 作x 轴的平行线,交PH 于点N ,当N 是线段PF 的三等分点时,求P 点坐标;(4)如图2,Q 是x 轴上一点,其坐标为4,05⎛⎫-⎪⎝⎭,动点M 从A 出发,沿x 轴正方向以每秒5个单位的速度运动,设M 的运动时间为t (0t >),连接AD ,过M 作MG AD ⊥于点G ,以MG 所在直线为对称轴,线段AQ 经轴对称变换后的图形为A Q '',点M 在运动过程中,线段A Q ''的位置也随之变化,请直接写出运动过程中线段A Q ''与抛物线有公共点时t 的取值范围.7.如图1,在Rt ABC △中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是_________,位置关系是_________;(2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4=AD ,10AB =,请直接写出PMN 面积的最大值.8.如图1,抛物线24y ax bx =+-与x 轴交于(3,0)A -、(4,0)B 两点,与y 轴交于点C ,作直线BC .点D 是线段BC 上的一个动点(不与B ,C 重合),过点D 作DE x⊥轴于点E .设点D 的横坐标为(04)m m <<.(1)求抛物线的表达式及点C 的坐标; (2)线段DE 的长用含m 的式子表示为 ;(3)以DE 为边作矩形DEFC ,使点F 在x 轴负半轴上、点G 在第三象限的抛物线上. ①如图2,当矩形DEFC 成为正方形时,求m 的值;②如图3,当点O 恰好是线段EF 的中点时,连接FD ,FC .试探究坐标平面内是否存在一点P ,使以P ,C ,F 为顶点的三角形与FCD ∆全等?若存在,直接写出点P 的坐标;若不存在,说明理由.9.已知抛物线2y ax bx c =++与x 轴交于点(1,0)A -,点(3,0)B ,与y 轴交于点(0,3)C ,顶点为点D .(1)求抛物线的解析式;(2)若过点C 的直线交线段AB 于点E ,且:3:5ACECEBS S=,求直线CE 的解析式(3)若点P 在抛物线上,点Q 在x 轴上,当以点D 、C 、P 、Q 为顶点的四边形是平行四边形时,求点P 的坐标; (4)已知点450,,(2,0)8H G ⎛⎫⎪⎝⎭,在抛物线对称轴上找一点F ,使HF AF +的值最小此时,在抛物线上是否存在一点K ,使KF KG +的值最小,若存在,求出点K 的坐标;若不存在,请说明理由.10.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ; (2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.11.新定义:在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的长方形的周长与面积相等,则这个点叫做“和谐点”.例如,如图①,过点P 分别作x 轴、y 轴的垂线,与坐标轴围成长方形OAPB 的周长与面积相等,则点P 是“和谐点”.(1)点M (1,2)_____“和谐点”(填“是”或“不是”);若点P (a ,3)是第一象限内的一个“和谐点”,3x ay =⎧⎨=⎩是关于x ,y 的二元一次方程y x b =-+的解,求a ,b 的值.(2)如图②,点E 是线段PB 上一点,连接OE 并延长交AP 的延长线于点Q ,若点P (2,3),2OBE EPQ S S ∆∆-=,求点Q 的坐标;(3)如图③,连接OP ,将线段OP 向右平移3个单位长度,再向下平移1个单位长度,得到线段11O P .若M 是直线11O P 上的一动点,连接PM 、OM ,请画出图形并写出OMP ∠与1MPP ∠,1MOO ∠的数量关系.12.如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于点,的解析式为,若将抛物线平移,使平移后的抛物线经过点, 对称轴为直线,抛物线与轴的另一个交点是,顶点是,连结.(1)求抛物线的解析式;(2)求证:∽(3)半径为的⊙的圆心沿着直线从点运动到,运动速度为1单位/秒,运动时间为秒,⊙绕着点顺时针旋转得⊙,随着⊙的运动,求的运动路径长以及当⊙与轴相切的时候的值.13.在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.①依题意将图2补全;②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……请你参考上面的想法,帮助小宇证明∠APE=2∠MAD.(一种方法即可)14.如图,正方形ABCD中,对角线AC、BD交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BO于H.连接OG、CG.(1)求证:AH=BE ;(2)试探究:∠AGO 的度数是否为定值?请说明理由; (3)若OG ⊥CG ,BG=32,求△OGC 的面积.15.在直角坐标平面内,O 为原点,点A 的坐标为(10),,点C 的坐标为(0)4,,直线CM x ∥轴(如图所示).点B 与点A 关于原点对称,直线y x b =+(b 为常数)经过点B ,且与直线CM 相交于点D ,联结OD . (1)求b 的值和点D 的坐标;(2)设点P 在x 轴的正半轴上,若POD 是等腰三角形,求点P 的坐标;16.如图,Rt △ABC 中,∠C =90°,AB =15,BC =9,点P ,Q 分别在BC ,AC 上,CP =3x ,CQ =4x (0<x <3).把△PCQ 绕点P 旋转,得到△PDE ,点D 落在线段PQ 上. (1)求证:PQ ∥AB ;(2)若点D 在∠BAC 的平分线上,求CP 的长;(3)若△PDE 与△ABC 重叠部分图形的周长为T ,且12≤T ≤16,求x 的取值范围.17.如图,在平面直角坐标系xOy 中,过⊙T 外一点P 引它的两条切线,切点分别为M ,N ,若60180MPN ︒︒≤∠<,则称P 为⊙T 的环绕点.(1)当⊙O 半径为1时,①在123(1,0),(1,1),(0,2)P P P 中,⊙O 的环绕点是___________;②直线y =2x +b 与x 轴交于点A ,y 轴交于点B ,若线段AB 上存在⊙O 的环绕点,求b 的取值范围;(2)⊙T 的半径为1,圆心为(0,t ),以3,(0)3m m m ⎛⎫> ⎪ ⎪⎝⎭为圆心,33m 为半径的所有圆构成图形H ,若在图形H 上存在⊙T 的环绕点,直接写出t 的取值范围. 18.如图,在平面直角坐标系xOy 中,直线y =12x+2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx+c 的对称轴是x =32-且经过A 、C 两点,与x 轴的另一交点为点B . (1)求抛物线解析式.(2)若点P 为直线AC 上方的抛物线上的一点,连接PA ,PC .求△PAC 的面积的最大值,并求出此时点P 的坐标.(3)抛物线上是否存在点M ,过点M 作MN 垂直x 轴于点N ,使得以点A 、M 、N 为顶点的三角形与△ABC 相似?若存在,求出点M 的坐标;若不存在,请说明理由.19.如图,在矩形ABCD 中,已知AB=4,BC=2,E 为AB 的中点,设点P 是∠DAB 平分线上的一个动点(不与点A 重合). (1)证明:PD=PE .(2)连接PC ,求PC 的最小值.(3)设点O 是矩形ABCD 的对称中心,是否存在点P ,使∠DPO=90°?若存在,请直接写出AP 的长.20.直线m∥n,点A、B分别在直线m,n上(点A在点B的右侧),点P在直线m上,AP=13AB,连接BP,将线段BP绕点B顺时针旋转60°得到BC,连接AC交直线n于点E,连接PC,且ABE为等边三角形.(1)如图①,当点P在A的右侧时,请直接写出∠ABP与∠EBC的数量关系是,AP 与EC的数量关系是.(2)如图②,当点P在A的左侧时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.(3)如图②,当点P在A的左侧时,若△PBC的面积为934,求线段AC的长.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)⊙O的半径为10,(2)AD长为19.2,(3)存在,四边形AGEF的面积的最大值为34.56.【解析】【分析】(1)如图1利用垂径定理构造直角三角形解决问题.(2)如图2在(1)基础上利用圆周角和圆心角的关系证明△OCH∽△DCK,求出Dk,再据垂径定理求得AD.(3)如图3以平行四边形AGEF的面积为函数,以AG边上的高为自变量,列出一个二次函数,利用二次函数的最值求解.【详解】(1)如图1连接OC ,因为OB AC ⊥,根据垂径定理知 HC=1112622AC =⨯= 在RT △BCH 中 ∵210BC = ∴由勾股定理知:2222BH (210)62BC HC =-=-=∴OH=OB-BH=OB-2 又∵OB=OC所以在RT △OCH 中,由勾股定理可得方程:2222)6OC OC -+=( 解得OC=10.(2)如图2,在⊙O 中:∵AC=CD ,∴OC ⊥AD (垂径定理) ∴AD=2KD ,∠HCK=∠DCK 又∵∠DKC=∠OHC=90° ∴△OCH ∽△DCK ∴KD DC HO OC= ∴DC 1248KD=8105HO OC =⨯==9.6 ∴AD=2KD=19.2.本题与⊙O 无关,但要运用前面数据.作FM ⊥AC 于M ,作DN ⊥AC 于N ,显然四边形AGEF 为平行四边形,设平行四边形AGEF 的面积为y 、EM=x 、DN=a (a 为常量), 先运用(2)的△OCH ∽△DCK ,得CK=7.2. 易得△DFE ∽△DAC , ∴DN-EM EFDN AC =(相似三角形对应高之比等于相似比) ∴DN EMAG=EF=AC DN- ∴AG=12()aa x - ∴平行四边形AGEF 的面积y=212()1212a x x x x a a -=-+(0<x <a ) 由二次函数知识得,当x=12a1222a-=-⨯时,y 有最大值. 把x=2a 代入到中得,12EF AC = ∴此时EF 、EG 、FG 恰是△ADC 的中位线 ∴四边形AGEF 的面积y 最大=111S 34.56222ADC AD CK ∆=⨯⨯=. 【点睛】本题主要考查与圆有关线段的计算、与二次函数有关的几何最值问题.(1)的关键是利用垂径定理构造直角三角形,最后用勾股定理进行计算.(2)的关键是运用与圆有的角的性质证明相似,再进行计算.(3)难点是分清图形的变与不变,选择恰当的变量并列出函数关系式.2.(1)2134y x x =-++;(2)(32,0);(3)①见解析;②CM =231或CM =123+【解析】(1)根据点C 在抛物线上和已知对称轴的条件可求出解析式;(2)根据抛物线的解析式求出点B 及已知点C 的坐标,证明△ABC 是等腰直角三角形,根据旋转的性质推出直线EF 与x 轴的夹角为45°,因此设直线EF 的解析式为y=x+b ,设点M 的坐标为(m ,0),推出点F (m ,6-m ),直线EF 与抛物线2134y x x =-++只有一个交点,联立两个解析式,得到关于x 的一元二次方程,根据根的判别式为0得到关于m 的方程,解方程得点M 的坐标.注意有两种情况,均需讨论.(3)①过点P 作PG ⊥x 轴于点G ,过点E 作EH ⊥x 轴于点H ,设点M 的坐标为(m ,0),由2PC =及旋转的性质,证明△EHM ≌△MGP ,得到点E 的坐标为(m-1,5-m ),再根据两点距离公式证明EA ED =,注意分两种情况,均需讨论;②把E (m-1,5-m )代入抛物线解析式,解出m 的值,进而求出CM 的长. 【详解】 (1)∵点()6,0C在抛物线上,∴103664b c =-⨯++,得到6=9b c +, 又∵对称轴2x =, ∴2122()4b b x a =-=-=⨯-, 解得1b =, ∴3c =,∴二次函数的解析式为2134y x x =-++;(2)当点M 在点C 的左侧时,如下图:∵抛物线的解析式为2134y x x =-++,对称轴为2x =,()6,0C∴点A (2,0),顶点B (2,4), ∴AB=AC=4,∴△ABC 是等腰直角三角形,∴∠1=45°;∵将MPC 逆时针旋转90︒得到△MEF , ∴FM=CM ,∠2=∠1=45°, 设点M 的坐标为(m ,0), ∴点F (m ,6-m ), 又∵∠2=45°,∴直线EF 与x 轴的夹角为45°, ∴设直线EF 的解析式为y=x+b ,把点F (m ,6-m )代入得:6-m=m+b ,解得:b=6-2m , 直线EF 的解析式为y=x+6-2m ,∵直线EF 与抛物线2134y x x =-++只有一个交点,∴262134y x m y x x =+-⎧⎪⎨=-++⎪⎩, 整理得:213204x m +-=,∴Δ=b 2-4ac=0,解得m=32, 点M 的坐标为(32,0). 当点M 在点C 的右侧时,如下图:由图可知,直线EF 与x 轴的夹角仍是45°,因此直线EF 与抛物线2134y x x =-++不可能只有一个交点. 综上,点M 的坐标为(32,0). (3)①当点M 在点C 的左侧时,如下图,过点P 作PG ⊥x 轴于点G ,过点E 作EH ⊥x 轴于点H ,∵2PC 2)知∠BCA=45°, ∴PG=GC=1, ∴点G (5,0),设点M 的坐标为(m ,0),∵将MPC 逆时针旋转90︒得到△MEF , ∴EM=PM ,∵∠HEM+∠EMH=∠GMP+∠EMH =90°, ∴∠HEM=∠GMP , 在△EHM 和△MGP 中,EHM MGP HEM GMP EM MP ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△EHM ≌△MGP (AAS ), ∴EH=MG=5-m ,HM=PG=1, ∴点H (m-1,0),∴点E 的坐标为(m-1,5-m );∴22(12)(50)m m --+--221634m m -+ 又∵D 为线段BC 的中点,B (2,4),C (6,0), ∴点D (4,2),∴22(14)(52)m m --+--221634m m -+ ∴EA= ED .当点M 在点C 的右侧时,如下图:同理,点E 的坐标仍为(m-1,5-m ),因此EA= ED . ②当点E 在(1)所求的抛物线2134y x x =-++上时,把E (m-1,5-m )代入,整理得:m 2-10m+13=0, 解得:m=523+m=523-, ∴CM =231或CM =123+. 【点睛】本题是二次函数综合题,熟练掌握二次函数的图象和性质、旋转的性质、分类讨论的思想是解题的关键. 3.(1)1b =;(2)120,4m m ;(3)71m =-;(4)03m <<或4m >.【解析】 【分析】(1)将A 点坐标代入函数解析式即可求得b 的值;(2)分别表示出P 、Q 、M 的坐标,根据Q 、M 的横坐标相同,它们重合时纵坐标也相同,列出方程求解即可;(3)分别表示出PQ 和MQ 的长度,根据矩形PQMN 是正方形时PQ MQ =,即可求得m 的值,再根据顶点在正方形内部,排除不符合条件的m 的值;(4)分1m ,13m <<,3m =,3m >四种情况讨论,结合图形分析即可. 【详解】解:(1)将点()3,0A 代入21322y x bx =-++ 得21303322b =-⨯++, 解得b=1,;(2)由(1)可得函数的解析式为21322y x x =-++, ∴213,22P m m m ⎛⎫-++ ⎪⎝⎭,∵PQ l ⊥于点Q , ∴233,122m m Q ⎛⎫ ⎪⎝-+⎭+, ∵M 是直线l 上的一点,其纵坐标为32m -+,∴3(3,)2m M -+, 若点Q 与点M 重合,则2133222m m m -++=-+, 解得120,4m m ;(3)由(2)可得|3|PQm ,223131)2222|(()||2|MQ m m mm m,当矩形PQMN 是正方形时,PQ MQ = 即212|2||3|m m m , 即22123m m m 或22123mm m ,解22123m m m 得1271,71m m , 解22123mm m 得3233,33m m ,又2131(1)2222y x x x =-++=--+, ∴抛物线的顶点为(1,2), ∵抛物线的顶点在该正方形内部,∴P 点在抛物线对称轴左侧,即1m <,且M 点的纵坐标大于抛物线顶点的纵坐标,即322m,解得12m <-,故m 的值为71;(4)①如下图当1m 时,若抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小, 则M 点的纵坐标应该小于P 点纵坐标,且P 点应该在x 轴上侧, 即2313222m m m 且213022m m -++>, 解2313222m m m得04m <<, 解213022m m -++>得13m -<<, ∴01m <≤,②如下图当13m <<时,若抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小, 则M 点的纵坐标应该小于P 点纵坐标, 即2313222mm m,解得04m <<, ∴13m <<;③当3m =时,P 点和M 点都在直线x=3上不构成矩形,不符合题意; ④如下图当3m >时,若抛物线在矩形PQMN 内的部分所对应的函数值y 随x 的增大而减小, 则M 点的纵坐标应该大于P 点纵坐标, 即2313222mm m,解得0m <或4m >, 故4m >,综上所述03m <<或4m >. 【点睛】本题考查二次函数综合,正方形的性质定理,求二次函数解析式.能分别表示出M 、P 、Q 的坐标并结合图形分析是解决此题的关键,注意分类讨论. 4.(1)抛物线的解析式为21142y x x =-,点F 的坐标为()20,;(2)4EF =;(3)点P 的坐标为()()()466121456---,,,,,或()22.-, 【解析】 【分析】(1)因为抛物线经过原点,A,B 点,利用待定系数法求得抛物物线的解析式,再令y=0,求得与x 轴的交点F 点的坐标。
2022-2023学年山东省济南市历城区稼轩中学九年级第一学期月考数学试卷

2022-2023学年济南市历城区稼轩中学九年级(上)月考数学试卷一、选择题(每题4分)1.如图是一根空心方管,它的俯视图是( )A .B .C .D .2.已知在Rt △ABC 中,∠C =90°,AB =5,BC =3,则cos B 的值是( ) A .35B .45C .34D .433.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( ) A .15个B .20个C .30个D .35个4.若关于x 的一元二次方程2304kx -=有实数根,则实数k 的取值范围是( ) A .k =0B .13k -≥且k ≠0C .13k -≥D .13k >-5.若()13,A y -,21,2B y ⎛⎫ ⎪⎝⎭,()32,C y 在二次函数22y x x c =++的图象上,则1y ,2y ,3y 的大小关系是( ) A .213y y y <<B .132y y y <<C .123y y y <<D .321y y y <<6.如图,AB 是⊙O 的直径,点D 在⊙O 上,若∠AOC =120°,则∠D 的度数是( )A .20°B .30°C .40°D .45°7.如图,点D (0,3),O (0,0),C (4,0)在⊙A 上,BD 是⊙A 的一条弦,则sin OBD ∠=( )A .12B .34C .45D .358.如图,当ab >0时,函数2y ax =与函数y bx a =+的图象大致是( )A .B .C .D .9.如图,在平面直角坐标系中,在△OAB 中,点A 在x 轴上,OA =OB =6,函数ky x=(k >0,x >0)的图象经过点B 与AB 边的中点D ,则k 的值为( )A .24B .C .36D .10.已知函数245y x ax =-+(a 为常数),当x ≥4时,y 随x 的增大而增大,()11,P x y ,()22,Q x y 是该函数图象上的两点,对任意的1215a x -≤≤和2215a x -≤≤,1y ,2y 总满足21254y y a -+≤,则实数a 的取值范围是( ) A .-1≤a ≤2B .2≤a ≤3C .1≤a ≤2D .2≤a ≤4二、填空题(每题4分)11.如图,在△ABC 中,DE ∥BC ,AD =2,BD =3,AC =10,则AE 的长为 .12.将抛物线25y x =先向右平移2个单位,再向上平移3个单位后,得到新抛物线的表达式是 。
中学初三年级第一次月考数学试题

2 中学初三年级第一次月考数学试题一、选择题(3×8=24)1、下列函数中,y 是x 的反比例函数的有( ) (1)y =-πχ (2)xy =2 (3)y =2x 2 (4)y = x1 (5)y =x 12+ (6)y =11+x (7)y =x 21- (8)y =21-x A.1个 B.2个 C.3个 D.4个 2、已知反比例函数y =xk 2-的图像位于第一、三象限,则k 的取值范围是( )A.k >2B.k ≥2C.k ≤2D.k <23、若点A (1,1y )B (2,2y )都是反从例函数y=xk (k >0)的图象上,则1y与2y 的大小关系是( )A.1y <2y B.1y ≤2y C.1y >2y D.1y ≥2y4、正比例函数y =x 6的图象与反比例函数y =x6的图像的交点位于( ) A.第一象限 B.第二象限 C.第二、四象限 D.第一、三象限 5、下列方程中,一元二次方程有( )① x x =5 ①(x -3)2-6=0 ①x 2 =1 ①7x (x -2)=7x 2 ①ax 2+bx +c=0 A.1个 B.2个 C.3个 D.4个 6、一元二次方程x 2-2x -4=0的根的情况是( ) A.有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根 D.没有实数根7、若一元二次方程2x (kx -4)-x 2-6=0有实数根,则k 的最小整数值是( )A.-1B.0C.1D.28、若关于x 的一元二次方程x 2+kx +4k 2-3=0的两个实数根分别是1x .2x ,且满足1x +2x =1x .2x ,则k 的值为( )A.-1或43B.-1C.43 D.不存在 二、填空题(3×6=18)9、如图,已知A 点是反比例函数y =xk (k ≠0)的图像上一点,AB①y 轴于B ,①ABO 的面积为5,则k 的值为 。
10、已知反比例函数y =x6在第一象限的图像,如图所示,点A 在其图象上,点B 在x 轴的正半轴上,连结A0、AB,且AO=AB,则①AOB 的面积= 11、若y =x 2与双曲线y =xk的一个交点是(36),则另一个交点是 12、若关于x 的一元二次方程kx 2+3x +1=0有两不相等的实数根,则k 的取值范围是13、关于x 的一元二次方程(m -2)x 2+2x +m 2+m -6=0有一个实数根为0,则m 的值是14、已知一个三角形的两边长分别是3cm 和7cm ,第三边长为acm ,且满足a 2-10a+21=0,则此三角形的周长为 。
2019-九年级数学上学期第一次月考试题华东师大版

2019-2020年九年级数学上学期第一次月考试题华东师大版一、选择题:(每题3分,共 30分) 1 、式子:①a ;②;③1 x ;④x 2 ;⑤x ;⑥5 x 2 1 ;⑦ a 2 2⑧ 3b 2 中是二次根式的代号为()A 、①②④⑥ B、②④⑧C 、②③⑦⑧D、①②⑦⑧2 、计算:18 ÷3 × 4的结果是()43A 、 0 B、 4 2C、 22 D、 323 、以下说法中,正确的选项是()A、假如ab cd ,那么 acB、ababbdbdC、方程 x 2x 20的根是 x 1 1, x 2 2D 、 (x1)2 x 14、若分式方程6m 1 有增根, 则它的增根是()( x 1)(x1)x 1A 、 0B 、 1C、- 1 D 、± 15 一元二次方程k2 x 23xk 2 4 0 有一个解为 0,则 k 的值( )A、±2B、2C、- 2D、随意实 数6、已 知 210 ,21 0 ,且,的值为()A 、2 B、 -2 C、-1 D、07 、若方程 x 24 xa 0 无实数根,则化简16 - 8a a 2 等于()A 、 4-aB 、 a-4C 、 -a-4D 、没法确立8 、若正比率函数 y=(a-1)x的图像过第一、 三象限, 化简 (1 a)2 的结果是()A 、 a-1B、1-aC、( a-1) 2D 、- ( 1-a) 29、某工厂改良工艺降低了某种产品的成本,两个月内从每件产品 250元,降低到了每件 160元,设均匀每个月的降低率为 x , 则可列方程( )A 、250( 1-x ) =160B 、250( 1-x ) 2=160C 、250( 1-x 2) =160D 、250( 1-2x )=160 10 、已知三个对于 y 的方程: y 2y a0 , (a 1) y 22y1 0 和 (a2) y 22y 1 0 ,若 此中起码有两个方程有实根,则实数a 的取值范围是( )A 、 a 2B 、 a1或 1 x 2C 、 a 1 D、1a 144二、填空题:( 每题3 分,共 18 分)11、若a 3 3 a 存心义,则 a =。
武汉市2019届10月九年级上月考数学试卷含答案解析.docx

武汉市 2019 届 10 月九年级上月考数学试卷含答案解析一、选择题(本大题共10 小题,每小题 3 分,共 30分)1.方程 4x2﹣ x+2=3 中二次项系数、一次项系数、常数项分别是()A. 4、﹣ 1、﹣ 1B. 4、﹣ 1、 2 C. 4、﹣ 1、3D. 4、﹣ 1、52.方程 x( x﹣ 1) =2 的解是()A. x=﹣ 1B. x=﹣ 2C. x1 =1, x2=﹣ 2D. x1=﹣1, x2=23.若 x , x是一元二次方程 x2+4x+3=0 的两个根,则x +x的值是()1212A. 4 B. 3 C.﹣ 4 D.﹣ 34.抛物线 y=2( x+3)2﹣5 的顶点坐标是()A.(﹣ 3,﹣ 5)B.(﹣ 3,5) C.( 3,﹣ 5) D.( 3, 5)5.如图,△ ABC中,∠ C=65°,将△ ABC绕点 A顺时针旋转后,可以得到△ AB′C′,且C′在边 BC上,则∠ B′C′B的度数为()A.56°B.50°C.46°D.40°6.若关于x 的一元二次方程为ax2+bx+5=0(a≠ 0)的解是x=1,则﹣ a﹣b 的值是()A. 2019B.C.D.7.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅年月退休金为1500 元,年达到2160元.设李师傅的月退休金从年到年年平均增长率为x,可列方程为()A.( 1﹣ x)2=1500B. 1500( 1+x)2=2160C. 1500( 1﹣ x)2=2160D. 1500+1500( 1+x) +1500(1+x)2=21608.如图,已知△ABC中,∠ C=90°, AC=BC=,将△ ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则 C′B的长为()A. 2B.C.1D. 19.已知α是一元二次方程2x 22x 3=0 的两个根中大的根,下面α 的估正确的是()A. 0<α<B.<α<1C. 1<α<D.<α<210.如:在△ABC中,∠ ACB=90°,∠ B=30°,AC=1, AC在直 l 上,将△ ABC点 A旋到位置①,可得到点P1,此 AP1=2;将位置①的三角形点P1旋到位置②,可得到点P2,此 AP2=2+;将位置②的三角形点P2旋到位置③,可得到点P3,可得到点P3,此 AP3=3+;⋯,按此律旋,直到得到点P 止,AP=()A. +672B. +671 C . +672D. +671二、填空(共 6 小,每小 3 分,共 18 分)11.在平面直角坐系中,点P( 2, 3)关于原点称点P′的坐是.12.如果二次函数y=( 1 2k)x23x+1 的象开口向上,那么常数k 的取范是.13.关于 x 的一元二次方程(p 1) x2x+p21=0 一个根0,数p 的是.14.明德小学了美化校园,准在一32 米, 20 米的方形地上修筑两条度相同的道路,余下部分作草坪,在有一位学生了如所示的方案,求中道路的是米,草坪面540 平方米.15.如图,抛物线y=ax2+bx+c 分别交坐标轴于A(﹣ 2, 0)、 B( 6, 0)、 C( 0, 4),则0≤ ax2 +bx+c< 4 的解集是.16.如图所示,在菱形ABCD中, AB=4,∠ BAD=120°,△ AEF为正三角形,点E、 F 分别在菱形的边BC、 CD上滑动,且 E、 F 不与 B、 C、 D重合.当点E、 F 在 BC、 CD上滑动时,则△CEF的面积最大值是.三、解答题(共8 小题,共 72 分)17.解方程: x2+5x=﹣ 2.18.已知抛物线y=x2﹣ 4x+5.求抛物线的开口方向、对称轴和顶点坐标.19.为了应对市场竞争,某手生产厂计划用两年的时间把某种型号的手机的生产成本降低64%,若每年下降的百分数相同,求这个百分数.20.已知一元二次方程x2﹣ 4x+k=0 有两个实数根.(1)求 k 的取值范围;(2)如果 k 是符合条件的最大整数,且一元二次方程x2﹣ 4x+k=0 与 x2+mx﹣ 1=0 有一个相同的根,求此时m的值.21.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣ 2, 3), B(﹣ 6, 0), C(﹣1, 0).(1)请直接写出点 B 关于点 A 对称的点的坐标;(2)将△ ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点 B 的对应点的坐标;(3)请直接写出:以A、 B、C 为顶点的平行四边形的第四个顶点 D 的坐标.22.某商场在 1 月至 12 月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元 / 件)与销售月份x(月)的关系大致满足如图的函数,销售成本 y2(元 / 件)与销售月份x(月)满足y2=,月销售量 y3(件)与销售月份x(月)满足y3 =10x+20.(1)根据图象求出销售价格y1(元 / 件)与销售月份x(月)之间的函数关系式;(6≤ x ≤12 且 x 为整数)(2)求出该服装月销售利润W(元)与月份x(月)之间的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤ x≤ 12 且 x 为整数)23.如图,等边三角形ABC和等边三角形DEC,CE和 AC重合, CE=AB.(1)求证: AD=BE;(2)若 CE绕点 C 顺时针旋转 30 度,连 BD交 AC于点 G,取 AB的中点 F 连 FG.求证:BE=2FG;(3)在( 2)的条件下AB=2,则 AG=.(直接写出结果)24.如图,开口向下的抛物线y=ax2+bx+c 交 x 轴于 A(﹣ 1, 0)、 B( 5, 0)两点,交y 轴于点 C( 0, 5)(1)求抛物线的解析式;(2)设抛物线的顶点为 D,求△ BCD的面积;(3)在( 2)的条件下, P、Q为线段 BC上两点( P 左 Q右,且 P、Q不与 B、 C 重合),PQ=2 ,在第一象限的抛物线上是否存在这样的点R,使△ PQR为等腰直角三角形?若存在,求出点R 的坐标;若不存在,请说明理由.- 学年九年级(上)月考数学试卷( 10 月份)参考答案与试题解析一、选择题(本大题共10 小题,每小题 3 分,共 30 分)1.方程 4x2﹣ x+2=3 中二次项系数、一次项系数、常数项分别是()A. 4、﹣ 1、﹣ 1B. 4、﹣ 1、 2C. 4、﹣ 1、3 D. 4、﹣ 1、5【考点】一元二次方程的一般形式.【分析】要确定一次项系数和常数项,首先要把方程化成一般形式.【解答】解:∵方程4x2﹣ x+2=3 化成一般形式是 4x2﹣ x﹣ 1=0,∴二次项系数为 4,一次项系数为﹣ 1,常数项为﹣ 1,故选: A.【点评】一元二次方程的一般形式是:ax2+bx+c=0( a,b, c 是常数且 a≠0)特别要注意 a ≠0 的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项, bx 叫一次项, c 是常数项.其中a,b, c 分别叫二次项系数,一次项系数,常数项.2.方程 x( x﹣ 1) =2 的解是()A. x=﹣ 1B. x=﹣ 2C. x1 =1, x2=﹣ 2D. x1=﹣1, x2=2【考点】解一元二次方程- 因式分解法.【分析】观察方程的特点:应用因式分解法解这个一元二次方程.【解答】解:整理得:x2﹣ x﹣ 2=0,(x+1)( x﹣ 2) =0,∴x+1=0 或 x﹣ 2=0,即x1 =﹣ 1, x2=2故选 D.【点评】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.3.若 x1, x2是一元二次方程x2+4x+3=0 的两个根,则x1+x2的值是()A. 4B. 3C.﹣ 4 D.﹣ 3【考点】根与系数的关系.【分析】根据x1+x 2=﹣即可得.【解答】解:∵x1, x2是一元二次方程x2+4x+3=0 的两个根,∴x1+x 2=﹣ 4,故选: C.【点评】本题主要考查一元二次方程根与系数的关系,x1, x2是一元二次方程ax2+bx+c=0(a≠ 0)的两根时, x1 +x2=﹣,x1x2=.4.抛物线y=2( x+3)2﹣5 的顶点坐标是()A.(﹣ 3,﹣ 5)B.(﹣ 3,5) C.( 3,﹣ 5) D.( 3, 5)【考点】二次函数的性质.【分析】由于抛物线y=a( x﹣ h)2 +k 的顶点坐标为(h, k),由此即可求解.2【解答】解:∵抛物线y=2(x+3)﹣ 5,故选 A.【点评】此题主要考查了二次函数的性质,解题的关键是熟练掌握抛物线的顶点坐标公式即可解决问题.5.如图,△ ABC中,∠ C=65°,将△ ABC绕点 A顺时针旋转后,可以得到△AB′C′,且C′在边 BC上,则∠ B′C′B的度数为()A.56°B.50°C.46°D.40°【考点】旋转的性质.【分析】根据旋转的性质和∠C=65°,从而可以求得∠ AC′B′和∠ AC′C的度数,从而可以求得∠ B′C′B的度数.【解答】解:∵将△ABC绕点 A 顺时针旋转后,可以得到△AB′C′,且C′在边 BC上,∴AC=AC′,∠ C=∠AC′B′,∴∠ C=∠AC′C,∵∠ C=65°,∴∠ AC′B′=65°,∠ AC′C=65°,∴∠ B′C′B=180°﹣∠ AC′B′﹣∠ AC′C=50°,故选 B.【点评】本题考查旋转的性质,解题的关键是明确题意,找出所求问题需要的条件.6.若关于x 的一元二次方程为ax2+bx+5=0(a≠ 0)的解是x=1,则﹣ a﹣b 的值是()A. 2019B.C.D.【考点】一元二次方程的解.【分析】已知了一元二次方程的一个实数根,可将其代入该方程中,即可求出 b 的值.【解答】解:∵一元二次方程为ax2+bx+5=0(a≠ 0)的解是 x=1,∴a+b+5=0,即 a+b=﹣ 5,∴﹣ a﹣ b=﹣( a+b)=﹣(﹣ 5) =2019,故选 A.【点评】此题主要考查了方程解的定义,所谓方程的解,即能够使方程左右两边相等的未知数的值.7.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅年月退休金为1500 元,年达到2160元.设李师傅的月退休金从年到年年平均增长率为x,可列方程为()A.( 1﹣ x)2=1500B. 1500( 1+x)2=2160C. 1500( 1﹣ x)2=21602D. 1500+1500( 1+x) +1500(1+x) =2160【专题】增长率问题.【分析】本题是关于增长率问题,一般用增长后的量=增长前的量×(1+增长率),如果设李师傅的月退休金从年到年年平均增长率为x,那么根据题意可用x 表示今年退休金,然后根据已知可以得出方程.【解答】解:如果设李师傅的月退休金从年到年年平均增长率为x,那么根据题意得今年退休金为:1500 ( 1+x)2,列出方程为: 1500 (1+x)2=2160.故选: B.【点评】考查了由实际问题抽象出一元二次方程,平均增长率问题,一般形式为a( 1+x)2=b, a 为起始时间的有关数量, b 为终止时间的有关数量.8.如图,已知△ABC中,∠ C=90°, AC=BC=,将△ ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则 C′B的长为()A. 2﹣B.C.﹣1D. 1【考点】旋转的性质.【分析】连接BB′,根据旋转的性质可得AB=AB′,判断出△ ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△ B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交 AB′于 D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解.【解答】解:如图,连接BB′,∵△ ABC绕点 A 顺时针方向旋转60°得到△ AB′C′,∴AB=AB′,∠ BAB′=60°,∴△ ABB′是等边三角形,∴A B=BB′,在△ ABC′和△ B′BC′中,,∴△ ABC′≌△ B′BC′(SSS),∴∠ ABC′=∠B′BC′,延长 BC′交 AB′于 D,则 BD⊥AB′,∵∠ C=90°, AC=BC=,∴AB==2,∴BD=2×=,C′D=× 2=1,∴BC′=BD﹣C′D=﹣1.故选: C.【点评】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出 BC′在等边三角形的高上是解题的关键,也是本题的难点.9.已知α是一元二次方程2x 2﹣ 2x﹣ 3=0 的两个根中较大的根,则下面对α 的估计正确的是()A. 0<α<B.<α<1C. 1<α<D.<α<2【考点】解一元二次方程- 公式法;估算无理数的大小.【分析】先求出方程的解,再求出的范围,最后即可得出答案.【解答】解:△=(﹣ 2)2﹣ 4× 2×(﹣ 3) =28,x==,由意得,α=,∵2<< 3∴<α< 2,故: D.【点】本考了解一元二次方程,估算无理数的大小的用,正确解出方程、掌握估算无理数的大小的方法是解的关.10.如:在△ABC中,∠ ACB=90°,∠ B=30°,AC=1, AC在直 l 上,将△ ABC点 A旋到位置①,可得到点P1,此 AP1=2;将位置①的三角形点P1旋到位置②,可得到点P2,此 AP2=2+;将位置②的三角形点P2旋到位置③,可得到点P3,可得到点P3,此 AP3=3+;⋯,按此律旋,直到得到点P 止,AP=()A. +672B. +671 C . +672D. +671【考点】旋的性;含30 度角的直角三角形;勾股定理.【】律型.【分析】先求出△ABC三的,再依次算AP 、 AP、 AP、⋯,每旋三次,A123到 P 的距离三角形的周,增加一次,度增加2,增加 2 次,度增加2+,增加3 ,度增加周3+;因此要算AP=的度,要先算除以3,商是多少,余数是多少,从而得出果.【解答】解:在Rt△ ABC中,∵∠ B=30°, AC=1,∴A B=2, BC= ,由旋得: AP1 =AB=2,AP =AP+P P =2+,2112AP =AP+P P +P P =3+,31 1 223⋯∵÷ 3=671⋯2,∴AP=671(3+)+2+=+672,故 A.【点】本是旋,也是形律;考了含30°角的直角三角形的性和勾股定理,此的解思路:①先表示出直角三角形各;②因要算AP的,所以从AP1、 AP2、 AP3、依次算,并律,如果看不出可以多算几个度.二、填空(共 6 小,每小 3 分,共 18 分)11.在平面直角坐系中,点P( 2, 3)关于原点称点P′的坐是(2,3).【考点】关于原点称的点的坐.【】常型.【分析】平面直角坐系中任意一点P(x, y),关于原点的称点是(x, y).【解答】解:根据中心称的性,得点P( 2, 3)关于原点的称点P′的坐是(2, 3).故答案:(2, 3).【点】关于原点称的点坐的关系,是需要的基本.方法是合平面直角坐系的形.12.如果二次函数y=( 1 2k)x23x+1 的象开口向上,那么常数k 的取范是k<.【考点】二次函数的性.【分析】由抛物开口向上,可得到关于k 的不等式,可求得k 的取范.【解答】解:∵二次函数y=( 1 2k) x23x+1 的象开口向上,∴1 2k> 0,解得 k<,故答案: k<.【点评】本题主要考查二次函数的性质,掌握二次函数的开口方向由二次项系数的正负决定是解题的关键.13.关于 x 的一元二次方程(p﹣ 1) x2﹣ x+p2﹣ 1=0 一个根为0,则实数p 的值是﹣1.【考点】一元二次方程的解.【专题】方程思想.【分析】根据一元二次方程的解的定义,将x=0 代入原方程,然后解关于p 的一元二次方程.另外注意关于x 的一元二次方程(p﹣ 1) x2﹣ x+p2﹣ 1=0 的二次项系数不为零.【解答】解:∵关于x 的一元二次方程(p﹣ 1) x2﹣ x+p2﹣ 1=0 一个根为0,∴x=0 满足方程( p﹣ 1) x2﹣ x+p2﹣ 1=0,∴p2﹣ 1=0,解得, p=1 或 p=﹣ 1;又∵ p﹣ 1≠0,即 p≠ 1;∴实数 p 的值是﹣ 1.故答案是:﹣ 1.【点评】此题主要考查了方程解的定义.此类题型的特点是,将原方程的解代入原方程,建立关于 p 的方程,然后解方程求未知数 p.14.明德小学为了美化校园,准备在一块长32 米,宽 20 米的长方形场地上修筑两条宽度相同的道路,余下部分作草坪,现在有一位学生设计了如图所示的方案,求图中道路的宽是 2 米时,草坪面积为 540 平方米.【考点】一元二次方程的应用.【专题】计算题;应用题.【分析】如果设路宽为xm,耕地的长应该为32﹣ x,宽应该为20﹣x;那么根据耕地的面积为 540m2,即可得出方程,求解即可.【解答】解:设道路的宽为x 米.依题意得:(32﹣ x)( 20﹣ x)=540,解之得 x1=2, x2=50(不合题意舍去).答:道路宽为2m.故答案为2.【点评】本题考查一元二次方程的应用,难度中等.可将耕地面积看作一整块的矩形的面积,根据矩形面积 =长×宽求解.215.如图,抛物线y=ax +bx+c 分别交坐标轴于A(﹣ 2, 0)、 B( 6, 0)、 C( 0, 4),则【考点】二次函数与不等式(组).【分析】根据点A、B 的坐标确定出对称轴,再求出点C的对称点的坐标,然后写出即可.【解答】解:∵A(﹣ 2, 0)、 B( 6,0),∴对称轴为直线x==2,∴点 C 的对称点的坐标为(4, 4),∴0≤ ax2+bx+c <4 的解集为﹣ 2≤ x<0 或 4< x≤ 6.故答案为:﹣ 2≤ x<0 或 4<x≤ 6.【点评】本题考查了二次函数与不等式,难点在于求出对称轴并得到 C 点的对称点的坐标.16.如图所示,在菱形ABCD中, AB=4,∠ BAD=120°,△ AEF为正三角形,点E、 F 分别在菱形的边BC、 CD上滑动,且 E、 F 不与 B、 C、 D重合.当点E、 F 在 BC、 CD上滑动时,则△CEF的面积最大值是.【考点】菱形的性质;等边三角形的性质.【分析】先求证AB=AC,进而求证△ ABC、△ ACD为等边三角形,得∠ 4=60°,AC=AB进而求证△ ABE≌△ ACF,可得 S△=S△,故根据S 四边形=S△+S△=S△+S△=S△即可解ABE ACF AECF AEC ACF AEC ABE ABC题;当正三角形AEF的边 AE与 BC垂直时,边AE最短.△ AEF的面积会随着AE的变化而变化,且当AE 最短时,正三角形AEF的面积会最小,又根据S△=S 四边形﹣S△,则△CEF AECF AEFCEF的面积就会最大.【解答】解:如图,连接AC,∵四边形ABCD为菱形,∠ BAD=120°,∠1+∠EAC=60°,∠3+∠EAC=60°,∴∠ 1=∠ 3,∵∠ BAD=120°,∴∠ ABC=60°,∴△ABC和△ACD为等边三角形,∴∠ 4=60°, AC=AB,∴在△ ABE和△ ACF中,,∴△ ABE≌△ ACF( ASA),∴S△=S△,ABE ACF∴S 四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,作AH⊥ BC于 H 点,则 BH=2,∴S=S = BC?AH= BC?=4 ,四边形 AECF △ ABC由“垂线段最短”可知:当正三角形AEF的边 AE与 BC垂直时,边 AE最短,∴△ AEF的面积会随着 AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又∵ S△CEF=S四边形AECF﹣ S△AEF,则此时△ CEF的面积就会最大,∴S△=S 四边形﹣S△=4﹣× 2×=.CEF AECF AEF故答案为:【点评】本题主要考查了菱形的性质、全等三角形判定与性质及三角形面积的计算,根据△ABE≌△ ACF,得出四边形AECF的面积是定值是解题的关键.三、解答题(共8 小题,共 72 分)2【考点】解一元二次方程- 配方法.【分析】利用配方法即可求出方程的解.【解答】解: x2+5x+=,(x+ )2= ,x=【点评】本题考查一元二次方程的解法,本题采用配方法求解,属于基础题型.18.已知抛物线y=x2﹣ 4x+5.求抛物线的开口方向、对称轴和顶点坐标.【考点】二次函数的性质.【分析】用配方法将抛物线的一般式转化为顶点式,直接写出开口方向,顶点坐标和对称轴.【解答】解:∵y=x 2﹣ 4x+5,∴y= ( x﹣ 2)2 +1,∵a=1> 0,∴该抛物线的开口方向上,∴对称轴和顶点坐标分别为:x=2,( 2,1).【点评】本题考查了抛物线解析式与二次函数性质的联系.顶点式y=a( x﹣h)2 +k,当 a >0 时,抛物线开口向上,当a< 0 时,抛物线开口向下;顶点坐标为(h, k),对称轴为x=h.19.为了应对市场竞争,某手生产厂计划用两年的时间把某种型号的手机的生产成本降低64%,若每年下降的百分数相同,求这个百分数.【考点】一元二次方程的应用.【专题】增长率问题.【分析】可设原来的成本为1.等量关系为:原来的成本×(1﹣每年下降的百分数)2=原来的成本×( 1﹣ 64%),把相关数值代入求合适解即可.【解答】解:设每年下降的百分数为x.1×( 1﹣ x)2=1×( 1﹣ 64%),∵1﹣ x> 0,∴1﹣ x=0.6 ,∴x=40%.答:每年下降的百分数为 40%.【点评】此题主要考查了一元二次方程的应用;求平均变化率的方法为:若设变化前的量为 a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a( 1± x)2=b.20.已知一元二次方程x2﹣ 4x+k=0 有两个实数根.(1)求 k 的取值范围;(2)如果 k 是符合条件的最大整数,且一元二次方程x2﹣ 4x+k=0 与 x2+mx﹣ 1=0 有一个相同的根,求此时m的值.【考点】根的判别式;一元二次方程的解.【专题】计算题.【分析】( 1)方程 x2﹣ 4x+k=0 有两个实数根,即知△≥0,解可求k 的取值范围;(2)结合( 1)中 k≤ 4,且 k 是符合条件的最大整数,可知k=4,把 k=4 代入 x2﹣4x+k=0中,易解x=2,再把 x=2 代入 x2+mx﹣ 1=0 中,易求m.【解答】解:(1)∵方程x2﹣ 4x+k=0 有两个实数根,∴△≥ 0,即16﹣ 4k≥ 0,解得 k≤ 4;(2)∵ k≤4,且 k 是符合条件的最大整数,∴k=4,解方程 x2﹣ 4x+4=0 得 x=2,把 x=2 代入 x2+mx﹣ 1=0 中,可得4+2m﹣ 1=0,解得 m=﹣.【点评】本题考查了根的判别式、解不等式,解题的关键是知道△≥0? 方程有两个实数根.21.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣ 2, 3), B(﹣ 6, 0), C(﹣1, 0).(1)请直接写出点 B 关于点 A 对称的点的坐标;(2)将△ ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点 B 的对应点的坐标;(3)请直接写出:以A、 B、C 为顶点的平行四边形的第四个顶点 D 的坐标.【考点】作图 - 旋转变换.【分析】( 1)点 B 关于点 A 对称的点的坐标为(2, 6);(2)分别作出点 A、 B、 C 绕坐标原点 O逆时针旋转 90°后的点,然后顺次连接,并写出点B 的对应点的坐标;(3)分别以 AB、 BC、 AC为对角线,写出第四个顶点D 的坐标.【解答】解:(1)点 B 关于点 A 对称的点的坐标为(2, 6);(2)所作图形如图所示:,点 B' 的坐标为:(0,﹣ 6);(3)当以 AB为对角线时,点 D坐标为(﹣ 7, 3);当以 AC为对角线时,点 D 坐标为( 3,3);当以 BC为对角线时,点 D 坐标为(﹣ 5,﹣ 3).【点评】本题考查了根据旋转变换作图,轴对称的性质,以及平行四边形的性质,熟练掌握网格结构,准确找出对应点的位置是解题的关键.22.某商场在 1 月至 12 月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元 / 件)与销售月份x(月)的关系大致满足如图的函数,销售成本 y2(元 / 件)与销售月份x(月)满足y2=,月销售量 y3(件)与销售月份x(月)满足y3 =10x+20.(1)根据图象求出销售价格y1(元 / 件)与销售月份x(月)之间的函数关系式;(6≤ x ≤12 且 x 为整数)(2)求出该服装月销售利润W(元)与月份x(月)之间的函数关系式,并求出哪个月份的销售利润最大?最大利润是多少?(6≤ x≤ 12 且 x 为整数)【考点】二次函数的应用.【分析】( 1)根据待定系数法,可得函数解析式;(2)根据销售额减去销售成本,可得销售利润,根据函数的性质,可得最大利润.【解答】解:( 1)设销售价格 y1(元 / 件)与销售月份 x(月)之间的函数关系式为y1=kx+b(6≤ x≤ 12),函数图象过( 6, 60)、( 12, 100),则,解得.故销售价格y1(元 / 件)与销售月份x(月)之间的函数关系式y1 =x+20(6≤ x≤12且x为整数);(2)由题意得 w=y1?y3﹣ y2?y3即w=(x+20 ) ?(10x+20 )﹣x?( 10x+20)化简,得w=20x2 +240x+400,∵a=20, x=﹣=﹣=﹣ 6 是对称轴,当 x>﹣ 6 时, w 随 x 的增大而增大,∴当 x=12 时,销售量最大,W最大 =20× 122+240× 12+400=6160,答: 12 月份利润最大,最大利润是6160 元.【点评】本题考查了二次函数的应用,利用了待定系数法求解析式,利用了函数的减区间求函数的最大值.23.如图,等边三角形ABC和等边三角形DEC,CE和 AC重合, CE=AB.(1)求证: AD=BE;(2)若 CE绕点 C 顺时针旋转 30 度,连 BD交 AC于点 G,取 AB的中点 F 连 FG.求证:BE=2FG;(3)在( 2)的条件下AB=2,则 AG=.(直接写出结果)【考点】旋转的性质;全等三角形的判定与性质.【专题】证明题.【分析】( 1)由三角形 ABC和等三角形 DEC都是等边三角形,得到∠ BCE=∠ACD=60°,CE=CD, CB=CA,则△ CBE≌△ CAD,从而得到 BE=AD.(2)过 B作 BT⊥ AC于 T,连 AD,则∠ ACE=30°,得∠ GCD=90°,而C E=AB,BT=AB,得 BT=CD,可证得Rt △ BTG≌ Rt △ DCG,有BG=DG,而 F 为 AB的中点,所以 FG∥ AD, FG= AD,易证 Rt△ BCE≌ Rt △ ACD,得到BE=AD=2FG;(3)由( 2) Rt △ BTG≌ Rt △DCG,得到 AT=TC,GT=CT,即可得到 AG= .【解答】解:(1)证明:∵三角形ABC和等三角形DEC都是等边三角形,∴∠ BCE=∠ACD=60°, CE=CD, CB=CA,∴△ CBE≌△ CAD,∴B E=AD.(2)证明:过 B 作 BT⊥ AC于 T,连 AD,如图:∵CE绕点 C 顺时针旋转30 度,∴∠ ACE=30°,∴∠ GCD=90°,又∵ CE=AB,而 BT=AB,∴B T=CD,∴R t △ BTG≌ Rt △ DCG,∴ BG=DG.∵F 为 AB的中点,∴FG∥ AD,FG=AD,∵∠ BCE=∠ACD=90°,CB=CA, CE=CD,∴R t △ BCE≌ Rt △ ACD.∴ BE=AD,∴B E=2FG;(3)∵ AB=2,由( 2) Rt△ BTG≌ Rt△ DCG,∴A T=TC, GT=CG,∴G T= ,∴AG= .故答案为.【点评】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了等边三角形的性质、三角形全等的判定与性质以及三角形中位线的性质.24.如图,开口向下的抛物线y=ax2+bx+c 交 x 轴于 A(﹣ 1, 0)、 B( 5, 0)两点,交y 轴于点 C( 0, 5)(1)求抛物线的解析式;(2)设抛物线的顶点为 D,求△ BCD的面积;(3)在( 2)的条件下, P、Q为线段 BC上两点( P 左 Q右,且 P、Q不与 B、 C 重合),PQ=2 ,在第一象限的抛物线上是否存在这样的点R,使△ PQR为等腰直角三角形?若存在,求出点R 的坐标;若不存在,请说明理由.【考点】待定系数法求二次函数解析式.【分析】( 1)直接把点 A(﹣ 1, 0)、 B( 5, 0), C( 0, 5)代入抛物线 y=ax2+bx+c ,利用待定系数法即可得出抛物线的解析式;(2)作 DE⊥ AB于 E,交对称轴于F,根据( 1)求得的解析式得出顶点坐标,然后根据S△BCD=S△ CDF+S△ BDF即可求得;(3)分三种情况:①以点 P 为直角顶点;②以点 R 为直角顶点;③以点 Q为直角顶点;进行讨论可得使△ PQR为等腰直角三角形时点 R 的坐标.【解答】解:( 1)∵抛物线 y=ax 2+bx+c 与 x 轴交于两点 A(﹣ 1, 0), B( 5, 0), C(0, 5)∴,解得.∴此抛物线的解析式为:y=﹣x2+4x+5;(2)由 y=﹣ x2 +4x+5=﹣( x﹣ 2)2+9 可知顶点D的坐标为( 2, 9),作DE⊥ AB于 E,交对称轴于 F,如图,∴E( 2, 0),∵B( 5, 0), C( 0, 5)∴直线 BC的解析式为y= ﹣ x+5,把x=2 代入得, y=3,∴F(2,3),∴DF=9﹣ 3=6,S△=S△+S△=×6× 2﹣× 6×(5﹣2)=× 6× 5=15;BCD CDF BDF(3)分三种情况:①以点 P 为直角顶点,∵P Q=2 ,∴RQ= PQ=4∵C( 0, 5), B( 5, 0),∴OC=OB=5,∴∠ OCB=∠OBC=45°,∵∠ RQP=45°∴RQ∥ OC可求得直线BC的解析式为设R( m,﹣ m2+4m+5),则2则 RQ=(﹣ m+4m+5)﹣(﹣解得 m=4, m=1,12∵点 Q在点 P 右侧,∴m=4,y=﹣ x+5,Q( m,﹣ m+5)m+5) =4∴R( 4, 5);②以点 R 为直角顶点,∵P Q=2 ,∴RQ=PQ=222设 R( m,﹣ m+4m+5)则 Q( m,﹣ m+5),则 RQ=(﹣ m+4m+5)﹣(﹣ m+5) =2,解得 m=,m=,12∵点 Q在点 P 右侧,∴m=,∴R(,);③以点 Q为直角顶点,∵P Q=2 ∴ PR= PQ=4∵C( 0, 5), B( 5, 0)∴OC=OB=5∴∠ OCB=∠OBC=45°∵∠ RPQ=45°,∴PR∥ OB设R( m,﹣ m2+4m+5),则 P( m﹣ 4,﹣ m2+4m+5),把P( m﹣ 4,﹣ m2+4m+5)代入 y=﹣ x+5,得﹣( m﹣ 4) +5=﹣ m2+4m+5解得 m=4, m=1,12此时点 P(0, 5)因为点 P 在线段 BC上运动,且不与B、C 重合,所以不存在以Q为直角顶点的情况.综上所述:当R ( 4, 5)或((,)时,△ PQR为等腰直角三角形.【点评】考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,顶点坐标,面积计算,等腰直角三角形的判定与性质,以及分类思想的应用,综合性较强,有一定的难度.。
2019届山东省九年级上学期10月月考数学试卷【含答案及解析】

2019届山东省九年级上学期10月月考数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 下列方程中,是一元二次方程的是()A.2x2﹣7=3y+1B.5x2﹣6y﹣2=0C.x﹣=+xD.ax2+(b﹣3)x+c+5=02. 三角形的两边长分别为2和6,第三边是方程x2﹣10x+21=0的解,则第三边的长为()A.7 B.3 C.7或3 D.无法确定3. 下列命题正确的是()A.一组对边相等,另一组对边平行的四边形一定是平行四边形B.对角线相等的四边形一定是矩形C.两条对角线互相垂直的四边形一定是菱形D.两条对角线相等且互相垂直平分的四边形一定是正方形4. 正方形具有而菱形不具有的性质是()A.对角线平分一组对角 B.对角线相等C.对角线互相垂直平分 D.四条边相等5. 若菱形两条对角线的长分别为6和8,则这个菱形的周长为()A.20 B.16 C.12 D.106. 关于x的方程3x2﹣2x+1=0的根的情况是()A.有两个相等的实数根 B.有两个不相等的实数根C.没有实数根 D.不能确定7. 如果关于x的一元二次方程x2+px+q=0的两根分别为x1=3,x2=1,那么这个一元二次方程是()A.x2+3x+4=0 B.x2﹣4x+3=0 C.x2+4x﹣3=0 D.x2+3x﹣4=08. 两个正四面体骰子的各面上分别标明数字1,2,3,4,如同时投掷这两个正四面体骰子,则着地的面所得的点数之和等于5的概率为()A. B. C. D.9. 2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为()A.2(1+x)2=9.5 B.2(1+x)+2(1+x)2=9.5C.2+2(1+x)+2(1+x)2=9.5 D.2(1+x)=9.5二、填空题10. 一元二次方程2x2+4x=1的二次项系数、一次项系数及常数之和为.11. ▱ABCD中,对角线AC、BD交于点O,若AC=8,BD=6,则边AB长的取值范围为.12. 顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是形.13. 从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是.14. 在△ABC中,已知∠A、∠B、∠C的度数之比为1:2:3,AB边上的中线长为4cm,则△ABC面积等于 cm2.15. 若关于x的方程3x2+mx+m﹣6=0有一根是0,则m= .16. 如图,矩形ABCD中,AC、BD相交于点O,AE平分∠BAD,交BC于E,若∠EAO=15°,则∠BOE的度数为度.17. 如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在E处,折痕为MN,则线段CN的长是.18. 如图,在▱ABCD中,AE平分∠B AD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长,四边形ABEF的面积.三、解答题19. 解方程(1)2x2+4x﹣3=0(配方法解)(2)5x2﹣8x+2=0(公式法解)(3)3(x﹣5)2=2(5﹣x)(4)(3x+2)(x+3)=x+14.20. 小明和小芳做配紫色游戏,如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;(2)若出现紫色,则小明胜.此游戏的规则对小明、小芳公平吗?试说明理由.21. 已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:(1)△ABE≌△ADF;(2)∠AEF=∠AFE.22. 某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?23. 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?24. D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?为什么?(3)当OA与BC满足时,四边形DGEF是一个矩形(直接填答案,不需证明.)25. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.
B.
C.
D.
11. 如图,在
中,
,
,点 、 分别是边 、 上点,连结 ,
将
沿 翻折得到
,点 的对称点 恰好落在边 上,若以点 、 、 为顶
点的三角形与
相似,则 的长为( ).
/
A.
B.
C. 或
D. 或
12. 如图, 、 是函数
( ).
①
≌
,②
,则
上两点, 为一动点,作
,③若 .
轴,
轴,下列说法正确的是
B.
C.
D.
6. 如图,四边形
和
边形
与四边形
是以点 为位似中心的位似图形,若 的面积比为( ).
,则四
A.
B.
C.
D.
7. 已知
是反比例函数,则关于函数图象说法错误的是( ).
A. 两支曲线关于原点对称
B. 两支曲线分别在第二、四象限
C. 当
时,
D. 图象经过点
8. 如图,线段 的两端点的坐标分别为
眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“ 男 女”的概率.
/
25. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升 ,加热到
停止加
热,水温开始下降,此时水温
与开机后用时
成反比例关系,直至水温降至 ,
饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为 时接通电源,
水温
与时间
的关系如图所示:
( 1 )分别写出水温上升和下降阶段 与 之间的函数关系式. ( 2 )怡萱同学想喝高于 的水,请问她最多需要等待多长时间?
26. 四边形
中,点 为 边上一点,点 为对角线 上的一点,且
.
( 1 )若四边形
为正方形.
1 如图 ,请直接写出
.
2将
图 绕点 逆时针旋转到图 所示的位置,连接 , ,猜想 与 的数
正面
A.
B.
C.
D.
3. 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线统计 图,那么符合这一结果的实验最有可能的是( ). 频率
A. 挪一枚质地均匀的硬币,落地时结果是“正面向上” B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是 C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
/
量关系并说明理由.
( 2 )如图 ,若四边形
为矩形,
针旋转
得到
写出 与 的数量关系.
,其它条件都不变,将
图 绕点 顺时
,连接 , ,请在图 中画出草图,并直接
/
27. 如图 ,反比例函数
作
轴,垂足为 .
图像经过等边
图 的一个顶点 ,点 坐标为 ,过点
图 ( 1 )求点 的坐标和 的值.
( 2 )若将
为
.
15. 若函数
与
的图象的交点坐标为
,则
的值为
.
16. 一个正棱柱的三视图如图所示,其俯视图为正三角形,则该三棱柱的体积是
.
/
正视图
左视图
俯视图
17. 如图,在 并延长交
中, 是 于点 ,则
边上的中线, 是 .
上一点,且
,连结 ,
18. 如图, 点,
是等边三角形,点 , 分别在 ,
,
,则 的长是
根据数据绘制了如下的表格和统计图:
等级
视力( )
频数
频率
合计 人数
根据上面提供的信息,回答下列问题:
等级
( 1 )统计表中的
,
.
( 2 )请补全条形统计图.
( 3 )根据抽样调查结果,请估计该校八年级学生视力为“ 级”的有多少人?
( 4 )该年级学生会宣传部有 名男生和 名女生,现从中随机挑选 名同学参加“防控近视,爱
睛贴着地面观察 点,使 , , 三点成一线,从 处退行 米到点 处,从 观察 点,使
, , 三点也成一线.请你利用以上的信息计算出 的高度(测量过程中,建筑物 ,
标杆 和 均与地面垂直).
/
24. 某学校八年级共 名学生,为了解该年级学生的视力情况,从中随机抽取 名学生的视力数据 作为样本,数据统计如下:
,则 平分
,④若
A. ①③
B. ②③
二、填空题
(本大题共6小题,每小题4分,共24分。)
13. 如图,点 在
的边 上,要使
C. ②④
D. ③④
,添加一个条件
.
14. 某鱼塘里养了 条鲤鱼、若干条草鱼和 条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕
捞到草鱼的频率稳定在 左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约
,
,以点
为位似中心,将线段
缩小为原来的 后得到线段 ,则端点 的坐标为( ).
/
A.
B.
C.
D.
9. 如图,在矩形 是( ).
中, 是 边的中点,且
于点 ,连接 ,则下列结论错误的
A.
B.
C.
D.
10. 如图,正方形
是一块绿化带,其中阴影部分
,
都是正方形的花圃.已知
自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( ).
( 2 )请直接写出不等式
的解集.
( 3 )点 为 轴上一动点,当
时,求点 的坐标.
22. 如图,点 , 在线段 上,
是等边三角形,
.
( 1 )说明线段 、 、
( 2 )求
的度数.
之间的数量关系.
23. 如图,要测量建筑物 的高度,可以采用以下方法:立两根高 米长的标杆 和 ,两杆之
间的距离
米,并使 , , 三点在一条直线上,从点 处退行 米到点 处,人的眼
.
上,且
, 与 相交于
三、解答题
(本大题共9小题,共78分。) 19. 如上右图是一根空心方管,请补全它的三视图.
20.
/
已知:
于,
于,
,Leabharlann 以 , , 为顶点的三角形与
相似时,求
, 的长?
,点 在 上移动,当
21. 如图,一次函数
为
.
图象与反比例函数
图象相交于 , 两点,已知点 的坐标
( 1 )求一次函数和反比例函数的解析式.
次数
/
D. 袋子中有 个红球和 个黄球,只有颜色上的区别,从中随机取出一个球是黄球
4. 如图,已知线段 ,过点 作 的垂线,并在垂线上取
;连接 ,以点 为圆
心, 为半径画弧,交 于点 ;再以点 为圆心, 为半径画弧,交 于点 ,则
的值是( ).
A.
5. 函数 A.
B.
C.
D.
与
在同一坐标系中的图象可能是( ).
2019~2020学年10月山东济南历城区济南稼轩初级中学 初三上学期月考数学试卷
一、选择题
(本大题共12小题,每小题4分,共48分。)
1. 已知:
,则
的值为( ).
A.
B.
C.
D.
2. 如图所示是张老师电动车的一个零件,张老师要求小亮按如图摆放位置画出它的左视图,小亮经 过仔细观察画出了正确的图形,则小亮画的图形是:( ).
沿直线 翻折,得到
,判断该反比例函数图象是从点 的上方经
过,还是从点 的下方经过,又或是恰好经过点 ,并说明理由.
( 3 )如图 ,在 轴上取一点 ,以 为边长作等边
,恰好使点 落在该反比例
函数图象上,连接 ,求
的面积.
图
扫码关注“学而思爱智康济南”微信公众号 回复【初三月考】获得答案解析及其他学校真题
