第4章 判别分析及MATLAB实现(2013)
判别分析及MATLAB应用

判别分析及MATLAB应用
摘要
本文针对线性判别分析(LDA),总结了LDA的基本原理、求解过程
和MATLAB应用。
首先介绍了LDA的基本原理,即在最大化类内方差和最
小化类间方差之间寻求一个平衡,以作为类间距离的度量;然后,详细介
绍了求解LDA的算法流程,包括LDA的假设、建立数学模型、求解驻点过
程等;最后,结合MATLAB示例,介绍了如何在MATLAB中实现LDA,并介
绍了各种LDA的实现方法。
关键词:线性判别分析(LDA);最大似然估计;MATLAB
1 研究背景
统计学习理论中有两种重要分类模型:支持向量机(Support Vector Machine,SVM)和线性判别分析(Linear Discriminant Analysis,LDA)。
LDA是一种分类模型,它假设每个类别的概率密度函数都是一个
多元正态分布,利用极大似然估计,将各类样本数据的IC。
概率密度函
数的参数估计出来。
LDA可以有效的将特征进行降维,以得到较好的分类
结果。
2 线性判别分析原理
LDA是基于极大似然估计的一种分类模型,假定样本数据服从多元正
态分布,其目的是在最大化类内方差和最小化类间方差之间寻求一个平衡,以作为类间距离的度量。
(1)LDA的假设
LDA的假设有如下几点:
a.样本空间中两类样本具有多元正态分布。
2013实验报告-判别分析

2013实验报告-判别分析判别分析是一种模式识别技术,用于评估两个或多个已知分类的观测量。
该技术使用统计学方法来找出哪些变量最能区分不同的分类,以使模型能够对新的未知观测进行分类。
它可以在许多领域得到广泛应用,如医学、金融、自然科学、工业和社会科学等。
该实验使用判别分析技术来分析一个小型的数据集,以演示如何使用判别分析。
该数据集包括50个观测和两个变量,每个观测属于两种不同类型的花。
该数据集是经典的鸢尾花数据集,用于评估机器学习算法的性能。
为了进行判别分析,我们首先将数据集拆分成训练数据和测试数据。
训练数据用来创建模型,测试数据用来评估模型的性能。
使用判别分析函数fitdiscr来拟合模型,并使用测试数据来计算模型的分类准确性。
模型对测试数据集中的观测进行分类,并与实际标签进行比较,以确定模型的准确性。
在本实验中,我们使用了线性判别分析方法来分析数据。
线性判别分析是一种适用于两个或多个类别变量的判别分析方法,它将每个类别视为一个概率分布并通过计算类之间和类内差异来找到线性判别向量。
该方法基于类间方差和类内方差之间的比较来确定最佳的线性判别方向。
线性判别分析假设每个类别的协方差是相等的,并且由于可能有多个线性判别向量,因此我们需要使用额外的标准方法(如鉴别分析)来决定哪个线性判别向量最能区分不同的类别。
本实验结果表明,所构建的模型能够从花萼和花瓣长度和宽度这四个变量中提取有用的信息,并对测试数据的类别进行了准确分类。
通过将测试数据与训练数据相比较,发现模型对测试数据的分类准确性为96%,这表明该模型能够很好地对新的未知观测进行分类。
总之,判别分析是一种有用的模式识别技术,可以很好地应用于许多实际场景。
本实验演示了如何使用判别分析技术来分析数据并构建一个使用线性判别分析方法的分类模型。
MATLAB 判别分析

判别分析在生产、科学研究和日常生活中,经常会遇到对某一研究对象属于哪种情况作出判断。
例如要根据这两天天气情况判断明天是否会下雨;医生要根据病人的体温、白血球数目及其它症状判断此病人是否会患某种疾病等等。
从概率论的角度看,可把判别问题归结为如下模型。
设共有n 个总体:n ξξξ,,,21L其中i ξ是m 维随机变量,其分布函数为),,(1m i x x F L ,n i ,,2,1L =而),,(1m x x L 是表征总体特性的m 个随机变量的取值。
在判别分析中称这m 个变量为判别因子。
现有一个新的样本点Tm x x x ),,(1L =,要判断此样本点属于哪一个总体。
Matlab 的统计工具箱提供了判别函数classify 。
函数的调用格式为:[CLASS,ERR] = CLASSIFY(SAMPLE,TRAINING ,GROUP, TYPE)其中SAMPLE 为未知待分类的样本矩阵,TRAINING 为已知分类的样本矩阵,它们有相同的列数m ,设待分类的样本点的个数,即SAMPLE 的行数为s ,已知样本点的个数,即TRAINING 的行数为t ,则GROUP 为t 维列向量,若TRAINING 的第i 行属于总体i ξ,则GROUP 对应位置的元素可以记为i ,TYPE 为分类方法,缺省值为'linear',即线性分类,TYPE 还可取值'quadratic','mahalanobis'(mahalanobis 距离)。
返回值CLASS 为s 维列向量,给出了SAMPLE 中样本的分类,ERR 给出了分类误判率的估计值。
例已知8个乳房肿瘤病灶组织的样本,其中前3个为良性肿瘤,后5个为恶性肿瘤。
数据为细胞核显微图像的10个量化特征:细胞核直径,质地,周长,面积,光滑度。
根据已知样本对未知的三个样本进行分类。
已知样本的数据为:13.54,14.36,87.46,566.3,0.0977913.08,15.71,85.63,520,0.10759.504,12.44,60.34,273.9,0.102417.99,10.38,122.8,1001,0.118420.57,17.77,132.9,1326,0.0847419.69,21.25,130,1203,0.109611.42,20.38,77.58,386.1,0.142520.29,14.34,135.1,1297,0.1003-1-待分类的数据为:16.6,28.08,108.3,858.1,0.0845520.6,29.33,140.1,1265,0.11787.76,24.54,47.92,181,0.05263解:编写程序如下:a=[13.54,14.36,87.46,566.3,0.0977913.08,15.71,85.63,520,0.10759.504,12.44,60.34,273.9,0.102417.99,10.38,122.8,1001,0.118420.57,17.77,132.9,1326,0.0847419.69,21.25,130,1203,0.109611.42,20.38,77.58,386.1,0.142520.29,14.34,135.1,1297,0.1003]x=[16.6,28.08,108.3,858.1,0.0845520.6,29.33,140.1,1265,0.11787.76,24.54,47.92,181,0.05263]g=[ones(3,1);2*ones(5,1)];[class,err]=classify(x,a,g)-2-。
判别分析及MATLAB实现

d(x, G) (x )T 1(x )
为n维向量x与总体G的马氏距离.
(4.1.2)
MATLAB中有一个命令:d=mahal(Y,X),计算X 矩阵每一个点(行)至Y矩阵中每一个点(行)的 马氏距离。其中Y的列数必须等于X的列数,但它们 的行数可以不同。X的行数必须大于列数。输出d是 距离向量。
af=[1.24,1.72;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;1.40,1.70;
1.48,1.82;1.54,1.82;1.56,2.08];
x=[1.24,1.8;1.28,1.84; 1.4,2.04];
% 输入原始数据
m1=mean(apf); m2=mean(af);
第8页/共57页
(3) 两个总体之间的马氏距离 设有两个总体G1,G2,两个总体的均值向量分别
为 1 , 2,协方差矩阵相等,皆为Σ,则两个总体之
间的马氏距离为
d (G1, G2 ) (1 2 )T 1(1 2 ) (4.1.3)
通常,在判别分析时不采用欧氏距离的原因在 于,该距离与量纲有关.例如平面上有A,B,C,D四个 点,横坐标为代表重量(单位:kg),纵坐标代表 长度(单位:cm),如下页图。
上述公式可以化简为: W(x)=(ma-mb)S-1(x-(ma+mb)/2)’
若W(x)>0,x属于G1;若W(x)<0,x属于G2 注意: 1.此处ma,mb都是行向量; 2.当x是一个矩阵时,则用ones矩阵左乘(ma+mb)/2以 后,方可与x相减.
第16页/共57页
※ Matlab中直接进行数据的判别分析命令为classify, 其调用格式 class = classify(sample,training,group, 'type')
FISHER线性判别MATLAB实现

Fisher 线性判别上机实验报告班级: 学号: 姓名:一.算法描述Fisher 线性判别分析的基本思想:选择一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起,不同类的样本相隔尽可能地远。
Fisher 线性判别分析,就是通过给定的训练数据,确定投影方向W 和阈值w0, 即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
线性判别函数的一般形式可表示成0)(w X W X g T += 其中Fisher 选择投影方向W 的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求。
如下为具体步骤:(1)W 的确定w S 样本类间离散度矩阵b在投影后的一维空间中,各类样本均值Tiim '= Wm样本类内离散度和总类内离散度 T Ti i ww S ' = W S W S ' = W S W 样本类间离散度Tbb S ' = W S W Fisher 准则函数为 max 2221221~~)~~()(S S m m W J F +-=(2)阈值的确定w 0是个常数,称为阈值权,对于两类问题的线性分类器可以采用下属决策规则: 令)()()(21x x x g g g -=则:如果g(x)>0,则决策w x 1∈;如果g(x)<0,则决策w x 2∈;如果g(x)=0,则可将x 任意分到某一类,或拒绝。
(3)Fisher 线性判别的决策规则 Fisher 准则函数满足两个性质:1.投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
2.投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出W :-1w 12W = S (m - m ) 。
这就是Fisher 判别准则下的最优投影方向。
Matlab的判别和转换函数

Matlab的判别和转换函数Matlab的判别和转换函数for i=1:10s1=int2str(i);x(i)=input(['please input x(' s1 ')'])endfor i=1:3for j=1:3s1=int2str(i);s2=int2str(j);x(i,j)=input(['please input x(' s1 ',' s2 ')'])endendISCHAR True for character array (string).ISCHAR(S) returns 1 if S is a character array and 0 otherwise.ISNUMERIC True for numeric arrays.ISNUMERIC(A) returns 1 if A is a numeric array and 0 otherwise.For example, sparse arrays, and double precision arrays are numeric while strings, cell arrays, and structure arrays are not.ISLOGICAL True for logical array.ISLOGICAL(X) returns 1 if X is a logical array and 0 otherwise.Logical arrays must be used to perform logical 0-1 indexing.ISNAN True for Not-a-Number.ISNAN(X) returns an array that contains 1's wherethe elements of X are NaN's and 0's where they are not.For example, ISNAN([pi NaN Inf -Inf]) is [0 1 0 0].ISEMPTY True for empty matrix.ISEMPTY(X) returns 1 if X is an empty array and 0 otherwise.An empty array has no elements, that is prod(size(X))==0.ISINF True for infinite elements.ISINF(X) returns an array that contains 1's where theelements of X are +Inf or -Inf and 0's where they are not.For example, ISINF([pi NaN Inf -Inf]) is [0 0 1 1].ISFINITE True for finite elements.ISFINITE(X) returns an array that contains 1's wherethe elements of X are finite and 0's where they are not.For example, ISFINITE([pi NaN Inf -Inf]) is [1 0 0 0].For any X, exactly one of ISFINITE(X), ISINF(X), or ISNAN(X) is 1 for each element.ISOBJECT True for MATLAB objects.ISOBJECT(A) returns 1 if A is a MATLAB object and 0 otherwise.ISSTRUCT True for structures.ISSTRUCT(S) returns 1 if S is a structure and 0 otherwise.ISCELL True for cell array.ISCELL(C) returns 1 if C is a cell array and 0 otherwise.ISJA VA True for Java object arraysISJA VA(J) returns 1 if J is a Java object array, and 0 otherwise.ISFIELD True if field is in structure array.F = ISFIELD(S,'field') returns true if 'field' is the name of a fieldin the structure array S.ISSPARSE True for sparse matrix.ISSPARSE(S) is 1 if the storage class of S is sparseand 0 otherwise.DOUBLE Convert to double precision.DOUBLE(X) returns the double precision value for X.If X is already a double precision array, DOUBLE hasno effect.DOUBLE is called for the expressions in FOR, IF, and WHILE loopsif the expression isn't already double precision. DOUBLE shouldbe overloaded for all objects where it makes sense to convert itinto a double precision value.INT2STR Convert integer to string.S = INT2STR(X) rounds the elements of the matrix X tointegers and converts the result into a string matrix.NUM2STR Convert number to string.T = NUM2STR(X) converts the matrix X into a string representation T with about 4 digits and an exponent if required. This is useful for labeling plots with the TITLE, XLABEL, YLABEL, and TEXT commands.T = NUM2STR(X,N) converts the matrix X into a string representation with a maximum N digits of precision. The default number of digits is based on the magnitude of the elements of X.T = NUM2STR(X,FORMAT) uses the format string FORMAT (see SPRINTF for details).Example:num2str(randn(2,2),3) produces the string matrix'-0.433 0.125'' -1.67 0.288'SPRINTF Write formatted data to string.[S,ERRMSG] = SPRINTF(FORMAT,A,...) formats the data in the real part of matrix A (and in any additional matrix arguments), under control of the specified FORMAT string, and returns it in the MATLAB string variable S. ERRMSG is an optional outputargument that returns an error message string if an error occurred or an empty matrix if an error did not occur. SPRINTF is the same as FPRINTF except that it returns the data in a MATLAB string variable rather than writing it to a file.FORMAT is a string containing C language conversion specifications. Conversion specifications involve the character %, optional flags, optional widthand precision fields, optional subtype specifier, and conversion characters d, i, o, u, x, X, f, e, E, g, G, c, and s.See the Language Reference Guide or a C manual for complete details.The special formats \n,\r,\t,\b,\f can be used to produce linefeed, carriage return, tab, backspace, and formfeed characters respectively.Use \\ to produce a backslash character and %% to produce the percentcharacter.SPRINTF behaves like ANSI C with certain exceptions and extensions.These include:1. ANSI C requires an integer cast of a double argument to correctly use an integer conversion specifier like d. A similiar conversion is required when using such a specifier with non-integral MATLAB values. Use FIX, FLOOR, CEIL or ROUND on a double argument to explicitly convert non-integral MATLAB values to integral values if you plan to use an integer conversion specifier like d. Otherwise, any non-integral MATLAB values will be outputted using the format where the integer conversion specifier letter has been replaced by e.2. The following non-standard subtype specifiers aresupported for conversion characters o, u, x, and X.t - The underlying C datatype is a float rather than an unsigned integer.b - The underlying C datatype is a double rather than an unsigned integer. For example, to print out in hex a double value use a format like '%bx'.3. SPRINTF is "vectorized" for the case when A is nonscalar. The format string is recycled through the elements of A (columnwise) until all the elements are used up. It is then recycled in a similar manner through any additional matrix arguments.See the reference page in the online help for other exceptions, extensions, or platform-specific behavior.Examplessprintf('%0.5g',(1+sqrt(5))/2) 1.618sprintf('%0.5g',1/eps) 4.5036e+15sprintf('%15.5f',1/eps) 4503599627370496.00000sprintf('%d',round(pi)) 3sprintf('%s','hello') hellosprintf('The array is %dx%d.',2,3) The array is 2x3.sprintf('\n') is the line termination character on all platforms. FPRINTF Write formatted data to file.COUNT = FPRINTF(FID,FORMAT,A,...) formats the data in the real part of matrix A (and in any additional matrix arguments), under control of the specified FORMAT string, and writes it to the file associated with file identifier FID. COUNT is the number of bytes successfully written. FID is an integer file identifier obtained from FOPEN. It can also be 1 for standard output (the screen) or 2for standard error. If FID is omitted, output goes to the screen.FORMAT is a string containing C language conversionspecifications. Conversion specifications involve the character %, optional flags, optional width and precision fields, optional subtype specifier, and conversion characters d, i, o, u, x, X, f, e, E, g, G, c, and s.For more details, see the FPRINTF function description in online help (search by Function Name for FPRINTF), or look up FPRINTF in a C language manual.The special formats \n,\r,\t,\b,\f can be used to produce linefeed, carriage return, tab, backspace, and formfeed characters respectively. Use \\ to produce a backslash character and %% to produce the percent character.FPRINTF behaves like ANSI C with certain exceptions and extensions. These include:1. Only the real part of each parameter is processed.2. ANSI C requires an integer cast of a double argument to correctlyuse an integer conversion specifier like d. A similiar conversionis required when using such a specifier with non-integral MATLAB values. Use FIX, FLOOR, CEIL or ROUND on a double argument to explicitly convert non-integral MATLAB values to integral values if you plan to use an integer conversion specifier like d.Otherwise, any non-integral MATLAB values will be outputted using the format where the integer conversion specifier letter has beenreplaced by e.3. The following non-standard subtype specifiers are supported forconversion characters o, u, x, and X.t - The underlying C datatype is a float rather than anunsigned integer.b - The underlying C datatype is a double rather than anunsigned integer.For example, to print out in hex a double value use a format like '%bx'.4. FPRINTF is "vectorized" for the case when A is nonscalar. Theformat string is recycled through the elements of A (columnwise) until all the elements are used up. It is then recycled in a similar manner through any additional matrix arguments.For example, the statementsx = 0:.1:1; y = [x; exp(x)];fid = fopen('exp.txt','w');fprintf(fid,'%6.2f %12.8f\n',y);fclose(fid);create a text file containing a short table of the exponential function:0.00 1.000000000.10 1.10517092...1.002.71828183See the reference page in the online help for other exceptions, extensions, or platform-specific behavior.See also FSCANF, SPRINTF, FWRITE, DISP, DIARY, SAVE, INPUT.。
2013 matlab教程ppt(全)340页

2013-4-21 Application of Matlab Language 5
2013-4-21 Application of Matlab Language 4
课程安排
课堂教学:共24学时;(1-12周) 上机试验:共24学时。
(2-13周,周二7-8节,九实401、402、403)
学习成绩: 1)上机实验成绩占30%; 2)考勤 10% ; 3) 考试60% (随堂考试)。
2013-4-21
Application of Matlab Language
3
本课程的目的( Objectives of This Course )
讲授MATLAB语言基础入门知识,介绍MATLAB产品的体系、MATLAB桌面工具 的使用方法,重点介绍MATLAB的数据可视化、数值计算的基本步骤以及如何使 用MATLAB语言编写整洁、高效、规范的程序。并涉及到一些具体的专业应用工
2013-4-21
Application of Matlab Language
11
Matlab版本的发展 • 1992年,支持Windows 3.x的MATLAB 4.0版本推出,增加了Simulink,Control, Neural Network,Signal Processing等专用工具箱。 • 1993年11月,MathWorks公司推出了Matlab 4.1,其中主要增加了符号运算功能。 当升级至Matlab 4.2c,这一功能在用户中得到广泛应用。 • 1997年,Matlab 5.0版本问世了,实现了真正的32位运算,加快数值计算,图形表现 有效。 • 2001年初,MathWorks公司推出了Matlab 6.0(R12)。 • 2002年7月,推出了Matlab 6.5(R13),在这一版本中Simulink升级到了5.0,性能有 了很大提高,另一大特点是推出了JIT程序加速器,Matlab的计算速度有了明显的 提高。 • 2005年9月,推出了MAILAB 7.1(Release14 SP3),在这一版本中Simulink升级到了 6.3,软件性能有了新的提高,用户界面更加友好。值得说明的是,Matlab V7.1版 采用了更先进的数学程序库,即‚LAPACK‛和‚BLAS‛。 目前,Matlab软件支持多种系统平台,如常见的WindowsNT/XP、UNIX、Linux 等。
Matlab 系统辨识 仿真 CH3,CH4,CH6程序注释与剖析
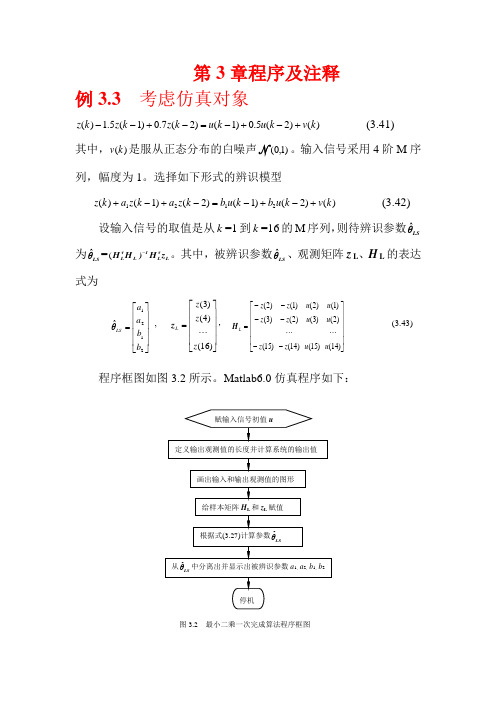
第3章程序及注释例3.3 考虑仿真对象)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (3.41) 其中,)(k v 是服从正态分布的白噪声N )1,0(。
输入信号采用4阶M 序列,幅度为1。
选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (3.42)设输入信号的取值是从k =1到k =16的M 序列,则待辨识参数LSθˆ为LS θˆ=L τL 1L τL z H )H H -(。
其中,被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H (3.43) 程序框图如图3.2所示。
Matlab6.0仿真程序如下:%二阶系统的最小二乘一次完成算法辨识程序,在光盘中的文件名:FLch3LSeg1.mu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16,步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on %画出输出观测值z的径线图形,并显示坐标网格u,z %显示输入信号和输出观测信号%L=14 %数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9) u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11)u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13)u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵H L赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15); z(16)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示θˆLS%Display Parametersa1=c(1), a2=c(2), b1=c(3),b2=c(4) %从θˆ中分离出并显示a1、a2、b1、LSb2%End程序运行结果:>>u =[ -1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]z =[ 0,0,0.5000,0.2500,0.5250,2.1125,4.3012,6.4731,6.1988,3.2670,-0.9386,-3.1949,-4.6352,6.2165,-5.5800,-2.5185]HL =0 0 1.0000 -1.0000-0.5000 0 -1.0000 1.0000-0.2500 -0.5000 1.0000 -1.0000-0.5250 -0.2500 1.0000 1.0000-2.1125 -0.5250 1.0000 1.0000-4.3012 -2.1125 1.0000 1.0000-6.4731 -4.3012 -1.0000 1.0000-6.1988 -6.4731 -1.0000 -1.0000-3.2670 -6.1988 -1.0000 -1.00000.9386 -3.2670 1.0000 -1.00003.1949 0.9386 -1.0000 1.00004.6352 3.1949 -1.0000 -1.00006.2165 4.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000ZL =[ 0.5000,0.2500,0.5250,2.1125,4.3012,6.4731,6.1988,3.2670,-0.9386,-3.1949,-4.6352,-6.2165,-5.5800,-2.5185]Tc =[ -1.5000,0.7000,1.0000,0.5000]Ta1 = -1.5000a2 = 0.7000b1 = 1.0000b2 =0.5000>>-11-1010-10010从仿真结果表3.1可以看出,由于所用的输出观测值没有任何噪声成分,所以辨识结果也无任何误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这时
AB 52 102 125 CD 102 12 101
显然 AB>CD 如果现在长度用mm为单位,重量的单位保持不变, 于是A点的坐标为(0,50),B点的坐标为(0,100),此时 计算线段的长度为
AB 502 102 2600 CD 100 1 10001
注意:
若S1,S2分别为两个样本的协方差矩阵,则在两个总 体协方差矩阵相等时,总体的协方差矩阵估计量
(n1 1) S1 (n2 1)S2 ˆ S n1 n2 2
(4.1.9)
其中n1,n2分别为两个样本的容量.得到判别法则: (4.1.11)
matlab判别步骤: 1.计算A、B两类的均值向量与协方差阵; ma=mean(A),mb=mean(B),S1=cov(A),S2=cov(B) 2.计算总体的协方差矩阵
(3) 两个总体之间的马氏距离 设有两个总体G1,G2,两个总体的均值向量分别 为 1 , 2,协方差矩阵相等,皆为Σ,则两个总体之 间的马氏距离为
d (G1 , G 2 ) ( 1 2 )T 1 ( 1 2 )
(4.1.3)
通常,在判别分析时不采用欧氏距离的原因在 于,该距离与量纲有关.例如平面上有A,B,C,D四个 点,横坐标为代表重量(单位:kg),纵坐标代表 长度(单位:cm),如下页图。
解:假定两总体的协方差相等,源程序如下:
apf=[1.14,1.78;1.18,1.96;1.20,1.86;1.26,2.;1.28,2;1.30,1.96]; af=[1.24,1.72;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;1.40,1.70; 1.48,1.82;1.54,1.82;1.56,2.08]; x=[1.24,1.8;1.28,1.84; 1.4,2.04]; % 输入原始数据 m1=mean(apf); m2=mean(af); s1=cov(apf); s2=cov(af); s=(5*s1+8*s2)/13; % 计算样本均值与协方差矩阵 for i=1:3 W(i)=(x(i,:)-1/2*(m1+m2))*inv(s)*(m1-m2)'; % 计算判别函数值 end;
例 (1989年国际数学竞赛A题)蠓的分类 蠓是一种昆虫,分为很多类型,其中有一种名为 Af,是能传播花粉的益虫;另一种名为Apf,是会传播 疾病的害虫,这两种类型的蠓在形态上十分相似, 很难区别. 现测得6只Apf和9只Af蠓虫的触角长度和 翅膀长度数据
Apf:(1.14,1.78), (1.18,1.96), (1.20,1.86), (1.26,2.00), (1.28,2.00), (1.30,1.96) ; Af:(1.24,1.72), (1.36,1.74), (1.38,1.64), (1.38,1.82), (1.38,1.90), (1.40,1.70), (1.48,1.82),(1.54,1.82), (1.56,2.下模型:
设有k个总体 G1 , G2 , , Gk ,它们都是 p元总体, T 其数量指标是 X ( X1, X 2 , , X p ) 1) 若总体 Gi 的分布函数是已知,对于任一新 样品数据 x ( x1, x2 , 总体 。 2) 通常各个总体 Gi 的分布是未知的,由从各 个总体取得的样本(训练样本)来估计。一般, 先估计各个总体的均值向量与协方差矩阵。
第4 章 判别分析(discriminant analysis)
§4.1 距离判别 及MATLAB实现
§4.2 Bayes判别
§4.3 判别分析 总结
计算与应用数学系, 中国石油大学(华东)理学院 丁永臻 2013
统计方法(判别分析):
判别分析—在已知研究对象分成若干类型,并已取 得各种类型的一批已知样品的观测数据,在此基础 上根据某些准则建立判别式,然后对未知类型的样 品进行判别分类。 距离判别法—首先根据已知分类的数据,分别计算 各类的重心,计算新个体到每类的距离,确定最短 的距离(欧氏距离、马氏距离) Fisher判别法—利用已知类别个体的指标构造判别 式(同类差别较小、不同类差别较大),按照判别 式的值判断新个体的类别 Bayes判别法—计算新给样品属于各总体的条件概率, 比较概率的大小,然后将新样品判归为来自概率最 大的总体
d 2 ( x, G2 ) d 2 ( x, G1 ) ( x 2 )T 1 ( x 2 ) ( x 1 )T 1 ( x 1 ) xT 1 x 2 xT 12 2T 12 xT 1 x 2 xT 11 1T 11 ) 2 xT 1 ( 1 2 ) 2T 12 1T 11 1T 12 2T 11 2 xT 1 ( 1 2 ) ( 1 2 )T 1 ( 1 2 ) 1 2[( x ( 1 2 )]T 1 ( 1 2 ) 2 2( x )T 1 ( 1 2 )
d1 ( x, y) | xi yi |
i 1
n
绝对距离
称
称
d 2 ( x, y )
2 ( x y ) i i i 1
n
欧氏距离
d r ( x, y) ( | xi yi | )
i 1
n
r 1/ r
为n维向量x,y之间的闵可夫斯基距离,其中 r ( r 0)
例4.1.1 (1989年国际数学竞赛A题)蠓的分类 蠓是一种昆虫,分为很多类型,其中有一种名为 Af,是能传播花粉的益虫;另一种名为Apf,是会传播 疾病的害虫,这两种类型的蠓在形态上十分相似, 很难区别. 现测得6只Apf和9只Af蠓虫的触角长度和 翅膀长度数据Apf:(1.14,1.78), (1.18,1.96), (1.20,1.86), (1.26,2.00), (1.28,2.00), (1.30,1.96) ; Af:(1.24,1.72), (1.36,1.74), (1.38,1.64), (1.38,1.82), (1.38,1.90), (1.40,1.70), (1.48,1.82),(1.54,1.82), (1.56,2.08). 若两类蠓虫协方差矩阵相等,试判别以下的三个 蠓虫属于哪一类? (1.24,1.8),(1.28,1.84),(1.4,2.04)
试判别以下的三个蠓虫属于哪一类? (1.24,1.8),(1.28,1.84),(1.4,2.04)
第4章 判别分析
判别分析的基本思想是根据已知类别的样本所提 供的信息,总结出分类的规律性,建立判别公式和 判别准则,判别新的样本点所属类型。本章介绍距 离判别分析、Bayes判别分析及其MATLAB软件的 实现。 4.1 距离判别分析 4.1.1 判别分析的概念 在一些自然科学和社会科学的研究中,研究对象 用某种方法已划分为若干类型,当得到的一个新样 品数据(通常是多元的),要确定该样品属于已知 类型中的哪一类,这样的问题属于判别分析.
1 其中 ( 1 2 ),令 W ( x) ( x )T 1(1 2 ) 2
于是距离判别准则为
x G1 , W ( x ) 0 x G2 , W ( x ) 0
(4.1.6)
由于总体的均值、协方差矩阵通常是未知的,数据 资料来自两个总体的训练样本,于是用样本的均值、 样本的协方差矩阵代替总体的均值与协方差.
, xn )T , y ( y1, y2 ,
T 1
, yn )T ,则称
d ( x, y ) ( x y ) ( x y )
为n维向量x,y之间的马氏距离.
(4.1.1)
其中 为总体协方差矩阵,通常取为实对称正定 矩阵. 显然,当为单位矩阵时马氏距离就是欧氏距离.
(2) 一个向量到一个总体的马氏距离 总体G 的均值向量为μ,协方差矩阵为Σ .则称
d ( x, G) ( x )T 1 ( x )
为n维向量x与总体G的马氏距离.
(4.1.2)
MATLAB中有一个命令:d=mahal(Y,X),计算X 矩阵每一个点(行)至Y矩阵中每一个点(行)的 马氏距离。其中Y的列数必须等于X的列数,但它们 的行数可以不同。X的行数必须大于列数。输出d是 距离向量。
即当 x 到 G1的马氏距离不超过到 G2 的马氏距 离时,判 x 来自 G1 ;反之,判来自 G2.
由于马氏距离与总体的协方差矩阵有关,所以利 用马氏距离进行判别分析需要分别考虑两个总体的 协方差矩阵是否相等. 1.两个总体协方差矩阵相等的情况 设有两个总体G1,G2,均值分别为 1 , 2 ,协方 差矩阵相等为Σ。考虑样品x到两个总体的马氏距 离平方差:
(n 1 1)S 1 (n 2 1)S 2 S n1 n 2 2
其中n1,n2分别为两个样本的容量. 3.计算未知样本x到A,B两类马氏平方距离之差 d=(x-ma)S-1(x-ma)’- (x-mb)S-1(x-mb)’ 4.若d<0,则x属于A类;若d>0,则x属于B类
上述公式可以化简为:
为常数。
显然,当r=2和1时闵可夫斯基距离分别为欧氏距 离和绝对距离.
2. 马氏距离 马氏距离是由印度统计学家马哈拉诺比斯(PC Mahalanobis)提出的,由于马氏距离具有统计意义, 在距离判别分析时经常应用马氏距离:
(1) 同一总体的两个向量之间的马氏距离 设有n维向量 x ( x1, x2 ,
W(x)=(ma-mb)S-1(x-(ma+mb)/2)’ 若W(x)>0,x属于G1;若W(x)<0,x属于G2 注意: 1.此处ma,mb都是行向量;
2.当x是一个矩阵时,则用ones矩阵左乘(ma+mb)/2以 后,方可与x相减.
※ Matlab中直接进行数据的判别分析命令为classify, 其调用格式 class = classify(sample,training,group, 'type')
