固体物理第5章
合集下载
固体物理 第五章 固体电子论基础1

5
5.一些金属元素的自由电子密度 一些金属元素的自由电子密度
元 素 Li Na K Cu Ag Mg Ca Zn Al In Sn Bi z 1 1 1 1 1 2 2 2 3 3 4 5 n/1028m-3 4.70 2.65 1.4 8.47 5.86 8.61 4.61 13.2 18.1 11.5 14.8 14.1 rs/10-10m 1.72 2.08 2.57 1.41 1.60 1.41 1.73 1.22 1.10 1.27 1.17 1.19 rs/a0 3.25 3.93 4.86 2.67 3.02 2.66 3.27 2.30 2.07 2.41 2.22 2.25
n= z
ρNA
M
ne2E j = nev = τ 2m
设电子平均自由程为l, 设电子平均自由程为 ,则 τ
2
zρNAe2E j= τ 2mM
(A m )
2
=l v
电流密度可写成
zρNAe E l j= × 2mM v
6.电导率σ 电导率
(A m )
2
j zρNAe l σ= = × 2mM v E
2
1.必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动 电子的运动不同于气体分子的运动, 电子的运动不同于气体分子的运动,不能用经典 理论来描述。 理论来描述。 2.电子的分布服从量子统计 即费米 狄拉克分布。 电子的分布服从量子统计, 即费米-狄拉克分布 狄拉克分布。 电子的分布服从量子统计 电子的分布不再服从经典的统计分布规律。 电子的分布不再服从经典的统计分布规律。 3.电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的 4.电子的能级是由一些能带组成。 电子的能级是由一些能带组成。 电子的能级是由一些能带组成
5.一些金属元素的自由电子密度 一些金属元素的自由电子密度
元 素 Li Na K Cu Ag Mg Ca Zn Al In Sn Bi z 1 1 1 1 1 2 2 2 3 3 4 5 n/1028m-3 4.70 2.65 1.4 8.47 5.86 8.61 4.61 13.2 18.1 11.5 14.8 14.1 rs/10-10m 1.72 2.08 2.57 1.41 1.60 1.41 1.73 1.22 1.10 1.27 1.17 1.19 rs/a0 3.25 3.93 4.86 2.67 3.02 2.66 3.27 2.30 2.07 2.41 2.22 2.25
n= z
ρNA
M
ne2E j = nev = τ 2m
设电子平均自由程为l, 设电子平均自由程为 ,则 τ
2
zρNAe2E j= τ 2mM
(A m )
2
=l v
电流密度可写成
zρNAe E l j= × 2mM v
6.电导率σ 电导率
(A m )
2
j zρNAe l σ= = × 2mM v E
2
1.必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动 电子的运动不同于气体分子的运动, 电子的运动不同于气体分子的运动,不能用经典 理论来描述。 理论来描述。 2.电子的分布服从量子统计 即费米 狄拉克分布。 电子的分布服从量子统计, 即费米-狄拉克分布 狄拉克分布。 电子的分布服从量子统计 电子的分布不再服从经典的统计分布规律。 电子的分布不再服从经典的统计分布规律。 3.电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的 4.电子的能级是由一些能带组成。 电子的能级是由一些能带组成。 电子的能级是由一些能带组成
中山大学固体物理第五章参考答案

定态薛定谔方 程为:
d 2 d2x
2m 2
E
U ( x)
0
U(x)
U0
1区 2区3区
b x
0 ca
1( x) Aeix Beix , 2( x) Aei'x Bei'x , 3( x) eika ( Aeix Beix ), 这里 2mE / , ' 2m(E U0) /
进行一些推导和必要简化,最后可 以得出下式
maU0b
2
sin
a
a
cos(
a)
cos(ka)
式中
2mE
而 k 2
是电子波的波矢。
上式就是电子的能量 E 应满足的方程,也是电子能量 E 与波矢 k 之间的关系式。
f( E)
E
图 5 f(E)函数图
由图看出,在允许取的 E值之间,有一些不允许取 的 E值,称为能隙。
– (2)试讨论分别同A、B两种材料组成的一维 超晶格量子阱的能带变化。*(如下图)
AB
ECA
EVA
8
a
a
ECB
克朗尼格-朋奈模型
EVB (基泰尔,固体物理导论,P119)
克朗尼格-朋奈模型
U(x)
周期性方势阱
U0
2区
1区 3区
b
x
0 ca
在 0 < x < a 一个周期的区域中,电子的势能为
0 (0 x c) U(x) U0 (c x a)
b=0, U0=∞, P=β2ba/2
见 Kittel 8版 p121Biblioteka 于本题,每个能带里有8条 小分能带
AB
8
a
a
固体物理第五章习题及答案

.
从上式可以看出,当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量 m* 变 为 . 此时电子的加速度
a= 1 F =0
m*
,
即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么?
[解答] 由本教科书的(5.53)式可知, 万尼尔函数可表示为
m* = 1 m 1 + 2Tn
Vn <1.
10. 电子的有效质量 m* 变为 的物理意义是什么?
[解答] 仍然从能量的角度讨论之. 电子能量的变化
(dE)外场力对电子作的功 = (dE)外场力对电子作的功 + (dE)晶格对电子作的功
m*
m
m
=
1 m
(dE ) 外场力对电子作的功
− (dE)电子对晶格作的功
i 2 nx
V (x) = Vne a
n
中, 指数函数的形式是由什么条件决定的?
[解答] 周期势函数 V(x) 付里叶级数的通式为
上式必须满足势场的周期性, 即
V (x) = Vneinx
n
显然
V (x + a) = Vnein (x+a) = Vneinx (eina ) = V (x) = Vneinx
Es (k)
=
E
at s
− Cs
−
Js
e ik Rn
n
即是例证. 其中孤立原子中电子的能量 Esat 是主项, 是一负值, − Cs和 − J s 是小量, 也是负 值. 13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?
福州大学固体物理第五章

2
2
2
εK
k
(k x k y k z )
2m
2m
这就是色散关系,能量随波矢的变化是抛物线函数。
对于一个三维晶体,需要的量子数为:
(1)波矢k(三个分量kx、ky、kz)
(2)自旋量子数 ms 1
2
给定了 k 就确定了能级,k 代表同能级上自旋相反的
一对电子轨道。
在波矢空间自由电子的等能面是一个球面
2 2
εk
(k x k y2 k z2 )
2m
在波矢空间是一球面方程,不同能量的等能面是一
系列同心球面。
➢费米能级和费米面:
在T=0K时,电子的能级与轨道填充时有两个原则:
① 先填能量低的能级
② 服从泡利原理
在T=0K时,由N个电子组成的自由电子系
2
1
3
相应的费米能:
2
kF
2
EF
(3 2 n) 2 / 3
2me
2m
2
也是由电子气的密度唯一地决定。
费米速度:
k F
vF
(3 2 n)1/ 3
m
m
也唯一决定于电子气密度,电子气的密度越大,
F .VF .k F
都越大。
思考: 晶体膨胀时,费米能级如何变化?
如一些典型金属的费米面参数:
面,即E到E+dE之间的体积,可以转化为半径k
到k+dk的两个球面之间的体积。转化公式:
k 2mE /
在波矢空间,波矢为k的球的球体体积为:4/3πk3,
每个k值占的体积为(2π/L)3,每个k又对应自旋相反的一
对电子,则:
2
2
εK
k
(k x k y k z )
2m
2m
这就是色散关系,能量随波矢的变化是抛物线函数。
对于一个三维晶体,需要的量子数为:
(1)波矢k(三个分量kx、ky、kz)
(2)自旋量子数 ms 1
2
给定了 k 就确定了能级,k 代表同能级上自旋相反的
一对电子轨道。
在波矢空间自由电子的等能面是一个球面
2 2
εk
(k x k y2 k z2 )
2m
在波矢空间是一球面方程,不同能量的等能面是一
系列同心球面。
➢费米能级和费米面:
在T=0K时,电子的能级与轨道填充时有两个原则:
① 先填能量低的能级
② 服从泡利原理
在T=0K时,由N个电子组成的自由电子系
2
1
3
相应的费米能:
2
kF
2
EF
(3 2 n) 2 / 3
2me
2m
2
也是由电子气的密度唯一地决定。
费米速度:
k F
vF
(3 2 n)1/ 3
m
m
也唯一决定于电子气密度,电子气的密度越大,
F .VF .k F
都越大。
思考: 晶体膨胀时,费米能级如何变化?
如一些典型金属的费米面参数:
面,即E到E+dE之间的体积,可以转化为半径k
到k+dk的两个球面之间的体积。转化公式:
k 2mE /
在波矢空间,波矢为k的球的球体体积为:4/3πk3,
每个k值占的体积为(2π/L)3,每个k又对应自旋相反的一
对电子,则:
《固体物理·黄昆》第五章(1)

每个代表点的体积
1 1 1 b1 ( b2 b3 ) N1 N2 N3
l1 l3 l2 k b1 b2 b3 N1 N2 N3
( 2 ) Vc
3
状态密度
Vc 3 ( 2 )
3
( 2 ) N N 简约布里渊区的波矢数目 3 ( 2 )
§5.2 周期势场下电子波函数的一般特性:布洛赫定理
布洛赫定理:当势场 V ( r ) 具有晶格周期性时,波动
方程的解具有以下性质
ik Rn (r Rn ) e (r )
了位相因子 e
k 为一矢量。当平移晶格矢量为 Rn ,波函数只增加
ik R n
H i ( r i ) E i ( r i )
能带理论的基本近似和假设:
3)周期性势场假设: 所有离子势场和其它电子的平均场是周期性势场
V ( r ) ( r ) u( r )
V ( r ) V ( r Rn )
在以上单电子近似核晶格周期性势场假定下,多 电子体系问题简化为在晶格周期性势场的单电子 问题:
1 2 3
布洛赫定理
ik Rm (r Rm ) e (r )
平移算符本征值的物理意义
(1) 1
e
ik a1
, 2 e
ik a 2
, 3 e
ik a 3
表征原胞之间电子波函数位相的变化 (2)平移算符本征值量子数
T和 H存在对易关系,则 H的本征函数同时也是各平移 算符T的本征函数 H E T1 1 , T2 2 , T3 3
平移算符的本征值 周期性边界条件
三个方向 a1 , a 2 , a 3 上的原胞数目
1 1 1 b1 ( b2 b3 ) N1 N2 N3
l1 l3 l2 k b1 b2 b3 N1 N2 N3
( 2 ) Vc
3
状态密度
Vc 3 ( 2 )
3
( 2 ) N N 简约布里渊区的波矢数目 3 ( 2 )
§5.2 周期势场下电子波函数的一般特性:布洛赫定理
布洛赫定理:当势场 V ( r ) 具有晶格周期性时,波动
方程的解具有以下性质
ik Rn (r Rn ) e (r )
了位相因子 e
k 为一矢量。当平移晶格矢量为 Rn ,波函数只增加
ik R n
H i ( r i ) E i ( r i )
能带理论的基本近似和假设:
3)周期性势场假设: 所有离子势场和其它电子的平均场是周期性势场
V ( r ) ( r ) u( r )
V ( r ) V ( r Rn )
在以上单电子近似核晶格周期性势场假定下,多 电子体系问题简化为在晶格周期性势场的单电子 问题:
1 2 3
布洛赫定理
ik Rm (r Rm ) e (r )
平移算符本征值的物理意义
(1) 1
e
ik a1
, 2 e
ik a 2
, 3 e
ik a 3
表征原胞之间电子波函数位相的变化 (2)平移算符本征值量子数
T和 H存在对易关系,则 H的本征函数同时也是各平移 算符T的本征函数 H E T1 1 , T2 2 , T3 3
平移算符的本征值 周期性边界条件
三个方向 a1 , a 2 , a 3 上的原胞数目
固体物理第五章
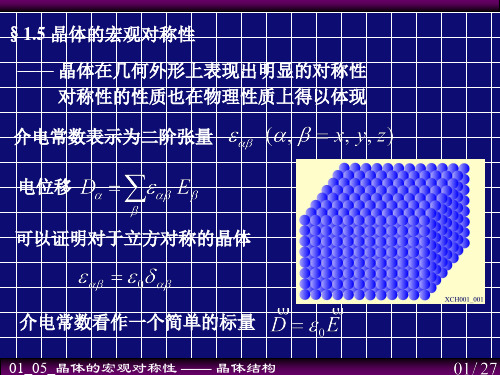
—— 绕z轴转θ角的正交矩阵 轴转θ 轴转
—— 中心反演的正交矩阵
—— 空间转动,矩阵行列式等于+1 空间转动,矩阵行列式等于+ —— 空间转动加中心反演,矩阵行列式等于-1 空间转动加中心反演,矩阵行列式等于-
01_05_晶体的宏观对称性 —— 晶体结构
对称操作 —— 一个物体在某一个正交变换下保持不变 —— 物体的对称操作越多,其对称性越高 物体的对称操作越多, 1 立方体的对称操作 1) 绕三个立方轴转动
01_05_晶体的宏观对称性 —— 晶体结构
所有正实数(0 除外)的集合 的集合, 正实数群 —— 所有正实数 除外 的集合,以普通乘法为 运算法则 所有整数的集合, 整数群 —— 所有整数的集合,以加法为运算法则
—— 一个物体全部对称操作的集合满足上述群的定义 一个物体全部对称操作 全部对称操作的集合满足上述群的定义 运算法则 —— 连续操作
平行轴(六角轴) 平行轴(六角轴)的分量 垂直于六角轴平面的分量 —— 由于六角晶体的各向异性,具有光的双折射现象 由于六角晶体的各向异性, —— 立方晶体的光学性质则是各向同性的
01_05_晶体的宏观对称性 —— 晶体结构
晶体的宏观对称性的描述 —— 原子的周期性排列形成晶格,不同的晶格表现出不 原子的周期性排列形成晶格, 同的宏观对称性 概括晶体宏观对称性的方法是考察晶体在正交变换的不变性 —— 三维情况下,正交变换的表示 三维情况下,
如果A为对称操作 如果 为对称操作 —— 这样可以简化 阶张量 这样可以简化n阶张量
01_05_晶体的宏观对称性 —— 晶体结构
—— 正四面体晶体上述结论亦然成立 —— 介电常数的论证和推导也适合于一切具有二阶张量形 式的宏观性质:如导电率、热导率……等 式的宏观性质:如导电率、热导率 等
固体物理:第五章 晶体中电子能带理论

电子在一个具有晶格周期性的势场中运动
V r V
r
Rn
其中 Rn 为任意格点的位矢。
2 2 2m
V r
E
2. 布洛赫定理
当势场具有晶格周期性时,波动方程的解具有如下性质:
(
r
Rn
)
eikRn
(
r
),
其中 k
为电子波矢,Rn
n1 a1 n2 a2 n3 a3
是格矢。
个能级分裂成N个相距很近的能级, 形成一个准连续的能带。 N个原子继续靠近,次外壳层电子也开始相互反应,能级 分裂成能带。
能带理论
能带论是目前研究固体中的电子状态,说明固体性质最重 要的理论基础。
能带理论是用量子力学的方法研究固体内部电子运动的理 论。它曾经定性地阐明了晶体运动的普遍特点,并进而说 明了绝缘体与半导体、导体的区别所在,解释了晶体中电 子的平均自由程问题。
原子中的电子处在不同的能级上,形成电子壳层
原子逐渐靠近,外层轨道发生电子的共有化运动——能级分裂
原子外壳层交叠的程度最大,共有化运动显著,能级分裂的很厉害, 能带很宽;
原子内壳层交叠的程度小,共有化运动很弱,能级分裂的很小,能 带很窄。
N个原子相距很远时,相互作用忽略不计。 N个原子逐渐靠近,最外层电子首先发生共有化运动,每
第五章 晶体中电子 能带理论
表征、计算和实验观测电子结构是固体物理学的核心问题; 这是因为原则上研究电子结构往往是进一步解释或预言许 多其他物理性质的必要步骤。
晶体电子结构的内涵是电子的能级以及它们在实空间和动 量空间中的分布。
玻尔的原子理论给出这样的原子图像:电子在一些特定的可能轨道 上绕核作圆周运动,离核愈远能量愈高,当电子在这些可能的轨道 上运动时原子不发射也不吸收能量,只有当电子从一个轨道跃迁到 另一个轨道时原子才发射或吸收能量,而且发射或吸收的辐射是单 频的。
固体物理第五章

三维晶体中单个电子在周期性势场中的运动问题处理 能量本征值的计算 能量本征值 选取某个具有布洛赫函数形式的完全集合 布洛赫函数 晶体中的电子的波函数按此函数集合展开 将电子的波函数代入薛定谔方程 确定展开式中的系数应满足的久期方程 求解久期方程得到能量本征值 电子波函数的计算 根据能量本征值确定电子波函数展开式中的 系数得到具体的波函数 在不同的能带计算模型和方法中采取的理论框架相 同,只是选取不同的函数集合
b1 , b2 , b3 ——倒格子基矢
满足 ai ⋅ b j = 2πδ ij
2π i
λ1 = eik ⋅a , λ2 = eik ⋅a , λ3 = eik ⋅a 平移算符的本征值
1 2
3
平移算符的本征值 λ1 = e
ik ⋅a1
, λ2 = eik ⋅a2 , λ3 = eik ⋅a3
ˆ ( R ) = T n1 (a )T n2 (a )T n3 (a ) 作用于电子波函数 ˆ ˆ ˆ 将T n 1 1 2 2 3 3
电子波函数
uk + Kn (r ) = =
n
=e
ik ⋅ Rn
- - -K h ⋅ Rn = 2πμ
∑
h
a ( k + K n + K h )e i K h ⋅ r a ( k + K l )e
n
∑
l
i ( K 43; K ( r ) = e i(k + K
=
)⋅ r
uk + Kn (r )
能带理论——单电子近似的理论
将每个电子的运动看成是独立的在一个等效势 运动 场中的运动 单电子近似 最早用于研究多电子原子 哈特里-福克自洽场方法 自洽场 能带理论的出发点 电子不再束缚于个别的原子,而在整个固体内运动 个别的原子 共有化电子
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Planck distribution Consider a set of identical harmonic oscillators in thermal equilibrium.
N n1 / N n exp( / k BT ) exp( / )
then
N n N 0 exp( n / )
n
1 exp( / ) 1
<n>
4
3
2
1
0
0
x k BT /
1
2
3
4
The energy of the phonons with wavevector K and polariztion p
U K , p nK , p K , p K , p exp( K , p / ) 1
N0 0 <n>
s
N n N 0 exp( n / )
n
1 d x s s x , and sx x x 1 x dx s 1 x s s
n
s exp( s / ) exp( s / )
s s
1 exp( / ) 1
The average excitation quantum number of an oscillator is
n
sN N
s s
s
s exp( s / ) exp( s / )
s s
s
N
N
s
s
The total number and the total energy inside the square are same as those of the oscillators.
U d D p ( )
p
K , p exp( K , p / ) 1
D p ( ) dN p / d
The lattice heat capacity is
Clat x 2 exp x U k B d D p ( ) 2 T (exp x 1 ) V p
Density of states in one dimension Consider vibrations of a 1d line of length L carrying N+1 particles at separation a.
There are two equivalent methods for enumerating the number of the mode. Method 1: fixed boundary conditions
Method 2: periodic boundary conditions
(N+1)
u( sa) u( sa L)
N1
N
s=1
2 3 4 . .
us u (0) exp[i ( sKa K , p t )],
with
2 4π 6π Nπ K 0, , , , ... , . L L L L
dN dN dK L d D( ) d dK d dK
1
The density of the state with the periodic boundary condition:
dN dN dK L d D( ) d dK d 2 dK
exp[ i ( K x x K y y K z z )] exp{i[ K x ( x L) K y ( y L) K z ( z L)]}
whence
2 4 N K x , K y , K z 0, , , ... , L L L
Therefore there is one allowed value of K per volume (2/L)3 in K space.
D ( ) (VK 2 / 2 2 )( dK / d ) V ( / v) 2 1 V 3 2 2 v 2 2 v 3
The cutoff frequency D:
D (6 2v 3 N he cutoff wavevector KD:
Phonon heat capacity
phonon gas
U the heat capacity at constant volume CV T V the lattice heat capacity Clat
The total energy of the phonons at a temperature ( kBT) in a crystal is the sum of the energies over all phonon modes:
for / a K / a
There are three polarizations p for each value of K: 2 transverse modes, 1 longitudinal mode. The number of allowed K values in a single branch for the 1st Brillouin zone equals to the number of the primitive cells. The number of modes equals to the total degrees of the freedom. The density of the state with the fixed boundary condition:
Chapter 5
Key points:
Phonons II. Thermal properties
• Phonon heat capacity • Density of state • Debye model and Einstein model • Thermal expansion • Thermal conductivity
Due to the fixed boundary condition, The wavevector K is
2 3 ( N 1) K , , , ... . L L L L The number of mode is equal to the number of particles allowed to move. There is one mode for ach interval K = /L, so that the number of modes per unit range of K is L/ for K /a, and 0 for K > /a. dN / dK L / , for 0 K / a
The total energy in thermal equilibrium is K , p U U K , p K p K p exp( K , p / ) 1 Suppose that the crystal has Dp( )d modes of a given polarization p in the frequency range to + d . Then the energy is
Method 2: periodic boundary conditions
Method 1: fixed boundary conditions
L
Fixed
s=0 1
Fixed a ui-1 … … …… i1 i i+1 …… N-1 N
us u (0) exp( iK , p t ) sin sKa
. .
.
..
. i+1 ui i
i1
.
..
.
a
For periodic boundary conditions the number of modes per unit range of K is L/2 for /a K /a, otherwise 0.
dN / dK L / 2 ,
U U K , p nK , p K , p
K p K p
where <nK,p> is the thermal equilibrium occupancy of phonons of wavevector K and polarization p, and is given by the Planck distribution function: 1 nK , p exp( / ) 1
There is NO wavevector larger than KD in Debye model.
The thermal energy for each polarization:
U p d D( p ) n( p ) p V 2 v
2 3
D
The total number of modes with wavevector less than K for a given polarization and a given branch is:
N ( K ) ( L / 2 )3 (4K 3 / 3)
The density of states for each polarization is
where
x / k BT
The central problem is to find D(), the number of modes per unit frquency range. D() is called the density of modes or density of states (DOS). The best practical way to obtain the density of state is to measure the dispersion relation vs K in selected crystal directions by inelastic neutron scattering and then to make a theoretical analytic fit to give the dispersion relation in general direction, from which D() may be calculated.
