云南师大附中2018届高考适应性月考(七)文科数学(含解析)
云南师大附中2018届高考适应性月考卷(七)

英语参考答案·第1页(共9页)1 云南师大附中2018届高考适应性月考卷(七)英语参考答案第一部分 阅读理解(共两节,满分40分)第一节 (共15小题;每小题2分,满分30分)1~5 ACBDB 6~10 DACBD 11~15 ACDAB第二节 (共5小题;每小题2分,满分10分)16~20 BADEG第二部分 语言知识运用(共两节,满分45分)第一节 (共20小题;每小题1.5分,满分30分)21~25 CBABD 26~30 ACACB 31~35 DBCDB 36~40 DCADA第二节 (共10小题;每小题1.5分,满分15分)41.are drawn42.to shop 43.Whatever 44.one/a 45.to 46.admiration 47.celebrated 48.symbols 49.Traditionally 50.which 第三部分 写作(共两节,满分35分)第一节 短文改错(共10小题;每小题1分,满分10分)Dear Li Lei ,I ’m proud to tell you what you heard of is true .As is proved ,that some UK primary schools will use 36 math textbooks ,exercise books ,①and teachers ’ guides publishing by the Shanghai Century Publishing (SCP ).The textbooks will be②publishedused in both Shanghai or the UK at a same time .It is the first time Chinese textbooks had been adopted③and ④the ⑤haveby a developed country in so a systematic and large-scale way .The textbooks have ∧listed as a sample⑥such ⑦beenby the National Centre for Excellence in the Teaching of Mathematics of the UK .Without SCP ’s英语参考答案·第2页(共9页)2 ⑧Withpermission ,British publisher Harper Collins ,the UK publisher of the textbooks ,will be responsibly⑨responsiblefor the promotion of the schoolbooks .Don ’t we take pride in you Chinese?⑩usYours , Li Hua第二节 书面表达(满分25分)【参考范文】Dear Jerry ,Tomorrow is the Chinese festival “Dragon Boat Festival ”.I would like to invite you to have the day with my family in my home .On “Dragon Boat Festival ”in China ,families conventionally get together to have a big dinner eating Zong Zi and other delicious foods to remember an outstanding man named Qu Yuan .How desperate I am to share the Chinese happiness and delicate fine dining with you .Meanwhile I will tell you Chinese stories behind the festival .I ’m sure you ’ll take an interest .If you can come ,I ’ll wait for you at 4:00 pm after school at the school gate .We ’ll take Bus 66 at the nearest stop .All my families really long for your acceptance and coming .Best wishes .Yours sincerely , Li Hua【解析】第一部分 阅读理解第一节A【语篇导读】娱乐类应用文。
云南省2018届高三数学试题(文科)

云南师大附中2018届高考适应性月考卷(七)文科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)题号123456789101112答案C D C D D A B B C A AB【解析】1.A =(33)-,,B 是自然数集,所以A B ={012},,,故选C .2.由反函数定义可知恒过点(21),,故选D .3.1z =,||z =∴C .4.由正弦定理可得外接圆半径22sin BC R A ==,故选D .5.S =,故选D .6.00m n =>,时表示直线,0m n >>时表示椭圆,0m n < 时表示双曲线,故选A .7.221q q =+且0q >,1q =∴,故选B .8.直线l :y x =与双曲线C 左右支各有一个交点,则1b a>,总基本事件数为16,满足条件的基本事件数为6,概率为38,故选B .9.由题可知若q 是假命题,则至少可选择BC ,与单选题矛盾,故q 是真命题;若p 是真命题,则至少可选择AB ,与单选题矛盾,故p 是假命题,故选C .10.由二进制数和十进制数的关系可得满足条件的数可表示为222 (04)a b c a b c ++<<≤≤,故10m =,故选A .11.设2112x A x ⎛⎫ ⎪⎝⎭,,2222x B x ⎛⎫ ⎪⎝⎭,,12AB l y kx =+:,联立得2210x kx --=,122x x k +=,121x x =-,2112AQ x l y x x =-:,2222BQ x l y x x =-:,121222x x x x Q +⎛⎫ ⎪⎝⎭,,QA QB ⊥,QF AB ⊥,所以①③正确,故选A .12.令()f x t =,由()f x 的图象可得,20t at b ++=的两根分别为1102t ⎛⎫∈ ⎪⎝⎭,,2112t ⎛⎫∈ ⎪⎝⎭,故01104210b a b a b >⎧⎪⎪++<⎨⎪++>⎪⎩,,,由线性规划可得5212a b ⎛⎫+∈-- ⎪⎝⎭,故选B .二、填空题(本大题共4小题,每小题5分,共20分)题号13141516答案125000π4π410π【解析】13.2500500=总数,故红嘴鸥总数为125000.14.π||||cos 4a b a b θθ== ,.15.令sin cos [1t t αα+=∈,,2sin 21t α=-,220t t -+=,解得t =11)2±=,t =,π4α=.16.可证A N BCN'⊥平面,π2BNC ∠=,BCN △外接圆半径为,外接球半径2r =,外接球的表面积为10π.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)解:(Ⅰ)已知1232n n n a a a ++++=,由于{}n a 是等差数列,设公差为d ,整理得212()33n n n n a a a a d +++-+-==,∴1d =,…………………………………(4分)∴1(1)n a a n d n =+-=.……………………………………………………………(6分)图2(Ⅱ)(1)n n n b a =-, n n n b n n ⎧=⎨-⎩,为偶数,,为奇数,数列{}n b 的前2018项和为20181009S =.……………………………………………(12分)18.(本小题满分12分)解:(Ⅰ) 116y y -≈, 2213y y -≈-, 339y y -≈-, 4417y y -≈,y981244 y3212127e 6−13−917残差图如图1.图1……………………………………………………………………………………(6分)(横坐标取为评分或因变量都给分)(Ⅱ)22121ˆ()575110.36892.75(ni i i n i i y y R y y ==∑-=-=-≈∑-,猫眼评分解释了36%的上座率.(若答模型拟合效果好坏也可以给分)………………………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:如图2,取DC 中点M ,连接AM ,BM ,3AC BC AD BD ====∵,DC AM ⊥∴,DC BM ⊥,BM AM M = ,DC ABM ⊥∴平面,AB ABM ⊂平面,CD AB ⊥∴.……………………………………………………………………………(6分)(Ⅱ)解:13BEF ABC S S =△△,13E BDF D BEF D ABC V V V ---==,AM BM ==,2ABM S =△,18233D ABC C BAM D BAM ABM V V V CM S ---=+== △,1839E BDF D ABC V --==.………………………………………………………………(12分)20.(本小题满分12分)解:(Ⅰ)由(0)D a -,关于y b =-对称得到点(2)C a b --,,(2)C a b --,在光线直线方程上,CF的斜率为,222211b a c a b c ⎧=⎪-⎪=⎨⎪=+⎪⎩,,2a b ==∴,,∴椭圆Γ的方程为22143x y +=.……………………………………………………(4分)(Ⅱ)由||||FP FM MP += 得π2MFP ∠=,直线AB l y kx k =+:,联立22143y kx k x y =+⎧⎪⎨+=⎪⎩,,得2222(34)84120k x k x k +++-=,222433434k k M k k ⎛⎫- ++⎝⎭,,34OM l y x k =-:,34m P m k -⎛⎫ ⎪⎝⎭,,直线FP 与直线AB 垂直1m ≠-,314(1)m k k m -=-+ ,4m =-.………………………………………………………………………………(12分)21.(本小题满分12分)解:(Ⅰ)()sin f x x x =-+,()cos f x x x '=+,(0)1f '=,(0)0f =,故()f x 在(0(0))f ,处的切线方程为y x =.…………………………………………(4分)(Ⅱ)连续函数()sin h x x x ax =-+,(0)0h =,[0π]x ∀∈,都有()0h x ≥成立,则必须满足(0)0h '≥,()cos h x x x a '=+-,解得1a ≤,π()cos 2sin 6h x x x a x a ⎛⎫'=+-=+- ⎪⎝⎭,ππ7π[0π]666x x ⎡⎤∈+∈⎢⎥⎣⎦,,,,π2sin [12]6x ⎛⎫+∈- ⎪⎝⎭,.当1a -≤时,()0h x '≥,()h x 在[0π],上单调递增,()(0)0h x h =≥;当11a -<≤时,由于在2π03⎡⎫⎪⎢⎣⎭,上()0h x '≥恒成立,()h x '在2ππ3⎡⎤⎢⎥⎣⎦,上单调递减,(π)0h '<且2π03h ⎛⎫' ⎪⎝⎭≥,存在唯一02ππ3x ⎡⎤∈⎢⎥⎣⎦,使得0()0h x '=,在0[0)x ,上()h x 单调递增,在0[π)x ,上()h x 单调递减,()(0)0h x h =≥,()(π)ππ0h x h a =->≥≥,1a ∴≤.…………………………………(12分)22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)2214C x y +=:,222194x y C +=:.………………………………………(5分)(Ⅱ)A B ,两点关于坐标原点O 对称,P 是曲线2C 上的动点,22222()()4444PA PB PA PB PO BA PA PB PO +---===- ,2[49]PO ∈ ,,所以PA PB 的取值范围为[05],.…………………………………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】(Ⅰ)解:已知x y ≤,||x y y x -=-,01x ≤≤,10x --≤≤,12y ≤≤,解得02y x -≤≤,0||2x y -≤≤.………………………………………………(5分)(Ⅱ)证明:[01]x ∈,,[12]y ∈,,2x x ≤,(1)(2)0y y --≤成立,即223y y +≤,22161623x y x y +++≥成立,故16383x y x y +++≥,即2216832x y x y --++≥.………………………………(10分)。
云南省师范大学附属中学2018年高三(上)学期第一次月考数学(理)试题(附答案)

云南师大附中2018届高考适应性月考卷(一)理科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.[1)A =+∞,,(1]B =-∞,,故选B . 2.1ii ||11i z z +===-,故,故选D .3.222()25+=++=a b a ab b ,所以||+=a b D . 4.π6πππ2πsin 2sin 2sin 23633y x y x x ⎛⎫⎛⎫⎛⎫⎛⎫=+−−−−−−−→=++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭向左平移个单位,故选C .5.285213a a a +==,所以5132a =,又17747()7352aa S a +===,所以45a =,32d =, 8a =11,故选D .6.当22x y ==,时,z 取得最大值4,故选A .7.由表中数据可得16555.4x y ==,,因为回归直线必过()x y ,,代入回归方程得ˆ43.6a=-,故选B .8.直线平分圆周,则直线过圆心(11),,所以有2a b +=,11111()222a b a b a b ⎛⎫+=++ ⎪⎝⎭≥2112⎫=⎪⎪⎝⎭(当且仅当b =时取“=”),故选D .9.作出sin y x =,|lg |y x =的图象如图1,由图象知有4个零点,故选C .图110.由正弦定理得:::sin :sin :sin a b c A B C =,又::cos :cos :cos a b c A B C =,所以有tan tan tan A B C ==,即A B C ==,所以ABC △是等边三角形,故选B .11.由三视图知:三棱锥S ABC -是底面边长为半径为R,则有:22)4R R =+,解得:R ,故选D .12.由题意知:32()e ln(1)x f x x x =+++在(0)+∞,上单调递增,()()f x t f x +>在(1)x ∈-+∞,上恒成立,必有2t ≥,则(21)f x t +=的根有2个,故选A .二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.36122112121C C rr r rr r T x x --+⎛⎫== ⎪⎝⎭,3602r -=,解得:4r =,代入得常数项为495.14.该程序执行的是11111111112913248102132481045S⎛⎫=+++=-+-++-=⎪⨯⨯⨯⎝⎭.15.由已知:22||||b bc b FM MN a a a ==-,,由||||F M M N =知:22bc b a a =,2c b e ==∴,∴.16.2211()3322b c AH AO AB AC AO ⎛⎫=+=+ ⎪⎝⎭uuu r uuu r uu u r uuu r uuu r g ,又22240b b c -+=,代入得:AH AO =uuu r uuu r g 2221421(4)3226b b b b b ⎛⎫-+=- ⎪⎝⎭,又22240c b b =-+>,所以02b <<,代入得AH AOuuu r uuu r g 的取值范围为203⎛⎫ ⎪⎝⎭,.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)(Ⅰ)证明:因为123n n a a +=+,所以132(3)n n a a ++=+,而11a =,故数列{3}n a +是首项为4,公比为2的等比数列.………………………(5分) (Ⅱ)解:由(Ⅰ)得数列{3}n a +是首项为4,公比为2的等比数列,即132n n a ++=,因此123n n a +=-. 所以1(21)2n n b n +=-,2311232(21)2n n S n +=⨯+⨯++-⨯,① 34221232(21)2n n S n +=⨯+⨯++-⨯,②①−②有231222(22)(21)2n n n S n ++-=+++--⨯,所以2(23)212n n S n +=-+.……………………………………………………………(12分)18.(本小题满分12分)解:(Ⅰ)5160626371748182688x +++++++==甲,5862646669717381688x +++++++==乙,222222222(5168)(6068)(6268)(6368)(7168)(7468)(8168)(8268)8s -+-+-+-+-+-+-+-=甲103=,222222222(5868)(6268)(6468)(6668)(6968)(7168)(7368)(8168)8s -+-+-+-+-+-+-+-=乙45=,所以乙组的成绩更稳定.…………………………………………………………………(6分) (Ⅱ)由题意知ξ服从参数为3,3,7的超几何分布,即(337)H ξ,,,ξ的取值可能为:0,1,2,3,3437C 4(0)C 35P ξ===,214337C C 18(1)C 35P ξ===,124337C C 12(2)C 35P ξ===,3337C 1(3)C 35P ξ===,ξ的分布列为:ξ0 1 2 3 P43518351235135ξ的数学期望:339()77E ξ⨯==.……………………………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:在长方体1111ABCD A B C D -中,因为11M N ACA D ,分别为,的中点,所以MN 为1A CD △的中位线, 所以MN ∥CD , 又因为CD ⊥平面11A ADD ,所以MN ⊥平面11A ADD .…………………………………………………………………(5分) (Ⅱ)解:在长方体1111ABCD A B C D -中,因为CD ⊥平面11A ADD , 所以1CA D ∠为1A C 与平面11A ADD 所成的角, 即1CA D ∠=30︒,又因为1A A ⊥平面ABCD ,所以1ACA ∠为1A C 与平面ABCD 所成的角,即145ACA∠=︒, 所以1MN =,2CD =,14A C =,1A A=AC =如图2,分别以AB ,AD ,1AA 所在直线为x ,y ,z 轴建立空间直角坐标系A xyz -, ∴A(0,0,0),D(0,2,0),1(22C ,,,1(00A ,,,C(2,2,0),B(2,0,0), 在正方形ABCD 中,BD ⊥AC ,∴BD uu u r是平面1A AC 的法向量,(220)BD =-,,uu u r . 设平面1ACD 的法向量为()n x y z =,,r,由(200)DC =,,,1(02DA =-,,,所以有2020x y =⎧⎪⎨-+=⎪⎩,,∴0x y =⎧⎪⎨=⎪⎩,,取z=1,得平面1ACD 的一个法向量为(021)n =,,. 设二面角1A ACD --的大小为α,则|cos |23α==.∴36sin =α.…………………………………………………………………………(12分)20.(本小题满分12分)解:(Ⅰ)00()P x y 设,,代入椭圆的方程有:2200221x y a b +=,整理得:2222002()b y x a a =--,又10y k x a=+,20y k x a=-,所以201222012y k k x a ==--,212212b k ka =-=-联立两个方程有,c e a ==解得:.………………………………(5分) (Ⅱ)由(Ⅰ)知222a b =,又1b =,所以椭圆C 的方程为22121x y +=.图2设直线l 的方程为:1x my =-,代入椭圆的方程有:22(2)210m y my +--=, 设1122()()M x y N x y ,,,, 1212222122m y y y y m m -+==++由韦达定理:,,121||||2OMNS OD y y =-==△所以,(1)t t =≥,则有221m t =-,代入上式有OMNS t t ==+△,当且仅当1t =,即0m =时等号成立,所以OMN △的面积的最大值为.…………………………………………………(12分)21.(本小题满分12分)(Ⅰ)解:22()21b x x bf x x x x ++'=++=,当0b ≥时,在12⎡⎫+∞⎪⎢⎣⎭,上()0f x '≥恒成立,所以()f x 在12⎡⎫+∞⎪⎢⎣⎭,上单调递增成立, 当0b <时,由220x x b ++=,解得x =,易知,()f x在0⎛ ⎝⎭上单调递减,在⎫+∞⎪⎪⎝⎭上单调递增, 由题意有,12≤,解得1b -≥. 综上所述,1b -≥.………………………………………………………………………(5分) (Ⅱ)证明:由(Ⅰ)知,当1b =-时,()f x 在12⎡⎫+∞⎪⎢⎣⎭,上单调递增, 对任意1n ≥,有112n n +≥成立,所以112n f f n ⎛⎫⎛⎫ ⎪ ⎪+⎝⎭⎝⎭≥,代入()f x 有23ln ln 21114n n n n n n ⎛⎫⎛⎫+-+ ⎪ ⎪+++⎝⎭⎝⎭≥, 整理得:2223ln 2ln (1)41n n n n n +⎛⎫-- ⎪++⎝⎭≥. ………………………………………………(12分) 22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)曲线C 的标准方程为:22143x y +=,直线l0y -.………………………………………………(5分)(Ⅱ)将直线l的参数方程化为标准方程:112()x t t y ⎧=+⎪⎪⎨⎪⎪⎩,为参数,,代入椭圆方程得:254120t t +-=,解得12625t t ==-,, 所以12114||11||||||3PA PB t t +=+=.……………………………………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)12(1)()3(12)21(2)x x f x x x x -<-⎧⎪=-⎨⎪->⎩,≤≤,,函数的图象如图3所示.………………(5分)(Ⅱ)由(Ⅰ)知()f x 的最小值是min ()3f x =,所以要使不等式2|1||2|2x x a a ++-+≥恒 成立,有232a a +≥, 解之得[31]a ∈-,.………………………………………………………………………(10分) 图3。
云南省昆明市云南师大实验中学2018年高三数学文月考试题含解析

云南省昆明市云南师大实验中学2018年高三数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 复数z满足z(l﹣i)=﹣1﹣i,则|z+1|=()A.0 B.1 C.D.2参考答案:C【考点】复数求模.【专题】转化思想;综合法;数系的扩充和复数.【分析】根据复数的运算性质计算即可.【解答】解:∵z(l﹣i)=﹣1﹣i,∴z(1﹣i)(1+i)=﹣(1+i)2,∴2z=﹣2i,∴z=﹣i,∴z+1=1﹣i,则|z+1|=,故选:C.【点评】本题考查了复数的化简与模的计算.2. 设等差数列{a n}满足,,S n是数列{a n}的前n项和,则使得的最大的自然数n是()A.7 B.8 C.9 D.10参考答案:C,解得,所以,所以,所以,则最大的自然数是9.故选C。
3.若不等式,对任意正整数恒成立,则实数的取值范围是( ).A. B. C.D.参考答案:答案:A4. 已知函数, 则的值是()A. B. C. D.参考答案:B5. 如图,一个空间几何体的正视图和俯视图都是周长为4,一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为()A.2πB.C.πD.参考答案:C【考点】L!:由三视图求面积、体积.【分析】由已知三视图得到几何体是两个圆锥的组合体,根据数据计算表面积.【解答】解:由已知三视图得到几何体是同底的两个圆锥的组合体,底面半径为,圆锥的高为,所以几何体的表面积为;故选C.6. 下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是()A.y=2x B.y=C.y=|x| D.y=﹣x2+1参考答案:D【考点】函数单调性的判断与证明;函数奇偶性的判断.【专题】函数思想;综合法;函数的性质及应用.【分析】由奇函数和偶函数图象的对称性,根据y=2x和的图象便可判断出A,B错误,而由y=x的单调性便可判断选项C错误,对于D,由偶函数的定义便可判断该函数为偶函数,由该二次函数的图象便可判断出在(0,+∞)上单调递减,从而得出D正确.【解答】解:A.根据y=2x的图象知该函数非奇非偶,∴该选项错误;B.根据的图象知该函数非奇非偶,∴该选项错误;C.x∈(0,+∞)时,y=|x|=x为增函数;即y=|x|在(0,+∞)上单调递增,∴该选项错误;D.显然y=﹣x2+1为偶函数,根据其图象可看出该函数在(0,+∞)上单调递减,∴该选项正确.故选:D.【点评】考查奇函数和偶函数图象的对称性,清楚y=2x和的图象,一次函数的单调性,偶函数的定义,以及二次函数的单调性的判断.7. 设函数的最小正周期为,则(A)在单调递减(B)在单调递减(C)在单调递增(D)在单调递增参考答案:A略8. 如图,在四面体ABCD中,AB=CD=2,AD=BD=3,AC=BC=4. 点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于EFGH,则四边形EFGH面积的最大值是()A. B. C. 1 D. 2参考答案:C作AB中点M,连接CM、DM如图所示,因为AC=BC,M为AB中点,所以;同理有AD=BD,M为AB中点,所以,所以,所以?。
2018年云南省高三高考适应性月考数学(文)试题Word版含答案

2018年云南省高三高考适应性月考数学(文)试题一选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.设集合(){}|ln 1A x y x ==-,集合(){}|ln 1B y y x ==-,则集合()R C A B = A. ()0,1 B. ()1,0- C. (),1-∞ D.()1,+∞ 2.在复平面内,复数12iz i=+的共轭复数对应的点位于 A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限3.已知平面向量,a b满足1,1,a a b a b =⋅=+= b =4.函数()32374f x x x x =---的图象在点()()1,1f --处的切线方程为A. 210x y -+=B. 210x y --=C. 230x y ++=D.230x y +-= 5.以下三个命题中,真命题的个数有()个 ①若11a b <,则a b >;②若a b c >>,则a c b c >;③函数()1f x x x=+有最小值2 A. 0 B. 1 C. 2 D. 36.设实数,x y 满足不等式组211y xy x y ≥⎧⎪-≤⎨⎪≥⎩,则目标函数2z x y =+的最大值为A. 1B. 2C. 3D. 47.元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图1所示,即最终输出的0,x =问一开始输入的x = A.34 B. 78 C. 1516 D. 31328.在长为5的线段AB 上任取一点P ,以AP 为边长作等边三角形,为 A.45 B. 35 C. 25 D.159.要得到函数2sin cos y x x x =的图象,可将函数sin 2y x =的图象A. 向左平移3π个单位 B. 向右平移3π个单位 C. 向左平移6π个单位 D. 向右平移6π个单位10.某几何体的三视图如图2所示,则此几何体的体积为 A.43 B. 83C. 4D. 811.小晶用圆、三角形、正方形按一定规律画图,前八个图形如图3所示,则猜测第2017个图形中共含有的正方形个数为A. 670B. 672C. 335D. 33612.已知函数()()1ln ,0,0x x x f x x x e--<⎧⎪=⎨≥⎪⎩,若方程()()()210f x mf x m m +-+=⎡⎤⎣⎦有四个不等的实数根,则m 的取值范围是 A. 415m -≤<B. 1m ≤-或1m >C. 1m =-或1m >D. 1m =-或01m <<二、填空题:本大题共4小题,每小题5分,共20分. 13.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若4cos ,,353A B a π===,则b = . 14.若P 为圆()2221x y -+=上的动点,则点P 到直线:20l x y -+=的最短距离为 .15.已知三棱锥A BCD -中,3,AB AC BD CD ====且BD CD ⊥,若点A 在平面BCD 内的投影恰好为点D ,则此三棱锥外接球的表面积为 .16.已知双曲线()222210,0x y a b a b -=>>的左、右焦点分别为12,F F ,点53,2P ⎛⎫⎪⎝⎭为双曲线上一点,若12PF F ∆的内切圆的半径为1,则双曲线的方程为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.若数列{}n a 满足111(,n nd n N d a a *+-=∈为常数),则称数列{}n a 为调和数列,现有一调和数列{}n b 满足1211,.2b b ==(1)求{}n b 的通项公式; (2)若数列2nn b c n =+,求{}n c 的前n 项和n S .18.(本题满分12分)心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. (1)求a ,并从频率分布直方图中求出成绩的众数和中位数;(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(]40,50这一段,另一个在(]50,60这一段的概率是多少?19.(本题满分12分)如图5所示,在直角梯形ABCD 中,//,90,1,AB CD ABC CD BC ∠===点E 为AD 边上的中点,过点D 作//DF BC 交AB 于点F ,现将此直角梯形沿DF 折起,使得A FD B --为直二面角,如图乙所示. (1)求证://AB 平面CEF ;(2)若AF ,求点A 到平面CEF 的距离.已知椭圆()222210x y a b a b +=>>过点1,2⎛ ⎝⎭(1)求椭圆的标准方程;(2)已知点()4,0P ,椭圆内部是否存在一个定点,过此点的直线交椭圆于,M N 两点,且12PM PN ⋅= 恒成立,若存在,求出此点,若不存在,说明理由.21.(本题满分12分)已知函数()22.xf x e mx x =--(1)若0m =,讨论()f x 的单调性; (2)若[)0,x ∈+∞时,()12ef x >-恒成立,求m 的取值范围.请考生在第22、23两题中任选一题作答,如果多做,则按照所做的第一题计分. 22.(本题满分10分)选修4-4:极坐标与参数方程已知直角坐标系xoy 中,直线过点()1,0P ,且倾斜角α为钝角,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标.曲线C 的极坐标方程为()2212sin 3ρθ+=(1)写出直线l 的参数方程和曲线C 的直角坐标方程; (2)若56πα=,直线l 与曲线C 相交于不同的两点,M N ,求MN 的长.23.(本题满分10分)选修4-5:不等式选讲 已知函数()(), 3.f x x g x m x ==-- (1)解关于的不等式()()10g f x m +->; (2)已知()()0,,c f a c f b c ><<,求证:()()21.f a b c f c ab +<+2018年云南省高三高考适应性月考数学(文)试题参考答案第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)【解析】 1.由题意,知,∴,故,故选D .2.因为,其共轭复数为,位于第四象限,故选D . 3.由题意,,故,故选B .4.,故,即切线斜率为2,又,故易得切线方程为,故选A .5.当时,①是假命题.当时,②是假命题.函数只有当时才会有最小值,③是假命题,故真命题个数为0,故选A.6.如图1,画出可行域,显然,目标函数在点时取得最大值,最大值为4,故选D.7.即解方程,解得,故选B.8.设,则正三角形面积为,若,则,由几何概型易得知,故选C.9.,则可由的图象向左平移个单位得到,故选C.10.如图2所示,可将此几何体放入一个正方体内,则四棱锥P−ABCD即为所求,易得体积为,故选B.11.通过观察发现一个三角形等于两个圆,一个正方形等于三个三角形,即一个正方形等于六个圆.又,故应有336个正方形,故选D.12.函数的图象如图3所示,令,由图中可知,对于任意,最多有三个解,要想有四个不等的实数根,则方程必有两个不等的实数根,故,故,或.不妨设这两个根为且,则由图象可得,要想有四个不等的实数根,则或或令,即或或解得或,故选D.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.∵,∴,由正弦定理得,即,故.14.最短距离为圆心到直线距离再减去半径.已知圆心为,则圆心到直线的距离为,半径为1,故最短距离为.15.∵平面,故,且知两两垂直,故可将此三棱锥放入一个长、宽、高分别为的长方体内,三棱锥的四个顶点亦为长方体的顶点,其外接球为长方体外接球.易得外接球半径为,故外接球表面积为.16.,且,故得.又,故,.又,联立化简得.又因点在双曲线上,所以,解得,故双曲线方程为.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)解:(Ⅰ)因为为调和数列,故为等差数列,又,故是以1为首项,1为公差的等差数列,…………………………(3分)故,故.…………………………(6分)(Ⅱ),…………………………(8分).………………………(12分)18.(本小题满分12分)解:(Ⅰ)由得.………………(2分)从频率分布直方图得知众数为75.…………………………(3分)40至70的频率为0.32,40至80的频率为0.68,故知中位数在70至80之间,设为,则,解得,故中位数亦为75.…………………………(6分)(Ⅱ)因为共有50个学生,故从频率分布直方图中易知(40,50]这一段有2人,(50,60]这一段有4人.通过列表可知,从这6个人中选2个人共有15种选法,从(40,50]和(50,60]这两段中各选一人共有8种选法,故由古典概型知概率为.……………………(12分)19.(本小题满分12分)(Ⅰ)证明:如图4所示,连接BD,FC交于点O,连接OE.因为BCDF为正方形,故O为BD中点.又E为AD中点,故OE为△的中位线.……………(3分),又平面CEF,∴平面CEF.…………………………(5分)(Ⅱ)解:如图5,连接FC,AC,取FD中点G,连接EG,CG.因为,易得.………………………(7分)因为原图形为直角梯形,折起后A−FD−B为直二面角,故易得平面平面.∴.又,故易得等腰△面积,而.…………………………(10分)设点A到平面CEF的距离为,∵,,即,解得.所以点A到平面CEF的距离为.…………………………(12分)20.(本小题满分12分)解:(Ⅰ)由题意知,.…………………(2分)又点在椭圆上,故椭圆标准方程为.…………………………(4分)(Ⅱ)假设存在.设点.当直线斜率存在且不为0时,设直线方程为.联立化简得.因为过椭圆内的点,故此方程必有两根.,…………………………(6分),,故得.…………………(8分)∵,故有,即,解得或,故直线方程为或.则直线恒过点或(6,0),因为此点在椭圆内部,故唯有点满足要求.…………………………(10分)当直线斜率为0时,过点的直线与椭圆的交点显然即为,,满足.当直线斜率不存在时,过点的直线与椭圆的交点M,N为,亦满足.综上,在椭圆内部存在点满足题目要求.…………………………(12分)21.(本小题满分12分)解:(Ⅰ)当时,.,令,得.易知在上单调递减,在上单调递增.…………………………(4分)(Ⅱ)恒成立,即恒成立.当时,对于任意都成立;…………………………(5分)当时,即恒成立.…………………………(6分)令,则,整理得…………………………(8分)令,注意到,,,故知在单调递增,.故知在单调递增,又.…………………………(10分)故知在(0,1)上为负,上为正.故知(0,1)上递减,上递增.故,故.…………………………(12分)22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)直线的标准参数方程为,曲线的直角坐标方程为.…………………………………(4分)(Ⅱ)∵,∴,,∴把直线代入中,可得.∵P(1,0)在椭圆内部,所以且点M,N在点异侧,设点M,N对应的参数分别为t1,t2,则,,∴.……………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】(Ⅰ)解:由得,∴,∴,∴不等式解集为.……………………………(5分)(Ⅱ)证明:要证,即证,只需证,只需证,只需证,只需证,只需证,又由题意知,,∴,,∴成立,故得证.………………………………(10分)。
云南省师范大学附属中学2018届高考适应性月考卷(二)数学(文)试卷及答案
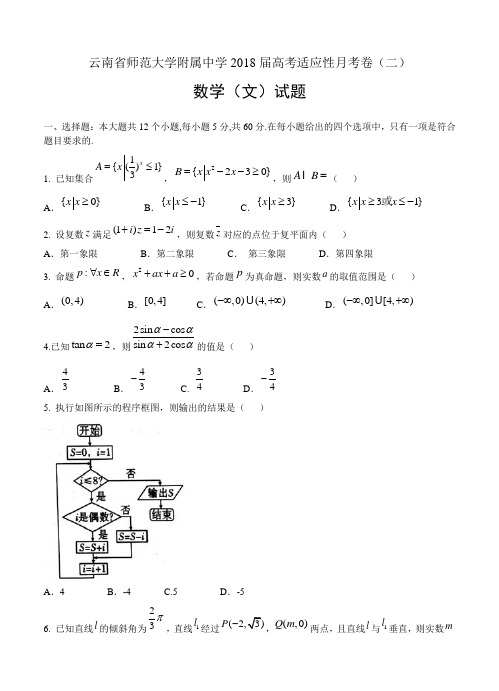
云南省师范大学附属中学2018届高考适应性月考卷(二)数学(文)试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合1{()1}3xA x=≤,2{230}B x x x=--≥,则A B=I()A.{0}x x≥B.{1}x x≤-C.{3}x x≥D.{31}x x x≥≤-或2. 设复数z满足(1)12i z i+=-,则复数z对应的点位于复平面内()A.第一象限B.第二象限C.第三象限D.第四象限3. 命题:p x R∀∈,20x ax a++≥,若命题p为真命题,则实数a的取值范围是()A.(0,4)B.[0,4]C.(,0)(4,)-∞+∞U D.(,0][4,)-∞+∞U4.已知tan2α=,则2sin cossin2cosαααα-+的值是()A.43B.43-C.34D.34-5. 执行如图所示的程序框图,则输出的结果是()A.4 B.-4 C.5 D.-56. 已知直线l的倾斜角为23π,直线1l经过(3)P-,(,0)Q m两点,且直线l与1l垂直,则实数m的值为( )A .-2B .-3 C. -4 D .-5 7.已知等差数列{}n a 中,48a =,1348a a a a +++=( )A .8B .16 C. 24 D .328.若实数,x y 满足不等式组2010220x x y x y -≤⎧⎪-+≥⎨⎪++≥⎩,则23z x y =+的最小值是( )A .-11B .-12 C. -13 D .-149.已知某空间几何体的三视图如图所示,则该几何体的表面积是( )A .122226+B .12226+ C. 12226+ D .122610.已知三棱锥P ABC -的所有顶点都在球O 的球面上,PA AB ⊥,PA AC ⊥,060BAC ∠=,2PA =,2AB =,3AC =,则球O 的表面积为( )A .403πB .303π C. 203π D .103π11. 点P 在椭圆22221(0)x y a b a b +=>>上,12,F F 是椭圆的两个焦点,01260F PF ∠=,且12F PF ∆的三条边2||PF ,1||PF ,12||F F 成等差数列,则此椭圆的离心率是( )A .45B .34 C. 23 D .1212.已知函数11()()2ln f x a x x x =--(a R ∈),()g x ax =-,若至少存在一个01[,1]x e ∈,使得00()()f xg x >成立,则实数a 的取值范围为( )A .(1,)+∞B .[1,)+∞ C. (0,)+∞ D .[0,)+∞ 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量(,2)a m =r ,(2,1)b =-r ,且()2a b b +⊥r r r,则m = .14.已知双曲线22221x y a b -=(0,0)a b >>的焦点与抛物线216x ay =的焦点重合,则双曲线的离心率为 .15.在ABC ∆中,3B π=,3AB =,2BC =,则cos A = .16. 已知函数23,30()ln(1),03x x x f x x x ⎧-+-≤≤=⎨+<≤⎩,若()()33g x f x ax a =--有三个零点,则实数a 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 在ABC ∆中,,,a b c 分别是角,,A B C 的对边,(2)cos cos 0b c A a C --=. (1)求角A 的大小;(2)若2a =,求ABC ∆的面积S 的最大值.18. 为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占47,女生中喜欢数学课程的占710,得到如下列联表. 喜欢数学课程 不喜欢数学课程 合计 男生 女生 合计(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,求抽取的学生中至少有1名是女生的概率..附:2 2()()()()()n ad bcka b c d a c b d-=++++,其中n a b c d=+++.2()P K k≥0.150 0.100 0.050 0.025 0.010 0.005 0.001 0k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 19. 如图,四棱锥P ABCD-的底面ABCD是平行四边形,PA⊥底面ABCD,3PA=,2AD=,4AB=,060ABC∠=.(1)求证:平面PBC⊥平面PAC;(2)若点,M N分别为,PA CD上的点,且35PM CNPA CD==,在线段PB上是否存在一点E,使得//MN平面ACE;若存在,求出三棱锥P ACE-的体积;若不存在,请说明理由.20. 已知函数1()ln1f x a xx=++.(1)当1a=时,求函数()f x的单调区间和极值;(2)是否存在实数a,使得函数()f x在[1,]e上的最小值为1?若存在,求出a的值;若不存在,请说明理由.21. 已知点A为圆228x y+=上一动点,AN x⊥轴于点N,若动点Q满足(1)OQ mOA m ON=+-u u u r u u u r u u u r(其中m为非零常数)(1)求动点Q的轨迹方程;(2)当2m =时,得到动点Q 的轨迹为曲线C ,斜率为-1的直线l 与曲线C 相交于B ,D 两点,求OBD ∆面积的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知直线l 经过点1(1,)2P ,倾斜角3πα=,在以原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=(1)写出直线l 的参数方程,并把曲线C 的极坐标方程化为直角坐标方程; (2)设l 与曲线C 相交于,A B 两点,求PA PB•的值.23.选修4-5:不等式选讲 设函数()221f x x x =--+.(1)解不等式()0f x ≤;(2)若对于x R ∀∈,使2()24f x m m -≤恒成立,求实数m 的取值范围.云南师大附中2018届高考适应性月考卷(二) 文科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)1.{|0}{|31}A x x B x x x ==-≥,≥或≤,∴{|3}A B x x =I ≥,故选C . 2.12i 13i 1i 22z -==--+,13i22z =-+,故选B . 3.对于20x x ax a ∀∈++R ,≥成立是真命题,∴240a a ∆=-≤,即04a ≤≤,故选B .4.∵tan 2α=,∴cos 0α≠,∴2sin cos 2tan 13sin 2cos tan 24αααααα--==++,故选C . 5.由题意可知输出结果为123484S =-+-+-⋅⋅⋅+=,故选A .6.∵11l l k k ==-g ,∴5m =-,故选D .7.∵13248622a a a a a a +=+=,,又2642a a a +=,∴13482642()432a a a a a a a +++=+==,故选D . 8.画出不等式组表示的可行域知,23z x y =+的最小值为14-,故选D .9.由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,PA ⊥平面ABCD ,2PA =,2AB =,4AD =,2BC =,经计算,PD =,PC =,DC =,∴PC CD ⊥,∴12222PAB S =⨯⨯=△, 12442PAD S =⨯⨯=△,122PBC S =⨯⨯△,12PCD S =⨯=△,1(24)262ABCD S =⨯+⨯= ∴122226S =++表,故选A .10.设ABC △外接圆半径为r ,三棱锥外接球半径为R ,∵2360AB AC BAC ==∠=︒,,,∴2222212cos602322372BC AB AC AB AC =+-︒=+-⨯⨯⨯=g g ,∴7BC 2sin60BCr ==︒ 72213,∴21r =,由题意知,PA ⊥平面ABC ,则将三棱锥补成三棱柱可得,22221101293PA R r ⎛⎫=+=+= ⎪⎝⎭,∴210404π4ππ33S R ==⨯=,故选A .11.设1122||||PF r PF r ==,,由椭圆的定义得:122r r a +=,∵12F PF △的三条边2PF ||, 112||||PF F F ,成等差数列,∴1222r c r =+,联立122r r a +=,1222r c r =+,解得12224233a c a cr r +-==,,由余弦定理得:2221212(2)2cos60c r r r r =+-︒g ,将12224233a c a c r r +-==,代入2221212(2)2cos60c r r r r =+-︒g 可得,222243a c c +⎛⎫=+ ⎪⎝⎭ 2422242123332a c a c a c -+-⎛⎫- ⎪⎝⎭g g g ,整理得:2220c ac a +-=,由c e a =,得2210e e +-=,解得:12e =或1e =-(舍去),故选D .12.若至少存在一个011e x ⎡⎤∈⎢⎥⎣⎦,,使得00()()f x g x >成立,则()()0f x g x ->在11e x ⎡⎤∈⎢⎥⎣⎦,有解,即112ln 2ln 0a a x ax x x x x ⎛⎫--+=+> ⎪⎝⎭在11e x ⎡⎤∈⎢⎥⎣⎦,上有解,即2ln a x x >-g 在11e x ⎡⎤∈⎢⎥⎣⎦,上至少有一个x成立,令()2lnh x x x=-g,()2(ln1)h x x'=-+,所以()h x在11e⎡⎤⎢⎥⎣⎦,上单调递减,则min()(1)0h x h==,因此0a>,故选C.13.(23)2(42)a b m b+=-=-r r r,,,,∵()2a b b+⊥r r r,∴(2)(4)320m-⨯-+⨯=,∴72m=.144a,∴2215ba=,∴双曲线的离心率4e==.15.在ABC△中,由余弦定理得2222212cos3223272AC AB BC AB BC B=+-=+-⨯⨯⨯=g g,∴AC=,由正弦定理得2sinsinBC BAAC==g,∵BC AC<,∴π3A B<=,∴cos A.16.由()|()|330g x f x ax a=--=,得|()|333(1)f x ax a a x=+=+,设3(1)y a x=+,则直线过定点(10)-,,作出函数|()|f x的图象(图象省略).两函数图象有三个交点.当30a≤时,不满足条件;当30a>时,当直线3(1)y a x=+经过点(3ln4),时,此时两函数图象有3个交点,此时ln434a=,ln26a=;当直线3(1)y a x=+与ln(1)y x=+相切时,有两个交点,此时函数的导数1()1f xx'=+,设切点坐标为()m n,,则ln(1)n m=+,切线的斜率为1()1f mm'=+,则切线方程为1ln(1)()1y m x mm-+=-+,即1ln(1)11my x mm m=-++++g,∵131am=+且3ln(1)1ma mm=-+++,∴1ln(1)11mmm m=-++++,即1ln(1)111mmm m+=+=++,则1em+=,即e1m=-,则1131eam==+,∴13ea=,∴要使两个函数图象有3个交点,则ln2163ea<≤.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分) 解:(Ⅰ)因为(2)cos cos 0b c A a C --=,所以2cos cos cos 0b A c A a C --=,由正弦定理得2sin cos sin cos sin cos 0B A C A A C --=, 即2sin cos sin()0B A A C -+=,又πA C B +=-,所以sin()sin A C B +=, 所以sin (2cos 1)0B A -=,在ABC △中,sin 0B ≠,所以2cos 10A -=,所以π3A =.(Ⅱ)由余弦定理得:222222cos a b c bc A b c bc =+-=+-,∴42bc bc bc -=≥,∴1sin 42S bc A ===,当且仅当b c =时“=”成立,此时ABC △为等边三角形,∴ABC △的面积S 18.(本小题满分12分)由题意得22120(40153035) 2.05770507545K ⨯⨯-⨯=≈⨯⨯⨯,∵2.057 2.706<,∴没有90%的把握认为喜欢数学课程与否与性别有关.)(Ⅱ)用分层抽样的方法抽取时,抽取比例是624515=,则抽取男生230415⨯=人,抽取女生215215⨯=人. 记抽取的女生为AB ,,抽取的男生为a b c d ,,,, 从中随机抽取2名学生共有15种情况:()()()()()()()()()()()A B A a A b A c A d B a B b B c B d a b a c ,,,,,,,,,,,,,,,,,,,,,,()()()()a d b c b d c d ,,,,,,,.其中至少有1名是女生的事件为:()()()()()()()()()A B A a A b A c A d B a B b B c B d ,,,,,,,,,,,,,,,,,,有9种情况.记“抽取的学生中至少有1名是女生”为事件M ,则93()155P M ==.19.(本小题满分12分)(Ⅰ)证明:由已知,得AC ==,∵2BC AD ==,4AB =,又222BC AC AB +=,∴BC AC ⊥.又PA ⊥底面ABCD ,BC ⊂平面ABCD ,则PA BC ⊥, ∵PA ⊂平面PAC ,AC ⊂平面PAC ,且PA AC A =I ,∴BC ⊥平面PAC .∵BC ⊂平面PBC ,∴平面PBC ⊥平面PAC .(Ⅱ)线段PB 上存在一点E ,使得MN ∥平面ACE .证明:在线段PB 上取一点E ,使35PE PB =,连接ME AE EC MN ,,,,∵35PM PE PA PB ==,∴ME AB ∥,且35ME AB =,又∵CN AB ∥,且35CN AB=,∴CN ME ∥,且CN ME =,∴四边形CEMN 是平行四边形,∴CE MN ∥,又CE ⊂平面ACE ,MN ⊄平面ACE ,∴MN ∥平面ACE .∴3111325552P ACE E PAC B PAC PAC V V V S BC ---====⨯⨯⨯=g △. 20.(本小题满分12分)解:由题意知函数的定义域为{|0}x x >,()1a x af x x x -'=-+=. (Ⅰ)当1a =时,11()1x f x x x -'=-+=, 当01x <<时,()0f x '<,当1x >时,()0f x '>,所以函数()f x 的单调递减区间是(01),,单调递增区间是(1)+∞,. 所以当1x =时,函数()f x 有极小值(1)ln1112f =++=,无极大值.(Ⅱ)①当1a ≤时,函数()f x 在[1e],为增函数, ∴函数()f x 在[1e],上的最小值为(1)ln1112f a =++=,显然21≠,故不满足条件; ②当1e a <≤时,函数()f x 在[1)a ,上为减函数,在[e]a ,上为增函数 故函数()f x 在[1e],上的最小值为()f x 的极小值()ln 1=1f a a a a =-++, 即e a =,满足条件;③当e a >时,函数()f x 在[1e],为减函数, 故函数()f x 在[1e],上的最小值为1(e)ln e 11e f a =++=,即e a =,不满足条件.综上所述,存在实数e a =,使得函数()f x 在[1e],上的最小值为1. 21.(本小题满分12分)解:(Ⅰ)设动点00()()Q x y A x y ,,,,则0(0)N x ,,且22008x y +=,① 又(1)OQ mOA m ON =+-u u u r u u u r u u u r ,得001x x y y m ==,,代入①得动点Q 的轨迹方程为222188x y m +=.(Ⅱ)当2m =时,动点Q 的轨迹曲线C 为22184x y +=.设直线l 的方程为y x b =-+,代入22184x y +=中,得2234280x bx b -+-=,由22(4)43(28)0b b ∆=--⨯⨯->,∴212b <, 设1122()()B x y D x y ,,,,2121242833b b x x x x -+==g ,,∵点O 到直线l 的距离d =||BD2211222OBD b b S d BD +-===g g △,当且仅当2212b b =-,即2612b =<时取到最大值.∴OBD △面积的最大值为22.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)直线l 的参数方程为:112()12x t t y ⎧=+⎪⎪⎨⎪=⎪⎩,为参数,,曲线C 的直角坐标方程为:2213x y +=.(Ⅱ)把直线l的参数方程11212x t y ⎧=+⎪⎪⎨⎪=+⎪⎩,,代入曲线C 的方程2213x y +=中,得221113322t ⎛⎫⎛⎫++= ⎪ ⎪ ⎪⎝⎭⎝⎭,即2104)50t t +-=, 设点A B ,所对应的参数分别为12t t ,,则1212t t =-g , ∴121211||||||||||22PA PB t t t t ===-=g g g .23.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)不等式()0f x ≤,即|2||21|x x -+≤,即2244441x x x x -+++≤,23830x x +-≥,解得133x x -≥或≤, 所以不等式()0f x ≤的解集为133x x x ⎧⎫-⎨⎬⎩⎭≥或≤. (Ⅱ)1321()|2||21|312232x x f x x x x x x x ⎧+<-⎪⎪⎪=--+=-+-⎨⎪-->⎪⎪⎩,,,≤≤,,,故()f x 的最大值为1522f ⎛⎫-=⎪⎝⎭,因为对于x ∀∈R ,使2()24f x m m -≤恒成立, 所以25242m m +≥,即24850m m +-≥, 解得1522m m -≥或≤,∴5122m ⎛⎤⎡⎫∈-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U ,,.。
2018届云南省云南师范大学附属中学高考适应性月考卷(二)数学(理)试题(解析版)

2018届云南省大理市云南师范大学附属中学高考适应性月考卷(二)数学(理)试题一、单选题1.已知集合,,则()A. B. C. D.【答案】C【解析】,∴,故选C.2.设复数满足,则复数对应的点位于复平面内()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B【解析】,,对应点为,故选B.3.命题,,若命题为真命题,则实数的取值范围是()A. B. C. D.【答案】B【解析】对于成立是真命题,∴,即,故选B.4.执行如图所示的程序框图,则输出的结果是()A. 4B. -4C. 5D. -5【答案】A【解析】由题意可知输出结果为,故选A.点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 5.已知直线的倾斜角为,直线经过,两点,且直线与垂直,则实数的值为()A. -2B. -3C. -4D. -5【答案】D【解析】∵,∴,故选D.6.若的展开式中常数项为,则实数的值为()A. B. C. -2 D.【答案】D【解析】的展开式通项为,令,则有,∴,即,解得,故选D.7.将函数()的图象向右平移个单位,得取函数的图象,若在上为减函数,则的最大值为()A. 2B. 3C. 4D. 5【答案】B【解析】由题意可得函数的解析式为,函数的一个单调递减区间是,若函数在区间上为减函数,则,只要,∴,则的最大值为,故选B.点睛:已知函数的单调区间,求参,直接表示出函数的单调区间,让已知区间是单调区间的子集;8.已知某空间几何体的三视图如图所示,则该几何体的表面积是()A. B. C. D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴,,,,∴,故选A.9.已知三棱锥的所有顶点都在球的球面上,,,,,,,则球的表面积为()A. B. C. D.【答案】A【解析】设外接圆半径为,三棱锥外接球半径为,∵,∴,∴,∴,∴,由题意知,平面,则将三棱锥补成三棱柱可得,,∴,故选A.点睛:空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.(2)若球面上四点构成的三条线段两两互相垂直,且,一般把有关元素“补形”成为一个球内接长方体,利用求解.10.点在椭圆上,是椭圆的两个焦点,,且的三条边,,成等差数列,则此椭圆的离心率是()A. B. C. D.【答案】D【解析】设,由椭圆的定义得:,∵的三条边成等差数列,∴,联立,,解得,由余弦定理得:,将代入可得,,整理得:,由,得,解得:或(舍去),故选D.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于的方程或不等式,再根据的关系消掉得到的关系式,而建立关于的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.11.已知函数,,如果对于任意的,都有成立,则实数的取值范围为( )A. B. C. D.【答案】C【解析】对于任意的,都有成立,等价于在,函数,,在上单调递减,在上单调递增,且,∴.在上,恒成立,等价于恒成立.设,,在上单调递增,在上单调递减,所以,所以,故选C .点睛:函数的双变元问题,任意的,都有成立,等价于在,函数,转化为两侧的函数最值问题,先求出最值好求的一边,,转化为恒成立,再变量分离;12.已知圆的半径为2,是圆上任意两点,且,是圆的一条直径,若点满足(),则的最小值为( )A. -1B. -2C. -3D. -4【答案】C【解析】因为,由于圆的半径为,是圆的一条直径,所以,,又,所以,所以,当时,,故的最小值为,故选C.二、填空题13.若实数满足不等式组,则的最小值为__________.【答案】【解析】画出不等式组表示的可行域知,的最小值为.和相交于一点A,,目标函数最小时即截距最小时由图像知在A点取得;故结果为14;14.设数列的前项和为,且,,则__________.【答案】【解析】①,②,①②得:,又∴数列首项为1,公比为的等比数列,∴.故结果为85;15.已知平面区域,,在区域内随机选取一点,则点恰好取自区域的概率是__________.【答案】【解析】依题意知,平面区域是一个边长为的正方形区域(包括边界),其面积为,,如图2,点恰好取自区域的概率.故结果为;点睛:考查集合概型,和积分,利用面积之比求出概率即可;16.已知函数,若有三个零点,则实数的取值范围是__________.【答案】【解析】由,得,设,则直线过定点,作出函数的图象.两函数图象有三个交点.当时,不满足条件;当时,当直线经过点时,此时两函数图象有个交点,此时,;当直线与相切时,有两个交点,此时函数的导数,设切点坐标为,则,切线的斜率为,则切线方程为,即,∵且,∴,即,则,即,则,∴,∴要使两个函数图象有个交点,则.点睛:对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.三、解答题17.在中,分别是角的对边,.(1)求角的大小;(2)若,求的面积的最大值.【答案】(1)(2)【解析】试题分析:(1)先根据正弦定理将边角关系转化为角的关系,再根据两角和正弦公式以及诱导公式化简得,最后根据三角形内角范围求角的大小;(2)由余弦定理得,再根据基本不等式得,最后根据面积公式得最大值试题解析:解:(Ⅰ)因为,所以,由正弦定理得,即,又,所以,所以,在中,,所以,所以.(Ⅱ)由余弦定理得:,∴,∴,当且仅当时“”成立,此时为等边三角形,∴的面积的最大值为.18.为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占,女生中喜欢数学课程的占,得到如下列联表.(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,若所选2名学生中的女生人数为,求的分布列及数学期望.附:,其中.【答案】(1),(2).【解析】试题分析:(1)计算K2的值,根据K2的值,,可得没有以上的把握认为“性别与喜欢数学课之间有关系”.(2)用样本容量乘以男生所占的比例,可得应抽取的男生数,用样本容量乘以女生所占的比例,可得应抽取的女生数.(Ⅰ)列联表补充如下:由题意得,∵,∴没有的把握认为喜欢数学课程与否与性别有关.(Ⅱ)用分层抽样的方法抽取时,抽取比例是,则抽取男生人,抽取女生人,所以的分布列服从参数的超几何分布,的所有可能取值为,其中.由公式可得,,,所以的分布列为:所以的数学期望为.19.如图,四棱锥P ABCD -的底面ABCD 是平行四边形, PA ⊥底面ABCD ,3PA =, 2AD =, 4AB =, 060ABC ∠=.(1)求证:平面PBC ⊥平面PAC ; (2)E 是侧棱PB 上一点,记PEPBλ=(01λ<<),是否存在实数λ,使平面ADE 与平面PAD 所成的二面角为060?若存在,求出λ的值;若不存在,请说明理由.【答案】(1)见解析,(2) 存在35λ=,使平面ADE 与平面PAD 所成的二面角为60︒. 【解析】试题分析:以A 为原点,分别以AD ,AC ,AP 所在直线为x ,y ,z 轴建立空间直角坐标系.求得A (0,0,0),D (2,0,0),P (0,0,3),B (﹣2,,0).设E (x ,y ,z ),由=λ,得E (﹣2λ,,3﹣3λ).求出平面ADE 与平面ADP的一个法向量,结合题意可得λ=.说明存在实数,使平面ADE 与平面PAD 所成的二面角为60°.(Ⅰ)证明:由已知,得AC =∵2BC AD ==, 4AB =, 又222BC AC AB +=,∴BC AC ⊥.又PA ⊥底面ABCD , BC ⊂平面ABCD , 则PA BC ⊥,∵PA ⊂平面PAC , AC ⊂平面PAC ,且PA AC A ⋂=, ∴BC ⊥平面PAC .∵BC ⊂平面PBC ,∴平面PBC ⊥平面PAC .(Ⅱ)解:以A 为坐标原点,过点A 作垂直于AB 的直线为x 轴, AB AP ,所在直线分别为y 轴, z 轴建立空间直角坐标系A xyz -,如图3所示.则()()()000040003A B P ,,,,,,,,,因为在平行四边形ABCD 中, 2460AD AB ABC ==∠=︒,,,则30DAx ∠=︒,∴)10D -,.又(01)PEPBλλ=<<,知()()0431E λλ-,,. 设平面ADE 的法向量为()111m x y z =,,,则·0{ ·0m AD m AE ==,,即()11110{4310y y z λλ-=+-=,, 取11x =,则1m ⎛= ⎝⎭ . 设平面PAD 的法向量为()222n x y z =,,,则·0{ ·0n AP n AD == ,,即22230 0z y =-=,, 取21y =,则10n ⎫=⎪⎪⎝⎭,.若平面ADE 与平面PAD 所成的二面角为60︒,则1cos cos602m n 〈〉=︒= ,11012+=, 2=,即2914λλ⎛⎫= ⎪-⎝⎭,解得3λ=(舍去)或35λ=. 于是,存在35λ=,使平面ADE 与平面PAD 所成的二面角为60︒. 点睛:本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角;20.已知函数.(1)当时,求函数的单调区间和极值;(2)是否存在实数,使得函数在上的最小值为1?若存在,求出的值;若不存在,请说明理由.【答案】(1)单调递减区间是,单调递增区间是.极小值,无极大值.(2)存在实数,使得函数在上的最小值为.【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值(2)先根据导函数是否变化分类讨论:当时,导函数恒为正,所以最小值为;当时,导函数先负后正,所以最小值为;当时,导函数为负,最小值为,最后根据最小值为1,解对应的值。
云南师大附中2018届高考适应性月考卷(五)文数-答案

当直线 l1 , l2 的斜率都存在时,不妨令直线 l1 的斜率为 k(k 0) ,由题意知 l1 的直线方程
为
y
k(x 1)
,联立方程
x2
4
y2 3
1,
消去
y
得
(3 4k 2 )x2
8k 2 x 4k 2
12 0
,设
y k(x 1),
A(x1,y1) , B(x2,y2 )
2.由 z
1 1
i i
1 1
i i
(1 i)2 (1 i)2 (1 i)(1 i)
4i 2
2i ,故选 A.
3.由雷达图可知平均最高气温低于 20 度的月份有一月、二月、十一月、十二月共四个,故选 C.
4.当 x≥0 时, f (x) f (x 2) ,所以当 x≥2 时, f (x 2) f (x 4) ,故而当 x≥2 时,有
的斜率
不存在时, | AB | 3 ,故 | AB | 存在最小值 3 ,故 D 选项不对,故选 D.
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
题号
13
14
15
16
答案
4
128
4
3
【解析】
13.由题意可知,线性区域是如图
5
的阴影部分,由
y
3 4
x
z 4
,
则
z 2 4 ,则圆台的高为 O1O2 7 , AC 5 2 ,所以圆
台的侧面积为
S侧
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
, ,
.
当 时, , 在 上单调递增, ;
当 时,由于在 上 恒成立, 在 上单调递减,
且 ,存在唯一 使得 ,
在 上 单调递增,在 上 单调递减, ,
, .……………………………………(12分)
22.(本小题满分10分)【选修4−4:坐标系与参数方程】
解:(Ⅰ) , .…………………………………………(5分)
3. , ,故选C.
4.由正弦定理可得外接圆半径 ,故选D.
5. ,故选D.
6. 时表示直线, 时表示椭圆, 时表示双曲线,故选A.
7. 且 , ,故选B.
8.直线 : 与双曲线 左右支各有一个交点,则 ,总基本事件数为16,满足条件的基本事件数为6,概率为 ,故选B.
9.由题可知若 是假命题,则至少可选择BC,与单选题矛盾,故 是真命题;若 是真命题,则至少可选择AB,与单选题矛盾,故 是假命题,故选C.
答案
【解析】
13. ,故红嘴鸥总数为125000.
14. .
15.令 , , ,解得
, , .
16.可证 , , 外接圆半径为 ,外接球半径 ,外接球的表面积为 .
三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
解:(Ⅰ)已知 ,
由于 是等差数列,设公差为 ,
(Ⅱ) 两点关于坐标原点 对称, 是曲线 上的动点,
, ,
所以 的取值范围为 .……………………………………………………(10分)
23.(本小题满分10分)【选修4−5:不等式选讲】
(Ⅰ)解:已知 , ,
, , ,
解得 , .…………………………………………………(5分)
(Ⅱ)证明: , , , 成立,
云南师大附中2018届高考适应性月考(七)
云南师大附中2018届高考适应性月考卷(七)
文科数学参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
C
D
D
A
B
B
C
A
A
B
【解析】
1. = , 是自然数集,所以 = ,故选C.
2.由反函数定义可知恒过点 ,故选D.
整理得 ,∴ ,……………………………………(4分)
∴ .…………………………………………………………………(6分)
(Ⅱ) ,
数列 的前2018项和为 .………………………………………………(12分)
18.(本小题满分12分)
解:(Ⅰ) , , , ,
9
8
12
44
3
21
21
27
6
−13
−9
17
残差图如图1.
,
, , ,
, ,
.………………………………………………………………………………(6分)
(Ⅱ)解: ,
,
, ,
,
.…………………………………………………………………(12分)
20.(本小题满分12分)
解:(Ⅰ)由 关于 对称得到点 , 在光线直线方程上,
的斜率为 , ,
∴椭圆 的方程为 .………………………………………………………(4分)
10.由二进制数和十进制数的关系可得满足条件的数可表示为 ,故 ,故选A.
11.设 , , ,联立得 , , , , , , , ,所以 正确,故选A.
12.令 ,由 的图象可得, 的两根分别为 , ,故 由线性规划可得 ,故选B.
二、填空题(本大题共4小题,每小题5分,共20分)
题号
13
14
15
16
即 , 成立,
故 ,即 .…………………………………(10分)
(Ⅱ)由 得 ,直线 ,
联立
得 ,
, , ,
直线 与直线 垂直 , ,
.…………………………………………………………………………………(12分)
21.(本小题满分12分)
解:(Ⅰ) , ,
, ,
故 在 处的切线方程为 .……………………………………………(4分)
(Ⅱ)连续函数 , ,
都有 成立,则必须满足 ,
图1
………………………………………………………………………………………(6分)
(横坐标取为评分或因变量都给分)
(Ⅱ) ,
猫眼评分解释了36%的上座率.
(若答模型拟合效果好坏也可以给分)…………………………………………………(12分)
19.(本小题满分12分)
(Ⅰ)证明:如图2,取 中点 ,连接 , ,
