FLUENT分析圆管弯头段的三维流动
Fluent验证案例001:旋转和静止同心圆筒之间的流动

Fluent验证案例001:旋转和静止同心圆筒之间的流动展开全文1.问题描述对两个同心圆柱体间的定常层流进行模拟。
内部圆筒以恒定的角速度旋转引起流动,外部圆筒保持静止。
流动是稳态的。
利用层流的解析方程可以计算出不同截面的切向速度。
这些数值可用于与仿真结果进行比较。
物性参数几何尺寸边界条件密度:1kg/m^3 内径:17.8mm 内壁角速度:1rad/s粘度:0.0002kg/m.s 外径:46.28mm2.解析解解析解可参考:F. M. White. Viscous Fluid Flow.Section 3-2.3. McGraw-Hill Book Co., Inc..New York, NY. 1991”设内径,角速度,外径,角速度。
这种几何结构使得只有切向速度不为零,变量和p只是半径r的函数。
这使得极坐标下的运动方程简化为如下:连续方程径向动量方程切向动量方程边界条件为:在处,,;在处,;切向动量方程解的形式如下:我们从边界条件可以得到和的值,且在本例中外壁保持静止,即,因此,切向动量方程的解为:3.1选择模型如图,在本例中我们选择层流模型。
3.2设置材料设置密度为1,粘度为0.0002。
3.3边界条件设置内壁面为运动壁面,运动形式为绝对,旋转,角速度为1。
3.4求解方法设置求解方法设置如图所示。
3.5接下来进行初始化和运行求解4.结果对比如图所示,fluent计算的数值解和解析解是比较吻合的。
操作视频见第二条推文。
案例文件链接:https:///s/1jdBLqltMnrJbzYjjYqwGGA提取码:rfuyend后记:本人将毕生致力于CFD,为我国的仿真事业做一点点贡献。
希望在有生之年可以看到国产的CAE软件大规模市场化,而不是被别人卡脖子。
长风破浪会有时,直挂云帆济沧海!。
fluent 案例教程-1圆管层流流动加有障碍通道内流动模拟

3.3 实验一:管内层流流动数值计算3.3.1 计算目的1、初步掌握软件的操作与边界条件设置方法;2、通过模拟计算了解圆管层流的入口段流动与充分发展段流动特点及边界层在入口处生长,然后,不断增加,直至两边相交于管中心线(管子足够长),管段进入充分发展段,在充分发展段形成抛物线分布等知识。
3.3.2 物理问题流体在水平圆管内流动,管径D =0.2 m 管长 L =8 m. 入流速度V in =1 m/ s 截面上速度认为一致,密度ρ=1 kg/ m 3, 粘性系数 µ= 2 x 10-3kg/(ms ). 雷诺数Re 100avg V D ρµ==,其中:V avg =1m/s 为入口平均速度, 应用Fluent 求解。
3.3.3 具体操作在GAMBIT 中创建如下物理模型。
首先,利用轴对称图形,我们创建四个节点。
然后连接各相邻节点,形成矩形。
再形成面。
运行GAMBIT ,选择求解器为Fluent5/6。
3.3.3.1 创建节点与面 (1)创建节点:((0,0.1进入界面:操作:> Vertex Command Button > Create Vertex进入界面:x=0;y=0;z=0,点击Apply. 便创建了vertex.1 (0,0,0)点。
重复操作,创建:V ertex 2: (0,0.1,0),Vertex 3: (8,0.1,0),Vertex 4: (8,0,0) 二维问题,Z轴省略默认为赋值为0。
操作:Global Control > Fit to Window Button可以查看整个图形,如下:(2)将节点连成线操作:> Edge Command Button > Create Edge选择矩形的两个点,点击Apply。
重复以上操作,可得4条线,得到一个矩形:(3)创建面操作:> Face Command Button > Form Face按下SHIFT键,鼠标点击每条边线,释放SHIFT键,则边线被选取,另外也可用以下方法进行操作:点击Edges右边的箭头:调入Edge List 窗口:点击ALL,选择所有边线,如下图。
2004-06 FLUENT流体工程仿真计算实例与应用 韩占忠 王敬 兰小平 北京理工大学出版社

前言回到顶部↑空气、水、油等易于流动的物质被统称为流体。
在力的作用下,流体的流动可引起能量的传递、转换和物质的传送,利用流体进行力传递、进行功和能转换的机械就称为流体机械。
比如,泵是一种将电能转换为流体动能并输送液体的机械;风机是一种将机械能或电能转换为风能的机械;水力发电机就是一种将水的势能和动能转换为电能的一种机械。
此类例子举不胜举,因此,流体机械与我们的生活和工作密切相关。
流体力学就是一门研究流体流动规律以及流体与固体相互作用的一门学科,研究的范围涉及到风扇的设计,发动机内气体的流动以及车辆外形的减阻设计,水利机械的工作原理,输油管道的铺设,供水系统的设计,乃至航海、航空和航天等领域内动力系统和外形设计等等。
自从1687年牛顿定律公布以来,直到本世纪50年代初,研究流体运动规律的主要方法有两种:一是实验研究,以实验为研究手段;另一种是理论分析方法,利用简单流动模型假设,给出某些问题的解析解。
前者耗费巨大,而后者对于较复杂的非线性流动现象目前还有些无能为力。
20世纪70年代以来,飞速发展起来的计算流体力学为实验研究和理论研究都起到了促进作用,也为简化流动模型提供了更多的依据,使很多分析方法得到发展和完善。
实验研究、理论分析方法和数值模拟已成为当前研究流体运动规律的三种基本方法。
任何流体运动的规律都是以质量守恒定律、动量守恒定律和能量守恒定律为基础的。
这些基本定律可由数学方程组来描述,如欧拉方程、N—S方程。
采用数值计算方法,通过计算机求解这些控制流体流动的数学方程,进而研究流体的运动规律,这样的学科就是计算流体力学。
尽管流动规律仍然满足质量守恒定律、动量守恒定律和能量守恒定律,但流体力学不同于固体力学,一个根本原因就在于流体的流动过程中发生了巨大的形变,使问题求解变得异常复杂。
其控制方程属于非线性的偏微分方程,除几个简单问题之外,一般来说很难求得解析解。
为此,对具体问题进行数值求解就成为研究流体流动的一个重要的研究方向和方法,其基础就是计算流体力学。
三维圆管流动状况的数值模拟分析

三维圆管流动状况的数值模拟分析毕业论⽂学⽣姓名:袁洪武学号:20082396学院:⼟⽊⼯程与⼒学学院专业年级:2008⼯程⼒学题⽬:三维圆管流动状况的数值模拟分析指导教师:蒋光彪副教授评阅教师:余敏讲师2012年 5 ⽉摘要在⼯程和⽣活中,圆管内的流动是最常见也是最简单的⼀种流动,圆管流动有层流和紊流两种流动状况。
雷诺数是判别流体流动状态的准则数。
本⽂⽤Fluent软件来模拟研究三维圆管的层流和紊流流动状况,主要对流速分布和压强分布作出分析。
⾸先在Gambit⾥建⽴物理模型,分别建⽴直圆管与90度弯圆管的物理模型,并划-⽅程[]1,分⽹格。
选⽤液体流动的质量守恒⽅程、动量守恒⽅程、能量守恒⽅程以及kε分别对层流和紊流采⽤不同的3种⼊⼝流速来对三维圆管内部流体进⾏模拟分析,并在FLUENT软件中以直观的⽅式表⽰出了层流和紊流各种不同速度在圆管中的流动状况,分析讨论其不同流速下的规律、特点。
并通过⼏种理论⽅式计算验证所得到的数值模拟结果的准确性。
结果证明所得到的数值模拟结果与圆管层流、紊流的理论数据相符合。
关键词FLUENT;光滑圆管;湍流;层流;雷诺数;数值模拟Title The numerical simulation and analysis of the flow in the 3D round tubeAbstract:In engineering and life, circular pipe flow is the most common and the simplest flow, and it contains two flow conditions-aminar and turbulent. Reynolds number is used to distinguish the fluid state criterion. This paper is to simulate study of three-dimensional pipe laminar and turbulent flow by Fluent software, which mainly makes analysis on the velocity distribution and the pressure distribution .First, establish physical model in the Gambit, respectively, set straight circular pipe and 90 degree bend pipe physical model, and then, mesh. Selecting liquid flow equation of mass conservation, momentum conservation equation and energy conservation equation of laminar flow and turbulent flow, we can, respectively, use 3 different entrance velocity to make simulation analysis of 3D pipe internal fluid. In Fluent software , this paper expresses the different velocity of laminar and turbulent flow in pipe flow condition in an intuitive way, discussing pattern and characteristics under different flow, and verifies the accuracy of the numerical results through several theoretical method.Results show that the numerical results are Conformed to the theory datas of Laminar and turbulent flow .Keywords:Fluent; Smooth pipe; Turbulent flow; Laminar flow; Reynolds number;Numerical simulation⽬录1 绪论 (1)1.1课题提出的意义 (1)1.2直接数值模拟⽅法简介 (1)1.3主要研究内容 (2)2直接数值模拟⽅法 (3)2.1FLUENT简介 (3)2.2FLUENT的计算过程 (5)2.3控制⽅程 (6)3 在GAMBIT建⽴中模型 (9)3.1直圆管 (9)3.290度弯管 (10)4 在FLUENT中求解计算层流流动 (11)4.1FLUENT的参数设置 (11)4.2直圆管层流计算结果及分析 (12)4.390度弯管层流计算结果及分析 (18)4.4圆管层流数值模拟结果的验证 (22)5 在FLUENT中求解计算紊流流动 (26)5.1FLUENT参数设置 (26)5.2直圆管紊流计算结果及分析 (26)5.390度弯管紊流计算结果及分析 (33)5.4圆管湍流数值模拟结果验证 (35)6 总结与展望 (38)6.1总结 (38)6.2展望 (38)参考⽂献 (39)致谢 (41)1 绪论1.1 课题提出的意义对实际⼯程中⼤量存在的边界形状复杂的区段内的流动,鉴于其复杂性和测量的困难性,实验往往只能给出总流的参数,却⽆法给粗区段内详细的流场信息,⽽数值模拟能够给出相关流场的具体信息[]2。
fluent实例:冷、热水混合器内的三维流动与换热
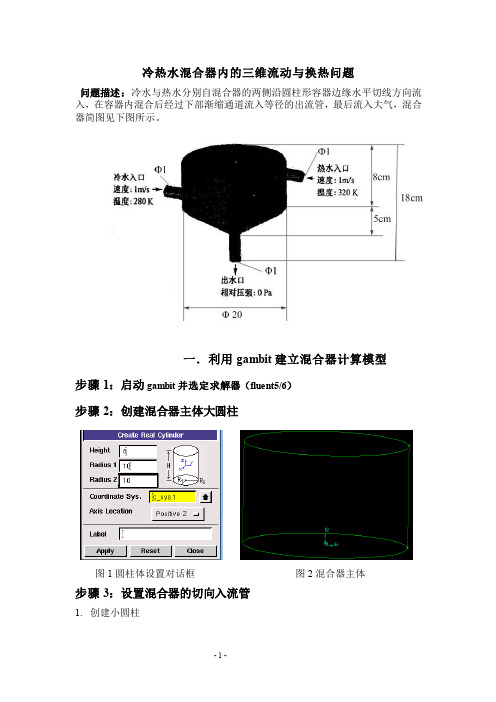
图 33 速度边界设置对话框
2.设置入口 2 的边界条件
图 34 速度入口 2 的设置对话框
- 16 -
2. 设置出流口的边界条件
图 35 出口边界设置对话框
步骤 5:求解初始化
图 36 初始化设置对话框
- 17 -
步骤 6:设置监视器
图 37 监视器设置对话框
步骤 7:保存 case 和 data 文件
步骤 8:求解计算
图 38 迭代计算设置对话框
- 18 -
图 39 残差曲线图
图 40 出口速度监控图
三. 计算结果的后处理 步骤 1:创建等(坐标)值面
1. 创建一个 z=4cm 的平面,命名为 surf-1 2. 创建一个 x=0 的平面,命名为 surf-2
- 19 -
图 41 等值面设置对话框
2.启动能量方程
图 28 能量方程设置对话框
2. 使用 k 湍流模型
- 13 -
图 29 湍流模型设置对话框
步骤 3 设置流体的材料属性
图 30 材料属性设置对话框
- 14 -
图 31 流体材料库对话框
步骤 4 设置边界条件
图 32 边界条件设置对话框
- 15 -
1. 设置入口 1 的边界条件
图 13 出流小管设置对话框
图 14 创建出流小管后的混合器
2.将其移动并与锥台相接
图 15 移动小出流圆管设置对话框
图 16 移动小出流圆管后的混合器
步骤 7 将混合器上部、渐缩部分和下部出流小管组合为一个整体
-5-
图 17 体积列表框
图 18 合并体积后的混合器
步骤 8:混合内区域划分网格
图 19 网格设置对话框
FLUENT算例——TurbulentPipeFlow(LES)圆管湍流流动(大涡模拟)

FLUENT 算例——TurbulentPipeFlow (LES )圆管湍流流动(⼤涡模拟)Turbulent Pipe Flow (LES) 圆管湍流流动(⼤涡模拟)以ANSYS 17.0为例问题描述考虑通过圆形截⾯直管道的流动问题,圆管直径,长度。
管道进⼝处的平均流速为,假设流体密度为定值,,流体动⼒粘性系数。
那么基于圆管直径、平均流速、流体密度、动⼒粘性系数算得该问题的Reynold数(Re)为接下来咱们⽤ANSYS FLUENT中的LES⽅法来求解该流动问题,绘制在距离进⼝处下游截⾯上随着半径变化的平均速度和均⽅根速度,并⽐较由LES⽅法和⽅法模拟得到的平均速度。
1 预分析和准备⼯作预分析在⼤涡模拟中,瞬时速度被分解为滤波后的分量以及剩余的残差分量,滤波后的速度分量表征了⼤尺度的⾮定常运动。
在LES中,⼤尺度的湍流运动被直接表征,⽽⼩尺度的湍流运动则⽤模型近似。
关于滤波速度的滤波⽅程可以从Navier-Stokes⽅程推出,由于残差操作,动量⽅程中的⾮线性对流项引⼊了⼀个应⼒张量的残差项,该残差应⼒张量需要通过构造模型来完成⽅程组的封闭,⽽FLUENT中提供了从易到难的多种模型。
既然咱们要求解,那么LES就是个⾮定常的模拟过程,需要在时域内向前推进。
为了收集统计平均量,⽐如平均和均⽅根(root mean square(r.m.s.))速度,咱们需要⾸先达到统计上的稳定状态(然后再开展统计平均的处理)。
作为对⽐,模型求得的平均速度也⼀并给出。
关于LES的详细理论和⽅程可以再很多湍流的书籍中找到。
准备⼯作LES是三维⾮定常计算(只能适⽤于三维问题和⾮定常问题),那么计算域是全部的管道。
在打开ANSYS之前,先创建⼀个⽂件夹turbulent_pipe_LES,然后⾥⾯在创建⼀个ICEM⽂件夹和FLUENT⽂件夹,分别⽤来存放ICEM的建模和画⽹格⽂件,以及FLUENT的计算⽂件。
2 构建⼏何模型打开ICEM CFD 17.0软件,在其中完成建模⼯作,咱们计算域是圆管内部流道,也就是⼀个圆柱体,让圆柱体的轴线沿着⽅向,进⼝截⾯位于上,圆⼼位于坐标原点。
FLUENT算例 (3)三维圆管紊流流动状况的数值模拟分析

三维圆管紊流流动状况的数值模拟分析在工程和生活中,圆管内的流动是最常见也是最简单的一种流动,圆管流动有层流和紊流两种流动状况。
层流,即液体质点作有序的线状运动,彼此互不混掺的流动;紊流,即液体质点流动的轨迹极为紊乱,质点相互掺混、碰撞的流动。
雷诺数是判别流体流动状态的准则数。
本研究用CFD 软件来模拟研究三维圆管的紊流流动状况,主要对流速分布和压强分布作出分析。
1 物理模型三维圆管长2000mm l =,直径100mm d =。
流体介质:水,其运动粘度系数62110m /s ν-=⨯。
Inlet :流速入口,10.005m /s υ=,20.1m /s υ= Outlet :压强出口Wall :光滑壁面,无滑移2 在ICEM CFD 中建立模型2.1 首先建立三维圆管的几何模型Geometry2.2 做Blocking因为截面为圆形,故需做“O ”型网格。
2.3 划分网格mesh注意检查网格质量。
在未加密的情况下,网格质量不是很好,如下图因管流存在边界层,故需对边界进行加密,网格质量有所提升,如下图2.4 生成非结构化网格,输出fluent.msh等相关文件3 数值模拟原理紊流流动当以水流以流速20.1m /s υ=,从Inlet 方向流入圆管,可计算出雷诺数10000υdRe ν==,故圆管内流动为紊流。
假设水的粘性为常数(运动粘度系数62110m /s ν-=⨯)、不可压流体,圆管光滑,则流动的控制方程如下:①质量守恒方程:()()()0u v w t x y zρρρρ∂∂∂∂+++=∂∂∂∂ (0-1)②动量守恒方程:2()()()()()()()()()()[]u uu uv uw u u ut x y z x x y y z z u u v u w p x y z xρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-2)2()()()()()()()()()()[]v vu vv vw v v v t x y z x x y y z z u v v v w px y z yρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-3)2()()()()()()()()()()[]w wu wv ww w w w t x y z x x y y z z u w v w w px y z zρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-4)③湍动能方程:()()()()[())][())][())]t t k k t k k k ku kv kw k k t x y z x x y yk G z zμμρρρρμμσσμμρεσ∂∂∂∂∂∂∂∂+++=+++∂∂∂∂∂∂∂∂∂∂+++-∂∂ (0-5)④湍能耗散率方程:212()()()()[())][())][())]t t k k t k k u v w t x y z x x y y C G C z z k kεεμμρερερερεεεμμσσμεεεμρσ∂∂∂∂∂∂∂∂+++=+++∂∂∂∂∂∂∂∂∂∂+++-∂∂ (0-6)式中,ρ为密度,u 、ν、w 是流速矢量在x 、y 和z 方向的分量,p 为流体微元体上的压强。
基于fluent圆管数值模拟

已知:圆管的横截面半径0.1m,长度为1m,水流以1m/s的速度从圆管的一端进入。
用fluent模拟管进出口流场模拟。
步骤:
1、用solidworks 画直径为100mm,长度为1000mm的图,另存为1.X_T格式,然后导入ICEM,导入步骤如下图:
选择单位为:Millimeter ,导入ICEM后如下图:
2、创建part,右击模型树Model/Parts/Creat Part,设置part的进口IN,出口OUT,管壁WALL。
Part设置完成后删除没有几何元素的空Part如下图:
创建几何图形的拓扑结构,如下图:创建Body,如下图:
3、定义网格参数
3.1 定义全局网格参数3.2 定义体网格全局参数
3.3 定义棱柱网络全局参数
保存几何模型。
File-geometry-save geometry as ,保存当前几何模型为1.tin
4、生成网格
4.1 生成网格
4.2 检查网络质量
质量检测结果,如下图:
4.3 导出网格
File-mesh-save mesh as,保存当前的网格文件为dz.uns。
步骤如下图:
5、求解计算
打开FLUENT,选择三维求解器
FILE--READ--CASE ,选择生成的网格dz.msh,如下图:
在fluent中的步骤如下图:
求解结果如下图:进口速度模拟:
出口速度模拟:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用FLUENT分析圆管弯头段的三维流动
摘要:简要介绍了Fluent的组成部分和使用步骤,并通过Fluent对黏性流体通过圆管弯头段的三维流动经典案例分析,介绍了用Fluent分析解决实际问题的具体过程,说明了用Fluent 分析流体力学的可行性,从而为解决其它复杂流体问题的优化分析提供了新的方法和科学依据。
关键词: Fluent ;圆管弯头;三维流动
1概述
CFD(计算流体力学)是应用数学方法描述物理和化学现象的一种数据模型模拟工具。
Fluent是目前国际上通用的商业CFD(计算流体动力学)软件包,在国际CFD市场上占主导地位,只要涉及流体、热传递及化学反应等工程问题,都可用Fluent进行解算。
Fluent[1I是用于计算复杂几何条件下流动和传热问题的程序。
它提供的无结构网格生成程序.把计算相对复杂的几何结构问题变得容易和轻松。
可以生成的网格包括二维的三角形和四边形网格。
三维的四面体、六面体及混合网格。
2Fluent程序组成部分和求解步骤
Fluent软件包由以下三部分组成:前处理器:Gambit用于网格生成.是具有强大组合建构模型能力的专用CFD前处理器:求解器是流体计算的核心.可对基于结构化或非结构化网格进行求解:后处理器具有强大的后处理功能。
求解步骤:①确定几何形状,生成计算网格(用Gambit,也可以读入其它指定程序生成的网格);②选择2D或3D来模拟计算;③输入网格;④检查网格;⑤选择解法器;⑥选择求解的方程,层流或湍流(或无粘流)、化学组分或化学反应、传热模型等;确定其它需要的模型:如风扇、热交换器、多孔介质等模型;⑦确定流体物性;⑧指定边界条件;⑨条件计算控制参数;⑩流场初始化;⑩计算;⑩检查结果:⑩保存结果,后处理等。
3 圆管弯头段的三维流动分析实例
1)问题描述
水在一个直径为100mm的
管道内以平均速度v=1m/s
流动,经过一个等径的90
度弯头后进入等径的圆形
管道结构,如图1所示。
对流动过程进行数值模拟
计算,并分析弯管的局部
损失。
图1 管路结构图
2)利用GAMBIT建立圆形弯管道计算模型
首先分别创建圆环和立方体并通过布尔交运算得到管道的弯头,然后再建立直管段来创建圆形玩管道,如图1所示。
设置边界层网格,如图2所示;划分面网格如图3所示;划分体网格如图4所示。
图2边界层网格图3入口端面网格图4管道网格图
3)利用FLUENT 3d求解器进行求解
首先启动FLUENT 3d求解器,读入网格文件;然后依次设置湍流模型、设置边界条件、
设置求解控制参数等等;最后设置残差监视器并设置最大迭代次数为100,经过58次迭代计算,残差达到收敛标准,残差监测曲线如图5所示。
图5残差监测曲线
4)利用FLUENT进行计算结果的后处理
⑪管道受到的水流作用力,沿X轴向和Y轴向的水流冲击力分别如图6和图7所示。
图6 沿X向作用力报告
图7沿X向作用力报告
⑫绘制压力分布云图和速度分布云图,如图8和图9所示.
图8 压力分布云图图9 速度分布云图
⑬显示速度矢量图
分别选择平面Z=0 和y=0的速度矢量图如图10和图11所示;并创建与YZ平面夹角为-45度的平面的速度矢量图,即为弯道截面上的速度矢量图,如图12所示。
⑭显示流体质点轨迹图,如图13所示。
图10 Z=0面的速度矢量图图11 y=0面的速度矢量图
图12 45度截面的速度矢量图图13 流体质点轨迹图
⑮弯头的阻力损失如图14所示。
图14弯头的阻力损失
由图10对话框可知,x=0和y=0平面上的面积加权平均压强分别为768.399Pa 和929.657Pa 。
⑯ 弯头的流动损失 (ⅰ)水头损失 929.657-768.399
0.016510009.81
p h g ρ∆=
==⨯mH 2O (ⅱ)弯头的局部损失系数 222229.810.0165
0.323312h gh v v g
ξ⨯⨯=
=== 4 结语
本文利用FLUENT 的三维流动的数值模拟计算功能,针对圆管弯头段的三维流动过程进行数值模拟计算,并分析计算出了弯管的局部损失。
通过对本经典实例的实际操作分析,使得我对FLUENT 软件的操作过程有了系统的掌握,对FLUENT 软件分析流体力学的优越性有了亲身的体会,并为今后的学习和解决复杂问题奠定了基础。
参考文献
[1] 韩占忠.王敬.兰小平 FLUENT 流体工程仿真计算实例与应用 2010. [2] 胡玉仙.基于FLUENT 软件的泵站进出水流道流动模拟研究. 2004. [3] 许承宣 工程流体力学 1998.。
