习题一 绘制典型信号及其频谱图
matlab绘制正弦信号频谱图(虚频谱、实频谱、单、双边相位谱、单、双边幅频谱)

matlab 绘制正弦信号频谱图(虚频谱、实频谱、单、双边相位谱、单、双边幅频谱)matlab绘制正弦信号频谱图(虚、实频谱、单、双边相位谱、单、双边幅频谱) ⾸先我们今天绘制的正弦信号的函数表达式:f(x)=sin(2*π*f*t),其中f=2. 我使⽤的是matlab2020b,打开matlab后,新建脚本。
我们先画出sin(2*π*f*t)信号的图像: 函数图像如下: 然后对函数进⾏快速傅⾥叶变换、计算实部虚部,绘制幅频谱、相频谱、实频谱、虚频谱。
代码如下:f=2;T =1/f;Fs =100; %采样率Ts =1/Fs;t =0:Ts:1-Ts; %t 范围0~1,步长0.01n =length(t);y =sin(2*pi*f*t); %正弦信号函数sinplot =figure;plot(t,y) %绘制函数图像 x 轴为时间t ,y 轴为信号函数xlabel('时间(s )') %x 轴名称ylabel('信号') %y 轴名称title('原信号图像') %图像顶部名称grid on[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3);%离散绘制幅频谱,取消原图像⼩圆圈,线条粗细3xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5]) %坐标显⽰范围:x 轴-2.5~2.5,y 轴-1.5~1.5CnR =real(Doain); %实部CnI =imag(Doain); %虚部Cn =(CnR.^2+CnI.^2).^(1/2); %幅值fain =tand(CnI./CnR)/3; %相位⾓fain =fain(1,48:54); %去除影响因素figurestem(Range,CnR) %离散绘制gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)axis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('信号')title('原信号图像')grid onfunction[X,freq]=cFFT(x,Fs) %修正N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end 绘制图像如下: 最后附上完整代码:f=2;T=1/f;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*f*t);sinplot=figure[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnI./CnR)/3;fain=fain(1,48:54);figurestem(Range,CnR)gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('信号')grid onfunction[X,freq]=cFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end延迟T/4后的代码fo=2;T=1/fo;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*fo*t-pi/2);sinplot=figure[Doain,Range]=centeredFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnR./CnI)*3.2;fain=fain(1,48:54);figurestem(Range,CnR,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI)gridaxis([-6,6,-2,2])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),abs(fain),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('双边相频谱')xlabel('Hz')figurefain2=fain(1,4:7);stem(Range(1,51:54),abs(fain2),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间(s)')ylabel('y')title('原信号图像')grid onfunction[X,freq]=centeredFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1; % N evenelsek=-(N-1)/2:(N-1)/2; % N oddendT=N/Fs;freq=k/T; %the frequency axisaccordinglyX=fft(x)/N;X=fftshift(X);End⽂件链接: (matlabxinhao1⽂件是本⽂所提到的信号,matlabxinhao2是将本⽂提到的信号延迟T/4之后的信号绘图。
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab 绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变)2、采样频率fs 可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab 编写如下程序:clear;clf; fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); % 信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; % 频率序列subplot(3,3,1),plot(f,yy); % 绘出随频率变化的振幅xlabel('频率八itHz');ylabel(' 振幅');title(' 图1:fs=100 ,N=1024') ; grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %y=fft(x,N); %对信号进行傅里叶变换信号yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; % 频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel(' 频率/\itHz');ylabel(' 振幅');title(' 图2:fs=100,N=1024 ,两种信号叠加'); grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N); yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel(' 频率/\itHz'); ylabel(' 振幅');title(' 图3:fs=100,N=1024 混入噪声');grid on;%改变采样点数N=128N=128; n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); % 信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; % 频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); % 绘出随频率变化的振幅xlabel('频率八itHz');ylabel(' 振幅');title(' 图4:fs=100 ,N=128' ) ;grid on;%改变采样频率为200Hz 时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); % 信号y=fft(x,N); % 对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); % 绘出随频率变化的振幅xlabel(' 频率/\itHz');ylabel(' 振幅');title(' 图5:fs=400 ,N=1024') ;grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); % 信号window=triang(N);% 生成三角窗函数x=x.*window';% 加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; % 频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel(' 频率/\itHz');ylabel(' 振幅');title(' 图6:fs=100,N=1024, 加三角窗函数'); grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); % 信号window=hamming(N);% 生成海明窗函数x=x.*window';% 加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n *fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); % 绘岀随频率变化的振幅xlabel('频率八itHz');ylabel('振幅');title('图7: fs=100 , N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024; n=0:N-1;t= n/fs;x=A*si n(2*pi*B*t+C); % 信号window=hanning(N);%生成汉宁窗函数x=x.*window';% 加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n *fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); % 绘岀随频率变化的振幅xlabel('频率八itHz');ylabel('振幅');title('图8: fs=100 , N=1024,加汉宁窗函数');grid on;三、运行结果如下:15圍丁:fs^lOO,忖=102気抑海明窗函謝團E: N=1O24,^jniJ?宁窗函謝16105 ■ ■■ ■ *°0L. ,■-B F■ . r ■ <10團X f尸ICO昨暹入嗥声20频率阳上图6: {5=100.1^=1024加三甬奮西数20.------------ 1-------- . --------- --------- □1Q 20 33 矶I频率用P频率堀2四、分析与结论:1) 从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
典型周期信号的频谱

2
T
证:an
T
8 T
4 0
f
(t) cosntdt
22
20
f (t) f (t) f (t) f (t T )
2
an T T f (t) cosntdt T T f (t) cosntdt
2
2
T
由复振幅cn 的表达式可知,频谱谱线顶点的联线所
sin x
构成的包络是 x 的形式----称为抽样函数。
1. 找出谐波次数为零的点(即包络与横轴的交点)
包络线方程为
cn
2E
T
sin 2
2
与横轴的交点由下式决定:
sin
2
0
即: ,2 ,3
2
2
0
2
4
6
2m
2f
f
f0
1, 2, 3
T
2 T
2
f (t)e jn1t dt
b.这样定义能确切的反映信号的频谱分布特性。 各个频率分量振幅之间的相对比例关系是固定不 变的。
2.几点说明
a.F ( j) 代表了信号中各频率分量振幅的相对
大小。
|
b.各频率分量的实际振幅为
F ( )
|
d
是无穷
小量。
C. F ( j )具有单位角频率振幅的量纲。
| f (t) | dt 存在。
六.周期和非周期矩形脉冲信号频谱的对比
1.它们都具有抽样函数 sin x 的形式。
2.
Cn
2E
T1
sin n1
2
n1
x
1.画出下列已调波的波形和频谱图(设ωc=5Ω)。(1)u(t)=(1+sinΩt
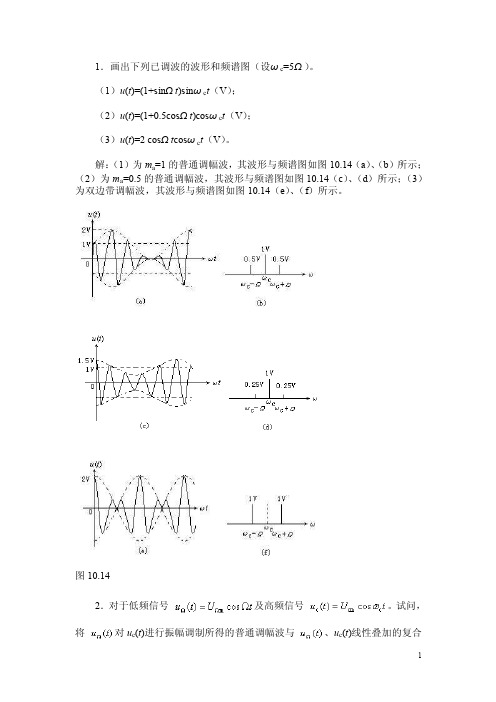
1.画出下列已调波的波形和频谱图(设ωc=5Ω)。
(1)u(t)=(1+sinΩt)sinωc t(V);(2)u(t)=(1+0.5cosΩt)cosωc t(V);(3)u(t)=2 cosΩt cosωc t(V)。
解:(1)为m a=1的普通调幅波,其波形与频谱图如图10.14(a)、(b)所示;(2)为m a=0.5的普通调幅波,其波形与频谱图如图10.14(c)、(d)所示;(3)为双边带调幅波,其波形与频谱图如图10.14(e)、(f)所示。
图10.142.对于低频信号及高频信号。
试问,将对u c(t)进行振幅调制所得的普通调幅波与、u c(t)线性叠加的复合信号比较,其波形及频谱有何区别?解:将对u c(t)进行振幅调制所得的普通调幅波的波形与频谱图参见图10.14(c)、(d),而与u c(t)线性叠加的复合信号的波形与频谱图如图10.15所示。
3.已知已调信号的频谱图如图10.16所示。
(1)说明各频谱所表示的已调信号类型;(2)写出它们的数学表达式和频谱宽度;(3)计算在单位电阻上各调制信号消耗的平均功率。
图10.16解:(1)图(a)为单音调制的普通调幅波;图(b)为双音调制的普通调幅波;图(c)为二次调制的普通调幅波。
(2)图(a)调幅波的数学表达式为(V)频谱宽度BW=1003-997=6(kH Z)同理,图(b)调幅波的数学表达式为(V)频谱宽度BW=1010-990=20(kH Z)图(c)中,第一次调制:两路频率为F=3kH Z的音频信号分别调制到f1=10kH Z 和f2=30kH Z的载频(称为副载频)上,第二次调制:将两路已调信号叠加,再调制到主载频f c=1000kH Z的载频上。
第一次调制:(V)(V)第二次调制:(V)频谱宽度BW=1033-967=66(kH Z)(3)图(a):(W)图(b):(W)图(c):(W)4.已知某普通调幅波的最大振幅为10V,最小振幅为6V,求其调幅系数m a。
信号系统习题及解答

第2章 信号系统习题及解答2-1 绘出下列各时间函数的波形图。
(1)1()(1)f t tu t =-(2)2()[()(1)](1)f t t u t u t u t =--+-(3)3()(1)[()(1)]f t t u t u t =---- (4)4()[(2)(3)]f t t u t u t =--- (5)5()(2)[(2)(3)]f t t u t u t =---- (6)6()()2(1)(2)f t u t u t u t =--+-解:2-5 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。
t图 题2-5(3)3()(36)f t f t =+ (5)511()36f t f t ⎛⎫=-- ⎪⎝⎭解:tt2-6 已知()f t 波形如图题2-6所示,试画出下列信号的波形图。
图 题2-6(4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解:2-7 计算下列各式。
(1)0()()f t t t δ+ (2)00()()d f t t t t t δ∞-∞+-⎰(3)24e (3)d t t t δ-+⎰(4)e sin (1)d tt t t δ∞-+⎰(5)d [e ()]d t t tδ- (6)0()()d f t t t tδ∞-∞-⎰(7)0()()d f t t t tδ∞-∞-⎰(8)00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰(9)00()(2)d t t u t t t δ∞-∞--⎰(10)(e )(2)d t t t t δ∞-∞++⎰(11)(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰(12)j 0e [()()]d t t t t tΩδδ∞--∞--⎰解:(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。
习题一 绘制典型信号及其频谱图
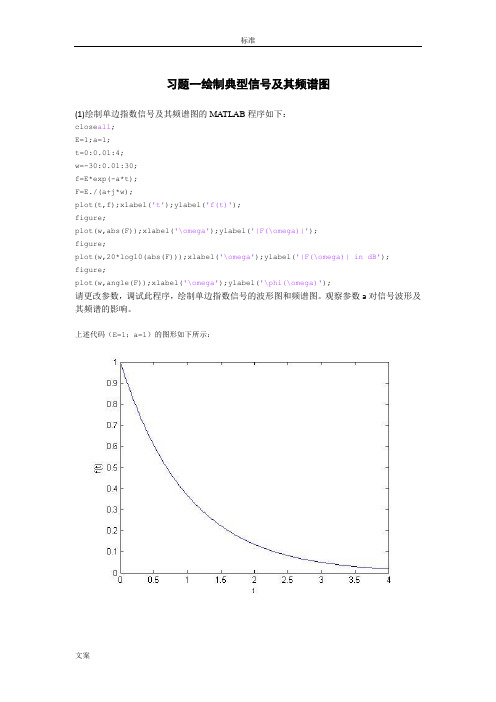
习题一绘制典型信号及其频谱图(1)绘制单边指数信号及其频谱图的MATLAB程序如下:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=E./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');请更改参数,调试此程序,绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
上述代码(E=1;a=1)的图形如下所示:现改变参数再绘制图形:①E=1;a=2;图形如下所示:②E=2;a=1; 图形如下所示:③E=2;a=2; 图形如下所示:由图可知,a越大,单边指数信号的波形图f(t)-t下降越快,其频谱图|F(ω)|-ω、|F(ω)| in dB-ω在ω=0处的峰值越小,φ(ω)-ω的初始近似水平段的值也越小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图,观察并对比各信号的频带宽度和旁瓣的大小。
①矩形脉冲代码如下:close all;E=1;tau=1;t=-4:0.1:4;w=-30:0.1:30;f=E*(t>-tau/2&t<tau/2)+0*(t<=-tau/2&t>=tau/2);F=(2*E./w).*sin(w*tau/2);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');图形如下所示:②升余弦脉冲代码如下:clear all; E=1;tau=1;t=-3:0.1:3;w=-30:0.1:30;f=(E/2*(1+cos(2*pi*t/tau))).*(t>-tau/2&t<tau/2)+0*(t>=tau/2|t<=-tau/2 );Sa=sin(w*tau/2)./(w*tau/2);F=E*tau/2*Sa./(1-(w*tau/2/pi).^2);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');图形如下所示:③三角脉冲代码如下:close all;E=1;tau=1;t=-3:0.1:3;w=-30:0.1:30;f=E*(1-2*abs(t)/tau).*(t<tau/2&t>-tau/2)+0*(t>=tau/2|t<=-tau/2);Sa=sin(w*tau/4)./(w*tau/4);F=E*tau/2*Sa.^2;plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');图形绘制如下:由图可知,三种信号中矩形脉冲相对频带宽度最小,升余弦脉冲和三角脉冲的频带宽度较为接近;旁瓣大小比较结果为:矩形脉冲>三角脉冲>升余弦脉冲。
作业和例题

1-1 以下信号,哪个是周期信号?哪个是准周期信号?哪个是瞬变信号?它们的频谱各具有哪些特征? (1)0cos2t f t e ππ-∙ (2)00sin 24sin f t f t π+ (3) 00cos22cos3f t f t ππ+解答:(1)瞬变信号。
频谱具有连续性、衰减性。
幅频谱是偶函数,相频谱是奇函数。
(2)准周期信号。
频谱具有离散性的特点。
(3)周期信号。
频谱具有离散性、收敛性、谐波性的特点。
1-6 已知某信号x(t)的频谱X(f),求00()cos2()m x t f t f f π>>的频谱,并作频谱图。
若0m f f <,频谱图会出现什么情况?解答:[]000001()cos 2()()()21[()()]2x t f t X f f f f f X f f X f f πδδ⇔*++-=++-频谱图:f若0m f f <,则频谱图会产生混叠现象。
习题1:已知信号 试画出其单边频谱和双边频谱。
单边频谱: ω-n A 、ωϕ-n 双边频谱:ω-n C 、ω-∠n C习题2:已知信号时域表达式问:(1)该信号是属于哪类信号?(2)画出其频谱图。
此信号属于周期信号。
f----=t At A t A A t x 0003sin 32sin 2sin 2)(ωπωπωπ)2t 3cos(cos 4)4cos(32)(2ππ+++++=t t t x 2t 3cos(2cos 24cos(34)(ππ+++++=t t t x )2cos(n n 2n sin n 2)(1n 01n 0πωπωπ++=-=∑∑∞=∞=t A A t A A t x例题:求周期方波信号的频谱。
方法1:利用定义求。
...)3,1n (n 2AC n ±±==π⎪⎪⎩⎪⎪⎨⎧--===-==∠...5,3,-1n 20n0...5,3,1n 2C R C I arctan C n e n m n ππ方法2:利用单边频谱和双边频谱的关系求。
信号系统习题及解答

第2章 信号系统习题及解答2-1 绘出下列各时间函数的波形图。
(1)1()(1)f t tu t =-(2)2()[()(1)](1)f t t u t u t u t =--+-(3)3()(1)[()(1)]f t t u t u t =---- (4)4()[(2)(3)]f t t u t u t =--- (5)5()(2)[(2)(3)]f t t u t u t =---- (6)6()()2(1)(2)f t u t u t u t =--+-解:2-5 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。
t图 题2-5(3)3()(36)f t f t =+ (5)511()36f t f t ⎛⎫=-- ⎪⎝⎭解:tt2-6 已知()f t 波形如图题2-6所示,试画出下列信号的波形图。
图 题2-6(4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解:2-7 计算下列各式。
(1)0()()f t t t δ+ (2)00()()d f t t t t t δ∞-∞+-⎰(3)24e (3)d t t t δ-+⎰(4)e sin (1)d tt t t δ∞-+⎰(5)d [e ()]d t t tδ- (6)0()()d f t t t tδ∞-∞-⎰(7)0()()d f t t t tδ∞-∞-⎰(8)00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰(9)00()(2)d t t u t t t δ∞-∞--⎰(10)(e )(2)d t t t t δ∞-∞++⎰(11)(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰(12)j 0e [()()]d t t t t tΩδδ∞--∞--⎰解:(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题一绘制典型信号及其频谱图
(1)绘制单边指数信号及其频谱图的MATLAB程序如下:
close all;
E=1;a=1;
t=0:0.01:4;
w=-30:0.01:30;
f=E*exp(-a*t);
F=E./(a+j*w);
plot(t,f);xlabel('t');ylabel('f(t)');
figure;
plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');
figure;
plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;
plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');
请更改参数,调试此程序,绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
上述代码(E=1;a=1)的图形如下所示:
现改变参数再绘制图形:①E=1;a=2;
图形如下所示:
②E=2;a=1; 图形如下所示:
③E=2;a=2; 图形如下所示:
由图可知,a越大,单边指数信号的波形图f(t)-t下降越快,其频谱图|F(ω)|-ω、|F(ω)| in dB-ω在ω=0处的峰值越小,φ(ω)-ω的初始近似水平段的值也越小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图,观察并对比各信号的频带宽度和旁瓣的大小。
①矩形脉冲
代码如下:
close all;
E=1;tau=1;
t=-4:0.1:4;
w=-30:0.1:30;
f=E*(t>-tau/2&t<tau/2)+0*(t<=-tau/2&t>=tau/2);
F=(2*E./w).*sin(w*tau/2);
plot(t,f);xlabel('t');ylabel('f(t)');
figure;
plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');
figure;
plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;
plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');
图形如下所示:
②升余弦脉冲代码如下:clear all; E=1;tau=1;
t=-3:0.1:3;
w=-30:0.1:30;
f=(E/2*(1+cos(2*pi*t/tau))).*(t>-tau/2&t<tau/2)+0*(t>=tau/2|t<=-tau/2 );
Sa=sin(w*tau/2)./(w*tau/2);
F=E*tau/2*Sa./(1-(w*tau/2/pi).^2);
plot(t,f);xlabel('t');ylabel('f(t)');
figure;
plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');
figure;
plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;
plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');
图形如下所示:
③三角脉冲
代码如下:
close all;
E=1;tau=1;
t=-3:0.1:3;
w=-30:0.1:30;
f=E*(1-2*abs(t)/tau).*(t<tau/2&t>-tau/2)+0*(t>=tau/2|t<=-tau/2);
Sa=sin(w*tau/4)./(w*tau/4);
F=E*tau/2*Sa.^2;
plot(t,f);xlabel('t');ylabel('f(t)');
figure;
plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');
figure;
plot(w,20*log10(abs(F)));xlabel('\omega');ylabel('|F(\omega)| in dB'); figure;
plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');
图形绘制如下:
由图可知,三种信号中矩形脉冲相对频带宽度最小,升余弦脉冲和三角脉冲的频带宽度较为接近;旁瓣大小比较结果为:矩形脉冲>三角脉冲>升余弦脉冲。
