第19章答案
第19章 爬行纲复习题答案

第19章爬行纲复习题一、填空题1、爬行动物的脊柱分化为(颈椎)、(胸椎)、(腰椎)、(荐椎)、(尾椎)5个部分。
2、爬行动物具有多枚颈椎,其中第一枚称为(环椎),第二枚称为(枢椎),具(2)枚荐椎。
3、爬行动物的牙齿按着生方式可分为(槽生齿)、(侧生齿)、(端生齿),鳄鱼牙齿的着生方式为(槽生)。
4、爬行动物的呼吸方式除具有吞咽呼吸外,又发展了(胸腹式呼吸)。
5、爬行动物心脏由(静脉窦)、(心房)、(心室)组成,其中(静脉窦)趋于退化,(心室)具有不完全的分隔,循环方式为(不完全的双)循环。
6、爬行类适应陆生的最主要特征是皮肤(干燥),缺乏(腺体),(角质层)层较厚,产大型(羊膜卵),(体内)受精。
7、从爬行动物开始,肌肉系统出现了陆生脊椎动物特有的(皮肤肌)和(肋间肌)。
8、五趾型附肢从(两栖)动物开始出现。
盲肠从(爬行)动物开始出现。
9、爬行动物的内耳司听觉感受的(瓶状囊)显著加长。
蜥蜴的听觉器官发达,出现了雏形的(外耳道);蛇类因穴居生活,声波沿地面通过头骨的(方骨)传递给(耳柱骨),从而使内耳产生听觉。
10、爬行动物的的代谢废物以(尿酸)形式排出。
11、胸廓是由(胸椎)、(胸骨)、(肋骨)三部分组成,最早出现胸廓的动物类群是(爬行类)。
二、选择题1、次生腭最完整的爬行动物是(A)。
A、鳄类B、龟类C、蜥蜴D、蛇类2、爬行类从外形上显著区别于两栖类的特征是(D)。
A、具有五趾型附肢B、有尾C、皮肤富有腺体D、皮肤干燥,有角质鳞片或盾片3、次生腭的作用是(D)。
A、使眼球不能下陷B、使头骨更加坚固C、使内鼻孔前移D、使内鼻孔后移,口腔和鼻腔分开4、具有1个枕骨髁的动物是(B)。
A、两栖类和爬行类B、鸟类和爬行类C、鸟类和哺乳类D、两栖类和哺乳类5、在下列动物中,具有颊窝的是(A)。
A、蝮蛇B、眼镜蛇C、蟒蛇D、乌梢蛇6、最早出现枢椎的动物是(B)。
A、两栖类B、爬行类C、鸟类D、哺乳类7、爬行动物的“盐腺”是(B)。
第19章 生存分析思考与练习参考答案

第19章生存分析思考与练习参考答案一、最佳选择题1. 下列有关生存时间的定义中正确的是( E )。
A.流行病学研究中,从开始接触某危险因素至某病发病所经历的时间B.乳腺增生症妇女治疗后阳性体征消失至首次复发的时间C.肺癌患者从手术治疗开始到死亡的时间D.急性白血病患者从治疗开始到缓解的时间E.以上均正确2. 教材表19-18表是急性白血病患者药物诱导后缓解至首次复发的随访记录。
教材表19-18 急性白血病患者药物诱导后缓解至首次复发的随访记录编号缓解日期终止观察日期结局生存时间/天1 2000.04.01 2000.09.06 复发1582 2001.11.05 2002.02.05 死亡913 2000.07.15 2000.12.10 复发1474 2001.05.20 2001.08.25 失访965 2002.09.03 2002.12.31 缓解119……………生存时间属删失数据的有(C)。
A.1号和3号B.1号和2号C.2号、4号和5号D.2号、3号和4号E.1号、2号和3号3. 下列有关log-rank检验的描述中正确的是(A)。
A.log-rank检验是各组生存率的整体比较B.log-rank检验是各组生存率某时间点的比较C.log-rank检验属生存曲线比较的参数法D.log-rank检验中,各组实际死亡数必等于理论死亡数E.log-rank检验的自由度为14. Log-rank检验与Breslow检验相比,( B )。
A.log-rank检验对组间死亡近期差异敏感B.log-rank检验对组间死亡远期差异敏感C.Breslow检验对组间死亡远期差异敏感D.两者对组间死亡远期差异同样敏感E.两者对组间死亡近期差异同样敏感5. Cox回归模型要求两个不同个体在不同时刻t的风险函数之比(D)。
A.随时间增加而增加B.随时间增加而减小C.开始随时间增加而增加,后来随时间增加而减小D.不随时间改变E.视具体情况而定二、思考题1. 生存分析的主要用途及其统计学方法有哪些?答:生存分析在生物医学领域主要解决如下问题。
第19章.一次函数--全品习题答案

19.1 函数19.1.1 变量与函数第1课时 变量(全品第61页) 教师详答1.A [解析] 由于100是不变的,所以是常量,而W 和n 是变化的,因此是变量.故选A . 2.y =0.5x 0.5 x ,y3.[全品导学号:07712121]S ,a 12,h4.解:(1)s =300-50t.(2)300,50是常量,t ,s 是变量.5.V ,R 43,π6.[全品导学号:07712122]解:S =12³3x =32x.常量:32;变量:S ,x.7.[全品导学号:07712123]解:(1)60是常量,S ,x 是变量. (2)R 是常量,V ,h 是变量.19.1 函数19.1.1 变量与函数第2课时 函数(全品第62页)教师详答1.D2.[全品导学号:07712124]C [解析] 根据函数的定义来判断,如果三角形的高一定,则给定一个底边长,相应地就确定了一个三角形的面积的值,所以①不具有函数关系;如果多边形给定一个边数值,相应地就确定了一个多边形的内角和的值,所以②具有函数关系;如果给定一个半径,相应地就确定了一个圆的面积,所以③具有函数关系;④中有两个变量x 和y ,如果给定一个x 值,相应地就确定了一个y 值,所以④具有函数关系.故选C .3.B [解析] 把x =a ,y =1代入,得1=2a -1,解得a =1. 4.解:(1)x 是自变量,y 是x 的函数.y =0.55x.(2)x 是自变量,y 是x 的函数.y =60x.(3)x 是自变量,Q 是x 的函数.Q =20+5x.5.D 6.x ≤237.[全品导学号:07712125]解:(1)Q =800-50t.(2)当抽完水时有0=800-50t ,解得t =16,所以自变量t 的取值范围为0≤t ≤16. (3)当t =10时,Q =800-50t =800-50³10=300(立方米). 答:10小时后,水池中还有300立方米的水.8.[全品导学号:07712126]解:m =n +19(1≤n ≤25,且n 为正整数). (1)m =2n +18 (2)m =3n +17(3)m =(n -1)b +a(1≤n ≤p ,且n 为正整数).19.1 函数 19.1.2 函数的图象第1课时 函数的图象及其画法(全品第63-64页)教师详答1.D2.(1)15 1.1 (2)10 (3)12 0.9 (4)18 (5)22253.[全品导学号:07712127]解:(1)时间t 路程s(2)由图可知:9时、12时所走的路程分别是4千米、15千米. (3)根据图象可得,该旅行者休息的时间为:10.5-10=0.5(时). (4)根据图象可得:(15-9)÷(12-10.5)=4(千米/时).答:他从休息后直至到达目的地这段时间的平均速度是4千米/时.4.C [解析] 根据函数图象的定义,如果点的坐标满足函数解析式,那么这个点就在这个函数的图象上,通过计算,可知选C .5.A [解析] 把x =2,y =3代入y =ax 2-x +1中,有3=4a -2+1,解得a =1.6.[全品导学号:07712128]5 [解析] 根据函数图象的定义知点P(3,m)和点Q(n ,2)都满足函数y =x +8的解析式,所以3+8=m ,n +8=2,解得m =11,n =-6,所以m +n =11+(-6)=5.7点(1,1),(2,3)在函数y =2x -1的图象上,点(-1,0),(-2,3)不在函数y =2x -1的图象上.8.[全品导学号:07712129]C [解析] 向上抛球的过程,球的速度开始最大,而后逐渐变为0,然后又增大,符合条件的图象是C .9.[全品导学号:07712130]C [解析] A 项,根据图象可得,乙前4秒行驶的路程为12³4=48(米),正确;B 项,根据图象可得,在0到8秒内甲的速度每秒增加4米,正确;C 项,根据图象可得,两车到第3秒时行驶的路程不相等,错误;D 项,在4至8秒内甲的速度都大于乙的速度,正确.故选C .10.80 [解析] 从图象可以看出,小明用20分钟行驶的路程是1600米,所以他步行回家的平均速度是80米/分.11(2)当x =-3时,y =12³(-3)2=2≠-2,∴点(-3,-2)不在函数y =12x 2的图象上.12.[全品导学号:07712131]解:(1)5 70 5 54 5(2)y 是x 的函数.理由:由图象可知,变量y 随着x 的变化而变化,同时对于每一个x ,按照图象,都有唯一的y 值与之相对应,符合函数的定义.(3)摩天轮的直径是70-5=65(m ).19.1 函数 19.1.2 函数的图象第2课时 实际问题中的函数图象(全品第65-66页)教师详答1.[全品导学号:07712132]C [解析] 两个变量之间,如果给定自变量一个值,另一个变量也有唯一的值与之对应,这样的两个变量之间的关系才是函数关系.选项中给定自变量x 一个值时,相应的另一个变量y 却得到了两个值.故C 项不能体现y 是x 的函数关系.2.B 3.B4.C [解析] 由题意知,前1小时路程随时间增大而增大,1小时后路程增加变快. 5.D [解析] 0<x ≤20,表示小强从家步行去车站,总路程为2千米,故A 正确;20<x ≤30,表示小强在车站等小明,用的时间是10分钟,故B 正确;30<x ≤60,表示两人一起乘公共汽车去学校,用的时间是30分钟,走的路程是15千米,所以公共汽车的平均速度是30千米/时,所以C 正确,D 不正确.6.C7.解:(1)声速与气温 气温 声速 气温 (2)随着T 的增大,v 也增大.(3)气温每升高5 ℃,声速增加3 m /s即气温每升高1 ℃,声速增加35m /s .∴v =331+35T.(4)当T =30 ℃时,v =331+35³30=331+18=349(m /s ),349³6=2094(m ).答:发生打雷的地方距小明大约有2094 m . 8.[全品导学号:07712133]D9.y =0.5x10.[全品导学号:07712134]8 [解析] 进水管进水的速度为20÷4=5(升/分),出水管出水的速度为5-(30-20)÷(12-4)=3.75(升/分),∴关闭进水管后,放完水经过的时间为30÷3.75=8(分).11.解:由题意可知s =240-30t(0≤t ≤8). 列表:函数图象如图所示:12.[全品导学号:07712135]; 当x >20时,y =3.3(x -20)+2.5³20=3.3x -16. (2)∵该户4月份的水费平均每吨2.8元, ∴该户4月份用水超过20吨.设该户4月份用水a 吨,根据题意,得 2.8a =3.3a -16,解得a =32. 答:该户4月份用水32吨.19.2 一次函数 19.2.1 正比例函数第1课时 正比例函数的概念(全品第67页)教师详答1.[全品导学号:07712136]D [解析] 路程=速度³时间,速度一定时,路程是时间的正比例函数.故选D .2.C3.A [解析] ∵y =x +2a -1是正比例函数,∴2a -1=0,解得a =12.故选A .4.y =-2x 正比例5.-236.-1 127.S =3x [解析] 由三角形的面积公式可得S =12³6x ,即S =3x.8.[解析] 判断一个函数是不是正比例函数,要看解析式能否转化为y =kx(k ≠0)的形式. 解:(1)y =28-5x ,y 不是x 的正比例函数.(2)y =x 2,y 不是x 的正比例函数.9.D [解析] 根据正比例函数的定义,形如y =kx(k ≠0)的函数是正比例函数.y =3x -1可转化为y +1=3x ,把y +1看成一个整体,则y +1与x 成正比例;y =-x 2中,k =-12,所以y 与x 成正比例;在y =2(x +1)中,把x +1看作一个整体时k =2,所以y 与x +1成正比例;在y =x +3中,把x +3看作一个整体时k =1,所以y 与x +3成正比例.综上可知D 项的说法不正确.故选D .10.[全品导学号:07712137]C11.[全品导学号:07712138]2 [解析] 由题意知y =2x +k -2,由正比例函数的定义得k -2=0,即k =2.12.[全品导学号:07712139]解:正比例函数必须满足y =kx(k 是常数,k ≠0)的形式,无常数项,所以解得所以函数解析式为y =-4x.19.2 一次函数 19.2.1 正比例函数第2课时 正比例函数的图象与性质(全品第68-69页)教师详答1.D [解析] 因为正比例函数y =kx(k ≠0)的图象是一条经过原点的直线,所以只有D 项的图象符合题意.故选D .2.B 3.B4.-2 [解析] 把(2,-4)代入y =kx ,得-4=2k ,解得k =-2. 5.[全品导学号:07712140]0.26.1 [解析] 因为函数图象过原点,所以-(4m -4)=0,解得m =1. 7.略 8.C9.A [解析] 由正比例函数的性质可知:当y 随x 的增大而减小时,k -1<0,即k <1.故选A .10.>11.[全品导学号:07712141][解析] 正比例函数的比例系数决定函数的增减性.解:(1)当5-2k>0,即k<52时,y 随x 的增大而增大.(2)当5-2k<0,即k>52时,y 随x 的增大而减小.12.D [解析] x 的取值为正整数,y 也为正整数.故选D .13.C [解析] 对于正比例函数y =kx ,当k<0时,y 随x 的增大而减小,所以当x 1<x 2时,y 1>y2,即y 1-y 2>0.14.[全品导学号:07712142]C [解析] 如图,过点A 作直线y =x 的垂线,当B 是垂足时,AB 最短.过点B 作BE ⊥OA ,垂足为E.因为直线y =x 是第一、三象限的平分线,所以∠AOB =45°.由AB ⊥OB ,可得∠OAB =∠AOB =45°,可得BO =AB.由BE ⊥OA ,可得AE =OE ,从而得BE =AE=OE =12,所以点B 的坐标为(-12,-12).15.减小 [解析] 点(2,-6)在正比例函数y =kx 的图象上,即当x =2时,y =-6,∴-6=2k ,解得k =-3.∵k <0,∴y 随x 的增大而减小.16.y =73x [解析] 根据正比例函数的概念,可得9t 2=1,解得t =±13.∵函数图象经过第一、三象限,∴1-4t>0,解得t<14,∴t =-13.将t =-13代入y =(1-4t)x9t 2,得y =73x.17.y =2x(答案不唯一) [解析] ∵正比例函数y =kx 的图象经过第一、三象限, ∴k >0,当k 取2时可得函数解析式为y =2x.18.[全品导学号:07712143]1319.解:(1)将x =1,y =2代入y =kx ,得k =2, 故正比例函数的解析式为y =2x.(2)当x =-1时,y =2³(-1)=-2. (3)∵0≤y ≤5,∴0≤2x ≤5,解得0≤x ≤52.20.[全品导学号:07712144]解:(1)函数的图象如图:(2)y 轴的夹角变小. (3)由(2)中的规律可知,k 1>k 2.周滚动练习(二)(全品第70-71页)教师详答1.B 2.C 3.C4.[全品导学号:07712145]C 5.C6.πr 2S 和r π7.二、四 0 -5 减小8.[全品导学号:07712146]2 [解析] 由题意知,当x =3时,y 与x 满足的解析式为y =-x +5.把x =3代入y =-x +5,得-3+5=2,所以当输入x =3时,输出的结果y =2.9.< [解析]∵P 1(1,y 1),P 2(2,y 2)是正比例函数y =13x 的图象上的两点,∴y 1=13,y 2=13³2=23.∵13<23,∴y 1<y 2. 10.x ≥-2且x ≠111.解:(1)y =0.1x. (2)x =28-5y. (3)y =4x. 其中(1)(3)中的y 是x 的正比例函数12.解:(1)观察图象可知:自变量x 的取值范围是0≤x ≤5. (2)观察图象可知:当x =5时,y 有最小值,最小值是2.5. (3)观察图象可知y 随着x 的增大而减小.13.[解析] 根据题意知小明和小刚行驶的时间是2.5小时,所以速度为502.5=20(千米/时),所以二人前1.5小时行驶了20³1.5=30(千米),修车后行驶的1小时行驶的路程为20千米,依此可画出图象.解:图象如图所示.14.解:(1)由题意得解得k =±2.当k 等于±2时,该函数是正比例函数.(2)当k =2时,正比例函数的图象经过第一、三象限,正比例函数的解析式为y =52x.(3)当k =-2时,正比例函数y 随x 的增大而减小,正比例函数的解析式为y =-32x.15.[全品导学号:07712147][解析] 两人行驶的路程s 是时间t 的函数.从图象可以看出骑自行车的人先出发却后到达乙地,行驶的路程都是100千米.解:(1)甲地与乙地相距100千米;骑摩托车的人用了2小时,骑自行车的人用了6小时;骑摩托车的人先到达乙地,早到了1小时.(2)骑自行车的人先匀速行驶了2小时,行驶40千米后休息了1小时,然后用3小时匀速到达乙地.骑摩托车的人在骑自行车的人出发3小时后出发,行驶2小时后到达乙地.(3)摩托车行驶的平均速度是50千米/时.19.2 一次函数19.2.2 一次函数第1课时一次函数的概念(全品第72页)教师详答1.C[解析] ①y=πx,②y=2x-1是一次函数,共2个.2.C3.[全品导学号:07712148]D4.5 -3 -3 55.6.D7.B8.[全品导学号:07712149]解:(1)当m=-3,n为任意实数时,它是一次函数.(2)当m=-3,n=2时,它是正比例函数.9.[全品导学号:07712150][解析] 从表格中可以看出一张方桌能坐4人,以后每多一张方桌可以多坐2个人.表中应填的数字为10,y与x之间的函数解析式是y=4+2(x-1)=2x +2.解:表中填10.(1)y=2x+2,y是x的一次函数.(2)把y=42代入y=2x+2中,得42=2x+2,解得x=20.答:需要20张这样的方桌.19.2 一次函数19.2.2 一次函数第2课时一次函数的图象与性质(全品第73-74页)教师详答1.A2.y=3x+2 [解析] 根据图象沿y轴向上平移的规律,得最终图象对应的函数解析式为y =3x-1+3=3x+2.3.C 4.D 5.C 6.D7.解:图象略.共同点:函数图象都是一条直线,且均交y轴于点(0,2).8.C9.A[解析] ∵k=-2<0,∴y随x的增大而减小.∵1<2,∴a>b.10.m>-211.四[解析] ∵在一次函数y=kx+2中,y随x的增大而增大,∴k>0.∵2>0,∴此函数的图象经过第一、二、三象限,不经过第四象限.12.[全品导学号:07712151]解:(1)由1-3m=0且m-1≠0,得m=13.(2)把(0,2)代入,得1-3m=2,解得m=-13.(3)由m-1<0,得m<1.13.[全品导学号:07712152]C14.A[解析] 分四种情况:①当a>0,b>0时,直线y=ax+b和y=bx+a均经过第一、二、三象限,选项中不存在此情况;②当a>0,b<0时,直线y=ax+b经过第一、三、四象限,直线y=bx+a经过第一、二、四象限,选项A符合此条件;③当a<0,b>0时,直线y =ax+b经过第一、二、四象限,直线y=bx+a经过第一、三、四象限,选项中不存在此情况;④当a<0,b<0时,直线y=ax+b经过第二、三、四象限,直线y=bx+a经过第二、三、四象限,t选项不存在此情况.故选A.15.答案不唯一,如y=-x+3 [解析] 设一次函数的解析式为y=kx+b.因为一次函数的图象过点(0,3),所以b=3.又因为函数y随x的增大而减小,所以k<0.16.-6 [解析] 函数y=2x+3的图象与x轴的交点坐标是(-32,0),函数y=4x-b的图象与x轴的交点坐标是(b4,0),所以-32=b4,解得b=-6.17.解:当x=0时,y=-6.当y=0时,即-12x-6=0,解得x=-12.所以点A,B的坐标分别为(-12,0),(0,-6),所以OA=||-12=12,OB=||-6=6,所以S =12OA ²OB =12³12³6=36.19.[全品导学号:07712154][解析] (1)在图中描出表中已知四对对应值的点,分析四个点的排列位置,猜想它们在同一直线上,y 与x 之间是一次函数关系,从表中对应值发现:19=17³1+2,36=17³2+2,53=17³3+2,70=17³4+2,…,所以y 与x 之间的函数解析式不难求得.(2)中的问题可利用(1)中求得的函数解析式解决.解:(1)如图所示.猜想y 与x 之间是一次函数关系.y 关于x 的函数解析式为y =17x +2(x 为正整数). (2)由(1)得y 与x 之间的函数解析式为y =17x +2,当y =1000时,17x +2=1000,解得x =581217,而x 为正整数,所以x ≈59.答:每根彩纸链至少要用59个纸环.19.2 一次函数 19.2.2 一次函数第3课时 一次函数解析式的求法(全品第75-76页)教师详答1.2.A 3.D 4.C5.[全品导学号:07712155]D [解析] ∵点B 在正比例函数y =2x 的图象上,横坐标为1,∴y =2³1=2,∴B(1,2),设这个一次函数的解析式为y =kx +b.∵一次函数的图象过点A(0,3),与正比例函数y =2x 的图象相交于点B(1,2),∴可得出方程组解得∴这个一次函数的解析式为y =-x +3. 6.310.D [解析] 设直线y =-3x 向上平移后得到直线AB ,则直线AB 的函数解析式可设为y =-3x +k ,把(m ,n)代入得n =-3m +k ,解得k =3m +n , ∵3m +n =10,∴k =10,∴直线AB 的函数解析式为y =-3x +10. 故选D .11.[全品导学号:07712156]y =2x +2 [解析] 由图象知OA =2,在Rt △AOB 中,OB =(5)2-22=1,所以点B 的坐标为(-1,0).将A(0,2),B(-1,0)的坐标代入y =kx +b 中,解得k =2,b =2,所以函数解析式为y =2x +2.12.(-1,0) [解析] 如图,作出点A(2,3)关于x 轴对称的点C(2,-3),连接CB 交x 轴于点P ,且可求得直线CB 的函数解析式为y =-x -1,当y =0时,-x -1=0,解得x =-1,∴点P 的坐标是(-1,0).13.[全品导学号:07712157]-23或516.[全品导学号:07712158]73≤k ≤3 [解析] 若直线y =kx -k(k ≠0)过点(2,3),则3=2k -k ,解得k =3;若直线y =kx -k(k ≠0)过点(4,7),则7=4k -k ,解得:k =73.因为直线y =kx -k(k ≠0)与线段AB 有交点,所以k 的取值范围为73≤k ≤3.19.2 一次函数 19.2.2 一次函数第4课时 一次函数的应用(全品第77-78页)教师详答1.C2.y =0.3x +6(0≤x ≤5)运送到B港口的物资为(80-x)吨,Array从乙仓库运送到A港口的物资为(100-x)吨,运送到B港口的物资为50-(80-x)=(x-30)(吨),∴总运费y与x之间的函数解析式为y=14x+20(100-x)+10(80-x)+8(x-30)=-8x+2560,x的取值范围是30≤x≤80.(2)由(1)得y=-8x+2560,∵-8<0,∴y随x的增大而减小,∴当x=80时,总运费最低,当x=80时,y=-8³80+2560=1920,即最低费用为1920元.此时方案为:把甲仓库的物资全部运往A港口,再从乙仓库运往A港口20吨物资,乙仓库余下的全部物资运往B港口.7.[全品导学号:07712161]解:(1)∵从甲仓库运送到A港口的物资为x吨,∴从甲仓库周滚动练习(三)(全品第79-80页)教师详答1.D[解析] ∵k=2>0,b=1>0,根据一次函数的图象即可判断函数图象经过第一、二、三象限,不经过第四象限.故选D.2.B3.C[解析] A项,令y=-2x+1中的x=-1,则y=3,∴一次函数的图象不过点(-1,2),即A项不正确;B项,∵k=-2<0,b=1>0,∴一次函数的图象经过第一、二、四象限,即B项不正确;C项,∵k=-2<0,∴一次函数中的y随x的增大而减小.∵令y=-2x+1中的x=1,则y=-1,∴当x>1时,y<0成立,即C项正确;D.∵k=-2<0,∴一次函数中y随x的增大而减小,即D项不正确.故选C.4.C[解析] ∵正比例函数y=kx的图象经过点(2,-3),∴-3=2k,解得k=-32,∴正比例函数的解析式是y=-32x,四个选项中只有C选项的点在正比例函数y=-32x的图象上.故选C.5.B[解析] 因为正比例函数y=kx的图象过第二、四象限,所以k<0,因此一次函数y =x+k中y随x的增大而增大,且其图象与y轴负半轴相交,即函数图象位于第一、三、四象限.故选B.6.[全品导学号:07712163]C[解析] ①乙晚出发1小时.②乙出发3-1=2(时)后追上甲.③甲的速度是123=4(千米/时).④乙在距A地12千米处追上甲,且乙的速度快,所以乙先到达B地.综上可知,有3个说法正确.故选C.7.y=30x30 x和y8.≠1 -19.< [解析] 一次函数y=2x+1中y随x的增大而增大,所以若x1<x2,则y1<y2.10.(0,-3) [解析] 将直线y=3x+2沿y轴向下平移5个单位长度可得y=3x+2-5,即y=3x-3,∴平移后直线与y轴的交点坐标为(0,-3).11.三12.[全品导学号:07712164]5 [解析] 由题意可知:从甲地匀速驶往乙地,所用时间为3.2-0.5=2.7(时),返回的速度是它从甲地驶往乙地的速度的1.5倍,返回用的时间为2.7÷1.5=1.8(时),所以a=3.2+1.8=5.13.解:(1)∵k>0时,函数y随x的增大而增大,即2a+4>0,解得a>-2,b为任意实数.(2)∵k<0,b<0时,函数图象经过第二、三、四象限,∴2a+4<0,-(3-b)<0,解得a<-2,b<3,∴当a<-2,b<3时,函数图象经过第二、三、四象限.14.解:(1)把(1,4)代入y=kx+3,得k+3=4,解得k=1,即这个一次函数的解析式为y=x+3.(2)∵k=1,∴原不等式可化为x+3≤6,解得x≤3.15.解:由题意,得y=27x+3. 当x=20时,y=27³20+3=543.16.解:(1)(3900-3650)÷5=250÷5=50(米/分),即小丽步行的速度为50米/分.(18-15)³50=150(米).即学校与公交站台乙之间的距离为150米.(2)设过C,D两点的直线的函数解析式为y=kx+b.∵C(8,3650),D(15,150),∴当8≤x ≤15时,y =-500x +7650.17.[全品导学号:07712165]解:(1)∵直线y =2x +1与直线y =kx -1垂直, ∴2k =-1,解得k =-12.(2)∵过点A 的直线与直线y =-13x +3垂直,∴可设过点A 的直线所对应的函数解析式为y =3x +b. 把点A 的坐标(2,3)代入,得3=3³2+b ,解得b =-3, ∴该直线所对应的函数解析式为y =3x -3.19.2 一次函数19.2.3 一次函数与方程、不等式第1课时 一次函数与一元一次方程、不等式(全品第81-82页)教师详答1.C2.(-3,0) [解析] 因为关于x 的方程mx +n =0的解为x =-3,所以-3m +n =0,即对于函数y =mx +n ,当x =-3时,y =0,∴点(-3,0)是直线y =mx +n 与x 轴的交点.3.x =2 [解析] 因为点(2,3)在一次函数y =kx +b 的图象上,所以3=2k +b ,即关于x 的方程kx +b =3的解为x =2.4.x =-15.解:(1)x =2.(2)x =0.(3)x =-1.6.[解析] 方程2x -6=0的解可以利用函数y =2x -6的图象与x 轴的交点坐标求得. 解:函数y =2x -6的图象如图所示.从函数图象上可以看出直线y =2x -6与x 轴的交点坐标是(3,0),所以方程2x -6=0的解是x =3.7.C 8.B 9.C10.≥211.[全品导学号:07712166]解:函数y =2x +6的图象如图:(1)当x =-3时,y =0,所以方程2x +6=0的解为x =-3. (2)当x >-1时,y >4,所以不等式2x +6>4的解集为x >-1. (3)当-4≤x ≤-2时,-2≤y ≤2.12.B [解析] 将一次函数y =12x 的图象向上平移2个单位长度,平移后的图象所对应的函数解析式为y =12x +2.令y =0,解得x =-4;令x =0,解得y =2,画出其图象如图所示.∴若y >0,则x的取值范围是13.-4 -11 [解析] 由题意,得3x +1=2x -3,解得x =-4.当x =-4时,y =3x +1=-11.14.-1<x<2 [解析] 两函数图象都在x 轴上方的自变量的取值在-1和2之间,所以-1<x<2.15.[全品导学号:07712167]y<-2 [解析] 因为一次函数y =kx +b 的图象过点(0,-4),所以y =kx -4.将(2,0)代入y =kx -4,得0=2k -4,解得k =2,所以y =2x -4.当x =1时,y =2³1-4=-2.根据图象可得当x<1时,y<-2.17.[全品导学号:07712169]解:(1)根据表中的数据可知y 与x 满足正比例函数关系.设y =kx ,将x =100,y =40代入y =kx ,得k =0.4,所以y =0.4x ,其他几组值也符合该函数解析式,所以函数的解析式为y=0.4x.(2)y =0.15x +200. (3)如图所示:19.2 一次函数19.2.3 一次函数与方程、不等式第2课时 一次函数与二元一次方程组(全品第83页)教师详答1.A [解析] 方法一:图中的两条直线分别为直线y =5x -1和直线y =2x +5,分别代入y =0和x =0,可求出两条直线与x 轴、y 轴的交点坐标,根据交点坐标知A 项是正确的.方法二:首先根据k 的值排除C 项和D 项,然后由直线的倾斜程度考虑B 项是否正确,于是把B 项中的交点坐标(3,7)代入直线解析式中,发现不成立.故选A .2.D6.[全品导学号:07712171]D [解析] 直线y =-23x -3与y 轴的交点为(0,-3).当a=-3时,直线y =a 与y =-23x -3交于y 轴上的点(0,-3);当a<-3时,直线y =a 与y =-23x -3的交点在第四象限,所以选D .7.[全品导学号:07712172]解:直线AB 和直线CD 所对应的函数解析式分别为y =2x +6和y =-12x +1,∴直线AB 与直线CD 的交点坐标为(-2,2).8.[全品导学号:07712173]解:∵直线y =-43x +4与y 轴交于点A ,∴点A 的坐标为(0,4).∵直线y =45x +45与x 轴交于点C ,∴点C 的坐标为(-1,0).∵直线y =-43x +4与直线y=45x +45相交于点B ,∴点B 的坐标为(32,2).∵直线y =-43x +4与x 轴交于点D ,∴点D 的坐标为(3,0),∴△ACD 的面积为12³4³4=8,△BCD 的面积为12³4³2=4,∴△ABC 的面积为8-4=4.专题训练(三) 一次函数易错题(全品第84页)教师详答1.-2 [解析] 根据一次函数的定义,得错误!解得m =-2.2.解:已知正比例函数y =(m -1)x5-m 2的图象经过第二、四象限,∴m -1<0,5-m 2=1, 解得m =-2.3.x =1或x =-1 [解析] 在x 轴上到y 轴的距离为1的点的坐标为(1,0)或(-1,0),不要忽略任何一种情况.4.-3≤m <2 [解析] 由一次函数y =(m -2)x +m +3的图象不经过第三象限, 可知它经过第二、四象限或第一、二、四象限, ∴错误!或错误! 解得-3≤m <2.5.[全品导学号:07712174]解:一次函数y =kx +4的图象与y 轴、x 轴的交点坐标分别是(0,4),⎝ ⎛⎭⎪⎫-4k ,0,图象与两坐标轴围成的三角形的面积是12³4³⎪⎪⎪⎪⎪⎪-4k =16,解得k =±12.所以这个一次函数的解析式是y =12x +4或y =-12x +4.6.D 7.C 8.C9.[全品导学号:07712175]解:若y 随x 的增大而增大,则当x =-3时,y =-1;当x =2时,y =9.所以错误! 解得错误!所以k +b =7.若y 随x 的增大而减小,则当x =-3时,y =9;当x =2时,y =-1. 所以错误!解得错误! 所以k +b =1.综上所述,k +b 的值是7或1.19.3 课题学习 选择方案(全品第85-86页)教师详答1.B [解析] 两函数图象的交点坐标为(2,4),即售出2件产品时,售价相同;在交点左侧,乙家较便宜;在交点右侧,甲家较便宜;买1件产品时,乙家的售价为2元.故选B .2.169网费3.解:(1)方案一:y =0.95x ;方案二:y =0.9x +300.(2)∵0.95³5880=5586(元),0.9³5880+300=5592(元),∴选择方案一更省钱. 4.[全品导学号:07712176]解:(1)∵购买大型客车x 辆,∴购买中型客车(20-x)辆. 根据题意,得y =62x +40(20-x)=22x +800. (2)依题意得20-x <x.解得x >10.∵y =22x +800,y 随着x 的增大而增大,x 为整数,∴当x =11时,购车费用最省,为22³11+800=1042(万元). 此时需购买大型客车11辆,中型客车9辆.答:购买大型客车11辆,中型客车9辆时,购车费用最省,该方案所需费用为1042万元. 5.解:(1)设甲种商品每件的进价为x 元,乙种商品每件的进价为y 元,根据题意,得答:甲种商品每件的进价为30元,乙种商品每件的进价为70元.(2)设该商场购进甲种商品m 件,则购进乙种商品(100-m)件,根据题意,得 m ≥4(100-m), 解得m ≥80.设卖完A ,B 两种商品商场的利润为w ,则w =(40-30)m +(90-70)(100-m)=-10m +2000,∵-10<0,w 随m 的增大而减小,∴当m =80时,w 取得最大值,最大利润为1200元. 故该商场获利最大的进货方案为甲商品购进80件、乙商品购进20件,最大利润为1200元. 6.解:(1)由题意知: 当0<x ≤1时,y 甲=22x ;当x >1时,y 甲=22+15(x -1)=15x +7. y 乙=16x +3.(2)①当0<x ≤1时,令y 甲<y 乙,即22x <16x +3,解得0<x <12;令y 甲=y 乙,即22x =16x +3,解得x =12;令y 甲>y 乙,即22x >16x +3,解得12<x ≤1.②当x >1时,令y 甲<y 乙,即15x +7<16x +3, 解得x >4;令y 甲=y 乙,即15x +7=16x +3, 解得x =4;令y 甲>y 乙,即15x +7>16x +3, 解得1<x <4.综上可知:当12<x <4时,选乙快递公司省钱;当x =4或x =12时,选甲、乙两家快递公司快递费一样多;当0<x <12或x >4时,选甲快递公司省钱.7.[全品导学号:07712177]解:(1)根据题意可知,参加演出的男生有x 人,参加演出的女生有(2x -100)人.总费用y 1(单位:元)和y 2(单位:元)与参演男生人数x 之间的函数解析式分别是:y 1=0.7[120x +100(2x -100)]+2200=224x -4800,y 2=0.8[100(3x -100)]=240x -8000.(2)当y 1>y 2时,即224x -4800>240x -8000,解得x <200; 当y 1=y 2时,即224x -4800=240x -8000,解得x =200; 当y 1<y 2时,即224x -4800<240x -8000,解得x >200.即当参演男生人数少于200人时,购买B 公司的服装比较合算;当参演男生人数等于200人时,购买两家公司的服装总费用相同,可在任一家公司购买;当参演男生人数多于200人时,购买A 公司的服装比较合算.8.[全品导学号:07712178]解:(1)y A =20x +25(200-x)=-5x +5000; y B =15(240-x)+18(60+x)=3x +4680.(2)∵y A -y B =(-5x +5000)-(3x +4680)=-8x +320. ∴当-8x +320>0,即x<40时,B 地的运费较少; 当-8x +320=0,即x =40时,两地的运费一样多; 当-8x +320<0,即x>40时,A 地的运费较少.(3)设两地运费之和为y 元,则y =y A +y B =(-5x +5000)+(3x +4680)=-2x +9680. 由题意知3x +4680≤4830, 解得x ≤50.∵-2<0,∴y 随x 的增大而减小, ∴x 为50时,y 有最小值,∴y 最小值=-2³50+9680=9580,∴在此情况下,当A 地运往甲、乙两仓库的猕猴桃分别为50吨、150吨;B 地运往甲、乙两仓库的猕猴桃分别为190吨、110吨时,才能使两地运费之和最少,最少费用是9580元.小结与思考(全品第87-88页)教师详答1.D 2.D 3.D4.D [解析] x =-3时,分母x +3为0,无意义.故选D . 5.y =2x -37.B [解析] 因为b <0,所以直线与y 轴交于负半轴.故选B .8.[全品导学号:07712179]B [解析] ∵直线y =-x +m 与y =nx +4n(n ≠0)的交点的横坐标为-2,直线y =nx +4n 与x 轴的交点坐标为(-4,0),∴关于x 的不等式组-x +m >nx +4n >0的解集为-4<x <-2,∴其整数解为-3.故选B . 9.一、三 [解析] 因为一次函数y =kx +b 的图象经过第二、三、四象限,所以k<0,b<0,所以kb>0,所以正比例函数y =kbx 的图象经过第一、三象限.10.>11.[全品导学号:07712180] 25 [解析] 由题意,得b =a +5,d =c +5,所以a(c -d)-b(c -d)=(a -b)(c -d)=(-5)³(-5)=25.12.4 [解析] 如图,在△ABC 中,BC 为底,AO 为高,且高为2,面积为4,故△ABC 的底边BC =8÷2=4.因为点B 的坐标为(0,b 1),点C 的坐标为(0,b 2),所以b 1-b 2即是BC 的长.13.A14.解:(1)设工厂生产x 件A 产品,则生产(50-x)件B 产品.根据题意,得解得30≤x ≤32. ∵x 为整数,∴x =30,31,32,∴有三种生产方案:①A:30件,B:20件;②A:31件,B:19件;③A:32件,B:18件.(2)方法一:当生产A种产品30件,B种产品20件时,利润为30³80+20³120=4800(元).当生产A种产品31件,B种产品19件时,31³80+19³120=4760(元).当生产A种产品32件,B种产品18件时,32³80+18³120=4720(元).故当生产A种产品30件,B种产品20件时,获得的利润最大.方法二:B产品生产得越多获得的利润越大,即生产A种产品30件,B种产品20件时,最大利润为30³80+20³120=4800(元).15.[全品导学号:07712181]解:(1)y=4x大+210.(2)①当x大=6时,y=4³6+210=234,∴y=3x小+234.②根据题意,得3x小+234≤260,解得x小≤823,∵x小为自然数,∴x小最大为8,即最多能放入8个小球.本章中考演练(全品第89-90页)教师详答1.B[解析] 根据题意,从20分钟到30分钟在书店里看书,离家距离没有变化,是一条平行于x轴的线段.故选B.2.A[分析] 由题意,得x≥0且x-2≠0,解得x≥0且x≠2.故选A.3.[全品导学号:07712182]C[解析] ∵点P(x,y)在第一象限内,且x+y=6,∴y=6-x(0<x<6,0<y<6).∵点A的坐标为(4,0),∴S=12³4³(6-x)=12-2x(0<x<6),∴选项C符合.故选C.4.A5.(-4,1)6.y=2x-2 [解析] 根据平移的规则可知:直线y=2x+1向下平移3个单位长度后所得直线的函数解析式为y=2x+1-3=2x-2.7.一[解析] ∵关于x的方程mx+3=4的解为x=1,∴m+3=4,解得m=1,∴直线y=(m-2)x-3为直线y=-x-3,∴直线y=(m-2)x-3一定不经过第一象限.8.二、四[解析] 由题意得|m|=1,且m-1≠0,解得m=-1,∴函数解析式为y=-2x.∵k=-2<0,∴该函数的图象经过第二、四象限.故答案为:二、四.9.-110.解:将x=-1,y=1代入y=kx+2,得1=-k+2,解得k=1.∴一次函数的解析式为y=x+2.当x=0时,y=2;当y=0时,x=-2,∴函数图象经过(0,2),(-2,0)两点,此函数图象如图所示.11.解:(1)∵点B 在直线l 2上, ∴4=2m ,∴m =2, ∴B(2,4).设直线l 1的函数解析式为y =kx +b ,∴直线l 1的函数解析式为y =12x +3.(2)可知C ⎝ ⎛⎭⎪⎫n ,12n +3,D(n ,2n), 当点C 在点D 上方时,有n2+3>2n ,解得n <2.12.解:(1)∵点A(2,0),AB =13,∴OB =AB 2-OA 2=3, ∴点B 的坐标为(0,3). (2)∵△ABC 的面积为4, ∴12³BC ³OA =4, ∴12³BC ³2=4,即BC =4. ∵OB =3,∴OC =4-3=1, ∴C(0,-1).设直线l 2的函数解析式为y =kx +b ,则∴该运动员从起点到第二次经过C 点所用的时间是7+68=75(分), ∴直线AB 经过(35,10.5),(75,2.1)两点. 设AB 所在直线的函数解析式为s =kt +b ,∴AB 所在直线的函数解析式为s =-0.21t +17.85.②该运动员跑完赛程用的时间即为直线AB 与x 轴交点的横坐标, ∴当s =0时,-0.21t +17.85=0,解得t =85. ∴该运动员跑完赛程用时85分钟.14.解:(1)设y B 关于x 的函数解析式为y B =k 1x +b(k 1≠0), 由线段EF 过点E(1,0)和点P(3,180),得∴y B 关于x 的函数解析式为y B =90x -90(1≤x ≤6). (2)设y A 关于x 的函数解析式为y A =k 2x(k 2≠0), 由题意,得180=3k 2,即k 2=60,∴y A =60x. 当x =5时,y A =5³60=300, 当x =6时,y B =90³6-90=450, 450-300=150(千克).答:如果A ,B 两种机器人各连续搬运5小时,那么B 种机器人比A 种机器人多搬运了150千克.自我综合评价(四)(全品第91-92页)教师详答1.D2.B [解析] 因为-2<0,所以y 随x 的增大而减小.因为3>-2,所以y 1<y 2. 3.B4.C [解析] 因为一次函数y =kx +b 的图象经过第二、三、四象限,所以k <0,b <0. 5.C 6.D7.x ≠1 [解析] 函数y =x +1x -1的自变量x 的取值范围是x -1≠0,即x ≠1.8.y =32x -29.x =2 [解析] 观察图象,由直线y =ax +b 与直线y =cx +d 相交于点(2,1),即可知关于x 的一元一次方程ax +b =cx +d 的解为直线y =ax +b 与直线y =cx +d 交点的横坐标,即x =2.10.4.5 [解析] 令x =0,可求直线l 1与y 轴的交点坐标是(0,4),直线l 2与y 轴的交点坐标是(0,-5),所以BC =4-(-5)=9.因为E ,F 分别是AB ,AC 的中点,所以EF =12BC =92.11.[全品导学号:07712184]0<m <3212.解:(1)设这个一次函数的解析式为y =kx +b , ∵该函数图象经过(-2,1)和(1,4)两点,∴这个一次函数的解析式为y =x +3. (2)当x =3时,y =3+3=6.13.解:(1)由y 1=-12x +1,可知当y =0时,x =2,∴点A 的坐标是(2,0), ∴AO =2.∵直线y 1=-12x +1与直线y 2=-32x 交于点B ,∴点B 的坐标是(-1,1.5), ∴△AOB 的面积=12³2³1.5=1.5.(2)由(1)可知交点B 的坐标是(-1,1.5), 由函数图象可知y 1>y 2时,x >-1. 14.[全品导学号:07712185]解:(1)令y =0,得x =-32,∴点A 的坐标为⎝ ⎛⎭⎪⎫-32,0. 令x =0,得y =3,∴点B 的坐标为(0,3). (2)设点P 的坐标为(x ,0), 依题意,得x =±3.∴点P 的坐标为(3,0)或(-3,0),∴S △ABP =12³⎝ ⎛⎭⎪⎫32+3³3=274,或S △ABP =12³⎝ ⎛⎭⎪⎫3-32³3=94,∴△ABP 的面积为274或94.15.解:(1)从小刚家到该景区乘车一共用了4 h . (2)设线段AB 所在直线的函数解析式为y =kx +b. ∵点A(1,80),B(3,320)在直线AB 上,∴y =120x -40(1≤x ≤3).(3)当x =2.5时,y =120³2.5-40=260, 380-260=120(km ).故小刚一家出发2.5小时时离目的地还有120 km . 16.解:(1)根据题意,得2000³2x +1600x +1000³(100-3x)≤170000. 解得x ≤261213. ∵x 为正整数, ∴x 最大为26. 答:商店至多可以购买冰箱26台.(2)设商店销售完这批家电后获得的利润为y 元,则y =(2300-2000)³2x +(1800-1600)x +(1100-1000)³(100-3x)=500x +10000. ∵k =500>0,∴y 随x 的增大而增大.∵x ≤261213且x 为正整数,∴当x =26时,y 取最大值,最大值为500³26+10000=23000.答:当购买冰箱26台时,商店销售完这批家电后获得的利润最大,最大利润为23000元.第十九章一次函数测试题。
《管理学》习题与答案——第19章 控制与控制过程

第十九章控制与控制过程一、教学要点1、控制的必要性。
2、控制的基本原理.3、种种类型控制的概念.4、预先控制、现场控制和成果控制的内涵,及其各自的优缺点。
5、有效控制有的基本特征。
6、控制过程的基本内容。
7、如何选择控制的重点?8、制定控制标准的方法。
9、纠偏措施应满足的要求.10、关键名词:控制、程序控制、跟踪控制、自适应控制、最佳控制、预先控制、现场控制、成果控制、适时控制、适度控制、客观控制、弹性控制、统计性标准、工程标准、评估性标准、二、习题(一)填充题1、控制是为了保证_________与_________适应的管理职能.2、控制工作的主要内容包括_________、_________和_________。
3、预先控制的内容包括_________和_________两个方面。
4、成果控制的主要作用,是通过总结过去的经验和教训,为_________提供借鉴.5、成果控制主要包括_________、_________、_________以及_________等内容。
6、企业应根据_________和_________来确定控制的范围和频度,建立有效的控制系统。
7、适度控制是指控制的_________、_________和_________要恰到好处。
8、控制的过程都包括三个基本环节的工作:_________、_________和_________。
9、一般来说,企业可以使用的建立标准的方法有三种:_________、_________、_________ 。
10、工程标准也是一种用统计方法制定的控制标准,不过它不是对历史性统计资料的分析,而是通过对_________ 。
11、在采取任何纠正措施以前,必须首先对_________。
12、一般地说,弹性控制要求企业制定_________和_________。
(二)选择题1、1、有效的控制要求_________A. 选择关键的经营环节B。
确定恰当的控制频度C。
第19章 生活用电动手动脑学物理参考答案
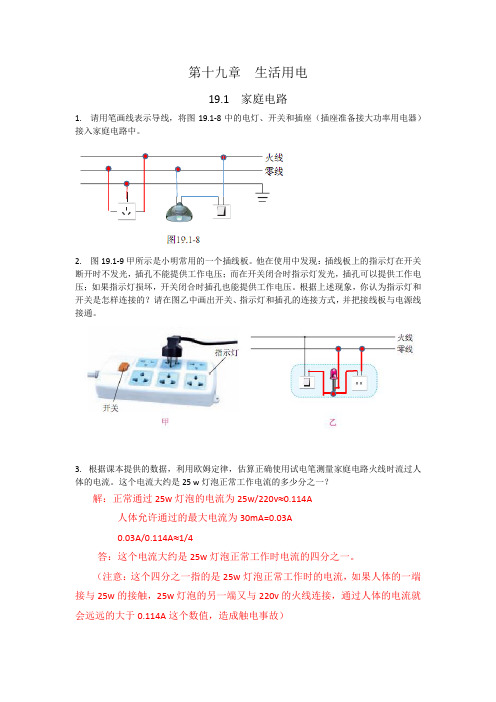
第十九章生活用电19.1 家庭电路1. 请用笔画线表示导线,将图19.1-8中的电灯、开关和插座(插座准备接大功率用电器)接入家庭电路中。
2. 图19.1-9甲所示是小明常用的一个插线板。
他在使用中发现:插线板上的指示灯在开关断开时不发光,插孔不能提供工作电压;而在开关闭合时指示灯发光,插孔可以提供工作电压;如果指示灯损坏,开关闭合时插孔也能提供工作电压。
根据上述现象,你认为指示灯和开关是怎样连接的?请在图乙中画出开关、指示灯和插孔的连接方式,并把接线板与电源线接通。
3.根据课本提供的数据,利用欧姆定律,估算正确使用试电笔测量家庭电路火线时流过人体的电流。
这个电流大约是25 w灯泡正常工作电流的多少分之一?解:正常通过25w灯泡的电流为25w/220v≈0.114A人体允许通过的最大电流为30mA=0.03A0.03A/0.114A≈1/4答:这个电流大约是25w灯泡正常工作时电流的四分之一。
(注意:这个四分之一指的是25w灯泡正常工作时的电流,如果人体的一端接与25w的接触,25w灯泡的另一端又与220v的火线连接,通过人体的电流就会远远的大于0.114A这个数值,造成触电事故)4. 你家里的空气开关是安装在家庭电路中哪个部位的?为什么要这样安装?答:安装在家庭电路的干路上,这样安装的好处是无论家庭电路中任何一个地方发生短路现象或者电流过大,都会自动切断整个电路。
19.2 家庭电路中电流过大的原因1. 如图19-2-6所示的甲、乙两个电路中,开关闭合后,输电线因电流过大而燃烧起来,甲、乙两图产生电流过大的原因是不同的。
其原因各是什么?答:甲图中电流过大的原因是:电路中用电总功率过大;乙图中电流过大的原因是发生了短路。
2. 电焊利用电流的热效应将焊条熔化,从而使金属部件连接在一起。
某电焊机输出电压40 V、输出功率2 000 w。
各种橡胶绝缘铜芯导线在常温下安全载流量(长时间通电时的最大安全电流)如下表。
第19章爬行纲答案

第19章爬行纲练习答案一、名词1. 羊膜卵amniotic egg:包括卵壳、卵膜、卵黄和胚胎等结构,在发育期间,发生羊膜、绒毛膜、尿囊膜等一系列胚膜结构的一种卵,它使羊膜动物获得了在陆地繁殖的能力。
2. 爬行动物reptile:是真正陆生脊椎动物的开始,是体被角质鳞片或盾片,完全用肺呼吸,以腹部贴地爬行,产大型羊膜卵,在陆地上繁殖的变温脊椎动物。
包括蜥蜴、蛇、龟、鳖、鳄等。
3. 颞窝(孔)与颊窝temporal fossa and facial pit:爬行动物头骨两侧眼眶后颞部的膜性硬骨的穿洞称为颞窝。
如蛇为双颞窝类。
蝮蛇的鼻孔与眼之间的颊部又一个陷窝,窝内有一个薄膜把腔分为内外二个室,为红外线感受器,被称为颞窝。
4. 红外线感受器infrared receptor:爬行类的蟒科蛇类和腹科蛇类在头部具有的特殊感受器,它具有对环境温度微小变化而发生反应的功能,这种热能感受器被称为红外线感受器。
如蟒蛇的唇窝和蝮蛇的颊窝。
5. 胸廓thorax(thoracic cage):脊椎动物从爬行类开始,胸椎、肋骨和胸骨借关节和韧带相互连接形成囊状结构的胸廓。
它保护内脏,加强呼吸。
6. 胸腹式呼吸thoracoabdominal breathing(respiration):爬行动物靠肋间肌和腹壁肌肉运动来扩大和缩小胸廓,从而完成呼吸动作,这种呼吸方式被称为胸腹式呼吸。
7. 次生腭secondary palate:脊椎动物从爬行动物开始,它的硬腭由前颌骨、上颌骨、腭骨的腭突和翼骨愈合组成,它位于脑颅底的口腔顶壁。
8. 闭锁式骨盆closed pelvis:爬行动物髂骨与荐椎的横突相连接,左右坐骨和耻骨在腹中线联合,构成的骨盆为闭锁式骨盆。
9. 同型齿与端生齿pleurodont and acrodont:绝大多数爬行动物的牙齿没有分化,都为同型的圆锥齿,这属于同型齿。
爬行动物低等种类如喙头蜥,其牙齿着生在颌骨的顶面,为端生齿。
第19章生存分析案例辨析及参考答案

第19章⽣存分析案例辨析及参考答案第19章⽣存分析案例辨析及参考答案案例19-1某医师收集30例肺癌术后患者的⽣存情况,有1例由于电话和地址错误⽆法随访到患者,他设计了以下⼏种处理⽅法:①把该病例去掉;②把这例患者写⼊SPSS数据,但末次随访时间空⽩,让SPSS⾃动去分析;③因为某⼀天(⽐如2006年9⽉1⽇)想随访这例患者但是没有随访到,所以将末次随访时间写为随访当天的⽇期。
另欲分析肺癌术后患者的中位⽣存期,计算结果为10个⽉,但是检查原始数据发现,⽣存时间为10个⽉的这个患者⼀直存活到随访结束,似乎与中位⽣存期的定义相⽭盾。
请问:(1)该医师对这例失访患者的处理是否恰当?为什么?正确的处理⽅法是什么?(2)另有1例患者死于脑梗死,⽣存分析时应如何处理?(3)该医师的发现是否与中位⽣存期的定义相⽭盾?为什么?案例辨析(1)该医师对这例失访患者的三种处理都不恰当。
(2)死于脑梗死的病例同样应当作为删失病例。
(3)属于概念不清⽽产⽣的怀疑。
正确做法(1)应作为删失病例,删失⽣存时间的计算为从⼿术切除到最后⼀次随访的时间。
(2)死于脑梗死的病例应当作删失病例,删失⽣存时间的计算为从⼿术切除到死于脑梗死的时间。
(3)该医师的发现与中位⽣存期的定义并不⽭盾,中位⽣存期不能与个体⽣存时间相混淆。
案例19-2 评价A、B两种治疗⽅案对某病的治疗效果,A组(group=0)12⼈,B组(group =1)13⼈。
患者分组后检查其肾功能(kidney),功能正常者记为0,异常者记为1。
治疗后⽣存时间为time(天),⽣存结局status=0表⽰删失,status=1表⽰死亡。
原始数据见教材表19-11。
教材表19-11 25例某病患者两种治疗⽅法的⽣存情况No. group kidney time status No. group kidney time status1 0 1 8 1 14 1 0 632 12 0 0 852 0 15 1 0 2 240 03 0 1 52 1 16 1 0 195 14 0 0 220 1 17 1 0 76 15 0 1 63 1 18 1 0 70 16 0 0 8 1 19 1 1 13 17 0 0 1 976 0 20 1 1 23 18 0 0 1 296 0 21 1 0 1 296 19 0 0 1 460 0 22 1 0 210 110 0 1 63 1 23 1 0 700 111 0 0 1 328 0 24 1 1 18 112 0 0 365 0 25 1 0 1 990 013 1 0 180 1甲医师以⽣存结局为观察指标,整理得A、B两组死亡情况(教材表19-12)。
华师大版八年级下册数学第19章 矩形、菱形与正方形含答案

华师大版八年级下册数学第19章矩形、菱形与正方形含答案一、单选题(共15题,共计45分)1、如图,在矩形ABCD中,M是BC边上一点,连接AM,过点D作,垂足为若,,则BM的长为A.1B.C.D.2、如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是()A.①②B.①③④C.①②④D.①②③④3、下列说法正确的是()A.有两个角为直角的四边形是矩形B.矩形的对角线相等C.平行四边形的对角线相等D.对角线互相垂直的四边形是菱形4、如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为()A.9B.9C.27D.275、如图,是北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13B.19C.25D.1696、如图,已知平行四边形ABCD的对角线的交点是0,直线EF过O点,且平行于AD,直线GH过0点且平行于AB,则图中平行四边形共有()A.15个B.16个C.17个D.18个7、如图,四边形ACED为平行四边形,DF垂直平分BE甲乙两虫同时从A点开始爬行到点F,甲虫沿着A﹣D﹣E﹣F的路线爬行,乙虫沿着A﹣C﹣B﹣F的路线爬行,若它们的爬行速度相同,则()A.甲虫先到B.乙虫先到C.两虫同时到D.无法确定8、如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为()A. B. C. D.39、下列判断错误的是()A.两组对边分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.两条对角线垂直且平分的四边形是正方形D.四条边都相等的四边形是菱形10、如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AG,EG,AE,将△ABG和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE=3,CG=4,则DE的长度为()A. B. C.3 D.11、如图,平行四边形ABCD对角线AC、BD交于点O,∠ADB=20°,∠ACB=50°,过点O的直线交AD于点E,交BC于点F当点E从点A向点D移动过程中(点E与点A、点D不重合),四边形AFCE的形状变化依次是()A.平行四边形→矩形→平行四边形→菱形→平行四边形B.平行四边形→矩形→平行四边形→正方形→平行四边形C.平行四边形→菱形→平行四边形→矩形→平行四边形D.平行四边形→矩形→菱形→正方形→平行四边形12、如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )A.四边形AEDF是平行四边形B.若∠BAC=90°,则四边形AEDF是矩形 C.若AD⊥BC且AB=AC,则四边形AEDF是菱形 D.若AD平分∠BAC,则四边形AEDF是矩形13、如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是()A.3 :4B.5 :8C.9 :16D.1 :214、如图,在△ABC中,∠A=∠B=45 ,AB=4,以AC为边的阴影部分图形是一个正方形,则这个正方形的面积为()A.2B.4C.8D.1615、如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠,折叠后顶点D 恰好落在边OC上的点F处.若点D的坐标为,则点E的坐标为()A. B. C. D.二、填空题(共10题,共计30分)16、工人师傅在做矩形零件时,常用测量平行四边形的两条对角线是否相等来检查直角的精确度,这是根据________.17、阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.小明发现,过点E作E F∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).请回答:BC+DE的值为________参考小明思考问题的方法,解决问题:如图3,已知▱ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________18、如图,O是边长为4的正方形ABCD的中心,将一块足够大,圆心角为直角的扇形纸板的圆心放在点O处,并将纸板的圆心绕点O旋转,则正方形ABCD被纸板覆盖部分的面积为 ________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CH3COOCH2
CH3COO CH3COO
O OCCH3
CH3C O O O
OOCCH3 CH2OOCCH3
CH2OOCCH3
蔗糖八乙酸酯
(四) 回答下列问题:
(1) 单糖是否均是固体?都溶于水?都不溶于有机溶剂?都有甜味?都有变旋光现象?
答:一般一般情况下,是。
(2) 下列两个异构体分别与苯肼作用,产物是否相同?
x
过量苯肼
蓝色
黄色结晶(脎)
x
(六) 有两个具有旋光性的丁醛糖(A)和(B),与苯肼作用生成相同的脎。用硝酸氧化, (A)和(B)都生成含有四个碳原子的二元酸,但前者有旋光性,后者无旋光性。试推 测(A)和(B)的结构式。
CHO
CHO
HO H
H OH
H OH
HO H
解:(A)的结构式为:
CH2OH 或 CHO
实物与镜像的关系。
α和β的δ-氧环式D-(+)-葡萄糖分子中均含有五个手性碳原子,其中有四个手性碳的构型相同,
只有苷原子的构型不同,所以它们互为差向异构体或异头物。
(二) 写出下列各化合物立体异构体的投影式(开链式):
CH2OH
HO O OH
C H2OH O
HO
OH
OH
(1)
OH (2)
OH OH
CHO
CHO H OH H OH H OH
CH3
解: (A)
CH2OH H OH H OH H OH
CH3 (B)
H3C O CH
H OH OH
(C)
OCH3
CH3
OHC O
H
(D)
OCH3 CH
CHO
CH2OH
HO CH2OHO HO
CH3OH
OH dry HCl
(2)
OH
CHO
HO CH2OHO HO OH
OCH3
H OH H OH
HNO3
(3)
CH2OH
CHO
内消旋酒石酸
HO H
NaBH4
H OH
(4)
CH2OH
旋光性丁四醇
HO CH2OHO HO OH
OCH3 HIO4
C H2OH O
HC
OH OCH3 OH O
(C)
(A)
溴水
(B)
或Fehling试剂
(C)
解:
(2) 葡萄和蔗糖
葡萄糖
溴水
不裉色
裉色 裉色
过量PhNHNH2
不成脎 成脎
裉色
葡萄糖
过量苯肼
黄色结晶(脎)
解: 蔗糖 (3) 麦芽糖和蔗糖
x 或 蔗糖
x
麦芽糖 溴水
蔗糖
解: (4) 蔗糖和淀粉
蔗糖
I2
淀粉
解:
裉色
麦芽糖
x 蔗糖 或
OHC
OCH3 + HCOOH
(5)
Ph
O
O HO
(6)
CHO
O PhCH2Cl
KOH
HO OCH3
O
Ph
O
O
O
PhCH2O
PhCH2O OCH3
HH
HIO4
H OH
CHO H H + HCOOH + HCHO
H OH
CHO
(7)
CH2OH
(8)
HOCH2 HO
HO
HO
HO O
CH2OH
(CH3CO)2O
HOCH2 OH
HO
O
HO
OH
HO C H2OH O
HO
OH
OH
答: (A)
-D-吡喃甘露糖
(B)
D-吡喃半乳糖
(五) 用化学方法区别下列各组化合物:
HOCH2 CH CH CH CH CHOCH3
OH OH OH
O
(1)
(A)
HOCH2 CH CH CH CH CHOH
OH OH OCH3 O
(B) HOCH2 CH CH CH CH CHOH
CHO H OH HO CH2OH
CH2OH
(八) 一种核酸用酸或碱水解后,生成D-戊醛糖(A)、磷酸以及若干嘌呤和嘧啶。用 硝酸氧化(A),生成内消旋二元酸(B)。(A)用羟氨处理生成肟(C),后者用乙酐处理 转变成氰醇的乙酸酯(D),(D)用稀硫酸水解给出丁醛糖(E),(E)用硝酸氧化得到内消 旋二元酸(F)。写出(A)至(F)的结构式。
(C)
CH2OH
COOH
H OH
H OH
(F)
COOH
(九) 有三种D型己醛糖(A)、(B)和(C),其中(A)和(B)经催化加氢生成光学活性的相 应醇;用苯肼处理,(A)和(B)生成不同的脎,而(B)和(C)生成相同的脎;但(B)和(C) 经催化加氢生成的相应醇不同。试写出(A)、(B)和(C)的结构式并命名。
异构化和逆羟醛缩合反应。所以,糖苷既不与Fehling试剂作用,也不与Tollens试剂作用。 糖苷无变旋光现象的原因同样归结为它不能形成氧环式和开链式的动态平衡。 (4) 什么叫差向异构体?它与异头物有无区别? 答:两个含有多个手性碳原子手性分子中,构造相同,只有一个手性碳的构型不同,而其它手性碳 的构型均相同时,这两个旋光异构体互为差向异构体; 两个末端手性碳的构型不同的差向异构体互为异头物。 (5) 酮糖和醛糖一样能与Tollens试剂或Fehling试剂反应,但酮不与溴水反应,为什么? 答:因为酮糖可以在碱性介质中发生差向异构化反应及逆羟醛缩合反应,使原来的酮糖转化为醛糖, 达到动态平衡,从而使原来的酮糖被氧化。而溴水不是碱性介质,不能使酮糖发生差向异构及 逆羟醛缩合反应,所以溴水不能氧化酮糖。 (6) 写出D-吡喃甘露糖(A)和D-吡喃半乳糖(B)最稳定的构象式(α-或β-吡喃糖)。
CHO
CHO
HOCH2
OH
HO CH2OH
H OH HO H
CH2OH
CH2OH
CHO HO CH2OH
H OH CH2OH
CHO HOCH2 OH
HO H CH2OH
CHO H OH HOCH2 OH
CH2OH
CHO HO H HO CH2OH
CH2OH
CHO HO H HOCH2 OH
CH2OH
第十九章 碳水化合物
(一) 写出D-(+)-葡萄糖的对映体。α和β的δ-氧环式D-(+)-葡萄糖是否是对映体? 为什么?
CHO
HO H
H OH
HO H
HO H
解:D-(+)-葡萄糖的对映体为
CH2OH (L- (-)-葡萄糖)。
α和β的δ-氧环式D-(+)-葡萄糖不是对映体,因为α和β的δ-氧环式D-(+)-葡萄糖之间不具有
OHC CH2 CH CH CH CH2
CH2 CH CH CH2 CH CHO
(A)
OH OH OH OH (B) OH OH OH
OH
答:产物不同。(A)与苯肼作用只能生成腙;(B)与过量苯肼作用可生成脎。 (3) 糖苷既不与Fehling试剂作用,也不与Tollens试剂作用,且无变旋光现象,试解释之。 答:糖苷是稳定的缩醛结构,不能形成氧环式和开链式的动态平衡,因而不能通过开链式发生差向
CHO
C=N [ 提示:H
(CH3CO)2O
OH
-H2O
COOH
H OH
H OH
H OH
H OH
H OH
H OH
解:(A)
CH2OH CN
(B)
CH2OH
H
OCOCH3
H
OCOCH3
H
OCOCH3
(D)
CH2OCOCH3
CHO
H OH
H OH
(E)
CH2OH
CN
] C=NOH
H OH
H OH
H OH
CHO H OH HO H H OH H OH
CH2OH 解: (A) D-葡萄糖
CHO HO H HO H
H OH H OH
CH2OH 或者: (A) D-半乳糖
CHO HO H HO H HO H
H OH CH2OH
(B) D-塔罗糖
CHO H OH HO H HO H H OH
CH2OH
(C) D-半乳糖
CHO HO H
H OH H OH H OH
CH2OH (B) D-阿卓糖
CHO H OH H OH H OH H OH
CH2OH (C) D-阿洛糖
(十) 光学活性化合物C5H10O4(A),有三个物性碳原子,构型均匀为R。(A)与NH2OH 生成肟。(A)用NaBH4处理得到光学活性化合物C5H12O4(B),(B)与乙酐反应得到四 乙酸酯;在酸存在下,(A)与甲醇作用生成C6H12O4(C),(C)与HIO4反应得到 C6H10O4(D),(D)经酸性水解得到乙二醛(OHC-CHO),D-α-羟基丙醛和甲醇。试写 出(A)~(D)的结构式。
CH2OH CHO
H OH
HO H
H OH
HO H
(B)的结构式为: CH2OH 或
CH2OH
(七) 化合物C5H10O5(A),与乙酐作用给出四乙酸酯,(A)用溴水氧化得到一个酸 C5H10O6,(A)用碘化氢还原给出异戊烷。写出(A)可能的结构式。(提示:碘化氢能 还原羟基或羰基成为烃基。)
解:(A)可能的结构式有:
CHO
H OH
H OH
HO H
H OH
HO H
H OH
