《统计学》统计综合指标(补充例题)
统计综合指标考试题及答案

统计综合指标考试题及答案一、选择题(每题2分,共20分)1. 以下哪项不是统计综合指标?A. 平均数B. 众数C. 方差D. 中位数答案:C2. 总体平均数的计算公式是:A. 总和 / 总数B. 总和 / 总数 + 1C. 总和× 总数D. 总数 / 总和答案:A3. 标准差是衡量数据的:A. 中心趋势B. 离散程度C. 偏态D. 峰态答案:B4. 以下哪个指标可以反映数据的偏态?A. 均值B. 方差C. 偏度D. 峰度答案:C5. 以下哪个指标表示数据的峰态?A. 均值B. 方差C. 偏度D. 峰度答案:D6. 以下哪个选项是计算众数的方法?A. 出现次数最多的数值B. 所有数值的总和除以数值的个数C. 所有数值的乘积除以数值的个数D. 所有数值的平方和除以数值的个数答案:A7. 以下哪个选项是计算中位数的方法?A. 将数据从小到大排序,取中间的数值B. 将数据从小到大排序,取平均数C. 将数据从大到小排序,取中间的数值D. 将数据从大到小排序,取平均数答案:A8. 以下哪个选项是计算方差的公式?A. 平均数的平方B. 每个数值与平均数差的平方和除以总数C. 每个数值与平均数差的绝对值和除以总数D. 每个数值与平均数差的平方和乘以总数答案:B9. 以下哪个选项是计算标准差的公式?A. 方差的平方根B. 方差的平方C. 方差的倒数D. 方差的对数答案:A10. 以下哪个选项是计算变异系数的公式?A. 标准差 / 平均数B. 方差 / 平均数C. 平均数 / 标准差D. 平均数 / 方差答案:A二、简答题(每题5分,共20分)1. 请简述什么是统计综合指标,并给出至少两个例子。
答案:统计综合指标是用来描述和概括数据集中趋势和离散程度的一系列数值指标。
例如,平均数可以反映数据的中心位置,而标准差可以衡量数据的离散程度。
2. 请解释什么是正态分布,并简述其特点。
答案:正态分布是一种连续概率分布,其形状呈对称的钟形曲线。
统计学综合指标

第四章统计综合指标一.单选题1、 某企业某种产品汁划规定单位成本降低5%,实际降低了 7%,则实际生产成本为计划完成 度得(A ) A. B. C. D.2、A. B ・ C. D. 3、 A.B.C.D. 5、C 、D 、6、 已知某企业职工消费支出,年支出6000元人数最多,平均年支出为5500元•该企业职工消 费支出分布属于(A )A. B. C. D ・7、 A. B. C. D.8、 加权算术平均数不但受标志值大小得影响,而且也受标志值出现得次数多少得影响。
因此, 下列情况中对平均数不发生影响得就是(D )A. B. C.97、9% 140% 102、2% 2%某月份甲工厂得工人出勤率属于(A ) 结构相对数 强度相对数比例相对数 计划完成相对数按全国人口平均得粮食产量就是(B ) 平均指标 强度相对指标 比较相对指标 结构相对指标若某总体次数分布呈轻微左偏分布,则有(B )成立。
A 、 x>B 、 X vMfVA/。
左偏分布 右偏分布 对称分布J 形分布用组中值代表组内变量值得一般水平有一:4^得假出性,即(B ) 各组得次数必须相等 变量值在本组内得分布就是均匀得 组中值能取整数各组必须就是封闭组 标志值比较小而次数较多时 标志值较大而次数较小时 标志值较大而次数较多时 标志值出现得次数柑等时D.9、已知某市场某种蔬菜早市、午市、晚市得毎公斤价格,在早市、午币、晚市得销售额基本 相同得情况下,计算平均价格可采取得平均数形式就是(C )简单算术平均数 加权算术平均数 简单调与平均数 加权调与平均数若各■个标忠值都扩大2倍,而频数都减少为原来得1/3,则平均数(A )扩大2倍减少到1/3 不变不能预期平均值得变化假立各个标志值都减去20个单位,那么平均值就会(A ) 减少20减少到1/20 不变不能预期平均值得变化如果单项式分配数列得各个标志值与它们得频数都缩小到原来得1/2,那么众数(A ) 缩小到原来得1/2缩小到原来得1/4 不变不能预期其变化如果单项式分配数列得并个标志值都增加一倍,而频数均减少一半,那么中位数(A ) 增加一倍 减少一半 不变不能预期其变化如果变量值中有一项为零,则不能计算(B )算术平均数调与平均数与几何平均数 众数中位数计算标准差时,如果从每个变量值中都减去任意数N 计算结果与原标准差相较(C ) 变大 变小 不变可能变大也可能变小假如把分配数列得频数换成频率,则标准差(C )减少增加 不变 无法确定不同总体间得标准差不能进行简单对比,这就是因为(D ) 平均数不一致离散程度不一致A. B. C. D ・ 10、 A. B. C. D ・ 11、A. B. C. D. 12、A. B ・C. D. 13、A.B ・C. D ・14、 A ・B. C. D. 15、 A. B. C. D. 16、C. 总体单位不一致D. 离差平方与不一致 20、两个总体得平均数不等,但标准差相等,则(B A. B. C. D ・21、 如果两个数列就是以不同得i|量单位来表示得,则比较其离差得il •:g 方法就是(D A. B. C. D ・22、 在下列成数数值中,哪一个成数数值得方差最小(D )A. 0、8B. 0、5C.0、3D. 0、123、 如果偏度值a 小于零,蜂度值B 小于3,可判断次数分布曲线为(C ) A. B. C. D.二、多选题 总量指标(ABCE)就是计算相对指标与平均指标得基础 就是反映国情与国力得重要指标 就是实行社会管理得重要依据 可用来比较现象发展得结构与效益水平某银行1999年底得居民储蓄存款额就是(ACE ) 综合指标 单位总量指标 标志总虽指标 时期指标 时点指标下列指标中属于时期指标得就是(AB ) 产品产量 销售收入平均数小,代表性大 平均数大,代表性大 两个平均数代表性相同 无法加以判断极差 标准差 平均差 标准差系数左偏分布,呈尖顶峰度 右偏分布,呈尖顶峰度 左偏分布,呈平顶峰度 右偏分布,呈平顶峰度职工人数设备台数下列指标中属于强度相对数得就是(BC )1992年末我国乡村总人口占全国总人口得72、37% 1992年我国农民家窓平均每百户拥有电冰箱2、17台1992年我国人口密度122人/平方公里1992年我国全部职工平均货币工资2711元A.B.C.D・2、A・B.C.D.E・3、A.B.C.D・4E. 1992年我国钢产量为美国同期得81、2%5、分子与分母不可互换计算得相对指标就是(ABCA.计划完成情况相对指标B.动态相对指标C.结构相对指标D.强度相对指标E.比较相对指标6、平均指标(ABDE )A.就是总体一般水平得代表值B.就是反映总体分布集中趋势得特征值C.就是反映总体分布离中趋势得特征值D.可用来分析现象之间得依存关系E.只能根摇同质总体计算7、卜•列属于平均指标得有(BC )A.人均国民收入B.人口平均年龄C.粮食单位面积产量D.人口密度E.人口自然增长率8、下列平均数要用几何平均法il•算得有(BCD )。
统计学综合指标

第四章统计综合指标一、单选题1.某企业某种产品计划规定单位成本降低5%,实际降低了7%,则实际生产成本为计划完成度的(A)C.比较相对指标D.结构相对指标5.若某总体次数分布呈轻微左偏分布,则有(B)成立。
A.x>M>o MeB.x<M<o MeC.x>M>e MoD.x<M<e Mo6.已知某企业职工消费支出,年支出6000元人数最多,平均年支出为5500元,该企业职工消费支出分布属于(A)A.左偏分布ArrayC.标志值较大而次数较多时D.标志值出现的次数相等时9.已知某市场某种蔬菜早市、午市、晚市的每公斤价格,在早市、午市、晚市的销售额基本相同的情况下,计算平均价格可采取的平均数形式是(C)2A.简单算术平均数B.加权算术平均数C.简单调和平均数D.加权调和平均数10.若各个标志值都扩大2倍,而频数都减少为原来的1/3,则平均A.缩小到原来的1/2B.缩小到原来的1/4C.不变D.不能预期其变化13.如果单项式分配数列的各个标志值都增加一倍,而频数均减少一半,那么中位数(A)A.增加一倍B.减少一半C.不变D.不能预期其变化A.减少B.增加C.不变D.无法确定19.不同总体间的标准差不能进行简单对比,这是因为(D)4A.平均数不一致B.离散程度不一致C.总体单位不一致D.离差平方和不一致20.两个总体的平均数不等,但标准差相等,则(B)B.0.5C.0.3D.0.123.如果偏度值a小于零,峰度值β小于3,可判断次数分布曲线为(C)A.左偏分布,呈尖顶峰度B.右偏分布,呈尖顶峰度C.左偏分布,呈平顶峰度D.右偏分布,呈平顶峰度二、多选题1.总量指标(ABCE)B.销售收入C.职工人数D.设备台数4.下列指标中属于强度相对数的是(BC)A.1992年末我国乡村总人口占全国总人口的72.37%6B.1992年我国农民家庭平均每百户拥有电冰箱2.17台C.1992年我国人口密度122人/平方公里D.1992年我国全部职工平均货币工资2711元E.1992年我国钢产量为美国同期的81.2%5.分子与分母不可互换计算的相对指标是(ABC)A.人均国民收入B.人口平均年龄C.粮食单位面积产量D.人口密度E.人口自然增长率8.下列平均数要用几何平均法计算的有(BCD)。
《统计学》第六章统计指数(补充例题)
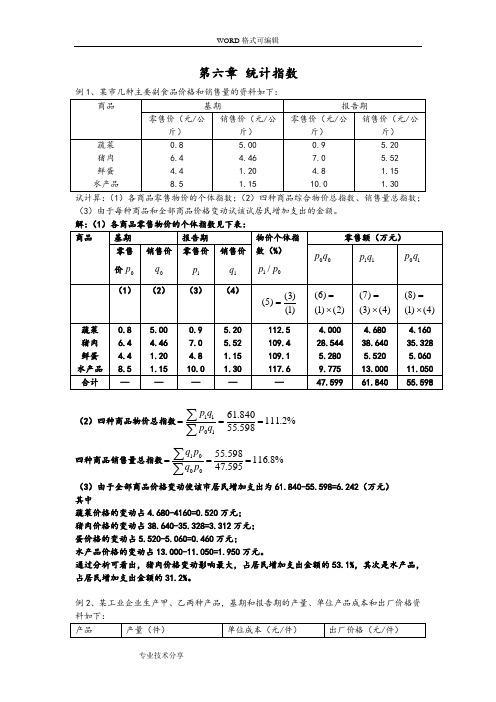
第六章 统计指数(3)由于每种商品和全部商品价格变动试该试居民增加支出的金额。
解:(1)各商品零售物价的个体指数见下表:(2)四种商品物价总指数%2.111598.55840.611011===∑∑qp q p四种商品销售量总指数%8.116595.47598.55001===∑∑pq p q(3)由于全部商品价格变动使该市居民增加支出为61.840-55.598=6.242(万元) 其中蔬菜价格的变动占4.680-4160=0.520万元; 猪肉价格的变动占38.640-35.328=3.312万元; 蛋价格的变动占5.520-5.060=0.460万元;水产品价格的变动占13.000-11.050=1.950万元。
通过分析可看出,猪肉价格变动影响最大,占居民增加支出金额的53.1%,其次是水产品,占居民增加支出金额的31.2%。
例2、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资试计算:(1)以单位成本为同度量因素的产量总指数 (2)以出厂价格为同度量因素的产量总指数 (3)单位成本总指数 (4)出厂价格总指数(1)以单位成本为同度量因素的产量总指数%7.1193100037100001===∑∑zq z q(2)以出厂价格为同度量因素的产量总指数%6.115550006360001===∑∑pq p q(3)单位成本总指数%2.14837100550001011===∑∑qz q z(4)出厂价格总指数%8.9963600635001011===∑∑qp q p例3、试根据例2的资料,从相对数和绝对数方面分析: (1)总成本变动受产量和单位成本变动的影响程度 (2)销售额变动受产量和出厂价格变动的影响程度 解:(1)总成本变动:总成本指数%4.1773100055000011===∑∑qz q z增加总成本∑∑=-=-2400031000550000011qz q z (元)其中由于产量变动的影响:产量指数%7.1193100037100001===∑∑zq z q由于产量增长而引起总成本增加:∑∑=-=-610031000371000001zq z q (元)由于单位成本变动的影响: 单位成本指数%2.1483710055000111===∑∑zq z q由于单位成本增长而引起总成本增加:∑∑=-=-1790037100550000111zq z q (元)177.4%=119.7%×148.2% 24000元=6100元+17900元计算表明,该厂两种产品总成本报告期比基期增长77.4%,是由于产品产量增加19.7%和单位成本提高48.2%两因素造成的。
统计学综合指标习题

A.
标志值比较小而次数较多时
B.
标志值较大而次数较小时
C.
标志值较大而次数较多时
标志值出现的次数相等时
9.已知某市场某种蔬菜早市、午市、晚市的每公斤价格,在早市、 计算平均价格可采取的平均数形式是()
10.若各个标志值都扩大2倍,而频数都减少为原来的1/3,
扩大2倍
第四章综合指标
一、单选题
1.某企业某种产品计划规定单位成本降低5%,实际降低了7%,则实际生产成本为计划的()
A.
%
B.
140%
C.
%
D.
2%
2.某月份甲工厂的工人出勤率属于(
A.
结构相对数
B.
强度相对数
C.
比例相对数
D.
计划完成相对数
3.按全国人口平均的粮食产量是(
A.
平均指标
B.
强度相对指标
C.
比较相对指标
D.
结构相对指标
4. 受极大值影响较大的平均数是(
A.
位置平均数
B.
几何平均数C.算术Fra bibliotek均数D.
调和平均数
A.X>Me>Mo
B.x<Me<Mo
C.x>Mo>Me
D.X<Mo<Me
6000元人数最多,平均年支出为5500元,该企业职工消费支出分布
各组必须是封闭组
8.加权算术平均数不但受标志值大小的影响,而且也受标志值出现的次数多少的影响。因此,下列情况中对
2021统计学原理-《统计学》第四章 综合指标试题(精选试题)

统计学原理-《统计学》第四章综合指标试题1、一组数据向某一中心值靠拢的倾向反映了数据的________。
2、________是一组数据中出现次数最多的变量值。
3、一组数据排序后处于中间位置上的变量值称________。
4、不受极端值影响的集中趋势度量指标有________、________和________。
5、一组数据的最大值与最小值之差称________。
6、________是一组数据的标准差与其相应的平均数之比。
7、数据分布的不对称性是________。
8、数据分布的平峰或尖峰程度称________9、计算比率的平均数一般用几何平均法,它实际上是各变量值对数的________。
10、Excel中计算中位数时选用的函数为________函数.11、某工厂13名工人某日生产零件数分别为(单位:件)10、11、13、11、14、11、12、11、15、16、12、12、13,则中位数为________;众数为________。
12、某百货公司连续几天的销售额如下:257、276、297、252、238、310、240、236、265,则其下四分位数是________。
13、一组数据分布的最高峰点所对应的变量值即为_______________。
14、当平均数大于中位数时,数据呈_______________分布。
15、若一组数据的,则其属于____________________分布。
16、如果一组数据服从标准正态分布,则峰态系数为____________。
17、_________________是一组数据中间位置上的代表值,不受数据极端值的影响。
18、假定一个总体由5个数据组成:3、7、8、9、13,该总体的方差为________。
19、某班共有25名学生,期末统计学课程的考试分数分别为:68、73、66、76、86、74、61、89、65、90、69、67、76、62、81、63、68、81、70、73、60、87、75、64、56,该班考试分数的下四分位数和上四分位数分别是________和________。
统计学第三章 综合指标练习题

统计学第三章综合指标练习题统计学第三章综合指标练习题前面章节及第三章综合指标一、选择题1、杭州地区每百人手机拥有量为90部,这个指标是a、比例相对指标b、比较相对指标c、结构相对指标d、强度相对指标2、某组与数据呈圆形正态分布,排序出来算术平均数为5,中位数为7,则该数据分布为a、左偏分布b、右偏分布c、对称分布d、无法判断3、平均值算术平均数的大小a主要受到各组标志值大小的影响,与各组次数多少毫无关系;b主要受到各组次数多少的影响,与各组标志值大小毫无关系;c既与各组标志值大小毫无关系,也与各组次数多少毫无关系;d既与各组标志值大小有关,也受到各组次数多少的影响4、已知一分配数列,最小组限为30元,最大组限为200元,不可能是平均数的为a、50元b、80元c、120元d、210元5、比较两个单位的资料,甲的标准差小于乙的标准差,则a两个单位的平均数代表性相同b甲单位平均数代表性大于乙单位c乙单位平均数代表性大于甲单位d不能确定哪个单位的平均数代表性大6、若单项数列的所有标志值都减少常数9,而次数都增加三分之一,则其算术平均数a、增加9b、增加6c、减少三分之一d、增加三分之二7、与变量值相同计量单位的是a全距b调和平均数c平均差d标准差e线性系数f算术平均数8、由于计量单位或者规模不同造成不可比,可能采用什么方法解决a比较对指标b平均指标c强度相对指标d比例相对指标f结构相对指标9、与变量值同比例变化的是a算术平均数b调和平均数c几何平均数d全距e标准差f平均差g标准差系数10、某数据集服从对称的正态分布,算术平均数为100,现分别增加2个极端值1和199,怎此数据集的分布将a维持等距的正态分布b左偏c右偏d无法推论11、人口普查中以每个居住地居民位调查单位,下面属标志的就是a性别b年龄c男性d人口总数e已婚12、对浙江财经学院学生的基本情况进行调查,属于数量标志的是a平均值开支b年龄c年级d体重e学生总数二、计算题1、已知甲小区居民平均年龄为37岁,标准差为12岁,现对乙小区居民年龄进行抽样调查,得到资料如下(保留1位小数):年龄(岁)人数(人)18以下1218-305030-506850以上40根据以上资料计算:(保留1位小数)(1)计算乙小区居民的平均年龄;(2)比较甲乙两小区平均年龄的代表性大小;2、已知某企业职工工资情况如下:工资(元)人数(人)1000以下201000-2000402000-30001003000-4000504000以上30根据资料计算该企业职工工资的平均数,众数和中位数。
第三章-综合指标练习试题

第三章统计综合指标一、名词解释1、总量指标2、时期指标3、相对指标4、强度相对指标5、算术平均数6-标致变异指标7、标准差系数二、填空1、总量指标是对总体和进行统计描述的基础数据,是从上认识客观事物的起点数据。
2、是统计中最常用的最基本的综合指标。
3、总量指标按照其反映的总体内容不同,可划分为和。
总量指标反映的时间状况不同,可分为总量指标和总量指标。
4、根据被研究对象的特点、性质和作用,总量指标的计量单位一般有三种,即、、。
实物单位是反映事物使用价值的计量单位,它又可以分为、、双重单位和。
5、相对指标的基本公式为:6、相对指标数值有两种计量形式:一是相对指标,二是相对指标。
7、无名数相对指标是指相对指标值后边没有计量单位,或者没有实质性的具体计量单位而只有抽象的计量单位。
具体有、、、。
8、根据不同的研究目的、任务和对比基础,相对指标可分为相对指标(与计划数对比)、相对指标、相对指标(与部分数额对比)、相对指标(与同类典型数额对比)、相对指标(与有联系的总体数额对比)、相对指标(与历史数额对比)。
9、在社会经济统计中,(也称为均值)是最常用的最基本的反映分布数列中各变量值分布的集中趋势的代表值。
它是在总量指标基础上计算出来的。
10、算术平均数依据计算方法不同,又分为算术平均数和算术平均数。
11、在不掌握各组单位数的资料及总体单位数的情况下,如果只掌握各组的标志值和各组的标志总量及总体总量,则用平均数的方法计算平均指标。
12、标志变异指标是反映总体各单位标志值差异程度的综合指标,它表明总体各单位标志值的和,又称。
13、按计算方法的不同,标志变异指标一般常用的有、、。
14、极差的计算公式:。
标准差的简单式计算公式:。
标准差的加权式计算公式:。
标准差系数的计算公式:。
15、对于不同水平即平均指标不相同的总体,不宜直接用标准差比较其标志变动度的大小,而需要利用进行比较。
16、标准差愈大,说明标志变动程度愈,因而平均数的代表性就愈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章统计综合指标(五)计算题例1、某集团公司所属各拖拉机厂某月生产情况如下表所示:厂别类型每台马力数产量(台)第1厂履带式3675履带式18105轮式28400第2厂履带式7585轮式1594轮式12150第3厂履带式4540履带式7525轮式2450 要求按产品类型和功率核算有关总量指标。
解:【分析】通常总量指标中首选核算实物量。
这里可以核算自然实物量、双重单位实物量和标志单位实物量。
从下面两表看出核算的过程及结果:(1)按自然单位和双重单位核算:产品类型产量(台)产量(台/马力)履带式330330/14640轮式694694/15610合计10241024/30250(2)按标准单位核算(以15马力拖拉机为标准单位):产品类型与功率产量(台)换算系数标准台数(1)(2)(3)=(1)÷15(4)=(2)×(3)履带式18马力105 1.212636马力75 2.418045马力40 3.012075马力110 5.0550小计330—976轮式12马力1500.80012015马力94 1.0009424马力50 1.6008028马力400 1.867747小计694—1041合计1024—2017例2、下面是某市年末户籍人口和土地面积的资料:单位:人户籍人口数 2001年 2002年 人口总数 男 女 1343599 682524 661075 1371588 695762 675826已知该土地面积1565平方公里,试计算全部可能计算的相对指标,并指出它们属于哪一种相对数。
解:计算结果列表如下:2001年 2002年 人口总数 男 女 (1)男性人口占总人口比重(%) (2)女性人口占总人口比重(%) (3)性别比例(%)男:女 (4)人口密度(人/平方公里) (5)人口增长速度(%) 1343599 682524 661075 50.8 49.2 103 858 — 1371588 695762 67582650.7 49.3 102 8762.1 在所计算的相对指标中:(1)、(2)为结构相对数,(3)为比例相对数,(4)为强度相对数,(5)为动态相对数。
例3、某服装公司产量如下:单位:万件 2002年 2003年计划 实际 重点企业产量成人的 儿童的 6.4 5.1 8.8 5.7 9.4 6.1 4.3 2.3 合计 11.5 14.5 15.5 6.6 计算所有可能计算的相对指标,并指出它们属于哪一种相对指标。
解:下面设计一张统计表,把所计算的相对指标反映在表中: 2002年 2003年 2003年比2002年增长(%)产量 比重 (%) 计划 实际 产量计划完成(%) 重点企业 产量 比重(%) 产量 比重(%) 产量 比重(%) (甲) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) 成人的 儿童的 6.4 5.1 56 44 8.8 5.7 61 39 9.4 6.1 61 39 106.8 107.0 4.3 2.3 65 35 46.9 19.6 合计 11.5 100 14.5 100 15.5 100 106.9 6.6 100 34.8所计算的相对指标中(2)、(4)、(6)、(9)均为结构相对数,(7)为计划完成程度相对数,(10)为动态相对数。
此外,还可把“成人的”产量与“儿童的”产量对比,计算比例相对数; 把重点企业产量与全公司产量对比,计算结构相对数。
例4、某地区2003年生产总值计划为上年的108%,2002-2003年动态相对数为114%,试确定2003年生产总值计划完成程度。
解:根据计划完成程度(%)=年计划生产总值年实际生产总值计划数实际数20032003=年实际生产总值年实际生产总值20022003=年实际生产总值年计划生产总值20022003÷%6.105%108%114==例5、某农场三种不同地段的粮食产量资料如下:地段 播种面积(亩) 收获量(公斤) 甲 乙 丙 60 50 40 48000 35000 24000 合计 150 107000 试计算每地段的单位面积产量和三地段的平均单位面积产量。
解:【分析】本题利用算术平均数的基本形式进行计算,直接用组标志总量除以组单位总量得出各地段平均单位面积产量。
再用标志总量除以单位总量得到三个地段的总平均收获率。
计算结果如下:地段 播种面积(亩) 收获量(公斤) 收获率(公斤/亩) 甲 乙 丙 60 50 40 48000 35000 24000 800 700 600 合计 150 107000 713 单位面积产量(收获率)=总收获率/总播种面积例6、某厂有102名工人,各组工人工资和工人数资料如下:技术级别 月工资(元) 工人数(人)1 2 3 4 5 546 552 560 570 585 57 15 18 40 2 合计 — 102 求工人平均工资和平均技术级别。
解:【分析】技术级别和月工资都是工人的标志,可通过工人数加权来计算平均技术级别和平均月工资。
工人的平均月工资计算列表如下:技术级别 月工资x (元)工人数f (人)工资总额xf (元)1 2 3 4 5 546 552 560 570 585 57 15 18 40 2 31122 8280 10080 5700 1170 合计—10256352)(47.55210256352元===∑∑fxf x例7、某管理局所属15个企业,某年某产品按平均成本的高低分组资料如下表: 按平均成本分组(元/件) 企业数(个) 各组产量在总产量中所占比重(%)10-12 12-14 14-18 2 7 6 22 40 38 合计 15 100 试计算15个企业的平均单位成本。
解:【分析】本题计算要求利用频率计算平均数的公式,资料是组距分配数列,须先计算组中值。
另外,本题还涉及权数的选择,企业数虽是次数,但它和分组标志值相乘无任何实际意义,因此,不能作权数。
只有采用产量比重作权数,才符合题目要求。
列表计算如下: 按平均单位成本分组(元) 组中值x 各组产量在总产量中所占比重(%)∑ff x 10-1212-14 14-18 11 13 16 22 40 38 2.42 5.20 6.08 合计— 10013.70平均单位成本∑∑=ffxx =2.42+5.20+6.08=13.70例8、某企业工人按劳动生产率高低分组的资料如下: 按劳动生产率分组(件/人) 生产工人数50-60 60-70 70-80 80-90 90以上 150 100 70 30 16 合计 366试计算该企业工人的平均劳动生产率。
解:【分析】本题是等距分配数列,要计算平均数首先要计算组中值。
最后一组为开口组,其组中值=下限+21相邻组距=95 列表计算如下: 按劳动生产率分组(件/人) 组中值x 生产工人数f产量xf (件)50-60 60-70 70-80 80-90 90以上 55 65 75 85 95 150 100 70 30 16 8250 6500 5250 2550 1520 合计—36624070平均劳动生产率36624070==∑∑ffxx =65.8(件/人)例9、某公司所属20个企业资金利润及有关资料如下表: 资金利润率(%) 组中值(%) 企业数 企业资金(万元)-10-0 0-10 10-20 20-30 -5 5 15 25 10 5 3 2 80 100 500 800 合计 — 20 1480 求平均利润率。
解:【分析】本题不宜以企业数为权数,应该以企业资金为权数,求得各组的实际利润,然后求平均利润率。
平均利润率:80050010080800%25500%15100%580%5+++⨯+⨯+⨯+⨯-==∑∑f xf x%65.181480276==这里276万元是全公司的利润总额,分母1480万元是全公司的资金,所得的平均利润率18.65%是符合实际的。
例10、2003年某月份甲乙两农贸市场某农产品价格及成交量和成交额的资料如下: 品种 价格(元/千克) 甲市场成交额(万元) 乙市场成交量(万千克) A B C 1.2 1.4 1.5 1.2 2.8 1.5 2 1 1 合计 — 5.5 4 试问该农产品哪一个市场的平均价格高。
解:【分析】给定的数据是被平均标志(价格)的分子(成交额),则用加权调和平均数计算;给定的是“分母”(成交量),则按加权算术平均数计算。
计算列表如下:价格x(元/千克)甲市场乙市场成交额M (万元) 成交量M/x (万千克)成交量f (万千克) 成交额xf (万元)1.2 1.4 1.5 1.22.8 1.5 1 2 1 2 1 1 2.4 1.4 1.5 合计 5.5 4 4 5.3两市场的平均价格如下:38.145.5===∑∑xM Mx 甲(元/千克) 33.143.5===∑∑fxf x 乙(元/千克)例11、某市场某种蔬菜早市、午市和晚市每千克价格分别为1.25元、1.20元和1.15元,试在下面的情况下求平均价格:(1)早市、午市和晚市销售量基本相同;(2)早市、午市和晚市销售额基本相同。
解:【分析】销售量基本相同,可以看作次数(f )相等,故平均价格可用简单算术平均数计算。
已知销售额即标志总量(m ),要用调和平均数计算平均价格。
这里早、午和晚市销售额基本相同,可用简单调和平均数计算。
(1)2.1315.120.125.1=++==∑∑nx x (元/千克)(2)199.115.1120.1125.111111=++++==∑xn x (元/千克)例12、某企业某月工人日产量资料如下表,试计算众数和中位数。
日产量分组(件) 工人数60以下 60-70 70-80 80-90 90-100 100以上 40 100 180 220 90 50 合计 680解:(1)众数:i L M ⨯∆+∆∆+=21108210)90220()180220(18022080≈⨯-+--+=(件)(2)中位数:i f S fL M mm e ⨯-+=-∑128222032026801080≈-⨯+=(件)例13、设甲乙两公司进行招员考试,甲公司用百分制记分,乙公司用五分制记分,有关资料如下表所示: 甲公司 百分制组别 参考人数(人) 乙公司 五分制组别 参考人数(人)60以下 60-70 70-80 80-90 90-100 100以上1 15 20 12 2 1 2345 13 13 17 16 合计 50 合计 50 问哪一个公司招员考试的成绩比较整齐? 解:【分析】要说明哪一个公司招员考试的成绩比较整齐,必须计算标准差系数。
