虚位移原理例题
第17章 虚位移原理

(e) (e) 动量定理 或 dK F 或 MaC F 质心运动定理 dt dLO mO ( F ) 0 动量矩定理 mO ( F ) dt
(e) F 0
还是静 力学方 程,无 意义。
2
动能定理
假设系统有一小的位移
dT 0
质点系自由度 = 自由质点系自由度 — 约束(方程)数
2. 以刚体作为基本单元 自由刚体系:OA、AB;自由度 = 3×2 = 6 约束方程: 约束数 = 5
xO 0, x A x A , yO 0, y A y A , yB 0
O
y
A
r
A
l
B
x
质点系自由度 = 6 — 5 = 1 质点系自由度 = 自由刚体系自由度 — 约束(方程)数
注1:通常两种方法各有侧重,有些问题用几何法容易,有些问题用解析
法容易。一般容易作运动学分析的问题宜选用几何法。
注2:解析法(变分法)相当于“绝对法”;而几何法(运动分析法)通
常要用到“合成运动”的方法。即两种方法“对应”于运动分析的两种方 法。 12
三、虚功 力在虚位移上所做的功称为虚功。
力: W F r F r cos Xx Yy Zz 或 W mP (F ) mP (F ) 指力 F 对轴或瞬心P之矩,特别对刚体此式常用。
16
解题步骤: (一)研究整体(不取分离体),并选广义坐标; (二)(若用几何法)画出系统一组虚位移,并用广义坐标虚位 移表示所有对应主动力的虚位移; (若用解析法,不画虚位移)画出直角坐标系,并求所有对 应主动力坐标的变分; (三)列解方程。 例1:本章开头例子 如图,系统平衡。已知Q、l、 ,求P。 分析:由几何法找“运动”关系比较难,而 结构规则,故用解析法较方便。 解:选 为广义坐标,建立坐标系如图。
第11章 虚位移原理—习题(1~17)

第11章 虚位移原理——习题1~1711-1 图示平面机构,圆盘的半径为r ,可绕其中心轴转动,直杆BC 和BD 的长度为l 1 = 2r ,直杆AB 的长度为l 2 = 3r ,试建立图示位置圆盘的虚转角θδ与滑块C 的虚位移C r δ之间的关系。
(题11-1答案:)11-2 在图示平面机构中,O 1A = AB = r ,O 2C = 2r ,BD = 4r ,C 为杆BD 的中点,试建立图示位置杆O 1A 的虚转角1δθ与杆O 2C 的虚转角2δθ之间的关系。
(题11-2答案:)11-3 如图所示曲柄摇杆机构,已知OA = OB = l ,试建立图示位置两杆虚转角之间的关系。
(题11-3答案:)11-4 在图示平面机构中,半径为R = 2r 的四分之一细圆环BD ,其上套一套筒A ,套筒与可绕轴O 转动的直杆OA 铰接,OA 的长度为l = 3r ,试建立图示题11-1图题11-2图位置杆OA 的虚转角与点D 的虚位移之间的关系。
(题11-4答案:)11-5 在如图所示平面机构中,O 1A = O 3C = O 3D = AB = l ,在图示位置,CB = O 2B =l 332,试建立该位置A 、D 两点虚位移之间的关系。
(题11-5答案:)11-6 在图示平面机构中,ABD 为边长等于a 的正三角形平板,O 1B 、O 2D 的杆长也均为a 。
机构在图示位置时,杆OE 与水平线成60◦角,A 、D 、O 2在同一水平线上,O 1B 位于铅垂位置,且OA = a ,试求此瞬时刚体O 1B 与OE 的虚转角之间的关系。
题11-3图题11-4图题11-5图题11-6图(题11-6答案:)11-7 在图示平面四连杆机构中,在杆AB 上垂直地作用有三角形分布载荷,其最大集度为q ,在杆OA 的中点作用有水平向左的主动力F ,且F = ql ,若不计各构件自重和各接触处摩擦,为使系统在图示位置平衡,所需施加的作用于杆BC 上的主动力偶矩M 的值。
理论力学:虚位移原理

y
B
内力虚功:W (Fs ) Fs
b
xE xD 2b sin 2b cos
l
A
FS D FS' E
CF
外力虚功:W (F ) FxC
xC 2l sin
xC 2l cos
x
根据虚位移原理:W 0
当0 2b
Fs
k(
0 )
b l
k ( xC
a)
当:xC a, 0
2020/12/9
变形体的虚位移原理:具有双面、理想约束处于静止的质 点系,在给定位置处于平衡的充分必要条件是,其所有外 力和内力在该位置任意给定的虚位移上所作的虚功之和等 于零。
2020/12/9
2
理论力学
§4-6 虚位移原理
例:机构如图所示,不计构件自重。 已知 AB = BC = l, 弹簧
刚度为k,当 AC = a 时,弹簧无变形。设在滑块上作用一水平
理论力学
习题:4-7、4-12、4-15
•变形体的虚位移原理
•质点系平衡的稳定性
2020/12/9
1
理论力学
§4-6 虚位移原理
三、变形体的虚位移原理
m1
F1
m2
F2
F1
m1
m2 F2
FN 1
FN 2
FN 1
FN 2
•外力(external force):质点系外部的物体作用于质点系上的力
•内力(internal force):质点系内部的作用力
V
nห้องสมุดไป่ตู้i1
V qi
qi
0
(*)
对于具有完整约束质点系的广义坐标的虚位移(变分)是独立的
工程力学 第23章虚位移原理习题解

习题 23-1 图
虚功式 即
− Mδθ − 2mgδy D + FδxB − Fk δxC = 0
l − Mδ θ − 2mg ( cosθ )δ θ + F (−l sin θ )δ θ − Fk (−l sin θ )δ θ = 0 2
A
δθ
δy E
D
3m 5m
F
ϕ
C
δrF δrG
ϕ
E
B
′ FN1 FN1
G
(a)
F1 δr D
F2
δr H δθ δrE δθ
ϕ ϕ
虚功式
′ δ rF sin ϕ = 0 − F1δ rD − FN 2δ rH − F2δ rE − FN2
A
5m
D
ϕ ϕ
H
FN2 ′ FN2
C
δrG
E
B
即
− F1 ⋅ 3δ θ − FN 2 ⋅ 4δθ − F2 ⋅ 2δθ − FN2 ⋅ 5δθ ⋅
y A = 5b cos
θ
2
+a
x
δϕ
b
M
C
b
5 θ δy A = − b sin δθ 2 2
θ
x B = 2b sin
θ
2
a
θ δxB = b cos δθ 2
A
mg
设丝杠的虚转角为 δ ϕ ,则
δϕ= 2π 2π b θ δ xB = cos δ θ h h 2
习题 23-2 图 (a)
y
虚功式 Mδ ϕ + mgδ y A = 0 以 δ y A , δ ϕ 的表达式代入上式,得
第14章 虚位移原理_例题

弹簧原长 (600 300 )mm
弹簧后来长
(600
300 cos
)mm
弹簧缩短
(
300 cos
300 )mm
弹簧力 F
k
(
300
ቤተ መጻሕፍቲ ባይዱcos
300 )
由虚 位移原理:
M • F •ra F •rB 0 M Frr 0 0
[M
1.5(
1 cos
1)
0.3
sin cos2
0] 0
解: 对系统:建立坐标系和受力分析 解析法:
yK 6l sin yK 6l cos (1)
虚功方程:M W 6l cos 0 (2)
所以: M 6Wl cos
例6: 书14-5
当OC绕轴O摆动时,滑块A沿曲柄滑动,从而带动杆AB在导槽
内移动,不计各构 件自 重与各处摩擦。OC a,OD l
rB 2a (2)
列虚功方程:
M PrD FBxrB 0
(3)
将(1)(2)代入(3),得:
M Pa FBx 2a 0
FBx
1 M 2 a
P
(2)求B 铰的垂直约束力: 解除B 铰的垂直约束,代之以垂直力 FBy 。 杆BCD 的速度瞬心在A
rD 5a
rB 2a
M PrD
F
、F
给出力
P
、
F
处的虚位移 rD、rB
几何法: rC cos rD
C
rC cos(90 2 ) rB cos
A
θ
θ rC D F
Fθ
rB
B
由虚功原理 PrD FrB 0 0
PrC cos F 2sinrC 0 (P cos 2F sin )rC 0
《理论力学》第十三章--虚位移试题及答案
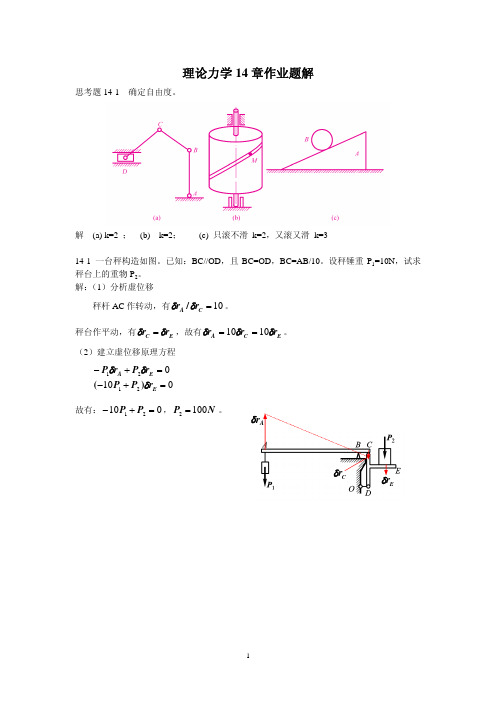
理论力学14章作业题解思考题14-1 确定自由度。
解 (a) k=2 ; (b) k=2; (c) 只滚不滑 k=2,又滚又滑 k=314-1 一台秤构造如图。
已知:BC//OD ,且BC=OD ,BC=AB/10。
设秤锤重P 1=10N ,试求秤台上的重物P 2。
解:(1)分析虚位移 秤杆AC 作转动,有10=C A r r d d /。
秤台作平动,有E C r r d d =,故有E C A r r r d d d 1010==。
(2)建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有:01021=+-P P ,N P 1002=。
Cr d Er14-5 OA=l ,OC=R满足的条件。
解: (用虚位移原理求解)(1) 运动分析(虚位移关系分析)A 处虚位移关系用合成运动的理论分析。
A 为动点,OC 为动系。
r e A r r r r r r d d d +=f d d cos A e r r =另外:R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知:AC=BC=EC=GC=DE=DG=l ,荷载F 2。
求平衡时的F 1。
解 用解析法,1个自由度,选q 为广义坐标。
建立坐标,如图。
(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解:(1) 接触D 处水平约束,代之约束力。
第十五章虚位移原理

F'
B
A
W
FN s 2Fl 0
2π
s
h
h s 2π
δs FN
FN h W (2Fl 2π ) 0
FN h 2 Fl 0 2π
1 FN 4π Fl h
例题
第15章 虚位移原理
例 题 1
例题
第15章 虚位移原理
2 1 2 1
2
2 1
y
x22 y22 l32 ( x1 x2 ) ( y1 y2 ) l
2 2 2
l2 m1
m2 (x ,y ) 2 2
l3 x
l1
(x1,y1)
例3:曲柄连杆机构 约束方程为:
2 2 xA yA r2
y
r φ
A (xA,yA) l
B x (xB,yB)
xC
xC
例题
第15章 虚位移原理
例 题 7
已知图所示结构,各杆都以光滑铰链连接,且有 AC=CE=BC=CD=DG=GE=l。在点G作用一铅直方向的力F,求 支座B的水平约束反力FBx。
sin ( ) M FAr cos FB r 0 cos
例:图示平面等腰三角形机构,在C点作用主动力P,系统 处于平衡,求A、B两处的约束反力。
A、B两处共有4个反力,应逐个求之。 先求哪个反力,则解除该方向的约束,代 之以对应的反力。暂时不求的则不要解除, 仍保持原约束的性质。
力学小魔术
一根重为F的均质杆简支于A,B支座上,支座的反力 分别为F/2。如果突然将支座B撤去,显然在重力矩 作用下AB杆将绕A点顺时针转动而掉下。现在,允 许在AB杆上采取一些措施,但不能对系统施加绕A 点的外力矩,使得在支座B撤去后,AB杆仍能维持 水平而不掉下。你能做到吗?
虚位移原理例题

虚位移原理例题虚位移原理是力学中的一个重要概念,它是描述物体在受力作用下发生位移的原理。
虚位移原理在力学、静力学、动力学等领域都有着广泛的应用。
下面我们通过一些例题来深入理解虚位移原理的应用。
例题一,弹簧振子。
一根质量为m的弹簧上挂着一个质量为M的物体,当物体受到外力F时,弹簧发生形变。
求弹簧的位移x。
解析,根据虚位移原理,我们可以假设弹簧的位移为x,那么弹簧所受的弹力为-kx,其中k为弹簧的弹簧系数。
根据牛顿第二定律,物体所受的合外力为F-kx,根据虚位移原理,这个合外力所做的虚功等于零。
因此,我们可以得到F-kx=0,解得x=F/k。
例题二,斜面上的物体。
一个质量为m的物体沿着无摩擦的斜面向下滑动,斜面的倾角为θ,斜面的高度为h。
求物体滑动的位移s。
解析,根据虚位移原理,我们可以假设物体沿着斜面滑动的位移为s,那么物体所受的重力分解成沿斜面方向的分力为mgsinθ,垂直斜面方向的分力为mgcos θ。
根据虚位移原理,物体所受的合外力为mgsinθ,这个合外力所做的虚功等于零。
因此,我们可以得到mgsinθs=0,解得s=0。
例题三,简谐振动。
一个质量为m的物体挂在一个弹簧上,弹簧的劲度系数为k。
求物体振动的最大位移A。
解析,根据虚位移原理,我们可以假设物体振动的位移为x,那么物体所受的弹力为-kx。
根据牛顿第二定律,物体所受的合外力为-mg-kx,根据虚位移原理,这个合外力所做的虚功等于零。
因此,我们可以得到-mg-kA=0,解得A=mg/k。
通过以上例题的分析,我们可以看到虚位移原理在力学问题中的重要作用。
它通过假设物体的虚位移,使得问题的分析变得简单而直观。
虚位移原理的应用不仅仅局限于上面的例题,它在静力学、动力学、弹性力学等领域都有着广泛的应用。
因此,掌握虚位移原理对于理解力学问题、解决实际问题具有重要意义。
总结:虚位移原理是力学中的一个重要概念,它描述了物体在受力作用下发生位移的原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6: 书15-5
当OC绕轴O摆动时,滑块A沿曲柄滑动,从而带动杆AB在导槽
内移动,不计各构 件自 重与各处摩擦。OC a,OD l 求机构平衡时力F1与F2的关系。
解:给出力
F1
、F2
处的虚位移 rC、rA
几何法:ra rA re rr rA cos re
rC
re
a l / cos
注意:几何法时,主动力与虚位移方向一致为正;
解析法时主动力、坐标变分各自沿坐标轴方向为正,力偶、角度逆时针为正。
例4 均质杆OA及AB在A点用铰连接,并在O点用固定铰 支座,如图所示。两杆各长2a和2b,各重P1及P2,设在B点
加水平力 F 以维持平衡,求两杆与铅直线所成的角及 。
解F1
由虚功原理 F1rC F2rA 0
F1
a
F2l cos2
φD x
O
解析法:建立如图直角坐标系 yA l tan
求变分 y A
l
cos2
又rC
由虚功原理 F1rC F2yA 0
a
F1
F2l
a cos2
B
F2
例7: 书15-7
滑套D套在光滑直杆AB上,并带动杆
一组虚位移,如图所示。 图示中:
rA rD rB
FrB cos P1rC sin P2rD sin 0
而 rC a , rB rD rA 2a
代入上式后,得:
(Fcos 2aP1asin P2 2asin ) 0
tg
P1
2F 2P2
讨论:其它可能虚位移与真实位移
例5 :升降机构,
已知: AO AB AC AD l ,
vB
2rA sin rB
解析法:
rB 2l sin
虚功方程 M FrB 0
arcsin M
2Fl
xB 2l cos xB 2l sin
( x轴向右为正,xB向右,
rB xB 2l sin)
当然,几何法
也可以假设 顺时针,
求解结果相同。
虚功方程 M FxB 0
M F 2l sin 0
(2Fl
h
2
FN )
0
由于 是任意的,有: 2Fl
也即:
h
2
FN
0
FN
4
l h
F
讨论: 1)利用约束力不做功避免了所有约束力的出现, 这是虚位移原理解题与矢量静力学解题相比的巨大优点。
2)本题求虚位移间关系的方法为:由物理关系直接给 出法。
例2 图示椭圆规机构,连杆AB长l,杆重和滑道摩擦不计, 铰链为光滑的,求在图示位置平衡时,主动力大小P和Q之间 的关系。
解:研究整个机构。 系统的所有约束都是 完整、定常、理想的。
1、几何法:使A发生虚位移 rA ,
B的虚位移 rB ,则由虚位移原理,
得虚功方程:
rA
PrA QrB 0
而 rA sin rB cos
rA
rB rA tg
(PQtg )rA 0
由rA的任意性,得 PQ tg
2、解析法 由于系统为单自由度,
由此解得:
tg
P1
2F 2P2
,
tg 2F
P2
解法二: 应用虚位移原理,几何法
先使 保持不变,而使 获得变分 ,得到系统的一
组虚位移,如图所示。
FrB cos P2rD sin 0
而 rB 2b , rD b
代入上式,得
tg
F 2b P2 b
2F P2
再使 保持不变,而使 获得变分 ,得到系统的另
CD在铅直滑道上滑动。已知=0o时,
弹簧等于原长,弹簧刚度系数为
5(kN/m),求在任意位置( 角)平衡
时,加在AB杆上的力偶矩M ?
解:这是一个已知系统平衡,求作用于系统上主动力之间关系 的问题。将弹簧力计入主动力,系统简化为理想约束系统,故 可以用虚位移原理求解。
选择AB杆、CD杆和滑套D的系统为研究对象。
统,取角及为广义坐标,现用两
种方法求解。 y
解法一: 应用虚位移原理,解析法
P1yC P2yD FxB 0 (a) 而 yC acos , yC asin
yD 2acos bcos , yD 2asin bsin xB 2asin 2bsin , xB 2acos 2bcos
代入(a)式,得:
K
CE DE FE EG FH l , HG IH HJ l ,
机构的平衡位置为 ,
试求力偶M与重物 W 间的关系。
解: 对系统:建立坐标系和受力分析 解析法:
yK 6l sin yK 6l cos (1)
虚功方程:M W 6l cos 0 (2)
所以: M 6Wl cos
re
300
cos
rr
re
tan
300sin cos2
去掉弹簧,暴露出弹簧力 F和
F
ra re
rB F rr
F
弹簧原长 (600 300 )mm
弹簧后来长
(600
300 cos
)mm
弹簧缩短
(
300 cos
300 )mm
例1:螺旋压榨机中螺杆的螺距为 h 。如果
在手柄上作用一在水平面内的力偶,其
力偶矩为 2Fl ,求平衡时作用于被压榨
物体上的压力。(忽略摩擦)
解:
1、对象:由手柄、螺杆及压板组成的系统
23、、分给析系受统力以:虚主位动移力:(F和, F’s有 )及,:压s板阻h力FN
2
4、列虚功方程:W
2Fl
FNs
(P1a sin P2 2a sin F 2a cos) (P2bsin F 2b cos ) 0
(P1asin P2 2asin F2a cos) (P2bsin F2bcos ) 0 由于 , 是彼此独立的,所以:
P1asin P2 2asin F2acos 0 P2 bsin F2bcos 0
机构。今在OA杆上作用力偶 M ,在滑块B上作用力 F ,使 机构处于平衡状态,如例图所示。试求平衡位置角 。 解:1、对象:系统
2、分析受力:M,F
3、给虚位移: , rB ,求虚位移关系:
几何法(虚位移投影法或者瞬心法):
rA l
OA vA
rA cos(90 ) rA sin 2 rB cos
可取为广义坐标。
xB lcos , yA lsin xB lsin , yA lcos
Py A QxB 0 ,
(Pcos Qsin )l 0
由于 任意,故 PQ tg
注意:几何法时,主动力与虚位移方向一致为正; 解析法时主动力、坐标变分各自沿坐标轴方向为正
OA vA vB
例3:两均质杆 OA AB l ,均不计重,构成曲柄滑块
