最新2019-苏教版高中数学教材分析-PPT课件
合集下载
教材解读ppt课件

❖ 示范画出了拼合后的图 形的示意图,并要求自 己思考具体说明以股为 边的正方形中的两条分 割线应该如何画? 或满 足什么位置与数量条件?
❖ 数列中蕴含的函数思想是研究数列的指导思 想,从函数的视角看数列概念,从函数的观 点研究了数列。关注了数列和数集的不同、 关注了斐波那契数列的通项公式是否存在问 题(存在)。对数列存在通项公式的情形下, 对其通项公式的不唯一性的认识强调了结合 实例进行引导。
❖ 小学五年级下圆中的圆的周长一课中, 圆的周 长是采用滚动、绳绕等方式进行测量,渗透
了“化曲为直”的数学思想方法。圆周率
是最早出现在中小学教材中的无理数.
❖ 勾股定理是苏科版八年级上第二章勾股定理 与平方根第一节,反映了现行教材对课程内 容采用综合体系的混合编写形式, 利于打通数 学内部各分支科目间的联系,使学生从整体 上认识、学习数学知识。其中还着重关注了 勾股定理的背景知识。
苏教版高中必修2教材中有一段内容:台体(棱台、圆台)
的体积可以转化为椎体的体积来计算(如图)。如果台体的上、
下底面积分别为 S , S ,高是 h ,可以推得它的体积是
V台体
1 3
h(S
SS S) 。
等差数列的定义
苏教版高中必修 5 教材上对等差数列的定义如下: 一般地,如果一个数列从第二项起,每一项减去它的 前一项所得的差都等于同一个常数,那么这个数列就叫做
中小学教材分析
《标准》为教材编写的依据,教材的编
写,从课程内容是否分科看,可分为分科体 系和综合体系。从课程内容发展上看,可分 为直线式和螺旋式两种不同的编排形式。新 的教材观——“用教材教”,而不是“教教 材”,是使用教材的指导思想之一。 我们要 解读教材,吃透教材,超越教材。
苏教版高中数学选择性必修一直线的斜率与倾斜角 课件

讲授新课
知识点三 三点共线
【例 3】(2022·吉林扶余市第一中学期末)若 a∈N,又三点 A(a,0),B(0,a+4),C(1,3)共线,
求 a 的值.
【解析】∵A、B、C 三点共线,∴直线 AC、BC 的斜率相等,
∴ 3 0 3 (a 4) ,解之得,a=±2. 1a 10
【跟踪训练】
当堂检测
知识点二 直线的斜率 斜率的定义
1..倾斜角不是 的直线,它的倾斜角的正切叫做这条直线的斜率, 常用 表示,即 .
2.概念解读:当直线 与x轴平行或重合时,a=0°,k=tan0°,a=0; 直线 与x轴垂直时,a=90°,k不存在。由此可知,一条直线 的倾斜 角 一定存在,但是斜率k不一定存在.
过两点 P1(x1,
y1) 、 P2 (x2 ,
y2 ) 的直线的斜率公式 k
y2 x2
y1 x1
( x1
x2 ) .
当堂检测
【概念解读】 对于上面的斜率公式要注意下面五点: (1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角 =90°, 直线与x轴垂直; (2)k与P1、P2顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同 时交换,但分子与分母不能交换; (3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得; (4)当y1=y2时,斜率k=0,直线的倾斜角 =0°,直线与x轴平行或重合; (5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
讲授新课
知识点一 直线的倾斜角
【例1】设直线 过原点,其倾斜角为 ,将直线 绕坐标原点沿逆时针方向 旋转45°,得到直线 ,则直线 1的倾斜角为 【答案】当0°≤ <135°时,为 +45°,当135°≤ <180°时,为 -135° 【解析】倾斜角的范围是[0°,180°),因此,只有当 +45°∈[0°, 180°),即当0°≤ <135°时, 的倾斜角才是 +45°,而当135°≤ <180°时, 的倾斜角为 -135°.故应选D.
苏教版高中数学必修一课件1.2 子集、全集、补集ppt版本

定义
文字语言 符号语言
设A⊆S,由S中不属于A的所有元素组成的集合 称为S的子集A的补集 ∁SA={x|x∈S,且x∉A}
图形语言
(1)A⊆S,∁SA⊆S; (2)∁S(∁SA)=A; 性质 (3)∁SS=∅,∁S∅=S; (4)A∪(∁SA)=S; (5)A∩(∁SA)=∅
题型探究
类型一 判断集合间的关系
解答
(2)若一个集合有n(n∈N)个元素,则它有多少个子集?多少个真子集? 验证你的结论. 解 若一个集合有n(n∈N)个元素,则它有2n个子集,2n-1个真子集. 如∅,有一个子集,0个真子集.
解答
反思与感悟
为了罗列时不重不漏,要讲究列举顺序,这个顺序有点类似于从1到 100数数:先是一位数,然后是两位数,在两位数中,先数首位是1的 等等.
本课结束
再见
2019/11/21
第1章 集合
1.2 子集、全集、补集
学习目标
1.理解子集、真子集、全集、补集的概念. 2.能用符号和Venn图,数轴表达集合间的关系. 3.掌握列举有限集的所有子集的方法,给定全集,会求补集.
内容索引
问题导学 题型探究 当堂训练
问题导学
知识点一 子集
思考
如果把“马”和“白马”视为两个集合,则这两个集合中的元 素有什么关系? 答案 所有的白马都是马,马不一定是白马.
12345
解析
答案
4.若A={x|x>a},B={x|x>6},且A⊆B,则实数a的取值范围是__[6_,__+__∞__).
12345
答案
5.设集合U={1,2,3,4,5,6},M={1,2,4},则∁UM等于_{_3_,_5_,6_}__.
2019-2020学年高中数学2.4逆变换与逆矩阵2.4.2二阶矩阵与二元一次方程组课件苏教版选修4_2
-38 -18.
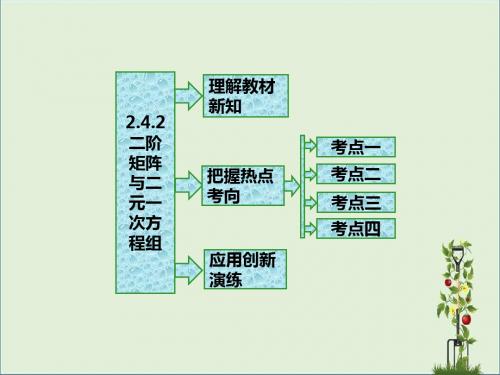
已知矩阵 A=ca db,利用行列式求矩阵 A 的逆矩阵的步骤 如下:
(1)首先计算 det(A)=ca db=ad-bc,当 det(A)≠0 时,逆 矩阵存在.
d (2)利用 A-1=de-tcA
detA
-b detaA,求出逆矩阵 A-1. detA
θ θ
-sin cos
θθ=cos2
θ-(-sin2
θ)=1.
2.若
x2 -1
1y2=xy
-yx,求 x+y 的值.
解:x2+y2=-2xy⇒x+y=0.
利用行列式求可逆矩阵的逆矩阵
[例 2] 已知 A=-11 22,B=-11 11,判断 AB 是否可
(3)二阶行列式0a 10=a,当 a=0 时,矩阵不可逆,当 a≠0 时,
1 矩阵可逆,逆矩阵为a
0
.
0 1
4.若矩阵 A=63 x92存在逆矩阵,求 x 的取值范围.
解:据题意 det(A)≠0,即36 9x2≠0. ∴3x2-54≠0. ∴x≠±3 2. 故 x 的取值范围是{x|x∈R 且 x≠±3 2}.
逆,若可逆求出逆矩阵. [思路点拨] 利用矩阵可逆的充要条件求解.
[精解详析]
AB=-11
2 1 2 -1
11=- -13
31.
因 det(AB)=- -13 31=-1+9=8≠0,故 AB 可逆,
1 ∴(AB)-1=83
8
二元一次方程组的行列式解法及矩阵解法
[例 3] 分别利用行列式及逆矩阵解二元一次方程组
3x-2y=1, -x+4y=3.
[思路点拨]
求出相应行列式的值,利用 x=DDx,y=DDy求
苏教版(2019)高中数学必修第一册课件2.1 命题、定理、定义 课件 - 副本

规律与方法
1.根据命题的定义,可以判断真假的陈述句是命题.命题的条件与结 论之间属于因果关系,真命题需要给出证明,假命题只需举出一个 反例即可. 2.任何命题都是由条件和结论构成的,可以写成“若p,则q”的形 式.含有大前提的命题写成“若p,则q”的形式时,大前提应保持 不变,且不写在条件p中.
题型三 命题的真假判断
例3有下列命题:
①若xy=0,则|x|+|y|=0;②若a>b,则a+c>b+c;③矩形的对角线互相
垂直. ④命题“若a,b是无理数,则a+b是无理数”是真命题
其中真命题共有
A.0个
√B.1个
C.2个
D.3个
解析 ①由xy=0得到x=0或y=0,所以|x|+|y|=0不一定成立,是假命题; ②当a>b时,有a+c>b+c成立,正确,所以是真命题; ③矩形的对角线不一定互相垂直,不正确,是假命题. ④若a,b互为相反数,则a+b=0,不正确,是假命题.
5.对于任意实数 a,b,c,d,有下列命题:
①若 a>b,c≠0,则 ac>bc;
②若 ac2>bc2,则 a>b;
③若 a>b,则1a<1b;
④若 a>b>0,c>d,则 ac>bd.
其中真命题的个数是( )
√A.1
B.2
C.3
D.4
解析
当c<0时,①错误;ac2>bc2,显然c2>0,因此②正确; 当a>0>b时,③错误; 当a=2,b=1,c=-1,d=-2时,显然④错误, 故选A.
跟踪训练2 已知命题:弦的垂直平分线经过圆心并且平分弦所对的弧,若 把上述命题改为“若p,则q”的形式,则p是_一__条__直__线__是__弦__的__垂__直__平__分__线__, q是_这__条__直__线__经__过__圆__心__且__平__分__弦__所__对__的__弧__. 解析 已知中的命题改为“若p,则q”的形式为“若一条直线是弦的垂 直平分线,则这条直线经过圆心且平分弦所对的弧”, p:一条直线是弦的垂直平分线; q:这条直线经过圆心且平分弦所对的弧.
2019版高中数学苏教版必修一课件:第三章 3.1.2 第2课时 指数函数及其性质的应用

解析 1 年后价格为 8 100×(1-13)=8 100×23=5 400(元), 2 年后价格为 5 400×(1-13)=5 400×23=3 600(元), 3 年后价格为 3 600×(1-13)=3 600×23=2 400(元). 答案 2 400元
知识点二 与指数函数复合的函数单调性 1.复合函数y=f(g(x))的单调性:当y=f(x)与u=g(x)有相同
规律方法 (1)对于底数相同、指数不同的两个幂的大小比较, 可以利用指数型函数的单调性来判断. (2)对于底数不同、指数相同的两个幂的大小比较,可以利用 指数型函数图象的变化规律来判断. (3)对于底数不同且指数也不同的幂的大小比较,应通过中间 值来比较. (4)对于三个(或三个以上)数的大小比较,则应先根据特殊值 0,1进行分组,再比较各组数的大小.
(2)分情况讨论: ①当 0<a<1 时,函数 f(x)=ax(a>0,a≠1)在 R 上是减函数, ∴x2-3x+1>x+6, ∴x2-4x-5>0, 根据相应二次函数的图象可得 x<-1 或 x>5; ②当 a>1 时,函数 f(x)=ax(a>0,a≠1)在 R 上是增函数, ∴x2-3x+1<x+6,∴x2-4x-5<0, 根据相应二次函数的图象可得-1<x<5. 综上所述,当 0<a<1 时,x∈(-∞,-1)∪(5,+∞); 当 a>1 时,(-1,5).
(1)1.72.5,1.73;(2)0.6-1.2,0.6-1.5; (3)2.3-0.28,0.67-3.1.
解 (1)(单调性法)由于1.72.5与1.73的底数都是1.7,故构造函 数y=1.7x,则函数y=1.7x在R上是增加的. 又2.5<3,所以1.72.5<1.73. (2)(单调性法)由于0.6-1.2与0.6-1.5的底数都是0.6,故构造函 数y=0.6x,则函数y=0.6x在R上是减少的. 因为-1.2>-1.5,所以0.6-1.2<0.6-1.5. (3)(中间量法)由指数型函数的性质,知 2.3-0.28<2.30=1, 0.67-3.1>0.670=1, 所以2.3-0.28<0.67-3.1.
函数的表示方法课件-2022-2023学年高一上学期数学苏教版(2019)必修第一册

(2)便于数形结合思想的应用
数值,而且有时误差较大
高中数学
必修第一册
配套江苏版教材
示例 下表是某校高一(1)班三名同学在高一学年六次数学测试的成绩及班级平均分表.
测试序号
姓名
1
2
3
4
5
6
小伟
98
87
91
92
88
95
小城
90
76
88
75
86
80
小磊
68
65
73
72
75
82
班级平均分
88.2
78.3
85.4
高中数学
必修第一册
配套江苏版教材
例6 某镇响应“绿水青山就是金山银山”的号召,因地制宜地将该镇打造成“生态水果特色镇”.经调
研发现:某珍稀水果树的单株产量W(单位:千克)与施用肥料x(单位:千克)满足如下关系:
配套江苏版教材
3.分段函数的图象
分段函数有几段,它的图象就由几条曲线组成,在同一直角坐标系中,根据每段的定义区间和表达式依次
画出图象,要注意每段图象的端点是空心点还是实心点.
示例 已知函数f(x)=1+
−
(-2<x≤2).
2
(1)用分段函数的形式表示f(x);(2)画出f(x)的图象;(3)写出函数f(x)的值域.
高中数学
必修第一册
配套江苏版教材
+ 1 2 , ≤ −1,
例5 已知函数f(x)= 2 + 2, −1 < < 1, 若f(a)>1,则实数a的取值范围是(
C )
1
, ≥ 1,
1
数值,而且有时误差较大
高中数学
必修第一册
配套江苏版教材
示例 下表是某校高一(1)班三名同学在高一学年六次数学测试的成绩及班级平均分表.
测试序号
姓名
1
2
3
4
5
6
小伟
98
87
91
92
88
95
小城
90
76
88
75
86
80
小磊
68
65
73
72
75
82
班级平均分
88.2
78.3
85.4
高中数学
必修第一册
配套江苏版教材
例6 某镇响应“绿水青山就是金山银山”的号召,因地制宜地将该镇打造成“生态水果特色镇”.经调
研发现:某珍稀水果树的单株产量W(单位:千克)与施用肥料x(单位:千克)满足如下关系:
配套江苏版教材
3.分段函数的图象
分段函数有几段,它的图象就由几条曲线组成,在同一直角坐标系中,根据每段的定义区间和表达式依次
画出图象,要注意每段图象的端点是空心点还是实心点.
示例 已知函数f(x)=1+
−
(-2<x≤2).
2
(1)用分段函数的形式表示f(x);(2)画出f(x)的图象;(3)写出函数f(x)的值域.
高中数学
必修第一册
配套江苏版教材
+ 1 2 , ≤ −1,
例5 已知函数f(x)= 2 + 2, −1 < < 1, 若f(a)>1,则实数a的取值范围是(
C )
1
, ≥ 1,
1
苏教版高中数学选择性必修一两条直线的交点 课件
数学(苏教版2019)
选择性必修第一册
第1章 直线与方程
1.4 两条直线的交点
学习目标 课程标准
重难点
能用解方程组的方法求 两直线的交点掌握两直 1.两条直线交点的求解 线相交的条件
当堂检测
知识回顾 一、两条直线的交点
几何元素及关系 点A 直线l
点A在直线l上 直线l1与l2的交点是A
代数表示 A(a,b) l:Ax+By+C=0 Aa+Bb+C=0 方程组的解是
1.判断下列各对直线的位置关系.若相交,求出交点坐标:
(1)l1:2x+y+3=0,l2:x-2y-1=0;
(2)l1:x+y+2=0,l2:2x+2y+3=0.
【解析】(1)解方程组 2x+y+3=0, x-2y-1=0,
得 x=-1, y=-1,
所以直线 l1 与 l2 相交,交点坐标为(-1,-1).
2x+y+2=0,
x=-10, 3
得 y=14. 3
所以
l1
与
l2
相交,且交点坐标为
(
10 3
,
14 3
)
.
2x-6y+3=0,① (2)解方程组 y=1x+1,②
32
②×6 整理得 2x-6y+3=0.
因此,①和②可以化成同一个方程,即①和②表示同一条直线,l1 与 l2 重合.
2x-6y=0,① (3)解方程组 y=1x+1,②
讲授新课
知识点一 两条直线的交点
判断下列各组直线的位置关系.如果相交,求出交点的坐标: (1)l1:5x+4y-2=0,l2:2x+y+2=0; (2)l1:2x-6y+3=0,l2:y=13x+12; (3)l1:2x-6y=0,l2:y=13x+12.
选择性必修第一册
第1章 直线与方程
1.4 两条直线的交点
学习目标 课程标准
重难点
能用解方程组的方法求 两直线的交点掌握两直 1.两条直线交点的求解 线相交的条件
当堂检测
知识回顾 一、两条直线的交点
几何元素及关系 点A 直线l
点A在直线l上 直线l1与l2的交点是A
代数表示 A(a,b) l:Ax+By+C=0 Aa+Bb+C=0 方程组的解是
1.判断下列各对直线的位置关系.若相交,求出交点坐标:
(1)l1:2x+y+3=0,l2:x-2y-1=0;
(2)l1:x+y+2=0,l2:2x+2y+3=0.
【解析】(1)解方程组 2x+y+3=0, x-2y-1=0,
得 x=-1, y=-1,
所以直线 l1 与 l2 相交,交点坐标为(-1,-1).
2x+y+2=0,
x=-10, 3
得 y=14. 3
所以
l1
与
l2
相交,且交点坐标为
(
10 3
,
14 3
)
.
2x-6y+3=0,① (2)解方程组 y=1x+1,②
32
②×6 整理得 2x-6y+3=0.
因此,①和②可以化成同一个方程,即①和②表示同一条直线,l1 与 l2 重合.
2x-6y=0,① (3)解方程组 y=1x+1,②
讲授新课
知识点一 两条直线的交点
判断下列各组直线的位置关系.如果相交,求出交点的坐标: (1)l1:5x+4y-2=0,l2:2x+y+2=0; (2)l1:2x-6y+3=0,l2:y=13x+12; (3)l1:2x-6y=0,l2:y=13x+12.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扩展了不等式的证明题和综合题的命题空间
07全国卷(理Ⅰ)20题:设函数f(x)=exe-x。(1)证明:f(x)的导数f‘(x)≥2;(2) 若对所有实数x≥0,都有f(x)≥ax,求a的取值 范围。
07重庆卷第20题:已知函数f(x)=ax4lnx+ bx4-c(x>0)在x=1处取得极值-3-c,其中a,b,c 不常数。(1)试确定a,b的值;(2)讨论函 数f(x)的单调区间;(3)若对任意x>0,不等 式f(x)≥-2c2恒成立,求c的取值范围。
些难且偏的“名题”上花时间,重点应在 已知算法时流程图的画法、算法语句的表 示,特别是流程图的读图、读码上进行训 练。
3.高等数学中的方法值得研究
从第23题看: 求导法证明等式; 积分法证明等式。
二、变化内容
1.引起知识结构的改变 (1)函数
导数对函数、不等式的影响: 传统的求值域、最值的技巧不需过多
(2)立体几何
也是老师欲罢不能的内容:传统意识 过强
立体几何是传统内容中变化最大的。增加 了三示图,距离不要求,角对文科考生不 要求,对理科考生只在40分内容中考,且 方法统一:用空间向量计算。这样,传统 的以距离、角(特别是二面角)为主体的 命题思路被打破了。
第一,尽管教材对证明(立几推理)的 要求弱化(对判定定理不要求证明),但我 们仍然应该予以重视,因为这是必然出现的 题型(当然不要搞得过难)。还要注意位置 关系的探索性问题的研究,如“在什么条件 下,两线、面具有垂直(平行)关系”等。
(4)数列
递推数列在本章全无研究,只是在 “推理与证明”一章中的习题中有涉及, 数列教学的重点?
江苏07与08两年的数列题值得研究: 一是等差、等比为载体,但难点不在对公 式的应用本身; 二是对项的性质的研究、项之间关系的研 究; 三是变形转化是关键; 四是推理能力(合情推理与逻辑推理)
(5)不等关系
一是虽然不要求会求一般曲线(轨迹)的 方程,但由于这个“一般”二字,说明求“特 殊”曲线的方程还是要求的,所以,已知曲线 的类型,根据适当条件求曲线方程应该是可以 考的。(08高考第18题:求圆的方程;曲线过 定点)
二是重心应放在圆锥曲线的定义、性质的 研究上,如椭圆的焦点、准线等性质;或曲线 上一个点与曲线的顶点、焦点等特殊点构成的 图形的性质、线段长度、图形面积等(第12题)
第三,体积、表面积的计算应该成为立 体几何考查的重心之一。要注意研究这样几 个方面的问题:一是求体积、面积的体现能 力的一些求法,如通过图形变换、等价转换 的方法求体积、面积;二是注意动图形(体) 的面积、体积的题型的研究(广东07年文科 即为此类试题),如不变量与不变性问题 (定值与定性)、最值与最值位置的探求等; 三是注意由三示图给出的几何体的相关问题 的研究。
强化
为传统的单调性、极值、最值增加了函数类型。
07 山 东 (43;blnx , 其 中 ab≠0. 证 明 : 当 ab>0 时 , 函数f(x)没有极值点;当ab<0时,函数f(x)有 且只有一个极值点,并求出极值。
08 江 苏 第 17 题 : 函 数 y=20/cosθ 10tanθ +10(0≤θ ≤π /4)的最小值
苏教版高中数学教材分析
泰州市教育局教研室 石志群
一、新增内容
新增内容:频率高,难度低; 传统内容:考试重心,区分所在
1.从高考试卷看:频率高,难度低 3:复数; 6:几何概型; 7:统计,流程图; 9:类比探究; 10:归纳推理
2。抓住关键,不做无用功
以算法为例: 不要在算法的概念、算法的设计及一
第四,在40分中如果考空间向量求角, 估计不应该难,因为时间只有30分钟,如 果考得过难,运算量很大,时间不允许。
第22题:运算很简单
这里牵涉另一问题:定比分点坐标公 式的去除产生的影响
(3)解析几何
解析几何部分由于初中数学取消了韦达定 理,高中数学又取消了定比分点坐标公式, 并且求一般曲线(轨迹)的方程也不作要 求,传统高考的重心—直线与圆锥曲线的 位置关系、求轨迹方程等题型都不重要了, 因此,解析几何寻找新的命题思路已成为 必然。
三是注意圆锥曲线与其他内容的结合, 如与导数的结合(如2019年江苏卷第19题)、 与 向 量 的 结 合 ( 如 2019 年 全 国 ( 理 Ⅱ ) 第 20 题)。
四是注意不能用韦达定理的直线与曲线的 交点问题:转化为方程组求解,更为本质。如 07 上 海 第 21 题 , 由 两 个 半 椭 圆 构 成 的 曲 线 , (1)、(2)题是关于焦点、顶点等性质的研 究,第(3)题就是直线与曲线相交问题,并 不需要韦达定理,而是直接求交点坐标,再用 中点坐标公式。
对函数的教学关键是使学生学会运用 运动、变化的观点和方法认识问题
函数教学的核心内容:函数的概念及 其表示(08第20题)、函数的图象与性质 (08第20题)、函数的值域与最值(08第 14、17题)
关键是学会多角度地运用函数思想分 析与解决问题,并将函数思想与方程观点、 数形结合思想有机结合
例:若不等式x2 + ax +1≥0对一切 x∈(0,1/2]成立,求a的最小值。
一是强化了与函数的联系; 第14题 第20题 均与不等式恒成立有关,涉及分式函
数的导数、绝对值函数的值域、指数函数 的单调性等
三、教材核心思想的把握
以函数为例: 函数是整个中学数学中最重要的核心
思想之一 从08试卷看:1、4、8、11、13、14、
17、18、20 全与函数有关,而19题中的 数列也是一种特殊函数
08高考第16题充分说明了这一点
第二,要重视与三示图有关的题目的训 练。对此,可能有这样几个命题方向:一是 读图(今年山东第3题、宁夏第8题),由三 示图还原几何体,甚至还要研究关于这个几 何体的体积、表面积及其中的线、面位置关 系等;二是补图,即告诉几何体,并作出三 示图的一部分,请补全三示图(由于〈教学 要求〉的限制,我估计让考生作三示图的可 能性极小)。前者在各种题型中都可能出现, 后者可能在填空题中出现。
