考研数学三(概率论与数理统计)-试卷20
[考研数学]概率论考试复习题
![[考研数学]概率论考试复习题](https://img.taocdn.com/s3/m/9b99419fd1d233d4b14e852458fb770bf78a3b74.png)
概率论与数理统计练习1一、选择题:1、设随机事件A 与B 满足A B ⊃,则( )成立。
A.()()P A B P A +=B.()()P AB P A =C.()()P B A P B =D.()()()P B A P B P A -=-2、甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,则目标被击中的概率为( B )。
A.0.5B.0.8C.0.55D.0.63、连续型随机变量X 的密度函数()f x 必满足条件( D )。
A.0()1f x ≤≤B.()f x 为偶函数C.()f x 单调不减D. ()1f x dx +∞-∞=⎰4、设12,,,n X X X 是来自正态总体2(,)N μσ 的样本,则22μσ+的矩估计量是( D )。
A. 211()n i i X X n =-∑ B. 211()1n i i X X n =--∑ C. 221()n i i X n X =-∑ D. 211n i i X n =∑ 5、设总体(,1)X N μ ,123,,X X X 为总体X 的一个样本,若^1231123X X CX μ=++为未知参数μ的无偏估计量,则常数C =( ) A.12 B. 13 C. 15 D. 16二、填空题:1、袋子中装有50个乒乓球,其中20个黄的,30个白的,现有两人依次随机地从袋中各取一球,取后不放回,则第二人取得黄球的概率是 0.42、设A ,B 为两个随机事件,()0.6P A =,()0.2P A B -=,则()P AB = 0.63、已知二维随机向量(,)X Y 的联合分布为则= 0.34、设总体X 服从正态分布2(2,)N σ,1216,,,X X X 是来自总体X 的一个样本,且161116i i X X ==∑,则48X σ-服从 5、若(,)X Y 服从区域22{(,)4}G x y x y =+≤上的均匀分布,则(,)X Y 的联合密度函数为三、计算题:1、设A ,B 为随机事件,且()P A p =,()()P AB P A B =,求()P B 。
2024考研(数学三)真题答案及解析完整版

2024考研(数学三)真题答案及解析完整版2024年全国硕士研究生入学考试数学(三)真题及参考答案考研数学三考什么内容?数学三在高等数学这一部分因为要求的内容相对较少,所以很多学校经济类、管理类专业在本科期间所用教材并非理工类专业通常会使用的《高等数学》同济大学版,更多的学校本科阶段的教材是中国人民大学版《微积分》。
而考数学三的同学中在实际复习过程中使用哪一本教材的都有)(函数、极限、连续、一元函数微分学、一元函数积分学、多元函数微积分学、无穷级数、常微分方程与差分方程);线性代数(行列式、矩阵、向量、线性方程组、矩阵的特征值和特征向量、二次型);概率论与数理统计(随机事件和概率、随机变量及其分布、多维随机变量及其分布、随机变量的数字特征、大数定律和中心极限定理、数理统计的基本概念、参数估计、假设检验)。
考研的考试内容有哪些一、考研公共课:政治、英语一、英语二、俄语、日语、数学一、数学二、数学三,考研公共课由国家教育部统一命题。
各科的考试时间均为3小时。
考研的政治理论课(马原22分、毛中特30分、史纲14分、思修18分、形势与政策16分)。
考研的英语满分各为100分(完型10分、阅读理解60分、小作文10分、大作文20分)。
数学(其中理工科考数一、工科考数二、经管类考数三)满分为150分。
数一的考试内容分布:高数56%(84分)、线代22%(33分)、概率22%(33分);数二的内容分布:高数78%(117分)、线代22%(33分);数三的内容分布:高数56%(84分)、线代22%(33分)、概率22%(33分)。
这些科目的考试知识点和考试范围在各科考试大纲上有详细规定,一般变动不大,因此可以参照前一年的大纲,对一些变动较大的科目,必须以新大纲为准进行复习。
二、考研专业课统考专业课:由国家教育部考试中心统一命题,科目包括:西医综合、中医综合、计算机、法硕、历史学、心理学、教育学、农学。
其中报考教育学、历史学、医学门类者,考专业基础综合(满分为300分);报考农学门类者,考农学门类公共基础(满分150分)。
考研数学(三)题库 概率论与数理统计(第一章 随机事件和概率)打印版【圣才出品】

A.P(A)-P(B)
B.P(A)-P(B)+P(AB)
C.P(A)-P(AB)
_
_
D.P(A)+P(A)-P(AB)
4 / 29
圣才电子书 十万种考研考证电子书、题库视频学习平台
【答案】C
_
_
【解析】P(A)=P[A(B∪B)]=P(AB)+P(AB)=P(A-B)+P(AB),故 P
9.假设事件 A 和 B 满足 P(B|A)=1,0<P(A),则( )。 A.A 是必然事件 B.P(A|B)=0 C.A 包含事件 B D.P(A-B)=0 【答案】D 【解析】因为 P(B|A)=1 且 P(A)>0,故 P(AB)=P(A),P(A-B)=P(A) -P(AB)=0。
10.对于任意两事件 A 和 B,P(A-B)=( )。
__
P(A∪B)=1。
1 / 29
圣才电子书 十万种考研考证电子书、题库视频学习平台
3.若 A、B 互斥,且 P(A)>0,P(B)>0,则下列式子成立的是( )。 A.P(A|B)=P(A) B.P(B|A)>0 C.P(AB)=P(A)P(B) D.P(B|A)=0 【答案】D 【解析】因为 A,B 互斥,故 AB=∅,P(AB)=0,P(B|A)=P(AB)/P(A)=0。
14.对于事件 A、B、C,如果 A B C ,则( )。
_ __
A.A∪B⊂C
__ _
B.AB⊃C
_
C.A∪B⊂C
D.AB⊂C
【答案】C
_
【解析】∵ A B C ∴ A B C ,即 A∪B⊂C。
15.对于事件 A、B,如果 A⊃B,P(B)>0,则( )。
A.P(B|A)=P(B)
考研数学三(概率论与数理统计)-试卷5

考研数学三(概率论与数理统计)-试卷5(总分:70.00,做题时间:90分钟)一、选择题(总题数:13,分数:26.00)1.选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
(分数:2.00)__________________________________________________________________________________________解析:2.设随机变量X的方差存在,并且满足不等式P{|X( )(分数:2.00)A.D(X)=2.B.P{|X—E(X)|<3}C.D(X)≠2.D.P{|X—E(X)|√解析:解析:由于事件{|X—E(X)|<3}是事件{|X—E(X)|≥3}的对立事件,且题设P{|X—E(X)|≥3}≤,因此一定有P{|X—E(X)|<3}≥选项D正确.进一步分析,满足不等式P{|X—E(X)|≥3}≤的随机变量,其方差既可能不等于2,亦可以等于2,因此选项A与C都不能选.若X服从参数n=8,p=0.5的二项分布,则有E(X)=4,D(X)=2.但是P{|X—E(X)|≥3}=P{|X一4|≥3}=P{X=0}+P{X=1}+P{X=7}+P{X=8}=因此选项B也不成立.故选D.3.已知随机变量X服从二项分布,且E(X)=2.4,D(X)=1.44,则二项分布的参数n,P的值为( )(分数:2.00)A.n:4,P=0.6.B.n=6,P=0.4.√C.n=8,P=0.3.D.n=24,P=0.1.解析:解析:因为X~B(n,P),所以E(X)=np,D(X)=np(1一P)组,得n=6,p=0.4,故选项B正确.4.对任意两个随机变量X和Y,若E(XY)=E(X).E(Y),则( )(分数:2.00)A.D(XY)=D(X).D(Y).B.D(X+Y)=D(X)+D(Y).√C.X与Y独立.D.X与Y不独立.解析:解析:因为 D(X+Y)=D(X)+D(Y)+2[E(XY)一E(X).E(Y)],可见E(XY)=E(X).E(Y),故选项B正确.对于随机变量X与Y,下面四个结论是等价的.①Cov(X,Y)=0;②X 与Y不相关;③E(XY)=E(X)E(Y);④D(X+Y)=D(X)+D(Y).5.已知随机变量X与Y均服从0—1分布,且E(XY)=则(分数:2.00)A.B.C. √D.解析:解析:因为X与Y均服从0一1分布,所以可以列出(X,Y)的联合分布如下:又已知E(XY)=.即P 22 = 从而P{X+Y≤1}=P 11 +P 12 +P 21 =1一P 22.故选项C正确.6.设二维随机变量(X,Y)满足E(XY)=E(X).E(Y),则X与Y( )(分数:2.00)A.相关.B.不相关.√C.独立.D.不独立.解析:解析:因E(XY)=E(x)E(Y),故cov(X,Y)=E(XY)一E(X)E(Y)=0X与Y不相关,故选项B正确.7.将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数,则X和Y的相关系数等于( ) (分数:2.00)A.一1.√B.0.D.1.解析:解析:根据题意,y=n—X,故ρXY =一1.应选A.一般来说,两个随机变量X与Y的相关系数ρXY满足|ρXY|≤1.若Y=aX+b(a,b为常数),则当a>0时,ρXY =1,当a<0时,ρXY =一1.8.对于任意两随机变量X和Y,与命题“X和Y不相关”不等价的是( )(分数:2.00)A.E(XY)=E(X).E(Y).B.Cov(X,Y)=0.C.D(XY)=D(X).D(Y).√D.D(X+Y)=D(X)+D(Y).解析:解析:因为Cov(X,Y)=E(XY)一E(X)E(Y)=0是“X和Y不相关”的充分必要条件,所以A与B等价.由D(X+Y)=D(X)+D(Y)的充分必要条件是Cov(X,Y)=0,可见选项B与D等价.于是,“X和Y不相关”与选项A,B和D等价.故应选C.9.假设随机变量X在区间[一1,1]上均匀分布,则U=arcsinX和V=arccosX的相关系数等于( )(分数:2.00)A.一1.√B.0.C.0.5.D.1.解析:解析:因为U=arcsinX和V=arccosX满足下列关系:即U是V的线性函数,且其增减变化趋势恰恰相反,所以其相关系数ρ=一1.应选A.10.X与Y的相关系数ρ=1,则P{X=0,Y=1}的值必为( )(分数:2.00)A.0.√D.1.11.设随机变量X和Y独立同分布,记U=X—Y,V=X+Y,则随机变量U与V必然( )(分数:2.00)A.不独立.B.独立.C.相关系数不为零.D.相关系数为零.√解析:解析:因为 Cov(U,V)=E(UV)一E(U).E(V) =E(X 2一Y 2 )一E(X一Y).E(X+Y) =E(X 2 )一E(Y 2 )一E 2 (X)+E 2 (Y) =D(X)一D(Y)=0.则所以U与V的相关系数为零,故选D.12.设随机事件A与B互不相容,0<P(A)<1,0<P(B)<1与Y的相关系数为ρ,则( ) (分数:2.00)A.ρ=0.B.ρ=1.C.ρ<0.√D.ρ>0.解析:解析:选项B不能选,否则选项D必成立.因此仅能在选项A、C、D中考虑,即考虑ρ的符号,而相关系数符号取决于Coy(X,Y)=E(XY)-E(X).E(Y),根据题设知E(X)=P(A),E(Y)=P(B),(因为P(AB)=0),所以Cov(X,Y)=一E(X).E(Y)<0,故选C.13.设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X一2Y的方差是( )(分数:2.00)A.8.B.16.C.28.D.44.√解析:解析:本题考查方差的运算性质,是一道纯粹的计算题.可根据方差的运算性质D(C)=0(C为常数),D(CX)=C 2 D(X)以及相互独立随机变量的方差性质D(X±Y)=D(X)+D(Y)自行推演.故选项D正确.二、填空题(总题数:14,分数:28.00)14.设连续型随机变量X的分布函数为E(X)=1,则D(X)= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:1)解析:解析:根据题意已知连续型随机变量X15.相互独立的随机变量X 1和X 2均服从正态分布D(|X 1—X 2 |)= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据题意随机变量X 1和X 2相互独立,且服从正态分布设Z=X 1—X 2,则Z~N(0,1),其概率密度函数为φ(z)= D(|X 1 -X 2 |)=D(|Z|)=E(|Z| 2 )一E 2 |Z|=E(Z 2 )-E 2 |Z|=D(Z)+E2 (Z)一E 2 |Z|,显然,D(Z)=1,E(Z)=0.16.设随机变量X和Y X和Y的协方差Cov(X,Y)= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:一0.1)E(X)=0.5,E(Y)=(一1)×0.3+1×0.3=0. E(XY)=一P{XY=一1}+P{XY=1}=一0.2+0.1=一0.1. Coy(X,Y)=E(XY)一E(X)E(Y)=一0.1—0=一0.1.17.已知随机变量X的分布函数F(x)在x=1处连续,且F(1)=若EY= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据离散型随机变量期望公式计算.由于F(x)在x=1处连续,故E(Y)=aP{X>1}+bP{X=1}+cP{X<1} =a[1一P{X≤1}]+bP{X=1}+cP{18.已知(X,Y)在以点(0,0),(1,0),(1,1)为顶点的三角形区域上服从均匀分布,对(X,Y)作4次独立重复观察,观察值X+Y不超过1出现的次数为Z,则EZ 2 = 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:5)解析:解析:根据题干可知(X,Y)的联合概率密度函数为令事件A=“X+Y≤1”,则Z是4次独立重复试验事件A发生的次数,故Z~B(4,P),其中如图4—119.已知某自动生产线一旦出现不合格产品就立即进行调整,经过调整后生产出的产品为不合格产品的概率是0.1,如果用X表示两次调整之间生产出的产品数量,则EX= 1。
青岛大学考研真题—概率论与数理统计
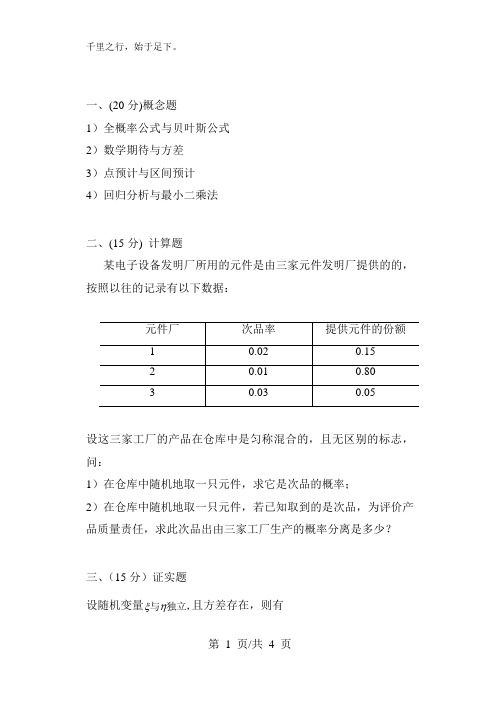
一、(20分)概念题1)全概率公式与贝叶斯公式2)数学期待与方差3)点预计与区间预计4)回归分析与最小二乘法二、(15分) 计算题某电子设备发明厂所用的元件是由三家元件发明厂提供的的,按照以往的记录有以下数据:设这三家工厂的产品在仓库中是匀称混合的,且无区别的标志,问:1)在仓库中随机地取一只元件,求它是次品的概率;2)在仓库中随机地取一只元件,若已知取到的是次品,为评价产品质量责任,求此次品出由三家工厂生产的概率分离是多少?三、(15分)证实题设随机变量独立,ξ且方差存在,则有与η22)()()(ηξηξηξξηE D D E D D D •+•+•=由此并可得ηξξηD D D •≥)(四、(15分) 计算题设二维随机变量),(ηξ的联合密度为 ⎩⎨⎧>>=--其它),(,00,0,43y x ke y x p y x问:1)求常数k;2)求相应的分布函数; 3)求),(2010<<<<ηξp 五、(15分)计算题设有A,B 两种不相关的证券,它们的收益与概率如下表:问:1)应如何投资这两种证券最佳(即要满意收益越大越好,风险越小越好)?2)若这两种证券相关,譬如相关系数5.0,-=B A ρ,结果又如何?六、 (15分)计算题假设某险种在投保时期内一共发生了N 次赔款,i ξ表示第i 次赔款额,则相应的赔款总量为:N S ξξξ+++=...21,其中N 为取非负整数值的随机变量,N ξξξ...,21,,具有相同的分布函数,且N,N ξξξ (21),互相自立,问: 1)推导赔款总量S 的数学期待及方差公式;2)若N 顺从参数3=λ的泊松分布,第i 笔赔款额i ξ的分布列如下表:计算赔款总量S 的范围。
七、(15分)证实题设{}n ξ为自立同分布的随机变量序列,每个随机变量的期待为a ,且方差存在,证实:a k n n nk k →+∑=1)1(2ξ(依概率收敛)八、(20分)计算题设总体ξ~),(2σμN ,2,σμ为未知参数,(n ξξξ,...,,21)是来自总体ξ的一个样本,问: 1)2,σμ的矩预计; 2)2,σμ的极大似然预计;3)以上两个预计是否无偏预计?若不是如何修正?九、(20分)计算题 针对一元线性回归模型i i i i x y εεβα,++=~n i N ,...,2,1),,0(2=σ求其中参数βα,的最小二乘预计及2σ的无偏预计,其中n x x x ,...,,21不全相同。
考研数学三(选择题)高频考点模拟试卷20(题后含答案及解析)

考研数学三(选择题)高频考点模拟试卷20(题后含答案及解析) 题型有:1.1.设函数f(x)=在(一∞,+∞)内连续,且=0,则常数a,b满足( )A.a<0,b<0。
B.a>0,b>0。
C.a≤0,b>0。
D.a≥0,b<0。
正确答案:D解析:因f(x)连续,故a+ebx≠0,因此只要a≥0即可。
再由=0.可知x→∞时,a+ebx必为无穷大(否则极限必不存在),此时需b则当x→0时f(x)是x 的A.等价无穷小B.二阶无穷小C.三阶无穷小D.四阶无穷小.正确答案:C解析:由题设[*]可知[*] 又有当x→0时[*]从而[*] 由于[*]故可知[*]即当x→0时f(x)是x的三阶无穷小.应选C.知识模块:函数、极限、连续3.设则x=0是f(x)的( ).A.连续点B.第一类间断点C.第二类间断点D.不能判断连续性的点正确答案:B解析:当x>0时,当x=0时,当x<0时,f(x)=x.因为f(0+0)=1,f(0—0)=0,所以x=0为f(x)的第一类间断点,选(B).知识模块:函数、极限、连续4.曲线y=【】A.没有渐近线.B.仅有水平渐近线.C.仅有铅直渐近线.D.既有水平渐近线也有铅直渐近线.正确答案:D 涉及知识点:微积分5.设随机变量X服从正态分布N(0,1),对给定的α∈(0,1),数uα满足P{X>uα}=α,若P{|X|<X}=α,则X等于( )A.B.C.D.正确答案:C解析:标准正态分布上α分位数的定义及条件P{X>uα}=α与P{|X|<x}=α,并考虑到标准正态分布概率密度曲线的对称性,可作出如图2—3及图2—4所示图形.如图2—4所示,根据标准正态分布的上α分位数的定义,可知,故选项C正确.知识模块:概率论与数理统计6.两曲线y=与y=ax2+b在点(2,)处相切,则( )A.B.C.D.正确答案:A解析:因两曲线相切于点(2,),故相交于该点.将x=2,y=代入y=ax2+b 中得=4a+b,又因为相切于该点,故切线斜率相等,即导数相等,所以=2ax,将x=2代入得知识模块:一元函数微分学7.设β,α1,α2线性相关,β,α2,α3线性无关,则( ).A.α1,α2,α3线性相关B.α1,α2,α3线性无关C.α1可用β,α2,α3线性表示D.β可用α1,α2线性表示正确答案:C 涉及知识点:一元函数积分学8.微分方程y’’-4y=x+2的通解为( ).A.B.C.D.正确答案:D解析:微分方程y’’-4y=0的特征方程为λ2-4=0,特征值为-2,2,则方程y’’-4y=0的通解为C1e-2x+C2e2x,显然方程y’’-4y=x+2有特解,选(D).知识模块:微积分9.设f(x)=,则( )A.f(x)在[1,+∞)单调增加.B.f(x)在[1,+∞)单调减少.C.f(x)在[1,+∞)为常数.D.f(x)在[1,+∞)为常数0.正确答案:C解析:按选项要求,先求f’(x).又f(x)在[1,+∞)连续,则f(x)=常数=f(1)=故选C.知识模块:一元函数微分学10.设级数都发散,则( ).A.B.C.D.正确答案:D解析:选(D).因为0≤|un|≤|un|,0≤|vn|≤|un|+|vn|,根据正项级数的比较审敛法知,知识模块:微积分11.设向量组α1,α2,α3线性无关,则下列向量组线性相关的是A.α1-α2,α2-α3,α3-α1.B.α1+α2,α2+α3,α3+α1.C.α1-2α2,α2-2α3,α3-2α1.D.α1+2α2,α2+2α3,α3+2α1.正确答案:A 涉及知识点:一元函数积分学12.设f(x)在(-∞,+∞)上有定义,x0≠0为函数f(x)的极大值点,则( ).A.x0为f(x)的驻点B.-x0为-f(-x)的极小值点C.-x0为-f(x)的极小值点D.对一切的x有f(x)≤f(x0)正确答案:B解析:因为y=f(-x)的图像与y=f(x)的图像关于y轴对称,所以-x0为f(-x)的极大值点,从而-x0为-f(-x)的极小值点,选(B).知识模块:微积分13.累次积分可以写成( )A.B.C.D.正确答案:D解析:由累次积分f(rcosθ,rsinθ)rdr可知,积分区域D为由r=cosθ为圆心在x轴上,直径为1的圆可作出D的图形如图4—3所示.该圆的直角坐标方程为故用直角坐标表示区域D为可见A、B、C均不正确,故选D.知识模块:多元函数微积分学14.设n维行向量α=(),矩阵A=E一αTα,B=E+2αTα,则AB=A.0.B.E.C.一E.D.E+αTα.正确答案:B解析:AB=(E一αTα)(E+2αTα)=E+2αTα一αTα一2αTααTα=E+αTα一2αT(ααT)α.注意ααT=,故AB=E.应选B.知识模块:线性代数15.函数z=f(x,y)=在(0,0)点( )A.连续,但偏导数不存在B.偏导数存在,但不可微C.可微D.偏导数存在且连续正确答案:B解析:从讨论函数是否有偏导数和是否可微入手.由于=0,所以fˊx (0,0)=0,同理fˊy(0,0)=0.令α=△z-fˊx(0,0)△x-fˊy(0,0)△y=当(△x,△y)沿y=x趋于(0,0)点时≠0,即α不是ρ的高阶无穷小,因此f(x,y)在(0,0)点不可微,故选(B).知识模块:多元函数微分学16.设矩阵A=(α1,α2,α3,α4)经行初等变换为矩阵B=(β1,β2,β3,β4),且α1,α2,α3线性无关,α1,α2,α3,α4线性相关,则( ).A.β4不能由β1,β2,β3线性表示B.β4能由β1,β2,β3线性表示,但表示法不唯一C.β4能由β1,β2,β3线性表示,且表示法唯一D.β4能否由β1,β2,β3线性表示不能确定正确答案:C解析:因为α1,α2,α3线性无关,而α1,α2,α3,α4线性相关,所以口。
考研数学三(概率统计)模拟试卷19(题后含答案及解析)

考研数学三(概率统计)模拟试卷19(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.将一枚硬币独立地掷两次,引进事件:A1={掷第一次出现正面},A2={掷第二次出现正面},A3={正、反面各出现一次},A4={正面出现两次},则事件A.A1,A2,A3相互独立B.A2,A3,A4相互独立C.A1,A2,A3两两独立D.A2,A3,A1两两独立正确答案:C解析:(本题的硬币应当设是“均匀”的)。
由题意易见:可见A1,A2,A3两两独立,故选(C)。
知识模块:概率与数理统计填空题2.设X1,X2,X3,X4是来自正态总体N(0,22)的简单随机样本,X=a(X1一2X2)2+b(3X3一4X4)2。
则当a=________,b=________时,统计量X服从χ2分布,其自由度为________。
正确答案:解析:∵E(X1一2X2)=EX1—2EX2=0D(X1一2X2)=DX1+4DX2=4+4×4=20E(3X3—4X4)=3EX3—4EX4=3×0—4×0=0D(3X3—4X4)=9DX3+16DX4=9X4+16×4=100与题目的X比较即得结果。
知识模块:概率与数理统计3.设总体X的概率密度为(一∞<x<+∞),X1,X2,…,Xn为总体X的简单随机样本,其样本方差为S2,则ES2=________。
正确答案:2解析:而E(S2)=DX,故ES2=2。
知识模块:概率与数理统计4.设X1,…,Xn是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知。
记则假设H0:μ=0的t检验使用的统计量t________。
正确答案:解析:知识模块:概率与数理统计解答题解答应写出文字说明、证明过程或演算步骤。
5.设二维随机变量(X,Y)的概率密度为求常数A及条件概率密度fY|X(y|x)。
考研数学三(概率论与数理统计)历年真题试卷汇编5(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编5(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(03年)将一枚硬币独立地掷两次,引进事件:A1={掷第一次出现正面},A2={掷第二次出现正面},A3={正、反面各出现一次},A4={正面出现两次},则事件【】A.A1,A2,A3相互独立.B.A2,A3,A4相互独立.C.A1,A2,A3两两独立.D.A2,A3,A4两两独立.正确答案:C 涉及知识点:概率论与数理统计2.(07年)某人向同一目标独立重复射击,每次射击命中目标的概率为p(0<P<1),则此人第4次射击恰好第2次命中目标的概率为【】A.3p(1-p)2.B.6p(1-p)2.C.3p2(1-p)2.D.6p2(1-p)2.正确答案:C解析:P{第4次射击恰好第2次命中目标}=P{前3次射击恰中1枪,第4次射击命中目标} =P{前3次射击恰中1枪}.P{第4次射击命中目标}=C31p(1-p)2.P=3p2(1-p)2 知识模块:概率论与数理统计3.(09年)设事件A与事件B互不相容,则【】A.P()=0.B.P(AB)=P(A)P(B).C.P(A)=1-P(B).D.P()-1.正确答案:D 涉及知识点:概率论与数理统计4.(14年)设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=【】A.0.1B.0.2C.0.3D.0.4正确答案:B解析:∵A与B独立,∴P(AB)=P(A)P(B).故0.3=P(A-B)=P(A)-P(AB)=P(A)-P(A)P(B) =P(A)[1-P(B)]=P(A)(1-0.5)=0.5(P(A) 得P(A)==06,P(B-A)=P(B)-P(AB)=P(B)-P(A)P(B)=0.5-0.6×0.5=0.2.知识模块:概率论与数理统计5.(15年)若A,B为任意两个随机事件,则【】A.P(AB)≤P(A)P(B).B.P(AB)≥P(A)P(B).C.P(AB)≤.D.P(AB)≥.正确答案:C解析:由ABA,ABB得P(AB)≤P(A),P(AB)≤P(B),两式相加即得:P(AB)≤.知识模块:概率论与数理统计6.(16年)设A,B为两个随机事件,且0<P(A)<1,0<P(B)<1,如果P(A|B)=1,则【】A.P()=1.B.P(A|)=0.C.P(A∪B)=1.D.P(B|A)=1.正确答案:A解析:由1=P(A|B)=,有P(B)=P(AB) 于是知识模块:概率论与数理统计7.(90年)设随机变量X和Y相互独立,其概率分布为则下列式子正确的是:【】A.X-YB.P{X-Y}=0C.P{X-Y}=D.P{X=Y}=1正确答案:C解析:P(X=Y)=P(X=-1,Y=-1)+P(X=1,Y=1) =P(X=-1)P(Y =-1)+P(X=1)P(Y=1) =知识模块:概率论与数理统计8.(93年)设随机变量X的密度函数为φ(χ),且φ(-χ)-φ(χ),F(χ)为X的分布函数,则对任意实数a,有【】A.F(-a)=1-∫0aφ(χ)dχB.F(-a)=-∫0aφ(χ)dχC.F(-a)=F(a)D.F(-a)=2F(a)-1正确答案:B解析:由概率密度的性质和已知,可得故选B.知识模块:概率论与数理统计9.(95年)设随机变量X~N(μ,σ2),则随着σ的增大,概率P(|X-μ|<σ) 【】A.单调增大.B.单调减小.C.保持不变.D.增减不定.正确答案:C解析:由已知X~N(μ,σ),得~N(0,1) 故P{|X-μ|<σ}==(1)Ф-Ф(-1) 故选C.知识模块:概率论与数理统计填空题10.(89年)设随机变量X的分布函数为则A=_______,P{|X|<}=_______.正确答案:1;解析:∵分布函数是右连续的,故得1=Asin ∴A=1 这时,F(χ)在(-∞,+∞)上都连续,于是知识模块:概率论与数理统计11.(91年)设随机变最X的分布函数为则X的概率分布为_______.正确答案:解析:F(χ)为一阶梯状函数,则X可能取的值为F(χ)的跳跃点:-1,1,3.P(X=-1)=F(-1)-F(-1-0)=0.4 P(X=1)=F(1)-F(1-0)=0.8-0.4=0.4 P(X=3)=F(3)-F(3-0)=1-0.8=0.2 知识模块:概率论与数理统计12.(94年)设随机变量X的概率密度为以Y表示对X的三次独立重复观察中事件{X≤}出现的次数P{Y=2}=_______.正确答案:解析:由题意,Y~B(3,p).其中p=故知识模块:概率论与数理统计13.(00年)设随机变量X的概率密度为若k使得P{X≥k}=,则k的取值范围是_______.正确答案:[1,3]解析:∵P(X≥k)=∫k+∞f(χ)dχ.可见:若k≤0,则P(X≥k)=1 若0<k<1,则P(X≥k)=若k>6,则P(X≥k)=0 若3<k≤6,则P(X ≥k)=若1≤k≤3,则P(X≥k)=综上,可知K∈[1,3].知识模块:概率论与数理统计14.(05年)从数1,2,3,4中任取一个数,记为X,再从1,…,X中任取一个数,记为Y,则P(Y=2}=_______.正确答案:解析:由题意,X的概率分布为而P(Y=2|X=1)=0,P(Y=2|X=2)=,P(Y=2|X=3)=,P(Y=2|X=4)=,故由全概率公式得知识模块:概率论与数理统计15.(05年)设二维随机变量(X,Y)的概率分布为若随机事件{X=0}与{X+Y=1}相互独立,则a=_______,b=_______.正确答案:0.4;0.1.解析:由题意知0.4+a+b+0.1=1,∴a+b=0.5 而P{X=0}=0.4+a,P{X+Y=1}=P{X=0,Y=1}+P{X=1,Y=0}=a+b=0.5,P{X =0,X+Y=1}=P{X=0,Y=1}=a 由P{X=0,X+Y=1)=P{X=0)P{X +Y=1} ∴a=(0.4+a)0.5,得a=0.4,从而b=0.1.知识模块:概率论与数理统计16.(06年)设随机变量X与Y相互独立,且均服从区间[0,3]上的均匀分布,则P{max(X,Y)≤1}=_______.正确答案:解析:由题意知X与Y的概率密度均为:则P(X≤1}=P{Y≤1}=∫-∞1f(χ)dχ=故P{max(X,Y)≤1}=P{X≤1,y≤1}=P{X≤1}P{y≤1}=知识模块:概率论与数理统计17.(99年)设随机变量Xij(i=1,2,…,n;n≥2)独立同分布,Eij=2,则行列式Y=的数学期望EY=_______.正确答案:0解析:由n阶行列式的定义知Y=,P1,…,Pn为(1,…,n)的排列,τ(p1p2…pn)为排列p1p2…pn的逆序数.而Xij(i,j=1,2,…,n)独立同分布且EXij=2,故知识模块:概率论与数理统计解答题解答应写出文字说明、证明过程或演算步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学三(概率论与数理统计)-试卷20(总分:64.00,做题时间:90分钟)一、选择题(总题数:12,分数:24.00)1.选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
(分数:2.00)__________________________________________________________________________________________ 解析:2.设二维随机变量(X 1,X 2 )的密度函数为f 1 (x 1,x 2 ),则随机变量(Y 1,Y 2 )(其中Y 1 =2X 1,Y 2 = )的概率密度f 2 (y 1,y 2 )等于(分数:2.00)A.B. √C.D.解析:解析:设(X 1,X 2 )的分布为F 1 (x 1,x 2 ),(Y 1,Y 2 )的分布为F 2 (y 1,y 2 ).故选项B正确.3.设随机变量X和Y都服从正态分布,且它们不相关,则( )(分数:2.00)A.X与Y一定独立.B.(X,Y)服从二维正态分布.C.X与Y未必独立.√D.X+Y服从一维正态分布.解析:解析:因为只有当(X,Y)服从二维正态分布时,X与Y与Y相互独立.本题已知X 和Y服从正态分布,不能推得(X,Y)服从二维正态分布,因此由不相关推不出X与Y一定独立,故排除选项A.若X和Y都服从正态分布且相互独立,则(X,Y)服从二维正态分布,但由题设并不知道X和Y是否相互独立,故排除选项B.同样,当X和Y都服从正态分布且相互独立时,才能推出X+Y服从一维正态分布,又排除选项D.综上可知,选择C.4.设相互独立的两随机变量X,Y均服从[0,3]上的均匀分布,则P{1<max(X,Y)≤2}的值为(分数:2.00)A.B.C. √D.解析:解析:P{1<max(X,Y)≤2}=P{max(X,Y)≤2}一P{max(X,Y)≤1} =P{X≤2,Y≤2}一P{X≤1,Y≤1}=P{X≤2}P{Y≤2}一故选项C正确.5.设相互独立的两随机变量X和Y分别服从E(λ)(λ>0)和E(λ+2)分布,则P{min(X,Y)>1}的值为( ) (分数:2.00)A.e -(λ+1)B.1一e -(λ+1)C.e -2(λ+1)√D.1一e -2(λ+1).解析:解析:P{min(X,Y)>1}=P{X>1,Y>1}=P{X>1}P{Y>1} =e -λ.e -(λ+2)=e -2(λ+1).故选项C正确.6.设相互独立的两随机变量X,Y,均服从E(1)分布,则P{1<min(X,Y)≤2}的值为( )(分数:2.00)A.e -1一e -2B.1一e -1C.1一e -2D.e -2一e -4.√解析:解析:P{1<min(X,Y)≤2}=P{min(X,Y)>1}一P{min(X,Y)>2} =P{X>1,Y>1}一P{X>2,Y>2} =P{X>1}P{Y>1}一P{X>2}P{Y>2} =e -1 .e -1—e -2 .e -2 =e -2—e -4.故选项D正确.7.设(X,Y)为二维随机变量,则下列结论正确的是( )(分数:2.00)A.若X与Y不相关,则X 2与Y 2不相关.B.若X 2与Y 3不相关,则X与Y不相关.C.若X与Y均服从正态分布,则X与Y独立和X与Y不相关等价.D.若X与Y均服从0—1两点分布,则X与Y独立和X与Y不相关等价.√解析:解析:对于选项D:设X~B(1,p),Y~B(1,Q),当X与Y独立时X与Y不相关.反之,当X与Y不相关,即E(XY)=E(X)E(Y)=pq由此可知X与Y独立.故此时X与Y独立和X 与Y不相关等价,故选项D正确.根据不相关的性质可排除选项A和B.对于选项C,当X与Y均服从正态分布时,(X,Y)未必服从二维正态分布,故选项C不正确.8.设随机变量X服从正态分布N(μ1,σ12 ),Y服从正态分布N(μ2,σ22 ),且P{|X一μ1 | <1}>P{|Y—μ2 | <1}.则必有( )(分数:2.00)A.σ1<σ2.√B.σ1>σ2.C.μ1<μ2.D.μ1>μ2.9.设随机变量(X,Y)服从二维正态分布,且X与Y不相关f X (x),f Y (y)分别表示X,Y的概率密度,则在Y=y,条件下,X的条件概率密度f X|Y (x|y)为( )(分数:2.00)A.f X (x).√B.f Y (y).C.f X (x)f Y (y).解析:解析:因为(X,Y)服从二维正态分布,且X与Y不相关,那么X与Y独立,且f(x,y)=f X(x)f Y(y).则故正确答案为A.10.随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为( )(分数:2.00)A.F 2 (x).√B.F(x)F(y).C.1一[1一F(x)] 2.D.[1一F(x)][1一F(y)].解析:解析:设Z的分布函数为F z(z),则F Z(x)=P(Z≤x)=P{max{X,Y}≤x}=P(X≤x)P(Y≤x)=F 2(x).故选项A正确.11.设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为记F Z (z)为随机变量Z=XY的分布函数,则函数F Z (z)的间断点个数为( )(分数:2.00)A.0.B.1.√C.2.D.3.解析:解析:根据题意可知, F Z(z)=P(XY≤z)=P(XY≤z|Y=0)P(Y=0)+P(XY≤z|Y=1)P(Y=1) = 一[P(XY≤z|Y=0)+P(XY≤z|Y=1)],由于X,Y独立,所以所以z=0为间断点,因此选项B正确.12.设F 1 (x),F 2 (x)为两个分布函数,其相应的概率密度f 1 (x)与f 2 (x)是连续函数,则必为概率密度的是( )(分数:2.00)A.f 1 (x)f 2 (x).B.2f 2 (x)F 1 (x).C.f 1 (x)F 2 (x).D.f 1 (x)F 2 (x)+f 2 (x)F 1 (x).√解析:解析:因为f 1 (x)与f 2 (x)均为连续函数,故它们的分布函数F 1 (x)与F 2 (x)也连续.根据概率密度的性质,应有f(x)非负,且∫ -∞+∞ f(x)dx=1.在四个选项中,只有D项满足.∫ -∞+∞ [f 1 (x)F2 (x)+f 2 (x)F 1(x)]dx =∫ -∞+∞ [F1 (x)F 2(x)]’dx =F 1 (x)F2 (x)| -∞+∞ =1—0=1,故选项D正确.二、填空题(总题数:11,分数:22.00)13.已知(X,Y)的联合概率密度为f(x, 1。
(分数:2.00)填空项1:__________________ (正确答案:正确答案:F(1,1))解析:解析:根据题设可知(X,Y)服从二维正态分布且密度函数为故X~N(0,2 2),Y~N(1,3 2),X与Y的相关系数ρ=0,所以X与Y独立,N(0,1),根据F分布典型模式知14.设随机变量X与Y0一1分布,则随机变量Z=max{X,Y}的分布律为 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据题意显然Z也是离散型随机变量,只取0,1两个值,且P{Z=0}=P{max(X,Y)=0}=P{X=0,Y=0}=P{X=0}P{Y=0}=P{Z=1}=1一P{Z=0}=所以Z15.设随机变量X和Y X的分布函数F(x)为 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据题意分布函数F(x)是F(x,y)的边缘分布函数,所以F(x)=F(x,+∞)=F(x,1),因此F(x)=16.已知随机变量X与Y独立同分布,且X的分布函数为F(x),记Z=max(X,Y),则(X,Z)的联合分布函数F(x,z)= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:已知X与Y独立且有相同分布F(x),所以(X,Z)的联合分布函数F(x,z)=P{X≤x,max(X,17.设(X,Y) ~N(μ,μ;σ2,σ2;0),则P{X<Y}= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])18.已知随机变量X与Y的联合概率分布为P{X+Y=1} =0.4,则α= 1;β= 2;P{X+Y<1} = 3;P{X 2 Y 2 =1}= 4.(分数:2.00)填空项1:__________________ (正确答案:正确答案:0.3)填空项1:__________________ (正确答案:0.1)填空项1:__________________ (正确答案:0.4)填空项1:__________________ (正确答案:0.3)解析:解析:根据题意得知,0.1+0.2+α+β+0.1+0.2=1及P{X+Y=1}=P{X=0,Y=1} +P{X=1,Y=0}=α+0.1=0.4解得α=0.3,β=0.1,于是 P{X+Y<=P{X=0,Y=一1}+P{X=0,Y=0}+P{X=1,Y=一1}=0.1+0.2+0.1=0.4: P{X 2 Y 2 =1}=P{X=1,Y=一1}+P{X=1,Y=1}=0.1+0.2=0.3.19.已知随机变量X与Y均服从0—1分布,且P{X+Y≤1}= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:因为X与Y均服从0一1分布,可以列出(X,Y)20.已知n维向量α1,α2,α3线性无关,则α1 +α2,α2 +2α3,Xα3 +Yα1线性相关的概率为 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:因为α1,α2,α3线性无关,所以“α1 +α2,α2 +2α3,Xα3 +Yα1线性相关” =X+2Y=0”,故所求的概率为21.设相互独立的两个随机变量X和Y均服从标准正态分布,则随机变量X—Y的概率密度函数的最大值等于 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据题意可知,X—Y~N(0,2),其概率密度函数f(x)的最大值在x=0处,22.已知随机变量X 1,X 2,…,X n相互独立,且都服从标准正态分布,Y 1 =X 1,Y 2 =X 2则Y 1一Y 2服从 1分布,参数为 2.(分数:2.00)填空项1:__________________ (正确答案:正确答案:正态)填空项1:__________________ (正确答案:[*])解析:解析:Y 1一Y 2=X 1一X 2+ ,所以Y 1一Y 2为相互独立正态变量和,且服从正态分布.23.设随机变量(X,Y)k= 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:根据概率密度性质∫ -∞+∞∫ -∞+∞ f(x,y)dxdy=1,则有∫ 02dx∫ 24 k(6一x一y)dy=1,又知由8k=1,得常数三、解答题(总题数:9,分数:18.00)24.解答题解答应写出文字说明、证明过程或演算步骤。
