2017届深圳中考复习《多结论几何综合题》专题试卷含解析
深圳中考数学试题与标准答案分析.doc

精品文档2017 年广东省深圳市中考数学试卷一、选择题1.(3 分)﹣ 2 的绝对值是()A.﹣ 2B.2C.﹣D.2.(3 分)图中立体图形的主视图是()A.B.C.D.3.(3 分)随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000 吨,将 8200000 用科学记数法表示为()A.8.2×105B.82× 105C. 8.2× 106D. 82×107 4.(3 分)观察下列图形,其中既是轴对称又是中心对称图形的是()A.B.C.D.5.(3 分)下列选项中,哪个不可以得到l1∥l2?()A.∠ 1=∠2B.∠ 2=∠ 3C.∠ 3=∠5D.∠ 3+∠ 4=180°6.(3 分)不等式组的解集为()A.x>﹣ 1 B.x<3 C.x<﹣ 1 或 x>3 D.﹣ 1<x<3 7.(3 分)一球鞋厂,现打折促销卖出 330 双球鞋,比上个月多卖10%,设上个月卖出 x 双,列出方程()A.10%x=330 B.(1﹣ 10%) x=330C.(1﹣10%)2 x=330 D.(1+10%)x=3308.(3 分)如图,已知线段 AB,分别以 A、B 为圆心,大于AB 为半径作弧,连接弧的交点得到直线 l,在直线 l 上取一点 C,使得∠ CAB=25°,延长 AC至 M,求∠ BCM 的度数为()A.40°B.50°C. 60°D.70°9.(3 分)下列哪一个是假命题()A.五边形外角和为 360°B.切线垂直于经过切点的半径C.(3,﹣ 2)关于 y 轴的对称点为(﹣ 3, 2)D.抛物线 y=x2﹣4x+2017 对称轴为直线 x=210.( 3 分)某共享单车前 a 公里 1 元,超过 a 公里的,每公里 2 元,若要使使用该共享单车50%的人只花 1 元钱, a 应该要取什么数()A.平均数B.中位数C.众数D.方差11.( 3 分)如图,学校环保社成员想测量斜坡CD 旁一棵树 AB 的高度,他们先在点 C 处测得树顶 B 的仰角为 60°,然后在坡顶 D 测得树顶 B 的仰角为 30°,已知斜坡 CD的长度为 20m, DE的长为 10cm,则树 AB 的高度是()m.A.20 B.30 C.30 D. 4012.( 3 分)如图,正方形ABCD的边长是 3,BP=CQ,连接 AQ,DP 交于点 O,并分别与边 CD,BC交于点 F,E,连接 AE,下列结论:①AQ⊥ DP;② OA2=OE?OP;③ S△AOD=S四边形OECF;④当 BP=1时,tan∠ OAE=,其中正确结论的个数是()A.1B.2C.3D.4二、填空题13.( 3 分)因式分解: a3﹣4a=.14.( 3 分)在一个不透明的袋子里,有 2 个黑球和 1 个白球,除了颜色外全部相同,任意摸两个球,摸到 1 黑 1 白的概率是.15.( 3 分)阅读理解:引入新数 i,新数 i 满足分配律,结合律,交换律,已知i2=﹣1,那么( 1+i)?( 1﹣ i)=.16.(3 分)如图,在 Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P 在 AC上,PM 交 AB 于点 E,PN 交 BC于点 F,当 PE=2PF时, AP=.三、解答题.(分)计算:| ﹣﹣2+.17 5 2| ﹣2cos45 °+(﹣ 1)18.( 6 分)先化简,再求值:(+)÷,其中x=﹣1.19.( 7 分)深圳市某学校抽样调查,A 类学生骑共享单车, B 类学生坐公交车、私家车等, C 类学生步行, D 类学生(其它),根据调查结果绘制了不完整的统计图.类型频数频率A 30 xB 18 0.15C m 0.40D n y( 1)学生共人, x= , y= ;( 2)补全条形统计图;( 3)若该校共有 2000 人,骑共享单车的有人.20.( 8 分)一个矩形周长为56 厘米.(1)当矩形面积为 180 平方厘米时,长宽分别为多少?(2)能围成面积为 200 平方米的矩形吗?请说明理由.21.( 8 分)如图,一次函数y=kx+b 与反比例函数 y=(x>0)交于A(2,4),B(a,1),与 x 轴, y 轴分别交于点 C,D.(1)直接写出一次函数 y=kx+b 的表达式和反比例函数 y= (x>0)的表达式;(2)求证: AD=BC.22.( 9 分)如图,线段AB 是⊙ O 的直径,弦 CD⊥ AB 于点 H,点 M 是上任意一点, AH=2, CH=4.(1)求⊙ O 的半径 r 的长度;(2)求 sin∠CMD;(3)直线 BM 交直线 CD于点 E,直线 MH 交⊙ O 于点 N,连接 BN 交 CE于点 F,求 HE?HF的值.23.(9 分)如图,抛物线 y=ax2+bx+2 经过点A(﹣ 1,0),B(4,0),交 y 轴于点 C;( 1)求抛物线的解析式(用一般式表示);( 2)点 D 为 y 轴右侧抛物线上一点,是否存在点 D 使 S△ABC= S△ABD?若存在请直接给出点 D 坐标;若不存在请说明理由;( 3)将直线 BC绕点 B 顺时针旋转 45°,与抛物线交于另一点E,求 BE的长.。
2017深圳中考数学试卷分析 (1)

2017年深圳中考数学试卷分析+考点分析+全真试题一、试卷分析2017年深圳中考数学已经圆满结束,考拉超级课堂研究院为大家整理了深圳中考真题、解析、答案以及试卷点评分析,紧扣热点、重视基础、难度适中、稳中有“新”、区分度明显是今年深圳中考数学的几大特点.1.紧扣热点:题目的载体和背景结合时事民生,将“一带一路”、共享单车等热点元素融入其中.2.重视基础、难度适中:同前几年深圳中考题型和考点分布基本一致,基础知识部分占全卷较大比重,选择题前11题均单独考察平行线判定、解不等式组、尺规作图、三角函数应用等基础内容;填空题前三道单独考察因式分解、概率、定义新运算,也属于基础知识;解答题前四题分别考察实数计算、分式化简求值、数据统计、一与二次方程的实际应用,难度适中。
全卷在注重基础知识考察的同时,重点突出函数、基本图形性质、图形间的基本关系等核心内容的考察.3.稳中有“新”:①选择题舍弃了前两年整式的运算,以求不等式组的解集代之;②舍弃了探索规律问题,取而代之的是考察面更广的定义新运算问题,该问题涵盖了整式的运算,同时还体现了高中的虚数的概念,对学生综合分析能力要求较高;③压轴填空第16题为直角三角形的构造相似问题,难点在于相似比的转化;④解答题21题考察反比例函数与一次函数综合,舍弃反比例函数求k值的考察,更注重函数综合的应用;⑤解答题22题舍弃了切线的证明,增加了计算的比重,以及增加了相似的综合运用能力.4.压轴题区分度明显:今年压轴题仍然出现在第12题(选择)、第16题(填空)、第22、23题(解答),整体考点与去年一致,分别有几何综合题、圆与相似、二次函数综合题,但难度比去年略有提高,具有明显的选拔性和区分度.例如最后一题综合了二次函数、动点与面积、图形的旋转等内容,题型与解法与往年略有不同,对于学生的数形结合思想、想象能力、计算能力的要求更高.二、考点分析试卷考查知识点、难度情况、分值题型题号涵盖知识点难度系数分值选择题1 绝对值★ 32 三视图★ 33 科学记数法★ 34 轴对称、中心对称图像★ 35 平行线的判定★ 36 解一元一次不等式组★ 37 一元一次方程的实际应用(销售利润)★ 38 尺规作图(中垂线)★ 39 命题与定理★ 310 数据分析(中位数)★ 311 三角函数的应用(测高)★★ 312 几何综合★★★ 3填空题13 因式分解★ 314 概率计算★ 315 定义新运算(虚数)★ 316 相似三角形★★★ 3解答题17 实数的计算★ 518 分式的化简求值★ 619 数据统计★720 一与二次方程的实际应用★★821 反比例函数与一次函数综合★★822圆的综合(勾股定理、圆周角定理、相似三角形)★★★9 23二次函数综合(二次函数解析式、面积问题、旋转)★★★9三、试题解析2017年深圳中考数学试卷第一部分选择题一、(本部分共12题,每小题3分,共36分,每小题给出4个选项,其中只有一个选项是正确的)1.-2的绝对值是()A.-2 B.2 C.-12D.12【考点】绝对值【解析】正数和0的绝对值是它们本身,负数的绝对值是它的相反数.【答案】B2.图中立体图形的主视图是()立体图形 A B C D 【考点】三视图【解析】三视图的主视图即从正面看到的图形.【答案】A3. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学计数法表示为( ) A .8.2×105 B .82×105 C .8.2×106 D .82×107【考点】科学计数法【解析】科学计数法要写成A ×10n 的形式,其中1≤A <10. 【答案】C4. 观察下列图形,其中既是轴对称又是中心对称图形的是( )A B C D【考点】图形变换【解析】A 为中心对称,B 为轴对称,C 为中心对称,D 既是轴对称又是中心对称. 【答案】D5. 下列选项中,哪个不可以得到l 1∥l 2?( )A .∠1=∠2B .∠2=∠3C .∠3=∠5D .∠3+∠4=180°【考点】平行线和相交线【解析】A 选项∠1与∠2是同位角相等,得到l 1∥l 2;B 选项∠2与∠3是内错角相等,得到l 1∥l 2;D 选项∠3与∠4是同旁内角互补,得到l 1∥l 2;C 选项∠3与∠5不是同位角,也不是内错角,所以得不到l 1∥l 2,故选C 选项. 【答案】C6. 不等式组32521x x -<⎧⎨-<⎩的解集为( )A .1x >-B .3x <C .1x <-或3x >D .13x -<< 【考点】不等式组解集【解析】解325x -<得:1x >-;解21x -<得:3x <,“大小小大取中间”,因此不等式组的解集为:13x -<<. 【答案】D7. 一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x 双,列出方程( )A .10330%x =B .()110330%x -=C .()2110330%x -=D .()110330%x +=【考点】一元一次方程,销售利润问题【解析】根据这个月的球鞋数量列等式关系. 【答案】D8. 如图,已知线段AB ,分别以A 、B 为圆心,大于12AB 为半径作弧,连接弧的交点得到直线l ,在直线l 上取一点C ,使得∠CAB =25°,延长AC 至M ,求∠BCM 的度数( ) A .40° B .50 C .60° D .70° 【考点】尺规作图【解析】根据尺规作图可知CA =CB ,再利用三角形外角和求出∠BCM 的度数. 【答案】B9. 下列哪一个是假命题( )A .五边形外角和为360°B .切线垂直于经过切点的半径C .(3,-2)关于y 轴的对称点为(-3,2)D .抛物线242017y x x =-+对称轴为直线x =2【考点】命题判断【解析】(3,-2)关于y 轴的对称点为(-3,-2) 【答案】C10. 某共享单车前a 公里1元,超过a 公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a 应该要取什么数( ) A .平均数 B .中位数 C .众数 D .方差 【考点】统计知识点【解析】使用该共享单车50%的人是数据的中位数 【答案】B11. 如图,学校环保社成员想测量斜坡CD 旁一棵树AB 的高度,他们先在点C 处测得树顶B 的仰角为60°,然后在坡顶D 测得树顶B 的仰角为30°,已知斜坡CD 的长度为20m ,DE 的长为10m ,则树AB 的高度是( )mA .203B .30C .303D .40【考点】三角函数的实际应用【解析】在Rt △CDE 中,CD =20,DE =10,∴101202sin DCE ∠==,∴∠DCE =30°,∵∠ACB =60°,∴∠ABC =30°,∠DCB =90°,∵∠BDF =30°,∴∠DBF =60°,∠DBC =30°,∴BC =203,∴AB =30,即树AB 的高度是30m .【答案】B12. 如图,正方形ABCD 的边长是3,BP =CQ ,连接AQ 、DP 交于点O ,并分别与边CD 、BC 交于点F ,E ,连接AE ,下列结论:①AQ ⊥DP ;②OA 2=OE ·OP ;③AODOECF S S =四边形,④当BP =1时,1316tan OAE ∠=. 其中正确结论的个数是( ) A .1 B .2C .3D .4【考点】四边形综合,相似,三角函数【解析】①易证△DAP ≌△ABQ ,∴∠P =∠Q ,可得∠Q +∠QAB =∠P +∠QAB =90°,即AQ ⊥DP ,故①正确; ②根据射影定理得2OA OD OP =•,明显OD ≠OE ,故②错误; ③易证△QCF ≌△PBE ,可得DF =EC ,∴△ADF ≌△DEC ,∴ADFDOFDECDOFS SSS-=-即AODOECF SS =四边形,故③正确; ④当BP =1时,AP =4,可得△AOP ∽△DAP ,则43PB PA EB DA ==,34BE =,则134QE =,易证△QOE ∽△PAD ,则1345QO OE QE PA AD PD ===,解得135QO =,3920OE =,AO =5-QO =125,∴1316OE tan OAE OA ∠==,故④正确. 【答案】C第二部分 非选择题二、填空题(本题共4题,每小题3分,共12分) 13. 因式分解:34a a -= . 【考点】因式分解【解析】提公因式与平方差公式相结合进行因式分解 【答案】()()22a a a +-14. 在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 . 【考点】概率【解析】利用树状图或者表格求概率 【答案】2315. 阅读理解:引入新数i ,新数i 满足分配率,结合律,交换律,已知i 2=-1,那么()()11i i +-= . 【考点】定义新运算【解析】化简()()11i i +-=1-i 2=1-(-1)=2【答案】216. 如图,在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,Rt △MPN ,∠MPN =90°,点P 在AC 上,PM 交AB 与点E ,PN 交BC 于点F ,当PE =2PF 时,AP = .【考点】相似三角形【解析】如图,作PQ ⊥AB 于点Q ,PR ⊥BC 于点R ,由等量代换,易得∠QPE =∠RPF ,∴△QPE ∽△RPF ,∵PE =2PF ,∴PQ =2PR =2BQ ,显然△AQP ∽△ABC ,∴AQ :QP :AP =AB :BC :AC =3:4:5,记PQ =4x ,则AQ =3x ,AP =5x ,PR =BQ =2x ,AB =AQ +BQ =3x +2x =5x =3,解得x =35,∴AP =5x =5×35=3.【答案】3三、解答题(共52分)17. 计算:()22224518cos ---+-+【考点】实数运算【解析】根据实数运算法则进行计算即可 【答案】原式=222212222212232--⨯++=--++=18. 先化简,再求值:22224x x x x x x ⎛⎫+÷ ⎪-+-⎝⎭,其中x =-1. 【考点】分式化简求值【解析】先将分式进行化简再进行求值 【答案】原式=()()()()()()2222222x x x x x x x x x++-+-•+-=3x +2把x =-1代入得:原式=3×(-1)+2=-1.19. 深圳市某学校抽样调查,A 类学生骑共享单车,B 类学生坐公交车、私家车,C 类学生步行,D 类学生(其它),根据调查结果绘制了不完整的统计图. 类型 频数 频率 A 30 x B 18 0.15 C m 0.40 Dny(1)学生共 人,x = ,y = ; (2)补全条形统计图;(3)若该校共有2000人,骑共享单车的有 人.【考点】统计图【解析】根据样本容量、频数与频率三者之间的关系进行计算即可.【答案】(1)18÷0.15=120人,x =30÷120=0.25,m =120×0.4=48,y =1-0.25-0.4-0.15=0.2,n =120×0.2=24;(2)如下图;(3)2000×0.25=500.20. 一个矩形周长为56厘米,(1)当矩形面积为180平方厘米时,长宽分别是多少? (2)能围成面积为200平方厘米的矩形吗?请说明理由. 【考点】一元二次方程应用题【解析】(1)设边长为x 厘米,则宽为(28-x )厘米,根据矩形的面积公式列等式关系,求解一元二次方程即可;(2)假设反正的方法进行判断合理与否. 【答案】(1)解:设长为x 厘米,则宽为(28-x )厘米, 列方程:x (28-x )=180, 解方程得110x =,218x =,答:长为18厘米,宽为10厘米;(2)解:设长为x 厘米,则宽为(28-x )厘米, 列方程得:x (28-x )=200,化简得:2282000x x -+=,224284200160b ac ∆=-=-⨯=-<,方程无解,所以不能围成面积为200平方厘米的矩形.21. 如图,一次函数y =kx +b 与反比例函数my x=(x >0)交于A (2,4)、B (a ,1),与x 轴、y 轴分别交于点C 、D .(1)直接写出一次函数y =kx +b 的表达式和反比例函数my x=(x >0)的表达式; (2)求证:AD =BC .【考点】反比例函数与一次函数的综合【解析】(1)根据A 点求出反比例函数解析式,从而得到B 点坐标,再由A 、B 点坐标求出一次函数解析式;(2)通过勾股定理计算AD 与BC 的边长进行比较. 【答案】(1)将A (2,4)代入my x=中,得m =8, ∴反比例函数的解析式为8y x=, ∴将B (a ,1)代入8y x=中得a =8, ∴B (8,1),将A (2,4)与B (8,1)代入y =kx +b 中,得8124k b k b +=⎧⎨+=⎩,解得125k b ⎧=-⎪⎨⎪=⎩, ∴152y x =-+;(2)由(1)知,C 、D 两点的坐标为(10,0)、(0,5),如图,过点A 作y 轴的垂线与y 轴交于点E ,过B 作x 轴的垂线与x 轴交于点F , ∴E (0,4),F (8,0),∴AE =2,DE =1,BF =1,CF =2, ∴在Rt △ADE 和Rt △BCF 中,根据勾股定理得,AD =225AE DE +=, BC =225CF BF +=, ∴AD =BC .22. 如图,线段AB 是⊙O 的直径,弦CD ⊥AB 于点H ,点M 是CBD 上任意一点,AH =2,CH=4.(1)求⊙O的半径r的长度;(2)求s i n∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE HF•的值.【考点】圆、三角函数、三角形【解析】(1)连接OC,勾股定理计算边长;(2)根据圆周角定理将∠CMD转化为∠AOC 即可求得答案;(3)连接OM,构造△EHM∽△NHF,利用相似比进行求值.【答案】(1)连接OC,在Rt△COH中,CH=4,OH=r-2,OC=r,由勾股定理得:(r-2)2+42=r2,解得:r=5;(2)∵弦CD与直径AB垂直,∴12AD AC CD==,∴∠AOC=12∠COD,∵∠CMD=12∠COD,∴∠CMD=∠AOC,∴sin∠CMD=sin∠AOC,在Rt△COH中,s i n∠AOC=45OHOC=,即s i n∠CMD=45;(3)连接AM,则∠AMB=90°,F在Rt △ABM 中,∠MAB +∠ABM =90°, 在Rt △EHB 中,∠E +∠ABM =90°, ∴∠MAB =∠E , ∵BM BM =,∴∠MNB =∠MAB =∠E , ∵∠EHM =∠NHF , ∴△EHM ∽△NHF ,∴HE HMHN HF=, ∴HE ·HF =HM ·HN , ∵AB 与MN 相交于点H ,∴HM ·HN =HA ·HB =HA ·(2r -HA )=2×(10-2)=16, 即HE ·HF =16.23. 如图,抛物线22y ax bx =++经过A (-1,0),B (4,0),交y 轴于点C . (1)求抛物线的解析式(用一般式表示);(2)点D 为y 轴右侧抛物线上一点,是否存在点D 使得23ABC ABDS S ∆=,若存在请直接给出点D 坐标,若不存在请说明理由;(3)将直线BC 绕点B 顺时针旋转45°,与抛物线交于另一点E ,求BE 的长.【考点】二次函数综合【解析】(1)待定系数求解析式;(2)先求出ABC S ∆,设D (m ,213222m m -++)(m>0),再用含有m 的代数式表示ABDS,即可求出m 的值,从而得到D 点坐标;(3)过C点作CF ⊥BC ,交BE 于点F ,过点F 作y 轴的垂线交y 轴于点H ,构造△CHF ≌△BOC ,求得F 点坐标,即可进行求解.【答案】(1)由题意得2016420a b a b -+=⎧⎨++=⎩,解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩,∴213222y x x =-++;(2)依题意知:AB =5,OC =2,∴1125522ABC S AB OC ∆=⨯=⨯⨯=,∵23ABC ABD S S ∆=,∴315522ABD S =⨯=,设D (m ,213222m m -++)(m >0),∵11522ABD D S AB y ==,∴211315522222m m ⨯⨯-++=, 解得:m =1或m =2或m =-2(舍去)或m =5, ∴D 1(1,3)、D 2(2,3)、D 3(5,-3);(3)过C 点作CF ⊥BC ,交BE 于点F ,过点F 作y 轴的垂线交y 轴于点H ,∵∠CBF =45°,∠BCF =90°,∴CF =CB , ∵∠BCF =90°,∠FHC =90°,∴∠HCF +∠BCO =90°,∠HCF +∠HFC =90°,即∠HFC =∠OCB ,∵CHF COB HFC OCB FC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CHF ≌△BOC (AAS ), ∴HF =OC =2,HC =BO =4,∴F (2,6),∴易求得直线BE :y =-3x +12,联立213222312y x x y x ⎧=-++⎪⎨⎪=-+⎩, 解得15x =,24x =(舍去),故E (5,-3), ∴()()22543010BE -+--。
广东省深圳市中考数学试卷(含详细解析)

2017年广东省深圳市中考数学试卷一、选择题1.(3分)﹣2的绝对值是()A.﹣2 B.2 C.﹣ D.2.(3分)图中立体图形的主视图是()A. B. C.D.3.(3分)随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()A.8.2×105B.82×105 C.8.2×106D.82×1074.(3分)观察下列图形,其中既是轴对称又是中心对称图形的是()A.B.C.D.5.(3分)下列选项中,哪个不可以得到l1∥l2?()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°6.(3分)不等式组的解集为()A.x>﹣1 B.x<3 C.x<﹣1或x>3 D.﹣1<x<37.(3分)一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()A.10%x=330 B.(1﹣10%)x=330 C.(1﹣10%)2x=330 D.(1+10%)x=330 8.(3分)如图,已知线段AB,分别以A、B为圆心,大于AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()A.40°B.50°C.60°D.70°9.(3分)下列哪一个是假命题()A.五边形外角和为360°B.切线垂直于经过切点的半径C.(3,﹣2)关于y轴的对称点为(﹣3,2)D.抛物线y=x2﹣4x+2017对称轴为直线x=210.(3分)某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()A.平均数B.中位数C.众数D.方差11.(3分)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m.A .20B .30C .30D .4012.(3分)如图,正方形ABCD 的边长是3,BP=CQ ,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ ⊥DP ;②OA 2=OE•OP ;③S △AOD =S 四边形OECF ;④当BP=1时,tan ∠OAE=,其中正确结论的个数是( )A .1B .2C .3D .4二、填空题13.(3分)因式分解:a 3﹣4a= .14.(3分)在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .15.(3分)阅读理解:引入新数i ,新数i 满足分配律,结合律,交换律,已知i 2=﹣1,那么(1+i )•(1﹣i )= .16.(3分)如图,在Rt △ABC 中,∠ABC=90°,AB=3,BC=4,Rt △MPN ,∠MPN=90°,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当PE=2PF 时,AP= .三、解答题17.(5分)计算:|﹣2|﹣2cos45°+(﹣1)﹣2+.18.(6分)先化简,再求值:(+)÷,其中x=﹣1.19.(7分)深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.类型频数频率A30xB180.15C m0.40D n y(1)学生共人,x=,y=;(2)补全条形统计图;(3)若该校共有2000人,骑共享单车的有人.20.(8分)一个矩形周长为56厘米.(1)当矩形面积为180平方厘米时,长宽分别为多少?(2)能围成面积为200平方米的矩形吗?请说明理由.21.(8分)如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=(x>0)的表达式;(2)求证:AD=BC.22.(9分)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.23.(9分)如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC =S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.2017年广东省深圳市中考数学试卷参考答案与试题解析一、选择题1.(3分)(2017•深圳)﹣2的绝对值是()A.﹣2 B.2 C.﹣ D.【考点】15:绝对值.【分析】根据绝对值的定义,可直接得出﹣2的绝对值.【解答】解:|﹣2|=2.故选B.【点评】本题考查了绝对值的定义,关键是利用了绝对值的性质.2.(3分)(2017•深圳)图中立体图形的主视图是()A. B. C.D.【考点】U2:简单组合体的三视图.【分析】根据主视图是从正面看的图形解答.【解答】解:从正面看,共有两层,下面三个小正方体,上面有一个小正方体,在中间.故选A.【点评】本题考查了学生的思考能力和对几何体三种视图的空间想象能力.3.(3分)(2017•深圳)随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()A.8.2×105B.82×105 C.8.2×106D.82×107【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n 是负数.【解答】解:将8200000用科学记数法表示为:8.2×106.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.(3分)(2017•深圳)观察下列图形,其中既是轴对称又是中心对称图形的是()A.B.C.D.【考点】R5:中心对称图形;P3:轴对称图形.【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.【解答】解:A、是中心对称图形,不是轴对称图形,选项不符合题意;B、是轴对称图形,不是中心对称图形,选项不符合题意;C、是中心对称图形,不是轴对称图形,选项不符合题意;D、是中心对称图形,也是轴对称图形,选项符合题意.故选D.【点评】此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.5.(3分)(2017•深圳)下列选项中,哪个不可以得到l1∥l2?()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°【考点】J9:平行线的判定.【分析】分别根据平行线的判定定理对各选项进行逐一判断即可.【解答】解:A、∵∠1=∠2,∴l1∥l2,故本选项错误;B、∵∠2=∠3,∴l1∥l2,故本选项错误;C、∠3=∠5不能判定l1∥l2,故本选项正确;D、∵∠3+∠4=180°,∴l1∥l2,故本选项错误.故选C.【点评】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.6.(3分)(2017•深圳)不等式组的解集为()A.x>﹣1 B.x<3 C.x<﹣1或x>3 D.﹣1<x<3【考点】CB:解一元一次不等式组.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式3﹣2x<5,得:x>﹣1,解不等式x﹣2<1,得:x<3,∴不等式组的解集为﹣1<x<3,故选:D.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.7.(3分)(2017•深圳)一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()A.10%x=330 B.(1﹣10%)x=330 C.(1﹣10%)2x=330 D.(1+10%)x=330【考点】89:由实际问题抽象出一元一次方程.【分析】设上个月卖出x双,等量关系是:上个月卖出的双数×(1+10%)=现在卖出的双数,依此列出方程即可.【解答】解:设上个月卖出x双,根据题意得(1+10%)x=330.故选D.【点评】本题考查了由实际问题抽象出一元一次方程,理解题意找到等量关系是解决本题的关键.8.(3分)(2017•深圳)如图,已知线段AB,分别以A、B为圆心,大于AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()A.40°B.50°C.60°D.70°【考点】N2:作图—基本作图;KG:线段垂直平分线的性质.【分析】根据作法可知直线l是线段AB的垂直平分线,故可得出AC=BC,再由三角形外角的性质即可得出结论.【解答】解:∵由作法可知直线l是线段AB的垂直平分线,∴AC=BC,∴∠CAB=∠CBA=25°,∴∠BCM=∠CAB+∠CBA=25°+25°=50°.故选B.【点评】本题考查的是作图﹣基本作图,熟知线段垂直平分线的作法是解答此题的关键.9.(3分)(2017•深圳)下列哪一个是假命题()A.五边形外角和为360°B.切线垂直于经过切点的半径C.(3,﹣2)关于y轴的对称点为(﹣3,2)D.抛物线y=x2﹣4x+2017对称轴为直线x=2【考点】O1:命题与定理.【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.【解答】解:A、五边形外角和为360°是真命题,故A不符合题意;B、切线垂直于经过切点的半径是真命题,故B不符合题意;C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;故选:C.【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.10.(3分)(2017•深圳)某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()A.平均数B.中位数C.众数D.方差【考点】WA:统计量的选择.【分析】由于要使使用该共享单车50%的人只花1元钱,根据中位数的意义分析即可【解答】解:根据中位数的意义,故只要知道中位数就可以了.故选B.【点评】本题考查了中位数意义.解题的关键是正确的求出这组数据的中位数.11.(3分)(2017•深圳)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m.A.20B.30 C.30D.40【考点】TA:解直角三角形的应用﹣仰角俯角问题.【分析】先根据CD=20米,DE=10m得出∠DCE=30°,故可得出∠DCB=90°,再由∠BDF=30°可知∠DBE=60°,由DF∥AE可得出∠BGF=∠BCA=60°,故∠GBF=30°,所以∠DBC=30°,再由锐角三角函数的定义即可得出结论.【解答】解:在Rt△CDE中,∵CD=20m,DE=10m,∴sin∠DCE==,∴∠DCE=30°.∵∠ACB=60°,DF∥AE,∴∠BGF=60°∴∠ABC=30°,∠DCB=90°.∵∠BDF=30°,∴∠DBF=60°,∴∠DBC=30°,∴BC===20m,∴AB=BC•sin60°=20×=30m .故选B . 【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.12.(3分)(2017•深圳)如图,正方形ABCD 的边长是3,BP=CQ ,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ ⊥DP ;②OA 2=OE•OP ;③S △AOD =S 四边形OECF ;④当BP=1时,tan ∠OAE=,其中正确结论的个数是( )A .1B .2C .3D .4【考点】S9:相似三角形的判定与性质;KD :全等三角形的判定与性质;LE :正方形的性质;T7:解直角三角形.【分析】由四边形ABCD 是正方形,得到AD=BC ,∠DAB=∠ABC=90°,根据全等三角形的性质得到∠P=∠Q ,根据余角的性质得到AQ ⊥DP ;故①正确;根据相似三角形的性质得到AO 2=OD•OP ,由OD ≠OE ,得到OA 2≠OE•OP ;故②错误;根据全等三角形的性质得到CF=BE ,DF=CE ,于是得到S △ADF ﹣S △DFO =S △DCE ﹣S △DOF ,即S △AOD =S 四边形OECF ;故③正确;根据相似三角形的性质得到BE=,求得QE=,QO=,OE=,由三角函数的定义即可得到结论. 【解答】解:∵四边形ABCD 是正方形,∴AD=BC ,∠DAB=∠ABC=90°,∵BP=CQ ,∴AP=BQ ,在△DAP 与△ABQ 中,,∴△DAP ≌△ABQ ,∴∠P=∠Q ,∵∠Q +∠QAB=90°,∴∠P +∠QAB=90°,∴∠AOP=90°,∴AQ ⊥DP ;故①正确; ∵∠DOA=∠AOP=90,∠ADO +∠P=∠ADO +∠DAO=90°,∴∠DAO=∠P ,∴△DAO ∽△APO , ∴,∴AO 2=OD•OP ,∵AE >AB ,∴AE >AD ,∴OD ≠OE ,∴OA 2≠OE•OP ;故②错误;在△CQF 与△BPE 中, ∴△CQF ≌△BPE ,∴CF=BE ,∴DF=CE ,在△ADF 与△DCE 中,,∴△ADF ≌△DCE ,∴S △ADF ﹣S △DFO =S △DCE ﹣S △DOF ,即S △AOD =S 四边形OECF ;故③正确;∵BP=1,AB=3,∴AP=4,∵△AOP∽△DAP,∴,∴BE=,∴QE=,∵△QOE∽△PAD,∴,∴QO=,OE=,∴AO=5﹣QO=,∴tan∠OAE==,故④正确,故选C.【点评】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,三角函数的定义,熟练掌握全等三角形的判定和性质是解题的关键.二、填空题13.(3分)(2017•深圳)因式分解:a3﹣4a=a(a+2)(a﹣2).【考点】55:提公因式法与公式法的综合运用.【专题】44 :因式分解.【分析】首先提取公因式a,进而利用平方差公式分解因式得出即可.【解答】解:a3﹣4a=a(a2﹣4)=a(a+2)(a﹣2).故答案为:a(a+2)(a﹣2).【点评】此题主要考查了提取公因式法和公式法分解因式,熟练掌握平方差公式是解题关键.14.(3分)(2017•深圳)在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是.【考点】X6:列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所摸到1黑1白的情况,再利用概率公式即可求得答案.【解答】解:依题意画树状图得:∵共有6种等可能的结果,所摸到的球恰好为1黑1白的有4种情况,∴所摸到的球恰好为1黑1白的概率是:=.故答案为:.【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.解题时注意:概率=所求情况数与总情况数之比.15.(3分)(2017•深圳)阅读理解:引入新数i,新数i满足分配律,结合律,交换律,已知i2=﹣1,那么(1+i)•(1﹣i)=2.【考点】4F:平方差公式;2C:实数的运算.【专题】23 :新定义.【分析】根据定义即可求出答案.【解答】解:由题意可知:原式=1﹣i2=1﹣(﹣1)=2故答案为:2【点评】本题考查新定义型运算,解题的关键是正确理解新定义,本题属于基础题型.16.(3分)(2017•深圳)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt △MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF 时,AP=3.【考点】S9:相似三角形的判定与性质.【分析】如图作PQ⊥AB于Q,PR⊥BC于R.由△QPE∽△RPF,推出==2,可得PQ=2PR=2BQ,由PQ∥BC,可得AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=3,求出x即可解决问题.【解答】解:如图作PQ⊥AB于Q,PR⊥BC于R.∵∠PQB=∠QBR=∠BRP=90°,∴四边形PQBR是矩形,∴∠QPR=90°=∠MPN,∴∠QPE=∠RPF,∴△QPE∽△RPF,∴==2,∴PQ=2PR=2BQ,∵PQ∥BC,∴AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,∴2x+3x=3,∴x=,∴AP=5x=3.故答案为3.【点评】本题考查相似三角形的判定和性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.三、解答题17.(5分)(2017•深圳)计算:|﹣2|﹣2cos45°+(﹣1)﹣2+.【考点】2C:实数的运算;6F:负整数指数幂;T5:特殊角的三角函数值.【分析】因为<2,所以|﹣2|=2﹣,cos45°=,=2,分别计算后相加即可.【解答】解:|﹣2|﹣2cos45°+(﹣1)﹣2+,=2﹣﹣2×+1+2,=2﹣﹣+1+2,=3.【点评】本题考查了有关负整数指数、特殊的三角函数值、乘方等知识的计算,属于常考题型,此类计算题要细心,熟练掌握特殊角的三角函数值,明确实数的运算法则.18.(6分)(2017•深圳)先化简,再求值:(+)÷,其中x=﹣1.【考点】6D:分式的化简求值.【分析】根据分式的运算法则即可求出答案.【解答】解:当x=﹣1时,原式=×=3x+2=﹣1【点评】本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.19.(7分)(2017•深圳)深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.类型频数频率A30xB180.15C m0.40D n y(1)学生共120人,x=0.25,y=0.2;(2)补全条形统计图;(3)若该校共有2000人,骑共享单车的有500人.【考点】VC:条形统计图;V5:用样本估计总体;V7:频数(率)分布表.【分析】(1)根据B类学生坐公交车、私家车的人数以及频率,求出总人数,再根据频数与频率的关系一一解决即可;(2)求出m、n的值,画出条形图即可;(3)用样本估计总体的思想即可解决问题;【解答】解:(1)由题意总人数==120人,x==0.25,m=120×0.4=48,y=1﹣0.25﹣0.4﹣0.15=0.2,n=120×0.2=24,(2)条形图如图所示,(3)2000×0.25=500人,故答案为500.【点评】本题考查条形图、频率分布表、样本估计总体等知识,解题的关键是记住频率=,频率之和为1,属于中考常考题型.20.(8分)(2017•深圳)一个矩形周长为56厘米.(1)当矩形面积为180平方厘米时,长宽分别为多少?(2)能围成面积为200平方米的矩形吗?请说明理由.【考点】AD:一元二次方程的应用.【分析】(1)设出矩形的一边长为未知数,用周长公式表示出另一边长,根据面积列出相应方程求解即可.(2)同样列出方程,若方程有解则可,否则就不可以.【解答】解:(1)设矩形的长为x厘米,则另一边长为(28﹣x)厘米,依题意有x(28﹣x)=180,解得x1=10(舍去),x2=18,28﹣x=28﹣18=10.故长为18厘米,宽为10厘米;(2)设矩形的长为x厘米,则宽为(28﹣x)厘米,依题意有x(28﹣x)=200,即x2﹣28x+200=0,则△=282﹣4×200=784﹣800<0,原方程无解,故不能围成一个面积为200平方厘米的矩形.【点评】考查一元二次方程的应用;用到的知识点为:长方形的长=周长的一半﹣宽.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.21.(8分)(2017•深圳)如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=(x>0)的表达式;(2)求证:AD=BC.【考点】G8:反比例函数与一次函数的交点问题.【分析】(1)先确定出反比例函数的解析式,进而求出点B的坐标,最后用待定系数法求出直线AB的解析式;(2)由(1)知,直线AB的解析式,进而求出C,D坐标,构造直角三角形,利用勾股定理即可得出结论.【解答】解:(1)将点A(2,4)代入y=中,得,m=2×4=8,∴反比例函数的解析式为y=,将点B(a,1)代入y=中,得,a=8,∴B(8,1),将点A(2,4),B(8,1)代入y=kx+b中,得,,∴,∴一次函数解析式为y=﹣x+5;(2)∵直线AB的解析式为y=﹣x+5,∴C(10,0),D(0,5),如图,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,∴E(0,4),F(8,0),∴AE=2,DE=1,BF=1,CF=2,在Rt△ADE中,根据勾股定理得,AD==,在Rt△BCF中,根据勾股定理得,BC==,∴AD=BC.【点评】此题是反比例函数与一次函数交点坐标问题,主要考查了待定系数法,勾股定理,解(1)的关键是掌握待定系数法求函数的解析式,解(2)的关键是构造直角三角形.22.(9分)(2017•深圳)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.【考点】MR:圆的综合题.【分析】(1)在Rt△COH中,利用勾股定理即可解决问题;(2)只要证明∠CMD=△COA,求出sin∠COA即可;(3)由△EHM∽△NHF,推出=,推出HE•HF=HM•HN,又HM•HN=AH•HB,推出HE•HF=AH•HB,由此即可解决问题.【解答】解:(1)如图1中,连接OC.∵AB⊥CD,∴∠CHO=90°,在Rt△COH中,∵OC=r,OH=r﹣2,CH=4,∴r2=42+(r﹣2)2,∴r=5.(2)如图1中,连接OD.∵AB⊥CD,AB是直径,∴==,∴∠AOC=∠COD,∵∠CMD=∠COD,∴∠CMD=∠COA,∴sin∠CMD=sin∠COA==.(3)如图2中,连接AM.∵AB是直径,∴∠AMB=90°,∴∠MAB+∠ABM=90°,∵∠E+∠ABM=90°,∴∠E=∠MAB,∴∠MAB=∠MNB=∠E,∵∠EHM=∠NHFM∴△EHM∽△NHF,∴=,∴HE•HF=HM•HN,∵HM•HN=AH•HB,∴HE•HF=AH•HB=2•(10﹣2)=16.【点评】本题考查圆综合题、垂径定理、勾股定理、相似三角形的判定和性质、相交弦定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考压轴题.23.(9分)(2017•深圳)如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC =S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.【考点】HF:二次函数综合题.【分析】(1)由A、B的坐标,利用待定系数法可求得抛物线解析式;(2)由条件可求得点D到x轴的距离,即可求得D点的纵坐标,代入抛物线解析式可求得D点坐标;(3)由条件可证得BC⊥AC,设直线AC和BE交于点F,过F作FM⊥x轴于点M,则可得BF=BC,利用平行线分线段成比例可求得F点的坐标,利用待定系数法可求得直线BE解析式,联立直线BE和抛物线解析式可求得E点坐标,则可求得BE的长.【解答】解:(1)∵抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),∴,解得,∴抛物线解析式为y=﹣x2+x+2;(2)由题意可知C(0,2),A(﹣1,0),B(4,0),∴AB=5,OC=2,∴S△ABC=AB•OC=×5×2=5,∵S△ABC =S△ABD,∴S△ABD=×5=,设D(x,y),∴AB•|y|=×5|y|=,解得|y|=3,当y=3时,由﹣x2+x+2=3,解得x=1或x=2,此时D点坐标为(1,3)或(2,3);当y=﹣3时,由﹣x2+x+2=﹣3,解得x=﹣2(舍去)或x=5,此时D点坐标为(5,﹣3);综上可知存在满足条件的点D,其坐标为(1,3)或(2,3)或(5,﹣3);(3)∵AO=1,OC=2,OB=4,AB=5,∴AC==,BC==2,∴AC2+BC2=AB2,∴△ABC为直角三角形,即BC⊥AC,如图,设直线AC与直线BE交于点F,过F作FM⊥x轴于点M,由题意可知∠FBC=45°,∴∠CFB=45°,∴CF=BC=2,∴=,即=,解得OM=2,=,即=,解得FM=6,∴F(2,6),且B(4,0),设直线BE解析式为y=kx+m,则可得,解得,∴直线BE解析式为y=﹣3x+12,联立直线BE和抛物线解析式可得,解得或,∴E(5,﹣3),∴BE==.【点评】本题为二次函数的综合应用,涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中求得D点的纵坐标是解题的关键,在(3)中由条件求得直线BE的解析式是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,有一定的难度.。
2017年深圳市中考数学真题试卷及详细答案(word版))

2017年广东省深圳市中考数学试卷一、选择题1.(3分)﹣2的绝对值是()A.﹣2 B.2 C.﹣D.2.(3分)图中立体图形的主视图是()A.B.C.D.3.(3分)随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()A.8.2×105B.82×105C.8.2×106D.82×107 4.(3分)观察下列图形,其中既是轴对称又是中心对称图形的是()A.B.C.D.5.(3分)下列选项中,哪个不可以得到l1∥l2?()A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°6.(3分)不等式组的解集为()A.x>﹣1 B.x<3 C.x<﹣1或x>3 D.﹣1<x<3 7.(3分)一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()A.10%x=330 B.(1﹣10%)x=330C.(1﹣10%)2x=330 D.(1+10%)x=3308.(3分)如图,已知线段AB,分别以A、B为圆心,大于AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为()A.40°B.50°C.60°D.70°9.(3分)下列哪一个是假命题()A.五边形外角和为360°B.切线垂直于经过切点的半径C.(3,﹣2)关于y轴的对称点为(﹣3,2)D.抛物线y=x2﹣4x+2017对称轴为直线x=210.(3分)某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()A.平均数B.中位数C.众数D.方差11.(3分)如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m.A.20B.30 C.30D.4012.(3分)如图,正方形ABCD 的边长是3,BP=CQ ,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ ⊥DP ;②OA 2=OE•OP ;③S △AOD =S 四边形OECF ;④当BP=1时,tan ∠OAE=,其中正确结论的个数是( )A .1B .2C .3D .4二、填空题13.(3分)因式分解:a 3﹣4a= .14.(3分)在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是 .15.(3分)阅读理解:引入新数i ,新数i 满足分配律,结合律,交换律,已知i 2=﹣1,那么(1+i )•(1﹣i )= .16.(3分)如图,在Rt △ABC 中,∠ABC=90°,AB=3,BC=4,Rt △MPN ,∠MPN=90°,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当PE=2PF 时,AP= .三、解答题17.(5分)计算:|﹣2|﹣2cos45°+(﹣1)﹣2+.18.(6分)先化简,再求值:(+)÷,其中x=﹣1.19.(7分)深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.类型频数频率A30xB180.15C m0.40D n y(1)学生共人,x=,y=;(2)补全条形统计图;(3)若该校共有2000人,骑共享单车的有人.20.(8分)一个矩形周长为56厘米.(1)当矩形面积为180平方厘米时,长宽分别为多少?(2)能围成面积为200平方米的矩形吗?请说明理由.21.(8分)如图,一次函数y=kx+b与反比例函数y=(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=(x>0)的表达式;(2)求证:AD=BC.22.(9分)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.23.(9分)如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC =S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.。
2017深圳中考数学试题及答案解析(K12教育文档)

(完整word版)2017深圳中考数学试题及答案解析(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)2017深圳中考数学试题及答案解析(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)2017深圳中考数学试题及答案解析(word版可编辑修改)的全部内容。
2016年广东省深圳市中考数学试卷第一部分选择题(本部分共12小题,每小题3分,共36分。
每小题给出4个选项,其中只有一个选项是正确的)1.下列四个数中,最小的正数是()A.-1 B。
0 C. 1 D。
22.把下列图形折成一个正方体的盒子,折好后与“中”相对的字是( )A.祝 B.你 C。
顺 D.利3.下列运算正确的是()A。
8a—a=8 B。
(-a)4=a4C。
a3×a2=a6 D.(a-b)2=a2-b24.下列图形中,是轴对称图形的是( )5.据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学计数法表示为( )A。
0.157×1010 B.1.57×108 C.1。
57×109 D.15.7×108 6.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是()A. ∠2=60° B。
∠3=60° C. ∠4=120° D. ∠5=40°7.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动.则第3小组被抽到的概率是( )A.71 B 。
2017年深圳市中考数学试卷含答案解析(Word版)
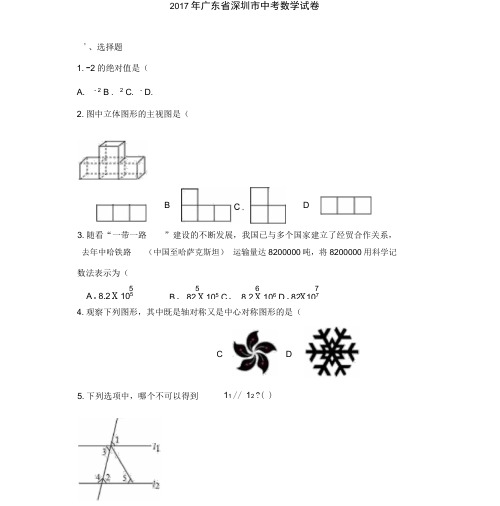
2017年广东省深圳市中考数学试卷'、选择题1.-2的绝对值是(A. - 2 B . 2 C. - D.2.图中立体图形的主视图是(3.随看“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为(5 A . 8.2 X 1055 6 7B . 82 X 105C . 8.2 X 106D . 82X1074.观察下列图形,其中既是轴对称又是中心对称图形的是(5.下列选项中,哪个不可以得到11 // 12?( )B .D. C.D.A. / 1= Z 2B. Z 2= Z 3C .Z 3= Z 5D . Z 3+ Z 4=180 °6.不等式组1Sift MJb... 的解集为7.—球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程()A. 10%x=330B.(1 —10%)x=330C. (1 —10%)2x=330 D . (1+10% )x=3308如图,已知线段AB,分别以A、B为圆心,大于AB为半径作弧,连接弧,dpql的交点得到直线I,在直线I上取一点C,使得/ CAB=25 ° ,延长AC至M,求/ BCM的度数为()A. 40 °B. 50 ° C . 60 ° D . 70 °9 •下列哪一个是假命题()A •五边形外角和为360 °B•切线垂直于经过切点的半径C.(3, —2)关于y轴的对称点为(-3, 2)D .抛物线y=x2—4x+2017对称轴为直线x=210 .某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数()A .平均数B .中位数C .众数D .方差11•如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点CB 60 ° D B 30 °处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡CD的长度为20m,DE的长为10cm,则树AB的高度是()m .A. 20豳・B. 30C. 30 逐D. 4012 •如图,正方形ABCD的边长是3, BP=CQ,连接AQ , DP交于点O,并分别与边CD , BC交于点F , E,连接AE,下列结论:①AQ丄DP :②OA 2=OE?OP ;③S△ AOD=S四边形OECF;④当BP=1时,tan Z OAE= ,其中正确结论的个数是()二、填空题313 .因式分解:a - 4a=14 .在一个不透明的袋子里,有2个黑球和1个白球,除了颜色外全部相同,任意摸两个球,摸到1黑1白的概率是15 •阅读理解:引入新数i,新数i满足分配律,结合律,交换律,已知i2=- 1,那么(1+i) ? (1 - i)=16 .如图,在Rt△ ABC 中,Z ABC=90 ° , AB=3 , BC=4 , Rt△ MPN , Z MPN=90点P在AC上,PM交AB于点E, PN交BC于点F,当PE=2PF时,AP=二、解答题17 •计算:一 -2 - 2cos45 ° (- 1)—2+ _ .裨| +诉:18.先化简,再求值:(,其中x= - 1 .19 .深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.类型频数频率A30xB180.15C m0.40D n y20 .一个矩形周长为56厘米.(1) 当矩形面积为180平方厘米时,长宽分别为多少?(2) 能围成面积为200平方米的矩形吗?请说明理由.21 .如图,一次函数y=kx +b与反比例函数y= ' (x>0)交于A (2, 4), B (a, X1), 与x轴,y轴分别交于点C , D.(1)直接写出一次函数y=kx +b的表达式和反比例函数y= (x>0)的表达式;CD丄AB于点H,点M是i上任意一(1 )求。
2017深圳中考数学试题及答案解析

2016年省市中考数学试卷第一部分 选择题(本部分共12小题,每小题3分,共36分。
每小题给出4个选项,其中只有一个选项是正确的)1.下列四个数中,最小的正数是( )A .—1 B. 0 C. 1 D. 2 2.把下列图形折成一个正方体的盒子,折好后与“中”相对的字是( )A .祝 B.你 C.顺 D.利 3.下列运算正确的是( )A.8a-a=8B.(-a)4=a 4C.a 3×a 2=a 6D.(a-b )2=a 2-b 2 4.下列图形中,是轴对称图形的是( )5.据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学计数法表示为( )A.0.157×1010B.1.57×108C.1.57×109D.15.7×1086.如图,已知a ∥b,直角三角板的直角顶点在直线b 上,若∠1=60°,则下列结论错误的是( )A. ∠2=60°B. ∠3=60°C. ∠4=120°D. ∠5=40° 7.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动。
则第3小组被抽到的概率是( ) A.71 B. 31 C. 211 D. 1018.下列命题正确是( )A.一组对边平行,另一组对边相等的四边形是平行四边形B.两边及一角对应相等的两个三角形全等C.16的平方根是4D.一组数据2,0,1,6,6的中位数和众数分别是2和69.施工队要铺设一段全长2000米,的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米。
设原计划每天施工x 米,则根据题意所列方程正确的是( )A.25020002000=+-x x B.22000502000=-+x x C.25020002000=--x x D.22000502000=--xx10.给出一种运算:对于函数nx y =,规定1-=n nx y 丿。
广东省深圳市2017届中考数学复习-多结论几何综合题专题

、单选题 多结论几何综合题专题试卷1、如图,△ ABC 和厶CDE 均为等腰直角三角形,点 B, C, D 在一条直线上,点 M 是 Of*AE 的中点,下列结论:①tan / AEC= :②S △ABC +S ^CD ^S △ACE ;③BML DM ④BM=DM 正 4、如图,把一张长方形纸片ABCD 沿对角线BD 折叠,使C 点落在E 处,BE 与AD相交于点F ,下列结论:①BD=A D+A £;②厶 ABF^A EDF ③二二=三④AD=BD?cos4° . AB AF 其中正确的一组是( 确结论的个数是( A 、1 个B 、C 、3 个D 、 A 、B、 C 、D、 ①② ②③ ①④ ③④ Rt △ ABC 中,AB=AC D E 是斜边 BC 上两点,且/ DAE=45,将△ ADC 2、如图,在 绕点A 顺时针旋转90°后,得到△ AFB 连接 EF,下列结论: jar ) ①厶AED^A AEF ②炭=总;③厶ABC 的面积等于四边形 AFBD 的面积; ④B F+D C UD F ⑤BE+DC=DEI 中正确的是 ( 5、如图,已知正方形 ABCD 勺边长为4,点E 、F 分别在边 AB BC 上,且AE=BF=1… … … a …CE DF 交于点 O .下列结论:①/ DOC=9°,② OC=O ,③tan / OCD= ,④S △ODC F SA 、 B、C 、D、 ①②④ ③④⑤ ①③④ ①③⑤ 四边形BEOF中, A 、1个 C 、3个正确的有(BDB3、如图,将等边厶ABC 沿射线 下列结论: ①AD= BC;②BD AC 互相平分; 数是( A 、 1 BC 向右平移到△ DCE 的位置,连接AD BD , ③四边形 ACED 是菱形;④BD£DE 其中正确的个 6、如图,已知正方形 延长EF 交AB 于G 连接DG ③厶GD OA BEF ④S △ BEF = A 、1 B 、2 C 、3ABCD 勺边长为12, BE=EC 将正方形边 CD 沿 DE 折叠到DF , 现在有如下 4个结论:①△ ADG2A FDG ②GB=2A0 .在以上4个结论中,正确的有()7、如图,?ABCD的对角线ACBD交于点O,AE平分/ BAD交BC于点E,且/ ADC=60 ,AB^BC,连接OE 下列结论:①/CAD=30 ;② S ?ABC=AB?AC③OB=AB ④OE= BC, 成立的个数有()A、4A、1个B 、2个C、3个D 、4个11、如图,在Rt△ ABC中,AB=CB BC L AC 把厶ABC折叠,使AB落在AC上,点B 与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE EF.下列结论:①tan / ADB=2②图中有4对全等三角形;③若将△ DEF沿EF折叠,则点D不一定落在AC上;④BD=BF⑤S四边形DFO=S A AOF ,上述结论中正确的个数是(8如图,AD>^ABC的角平分线,DE DF分别是△ ABD和厶ACD的高,得到下列四个结论: A 、① OA=OD ② ADL EF;③当/A=90°时,四边形AEDF是正方B、形; ④ AE+DF=AF+DE 其中正确的是(A、②③B、②④C、①③④C、D、12、1个2个3个4个如图,将等边厶ABC绕点D、②③④列结论:①AC=AD②BD L AC③四边形其中正确的个数是()9、如图, G E分别是正方形ABCD的边AB, BC的点,且AG=CE AE! EF, AE=EF A 、现有如下结论:①B E4 GE ②厶AGE^A ECF ③/ FCD=45 ; ④厶GB0A ECH 其中,正B、)ACED是菱形.C顺时针旋转C、D、确的结论有( )A、1个B、2个C、3个D、4个10、如图,PA=PBOEL PA OFLPB则以下结论:①OP是/ APB的平分线;13、23女口图,CB=CA/ ACB=90 ,点D在边BC上为正方形,过点F作FGL CA交CA的延长线于点(与B C不重合),四边形ADEFG连接FB,交DE于点Q 给出以下结论:①AC=FG②S △ FAB:S 四边形CBF=1 : 2;③/ ABC M ABF ④AD2=FQ?AC②PE=P®CA=BD④CD// AB其中正确的有()个.A 、 2B 、 3C 、 4D 、 516、如图,在正方形 ABCD 中, E 、F 分别为BC CD 的中点,连接 AE BF 交于点G, 将A BCF 沿BF 对折,得到△ BPF 延长 FP 交BA 延长线于点 Q,下列结论正确的个其中正确的结论的个数是( )③S A AGD =S^OGD ④四边形 AEFG 是菱形;⑤BE=20G ⑥若 S A OG =1 ,则正方形ABCC 的14、如图,矩形 ABCD 中, O 为AC 中点,过点 0的直线分别与 AB CD 交于点E 、F , 连结BF 交AC 于点 M 连结 DE BO 若/ COB=60 , FO=FC 则下列结论:①FB 垂△AOE: S A BCM =2 : 3 . 其中正确结论的个数是( 直平分 0C ②厶E0B2A CMB ③DE=EF ④S数是()①AE=BF ② AE! BF ;③ sin / BQP=A 、4B 、3C 、2D、14:④S 四边形 ECF (=2S BGE .A 、4个B 、 3个C 、 2个D 、 1个 15、( 2016?攀枝花)如图,正方形纸片 ABCD 中,对角线AC BD 交于点0,折叠 正方形纸片ABCD 使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后折痕 DE分别交 AB AC 于点E 、G,连结GF,给出下列结论: ①/ ADG=22.5 ;②tan / AED=217、如图所示,抛物线 y=ax 2+bx+c (a *0)与x 轴交于点 A (- 2, 0)、B( 1, 0), 直线x= - 0.5与此抛物线交于点 C,与x 轴交于点M 在直线上取点 D,使MD=M , 连接AC BC AD BD,某同学根据图象写出下列结论: ① a - b=0;② 当-2v x v 1 时,y >0; ③ 四边形ACBD 是菱形; ④ 9a - 3b+c > 0面积是6+4 ,其中正确的结论个数为(B 、 2C 、 3D 、A 、1A 、①②③ B 、②③④C 、 ①②④D 、①③④B 、 C、 D 、 ①②④ ①③④ ①②③ 18、如图,正方形 ABCD 中, AB=6,点E 在边CD 上,且 CE=2DE 将厶ADE 沿AE 对 折至△ AFE 延长 EF 交边BC 于点G,连结 AG CF.下列结论:①△ AB®A AFQ ②BG=GC ③EG=DE+BG ④AG/ CF ;⑤S △FGC =3.6 .其中正确结论的个数是( )B 、 3C 、 4D 、5 CF 19、如图,AB 是OO 的直径,弦 CD£AB 于点G,点F 是CD 上一点,且满足亍 = ,连接AF 并延长交OO 于点E ,连接AD, DE,若CF=2 AF=3,给出下列结论: ①厶 AD MA AED ② FG=2 ③tanE= ④S △DE =4,其中正确的是(20、如图,在OO 中,AB 是直径,点D 是OO 上一点,点C 是弧AD 的中点,弦CELAB 于点E ,过点D 的切线交EC 的延长线于点 G 连接AD 分别交CE CB 于点P 、Q 连接AC 给出下列结论:①/ DAC M ABC ②AD=CB ③点 ④AC f =AE?AB ⑤CB// GD 其中正确的结论是( )A 、①③⑤B 、②④⑤ C 、①②⑤ D 、①③④答案解析部分P 是厶ACQ 的外心; GA £0 BAB a XC b D一、单选题1、【答案】D【考点】等腰三角形的性质,梯形中位线定理,锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ ABS A CDE的对应边成比例知-二’2.C知,十云=77;b;然后由直角三角形中的正切函数,得tan / AEC^r ,再由等量代换求得tan / AEC= ;②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2>2ab ( a=b时取等号)解答;③、④通过作辅助线MN构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答. 【解答】解:•••△ ABC和厶CDE均为等腰直角三角形,••• AB=BC CD=DE•••/ BAC M BCA M DCE M DEC=45 ,•••/ ACE=90 ;•/△ABC^A CDE••- 一汀「一「JAC①• tan / AEC=-• tan / AEC= ;故本选项正确;| 2 | 2 | 2②.「S A ABC= a , S A CD :梯形ABDS A ABC+S^CDE=— (a +b)》ab ( a=b 时取等号),•S △ABc+S\CDE》S A ACE;故本选项正确;④过点M作MN垂直于BD垂足为N「•点M是AE的中点,则MN为梯形中位线,•N为中点,•△ BMD为等腰三角形,• BMkDM故本选项正确;③又MN= (AB+ED)= ( BC+CD)•••/ BMD=90 ,即BML DM故本选项正确.故选D.【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点•在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.2、【答案】C【考点】全等三角形的判定,勾股定理,相似三角形的判定,旋转的性质【解析】【分析】①根据旋转的性质知/ CAD M BAF AD=AF因为/ BAC=90 , / DAE=45,所以/ CAD M BAE=45,可得/ EAF=45 =M DAE 由此即可证明△AEF^A AED②当△ ABE^A ACD时,该比例式成立;③根据旋转的性质,△ AD QA ABF进而得出厶ABC 的面积等于四边形AFBD的面积;④据①知BF=CD EF=DE / FBE=90,根据勾股定理判断.⑤根据①知道△ AEF^A AED得CD=BF DE=EF由此即可确定该说法是否正确;【解答】①根据旋转的性质知/ CAD M BAF AD=AF•••/ BAC=90,/ DAE=45 ,•••/ CAD M BAE=45 .•••/ EAF=45 ,•△AED^A AEF;故本选项正确;②••• AB=AC•M ABE M ACD•当/ BAE M CAD 时,△ABE^A ACD•坐型= ;当/ BA字/ CAD时,△ABE与A ACD不相似,即工卞7;•••此比例式不一定成立;故本选项错误;③根据旋转的性质知△ AD QA AFB•S △ABC=S^ABD+S A ABF=S四边形AFBD , 即三角形ABC的面积等于四边形AFBD的面积; 故本选项正确;④•••/ FBE=45 +45° =90°•BE2+BF2=EF2 ,•••△ ADC绕点A顺时针旋转90°后,得到△ AFB•••△AFB^A ADC•BF=CD又••• EF=DE•BE2+DC:=D^ ,故本选项正确;⑤根据①知道△ AEF^A AED得CD=BF DE=EF•BE+DC=BE+BF DE=EF 即BE+DO DE,故本选项错误;综上所述,正确的说法是①③④;故选C.【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识,解题时注意旋转前后对应的相等关系.3、【答案】D【考点】等边三角形的性质,菱形的判定与性质,平移的性质【解析】【解答】•••△ ABC △ DCE是等边三角形,•/ ACB=M DCE= 60° ,AC=CD , •/ ACD= 180°—M ACB-M DCE= 60°,「.A ACD 是等边三角形,• AD= AC= BC , 故①正确;由①可得A» BC , •/ AB= CD , •四边形ABCD是平行四边形,• BD AC互相平分,故②正确;由①可得AD= AC= CE= DE ,故四边形ACED是菱形,即③正确;•••四边形ACED是菱形,• ACLBD , •/ AC// DE ,• /BDE=M COD= 90°,「. B D L DE , 故④正确;综上可得①②③④正确,共4个,故选D.【分析】先求出/ ACD= 60°,继而可判断△ ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;根据①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC L BD ,再根据平移后对应线段互相平行可得/ BDE=M COD= 90°,进而判断④正确.4、【答案】B【考点】勾股定理,翻折变换(折叠问题),相似三角形的判定与性质,特殊角的三角函数值【解析】【解答】①•••△ ABD为直角三角形,• BD2=A D+A B ,不是BD=AD+A B", 故说法错误;②根据折叠可知:DE=CD=AB M A=M E,M AFB=Z EFD •△ ABF^A EDF 故说法正确;③根据②可以得到△ ABF^A EDF • H7 =,故说法正确;④在Rt△ ABD 中,M AD字45°, • AD^ BD?COS45 ,故说法错误.所以正确的是②③.故选B.【分析】①直接根据勾股定理即可判定是否正确;②利用折叠可以得到全等条件证明△ ABF^A EDF;③利用全等三角形的性质即可解决问题;④在Rt△ ABD中利用三角函数的定义即可判定是否正确•此题主要考查了折叠问题,也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义, 它们的综合性比较强,对于学生的综合能力要求比较高,平时加强训练.5、【答案】C【考点】全等三角形的判定与性质,勾股定理,正方形的性质,锐角三角函数的定义【解析】【解答】解:•••正方形ABCD勺边长为4,••• BC=CD=4 / B=Z DCF=90 ,•/ AE=BF=1•BE=CF=4 1=3, 在厶EBC和厶FCD中,i BC=CDI BE = CF•••△ EBC^A FCD( SAS ,•••/ CFD M BEC•••/ BCE y BEC M BCE y CFD=90 ,•••/ DOC=90 ;故①正确;若OC=OE•••DF丄EC• CD=DE•/ CD=A B DE(矛盾),故②错误;•••/ OCD乂CDF=90,/ CDF f DFC=90 ,•••/ OCD W DFC• tan / OCD=ta M DFC= 士= ,故③正确;•/△EBC^A FCD•・S △EBC=S\FCD ,•S △EBC- S A FO(=S\FCD— S^FOC , 即S^OD=S四边形BEOF • 故④正确.故选C.【分析】由正方形ABCD勺边长为4 , AE=BF=1利用SAS易证得△ EBC^^ FCD然后全等三角形的对应角相等,易证得①/ DOC=90正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得/ OCD N DFC即可求得③正确;由①易证得④正确.6、【答案】C【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】由折叠可知,DF=DC=DA / DFE2 C=90 ,•••/ DFG M A=90°,•△ ADG^^ FDG ①正确;••正方形边长是•BE=EC=EF=6 设AG=FG=x 贝U 由勾股定理得:即:(x+6)2=62+ (12 —x)解得:x=4• AG=GF=4 BG=8 BG=2AG ②正确;BE=EF=6 △ BEF是等腰三角形,易知△ GED不是等腰三角形,③错误;1 EF 6 7^S A GBE= X 6X 8=24, S A BEF=亍?S A GBE= = ,④正确.故选:C.【分析】根据正方形的性质和折叠的性质可得AD=DF / A=Z GFD=90,于是根据“HL'判定△ ADG^^ FDG 再由GF+GB=GA+GB=12EB=EF △ BGE为直角三角形,可通过勾股定理列方程求出AG=4 BG=8进而求出厶BEF的面积,再抓住△ BEF是等腰三角形,而△ GED显然不是等腰三角形,判断③是错误的.7、【答案】C【考点】等边三角形的判定与性质,含30度角的直角三角形,平行四边形的性质【解析】【解答】•••四边形ABCD是平行四边形,•••/ ABC M ADC=60 ,12,EG=x+6 BG=12- x, E G=B£+B G ,2/ BAD=120 AE 平分/ BAD •/ BAE M EAD=60 ABE 是等边三角形,•AE=AB=B, •/ AB=£B C,• A E J BC,:M BAC=90,•/ CAD=30,故①正确;••• ACL AB z.S ?ABC=AB?AC故②正确,•/ AB寺BC OB= BD,v BD> BC, • AB^ OB 故③错误;:CE=BE CO=OA•••0E= AB • OE= BC,故④正确.故选:C.【分析】由四边形ABCD是平行四边形,得到/ ABC M ADC=60 , M BAD=120 ,根据AE平分/ BAD得到/ BAE M EAD=60推出△ ABE 是等边三角形,由于AB= BC,得到AE= BC,得到△ ABC是直角三角形,于是得到/ CAD=30 ,故①正确;由于AC L AB得到S ABC=AB?AC故②正确,根据AB= BC, 0B= BD且BD>BC,得到AB^ OB故③错误;根据三角形的中位线定理得到0E= AB,于是得到0E= BC,故④正确.&【答案】D【考点】全等三角形的判定与性质,角平分线的性质,正方形的判定【解析】【解答】如果OA=OD则四边形AEDF是矩形,M A=90°,不符合题意,•①不正确;••• AD是厶ABC的角平分线,•/ EAD M FAD在厶AED 和厶AFD中,(ZEAD= /FADj ZAFD = 90°•••△ AED^A FD (AAS , • AE=AF DE=DF〔AD—AD/ AE =AF• AE+DF=AF+DE「.④正确;在厶AEO 和厶AFO 中,■- ■「:I•△ AEZ A AF0( SAS , • EO=FO 又:AE=AF • AO 是EF 的中垂线,• AD L EF,•••②正确;•••当/ A=90°时,四边形AEDF的四个角都是直角,•四边形AEDF是矩形,又T DE=DF •四边形AEDF是正方形,.••③正确.综上,可得正确的是:②③④.故选:D.【分析】①如果OA=OD则四边形AEDF是矩形,M A=90°,不符合题意,所以①不正确.②首先根据全等三角形的判定方法,判断出△ AED^A AFD AE=AF DE=DF然后根据全等三角形的判定方法,判断出△ AEO^A AFO即可判断出AD L EF.③首先判断出当/ A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形, 然后根据DE=DF判断出四边形AEDF是正方形即可.④根据厶AED^A AFD判断出AE=AF DE=DF即可判断出AE+DF=AF+D成立,据此解答即可.9、【答案】B【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质【解析】【解答】•••四边形ABCD是正方形,•••/ B=M DCB=90 , AB=BC :AG=CE• BG=BE 由勾股定理得:BE= GE •••①错误;T BG=BE / B=90°,•M BGE M BEG=45 , AGE=135 , GAE M AEG=45 , •/ AE! EF,•M AEF=90 , BEG=45 , AEG M FEC=45 , GAE M FEC\G=CE在厶GAE和厶CEF中* ZG怔二ZCEF •△ GAE^A CEF •••②正确;AE=EFL•M AGE M ECF=135 , FCD=135 - 90° =45°, •••③正确;T M BGE M BEG=45 , M AEG M FEC=45 , •/ FEG 45°, •△ GBE 和厶ECH不相似,•④错误;即正确的有2个•故选B.【分析】根据正方形的性质得出M B=M DCB=90 , AB=BC求出BG=BE根据勾股定理得出BE= GE即可判断①;求出M GAE M AEG=45 ,推出M GAE M FECr根据SAS推出厶GAE^A CEF即可判断②;求出M AGE M ECF=135 ,即可判断③;求出M FEG45°,根据相似三角形的判定得出△ GBE 和A ECH不相似,即可判断④.10、【答案】A【考点】全等三角形的判定与性质,圆心角、弧、弦的关系,相似三角形的判定与性质【解析】【解答】连接OR OC OA OD OB CD AB.T PC?PA=PD?PB相交弦定理),PA=PB(已知),••• PC=PD「. AC=BD 在厶AOC 和厶BOD中,•••/ AOC M BOD(等弦对等角),OA=OB半径),OD=OC半径),•△ AO QA BOD•••③CA=BD OE=OF 又T OEL PA OF L PB•••①OP是/ APB的平分线;.••②PE=PF在厶PCD和厶PAB中,PC: PA=PD PB/ DPC M BPA PC SA PAB PDC=PB A・••④CD// AB综上所述,①②③④均正确,故答案选 A.【分析】①通过证明△ AO QA BOD再根据全等三角形的对应高相等求得OE=OF再根据角平分线的性质证明OP是/APB的平分线;②由角平分线的性质证明PE=PF③通过证明△ AO QA BOD再根据全等三角形的对应边相等求得CA=BD④通过证明厶PCDo^ PAB再根据相似三角形的性质对应角相等证得/ PDC=PBA然后由平行线的判定得出结论CD// AB 11、【答案】C【考点】全等三角形的判定与性质,翻折变换(折叠问题),锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE而DC> DE •- DC> BD, • tan / AD申2 , 故①错误;②图中的全等三角形有厶ABF^A AEF, △ ABD^A AED △ FBD^A FED (由折叠可知)•/ OBL AC AOB M COB=90 ,在Rt △ AOB和Rt △ COB中,AB="CB" ,BO=BO ,• Rt△ AOB2 Rt△ COB( HL),则全等三角形共有4对,故②正确;③••• AB=CB BOL AC 把厶ABC 折叠,•••/ ABO M CBO=45 , / FBD2 DEF•••/ AEF=/ DEF=45,•将△ DEF沿EF折叠,可得点D一定在AC上 ,故③错误;④••• OBLAC 且AB=CB• BO为/ ABC 的平分线,即/ ABO M OBC=45 ,由折叠可知,AD是/ BAC的平分线,即/ BAF=22.5°,又•••/BFD为三角形ABF的外角,•M BFD M ABO M BAF=67.5°,易得/ BDF=180 -45° -67.5 ° =67.5 ° ,•M BFD M BDF• BD=BF故④正确;⑤连接CF, •/△ AOF和A COF等底同高,•S △AOF=S^COF ,TM AEF M ACD=45 ,• EF// CD•・S △EFD=S\EFC ,=S^COF ,•・S四边形DFO•S 四边形DFO=S^AOF ,故⑤正确;故正确的有3个.故选C.12、【答案】D【考点】等边三角形的性质,菱形的判定,旋转的性质【解析】【解答】解:T将等边△ ABC绕点C顺时针旋转120°得到△ EDC•M ACE=120 , M DCE M BCA=60 , AC=CD=DE=CE•M ACD=120 - 60°=60°,•△ ACD是等边三角形,• AC=AD AC=AD=DE=CE•四边形ACED是菱形,T将等边△ ABC绕点C顺时针旋转120°得到△ EDC AC=AD• AB=BC=CD=AD•四边形ABCD是菱形,• BDL AC •①②③都正确,故选D.【分析】根据旋转和等边三角形的性质得出M ACE=120 , M DCE M BCA=60 , AC=CD=DE=CE求出厶ACD是等边三角形,求出AD=AC根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出ACL BD本题考查了旋转的性质,菱形的性质和判定,等边三角形的性质和判定的应用,能灵活运用知识点进行推理是解此题的关键.13、【答案】D【考点】全等三角形的判定与性质,矩形的判定与性质,正方形的性质,相似三角形的判定与性质,等腰直角三角形【解析】【解答】解::•四边形ADEF为正方形,•••/ FAD=90 , AD=AF=EF•••/ CAD# FAG=90 ,•/ FGL CA•••/ C=90 =Z ACB•••/ CAD# AFG在厶FGA和厶ACD中,£ .F L H\ AF^AD•△FGA^A ACD( AAS ,• AC=FG①正确;•/ BC=AC• FG=BC•••# ACB=90 , FGLCA• FG// BC•四边形CBFG是矩形,•CBF=90 , S^FAB=£FB?FG= g s 四边形CBFG , ②正确;•/ CA=CB # C=# CBF=90 ,•# ABC# ABF=45,③正确;•••# FQE# DQB# ADC / E=# C=90 ,•△AC SA FEQ• AC AD=FE FQ• AD?FE=AD=FQ?AC ④正确;故选:D.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键•由正方形的性质得出•FAD=90 , AD=AF=EF 证出# CAD# AFG 由AAS证明△ FGA^A ACD,得出AC=FG①正确;证明四边形CBFG是矩形,得出S^FAB F—FB?FG= S四边形CEFG , ②正确;由等腰直角三角形的性质和矩形的性质得出/ ABC# ABF=45,③正确;证出△ AC SA FEQ得出对应边成比例,得出D?FE=AD=FQ?AC④正确.14、【答案】B【考点】全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,矩形的性质【解析】【解答】解:①:•矩形ABCD中, 0为AC中点,• 0B=0,•••# COB=60 ,•△ OBC是等边三角形,• OB=BC•/ FO=FC• FB垂直平分OC故①正确;②••• FB垂直平分OC•△ CMB^ OMB•/ OA=OC / FOC# EOA / DCO# BAQ•△FOC^A EOA• FO=EO易得OBL EF,•△ OMIB △ OEB•△EOB2A CMB故②正确;③由△ OM BA OEB2A CMB 得/ 仁/ 2=# 3=30°, BF=BE •△ BEF是等边三角形,• BF=EF•/ DF/ BE 且DF=BE•四边形DEBF是平行四边形,••• DE=BF••• DE=EF故③正确;④在直角厶BOE中I / 3=30°• BE=2OE•••/ OAE/ AOE=30 ,• AE=OE• BE=2AE•S A AOE:S A BCI\=S A AOE &B0E=1 : 2 ,故④错误;所以其中正确结论的个数为3个;【分析】①利用线段垂直平分线的性质的逆定理可得结论;②证△OM^A OEB 得厶EOB2^ CMB③先证△ BEF是等边三角形得出BF=EF,再证?DEBF得出DE=BF所以得DE=EF④由②可知△ BCI WA BEO则面积相等,△ AOE 和A BEO属于等高的两个三角形,其面积比就等于两底的比,即&AOE:S^BOE=AE: BE由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE得出结论S MOE:S^BO=AE: BE=1: 2.本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.15、【答案】B【考点】菱形的判定与性质,翻折变换(折叠问题),等腰直角三角形【解析】【解答】解:•••四边形ABCD是正方形,•••/ GAD/ADO=45 ,由折叠的性质可得:/ ADG= —/ADO=22.5 ,■■■-故①正确.•••由折叠的性质可得:AE=EF / EFD/ EAD=90 ,• AE=E R BE,1 AD•AE<豆A B •后〉2,故②错误.•// AOB=90 ,• AG=F3 OG △ AGD与△ OGD同高,•S A AGD〉S^OGD , 故③错误.•// EFD/ AOF=90 ,• EF// AC•/ FEG/ AGE•// AGE/ FGE•/ FEG/ FGE• EF=GF•/ AE=EF•AE=GF 故④正确.•/ AE=EF=GF AG=GF• AE=EF=GF=AG•四边形AEFG是菱形,•/ OGF/ OAB=45 ,•EF=GF= V2OQ • BE=近EF= 5/2 X 近OG=2OG 故⑤正确.•••四边形AEFG是菱形,• AB// GF AB=GF•••/ BAO=45 , / GOF=90 ,•△ OGF时等腰直角三角形.•「S △OGF=1 ,O G=1,解得0G= J j,「. BE=2OG=2 ], GF= - - . _=〒=2, ••• AE=GF=2 ••• AB=BE+AE=2 匚+2 , •-S正方形ABC=AB2= (2 V2+2)2=12+8 血,故⑥错误.•其中正确结论的序号是:①④⑤. 故选B.【分析】①由四边形ABCD是正方形,可得/ GAD M ADO=45,又由折叠的性质,可求得/ ADG的度数;②由AE=Ef< BE,可得AD> 2AE③由AG=G>OG可得△ AGD的面积>△ OGD的面积;④由折叠的性质与平行线的性质,易得△ EFG是等腰三角形,即可证得AE=GF⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG⑥根据四边形AEFG是菱形可知AB// GF, AB=GF再由/ BAO=45 , / GOF=90可得出△ OGF时等腰直角三角形,由S MG=1求出GF的长, 进而可得出BE及AE的长,利用正方形的面积公式可得出结论. 此题考查的是四边形综合题,涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识•此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.16、【答案】B【考点】全等三角形的判定与性质,正方形的性质,翻折变换(折叠问题),相似三角形的判定与性质【解析】【解答】解:••• E, F分别是正方形ABCD边BC, CD的中点,• CF=BE在厶ABE和厶BCF中,I AB=BC£_-L?S Z57/,( BE=CF• Rt△ ABE^ Rt△ BCF( SAS ,•••/ BAE K CBF AE=BF 故①正确;又•••/ BAE K BEA=90 ,•/ CBF K BEA=90 ,•K BGE=90 ,• AE1BF,故②正确;根据题意得,FP=FC / PFB=/ BFC / FPB=90•/ CD// AB•/ CFB K ABF,•/ ABF K PFB• QF=QB令PF=k (k > 0),贝U PB=2k在Rt△ BPQ中,设QB=x•x 2= (x - k) 2+4k2,5k• x= ,BP 4• sin= K BQP= =,故③正确;•••/ BGE K BCF / GBE K CBF•△BG0A BCF•/ BE= BC, BF= BC,一r• BE BF=1: ,•△ BGE的面积:△ BCF的面积=1: 5 ,•S四边形ECF=4S^BGE , 故④错误.故选:B.【分析】首先证明厶ABE^A BCF再利用角的关系求得/ BGE=90 ,即可得到①AE=BF②AE1 BF;A BCF沿BF对折,得到△ BPF利用角的关系求出QF=QB解出BP, QB根据正弦的定义即可求解;根据AA可证△ BGE与厶BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解. 本题主要考查了四边形的综合题,涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点,解决的关键是明确三角形翻转后边的大小不变,找准对应边,角的关系求解.17、【答案】D【考点】二次函数的图象,二次函数的性质,菱形的判定【解析】【解答】解:①T抛物线y=ax2+bx+c (0)与x轴交于点A (- 2, 0)、B (1, 0),•••该抛物线的对称轴为x= - #= =-0.5 ,••• a=b, a - b=0,①正确;②•••抛物线开口向下,且抛物线与x轴交于点A (- 2, 0)、B (1, 0),•当-2v x v 1时,y > 0,②正确;③•••点A、B关于x=0.5对称,•AM=B M又••• MC=MD且CDLAB•四边形ACBD是菱形,③正确;④当x= - 3时,y v 0,即y=9a - 3b+c v 0,④错误.综上可知:正确的结论为①②③.故选D.【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=- 三=-0.5,由此即可得出a=b,①正确;②根据抛物线的开口向下以及抛物线与x轴的两交点坐标,即可得出当- 2v x v 1时,y>0,②正确;③由AB关于x=0.5对称, 即可得出AM=BM再结合皿。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则点 D 不一定 落在 AC 上; ④BD=BF ; ⑤ S 四边形 DFOE=S△AOF , 上述结论中正确
的个数是(
)
A、1 个
B、2 个
C、3 个
D、4 个
12、如图,将等边 △ ABC 绕点 C 顺时针旋转 120 °得到 △EDC ,连接 AD , BD .则 下列结论:
① AC=AD ; ② BD ⊥AC ; ③ 四边形 ACED 是菱形.
② GB=2AG ;③△ GDE ∽△ BEF ;④S△ BEF= .在以上 4 个结论中, 正确的有( )
A、1
B、2
C、3
D、4
A、1
B、2
C、 3
D 、4
7、如图, ? ABCD 的对角线 AC 、 BD 交于点 O, AE 平分 ∠BAD 交 BC 于点 E, 且 ∠ ADC=6°0 ,AB= BC ,连接 OE.下列结论: ①∠ CAD=3°0 ;② S? ABCD =AB?AC ;
其中正确的结论的个数是( )
则正方形 ABCD 的面积是 6+4 ,其中正确的结论个数为(
)
A、1 B、2 C、 3 D、4 14、如图,矩形 ABCD 中, O 为 AC 中点,过点 O 的直线分别与 AB 、 CD 交于点 E、F,连结 BF 交 AC 于点 M ,连结 DE、BO .若 ∠COB=60°,FO=FC ,则下列结 论:① FB 垂直平分 OC ;②△ EOB≌△ CMB ;③ DE=EF ;④ S△AOE :S△BCM =2:3.其
2017 届中考复习多结论几何综合题专题试卷
一、单选题
1、如图, △ ABC 和△ CDE 均为等腰直角三角形,点 B, C, D 在一条直线上,点
M 是 AE 的中点,下列结论:① tan∠AEC=
;② S△ABC +S△ CDE≥S△ ACE ;③BM ⊥ DM ;
④ BM=DM .正确结论的个数是(
D、4 个
A 、 ①②④
B、 ③④⑤
C、 ①③④
D、 ①③⑤
3、如图,将等边 △ABC 沿射线 BC 向右平移到 △DCE 的位置,连接 AD 、 BD ,
则下列结论:
① AD = BC ;② BD 、AC 互相平分; ③ 四边形 ACED 是菱形; ④ BD ⊥DE ;其中正
确的个数是(
).
6、如图,已知正方形 ABCD 的边长为 12,BE=EC ,将正方形边 CD 沿 DE 折叠到 DF,延长 EF 交 AB 于 G,连接 DG ,现在有如下 4 个结论: ①△ ADG ≌△ FDG ;
)
A 、 1 个 B、 2 个 C、 3 个 D、 4 个
4、如图,把一张长方形纸片 ABCD 沿对角线 BD 折叠,使 C 点落在 E 处, BE 与
AD 相交于点 F,下列结论:
① BD=AD
2ห้องสมุดไป่ตู้
+AB
2; ②△
ABF
≌△
EDF ;③
=
④ AD=BD?cos4°5 .
其中正确的一组是(
)
A 、 ①② B 、 ②③ C、 ①④ D 、 ③④
中正确结论的个数是(
)
A、2
B、3
C、4
D、5
16、如图,在正方形 ABCD 中, E、 F 分别为 BC 、 CD 的中点,连接 AE , BF 交于 点 G,将 △ BCF 沿 BF 对折,得到 △ BPF,延长 FP 交 BA 延长线于点 Q,下列结论
正确的个数是(
)
① AE=BF ; ② AE ⊥BF ; ③ sin∠ BQP= ; ④ S 四边形 ECFG=2S△ BGE .
8、如图, AD 是 △ ABC 的角平分线, DE ,DF 分别是 △ABD 和 △ ACD 的高,得到
下列四个结论:
① OA=OD ; ② AD ⊥ EF; ③ 当 ∠ A=90°时,四边形 AEDF 是正方
形; ④ AE+DF=AF+DE . 其中正确的是(
)
A 、 ②③ B、 ②④ C、 ①③④ D、 ②③④
2、如图,在 Rt△ABC 中, AB=AC , D 、E 是斜边 BC 上两点,且 ∠ DAE=45°,将 △ ADC 绕点 A 顺时针旋转 90 °后,得到 △ AFB ,连接 EF,下列结论:
①△ AED ≌△ AEF ;②
=
;③△ ABC 的面积等于四边形 AFBD 的面积;
④ BE 2+DC 2=DE 2 ⑤ BE+DC=DE; 其中正确的是 ( )
其中正确的个数是(
)
A、0 B、1 C、2 D、3 13、如图, CB=CA ,∠ ACB=90°,点 D 在边 BC 上(与 B、 C 不重合),四边形 ADEF 为正方形,过点 F 作 FG⊥ CA ,交 CA 的延长线于点 G,连接 FB,交 DE 于 点 Q,给出以下结论: ① AC=FG ; ②S△ FAB : S 四边形 CBFG =1: 2; ③∠ ABC= ∠ABF ; ④AD 2 =FQ?AC,
③ OB=AB ; ④OE= BC ,成立的个数有(
)
A、1 个 C、 3 个
B、2 个 D、 4 个
10、如图, PA=PB , OE⊥ PA, OF⊥PB,则以下结论: ① OP是∠ APB 的平分线;
② PE=PF③CA=BD ; ④ CD∥ AB ;其中正确的有(
)个.
A、4 C、2
B、3 D、1
11、如图,在 Rt△ ABC 中, AB=CB ,BO⊥ AC ,把 △ ABC 折叠,使 AB 落在 AC
上,点 B 与 AC 上的点 E 重 合,展开后, 折痕 AD 交 BO 于点 F,连接 DE、EF.下
列结论: ① tan∠ ADB=2 ; ②图中有 4 对全等三角形; ③ 若将 △ DEF 沿 EF 折叠,
9、如图, G, E 分别是正方形 ABCD 的边 AB ,BC 的点,且 AG=CE , AE ⊥ EF, AE=EF ,现有如下结论: ① BE= GE; ②△ AGE ≌△ ECF; ③∠ FCD=45° ; ④△ GBE ∽△ ECH ,其中,
正确的结论有(
)
A、1 个 C、 3 个
B、2 个 D、4 个
5、如图,已知正方形 ABCD 的边长为 4,点 E、F 分别在边 AB 、BC 上,且 AE=BF=1 ,
CE、 DF 交于点 O.下列结论: ①∠ DOC=90°, ②OC=OE , ③ tan∠ OCD= ,
④ S△ODC =S 四边形 BEOF 中,正确的有(
)
A、1 个
B、2 个
C、3 个
