【冀教版】七年级下册:8.4《整式的乘法》导学案(3)
冀教初中数学七年级下册《8.4整式的乘法》课堂教学课件 (3)

(1)(x-2)(x+1) (2)
解(1) (x-2)(x+1) =x2 +x-2x-2
1 a 2(3a 2) 3
=x2-x-2
a2 2 a 6a 4
3
a 2 20 a 4 3
所得积的符号由这两项的符号来确定: 负负得正,一正一负得负。
最后的结果要合并同类项。
例6:计算:(1)(x+3y)(2x-y) (2) (-3x+2b)(2x-4b)
的组合,其面积是
(M+N)(A+B)=M(A+B) + N(A+B) 的 理解
(m+n)(a+b)、m(a+b)+n(a+b) , 这些不同的式子都表示了最大 的长方形的面识,应该相等。
b
b
a
m ab
m
n
能用 “单项式乘以多项式” 来理解这两个式子的相等吗?
在 (m+n) x =mx+nx 中,将等号两端的 x换成(a+b)
最后的计算结果要化简 ̄合 ̄并 ̄同类项 。
中小学精品教学资 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
解(1)(x+3y)(2x-y) =2x2-xy+6xy-3y2 =2x2+5xy-3y2
(2) (-3x+2b)(2x-4b) =-6x2+12bx+4bx-8b2
=-6x2+16bx-8b2
多项式乘以多项式的 依据是什么? 如何进行多项式与多项式乘法运算?
运用多项式乘法法则,要有序地逐项相 乘,不要漏乘,并注意项的符号.
【冀教版】七年级数学下册:8.4《整式乘法》导学案(3)

8.4 整式的乘法(一)学习目标:知识目标:1.探究并掌握单项式与单项式的乘法法则。
2.运用单项式与单项式的乘法法则进行有关计算。
能力目标:发展学生的归纳概括能力。
情感目标:通过对单项式与单项式的乘法法则的探究,体验成功的喜悦,增强学好数学的自信心。
学习重难点:学习重点:单项式与单项式的乘法法则的探究与运用。
学习难点:单项式与单项式的乘法法则的探究。
预习导航:(预习课本,完成下列问题)1.等于多少? 等于多少?2.中有几个相乘? 几个相乘? 共有几个? 积等于多少? 3. 进行单项式与单项式的乘法运算时,你认为如何处理它们的系数?如何处理相同字母的幂?其余字母如何处理?一、复习导入二、试着做做 1.什么叫单项式?2.根据乘法的运算律和同底数幂的乘法,完成下列各题: (1)(2) (3)(4) 三、归纳概括1.单项式是由系数和字母组成的(相乘关系),两个单项式各有自己的系数,它们可能有相同的字母,也可能有不相同的字母,在它们相乘时:(1)系数应当怎么办?(2)相同的字母应当怎么办?(3)不相同的字母应当怎么办?2.你认为如何进行单项式与单项式的乘法运算?师:在上学期,我们学习了单项式与单项式相加(即合并同类项),那么,如何进行单项式与单项式的乘法运算呢?“试着做做”从复习单项式的概念入手,然后从4个具体算式开始,让学生动手参与,从中逐渐去感悟单项式与单项式的乘法运算方法。
(填空中注意小括号的用法)由学生自己在计算操作的基础上,经过思考、交流,归纳概括出单项式与单项式的乘法法则。
1.应使学生真正经历这一过程,以促进学生的观察能力和归纳概括能力的发展; 2.应使学生真正的去理解法9897-p 32a a ⋅a a 32⋅abc b a 322⋅a b c ()()____222aa a a a =⋅⋅=⋅______________________32===⋅a a _______________________32==⋅ab a ____________________________542==⋅yz x xy则,而不是单纯的背和记; 3.教师要注意对学生的表述加以规范;4.结合学生情况,可采用讨论、纠正、补充等方法,最终取得正确结论。
七年级数学下册 第八章 整式的乘法 全章学案 (新版)冀教版

同底数幂的乘法学习目标:(1)理解同底数幂的乘法,会用这一性质进行同底数幂的乘法运算.(2)体会从具体到抽象,特殊到一般的思想方法在研究数学问题中的作用.重点:同底数幂的乘法运算性质及其运用.难点:同底数幂的乘法运算性质的理解与推导.一.章前图解读,新课引入为改善生活环境,将某绿地进行扩大,你有几种方法表示扩大后的绿地面积?二.自主学习,导学共研(认真阅读教材,独立完成问题1-3)1.感受学习同底数幂的乘法的必要性 问题1 一种电子计算机每秒可进行一千万亿(1510)次计算,它工作310秒可进行多少次运算?(科学记数法:形如10n a ⨯的形式,n 为正整数,1≤a <10)2.探索并推导同底数幂的乘法的性质问题2 根据乘方的意义填空,观察计算结果,你能发现什么规律?(1)52(222⨯= ) (2)32(a a a ⋅= ) (3)(555m n ⨯= )问题3 你能将上面发现的规律推导出来吗?3.巩固同底数幂的乘法的运算性质例1计算:(1)25x x ⋅; (2)6a a ⋅; (3)43(2)(2)(2)-⨯-⨯-; (4)31m m x x +⋅.练习1辨一辨 判断下列计算是否正确,并简要说明理由:(1)3710n n n ⋅=;(2)358a a a +=;(3)5420y y y ⋅=;(4)22x x x ⋅=;(5)4442b b b ⋅=.例2计算:34()()x y x y +⋅+; 变式练习:54()()m n n m -⋅-.练习2练一练 计算:(1)678()()x x x -⋅⋅-; (2)32()()()x y x y y x -⨯-⨯-.例3计算:(1)(x )5x ⋅8x = (2)2(()()()n n a b a b a b ++=+⋅+ )(2)已知23,25m n ==,求2m n +的值.练习3变一变:已知23x a +=,用含a 的代数式表示3x .三、提升巩固,悟学反思1.归纳小结我们一起回顾本节课所学的主要内容,并请回答以下问题:(1)本节课学习了哪些主要内容?(2)同底数幂的乘法的运算性质是怎么探究并推导出来的?在运用时要注意什么?2.课堂反馈题型一 应用同底数幂的乘法法则进行计算(1)83a a ⋅= (2)5x x -⋅=(3)1013(2)(2)-⋅-= (4)432y y y y ⋅⋅⋅=题型二 判断并改正(1)236a a a ⋅= (2)2m m m x x x ⋅=(3)23n n n x x x += (4)325m m m +=题型三 同底数幂知识的灵活应用(1)22n y +可以写成( )A .12n y +B .22n y y ⋅C .21n y y +⋅D .22n y y +(2)若3,2m n x x ==,则m n x +的值是( )A .5B .6C .-5D .-6(3)若2282n ⨯=,则n 的值是 .3.课后思考(1)已知9m n m n x x x +-⋅=,求m 的值.(2)已知23,22,212a b c ===,求a 、b 、c 之间的关系.4.布置作业(1)已知5m a =,125n a =,求m n a +的值;(2)若8,64m n k k ==,则m n k += .积的乘方学习目标:1.通过探索积的乘方的运算性质,进一步体会和巩固幂的意义.2.积的乘方的推导过程的理解和灵活运用.学习重点:积的乘方的运算.学习方法:采用“探究──交流──合作”的方法,让学生在互动中掌握知识.学习过程:一、情境引入:计算:(1)(x4)3 = (2)a·a5 = (3)x7·x9(x2)3=二、探索新知活动:参考(2a3)2的计算,说出每一步的根据。
七年级数学下册第八章整式的乘法8.4《整式的乘法(3)课件(新版)冀教版

☾ 两项相乘时,
先定符号. 所得积的符号由这
两项的符号来确定:
(2) (3x -1)(2x+1)
负负得正 一正一负得负.
=3x•2x +3x• 1-1•2x - 1 最后的结果要
= 6x2 +3x -2x −1
合并同类项.
= 6x2 +x−1.
【例6】计算:
(1)(x−3y)(x+7y), (2)(2x + 5y)(3x−2y).
由于(m+n)(a+b)和 (ma+mb+na+nb)表示同一块地的 面积,故有:
(m+n)(a+b)= ma + mb + na+ nb
如何进行多项式与多项式相乘的 运算 ?
实际上,把(m+n)看成一个整体,有:
(m+n)(a+b) = (m+n)a+(m+n)b
= ma+mb+na+nb
问题 & 探索
整式的乘法(3)
回顾与思考 回顾 & 思考☞
如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的各项,
② 再把所得的积相加.
进行单项式与多项式乘法运算时,要注意什么?
① 不能漏乘: 即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
讨论 探究:
(a+b) x= ? (a+b)x=ax+bx
6 5
活动& 探索
填空:(x + 2)( x + 3) x2 + __ x + __ (x - 2)( x + 3) x2 + _1_ x + (_-_6) (x + 2)( x - 3) x2 +(_-1_)x + _(-_6) (x - 2)( x - 3) x2 + (_-_5)x + _6_
冀教版数学七年级下册8.4《整式的乘法》教案

《整式的乘法》教案教学目的1、让学生通过适当的尝试,获得直接的经验,体验单项式与单项式的乘法运算规律,总结运算法则;2、使学生能正确区别各单项式中的系数,同底数幂和不同底数幂的因式;3、让学生感知单项式法则对两个以上单项式相乘同样成立,知道单项式乘法的结果仍是单项式;4、理解并会灵活进行多项式乘法运算.重点对单项式运算法则的理解和应用;单项式与多项式乘法的应用;多项式与多项式相乘的法则和应用.难点尝试与探究单项式与单项式的乘法运算规律;单项式与多项式乘法的运算;探索多项式与多项式相乘的法则,注意多项式与多项式相乘的运算中“漏项”、“符号”的问题.教学过程【一】一、知识回顾:1、口述幂的几个法则;2、幂的运算法则的联系和区别.二、计算观察:试一试:计算:32321210510225.x x ⨯⨯⨯g ()()();() 通过上题的计算,启发引导学生归纳得出:1、系数相乘作为积的系数;2、相同字母的因式,应用同底数幂的运算法则,底数不变,指数相加;3、只在一个单项式里含有的字母,连同它的指数也作为积的一项;4、单项式与单项式相乘积仍是单项式.三、举例应用:例1计算(1)233(2)x y x y -g (2)232(5)(4)a b b c --g四、创设情境:问题讨论:1、a a g可以看作是边长为a 的正方形的面积,a ab g 可以做怎么样的理解; 2、其他的,请你举出例子.五、随堂练习:P80 1、2、3六、课堂小结:1、本节内容是单项式乘以单项式,重点是放在对运算法则的理解和应用上,请问:你能归纳出单项式乘以单项式的运算法则吗?2、在应用单项式乘以单项式运算法则时,应注意什么?【二】旧知识的复习:1.单项式与单项式相乘的法则?(学生举例说明)2.什么叫多项式?指出多项式的各项?(学生举例说明)强调:多项式的每一项包括它前面的性质符号.新知识的教学:1.问题的提出:试一试:计算22235a a b -- ()=? (学生动手完成后,汇报结果)议一议:(1)这是什么运算?(板书课题)(2)运算过程中的根据是什么?(3)你能总结出它的运算法则吗?(学生小组商议后选代表回答,并总结出法则的语言叙述及式子表示)法则:单项式与多项式相乘:就是用单项式分别去乘多项式的每一项;再把所得的积相加.式子表示:()m a b c ma mb mc ++=++(m 表示单项式,a b c ++表示多项式) 几何图形解释()m a b c ++=mc mb ma ++:mb m a b c ma mc。
【冀教版】七年级数学下册:8.4《整式乘法》导学案(2)

8.4 整式的乘法(二)学习目标:知识目标:1.探究并掌握单项式与多项式的乘法法则。
2.运用单项式与多项式的乘法法则进行有关计算。
能力目标:发展学生的归纳概括能力。
情感目标:通过对单项式与多项式的乘法法则的探究,体验成功的喜悦,增强学好数学的自信心。
学习重难点:学习重点:单项式与多项式的乘法法则的探究与运用。
学习难点:单项式与多项式的乘法法则的探究。
预习导航:(预习课本,完成下列问题)1.等于多少? 等于多少? 你运用了什么运算律?2. 如果把括号前的数字换成字母,上述的运算律还适用吗? 等于多少? 呢?3. 你认为如何进行单项式与多项式的乘法运算?一、复习导入二、猜想验证1.利用整式的加减法则计算:(1)3(a+b) (2)7x-(-5x+9)(3)2a+2(3a-b-2c) (4)x-3(2x+5y-6)2.猜想:m(a+b)= .3.上述结果可以用右图说明: (1)这个长方形的长为(a+b ),宽为m ,则 其面积为 。
(2)这个长方形的面积又可以看做宽为m ,长分别为a ,b 的两个长方形面积的和,即 。
(3)用等号把两个结果连起来,即 = 。
三、归纳概括1.计算mn(a+b-c),并按右图所示,谈一谈单项式与多项式相乘的过程及其结果表示的几何意义。
a b m 10099-p ()b a +-3()n m +5()n m x +3()223y x xy +c试一试:议一议:如何进行单项式与多项式的乘法运算?归纳:单项式与多项式相乘,用单项式去乘 ,再把积 。
即学即用:下列计算是否正确?如果不正确,应怎样改正?(1)(2)(3)(4)四、展示交流 例3计算:(1) (2)例4 先化简,再求值:.议一议:上述运算中你出现了什么错误?你认为单项式与多项式的乘法运算应注意那些问题?归纳概括环节仍以实例导入,让学生自己试着归纳概括单项式乘多项式的运算法则,必要时,也可以由以下问题作引导:1.在你做单项式和多项式相乘时,是借助什么运算律来进行的? 2.在运用这个运算律后,是将单项式乘多项式转化成了什么运算? 3.怎样用这个单项式和这个多项式来说明相乘的结果?最终得出:借助乘法分配率,可以把单项式乘多项式转化成单项式乘单项式。
2024年七年级数学下册第8章整式乘法8.4整式的乘法2单项式与多项式相乘教案(新版)冀教版
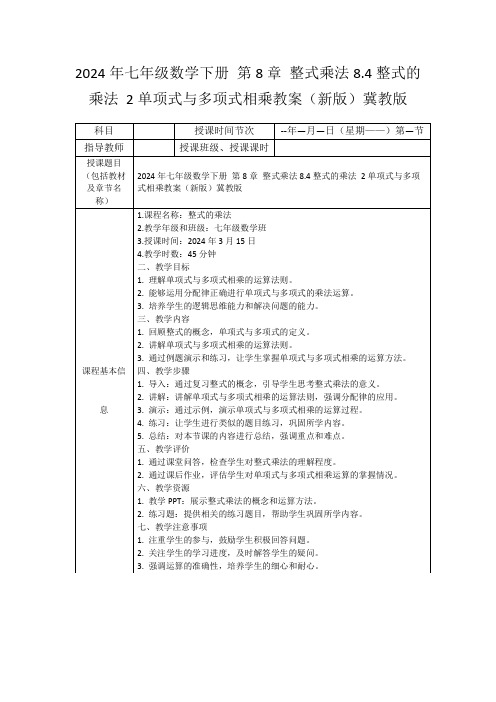
1.单项式与多项式相乘的运算
【例题1】计算:2x * (3x + 4)
【解题步骤】
首先,将单项式2x与多项式的每一项相乘,即:
2x * 3x = 6x^2
2x * 4 = 8x
然后,将乘法的结果相加,得到最终答案:
6x^2 + 8x
【例题2】计算:-3 * (x^2 + 2x - 1)
【解题步骤】
然而,在教学过程中我也发现了一些需要改进的地方。例如,在讲解分配律的应用时,我可能需要更直观地展示和解释,以便学生更好地理解和掌握。此外,在布置课后作业时,我可能需要更多地考虑学生的个体差异,布置不同难度的题目,以满足不同学生的学习需求。
针对这些反思,我计划在未来的教学中进行改进。首先,我会在讲解分配律的应用时,采用更直观的方式,例如通过具体的例子和实物模型,让学生更好地理解分配律的意义和应用。其次,我会根据学生的学习情况,合理布置课后作业,既能够巩固学生的知识,又能够挑战学生的思维。最后,我会继续探索和尝试更多的教学方法和手段,以激发学生的学习兴趣和主动性,提高教学效果。
1.课程名称:整式的乘法
2.教学年级和班级:七年级数学班
3.授课时间:2024年3月15日
4.教学时数:45分钟
二、教学目标
1.理解单项式与多项式相乘的运算法则。
2.能够运用分配律正确进行单项式与多项式的乘法运算。
3.培养学生的逻辑思维能力和解决问题的能力。
三、教学内容
1.回顾整式的概念,单项式与多项式的定义。
2.课后探究题目:
鼓励学生进行课后自主学习和探究,布置以下探究题目:
题目1:请你举例说明整式乘法在生活中的应用,并尝试用所学的知识解决实际问题。
冀教版数学七年级下册:8.4.3整式的乘法3 导学案设计 (无答案 )

课题名称:8.4整式的乘法课型:新授课主备人:XXX 使用人:使用时间:导学目标1.会进行多项式与多项式的乘法运算2.灵活运用多项式乘以多项式的运算法则自主学习1.学生复习单项式×多项式运算法则整式的乘法实际上就是单项式×单项式、单项式×多项式、多项式×多项式2张伯伯准备把长为m米、宽为a米的长方形鱼塘进行扩建,使得长再增加n米,宽再增加b米,求扩建后鱼塘的面积.合作探究一起探究:1.求扩建后鱼塘的面积有哪些方法?将计算过程和结果写出来2、探索法则与应用(m+n)(a+b)=(m+n)a+(m+n)b=ma+na+mb+nb或(m+n)(n+b)=m(a+b)+n(a+b)=ma+mb+na+nb提问:多项式与多项式相乘是怎样化为单项式与单项式相乘的?2.例题讲解例5计算:(1))1)(2(+-χχ;(2))2a3(2a31-⎪⎭⎫⎝⎛-.例6计算:(1))y2)(3y(-+χχ;(2))4b2)(2b3(-+-χχ.强调法则的应用小结本节课学习了哪些内容?你有哪些收获?1.多项式×多项式2.整式的乘法课堂检测1.计算(1)(X+2)(2X-4) (2)(X+2Y)(3a+4b)2.先化简,再求值:5X(2X+1)-(2X+3)(5X-1).其中,X=13.3、P84习题A,B组反思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.4 整式的乘法
第3课时多项式乘多项式
【学习目标】
1.知道多项式乘以多项式的法则,并能解释法则的实际意义;
2.正确进行多项式乘以多项式的计算,并能简化代数式.
【学习重点】
正确进行多项式乘以多项式的计算,并能简化求代数式的运算.
【学习难点】
正确进行多项式乘以多项式的计算,并能简化求代数式的运算.
【预习自测】
单项式乘单项式的法则?单项式乘多项式的法则?
一、选择题
计算(2a-3b)(2a+3b)的正确结果是( )
A.4a2+9b2B.4a2-9b2C.4a2+12ab+9b2 D.4a2-12ab+9b2
若(x+a)(x+b)=x2-kx+ab,则k的值为( )
A.a+b B.-a-b C.a-b D.b-a
计算(2x-3y)(4x2+6xy+9y2)的正确结果是( )
A.(2x-3y)2B.(2x+3y)2C.8x3-27y3D.8x3+27y3
(x2-px+3)(x-q)的乘积中不含x2项,则( )
A.p=q B.p=±q C.p=-q D.无法确定
若0<x<1,那么代数式(1-x)(2+x)的值是( )
A.一定为正B.一定为负C.一定为非负数D.不能确定
计算(a2+2)(a4-2a2+4)+(a2-2)(a4+2a2+4)的正确结果是( )
A.2(a2+2) B.2(a2-2) C.2a3 D.2a6
方程(x+4)(x-5)=x2-20的解是( )
A.x=0 B.x=-4 C.x=5 D.x=40
若2x2+5x+1=a(x+1)2+b(x+1)+c,那么a,b,c应为( )
A.a=2,b=-2,c=-1 B.a=2,b=2,c=-1
C.a=2,b=1,c=-2 D.a=2,b=-1,c=2
若6x2-19x+15=(ax+b)(cx+b),则ac+bd等于( )
A.36 B.15 C.19 D.21
(x+1)(x-1)与(x4+x2+1)的积是( )
A.x6+1 B.x6+2x3+1 C.x6-1 D.x6-2x3+1
【合作探究】
活动1 探究多项式乘以多项式的法则
请结合课本83页图8-4-3,完成“一起探究”
请总结:我们如何计算多项式乘以多项式:
运算法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积项加.
活动2 练习多项式乘以多项式
例5;例6见课本84页,请做课后练习第1 、 2题.
【解难答疑】
二、填空题
(3x -1)(4x +5)=__________.
(-4x -y )(-5x +2y )=__________.
(x +3)(x +4)-(x -1)(x -2)=__________. (y -1)(y -2)(y -3)=__________. (x 3+3x 2+4x -1)(x 2-2x +3)的展开式中,x 4
的系数是__________.
若(x +a )(x +2)=x 2
-5x +b ,则a =__________,b =__________.
若a 2
+a +1=2,则(5-a )(6+a )=__________.
当k =__________时,多项式x -1与2-kx 的乘积不含一次项.
若(x 2+ax +8)(x 2-3x +b )的乘积中不含x 2和x 3
项,则a =_______,b =_______.
如果三角形的底边为(3a +2b ),高为(9a 2-6ab +4b 2
),则面积=__________. 【反馈拓展】
1、计算:(1)(0.6-x)(1-x); (2)(2x+y)(x-y).
2、 (2x -1)(x -2)
计算:
5x (2x +1)-(2x +3)(5x -1)
一个长方形的长为2xcm ,宽比长少4cm ,若将长方形的长和宽都扩大3cm ,则面积比原来增大多少?
5.解方程:
6.先化简,再求值:,其中=-2.
7、一家住房结构如图10-1-1所示,图中标了有关尺寸(墙体厚度忽略不计,单位: 米) 房屋的主人计划把卧室以外的地面都铺上地砖,如果他选用地砖的价格是a 元/平方米,
()()____________2=-+b a b a 2
(10)(8)100x x x +-=-()()(
)2
2
21414122x
x x x x x ----+-x
则买地砖至少需用多少元(结果用代数式表示)?
【中考链接】 化简,再先求值:
,其中=-3.
本节知识点回顾
多项式与多项式相乘(多项式的乘法)
运算法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加. 注意事项:(1)切记不可漏项;
符号问题:多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注 意确定积中各项的符号;
(3)掌握一些特殊类型的规律进行简便运算是非常重要的,
如:,这一特点要记熟,应用时极方便;
(4)多项式乘以多项式的结果仍然是一个多项式.
【总结反思】
1.本节课我学会了: 还有些疑惑:
2.做错的题目有: 原因:
()()()()5.0232143++--+a a a a a 2
()()()x a x b x a b x ab ++=+++图10-1-1
卫 生 间
卧 室
客厅 厨房 4x
2y y 4y
2x
x。
