角平分线辅助线专题练习
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
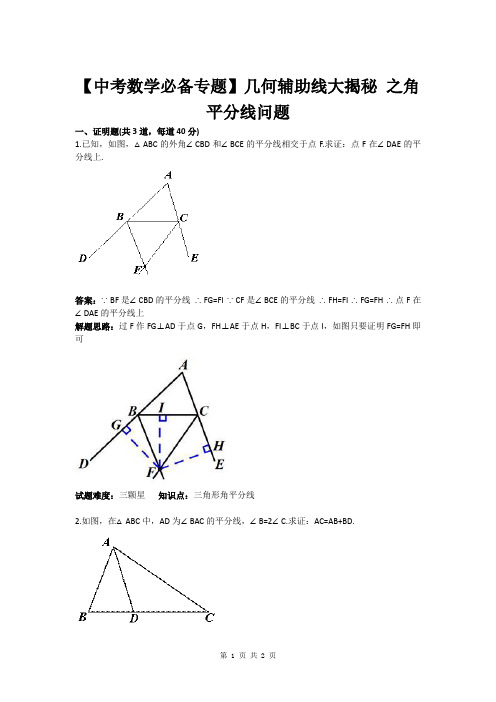
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
2024辽宁中考数学二轮专题复习 微专题 遇到角平分线如何添加辅助线(课件)

2. 如图,AB∥CD,∠ABC的平分线与∠BCD的平分线相交于点E, AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若 AD=8,则PE的最小值为___4___.
第2题图
3. 如图,∠MON=30°,OP平分∠MON,过点P作PQ∥OM交ON于 点Q.若OQ=4,则点P到OM的距离为___2__.
微专题 遇到角平分线如何添加辅助线
方法一 过角平分线上一点向角两边作垂线
方法解读 如图,已知∠MON,点P是∠MON平分线上一点.
过角平分线上的点向角两边作垂线. 已知PA⊥OM, 添加辅助线,作PB⊥ON于点B.
结论:PA=PB,OA=OB,∠APO=∠BPO等.
1. 如图,在Rt△ABC中,∠C=90°4 ,AD平分∠BAC交BC于点D,若 AC=4,BC=3,则CD的长为____3____.
第7题图
方法四 作角平分线的垂线,构造等腰三角形
方法解读 过角平分线上的点作角平分线的垂线,三线合一试试看. 已知AP⊥OP,延长AP交ON于点B.
结论:__R_t_△__A_O__P_≌__R_t_△__B_O__P_,__O_A__=__O_B_,__A__P_=__B_P__. __
8. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD. 若BD=1,BC=3,则AC的长为__5___.
结论:____△__A__O_P_≌__△__B__O_P_,__A__P_=__B_P______
6. 如图,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,若AC= 16,AD=8,则线段BC的长为__2_4___.
第6题图
7. 如图,四边形ABCD中,AC平分∠BAD,∠B+∠ADC=180°, 若BC=2,则DC的长为__2___.
角平分线四大辅助线模型 总结+习题+解析

角平分线四大辅助线模型角平分线的性质为证明线段或角相等开辟了新的途径,同时也是全等三角形知识的延续,又为后面角平分线的判定定理的学习奠定了基础.涉及到角平分线的考点主要是性质、判定以及四大辅助线模型,在初二上期中、期末考试中都是经常考察的方向。
角平分线性质:角平分线上的点到角两边的距离相等.角平分线判定:到角的两边距离相等的点在角的角平分线上.四大模型1、角平分线+平行线,等腰三角形必出现已知:OC平分∠AOB,CD∥OB交OA于D.则△ODC为等腰三角形,OD=CD.2、角平分线+两垂线,线等全等必出现已知:OC平分∠AOB.辅助线:过点C作CD⊥OA,CE⊥OB.则CD=CE,△ODC ≌△OEC.3、角平分线+一垂线,中点全等必出现已知:OC平分∠AOB,DC垂直OC于点C.辅助线:延长DC交OB于点E.则C是DE的中点,△ODC ≌△OEC.4、角平分线+截长补短线,对称全等必出现已知:OC平分∠AOB,截取OE=OD,连接CD、CE.则△ODC和△OCE关于OC对称,即△ODC ≌△OEC.【核心考点一】角平分线的性质与判定1.(2016•张家界模拟)如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上一个动点,若3PA =,则PQ 的最小值为( )A B .2 C .3 D .【分析】首先过点P 作PB OM ⊥于B ,由OP 平分MON ∠,PA ON ⊥,3PA =,根据角平分线的性质,即可求得PB 的值,又由垂线段最短,可求得PQ 的最小值.2.(2016秋•抚宁县期末)如图,在ABC ∆中,AD 是它的角平分线,8AB cm =,6AC cm =,则:(ABD ACD S S ∆∆= )A .3:4B .4:3C .16:9D .9:16【分析】利用角平分线的性质,可得出ABD ∆的边AB 上的高与ACD ∆的AC 上的高相等,估计三角 形的面积公式,即可得出ABD ∆与ACD ∆的面积之比等于对应边之比.3.(2017春•崇仁县校级月考)如图,在ABC ∆中,90ACB ∠=︒,BE 平分ABC ∠,DE AB ⊥于点D ,如果3AC cm =,那么AE DE +等于( )。
8年级数学人教版上册同步练习角的平分线的性质(含答案解析)

8年级数学人教版上册同步练习角的平分线的性质(含答案解析)专题一利用角的平分线的性质解题1.如图,在△ABC中,AC=AB,D在BC上,若DF⊥AB,垂足为F,DG⊥AC,垂足为G,且DF=DG.求证:AD⊥BC.2.如图,已知CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC.求证:OB=OC.3.如图,在Rt△ABC中,∠C=90°,21∠∠,AD是∠BAC的角平分线,DE⊥ABBAC B∶∶于点E,AC=3 cm,求BE的长.专题二角平分线的性质在实际生活中的应用4.如图,三条公路把A﹨B﹨C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,则这个集贸市场应建在()A.在AC﹨BC两边高线的交点处B.在AC﹨BC两边中线的交点处C.在∠A﹨∠B两内角平分线的交点处D.在AC﹨BC两边垂直平分线的交点处5.如图,要在河流的南边,公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1cm(指图上距离),则图中工厂的位置应在__________,理由是__________.6.已知:有一块三角形空地,若想在空地中找到一个点,使这个点到三边的距离相等,试找出该点.(保留作图痕迹)状元笔记【知识要点】1.角的平分线的性质角的平分线上的点到角的两边的距离相等.2.角的平分线的判定角的内部到角的两边的距离相等的点在角的平分线上.【温馨提示】1.到三角形三边距离相等的点是三角形三条角平分线的交点,不是其他线段的交点.2.到三角形三边距离相等的点不仅有内角的平分线的交点,还有相邻两外角的平分线的交点,这样的点共有4个.【方法技巧】1.利用角的平分线的性质解决问题的关键是:挖掘角的平分线上的一点到角两边的垂线段.若已知条件存在两条垂线段——直接考虑垂线段相等,若已知条件存在一条垂线段——考虑通过作辅助线补出另一条垂线段,若已知条件不存在垂线段——考虑通过作辅助线补出两条垂线段.2.利用角平分线的判定解决问题的策略是:挖掘已知图形中一点到角两边的垂线段.若已知条件存在两条垂线段——先证明两条垂线段相等,然后说明角平分线或角的关系;若已知条件存在一条垂线段——考虑通过作辅助线补出另一条垂线段,再证明两条垂线段相等;若已知条件不存在垂线段——考虑通过作辅助线补出两条垂线段后,证明两条垂线段相等.参考答案:1.证明:∵DF AB DG AC DF DG ⊥⊥=,,,∴AD 是BAC ∠的平分线,∴BAD CAD =∠∠.在ABD △和ACD △中,⎪⎩⎪⎨⎧=∠=∠=(公共边)(已求)已知)AD AD DAC DAB AC AB (∴SAS)ABD ACD (△≌△.∴ADB ADC =∠∠.又∵180BDA CDA +=︒∠∠,∴90BDA =︒∠,∴AD BC ⊥.2.证明:∵AO 平分∠BAC ,OD ⊥AB ,OE ⊥AC ,∴OD =OE ,在Rt △BDO 和Rt △CEO 中,⎪⎩⎪⎨⎧∠=∠=∠=∠,,COE DOB OEOD CEO BDO ∴(ASA)BDO CEO △≌△.∴OB =OC .3.解:∵∠C =90°,∴∠BAC +∠B =90°,又DE ⊥AB ,∴∠C =∠AED =90°,又21BAC B =∶∶∠∠,∴∠A =60°,∠B =30°, 又∵AD 平分∠BAC ,DC ⊥AC ,DE ⊥AB ,∴DC =DE ,∴3AE AC ==cm .在Rt △DAE 和Rt △DBE 中,⎪⎩⎪⎨⎧=∠=∠∠=∠.DE DE BEDAED B DAE∴△DAE ≌△DBE (AAS ),∴3BE AE == cm . 4.C 解析:根据角平分线的性质,集贸市场应建在∠A ﹨∠B 两内角平分线的交点处.故选C .5.∠A 的角平分线上,且距A1cm 处 角平分线上的点到角两边的距离相等6.解:作两个角的平分线,交点P 就是所求作的点.。
角平分线的性质专项练习(含解析)
角平分线的性质专项练习一、单选题知识点一:角平分线的有关证明1.在Rt ABC 中,90B ︒∠=,AD 平分BAC ∠,交BC 于点D ,DE AC ⊥,垂足为点E ,若3BD =,则DE 的长为( )A .3B .32C .2D .62.如图,在△ABC 中,AB =6,BC =5,AC =4,AD 平分∠BAC 交BC 于点D ,在AB 上截取AE =AC ,则△BDE 的周长为( )A .8B .7C .6D .53.如图,在ABC 中,90,C AD ∠=平分,BAC DE AB ∠⊥于点,E 给出下列结论.CD ED =①;,AC BE AB +=② ③BDE BAC ∠=∠, DA ④平分CDE ∠,::BDE ACD S S AB AC =⑤其中正确的有( )个A .5B .4C .3D .2知识点二:角平分线的性质定理4.如图,在Rt ABC ∆中,90B =∠,以点A 为圆心,适当长为半径画弧,分别交AB AC 、于点,D E ,再分别以点D E 、为圆心,大于12DE 为半径画弧,两弧交于点F ,作射线AF 交边BC 于点1,4BG AC ==,则ACG ∆的面积是( )A .1B .32C .2D .525.如图,在△ABC 中,AB =AC ,AD 是中线,DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F ,则下列四个结论中:①AB 上任一点与AC 上任一点到D 的距离相等;②AD 上任一点到AB ,AC 的距离相等;③∠BDE =∠CDF ;④∠1=∠2;其中正确的有( )A .1个B .2个C .3个D .4个6.如图,AB ∥CD ,BP 和CP 分别平分∠ABC 和∠DCB ,AD 过点P ,且与AB 垂直.若AD =8,则点P 到BC 的距离是( )A .8B .6C .4D .27.如图,已知在四边形ABCD 中,90BCD ∠=︒,BD 平分ABC ∠,6AB =,9BC =,4CD =,则四边形ABCD 的面积是( )A.24 B.30 C.36 D.42知识点三:角平分线判定定理=,则()8.如图,AC AD=,BC BDA.CD垂直平分AD B.AB垂直平分CDC.CD平分ACB∠D.以上结论均不对9.如图,已知AB∥CD,PE⊥AB,PF⊥BD,PG⊥CD,垂足分别E、F、G,且PF=PG=PE,则∠BPD=().A.60°B.70°C.80°D.90°10.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系下列说法正确的是()A.一定相等B.一定不相等C.当BD=CD时相等D.当DE=DF时相等11.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A .线段CD 的中点B .OA 与OB 的中垂线的交点C .OA 与CD 的中垂线的交点 D .CD 与∠AOB 的平分线的交点知识点四:角平分线性质的实际应用12.如图,在ABC ∆中,90︒∠=C ,8AC =,13DC AD =,BD 平分ABC ∠,则点D 到AB 的距离等于( )A .4B .3C .2D .113.如图,Rt △ABC 中,∠C=90°,AD 平分∠BAC ,交BC 于点D ,若AB=14,S △ABD=14,则CD=( )A .4B .3C .2D .114.如图,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为E ,S △ABC =7,DE =2,AB =4,则AC 长是( )A .6B .5C .4D .3知识点五:尺规作图-角平分线15.尺规作图作AOB ∠的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得OCP ODP ≌的根据是( )A .SASB .ASAC .AASD .SSS16.如图,在ABC ∆中,,40AC BC A =∠=︒,观察图中尺规作图的痕迹,可知BCG ∠的度数为()A .40︒B .45︒C .50︒D .60︒17.如图1,已知ABC ∠,用尺规作它的角平分线.如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ;第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在ABC ∠内部交于点P ;第三步:画射线BP .射线BP 即为所求.下列正确的是( )A .a ,b 均无限制B .0a >,12b DE >的长C .a 有最小限制,b 无限制D .0a ≥,12b DE <的长18.如图,观察图中尺规作图痕迹,下列说法错误的是( )A .OE 是AOB ∠的平分线B .OC OD =C .点C,D 到OE 的距离不相等D .AOE BOE ∠=∠二、填空题 知识点一:角平分线的有关证明19.如图,已知△ABC 的周长是21,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =4,△ABC 的面积是_____.20.如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限,且MA 平分∠BAO ,做射线MB ,若∠1=∠2,则∠M 的度数是_______。
角平分线辅助线专题练习

角平分线专1、轴对称性:内容:角是一个轴对称图形,它的角平分线所在的直线是它的对称轴. 思路和方法:边角等根本结构:如图,2、角平分线的性质定理:注意两点⑴距离相等〔2〕一对全等三角形3、定义:带来角相等.4、补充性质:如图,在AABC中.AD平分NBAC,那么有AB: AC=BD:DC例题2:如图,在△ABC中,NA等于6(r.BE平分NABC.CD平分NACB求证:DH=EH例题3:如图1, BC>AB.BD平分NABC,且NA+/C=180O, 求证:AD=DC.:思路一:利用“角平分线的对称性〞来构造由于角是轴对称图形,角平分线是其对称轴,因此,题中假设有角平分线,一般可以利用其对称性来构成全等三角形.证法1:如图1,在BC上取BE = AB,连结DE,〈BD平分B耳佟1ZAB C, AZAB D = ZDBE, X BD=BD.AAABD^AEBD (SA S),,NA=NDBE,A D =D E,又NA+NC=1 8 0°, ZDE B+ZDEC=1 8 0°,,NC=NDEC.DE = DC,那么AD=DC. A n证法2:如图2,过A作BD的垂线分别交BC、81)于£、F, ?\连结DE,由BD平分NABC,易得4ABF/△ EBF,那么AB=B E, 1 / \BD 平分NABC,BD=BD, AAABD^AEB D(SAS ) , / \/ \,AD = ED, NBAD=NDEB.又NBAD+NC=1 8 0., B 图CZBED+ ZCED = 180°,A ZC= ZDEC,那么DE=DC, A AD=DC. g 说明:证法1,2,都可以看作将△ ABD沿角平分线BD折向BC而构成/'、、全等三角形的. / \证法3:如图3,延长BA至E,使BE=BC,连结DE, J\r)YBD 平分NABC,,NCBD=NDBE,又BD=BD, /•△CB D/aEBDA ZC=ZE, CADE,又NBA D+NC= 1 8 0(),NDAB + ND A E= 1 80°, \ AZE=ZDA E, DE=DA,那么AD=DC. R 图3C 说明:证法3是4CBD沿角平分线BD折向BA而构成全等三角形的.思路二:利用“角平分线的性质〞来构造由于角平分线上的点到角的两边的距离相等,所以根据这个性质,可以过角平分线上一点向角的两边作垂线而构成两个全等的直角三角形.证法4:如图4.从D分别作BC、BA的垂线,垂足为E、F,・.,BD平分NABC,,DE=DF,又NB AD+NC = 18O°, ZBAD+ZFAD=I 8 00, A ZFAD=Z CAFAD^AEC D〔AA S 〕,那么AD=DC.例题4:如图 5 ,在△血中, 求证:AC^CD= AB证实:在AB上截取AE二AC, 丁月〃平分NC45,,NC月氏NDAB, AD=AD, :.ACAD^AEAD9AZZ»E4=90O ,VZC=90°, AU5C,,N6=45°,,/年N BDE^X 5 °,密BE, :.AaCkg密AE+BE=AB,即AC+CI^A 13.例题5.己知:如图6,在Rt△月3.中,NG=9〔T ,沿过6点的一条直线班折会这个三角形,使.点与四边上的一点,重合,当N月满足什么条件时,点〃恰为力6中点?写出一个你认为适当的条件,并利用此条件证实 .为四中点.解:当N#30°时,点.恰为弱的中点・, Z C=90°〔〕,,N烟二6 0.〔直角三角形两锐角互余〕.又△外〔〕,,/第F/%后30°,且/£〃后NX9 0°〔全等三角形对应角相等〕,・・・N〃8斤N/〔等量代换〕.•・•用后月£〔等角对等边〕,又N 劫5=900 , 即及ZLHR,〃是月夕的中点〔三线合一〕.角平分线定理使用中的几种辅助线作法一、角平分线,构造三角形例题、如下图,在AA BC中,NAR C=3NC, AD是NBAC的平分线,BE_L AD于求证:3E」(AC-AB) 2证实:延长BE交AC于点F.由于角是轴对称图形,对称轴是角的平分线所在的直线, 所以A D为NBA C的对称轴,又由于BE_LA D于F,所以点B和点F关于AD对称,所以BE=FE=1B F.AB=AF,NABF=NAFB°2由于NABF+NFBC=NABC = 3NC,ZABF = ZAFB=ZFBC+ZC,所以ZFBC+ ZC+ZF B C=3 NC,所以NFBC=NC,所以FB=FC,所以BE=1 F C = L(AC-AF) =,(AC-AB), 2 2 2所以BE = g(AC — A8).二、一个点到角的一边的距离,过这个点作另一边的垂线段如下图,N1 = N2,P为BN上的一点,并且PD_LBC于D, AB+BC=2BDo求证:NBAP+NB C P = 180 °. 证实:经过点P作PE_LAB于点E.由于PE_L AB.PD_LBC, N1 = N2, 所以PE=PD,R t APBE 和RtZkPBC 中BP = BPPE = PD所以R t △PBETRt^PBC(HL),所以BE=BD Q由于AB+BC=2BD.BC = CD + BD,A B =B E-AE.所以AE=CDc由于PE_LAB.PD_L BC,所以NPEB = NPDB=9 0 0 .在AP AE 和RtZ^PCD 中PE = PDNPEB = ZPDCAE = DC所以APAEgR t APCD.所以NPCB=NEAP.j由于NBAP+NEAP= 180°,所以NBAP+NBCP=18O° °三、角平分线和其上面的一点,过这一点作角的两边的垂线段例题、如下图,在△ ABC中,PB、PC分别是NAB C的外角的平分线,求证:Z 1 =Z2证实:过点P作PE1AB于点E, P G ±AC于点G. PF±BC 于点F.由于P在NEBC的平分线上,PE_LAB. PH± BC,所以PE=PFo同理可证PF=PG0所以PG=PE.又PE_LAB.PGJ. AC,所以PA是NBAC的平分线,所以N1 = N2.与三角形的角平分线有关的结论的探究三角形的内角和等于18 0*三角形的外角等于和它不相邻的两个内角的和.应用以上定理和推论可以探究与三角形的角平分线有关的结论.从结论的探究过程中,希望同学们能从中得到有益的启示:在平时的数学学习中,要学会运用所学知识去探索新的结论,学会探究,从而不断地提升自己的数学发现与创新的水平,提升数学学习水平.探究一:在A48C中,NA, NB的平分线交于点P,试探究ZBPC与NA的关系?探究:由于NBPC在ABPC中,由三角形的内角和定理,有:NBPC = 180°-(ZPBC + ZPCB)而由B P, CP分别是NABC和NAC B的角平分线知:ZPBC=-ZABC, ZPCB=-ZACB2 2(\ \ 1所以ABPC = 180°- -ZABC +-ZACB = 180° -一(NA8C + ZACB) \ 2 2 7 2而在在A48C中,ZABC+ ZA = 180° - ZA所以/BPC = 180°--(180°-zS4)= 90°+-ZA2 2故有结论一:在中,NA, NB 的平分线交于点P,那么有N8PC=90°+L/A, 2探究二:在AA8C 中,BP 是NABC 的平分线,C P 是A ABC 的外角/ ACE 的平分线, 试探究:N BPC 与NA 的关系?探究:由CP 是△ A B C 的外角ZAC E 的平分线, 所以有:NBPC=NPCE-NBPC又BP 是NABC 的平分线,CP 是NAC E 的平线所以:NPBC=L Z ABC, ZPC E = -ZACE 22 所以 NBPC 二 2 2= -(ZACE-ZABC )=-ZA 2 2故有结论二:在AA8C 中,BP 是NABC 的平分线,CP 是AABC 的外角NACE 的平分线,探究三:在AA8C 中,BP, CP 分别是A ABC 的两个 外角的平分线,试探究:NBPC 与NA 的关系?探究:由于NBPC 在ABPC 中,由三角形的内角和定 理,有:NBPC = 180° -(ZPBC + ZPCB )由BP, CP 分别是A ABC 的两个外角的平分线,有:NP BC 二ZPCB=izBCF 2 2WZABC+ZCBE=18 0 °, ZAC B + ZBCF=1 8 0°,所以NA BC+ZCBE+ZACB+ZBC F=36 00所以NEBC+/FCB= 3 6 0°-(ZACB+ZABC) = 360° -(180° -zL4)= 180° + ZA所以 /BPC = 180° - l(ZEBC+ ZFCB) = 180°-1(180° + ZA )= 90(,-|zA故有结论三:在A48C 中,BP, CP 分别是A ABC 的两个外角的平分线,那么有 N8PC=900—L/A . 2线段垂直平分线的性质定理及其逆定理角平分线的性质定理及其逆定理水平测试一、选择题1.以下说法,错误的选项是(那么有:ABPC = -^A. 2AA.三角形任意两个角的平分线的交点到这个三角形的三边的距离都相等B.三角形任意两个角的平分线的交点必在第三个角的平分线上C.三角形两个角的平分线的交点到三角形的三个顶点的距离都相等D.三角形的任意两个角的平分线的交点都在三角形的内部2.假设一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是〔.〕3.如下图,在RtZXABC中,NAC8 = 90,3C的中垂线交斜边A3于.,A8 = 7.8, AAC = 3.9,那么图中有多少个角等于60.3〕A.2[ZB. 3 个C. 4 个.D. 5 个4.等腰△A8C两腰A8, AC的垂直平分线交于点.,以下各式不正确的选项是〔〕A. OA_L8CgB. OA平分N8AC*C. = O4 = 3C5.△A8C中,A8 = AC, A3的垂直平分线交AC于£〕,△A8C和△08.的周长分别是6 0 cm和38cm,那么△ ABC的腰长和底边的长分别是〔〕A. 24cm 和12cmB. 1 6 cm 和22cm C . 2 0cm 和16cm D . 22 cm 和16 cm6.将一张长方形纸片按如下图的方式折叠,BC, BD为折痕,那么NCBD的度数为〔〕A. 60°B. 75°C. 90°D. 9 5°7.假设△A8C三条角平分线的交点到三顶点的距离相等,那么该三角形一定为〔〕A.等腰三角形,但不一定是等边三角形.B.直角三角形.C.等腰直角三角形.D.等边三角形.8.如图,△ ABC中,AD为NBAC的平分线,DE±AB, DF±AC,E. F为垂足,在以下结论中:①AAD Eg4ADF;②^BDE乌ZkCDF ;③△ABDgZkACD;④AE=AF;⑤BE=CF:⑥BD二CD.其中正确结论的个数是〔〕A. UB.2<3oD. 49.产点在ZAO3的平分线上,NAO8 = 60 , OP = 10cm,那么P点到边OA , OB的距离分别是〔〕A. 5cm, 5>/3 cm B . 4cm, 5cm C. 5cm, 5cm D. 5 cm, 10 c m1 0.如图,Z^ABC中,/C=90〕BD平分NABC交AC于D, D E是AB的垂直平分线,DE二1B2 D,且DE=L5cm,那么AC等于〔〕A. 3cm°B・ 7. 5 c m C. 6cm D. 4. 5 cmC D二、填空题1.线段AB和它外一点P,假设P A=PB,那么点P在A B的;假设点P 在A B 的,那么PA=PB.2.如图,△ ABC中,E歹是A8的垂直平分线交于O, BF = 12 , C尸=3H那么AC =・A3. 如图,448c = 50" AO垂直平分线段8C于点.,NABC的平分线8石交AO于点E,连结EC,那么NAEC的度数是4.如下图,在△A3C中,NC = 90 , OE是A3的垂直平分线,AB = 2AC .3c = 18cm,那么CE的长度为,..5.在锐角三角形A8C中,NA = 60 , A3, AC两边的垂直平分线相交于点.,那么N3OC 的度数是.3.6.ZXA8C中,NC = 90 , AO平分N84C,交BC于D,假设DC = 7 ,那么.到A3的距离是•7.ZkA8C的三边长分别为3cm、4cm、5cm,假设.为△ 48C三内角平分线交点,那么点.到斜边AB的距离等于.8.如图,30平分NC8A, CO平分NAC3, MN〃8C,且过点O,假设A3 = 12, AC = 14,那么AAMN的周长是A9 .如图,3.是Z48C 的平分线,.七于E, S/版.=36m? , AB = 18cm >BC = 12cm,那么DE 的长是.1 0.如图,△ABC 中,ZC = 90 , AC = BC f AO 平分 N84c 交 BC 于.,DE LAB 于E,且AB = 10cm,那么△0E3的周长是“ »三、解做题1 .如下图,直线.4,表示两条相互交叉的公路.点何,N 表示两个蔬菜基地.现 要建立一个蔬菜批发「6场,要求它到两个基地的距离相等,并且到公路04,的距离相 等,请你作图说明此批发市场应建在什么地方?2 . 如图△ A8C 中,胡= 3C, N8 = 120°, A8的垂直平分线交AC 于.,求3 .用三角尺画角平分线:如图,NA0B 是一个任意角,在义M N 作0&0B 的垂线,交点为P,画射线0P,那么这条射线即%角平分 线.请解释这种做法的道理.你还能举出哪些作角平分线的方法, 并说明这种做法的道理.证:AO = ‘OC. 2 BA4.如下图,是△A3C的角平分线,.石_LA3,_L AC,垂足分别是E , F.求证:AO垂直平分族.四、探索题1 .如图,在△ABC中,N4 = 90 , AB = AC,是NA3C的平分线,请你猜测图中哪两条线段之和等于第三条线段,并证实你的猜测的正确性(证实你的猜测需要用题中所有的2.如下图,在等腰△ABC中,AB = AC, ZBAC = 120 .(1)请你作出两腰的垂直平分线.(2)假设A3边的垂直平分线与A8, 3c分别交于点.,E, AC边上的垂直平分线与AC, 8c分别相交于点G, F ,那么△4后是什么形状?你能证实吗?(3)连结.6, DG与BC有什么关系?(4)假设ZX7 = 5cm,试求的周长.答案:一、1 D; 2 C; 3D: 4D; 5D: 6C;7D;8 B ;9C; 10D.二、1 .垂直平分线上;垂直平分线上;2. 15; 3. 115°; 4. 12cm; 5. 120 ; 6. 7 ; 7.112c m;8. 26: 9. —cm ; 10. 10cm .三、L解:分别作ZAOB的平分线OC和线段MN的垂直平分线DE,那么射线OC与直线DE的交点、P即为批发巾场应建的地方.2.证实:连接8..A3的垂直平分线交AC于•••QA = O3又BA = BC, N8 = 120 , ZA = ZC = 30 ••• ZA = ZABD = 30 , /DBC = 90RtZXOBC中,有8.= !..,A AD = -DC.2 23.解:30M=ON, 0P=0P, A RtAOMP^RtAONP〔HL〕 , AZM0P=ZN0P,,射线OP是ZAOB 的平分线.4.证实:♦・♦4〕是△ABC的角平分线,DE-LAB,.产_LAC,二.七=./〔角平分线上的点到角的两边距离相等〕.••• NDEF = /DFE 〔等角对等边〕.: NAEZ〕 = NAEO = 90 〔垂直定义〕,••• ZAEF = ZAFE〔等角的余角相等〕.AE = AF〔等角对等边〕•••A,.在族的中垂线上〔和一条线段两个端点距离相等的点,在这条线段的垂直平分线上〕.即AO是七厂的中垂线.四、1 .解:猜测结论:A8 + A£> = 8C,过.作.E_L3C于E.•••3.平分ZA8C, ZA = 90 , :.AD = DE.:.Z\ABD 94EBD,, AB = BE.•.・ AB = AC, :. ZC = 45、:.DE = EC.:.AD = EC. AB + AD = BC.2.解:〔1〕如下图.(2)△AE/是等边三角形.证实:•・• AB = AC , ABAC = 120 , J ZB = ZC = 30 .•・• DE垂直平分线AB, :.EB = EA,:./BAE = /B = 30 , ••• AAEF = 60 .同理可证NAEE = 60.•♦•△AE尸是等边三角形.⑶由于点D、G分别是AB、AC的中点,所以DG是中位线,那么0G =L B C.2〔4〕*:AE = BE, AF = FC f的周长为:AE+EF + AF = BE+EF + FC = BC.又••♦8C = 2ZX7 = 10cm.,八4£月的周长为10cm.选做题1. AiABC中,ZB = 22.5J , ZC = 60 , A3的垂直平分线交8.于.,交AB于F, BD = 60, AE_L3C于心求反?的长.解:连结AO.月是A8的垂直平分线,••• AD = BD = 672 〔线段垂直平分线上的点到线段两个端点的距离相等〕•\ Nl = NB = 22.5 〔等边对等角〕••• N2 = N1 + N8 = 45"••• Z3 = 90 - Z2 = 90 -45° = 45 ,,Z2 = N3••• A七二.石〔等角对等边〕9:DE2+AE2=AD2〔勾股定理〕2AE2 = 〔6yj2〕29:.AE = 6.在R t/\ACE中,ZC = 60,•二Z4 = 30•♦.AC = 2CE〔30所对的直角边等于斜边的一半〕9: AC2-EC2 =AE2〔勾股定理〕A 〔2CE〕2一CE2 = AE2,•二3CE2 = AE2,:.CE2=\l y:.CE = 2y/3.2 .如图,NA = 90.. AD//BC. P 是AB的中点,P 1〕平分NADC.求证:CP平分NDCB.证实:过点P作P E _L D C,垂足于E, ,N3 = N4 = NA = 90°,•••PD平分NADC, A Z1 = Z2,,PA = PE,•・・P为AB的中点,、:• PA = PB, PE = PB,•: AD // BC, ZA = 90° ,•・・P点在NDCB的平分线上.,CP 平分NDCB.3. CE, 3尸分别是锐角三角形ABC的NAC8, NA8C的平分线,AFL3F于尸,AELC石于E,试说明:(1) EF//BC ; (2) EF = -(AB + AC-BC).提示:由于8/是角平分线,且A所,所以延长A尸交8c于N,那么有△A8V是等腰三角形,从而尸是AN的中点,且A3 = 8N,同理E是AW的中点,且AC = CM,所以EF 〃 BC,且EF = L 〔BN + CM - CB〕 = L 〔AB + AC - BC〕.2 2备用题1.如果三角形内的一点到三边的距离相等,那么这点是〔〕CA.是三条边中垂线的交点B.是三角形三条边的中线的交点C.是三角形三个内角平分线的交点D.是三角形三条边上的高的交点2.如图,ZXABC中,NC AB=120° , AB, AC的垂直平分线分别交BC于点E、F,那么NEAF等于3.如果△ABC的边3c的垂直平分线经过顶点A,与3c相交于点.,且A8 = 2AQ,那么△A8C中必有一个内角的度数为〔〕DA. 45、B. 60 *C. 90 oD. 1204 .如图,RtZkACB, NC = 90 , AO平分NC43, 于E,那么以下结论中不正确的是〔〕BA. BD+ED = BCB. DE 平分NADBC. A.平分NEOCA D. ED + AC>AD5.等腰三角形内有一点P到底边的两端点距离相等,那么连结顶点和P的直线一定把底边.垂直平分5 .如图,在Rt^ABC中,N8 = 90>,石.垂直平分AC交AC于点.,交BC于息E,已知N£AB:4AC = 2:5,求NC 的度数.解:设ZE48=2A-,那么々AC = 5x, :.ZC = ZEAC = 3x.而NC + N8AC = 90 , A5x + 3x = 90 , x = 11.25\ ZC = 33.75?6 .如下图,AO是N84c的平分线,DE±AB于E,.尸_L AC于尸,且80 = 8. 求证:BE = CF.证实:♦「A.是N84C的平分线,.石_LA3, DF A.AC ,.七=.尸.(角平分线上的点到这个角两边的距离相等)又•/ BD = CD y:. RtADBE • RtADCF(HL):.BE = CF.7.如图,在△A8C中,NC = 90 ,点.是斜边A8的中点,AB = 2BC, DE±AB交47于£求证:8E平分乙43c.E证实:是A8的中点,2•/ AB = 2BC, /. BC = -AB, :.BD = BC .2又,? DE .LAB, ZC = 90,, ZC = ZBDE = 90 ,又BE = BE, :・RtABDEMRtABCE(HL), :.NDBE = /EBC, :・BE斗分/ABC.角平分线性质定理之应用三角形的角平分线是三角形的主要线段之一,它在几何的计算或证实中,起着“桥梁〞的作用.那么如何利用三角形的角平分线解题呢?下而举例说明.一、由角平分线的性质联想两线段相等例1如图1, AB>AC, NA的平分线与BC的垂直平分线相交于D,自D作DE_LAB, DFJ_AC,垂足分别为E, F.求证:BE=CF.证实连结DB, DC.•••D在NA的平分线上,,DE=DF.••• D在BC的垂直平分线上,.・.BD=DC.又NBED=/CFD=90° ,/.RtABDE^ R tACD F , ABE=CF.二、由角平分线的轴对称性构造全等三角形例2 如图2,BC>AB, BD平分NABC,且A D二DC 求证:ZA+ZC= 1 8 0° .图1证实延长BA至F,使BF=BC.由BD平分NABC在△ F B D 与ZkCBD 中,BF=B C ZABD=Z C BD BD= B D AAFBD^ACBD,A ZC=Z F , DF=CD=AD, NF=DAF, .-.ZA + ZC=ZBAD+ZDAF=180° . 三、过角平分线上一点作一边的平行线,构成等腰三角形例3 :如图3, NABC的平分线BF与NACB的平分线CF相交于点F,过F作DE 〃BC,交AB 于D,交AC于E,求证:BD+CERE.证实:TBF是N ABC的平分线AZDBF=ZCBF 又•.•DE〃BC 万.\ZDFB=ZCBF,NDBF=NDFB,BD二FD,同理C E= F E.ABDrC E=DF+FE=DE四、实际生活中的应用例4如图4,有三条公路I>.两两相交,要选择一地点建一座加油站,是加油站到三条公路的距离相等,应如何选择建加油站的地址?这样的位置有几种选择?解析:分别作△ A 两内角的平分线,它们相交于一点,根据角图4 性质知,这个点到三条公路的距离相等:或者分别作△ A8C相邻两外角的平分线,它们的交点到三条公路的距离也相等,这样点共有三个,所以建加油站的位置共有4种选择.角平分线携“截长补短〞显精彩角的平分线具有其特有的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法〞又是解决这一类问题的一种特殊方法,利用此种方法常可使思路豁然开朗.请看几例. 例1 如图1-1,月〃〃5C,点6在线段也上,4ADF4CDE, 4DCF4 E CB.求证:CD=AD+BC.分析:结论是CD=AD-BC y可考虑用“截长补短法〞中的“截长〞,即在.〃上截取C5, 只要再证£代期即可,这就转化为证实两线段相等的问题,从而到达简化问题的目的.证实:在⑦上截取.尸二6G如图1一2在△尸CE与△屈为中,CF = CB•ZFCE = ZBCECE = CEJXFCMXBCE (SAS) , AZ2=Z1.又,:AD〃BC, :.ZADC+ZBCI^ 1 80 °,,/〃口+N C 〃品9 0° , AZ2+Z3 = 9 0° , Z 1 +Z4=9 0° , AZ3 = Z4.在与△山店中,ZFDE=ZADEDE = DEN3 = N4:AFD厘AADEgSA) , :.DF^DA,•/ CD= D F+ CF, :. CH2 BC.图1-1 B图1-2例2,如图2-1, N1 = N2,尸为民V 上一点,且尸于点〃/夕+/U2放求证:/8“斗N5C 尸=1800.分析:证两个角的和是180°,可把它们移到一起,让它们是邻补角, 后4因而此题适用“补短〞进行全等三角形的构造.证实:过点尸作PE 垂直B A 的延长线于点瓦如图2-2• ••/1 = /2,且产〃,BC,:・PE=PD,在 RtXB P E 与 RtABPD 中,PE = PDBP=BP:.RtABP 的 RtABPDim, :・BFBD.• : A 历B C=2BD, :. AB+ B D+g B 步% ;.A 济DC=BE 即 DC= B&AB =AS.在了亡△ APE 与RtXCP 〃中,PE=PD• ZPEA = ZPDCAE=DC:.RtXAP 厘Rt4CPD0&,:.N/MFN PCD又♦: NBA 用NR1£=18O° , ;♦/8AP+NBC 尸=180°例3己知:如图3-1,在△嫉中,NO2N6, Z1=Z2.求证:冷力C+ CD.分析:从结论分析,“截长〞或“补短〞都可实现问题的转化,即延 长月.至£使.48 或在月月上截取止 证实:方法一(补短法)延长力.到左 使〃RCE,那么=NC£〃 /.』ACB=24E,• :乙AC B 之4 B, :. Z5= Z F,在 4ABDW4AED 中,21 = Z2• NB = NEAD=AD:.XABDQXAED (AAS) , :.AB=AE.又 A E=AC+C 匹AC+DC, :. AB^AC^r DC. 方法二〔截长法〕在四上截取AF^A C,如图3- 3在与△?! C,中, AF = AC< Zl = Z2AD=AD:AAF 哈△ACD(SAS ) , :.DF=DC, N /尸氏N / CD. 又•: 4ACB= 2/B,:・/FD 斤4B, :.FD= FB.即证实N6c AN BD图3-2<: AB = AF〞 B=AHFD, :. A&^A&CD.上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰中选择适宜思路进行分析.让掌握学生掌握好“截长补短法〞对于更好的理解数学中的化归思想有较大的帮助.角平分线问题中的一题多解如图1 所示,在△ ABC 中,/C=2NB./ 1 =Z 2 o求证:AB=AC+C D o证法一:截取法.就是在较长的线段中截取一段与求加法运算的两条线段中的一条相等, 然后证实另一段等于加法运算的另一条线段.如图2所示,在AB上截取AE=AC,连结DE.在aAED和4ACD中AE = AC<Z1 = Z2AD = AD所以△AEDgAACD.所以ED=CD, Z3=ZC<,图2由于N3=NB+N4,NC=2NB,所以NB=N4,所以BE=DE0所以AB=AE+BE=AC+DE=AC+C D.证法二、补短法.就是在较短的一条线段的根底上通过延长在截取的方法将求和的两条线段连结在一起.本种方法是延长AC,再在延长线上截取CF=CD O如图3所示,延长AC到点F,使CF=CD,连结DF.由于C F=CD,所以N3 = NF,由于NACB=N3+NF, 所以NACB=2NF0 又由于NACB=2 NB, 所以NB=NF,在4ABD和4AFD中Z1 = Z2<NB ="AD = AD所以△ABDTZkA FD,所以AB=AF.由于AF=AC+CF=AC+CD,所以AB= A C+CDo第三种方法:也是属于补短法,本种方法是延长DC,再在延长线上截取CM=AC.证实:延长DC,在DC的延长线上截取CM=AC,连结AM.由于由于CM=CA,所以N3=NM.由于NAC B = N3 +NM, 所以NACB=2 NM=2N3,又由于N ACB=2NB,所以NB = NM=N3,所以AB=AM.由于N4=NB + N1,N D AM=N2+N3,N 1=Z2所以N4=NDAM,所以AM= DM=DC+CM=DC + AC,所以AB = DC+AC0练习:如图5所示,在AABC中,BC边的垂直平分线DF交△ B A C的外角平分线AD于点D.F为垂足.DE_L AB 于E,并且AB>AC,求证:BE-AC=AEo提示:可以将减法运算转化为加法运算,然后利用“截长〞或者“补短〞法解决问题,。
中考数学全等三角形角平分线辅助练习题附解析
中考数学全等三角形角平分线辅助练习题附解析一、全等三角形角平分线辅助1.如图1,在ABC 中,AF ,BE 分别是BAC ∠和ABC ∠的角平分线,AF 和BE 相交于D 点.(1)求证:CD 平分ACB ∠;(2)如图2,过F 作FP AC ⊥于点P ,连接PD ,若45ACB ∠=︒,67.5PDF ∠=︒,求证:PD CP =;(3)如图3,若23180BAF ABE ∠+∠=︒,求证:BE BF AB AE -=-.2.已知:如图,//AC BD ,AE ,BE 分别平分CAB ∠和ABD ∠,点E 在CD 上.用等式表示线段AB 、AC 、BD 三者之间的数量关系,并证明.3.直线MN 与直线PQ 垂直相交于点O ,点A 在射线OP 上运动(点A 不与点O 重合),点B 在射线OM 上运动(点B 不与点O 重合).(1)如图1,已知AE 、BE 分别是∠BAO 和∠ABO 的角平分线,①当∠ABO =60°时,求∠AEB 的度数;②点A 、B 在运动的过程中,∠AEB 的大小是否会发生变化?若发生变化,请说明变化的情况:若不发生变化,试求出∠AEB 的大小;(2)如图2,延长BA 至G ,已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线所在的直线分别相交于E 、F ,在△AEF 中,如果有一个角是另一个角的3倍,请直接写出∠ABO 的度数.4.如图,∠D=∠C=90°,点E是DC的中点,AE平分∠DAB,∠DEA=28°,求∠ABE的大小.5.如图,已知等腰直角三角形ABC中,AB=AC,∠BAC=90°,BF平分∠ABC,CD⊥BD交BF的延长线于点D,试说明:BF=2CD.∠和6.如图1,点A是直线MN上一点,点B是直线PQ上一点,且MN//PQ.NAB ABQ∠的平分线交于点C.⊥;(1)求证:BC AC(2)过点C作直线交MN于点D(不与点A重合),交PQ于点E,+=;①若点D在点A的右侧,如图2,求证:AD BE AB②若点D在点A的左侧,则线段AD、BE、AB有何数量关系?直接写出结论,不说理由.7.在平面直角坐标中,等腰Rt△ABC中,AB=AC,∠CAB=90°,A(0,a),B(b,0).-+(a-2)2=0,求△ABO的面积;(1)如图12a b(2)如图2,AC 与x 轴交于D 点,BC 与y 轴交于E 点,连接DE ,AD=CD ,求证:∠ADB=∠CDE ;(3)如图3,在(1)的条件下,若以P (0,-6)为直角顶点,PC 为腰作等腰Rt △PQC ,连接BQ ,求证:AP ∥BQ .8.如图所示,在四边形ABCD 中,AC 平分,DAB CD CB ∠=,求证:180B D ∠+∠=.9.如图,OA=OB ,∠AOB=90°,BD 平分∠ABO 交OA 于点D ,AE ⊥BD 于E ,求证:BD=2AE.10.如图,在ABC ∆中,AB AC >,AD 平分BAC ∠交BC 于D ,求证:AB AC BD CD ->-.【参考答案】***试卷处理标记,请不要删除一、全等三角形角平分线辅助1.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)过D 点分别作三边的垂线,垂足分别为G 、H 、K ,根据角平分线的定义可证得DG=DH=DK ,从而根据角平分线的判定定理可证得结论;(2)作DS AC ⊥,DT BC ⊥,在AC 上取一点Q ,使QDP FDP ∠=∠,通过证明SQD TFD △≌△和QDP FDP △≌△得到22.5PDC PCD ∠=∠=︒,从而根据等角对等边判断即可;(3)延长AB 至M ,使BM BF =,连接FM ,通过证明AFC AFM △≌△得到AC AM =,再结合CE EB =即可得出结论.【详解】(1)证明:如图所示,过D 点分别作三边的垂线,垂足分别为G 、H 、K ,∵AF ,BE 分别是BAC ∠和ABC ∠的角平分线,∴DG DH DK ==,∴CD 平分ACB ∠;(2)证明:如图,作DS AC ⊥,DT BC ⊥,在AC 上取一点Q ,使QDP FDP ∠=∠. ∵CD 平分ACB ∠,∴DS DT =,∵67.5QDP FDP ∠=∠=︒,45ACB ∠=︒,∴13545180QDF ACB ∠+∠=︒+︒=︒,在四边形QDFC 中,180CQD DFC ∠+∠=︒,又∵180DFT DFC ∠+∠=︒,∴CQD DFT ∠=∠,在SQD 和TFD △中,90CQD DFT DS DTDSQ DTF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴SQD TFD △≌△,∴QD FD =,在QDP △和FDP 中QD FD QDP FDP DP DP =⎧⎪∠=∠⎨⎪=⎩∴QDP FDP △≌△,∴45QPD FPD ∠=∠=︒又∵QPD PCD PDC ∠=∠+∠,22.5PCD ∠=︒,∴22.5PDC PCD ∠=∠=︒,∴CP PD =;(3)证明:延长AB 至M ,使BMBF =,连接FM . ∵AF ,BE 分别是BAC ∠和ABC ∠的角平分线, ∴22180BAF ABE C ∠+∠+∠=︒,又∵23180BAF ABE ∠+∠=︒,∴C ABE CBE ∠=∠=∠,∴CE EB =,∵BM BF =,∴BFM BMF ABE CBE C ∠=∠=∠=∠=∠,在AFC △和AFM △中,C BMF CAF BAF AF AF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴AFC AFM △≌△,∴AC AM =,∴AE CE AB BM +=+,∴AE BE AB BF +=+,∴BE BF AB AE -=-.【点睛】本题考查角平分线的性质与判断,以及全等三角形的判定与性质,灵活结合角平分线的性质构造辅助线是解题关键.2.AB=AC+BD ,证明见详解.【分析】延长AE ,交BD 的延长线于点F ,先证明AB=BF ,进而证明△ACE ≌△FDE ,得到AC=DF ,问题得证.【详解】解:延长AE ,交BD 的延长线于点F ,∵//AC BD ,∴∠F=∠CAF ,∵AE 平分CAB ∠,∴∠CAF=∠BAF ,∴∠F=∠BAF ,∴AB=BF ,∵BE 平分ABF ∠,∴AE=EF,∵∠F=∠CAF,∠AEC=∠FED,∴△ACE≌△FDE,∴AC=DF,∴AB=BF=BD+DF=BD+AC.【点睛】本题考查了等腰三角形的判断与性质,全等三角形的判定与性质,根据题意添加辅助线构造等腰三角形和全等三角形是解题关键.3.(1)①135°②∠AEB的大小不会发生变化,∠AEB=135°,详见解析(2)∠ABO=60°或45°【分析】(1)①根据三角形内角和定理、角分线定义,即可求解;②方法同①,只是把度数转化为角表示出来,即可解答;(2)根据三角形内角和定理及一个外角等于与它不相邻的两个内角和,利用角的和差计算即可求得结果,要对谁是谁的3倍分类讨论..【详解】(1)如图1,①∵MN⊥PQ,∴∠AOB=90°,∵∠ABO=60°,∴∠BAO=30°,∵AE、BE分别是∠BAO和∠ABO的角平分线,∴∠ABE=12∠ABO=30°,∠BAE=12∠BAO=15°,∴∠AEB=180°﹣∠ABE﹣∠BAE=135°.②∠AEB的大小不会发生变化.理由如下:同①,得∠AEB=180°﹣∠ABE﹣∠BAE=180°﹣12∠ABO﹣12∠BAO=180°﹣12(∠ABO+∠BAO)=180°﹣12×90°=135°.(2)∠ABO的度数为60°.理由如下:如图2,∵∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F,∴∠OAE+∠OAF=12(∠BAO+∠GAO)=90°,即∠EAF=90°,又∵∠BOA=90°,∴∠GAO>90°,①∵∠E=13∠EAF=30°,∠EOQ=45°,∠OAE+∠E=∠EOQ=45°,∴∠OAE=15°,∠OAE=12∠BAO=12(90﹣∠ABO)∴∠ABO=60°.②∵∠F=3∠E,∠EAF=90°∴∠E+∠F=90°∴∠E=22.5°∴∠EFA=90-22.5°=67.5°∵∠EOQ=∠EOM= ∠AOE= 45°,∴∠BAO=180°-(180°-45°-67.5°)×2=45°∴∠ABO=90°-45°=45°【点睛】本题考查了三角形内角和定理及外角的性质、角分线定义,解决本题的关键是灵活运用三角形内角和外角的关系.4.28°【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,即可求得∠ABE的度数.【详解】如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,∴∠BEC=90°-∠AED=62°,∴Rt△BCE中,∠CBE=28°,∴∠ABE=28°.【点睛】考查了平行线的性质与判定、角平分线上的点到角的两边距离相等的性质、到角的两边距离相等的点在角的平分线上的性质,解题关键是熟记各性质并作出辅助线.5.见解析【分析】作BF的中点E,连接AE、AD,根据直角三角形得到性质就可以得出AE=BE=EF,由BD 平分∠ABC就可以得出∠ABE=∠DBC=22.5°,从而可以得出∠BAE=∠BAE=∠ACD=22.5°,∠AEF=45°,由∠BAC=90°,∠BDC=90°就可以得出A、B、C、D四点共圆,求出AD=DC,证△ADC≌△AEB推出BE=CD,从而得到结论.【详解】解:取BF的中点E,连接AE,AD,∵∠BAC=90°,∴AE=BE=EF,∴∠ABD =∠BAE ,∵CD ⊥BD ,∴A ,B ,C ,D 四点共圆,∴∠DAC =∠DBC ,∵BF 平分∠ABC ,∴∠ABD =∠DBC ,∴∠DAC =∠BAE ,∴∠EAD =90°,∵AB =AC ,∴∠ABC =45°,∴∠ABD =∠DBC =22.5°,∴∠AED =45°,∴AE =AD ,在△ABE 与△ADC 中,ABE DAC BAE ACD AE AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADC ,∴BE =CD ,∴BF =2CD .【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,直角三角形的性质,角平分线的性质,正确的作出辅助线是解题的关键.6.(1)见解析;(2)见解析;(3)BE AD AB =+【分析】(1) 由平行线性质可得∠NAB+∠ABQ=180°,再由角平分线定义可得11,22∠=∠∠=∠BAC NAB CBA ABQ ,再利用三角形内角和定理即可得∠C=90°,即可证明BC ⊥AC;(2) ①延长AC 交PQ 点F ,先证明AC=FC,再证明△ACD ≌△FCE,即可得AD+BE=AB; ②方法与①相同.【详解】解:(1)∵MN ∥PQ∴∠NAB+∠ABQ=180°∵AC 平分∠NAB ,BC 平分∠ABQ ∴11,22∠=∠∠=∠BAC NAB CBA ABQ ∴∠BAC+∠ABC=12180⨯︒=90°在△ABC中,∵∠BAC+∠ABC+∠C=180°∴∠C=180°- (∠BAC+∠ABC) =180°-90°=90°∴BC⊥AC;(2)①延长AC交PQ于点F∵BC⊥AC∴∠ACB=∠FCB=90°∵BC平分∠ABF∴∠ABC=∠FBC∴BC=BC∴△ABC≌△FBC∴AC=CF,AB=BF∵MN∥BQ∴∠DAC=∠EFC∵∠ACD=∠FCE∴△ACD≌△FCE∴AD=EF∴AB=BF=BE+EF=BE+AD即:AB=AD+BE②线段AD,BE,AB数量关系是:AD+AB=BE 如图3,延长AC交PQ点F,∵MN//PQ .∴∠AFB=∠FAN,∠DAC=∠EFC∵AC平分∠NAB∴∠BAF=∠FAN∴∠BAF=∠AFB∴AB=FB∵BC ⊥AC∴C 是AF 的中点∴AC=FC在△ACD 与△FCE 中DAC EFC AC FCACD FCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ACD FCE ASA ≅∴AD=EF∵AB=FB=BE-EF∴AD+AB=BE【点睛】本题考查了平行线性质,全等三角形性质判定,等腰三角形性质等,解题关键正确添加辅助线构造全等三角形.7.(1)△ABO 的面积=4;(2)证明见解析;(3)证明见解析.【分析】(1)根据绝对值和偶次方的非负性求出a ,b ,根据三角形的面积公式计算;(2)作AF 平分∠BAC 交BD 于F 点,分别证明△ACE ≌△BAF ,△CED ≌△AFD ,根据全等三角形的性质证明;(3)过C 点作CM ⊥y 轴于M 点,过D 点作DN ⊥y 轴于N 点,证明△ACM ≌△BAO ,根据全等三角形的性质得到CM=AO=2,AM=BO=4,证明四边形ONQB 为平行四边形,得到答案.【详解】解:(1)∵+(a-2)2=0,∴2a-b=0,a-2=0,解得,a=2,b=4,∴A (0,2),B (4,0),∴OA=2,OB=4,∴△ABO 的面积=12×2×4=4;(2)作AF 平分∠BAC 交BD 于F 点,∵AB=AC ,∠CAB=90°,∴∠C=∠ABC=∠DAF=∠BAF=45°,∵∠CAE+∠BAO=∠ABF+∠BAO=90°,∴∠CAE=∠ABF ,在△ACE 和△BAF 中,CAE ABF AC AB ACE BAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ACE ≌△BAF (ASA ),∴CE=AF ,在△CED 和△AFD 中,CD AD C DAF CE AF =⎧⎪∠=∠⎨⎪=⎩,∴△CED ≌△AFD (SAS )∴∠CDE=∠ADB ;(3)过C 点作CM ⊥y 轴于M 点,过D 点作DN ⊥y 轴于N 点,则∠AMC=∠BOA=90°,∵∠CAM+∠BAO=∠ABO+∠BAO=90°,∴∠CAM=∠ABO ,在△ACM 和△BAO 中,CAM ABO CMA AOB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACM ≌△BAO (AAS ),∴CM=AO=2,AM=BO=4,∵A (0,2),P (0,-6),∴AP=8,∴PM=AP-AM=4,在△PCM 和△QPN 中,CPM PQN PMC QNP PC PQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,△PCM ≌△QPN (AAS ),∴NQ=PM=4,∴四边形ONQB 为平行四边形,∴AP ∥BQ .【点睛】本题考查的是全等三角形的判定和性质,非负数的性质,掌握全等三角形的判定定理和性质定理是解题的关键.8.详见解析【解析】【分析】过点C 分别作CE AB ⊥于E ,CF AD ⊥于F ,由条件可得出△CDF ≌△CEB ,可得∠B=∠FDC ,进而可证明∠B+∠ADC=180°.【详解】证明:过点C 分别作CE AB ⊥于E ,CF AD ⊥于F ,∵AC 平分∠BAD ,CE ⊥AB 于E ,CF AD ⊥于F ,∴CF=CE ,在Rt △CDF 与Rt △CEB 中,CF=CE CD=CB⎧⎨⎩ ∴CBE CDF ∆∆≌, CBE CDF ∴∠=∠,180ADC CDF ∠+∠=︒,A C 180B D ∴∠+∠=︒ .【点睛】本题考查全等三角形的判定和性质,关键是根据HL 证明△CDF ≌△CEB 进而得出∠B=∠FDC .9.详见解析【分析】延长BO ,AE 并交于F ,证△ABE ≌△FBE ,推出AE=EF ,证△BOD ≌△AOF 推出BD=AF 即可.【详解】延长BO ,AE 并交于F ,∵BD 平分∠ABO ,AF ⊥BD ,∴∠1=∠2,∠AEB=∠FEB=90°,在△ABE 和△FBE 中1=2BE BEAEB FEB ∠∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABE ≌△FBE ,∴AE=EF ,∵∠AOB=90゜,∠AED=90°,∠ADE=∠BDO ,∴∠2=∠OAF ,∵∠AOB=90°,∴∠DOB=∠FOA=90°,∴在△OBD 和△OAF 中2=FAO BO AOBOD AOF ∠∠⎧⎪=⎨⎪∠=∠⎩, ∴△OBD ≌△OAF ,∴BD=AF ,∵AE=EF ,∴BD=2AE .【点睛】本题考查了全等三角形的性质和判定的应用,正确添加辅助线构建全等三角形是解题的关键.10.详见解析【解析】【分析】可以在AB 上截取AE=AC ,构造三角形全等,再结合三角形三边关系可证得结论.【详解】在AB 上截取AE=AC ,则BE=AB-AC ,在△AED 和△ACD 中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△AED ≌△ACD(SAS),∴DE=DC ,在△BDE 中,BD-DE <BE(三角形两边之差小于第三边),∴BE>BD-CD ,即AB-AC>BD-CD.【点睛】本题考查了全等三角形的判定与性质,三角形三边关系,构造三角形全等是解题的关键.。
提分专题四 遇到角平分线如何添加辅助线
A.①③
√
B.①②③
第3题图
)
C.①②
D.①④
方法 四 作垂线构造等腰三角形、全等三角形
方法分析
过角平分线上一点,作角平分线的垂线,构造两个全等
的直角三角形和一个等腰三角形
图示
条件及结论
条件:如图, 是 ∠ 的平分线, ⊥ .
结论: Rt △ ≌ Rt △ , △ 为等腰三角形
遇到角平分线如何添
提分专题四
加辅助线
方法 一 过角平分线上的点向两边作垂线
方法分析
过角平分线上一点,作角两边的垂线,得线段相等和三角
形全等,进而求线段长或面积
图示
条件:如图, 是 ∠ 的平分线, ⊥ ,
条件及结论 ⊥ .
结论: = , △ ≌△
针对训练
1.如图, , , 分别平分 ∠ , ∠ , ∠ , ⊥ 于点
, = 3 , △ 的面积为36,则 △ 的周长为(
A.48
B.36
ቤተ መጻሕፍቲ ባይዱ
√
C.24
第1题图
D.12
)
方法 二 截取线段构造全等三角形
方法分析
在角一边上截取与角另一边上相等的线段,构造全等三角
3或7
,则 的长为______.
第2题图
方法 三 作平行线构造等腰三角形
方法分析
过角平分线上一点,作与角的一边平行的直线,构造等腰
三角形
图示
条件:如图, 是 ∠ 的平分线, 为 上一点,
条件及结论 // 交 于点 .
结论: △ 为等腰三角形, =
针对训练
2024年中考数学二轮复习题型突破课件—与角平分线有关的辅助线问题
180°- ∠BFD = 80°.∴ ∠FDC = 60°.∵ ∠EDC =
∠ADB=180°-∠1-∠A=180°-20°-100°=60°,
∴ ∠EDC = ∠FDC. 又 ∵ CD = CD , ∴
△DCE≌△DCF.∴ CE=CF.∴ BC=BF+CF=AB
积是
16
.
第3题
1
2
3
4
5
6
7
4. 如图,∠ADE=∠BDE=15°,EF∥DB,EC⊥DB于点C.若EC= 3,
则EF的长为
2
.
第4题
1
2
3
4
5
6
7
5. 如图,在△ABC中,AD是∠BAC的平分线,BE是△ABD的边AD上的
中线.若△ABC的面积是24,AB=5,AC=3,则△ABE的面积是
2024年中考数学二轮复习题型突破—与角平分线有关的辅助线问
题
主讲人:XXX
类型1 作垂线
模型解读:如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点
A,PB⊥ON于点B,则PA=PB,△OAP≌△OBP.
典例1 如图,∠AOB=30°,OC平分∠AOB,CD⊥OA于点D,CE∥AO
交OB于点E,OE=20cm,求CD的长.
∠NBD.在△CDM和△BDN中,∵ ∠CMD=∠BND=90°,∠MCD=
∠NBD,DM=DN,∴ △CDM≌△BDN.∴ CD=BD
第6题答案
1
2
3
4
5
6
7
7. 如图,在△ABC中,∠BAC=60°,∠ABC=80°,∠BAC与∠ABC的平
22.第四章 微专题 遇到角平分线如何添加辅助线
微专题 遇到角平分线如何添加辅助线 例2 如图,在△ABC中,AD平分∠BAC,E是BC的中点,AD⊥BD,若 AC=7,AB=3,则DE的长为 2 .
例2题图
微专题 遇到角平分线如何添加辅助线
例3 如图,在四边形ABCD中,AC为∠BAD的平分线,BC=2,若∠B =2∠D=120°,求CD的长.
在△ABD和△ACF中,
∠ABD=∠ACF
AB=AC
,
∠BAD=∠CAF=90°
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵BD平分∠ABC,
∴∠EBC=∠EBF,
第5题图
F
微专题 遇到角平分线如何添加辅助线
在△BCE和△BFE中,
∠EBC=∠EBF
BE=BE
,
∠CEB=∠FEB
∴△BCE≌△BFE(ASA),
微专题 遇到角平分线如何添加辅助线
例5
一题多解法 如图,在△ABC中,AB=3,BC=6,BD平
分∠ABC,求
CD AD
的值.
解:如图,过点D作DE∥AB交BC于点E,
则∠ABD=∠BDE,
∵BD平分∠ABC, ∴∠ABD=∠DBC, ∴∠BDE=∠DBE,Байду номын сангаас∴DE=BE,
E
例5题图
微专题 遇到角平分线如何添加辅助线
AC上,连接DE,DF,DE=4,若∠BAC+∠EDF=180°,则DF的长
为___4____.
第4题图
解题关键点 在AB上截取AG=AF,连接DG,构造全等三角形.
微专题 遇到角平分线如何添加辅助线
5.如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BD是∠ABC的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DABC角平分线专题1、 轴对称性:内容:角是一个轴对称图形,它的角平分线所在的直线是它的对称轴。
思路和方法:边角等 造全等,也就是在角的两边上取相等的线段 构造全等三角形 基本结构:如图,2、 角平分线的性质定理:注意两点(1)距离相等 (2)一对全等三角形3、 定义:带来角相等。
4、 补充性质:如图,在△AB C中,AD 平分∠BAC ,则有AB:AC=BD:DC针对性例题:例题1:如图,AB=2AC ,∠BAD=∠DAC ,DA =DB求证:DC ⊥ACB例题2:如图,在△AB C中,∠A等于60°,BE 平分∠ABC,C D平分∠ACB 求证:DH=E H例题3:如图1,B C>A B,BD 平分∠A BC,且∠A+∠C=1800, 求证:AD=D C.:思路一:利用“角平分线的对称性”来构造因为角是轴对称图形,角平分线是其对称轴,因此,题中若有 角平分线,一般可以利用其对称性来构成全等三角形.证法1:如图1,在BC 上取B E=AB,连结DE ,∵BD 平分∠A BC,∴∠A BD=∠D BE ,又BD=BD,∴△ABD ≌△EBD (S AS),∴∠A =∠DB E,AD=D E,又∠A+∠C=1800,∠D EB+∠DE C=1800,∴∠C=∠D EC,D E=DC ,则AD =DC . 证法2:如图2,过A 作BD 的垂线分别交BC 、B D于E 、F ,连结DE,由BD 平分∠ABC ,易得△ABF ≌△EBF,则AB=B E,BD 平分∠A BC,BD =BD ,∴△ABD ≌△E BD(SA S),∴AD =ED ,∠BAD =∠DEB,又∠BA D+∠C=1800, ∠BED+∠CE D=1800,∴∠C=∠DEC ,则DE=DC,∴AD=DC . 说明:证法1,2,都可以看作将△AB D沿角平分线BD 折向B C而构成 全等三角形的.证法3:如图3,延长BA 至E ,使BE=B C,连结D E, ∵BD 平分∠A BC,∴∠CBD =∠DBE ,又BD=BD ,∴△CB D≌△EBD (SAS), ∴∠C=∠E ,CD=DE,又∠BA D+∠C=1800,∠DA B+∠D AE=1800, ∴∠E=∠D AE,DE =DA ,则AD=DC . 说明:证法3是△CBD 沿角平分线B D折向B A而构成全等三角形的.B AC D E 图1B ACDEF 图2B ACD E图3思路二:利用“角平分线的性质”来构造由于角平分线上的点到角的两边的距离相等,所以根据这个性质,可以 过角平分线上一点向角的两边作垂线而构成两个全等的直角三角形.证法4:如图4,从D 分别作BC 、BA 的垂线,垂足为E、F ,∵BD 平分∠ABC ,∴DE =D F,又∠B AD +∠C=1800,∠BAD+∠FAD=1800, ∴∠FAD=∠C,∴△FAD ≌△E CD(AA S),则AD=DC .例题4 已知:如图5,在△ABC 中,∠C =90°,AC =BC,AD 平分∠CAB .求证:AC +CD =AB证明:在AB 上截取A E=AC,∵A D平分∠CAB ,∴∠CAD = ∠DAB ,AD=AD , ∴△CA D≌△EAD ,∴∠DEA =90°,∵∠C =90°,AC =BC ,∴∠B=45°, ∴∠B =∠BDE =45°∴DE =B E,∴AC +CD =AE +DE =AE +BE =AB ,即AC +CD =AB.例题5.已知:如图6,在Rt △ABC 中,∠C =90°,沿过B 点的一条 直线BE 折叠这个三角形,使C 点与AB 边上的一点D 重合, 当∠A 满足什么条件时,点D 恰为AB 中点?写出一个你认为适当的条件,并利用此条件证明D 为AB 中点.解:当∠A =30°时,点D 恰为AB 的中点.∵∠A =30°,∠C=90°(已知),∴∠CBA =60°(直角三角形两锐角互余).又△BEC ≌△B ED (已知),∴∠CBE =∠DBE =30°,且∠E DB =∠C =90°(全等三角形对应角相等),∴∠DBE =∠A(等量代换).∵BE =A E(等角对等边),又∠EDB =90°,即ED ⊥A B,∴D是A B的中点(三线合一).B ACD FE 图4角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形例题、如图所示,在△ABC 中,∠A BC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
求证:1()2BE AC AB =- 证明:延长BE 交AC 于点F。
因为角是轴对称图形,对称轴是角的平分线所在的直线,所以A D为∠B AC的对称轴, 又因为BE ⊥AD于F,所以点B 和点F 关于AD 对称, 所以BE=FE =12B F,AB=A F,∠ABF=∠AF B。
因为∠ABF+∠FBC =∠AB C=3∠C ,∠AB F=∠AFB=∠F BC+∠C , 所以∠FBC +∠C+∠F BC=3∠C , 所以∠FBC=∠C ,所以FB=FC ,所以BE =12FC=12(A C-A F)=12(AC -AB), 所以1()2BE AC AB =-。
二、已知一个点到角的一边的距离,过这个点作另一边的垂线段如图所示,∠1=∠2,P为BN 上的一点,并且P D⊥BC 于D ,A B+BC=2BD 。
求证:∠BAP+∠BCP=180°。
证明:经过点P作PE ⊥AB 于点E 。
因为PE ⊥AB,P D⊥BC ,∠1=∠2, 所以P E=P D。
在R t△PBE 和Rt △PBC 中BP BPPE PD=⎧⎨=⎩ 所以Rt△PBE ≌Rt △PB C(HL ), 所以BE=BD 。
因为AB+BC=2BD,B C=CD +BD,A B=B E-AE, 所以AE=CD 。
因为PE ⊥AB,P D⊥BC, 所以∠PE B=∠PDB=90°. 在△PAE 和Rt △PCD 中21F EDCBANPE DCBAPE PD PEB PDC AE DC =⎧⎪∠=∠⎨⎪=⎩所以△PAE ≌R t△PCD, 所以∠PCB=∠E AP 。
因为∠BAP+∠EAP =180°, 所以∠BAP+∠B CP=180°。
三、已知角平分线和其上面的一点,过这一点作角的两边的垂线段例题、如图所示,在△ABC 中,PB 、PC 分别是∠A BC的外角的平分线,求证:∠1=∠2证明:过点P 作PE ⊥AB 于点E,PG⊥AC 于点G ,PF ⊥BC 于点F .因为P在∠EBC 的平分线上,PE ⊥AB ,PH ⊥BC, 所以PE=PF 。
同理可证PF=PG 。
所以PG=PE,又PE ⊥AB,PG ⊥AC,所以PA 是∠BAC 的平分线, 所以∠1=∠2。
与三角形的角平分线有关的结论的探究三角形的内角和等于1800,三角形的外角等于和它不相邻的两个内角的和。
应用以上定理和推论可以探究与三角形的角平分线有关的结论。
从结论的探究过程中,希望同学们能从中得到有益的启示:在平时的数学学习中,要学会运用所学知识去探索新的结论,学会探究,从而不断地提高自己的数学发现与创新的能力,提高数学学习水平。
探究一:在ABC ∆中,∠A ,∠B的平分线交于点P,试探究 ∠BPC 与∠A 的关系?探究:因为∠BPC 在ΔBPC 中,由三角形的内角和定理,有:()PCB PBC BPC ∠+∠-=∠0180而由BP,CP 分别是∠ABC 和∠AC B的角平分线 知:∠PBC =ABC ∠21,∠PCB =ACB ∠21所以()ACB ABC ACB ABC BPC ∠+∠-=⎪⎭⎫⎝⎛∠+∠-=∠21180212118000而在在ABC ∆中,A ACB ABC ∠-=∠+∠0180 所以()A A BPC ∠+=∠--=∠219018021180000G21PFECB ACBA故有结论一:在ABC ∆中,∠A,∠B的平分线交于点P ,则有A BPC ∠+=∠21900。
探究二:在ABC ∆中,BP 是∠AB C的平分线,C P是ΔAB C的外角∠ACE 的平分线, 试探究:∠BPC 与∠A 的关系?探究:由CP 是ΔA BC的外角∠A CE的平分线, 所以有:∠BPC=∠PCE -∠BP C又BP 是∠ABC 的平分线,CP 是∠AC E的平线所以:∠PBC=ABC ∠21,∠P CE=ACE ∠21所以∠B PC=ACE ∠21-ABC ∠21()A ABC ACE ∠=∠-∠=2121 故有结论二:在ABC ∆中,BP 是∠ABC 的平分线,CP 是ΔABC 的外角∠ACE 的平分线,则有:A BPC ∠=∠21。
探究三:在ABC ∆中,B P, CP 分别是ΔA BC 的两个外角的平分线,试探究:∠BPC 与∠A 的关系?探究:因为∠B PC 在ΔB PC 中,由三角形的内角和定理,有:()PCB PBC BPC ∠+∠-=∠0180由BP , CP 分别是ΔABC 的两个外角的平分线,有: ∠PBC=EBC ∠21,∠PCB=BCF ∠21而∠ABC+∠CBE =1800,∠AC B+∠B CF =1800,所以∠ABC+∠CB E+∠ACB+∠B CF=3600所以∠EBC+∠FCB=3600-(∠AC B+∠AB C)()A A ∠+=∠--=0180180360所以()()A A FCB EBC BPC ∠-=∠+-=∠+∠-=∠219018021180211800000故有结论三:在ABC ∆中,BP , CP 分别是ΔABC 的两个外角的平分线,则有A BPC ∠-=∠21900。
线段垂直平分线的性质定理及其逆定理 角平分线的性质定理及其逆定理 水平测试一、选择题1.下列说法,错误的是( )EC BAFPE AA.三角形任意两个角的平分线的交点到这个三角形的三边的距离都相等B.三角形任意两个角的平分线的交点必在第三个角的平分线上C.三角形两个角的平分线的交点到三角形的三个顶点的距离都相等D.三角形的任意两个角的平分线的交点都在三角形的内部2.若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是(ﻩ) A .锐角三角形ﻩﻩB.钝角三角形ﻩ C.直角三角形 ﻩD .不能确定3.如图所示,在R t ABC △中,90ACB ∠=,BC 的中垂线交斜边AB 于D ,7.8AB =,3.9AC =,则图中有多少个角等于60(ﻩ)A.2个ﻩ B.3个 C .4个ﻩ D .5个4.等腰△ABC 两腰AB ,AC 的垂直平分线交于点O ,下列各式不正确的是( ) A .OA BC ⊥ﻩﻩB.OA 平分BAC ∠ﻩ C.OB OC =ﻩ D .OA BC =5.已知△ABC 中,AB AC =,AB 的垂直平分线交AC 于D ,△ABC 和△DBC 的周长分别是60cm 和38cm ,则△ABC 的腰长和底边BC 的长分别是( )A.24cm 和12cmB.16cm 和22c m C.20c m和16cm D.22cm 和16cm 6.将一张长方形纸片按如图所示的方式折叠,BC ,BD 为折痕,则∠CBD 的度数为( ) A.60° B.75° C .90° D.95°7.若△ABC 三条角平分线的交点到三顶点的距离相等,则该三角形一定为( )A .等腰三角形,但不一定是等边三角形.B .直角三角形. C.等腰直角三角形. D.等边三角形.8. 如图,△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB ,DF ⊥A C,E 、F 为垂足,在以下结论中:①△A DE≌△ADF;②△BDE ≌△CD F;③△A BD ≌△A CD;④AE =A F;⑤BE=CF ;⑥BD=CD .其中正确结论的个数是( ) A.1ﻩB.2ﻩC.3ﻩD.49.已知P 点在AOB ∠的平分线上,60AOB ∠=,10OP =cm ,那么P 点到边OA ,OB 的距离分别是( )A .5c m,53cm B.4cm,5cm C .5cm,5cm D .5cm ,10cm10.如图,△AB C中,∠C=90º,BD 平分∠A BC 交AC 于D,DE是AB 的垂直平分线,DE=21B D,且DE =1.5cm,则AC 等于( ) A.3cm ﻩB.7.5cm C.6cm D .4.5cmAC DB BEA BCD EF二、填空题1.已知线段AB 和它外一点P,若PA=PB,则点P在A B的____________________;若点P 在AB的____________________,则P A=P B.2.如图,△ABC 中,EF 是AB 的垂直平分线交于D ,12BF =,3CF =,则AC = .3. 如图,50ABC AD ∠=,垂直平分线段BC 于点D ABC ∠,的平分线BE 交AD 于点E ,连结EC ,则AEC ∠的度数是 .4.如图所示,在ABC △中,90C ∠=,DE 是AB 的垂直平分线,2AB AC =,18cm BC =,则BE 的长度为 ﻩﻩ .5.在锐角三角形ABC 中,60A ∠=,AB ,AC的度数是ﻩﻩ.6.△ABC 中,90C ∠=,AD 平分BAC ∠,交BC 于D ,若7DC =,则D 到AB 的距离是 .7.△ABC的三边长分别为3cm 、4cm 、5cm ,若O 为△ABC 三内角平分线交点,则点O 到斜边AB 的距离等于 .8.如图,已知BO 平分CBA ∠,CO 平分ACB ∠,MN BC ∥,且过点O ,若12AB =,14AC =,则AMN △的周长是 ﻩﻩ.BE9.如图,BD 是ABC ∠的平分线,DE AB ⊥于E ,236m ABC S =△,18cm AB =,12cm BC =,则DE 的长是.10.如图,ABC △中,90C ∠=,AC BC =,AD 平分BAC ∠交BC 于D ,DE AB ⊥于E ,且10cm AB =,则DEB △的周长是ﻩ ﻩﻩ.三、解答题1.如图所示,直线OA ,OB 表示两条相互交叉的公路.点M ,N 表示两个蔬菜基地.现要建立一个蔬菜批发市场,要求它到两个基地的距离相等,并且到公路OA ,OB 的距离相等,请你作图说明此批发市场应建在什么地方?2. 如图△ABC 中,BA BC =,120B ∠=,AB 的垂直平分线交AC 于D ,求证:12AD DC =.3.用三角尺画角平分线:如图,∠AOBM 、N 作OA,OB 的垂线,交点为P ,画射线OP,线.并说明这种做法的道理.D4.如图所示,已知AD 是△ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F . 求证:AD 垂直平分EF .四、探索题1.如图,在ABC △中,90A ∠=,AB AC =,BD 是ABC ∠的平分线,请你猜想图中哪两条线段之和等于第三条线段,并证明你的猜想的正确性(证明你的猜想需要用题中所有的条件).2.如图所示,在等腰ABC △中,AB AC =,120BAC ∠=.(1)请你作出两腰的垂直平分线.(2)若AB 边的垂直平分线与AB ,BC 分别交于点D ,E ,AC 边上的垂直平分线与AC ,BC 分别相交于点G ,F ,则AEF △是什么形状?你能证明吗? (3)连结DG ,DG 与BC 有什么关系?(4)若5cm DG =,试求AEF △的周长.答案:一、1D;2C;3D ;4D ;5D;6C;7D;8B;9C;10D .二、1. 垂直平分线上;垂直平分线上;2.15;3.115°;4.12cm ;5.120;6.7;7.1cm;8.26;9.12cm 5;10.10cm.D三、1.解:分别作AOB ∠的平分线OC 和线段MN 的垂直平分线DE ,则射线OC 与直线DE 的交点P 即为批发市场应建的地方.2.证明:连接BD .AB 的垂直平分线交AC 于D ,DA DB =∴ 又BA BC =,120B ∠=,30A C ∠=∠=∴30A ABD ∠=∠=∴,90DBC ∠=∴Rt △DBC 中,有12BD DC =,12AD DC =∴. 3.解:∵OM=ON ,O P=OP,∴Rt △OMP ≌Rt △ONP(HL ),∴∠MO P=∠NOP ,∴射线O P是∠AOB 的平分线.4.证明:AD ∵是ABC △的角平分线, DE AB ⊥,DF AC ⊥,DE DF =∴(角平分线上的点到角的两边距离相等). ∴DEF DFE ∠=∠(等角对等边).90AED AFD ∠=∠=∵(垂直定义),AEF AFE ∠=∠∴(等角的余角相等). AE AF =∴(等角对等边)∴A ,D 在EF 的中垂线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上).即AD 是EF 的中垂线.四、1.解:猜想结论:AB AD BC +=,过D 作DE BC ⊥于E .BD ∵平分ABC ∠,90A ∠=,AD DE =∴. ABD EBD ∴△≌△,AB BE =∴. AB AC =∵,45C ∠=∴,DE EC =∴. AD EC =∴,AB AD BC +=.2.解:(1)如图所示.(2)AEF △是等边三角形.证明:AB AC =∵,120BAC ∠=,30B C ∠=∠=∴.DE ∵垂直平分线AB ,EB EA =∴,30BAE B ∠=∠=∴,60AEF ∠=∴.D同理可证60AFE ∠=.AEF ∴△是等边三角形.(3)因为点D 、G 分别是AB、AC 的中点,所以DG 是中位线,则12DG BC =. (4)AE BE =∵,AF FC =,AEF ∴△的周长为:AE EF AF BE EF FC BC ++=++=. 又210cm BC DG ==∵.AEF ∴△的周长为10cm .选做题1.ABC △中,22.5B ∠=,60C ∠=,AB 的垂直平分线交BC 于D ,交AB 于F,BD =AE BC ⊥于E ,求EC 的长.解:连结AD .DF ∵是AB 的垂直平分线,AD BD =∴=线段垂直平分线上的点到线段两个端点的距离相等)122.5B ∠=∠=∴(等边对等角) 2145B ∠=∠+∠=∴.又AE BC ∵⊥,3902904545∠=-∠=-=∴,∠∴AE DE ∴=(等角对等边) 222DE AE AD +=∵(勾股定理)222AE =∴,6AE =∴.在R t ACE △中,60C ∠=,430∠=∴2AC CE =∴(30所对的直角边等于斜边的一半)222AC EC AE -=∵(勾股定理)222(2)CE CE AE -=∴,223CE AE =∴,212CE =∴,CE =∴.2.如图,90A AD BC =︒,∠∥,P 是AB的中点,PD平分∠ADC. 求证:CP 平分∠DCB.证明:过点P 作P E⊥DC,垂足于E, ∴3490A ===︒∠∠∠,AD 21∵PD平分∠AD C,∴12=∠∠, ∴PA PE =,∵P为AB 的中点, ∴PA PB PE PB ==,, ∵90AD BC A =︒,∥∠, ∴P 点在∠DCB 的平分线上. ∴CP 平分∠DCB.3. CE BF ,分别是锐角三角形AB C的ACB ∠,ABC ∠的平分线,AF BF ⊥于F ,AE CE ⊥于E ,试说明:(1)EF BC ∥;(2)1()2EF AB AC BC =+-.提示:由于BF 是角平分线,且AF BF ⊥,所以延长AF 交BC 于N ,则有ABN △是等腰三角形,从而F 是AN 的中点,且AB BN =,同理E 是AM 的中点,且AC CM =,所以EF BC ∥,且11()()22EF BN CM CB AB AC BC =+-=+-.备用题1.如果三角形内的一点到三边的距离相等,则这点是( )CA .是三条边中垂线的交点B.是三角形三条边的中线的交点C.是三角形三个内角平分线的交点D.是三角形三条边上的高的交点2.如图,△ABC 中,∠CAB =120º,A B,AC 的垂直平分线分别交BC 于点E 、F,则∠EAF 等于( )CA .40º B.50º C.60º D.80º3.如果ABC △的边BC 的垂直平分线经过顶点A ,与BC 相交于点D ,且2AB AD =,则ABC △中必有一个内角的度数为( )D A.45ﻩB.60ﻩ C .90ﻩ D.1204.如图,Rt △ACB ,90C ∠=,AD 平分CAB ∠,DE AB ⊥于E ,则下列结论中不正确的是( )BA BA .BD ED BC += B.DE 平分ADB ∠ C.AD 平分EDC ∠ D.ED AC AD +>5.等腰三角形内有一点P 到底边的两端点距离相等,则连结顶点和P 的直线一定把底边 .垂直平分5.如图,在R t ABC △中,90B ∠=,ED 垂直平分AC 交AC 于点D ,交BC 于点E ,已知:2:5EAB BAC ∠∠=,求C ∠的度数.解:设2EAB x ∠=,则5BAC x ∠=,3C EAC x ∠=∠=∴.而90C BAC ∠+∠=,5390x x +=∴,11.25x =,33.75C ∠=∴.6.如图所示,AD 是BAC ∠的平分线,DE AB ⊥于E ,DF AC ⊥于F ,且BD CD =. 求证:BE CF =.证明:AD ∵是BAC ∠的平分线,DE AB ⊥,DF AC ⊥ DE DF =∴.(角平分线上的点到这个角两边的距离相等)又BD CD =∵,Rt Rt HL DBE DCF ∴△≌△()BE CF =∴.7.如图,已知在△ABC 中,90C ∠=,点D 是斜边AB 的中点,2AB BC =,DE AB ⊥交AC 于E .求证:BE 平分ABC ∠.BAC证明:D ∵是AB 的中点,12BD AB =∴, 2AB BC =∵,12BC AB =∴,BD BC =∴. 又∵DE AB ⊥,90C ∠=,90C BDE ∠=∠=∴, 又BE BE =,∴Rt △BDE ≌Rt △BCE (HL ), DBE EBC ∠=∠∴,BE ∴平分ABC ∠.角平分线性质定理之应用三角形的角平分线是三角形的主要线段之一,它在几何的计算或证明中,起着“桥梁”的作用.那么如何利用三角形的角平分线解题呢?下面举例说明. 一、由角平分线的性质联想两线段相等例1 如图1,A B>AC,∠A 的平分线与BC 的垂直平分线相交于D,自D 作DE ⊥AB ,D F⊥AC ,垂足分别为E,F.求证:B证明 连结DB ,DC.∵D 在∠A 的平分线上,∴D E=DF .∵D在BC 的垂直平分线上,∴BD = 又∠BED =∠CFD =90°, ∴Rt △BDE ≌Rt △CD F,∴BE=CF.例2 如图2,BC >AB ,B D平分∠AB C, 求证:∠A+∠C=180°.证明 延长BA 至F ,使BF =BC .由BD 在△FBD 与△CBD 中,BF=B C ∠ABD=∠CBD BD=BD ∴△FBD ≌△CB D,∴∠C=∠F,D F=CD=AD ,∠F=DAF , ∴∠A+∠C=∠B AD+∠DA F=180°.三、过角平分线上一点作一边的平行线,构成等腰三角形例3 已知:如图3,∠ABC 的平分线B F与∠ACB 的平分线CF 相交于点F ,过F 作DE ∥B C,交A B于D,交A C于E,求证:BD+CE=DE .证明:∵BF 是∠ABC 的平分线 ∴∠DBF=∠C BF ∴∠DFB=∠CBF∴∠DBF=∠DFB ∴BD=FD,同理CE=FE.∴BD+CE=DF+F E=D E.ADBCE图1-1四、实际生活中的应用例4 如图4,有三条公路1l 、2l 、3l 两两相交,要选择一地点建一座加油站,是加油站到三条公路的距离相等,应如何选择建加油站的地址?这样的位置有几种选择?解析:分别作△A BC 两内角的平分线,它们相交于一点,根据角平分线的性质知,这个点到三条公路的距离相等;或者分别作△ABC 相邻两外角的平分线,它们的交点到三条公路的距离也相等,这样点共有三个,所以建加油站的位置共有4种选择..角平分线携“截长补短”显精彩角的平分线具有其特有的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,利用此种方法常可使思路豁然开朗.请看几例. 例1 如图1-1,A D∥B C,点E 在线段AB 上,∠A DE =∠CDE ,∠D CE =∠ECB .求证:CD =AD +BC . 分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在C D上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.证明:在CD 上截取C F=BC ,如图1-2 在△FC E与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠A DC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF+CF ,∴CD =AD +BC .图4 ADB CE F1234图1-2例2 已知,如图2-1,∠1=∠2,P 为BN 上一点,且P D⊥BC 于点D ,AB+BC =2BD .求证:∠BAP +∠B CP=180°.分析:证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠B CP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直B A的延长线于点E ,如图2-2 ∵∠1=∠2,且P D⊥BC ,∴P E=PD , 在Rt △B PE与Rt △BPD 中,⎩⎨⎧==BPBP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +B C=2BD ,∴AB +B D+DC =BD +BE ,∴AB +DC =BE 即DC =BE -A B=AE .在Rt △APE 与Rt △C PD中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △C PD (SAS),∴∠P AE =∠PCD又∵∠B AP +∠PAE =180°,∴∠BA P+∠B CP=180° 例3 已知:如图3-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC+CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使C E=CD ,或在A B上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =C E,则∠C DE=∠C ED,如图3-2 ∴∠AC B=2∠E ,∵∠A CB=2∠B,∴∠B =∠E, 在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△AB D≌△AE D(A AS ),∴A B=AE . 又A E=AC+CE =AC +D C,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =A C,如图3-3 在△AF D与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SA S),∴DF =DC ,∠AFD =∠ACD . 又∵∠AC B=2∠B ,∴∠FDB =∠B ,∴FD =FB .ABCDP12N图2-1DCB A 12图3-1EDCB A 12图3-2FDCBA 12图3-3P12NABCDE 图3-22-2∵A B=AF +FB=AC +FD ,∴AB =AC +C D. 上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
