分子的平均平动动能
分子动理论气体分子平均动能
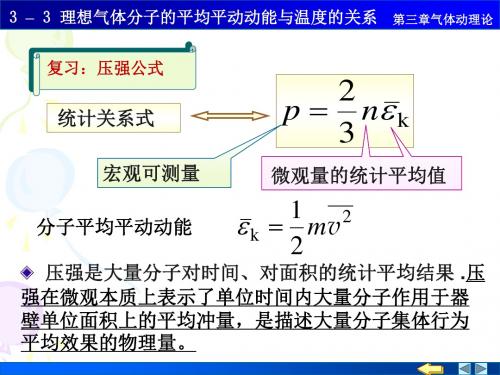
32 103 26 m 5 . 31 10 kg 23 N A 6.02 10 (3)
3 3 k kT 1.38 10 23 ( 27 273) 6.21 10 21 J 2 2
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
子数相等。
分子数 密度
k=R/NA=1.38×10-23J· K-1
称为玻耳斯曼常量
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
二、理想气体分子的平均平动动能与温度的关系
阿伏加德罗定律:
p nkT
2 1 2 理想气体压强公式 p n mv 3 2 1 3 2 k m v kT 分子平均平动动能 2 2
容器内不同气体的温度相同分子的平均平动动能也相同即kknkk?????????????????21而分子数密度满足????inn故压强为??????????????????????????????????????????????ikiikikikpnnnnp????????32323232即容器中混合气体的压强等于在同样温度体积条件下组成混合气体的各成分单独存在时的分压强之和
例 利用理想气体的温度公式说明Dalton 分压定律。
解:容器内不同气体的温度相同,分子的平均平动动能也 相同,即
k1 k 2 kn k
而分子数密度满足
n ni
故压强为 2 2 2 2 P n k ni k ni k ni ki Pi 3 3 3 3 即容器中混合气体的压强等于在同样温度、体积条件下组成 混合气体的各成分单独存在时的分压强之和。这就是Dalton 分压定律。
分子的平均平动动能

F引 F引
r0
F合
r
F引
r0 平衡距离
F斥
(2)当r<r0时,随r的减小,F引、F斥都增大,F斥比F引增 大得快,F斥>F引,分子力表现为斥力,r减小,分子力增大
F
F斥
r>r0
F斥
F引
F引
F斥
0
r0
F合
r
F引
(3)当r>r0时,随r 的增加,F引、F斥都减小,F斥 比F引减小得快,F斥<F引,分子力表现为引力
第四步: 计算N个分子给器壁的平均冲力:
mv m N 2 vx F Fi l x i 1 lx i i 1
该面所受压强
F 1 P S l x l y lz
N
2 x
Nm 1 ( mv V N i
N 2 ix
2 v ix ) nm v i
N
_____
2 x
定义分子速率平均值
v
则
v
i
i
N
;
定义分子速率平方的平均值
vx v y vz ; 2 v i 2
v
2 z
i
N
; v2
v v v ;
2 x 2 y 2 z
则
1 2 v v v v ; v x v y vz v 3
2 2 x 2 y
2
2
2
注意:统计规律有涨落 (fluctuation), 统计对象的数量越大,涨落越小。
微观理论,从分子热运动观点出发,依赖微 观粒子的力学规律,运用统计方法研究气体 分子热运动的宏观性质和变化规律。寻求宏 观量与微观量之间的关系,揭示气体宏观热 现象及其规律的微观本质。
分子的平均动能和平均平动动能

分子的平均动能和平均平动动能分子的平均动能和平均平动动能,听上去像是科学课上的难题,实际上却是我们生活中无处不在的小秘密。
想象一下,空气中那些看不见的小家伙,分子们正像在狂欢派对上,兴奋得乱舞呢。
每个分子都是小小的舞者,它们的动能就像是舞池里的热情,越多越好。
这种动能不是凭空而来的,而是温度的结果,温度越高,分子就越活跃,像是喝了咖啡的小伙伴,嗨得不得了。
我们先说说“平均动能”这回事。
分子们就像一群在操场上玩耍的小朋友,个个都有自己的速度。
有人慢悠悠,有人飞快。
这样一来,要想知道这些小家伙的平均水平,就得把它们的动能加起来,然后除以总数。
想象一下,算得不容易,有点像聚会后算账,喝了多少、吃了多少,最后还得分个清楚。
但是别担心,科学家们早就把这套公式搞定了,简单明了。
再来聊聊“平均平动动能”。
说白了,就是分子在特定方向上的运动能量。
好比你在马路上走路,走得快快的,偶尔停下来看看风景。
分子们也是,虽然它们总是转来转去,但我们关注的,是它们在某个方向上走的速度。
像是赛车,冲刺的时候速度很快,停下来的那一瞬间,动能就降到最低。
换句话说,分子在某个方向上的运动就是它们的平动,动能就是它们的实力。
要知道,温度不仅仅是数字,它是个大角色。
在炎热的夏天,分子的动能像火焰一样旺盛,碰撞得热火朝天,感觉连空气都在冒烟。
而在寒冷的冬天,分子的动能就像缩进了被窝里,懒洋洋的,基本上就是个“冬眠”的状态。
这些分子的表现,就决定了我们周围的温度和状态。
你可别小看这动能,有它在,冰水也能化开,空气也能流动,所有的变化都和这小小的动能息息相关。
想象一下,科学家们通过研究这些分子的动能,揭示了许多自然现象的奥秘。
比如说,水为什么会蒸发,冰为什么会融化,这些背后都藏着动能的秘密。
当分子们的动能达到了一定程度,它们就会开始挣脱束缚,水分子从液态变成气态,像是蝴蝶破茧而出。
科学家们用这些发现推动了许多技术的发展,比如空调、冰箱,甚至是航天科技。
理想气体分子的平均平动动能与温度的关系
§12-4 理想气体分子的平均平动动能 与温度的关系
§12-4
理想气体分子的平均平动动能与温度的关系
一、气体温度和平均平动动能的关系
根据理想气体状态方程,可得:
PV vRT
2 P n nkT 3
2019年3月20日星期三
vRT vN A kT P nkT V V
3 kT 2
2019年3月20日星期三
理学院 物理系
2019年3月20日星期三
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系来自三、气体分子的方均根速率
3 1 2 kT m v 2 2
3kT 3 RT v m
2
00C时气体分子的方均根速率 气体种类 方均根速率(m/s) O2 4.61×102 N2 4.93×102 H2 1.84×103 CO2 3.93×102 H2O 6.15×102
理学院 物理系
大学物理
§12-4
理想气体分子的平均平动动能与温度的关系
3 二、 2 kT
的物理意义
1.平均平动动能只与温度有关。 2.温度具有统计的意义,只能用于大量分子,对单个 分子谈温度是无意义的。 3.当两种气体具有相同的温度时,它们相应的平均平 动动能相等。 若使这两种气相接触,两种气体间将没有宏观的能量 传递,它们各自处于热平衡状态。即温度是表征气体 处于热平衡状态的物理量。这也就是热力学第零定 律的微观解释。
分子平均平动动能-精品

12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
分子平均平动动能:
k
1mv2 2
3kT 2
微观量的统计平均 宏观可测量量
第十二章 气体动理论
1
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
温度 T 的物理意义
第十二章 气体动理论
4
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
2 理想气体体积为 V ,压强为 p ,温度为 T . 一个分子 的质量为 m ,k 为玻耳兹曼常 量,R 为摩尔气体常量,则该理想气体的分 子数为:
(A) pV m (B) pV(kT)
(C) pV(RT) (D) pV(mT)
k
1mv2 2
3kT 2
(1)温度是分子平均平动动能的量度.
k T
(2)温度是大量分子的集体表现.
(3)在同一温度下各种气体分子平均平 动动能均相等.
第十二章 气体动理论
2
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
热运动与宏观运动的区别:温度所 反映的是分子的无规则运动,它和物体 的整体运动无关,物体的整体运动是其 所有分子的一种有规则运动的表现.
解 p nkT
N nV pV kT
第十二章 气体动理论
5
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
讨论
1 一瓶氦气和一瓶氮气质量密度相同,分子 平均平动动能相同,且都处于平衡状态,则:
7-3 理想气体分子的平均平动动能与温度的关系

t 2 0 C时气体分
0
3 3 23 kT1 1.38 10 1273 J 2 2 2.64 1020 J T2 273K 3 3 kT 2 1.38 10 23 273 J 2 2 5.65 1021 J
第7章 气体动理论
第7章 气体动理论
返回
7
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
0
[例7-6] 试计算 0 C 时氧分子的方均根速率.
解 已知 T 273 K ,氧气的摩尔质量
M mol 32103 kg mol1
可求得
vrms 3RT 3 8.31 273 1 1 m s 461 ms 3 M mol 32 10
第7章 气体动理论
返回
8
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
讨论
1 一瓶氦气和一瓶氮气密度相同,分子平均 平动动能相同,而且都处于平衡状态,则:
(A)温度相同、压强相同. (B)温度、压强都不同. (C)温度相同,氦气压强大于氮气压强. (D)温度相同,氦气压强小于氮气压强. N k 解 p nkT kT T V m
(C) pV ( RT ) 解 (D) pV (m T )
pV N nV kT
第7章 气体动理论
返回
10
p nkT
返回
5
南通大学
Nantong University
7-3 理想气体分子的平均平动动能与温度的关系
[例7-5] 在多高温度下,气体分子的平均平 动能等于一个电子伏特? 解 电子伏特(eV)是一种能量单位,它指 的是,一个电子在电场中通过电位差为lv(伏 特 ) 的区间时,由于电场力做功所获得的能 量.
12-4理想气体分子的平均平动动能与温度的关系

1 2
m 1 v12
1 2
m2
v22
v12 m2
v22
m1
•当温度T=0时,气体的平均平动动能为零,这时气体
分子的热运动将停止。然而事实上是绝对零度是不可 到达的(热力学第三定律),因而分子的运动是用不停 息的。
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
(A) pV m (B) pV (kT )
(C) pV (RT ) (D) pV (mT )
解 p nkT
N nV pV kT
第十二章 气体动理论
6
分子平均平动动能:
k
1 2
mv2
3 2
kT
微观量的统计平均 宏观可测量量
第十二章 气体动理论
1
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
温度 T 的物理意义
k
1 mv2 2
3 kT 2
(1)温度的微观本质:温度是分子平均平动动能的量度.
k T
(2)温度是大量分子的集体表现.单个分子的温度无意义。
大学物理124理想气体分子的平均平动动能与温度的关系理学院物理系2019323方均根速率ms气体种类第十二章气体动理论124理想气体分子平均平动动能与温度的关系物理学第五版a温度相同压强相同
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
p
2 3
n k
理想气体物态方程 p nkT
(3)同一温度下各种气体分子平均平动动能均相等.
(4)温度的实质:分子热运动剧烈程度的宏观表现。
理想气体分子的平均平动动能与温度的关系

V
m
第十二章 气体动理论
4
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
2 理想气体体积为 V ,压强为 p ,温度为 T . 一个分子 的质量为 m ,k 为玻耳兹曼常 量,R 为摩尔气体常量,则该理想气体的分 子数为:
(A) pV m (B) pV (kT )
(C) pV (RT ) (D) pV (mT )
第十二章 气体动理论
3
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
讨论
1 一瓶氦气和一瓶氮气密度相同,分子平均 平动动能相同,而且都处于平衡状态,则:
(A)温度相同、压强相同.
(B)温度、压强都不同.
(C)温度相同,氦气压强大于氮气压强.
(D)温度相同,氦气压强小于氮气压强.
解 p nkT N kT k T
解 p nkT
N nV pV kT
第十二章 气体动理论
5
k
1 mv2 2
ห้องสมุดไป่ตู้
3 kT 2
(1)温度是分子平均平动动能的量度.
k T
(2)温度是大量分子的集体表现.
(3)在同一温度下各种气体分子平均平 动动能均相等.
第十二章 气体动理论
2
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
注意
热运动与宏观运动的区别:温度所 反映的是分子的无规则运动,它和物体 的整体运动无关,物体的整体运动是其 中所有分子的一种有规则运动的表现.
物理学
12-4 理想气体分子平均平动动能与温度的关系
第五版
理想气体压强公式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n m / M P1V1 / RT1 4.41102 mol
查表知氧气的定压摩尔热容
Cp,m 29.44J mol-1 K-1
定体摩尔热容
CV ,m 21.12J mol-1 K-1
(1)等压过程中氧气(系统)吸热
QP pdV E nCp,m (T2 T1) 129.8J
S 2v0 N f (v)dv = N 0
即曲线下面积表示系统分子总数N
(2)从图中可知,在0到 v0 区间内, Nf (v) = av/v0 而在 v0 到 2v0 区间,Nf (v) = a 则利用归一化条件有
N v0 avdv + 2v0 adv
0 v0
v0
a = 2N / 3v0
v0 av3 dv + 0 Nv0
2v0 v0
av2 dv) N
=
31 36
mv02
18 目前实验室获得的极限真空约为1.33×10-11Pa, 这与距地球表面1.0×104km处的压强大致相等。试求在 27oC时单位体积中的分子数及分子的平均自由程。(设 气体分子的有效直径d=3.0×10-8cm)
解:由分析知 Z p ,当压强由 p0 降为 p0 / 2时
平均碰撞频率为
Z
Z0
p0 / 2 p0
Z0 / 2
又因1 / p ,故当压强减半时,平均自由程为
0
p0 / 2 p0
20
6-10 一压强为1.010 5pa,体积为1.010-3m3的 氧气自0℃加热到100℃,问:(1)当压强不变时, 需要多少热量?当体积不变时,需要多少热量?(2) 在等压或等体过程中各作了多少功?
式中符号表示系统向外放热252J
6-16 如图所示,使1mol氧气(1)由A等温 地变到B;(2)由A等体地变到C,再由C等压地 变到B. 试分别计算氧气所作的功和吸收的热量.
解 (1)沿AB作等温膨胀的过程中,系统作功
WAB
m M
RT
ln(VB ) VA
PAVA
ln(VB VA
)
2.77 103 J
可知在等温过程中,氧气吸收的热量为
QAB WAB 2.77 103 J
(2)沿A到C再到B的过程中系统做功和吸热分别为
WACB WAC WCB WCB PC (VB VC ) 2.0 103 J
QACB WACB 2.0 103 J
P(105Pa) A
13.18 马文蔚(5版)P257
C
B
V(10-3m3)
2
解:(2)由A到C为等体过程,则:
QAC=μCV(TC-TA)=μ·5/2·(PCVC-PAVA) =2.5×(1×1×2-2×1×2)×103 = -5000J
WAC=0 由C到B为等压过程,有
QCB= μCP(TB-TC)=μ·7/2·(PBV-BPCVC) =……=7000J
(3)速率在 v0 / 2 到 3v0 / 2 间隔内的分子数为
N
v0
avdv +
3v0
/2
adv
=
7N
/
12
v v0 / 2 0
v0
(4)分子速率平方的平均值按定义为
v2
N v2dN
0
v2 f (v)dv
N
0
故分子的平均平动动能为
k
1 mv2 2
1 m( 2
14 有N个质量均为m的同种气体分子,它们的速率 分布如图所示. (1)说明曲线与横坐标所包围面积的
含义(2)由N和 v0求a值;(3)求在速率v0 / 2 到v0 / 3
间隔内的分子数;(4)求分子的平均平动动能.
解(1)由于分子所允许的速率在0到 2v0 的范围内, 由归一化条件可知图中曲线下的面积
WBC=0 由C到D为等压过程,有
QCD= μCP(TD-TC)=μ·7/2·(PDVD-PCVC)
QDA=μCV(TD-TA)=250J WDA=0 由A到B为等压过程,有
QAB= μCP(TB-TA)=700J WAB=P(VB-VA)=200J
=……= -350J
WCD=P(VD-VC)=……=-100J
解 系统经ABC过程所吸收的热量及对外所作的功分别为
QABC 326J
WABC 126J
则由热力学第一定律可得由A到C过程中系统内能的增量
EAC QABC WABC 200J
由此可得从C到A系统内能的增量为
ECA 200J
从C到A,系统所吸收的热量为
QCA ECA WCA 252J
WCB=P(VB-VC)=……=2000J
或者:
由热力学第二定律: QACB=WACB+△EACB=2000J
P(105Pa)
A
B
D
C
1
2
解:由B到C为等体过程,则:
V(10-3m3) 同理,由D到A为等体过程,则:
QBC=μCV(TC-TB)=μ·5/2·(PCVC-PBVB) =2.5×(2×1-2×2)×102 = -500J
6-19 0.32kg的氧气作图中所示循环ABCDA,设V2=2V1, T1=300K,T2=200K,求循环效率. (已知氧气的定体摩 尔热容的实验值Cv, m=21.1 J·mol-1·K-1)
解:由理想气体物态方程 p nkT 得分子数密度为
n p / kT 3.21109 m3
分子的平均自由程为 kT 7.8 108 m
2 πd2p
可见分子间几乎不发生碰撞
20 如果理想气体的温度保持不变,当压强降 为原值的一半,分子的平均碰撞频率和平均自由 程如何变化?
等体过程中氧气(系统)吸热
QV E nCV ,m (T2 T1) 93.1J
m
dW PdV RdT
(2)在等压过程中 m T2
M
W dW RdT 36.6J M T1
而在等体过程中,因气体的体积不变,故做功为
WV p(V )dV 0
6-11 如图所示,系统从状态A沿ABC变化到状态C 的过程中,外界有326J的热量传递给系统,同时系统 对外作功126J. 如果系统从状态C沿另一曲线CA回到 状态A,外界对系统作功为52J,则此过程中系统是吸 热还是放热?传递热量是多少?
