二次函数的应用题
(完整版)二次函数应用题(含答案)整理版
(完整版)二次函数应用题(含答案)整理版题目1：某公司的销售额可以用二次函数$y=-2x^2+20x$来表示，其中$x$表示月份（从1开始），$y$表示对应月份的销售额。
求解下列问题：问题1：请计算公司第6个月的销售额。
解答：将$x=6$代入二次函数中，可得：$y=-2\times6^2+20\times6=-72+120=48$所以公司第6个月的销售额为48。
问题2：请问公司销售额最高的月份是哪个月？解答：二次函数$y=-2x^2+20x$是一个开口朝下的抛物线，最高点即为销售额最高的月份。
通过求导数，我们可以找到函数的最高点。
首先，求导得到一次函数$y'=-4x+20$，令$y'=0$，解方程可得$x=5$。
因此，公司销售额最高的月份是第5个月。
题目2：一架火箭从地面起飞后，高度$h$（以米为单位）随时间$t$（以秒为单位）变化的规律可以用二次函数$h=-5t^2+100t$表示。
求解下列问题：问题1：请问火箭多少秒后达到最大高度？解答：同样地，通过求导数，我们可以找到火箭高度的最高点。
将二次函数$h=-5t^2+100t$求导得到一次函数$h'=-10t+100$，令$h'=0$，解方程可得$t=10$。
因此，火箭在10秒后达到最大高度。
问题2：请计算火箭达到最大高度时的高度。
解答：将$t=10$代入二次函数中，可得：$h=-5\times10^2+100\times10=-500+1000=500$所以火箭达到最大高度时的高度为500米。
以上是对二次函数应用题的解答，希望能帮助到您。
二次函数应用题
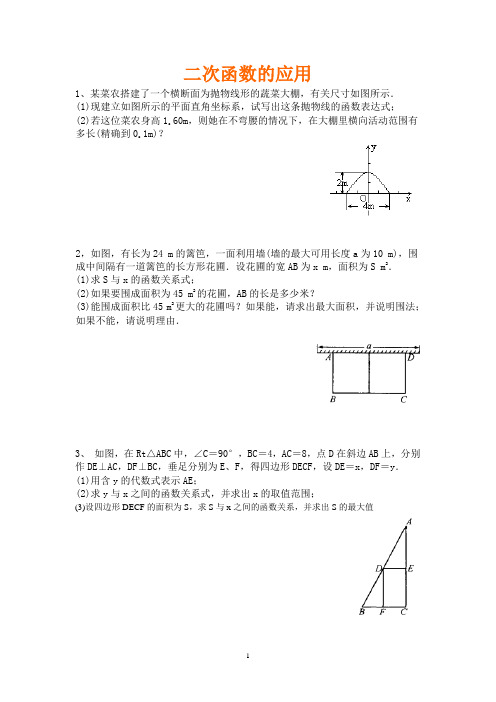
二次函数的应用1、某菜农搭建了一个横断面为抛物线形的蔬菜大棚，有关尺寸如图所示．(1)现建立如图所示的平面直角坐标系，试写出这条抛物线的函数表达式；(2)若这位菜农身高1.60m，则她在不弯腰的情况下，在大棚里横向活动范围有多长(精确到0.1m)？2，如图，有长为24 m的篱笆，一面利用墙(墙的最大可用长度a为10 m)，围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x m，面积为S m2．(1)求S与x的函数关系式；(2)如果要围成面积为45 m2的花圃，AB的长是多少米？(3)能围成面积比45 m2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．3、如图，在Rt△ABC中，∠C＝90°，BC＝4，AC＝8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE＝x，DF＝y．(1)用含y的代数式表示AE；(2)求y与x之间的函数关系式，并求出x的取值范围；(3)设四边形DECF的面积为S，求S与x之间的函数关系，并求出S的最大值4、在体育测试时，初三的一名高个子男同学掷铅球，已知铅球所经过的路线是某个二次函数图象一部分，如图所示，如果这个男同学的出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标(6，5)．(1)求这个二次函数的关系式；(2)该男同学把铅球掷出去多远？(精确到0.01 m，)5、有一抛物线型的立交桥，这个桥拱的最大高度为16 m，跨度为40 m．现把它的图形放在平面直角坐标系里，如图所示，若在离跨度中点M 5 m处垂直竖立一铁柱支撑拱顶，该铁柱应取多长？6、如图，在矩形ABCD中，AB＝6 cm，BC＝12 cm，点P从A出发，沿AB边向点B以1 cm/s的速度移动．同时Q从B出发，沿BC边向C以2 cm/s的速度移动，如果P、Q两点分别到达B、C两点后就停止移动，回答下列问题：(1)运动开始第几秒时，△PBQ的面积等于8 cm2？(2)设运动开始到第t s时，五边形APQCD的面积为S cm2，写出S与t的函数关系式．(3)t为何值时，S最小？求出S的最小值7、如图，△ABC是一等腰三角形铁板，其中AB＝AC＝20cm，BC＝24cm．若在△ABC上截出一个矩形零件DEFG，使EF在边BC上，若D、G分别在边AB、AC上(1)＝y cm2，试求y关于x的函数关系式；设EF＝x cm，S矩形DEFG(2)当x为多少时，矩形DEFG的面积最大？8、某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支(不含进价)总计120万元．在销售过程中发现，年销售量y(万件)与销售单价x(元)之间存在着如图1所示的一次函数关系．(1)求y关于x的函数关系式；(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利＝年销售额－年销售产品总进价－年总开支)．当销售单价x为何值时，年获利最大？并求这个最大值；(3)若公司希望该种产品一年的销售获利不低于40万元，借助图2中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？9、某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w＝－2x＋240．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：（1）求y与x的关系式；（2）当x取何值时，y的值最大？（3）如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？解：10．已知：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），解答下列问题：（1）当t为何值时，△PBQ是直角三角形?（2）设四边形APQC的面积为y（cm2），求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出相应的t值；不存在，说明理由；（3）设PQ的长为x（cm），试确定y与x之间的关系式．BC。
二次函数应用题(含答案)
1、小迪善于不断改进学习方法的小迪发现，对解题进行回顾反思，学习效果更好．某一天小迪有20分钟时间可用于学习．假设小迪用于解题的时间x （单位：分钟）与学习收益量y 的关系如图1所示，用于回顾反思的时间x （单位：分钟）与学习收益y 的关系如图2所示（其中OA 是抛物线的一部分，A 为抛物线的顶点），且用于回顾反思的时间不超过用于解题的时间．（1）求小迪解题的学习收益量y 与用于解题的时间x 之间的函数关系式；（2）求小迪回顾反思的学习收益量y 与用于回顾反思的时间x 的函数关系式；（3）问小迪如何分配解题和回顾反思的时间，才能使这20分钟的学习收益总量最大？2、如图，一位篮球运动员在离篮圈水平距离4 m 处跳起投篮，球沿一条抛物线运行，当球运行的水平距离为2.5 m 时，达到最大高度3.5 m ，然后准确落入篮框内．已知篮圈中心离地面距离为3.05 m ．（1） 建立图中所示的直角坐标系，求抛物线所对应的函数关系式；（2） 若该运动员身高1.8 m ，这次跳投时，球在他头顶上方0.25 m 处出手．问：球出手时，他跳离地面多高？（图1） （图2） （第14题）3、某跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为已知条件）.在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面米，入水处距池边的距离为4米，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误.（1）求这条抛物线的解析式；（2）在某次试跳中，测得运动员在空中的运动路线是（1）中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为米，问此次跳水会不会失误？并通过计算说明理由4、如图所示是永州八景之一的愚溪桥，桥身横跨愚溪，面临潇水，桥下冬暖夏凉，常有渔船停泊桥下避晒纳凉．已知主桥拱为抛物线型，在正常水位下测得主拱宽24m，最高点离水面8m，以水平线AB为x轴，AB的中点为原点建立坐标系．①求此桥拱线所在抛物线的解析式．②桥边有一浮在水面部分高4m，最宽处的河鱼餐船，试探索此船能否开到桥下?说明理由．1、（1）由题图，设y=kx，当x=l，时y=2，解得k=2，所以y=2x（0≤x≤20）即小迪解题的学习收益量y与用于解题的时间x之间的函数关系式是y=2x；（2）由题图，当0≤x<4时，设y=a（x-4）2+16，当x=0时，y=0，所以0=16a+16，所以a=-1，所以y=-（x-4）2+16，即y=-x2+8x；当4≤x≤10时，y=16，因此y=即小迪回顾反思的学习收益量y用于回顾反思的时间x的函数关系式是y=（3）设小迪用于回顾反思的时间为x（0≤x≤10）分钟，学习收益总量为y，则他用于解题的时间为（20-x）分钟，当0≤x<4时，y=-x2+8x+2（20-x）=-x2+6x+40=-（x-3）2+49，当x=3时，y最大=49，当4 ≤x≤10时，y=16+2（20-x）=56-2x，y随x的增大而减小，因此当x=4时，y最大=48，综上，当x=3时，y最大=49，此时20-x=17，答：小迪用于回顾反思的时间为3分钟，用于解题的时间为17分钟时，学习收益总量最大。
二次函数应用题专题(带答案)
二次函数应用题专题(带答案)0)时，可用交点式y=a(x-x1x-x2求其解析式。
4)根据问题要求，利用解析式求出所需的未知量。
三、练1、一枚炮弹在发射点上空爆炸，爆炸点离发射点水平距离1800米，爆炸高度为400米，求炮弹的初速度和仰角。
2、一架飞机以900km/h的速度飞行，飞行高度为2km，发现前方有一座山峰，山顶离飞机水平距离为10km，求飞机的爬升率和俯冲率。
3、一个人从距离地面20米的悬崖上抛出一个物体，物体抛出初速度为20m/s，抛出角度为60度，求物体落地点到悬崖的水平距离。
XXX：1、设炮弹飞行时间为t，初速度为v，仰角为θ，则可列出方程组：x=vtcosθy=vtsinθ-1/2gtx2y21800)2400)=xxxxxxx解得v600m/s，θ≈48.6°。
2、设飞机的爬升率和俯冲率分别为a和b，则可列出方程组：tan(θ-a)=4000/tan(θ+b)=2000/解得a≈2.5°，b≈1.4°。
3、设物体落地点到悬崖的水平距离为d，则可列出方程：d=vcosθtt=2vsinθ/g代入可得d≈40.8m。
评析：二次函数应用题需要学生熟练掌握建立坐标系、求解析式、利用解析式求未知量的方法，同时也需要学生对物理知识有一定的掌握，如抛物线运动、平抛运动等。
练中的例题和练题都体现了这些要点，可以帮助学生加深对二次函数应用的理解和掌握。
在教学过程中，可以引导学生多思考实际问题中的数学应用，提高他们的应用能力和解决问题的能力。
例2、某商场购进一批单价为16元的日用品，经试验发现，若按每件20元的价格销售时，每月能卖360件，若按每件25元的价格销售时，每月能卖210件，假定每月销售件数y(件)是价格x(元/件)的一次函数．1)求y与x之间的关系式；2)在商品不积压，且不考虑其他因素的条件下，问销售价格定为多少时，才能使每月获得最大利润？每月的最大利润是多少？解：(1)依题意设y=kx+b，则有 y= -30x+960 (16≤x≤32)．2)每月获得利润P=(-30x+960)(x-16)=30(-x+32)(x-16)=-30+48x-512+1920．所以当x=24时，P有最大值，最大值为1920．答：当价格为24元时，才能使每月获得最大利润，最大利润为1920元．注意：数学应用题来源于实践，用于实践，在当今社会市场经济的环境下，应掌握一些有关商品价格和利润的知识，总利润等于总收入减去总成本，然后再利用一次函数求最值．例3、在体育测试时，初三的一名高个子男同学推铅球，已知铅球所经过的路线是某个二次函数图像的一部分，如图所示，如果这个男同学的出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标为(6，5)1)求这个二次函数的解析式；2)该男同学把铅球推出去多远？(精确到0.01米)解：(1)设二次函数的解析式为 y=ax^2+bx+c。
二次函数应用题
二次函数应用题1、某食品零售店为食品厂代销一种面包，未售出的面包可退回厂家，经统计销售情况发现，当这种面包单价定为7角时，每天卖出160个，在此基础上，这种面包单价每提高1角，该零售店每天就会少卖出20个，该零售店每个面包的成本是5角．（1）如果每天卖出面包100个，那么这种面包的单价定为多少？这天卖面包的利润是多少？（2）如果每天销售这种面包获得的利润是48元，那么这种面包的单价是多少？2、某工厂生产的某种产品按质量分为10个档次，第一档次（最低档次）的产品一天可生产80件，每件产品的利润为10元，每提高一个档次，每件产品的利润增加2元．（1）当每件产品的利润为16元时，此产品质量在第几档次？（2）由于生产工序不同，此产品每提高一个档次，一天的产量减少4件．若生产某档次产品一天的总利润为1200元，问该工厂生产的是第几档次的产品？3、某宾馆有30间房间要出租，经过一段时间的经营发展，当每间房的租金为每日200元时，恰好全部租出．在此基础上，当每间房的租金每日提高10元时，就少租出一间，已知该宾馆每日平均每间房需支出各种费用150元，设每间房每日租金为x元，该宾馆出租房间的日收益为y元．（1）用含x的代数式表示每日未租出的房间数；（2）求y与x之间的函数关系式；（3）当x为何值时，该宾馆日收益最大，最大的日收益是多少？4．某商场购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出500个，根据销售经验，售价每提高1元，销售量相应减少10个．（1）假设销售单价提高x元，那么销售300个篮球所获得的利润是_______ 元；这种篮球每月的销售量是_______ 个．（用含x的代数式表示）（2）若每月销售这种篮球的最大利润是8000元，要使顾客得到实惠，则商场需要涨价多少？5．国家发改委公布的《商品房销售明码标价规定》，从2011年5月1日起商品房销售实行一套一标价．商品房销售价格明码标价后，可以自行降价、打折销售，但涨价必须重新申报．某市某楼盘准备以每平方米5000元的均价对外销售，由于新政策的出台，购房者持币观望．为了加快资金周转，房地产开发商对价格两次下调后，决定以每平方米4050元的均价开盘销售．（1）求平均每次下调的百分率；（2）某人准备以开盘均价购买一套100平方米的房子，开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.5元．请问哪种方案更优惠？6. 某商场在销售旺季临近时，某品牌的童装销售价格呈上升趋势，假如这种童装第1周的售价为50元/件，并且每周涨价2元/件，从第6周开始，保持60元/件的稳定价格销售，直到第11周结束，该童装不再销售．（1）求销售价格y（元）与周次x之间的函数关系式；（2）若该品牌的童装每周进货一次，并于进货当周售完，且这种童装每件进价z（元）与周次x之间的关系为z=-1/8 (x-8)2+12，(1≤x≤11，x为整数)，那么该品牌童装在第几周售出后，每件获得的利润最大？并求每件的最大利润．答案及提示1、解：（1）设这种面包单价为x角，得 160-（ x-7）×20=100，解得x=10，利润为100×（10-5）=500角=50元，答：这种面包的单价定为10角，这天卖面包的利润是50元．…（5分）（2）设这种面包单价为y角，由题意得，[160-20（y-7）]（y-5）=480，化简得，y2-20y+99=0，解得 y1=9，y2=11，答：这种面包的单价定为9角或11角（0.9元或1.1元）．2、解：（1）当每件利润是16元时，提高了（16-10）÷2=3个档次，∵提高3个档次，∴此产品的质量档次是第4档次．（2）设生产产品的质量档次是在第x档次时，一天的利润是y，由题意可得y=[10+2（x-1）][80-4（x-1）]，整理得y=-8x2+136x+672，当利润是1200元时，即=-8x2+136x+672=1200，解得：x1=6，x2=11（11＞10，不符合题意，舍去），答：当生产产品的质量档次是在第6档次时，一天的总利润为1200元．3、解：由题意得（1）x-200/10（2）y=x（30-x-200/10）-150×30=-1/10x2+50x-4500；（3）y=1/10x2+50x-4500=-1/10（x-250）2+1750∴当x=250时，y最大=1750（12分）．4、解：（1）销售一个篮球的利润为50-40+x=10+x（元），∴销售300个篮球所获得的利润是300×（10+x）元，这种篮球每月的销售量是500-10x，故答案为300×（10+x）；（500-10x）；（2）（10+x）（500-10x）=8000，（10+x）（50-x）=800，-x2+40x-300=0，x2-40x+300=0，（x-10）（x-30）=0，解得x1=10，x2=30，要使顾客得到实惠，∴x=10．答：要使顾客得到实惠，应涨价10元．5、解：（1）设平均每次下调的百分率为x．5000×（1-x）2=4050．（1-x）2=0.81，∴1-x=±0.9，∴x1=0.1=10%，x2=1.9（不合题意，舍去）．答：平均每次下调的百分率为10%；（2）方案一的总费用为：100×4050×9.8/10=396900元；方案二的总费用为：100×4050-2×12×1.5×100=401400元；∴方案一优惠．6、解：（1）由题意得，童装销售价格呈上升趋势，且第一周的售价为每件50元，并且从第二周开始每周涨价2元，直到第6周结束，当1≤x≤6时，y=50+2（x-1）=2x+48；当6≤x≤11时，y=60；（2）设每件获得利润为w元，则当1≤x≤6时，w=y-z，=2x+48+1/8（x-8）2-12=1/8x2+44，∵1/8＞0，∴当x＞0时，w随x的增大而增大，∴当x=6时，w最大=48.5．当6≤x≤11时，w=y-z，=60+1/8（x-8）2-12=1/8（x-8）2+48∵1/8＞0，∴当x＞8时，w随x的增大而增大，∴当x=11时，w最大=49 *1/8．答：该品牌童装在第11周售出后，每件获得的利润最大，每件的最大利润为49*1/8元．。
二次函数的应用题及解析
二次函数的应用题及解析二次函数是数学中重要的函数之一，广泛应用于各个领域。
本文将探讨几个常见的二次函数应用题，并进行详细解析。
问题一：某天气预报显示，一天内温度的变化服从二次函数关系。
已知该地点上午8时的温度为15摄氏度，下午2时的温度为25摄氏度，晚上8时的温度为18摄氏度。
问该地点第二天早上6时的温度是多少摄氏度？解析：根据已知条件构建二次函数的关系式。
假设时间为x，温度为y，则可以得出二次函数表达式为：y = ax^2 + bx + c。
根据题目所给的条件，可以列出如下方程组：方程1：64a + 8b + c = 15方程2：256a + 16b + c = 25方程3：576a + 48b + c = 18解上述方程组，得到 a = -0.005, b = 0.16, c = 15.16。
带入x = 22（第二天早上6时的时间），计算二次函数的值，即可得到第二天早上6时的温度为20.62摄氏度。
问题二：某公司销售某款产品，预测未来几个月的销售情况。
已知该产品销售量符合二次函数模型。
已知该产品2月份的销售量为2000件，5月份的销售量为3000件，8月份的销售量为4000件。
预测11月份的销售量是多少件？解析：同样地，假设时间为x，销售量为y，构建二次函数关系式：y = ax^2 + bx + c。
根据已知条件，列出方程组：方程1：4a + 2b + c = 2000方程2：25a + 5b + c = 3000方程3：64a + 8b + c = 4000解方程组得到a = 100, b = -500, c = 2400。
带入x = 14（11月份的时间），计算二次函数的值，可得到预测11月份的销售量为3400件。
通过以上两个实例，我们可以看到二次函数在温度预测和销售预测中的应用。
根据给定的条件，构建二次函数关系式，并解方程组可以得到问题所求的结果。
通过这种方法，我们可以更加准确地评估和预测未来的发展趋势。
二次函数的应用题
二次函数综合应用1.某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满。
当每个房间每天的房价每增加10元时，就会有一个房间空闲。
宾馆需对游客居住的每一个房间每天支出20元的各种费用，根据规定，每个房间每天的房价不得高于340元。
设每个房间的房价每天增加x元。
（1）设一天定住的房间数为y间，写出y与x的函数解析式及自变量x的取值范围（2）设宾馆一天的利润为w元，求w与x的函数解析式（3）一天定住房价多少个时，宾馆的利润最大？最大利润为多少元？2.某商场经营某种品牌的童装，购进时的单价是60元．根据市场调查，在一段时间内，销售单价是80元时，销售量是200件，而销售单价每降低1元，就可多售出20件．(1)写出销售量y件与销售单价x元之间的函数关系式；(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式；(3)若童装厂规定该品牌童装销售单价不低于76元，且商场要完成不少于240件的销售任务，则商场销售该品牌童装获得的最大利润是多少？3.某商厦将进货价30元的书包以40元售出，平均每月能售出600个。
调查表明：这种书包的售价每上涨1元，其销售量就减少10个。
（1）求出销售量y个与销售单价x元之间的函数解析式（2）求出销售这种书包获得利润z元与销售单价x元之间的函数关系式（3）若商厦规定销售这种书包的单价不高于62元，且商厦的进货成本不高于12000元，当销售单价定为多少元时，可获得最大利润？最大利润是多少？26．某商店经销一种销售成本为每千克40元的水产品，根据市场分析，若按每千克50元销售，一个月能售出500千克，销售单价每涨1元，月销量就减少10千克.针对这种水产品的销售情况，请解决下列问题：（1）当销售单价为每千克55元时，计算月销售量和月销售利润；（2）设销售单价为每千克x元，月销售利润为y元，求y与x间的函数关系式；（3）商店想在月销售成本不超过10000元的情况下，使得月利润达到8000元，销售单价应为多少？4. 一座拱桥的轮廓是抛物线型（如图1所示），拱高6m，跨度20m，相邻两支柱间的距离均为5m．（1）将抛物线放在所给的直角坐标系中（如图2所示），求抛物线的解析式；（2）求支柱EF的长度；（3）拱桥下地平面是双向行车道（正中间是一条宽2m的隔离带），其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车（汽车间的间隔忽略不计）？请说明你的理由．x图15. 我市某工艺厂为配合北京奥运，设计了一款成本为20元∕件的工艺品投放市场（1）把上表中x 、y 的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y 与x 的函数关系，并求出函数关系式；（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（利润=销售总价-成本总价）（3）当地物价部门规定，该工艺品销售单价最高不能．．超过45元/件，那么销售单6. 随着开发区近几年城市建设的快速发展，对花木的需求量逐年提高。
二次函数实际应用题
二次函数实际应用题1.端午节前夕，某超市从厂家分两次购进A、B两种品牌的粽子，两次进货时，两种品牌粽子的进价不变.第一次购进A品牌粽子 100袋和B品牌粽子 150袋，总费用为 7000元；第二次购进A品牌粽子 180袋和B品牌粽子120袋,总费用为 8100元。
(1)求A、B两种品牌粽子每袋的进价各是多少元；(2)当B品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对B品牌粽子进行降价销售，经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋，当B品牌粽子每袋的销售价降低多少元时，每天售出B品牌粽子所获得的利润最大?最大利润是多少元?2.某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15，且x为整数).当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件.(1)求y与x之间的函数关系式。
(2)若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为多少元?(3)设该商店销售这种消毒用品每天获利w(元)，当每件消毒用品的售价为多少元时，每天的销售利润最大?最大利润是多少元?3.某超市购进一批水果，成本为8元/kg，根据市场调研发现，这种水果在未来10天的售价m(元/kg)与时间第x天之间满足函数关系式m=12x+18(1≤x≤10)x为整数)，又通过分析销售情况，发现每天销售量y(kg)与时间第x天之间满足一次函数关系，下表是其中的三组对应值.(1)求y与x的函数解析式；(2)在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元?4.丹东是我国的边境城市，拥有丰富的旅游资源. 某景区研发一款纪念品，每件成本为30元，投放景区内进行销售，规定销售单价不低于成本且不高于 54元，销售一段时间调研发现，每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系，部分数据如下表所示：5.某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个。
二次函数的应用题(含答案)
二次函数的应用题(含答案)1．如图，抛物线y=x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．（1）求此抛物线的解析式；（2）写出顶点坐标及对称轴；（3）若抛物线上有一点B，且S△OAB=3，求点B的坐标．2．如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3，（1）求抛物线所对应的函数解析式；（2）求△ABD的面积；（3）将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．3．如图，已知二次函数L1：y=x2﹣4x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C．（1）写出A、B两点的坐标；（2）二次函数L2：y=kx2﹣4kx+3k（k≠0），顶点为P．①直接写出二次函数L2与二次函数L1有关图象的两条相同的性质；②是否存在实数k，使△ABP为等边三角形？如果存在，请求出k的值；如不存在，请说明理由；③若直线y=8k与抛物线L2交于E、F两点，问线段EF的长度是否会发生变化？如果不会，请求出EF的长度；如果会，请说明理由．4．如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3．（1）求抛物线的解析式．（2）若点D（2，2）是抛物线上一点，那么在抛物线的对称轴上，是否存在一点P，使得△BDP的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．5．如图，抛物线y=﹣x 2+bx+c 经过坐标原点，并与x 轴交于点A （2，0）． （1）求此抛物线的解析式； （2）写出顶点坐标及对称轴；（3）若抛物线上有一点B ，且S △OAB =8，求点B 的坐标．6．如图，在平面直角坐标系中放置一直角三角板，其顶点为A （0，1），B （2，0），O （0，0），将此三角板绕原点O 逆时针旋转90°，得到△A ′B ′O ．（1）一抛物线经过点A ′、B ′、B ，求该抛物线的解析式；（2）设点P 是在第一象限内抛物线上的一动点，是否存在点P ，使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍？若存在，请求出P 的坐标；若不存在，请说明理由．（3）在（2）的条件下，试指出四边形PB ′A ′B 是哪种形状的四边形？并写出四边形PB ′A ′B 的两条性质．7．某汽车租赁公司拥有20辆汽车．据统计，当每辆车的日租金为400元时，可全部租出；当每 辆车的日租金每增加50元，未租出的车将增加1辆；公司平均每日的各项支出共4800元．设公司每日租出工辆车时，日收益为y元．（日收益=日租金收入一平均每日各项支出） （1）公司每日租出x 辆车时，每辆车的日租金为 _________ 元（用含x 的代数式表示）； （2）当每日租出多少辆时，租赁公司日收益最大？最大是多少元？ （3）当每日租出多少辆时，租赁公司的日收益不盈也不亏？8．某工厂生产一种合金薄板（其厚度忽略不计），这写薄板的形状均为正方向，边长在（单位：cm）在5～50之间．每张薄板的成本价（单位：元）与它的面积（单位：cm2）成正比例，每张薄板的出厂价（单位：元）有基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的．浮动价与薄板的边长成（2）已知出厂一张边长为40cm的薄板，获得的利润为26元（利润=出厂价﹣成本价），①求一张薄板的利润与边长之间满足的函数关系式．②当边长为多少时，出厂一张薄板所获得的利润最大？最大利润是多少？9．牡丹花会前夕，我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，得到如下数据：（2）当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？（3）菏泽市物价部门规定，该工艺品销售单价最高不能超过35元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？答案得×，解得±；x得，﹣，﹣+解得，y=﹣时，×+1=，故，5．（2012•黑龙江）解：（1）把（0，0），（2，0）代入y=﹣x2+bx+c，得，解得b=2，c=0，所以解析式为y=﹣x2+2x；（2）∵a=﹣1，b=2，c=0，∴﹣=﹣=1，==1，∴顶点为（1，1），对称轴为直线x=1；（3）设点B的坐标为（a，b），则×2|b|=8，∴b=8或b=﹣8，∵顶点纵坐标为1，8＞1（或﹣x2+2x=8中，x无解），∴b=﹣8，∴﹣x2+2x=﹣8，解得x解：（1）△A′B′O是由△ABO绕原点O逆时针旋转90°得到的，又A（0，1），B（2，0），O（0，0），∴A′（﹣1，0），B′（0，2）．设抛物线的解析式为：y=ax2+bx+c（a≠0），∵抛物线经过点A′、B′、B，∴，解得：，∴满足条件的抛物线的解析式为y=﹣x2+x+2．（2）∵P为第一象限内抛物线上的一动点，设P（x，y），则x＞0，y＞0，P点坐标满足y=﹣x2+x+2．连接PB，PO，PB′，∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB，=×1×2+×2×x+×2×y，=x+（﹣x2+x+2）+1，=﹣x2+2x+3．假设四边形PB′A′B的面积是△A′B′O面积的4倍，则4=﹣x2+2x+3，即x2﹣2x+1=0，解得：x1=x2=1，此时y=﹣12+1+2=2，即P（1，2）．∴存在点P（1，2），使四边形PB′A′B的面积是△A′B′O面积的4倍．（3）四边形PB′A′B为等腰梯形，答案不唯一．①等腰梯形同一底上的两个内角相等；②等腰梯形对角线相等；③等腰梯形上底与下底平行；④等腰梯形两腰相等．或用符号表示：①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′；②PA′=B′B；③B′P∥A′B；④B′A′=PB．由表格中的数据，得，解得﹣＜==35解：（1）画图如图：由图可猜想y与x是一次函数关系，设这个一次函数为y=kx+b（k≠0），∵这个一次函数的图象经过（20，500）、（30，400）这两点，∴，解得：，∴函数关系式是y=﹣10x+700．（2）设工艺厂试销该工艺品每天获得的利润是W元，依题意得：W=（x﹣10）（﹣10x+700），=﹣10x2+800x﹣7000，=﹣10（（x﹣40）2+9000，∴当x=40时，W有最大值9000．（3）对于函数W=﹣10（（x﹣40）2+9000，当x≤35时，W的值随着x值的增大而增大，故销售单价定为35元∕件时，工艺厂试销该工艺品每天获得的利润最大．。
二次函数实际应用题
二次函数的应用练习题1．某食品零售店为仪器厂代销一种面包，未售出的面包可退回厂家，经统计销售情况发现，当这种面包的单价定为7角时，每天卖出160个。
在此基础上，这种面包的单价每提高1角时，该零售店每天就会少卖出20个。
考虑了所有因素后该零售店每个面包的成本是5角。
设这种面包的单价为x（角），零售店每天销售这种面包所获得的利润为y（角）。
⑴用含x的代数式分别表示出每个面包的利润与卖出的面包个数；⑵求y与x之间的函数关系式；⑶当面包单价定为多少时，该零售店每天销售这种面包获得的利润最大？最大利润为多少？2．某机械租赁公司有同一型号的机械设备40套。
经过一段时间的经营发现：当每套机械设备的月租金为270元时，恰好全部租出。
在此基础上，当每套设备的月租金每提高10元时，这种设备就少租出一套，且没租出的一套设备每月需支出费用（维护费、管理费等）20元。
设每套设备的月租金为x（元），租赁公司出租该型号设备的月收益（收益＝租金收入－支出费用）为y（元）。
用含x的代数式表示未出租的设备数（套）以及所有未出租设备（套）的支出费求y与x之间的二次函数关系式；当月租金分别为300元和350元式，租赁公司的月收益分别是多少元？此时应该出租多少套机械设备？请你简要说明理由；请把（2）中所求出的二次函数配方成的形式，并据此说明：当x为何值时，租赁公司出租该型号设备的月收益最大？最大月收益是多少？3．某商店购进一批单价为18元的商品，如果以单价20元出售，那么一个星期可售出100件。
根据销售经验，提高销售单价会导致销售量减少，即当销售单价每提高1元，销售量相应减少10件，如何提高销售单价，才能在一个星期内获得最大利润？最大利润是多少？4．某市城建部门经过长期市场调查发现，该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x；年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=―10；如年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；在(1)的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议。
二次函数应用题
二次函数应用题1. 一自动喷灌设备的喷流情况如图所示，设水管AB 在高出地面5.1米的B 处有一自动旋转的喷水头，一瞬间流出的水流是抛物线状，喷头B 与水流最高点C 连线成 45角，水流最高点C 比喷头高2米，求水流落点D 到A 点的距离。
2. 某跳水队员进行10米跳台跳水训练时，身体所示坐标系下经过原点O 的一条抛物线，图中标出的数据为已知条件），在跳某个规定动作时，正常情况下，该运动员在空中最高出距水面3210米，入水处距池边的距离为4米，同时，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误，(1)求这条抛物线的解析式；(2)在某次试跳中，测得运动员在空中调整好入水姿势时，距池边的水平距离为533米，问此次跳水会不会失误并通过计算说明理由。
3. 某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润s （万元）与销售时间t （月）之间的关系（即前t 个月的利润总和s 与t之间的关系）．根据图象提供的信息，解答下列问题：（1）由已知图象上的三点坐标，求累积利润s （万元）与时间t （月）之间的函数关系式； （2）求截止到几月末公司累积利润可达到30万元；（3）求第8个月公司所获利润是多少万元？) 第3题图4. 华联商场以每件30元购进一种商品，试销中发现每天的销售量y（件）与每件的销售价x（元）满足一次函数y=162-3x.（1）写出商场每天的销售利润w（元）与每件的销售价x（元）的函数关系式；（2）如果商场要想获得最大利润，每件商品的销售价定为多少为最合适？最大销售利润为多少？5．如图，有一座抛物线型拱桥，在正常水位时水面AB的宽是20米，如果水位上升3米时，水面CD的宽为10米，（1）建立如图所示的直角坐标系，求此抛物线的解析式；（2）现有一辆载有救援物质的货车从甲地出发，要经过此桥开往乙地，已知甲地到此桥280千米，（桥长忽略不计）货车以每小时40千米的速度开往乙地，当行驶到1小时时，忽然接到紧急通知，前方连降大雨，造成水位以每小时0.25米的速度持续上涨，（货车接到通知时水位在CD处），当水位达到桥拱最高点O时，禁止车辆通行；试问：汽车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过多少千米？6. 某商场经营一批进价为2元的小商品，在市场营销中发现日销售单价x元与日销售量y（1（2）设经营此商品日销售利润（不考虑其他因素）为p元，根据销售规律，试求日销售利润p元与销售单价x元之间的函数关系式，问日销售利润p是否存在最大值或最小值？若有，试求出；若无，请说明理由；7.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行销和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两方面的信息（如甲、乙两图）注：甲、乙两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本，生产成本月份最低；甲图的图象是线段，乙图的图象是抛物线.请根据图象提供的信息说明，解决下列问题：⑴在3月份出售这种蔬菜，每千克的收益是多少？⑵哪个月出售这种蔬菜，每千克的收益最大？说明理由.（收益=售价-成本）8.如图，一单杆高2.2m ，两立柱之间的距离为1.6m ，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状。
二次函数应用题集锦
二次函数应用题集锦一、二次函数的实际应用--商品问题1.已知某商品的进价为每件40元，售价是每件60元，每星期可卖出300件。
据市场调查反映：如果调整价格，每涨价1元，每星期要少卖出10件。
要想获得最大利润，该商品应定价为多少元？分析：若设销售单价定为x元，每周的利润为y元。
那么每件商品的利润可表示为(x-40)元，每周的销售量可表示为[300-10(x-60)]件，一周的利润可表示为y=(x-40)[300-10(x-60)] 元，要想获得最大利润可得Y=（x-40)[300-10(x-60)]=(x-40）(900-10x)=-10x²+1300x-36000=-10(x-65)²+6250所以当x=65时，所获得的利润最大为6250元，即商品定价为65元时，可获得最大利润为6250元。
如设销售单价涨了x元，那么每件商品的利润可表示为（20+x) 元，每周的销售量可表示为（300-10x) 件，一周的利润可表示为(20+x)(300-10x) 元，每周获得利润为y=(20+x)(300-10x) =-10(x-5)²+6250当x=5时y的最大值为6250，即当定价：60+5=65元时可获得最大利润为6250元。
2.已知某商品的进价为每件40元。
现在的售价是每件60元，每星期可卖出300件。
市场调查反映：如调整价格，每涨价一元，每星期要少卖出10件；每降价一元，每星期可多卖出20件。
如何定价才能使利润最大？解：设每件涨价为x元时获得的总利润为y元，则y =(60-40+x)(300-10x)=(20+x)(300-10x) （0≤x≤30)=-10x²+100x+6000=-10(x²-10x-600)=-10［(x-5)²-25-600］=-10(x-5)²+6250当x=5时，y的最大值是6250定价:60+5=65（元）第二问解:设每件降价x元时的总利润为y元.y=(60-40-x)(300+20x)=(20-x)(300+20x)=-20x²+100x+6000=-20（x²-5x-300）=-20（x-2.5）²+6125 （0≤x≤20）所以定价为60-2.5=57.5时利润最大,最大值为6125元.答:综合以上两种情况，定价为65元时可获得最大利润为6250元.已知某商品的进价为每件40元。
二次函数应用题(经典题)
二次函数应用题1如图，抛物线与x 轴交于A （-1，0）、B （3，0）两点，与y 轴交于点C （0，-3），设抛物线的顶点为D ．（1）求抛物线的解析式；（2）求抛物线顶点D 的坐标；（3）探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与△BCD 相似？若存在，请指出符合条件的点P 的位置，并直接写出点P 的坐标；若不存在，请说明理由．2.如图，抛物线y=x2+bx+c 与x 轴交于A （-1，0）、B （3，0）两点，直线l 与抛物线交于A 、C 两点， 其中C 点的横坐标为2．（1）求抛物线的解析式及直线AC 的解析式；（2）P 是线段AC 上的一个动点，过P 点作x 轴的垂线交抛物线于E 点，求线段PE 长度的最大值； （3）点G 是抛物线上的动点，在x 轴上是否存在点F ，使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F 点坐标；如果不存在，请说明理由．．3.抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3，0)两点，（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由.（3）在（1）中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.4.（2009年滨州）某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：（1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；（2）当降价多少元时，每星期的利润最大？最大利润是多少？（3）请画出上述函数的大致图象．5．如图，在平面直角坐标系中，OB⊥OA，且OB＝2OA，点A的坐标是(－1，2)．（1）求点B的坐标；（2）求过点A、O、B的抛物线的表达式；（3）连接AB，在（2）中的抛物线上求出点P，使得S△ABP＝S△ABO．6.在平面直角坐标系中，二次函数y=ax2+bx+2的图象与x轴交于A（-3，0），B（1，0）两点，与y 轴交于点C．（1）求这个二次函数的关系解析式；（2）点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；（3）在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；7.某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨x 元（x为正整数），每个月的销售利润为y元．（1）求y与x的函数关系式并直接写出自变量x的取值范围；（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？（3）每件商品的售价定为多少元时，每个月的利润恰为2200元？根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元？8.如图，已知抛物线与x 轴交于A （－1，0）、E （3，0）两点，与y 轴交于点B （0，3）．（1）求抛物线的解析式；（2）设抛物线顶点为D ，求四边形AEDB 的面积；（3）△AOB 与△DBE 是否相似？如果相似，请给以证明； 如果不相似，请说明理由．9、一开口向上的抛物线与x 轴交于A （2m -，0），B （m ＋2，0）两点，记抛物线顶点为C ，且AC ⊥BC ．（1）若m 为常数，求抛物线的解析式；（2）若m 为小于0的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点？（3）设抛物线交y 轴正半轴于D 点，问是否存在实数m ，使得△BCD 为等腰三角形？若存在，求出m 的值；若不存在，请说明理由．10.（2）、图14（3）为解答备用图］（1）k = ，点A 的坐标为 ，点B 的坐标为 ； （2）设抛物线22y x x k =-+的顶点为M ，求四边形ABMC 的面积；（3）在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；（4）在抛物线22y x x k =-+上求点Q ，使△BCQ 是以BC 为直角边的直角三角形．O BACD xy第25题图图14（1）图14（2）图14（3）11.已知，如图抛物线y＝ax2＋3ax＋c(a>0)与y轴交于C点，与x轴交于A、B两点，A点在B点左侧．点B的坐标为(1,0)，OC＝3OB.(1)求抛物线的解析式；(2)若点D是线段AC下方抛物线上的动点，求四边形ABCD的面积的最大值；(3)若点E在x轴上，点P在抛物线上，是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．12.如图所示．某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造．已知△ABC的边BC长120米，高AD长80米。
中考经典二次函数应用题(含答案)
二次函数应用题1、某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.（1）求商家降价前每星期的销售利润为多少元？（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？2、某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？3、张大爷要围成一个矩形花圃．花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD ．设AB 边的长为x 米．矩形ABCD 的面积为S 平方米．（1）求S 与x 之间的函数关系式（不要求写出自变量x 的取值范围）．（2）当x 为何值时，S 有最大值？并求出最大值．（参考公式：二次函数2y ax bx c =++（0a ≠），当2bx a=-时，244ac b y a -=最大(小)值)4、某电视机生产厂家去年销往农村的某品牌电视机每台的售价y （元）与月份x 之间满足函数关系502600y x =-+，去年的月销售量p （万台）与月份x 之间成一次函数关系，其中两个月的销售情况如下表：月份 1月 5月 销售量 3.9万台 4.3万台（1）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？（2）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了%m ，且每月的销售量都比去年12月份下降了1.5m%．国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴．受此政策的影响，今年3至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台．若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元，求m 的值（保留一位小数）．5.831 5.9166.083 6.164）5、某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y （件）与销售单价x （元）符合一次函数y kx b =+，且65x =时，55y =；75x =时，45y =． （1）求一次函数y kx b =+的表达式；（2）若该商场获得利润为W 元，试写出利润W 与销售单价x 之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润不低于500元，试确定销售单价x 的范围．6、某商场在销售旺季临近时 ，某品牌的童装销售价格呈上升趋势，假如这种童装开始时的售价为每件20元，并且每周（7天）涨价2元，从第6周开始，保持每件30元的稳定价格销售，直到11周结束，该童装不再销售。
二次函数应用题
二次函数应用题1、某校九年级的一场篮球比赛中，如图所示，队员甲正在投篮，已知球出手时离地面高m，与篮圈中心的水平距离为7 m，当球出手后水平距离为4 m时到达最大高度4 m．设篮球的运动轨迹为抛物线，篮圈距地面3 m．(1)请你建立适当的平面直角坐标系，并判定此球能否准确投中？(2)此时，若对方队员乙在甲面前1 m处跳起盖帽拦截，已知乙的最大摸高为2.9 m，那么他能否获得成功？2、如图所示，一位篮球运动员在离篮圈水平距离为4 m处跳起投篮，球沿一条抛物线运行，当球运行的水平距离为2.5 m时，达到最大高度3.5 m，然后准确落入篮框内．已知篮圈中心离地面距离为3.05 m．(1)建立如图所示的直角坐标系，求抛物线所对应的函数关系式；(2)若该运动员身高1.8 m，这次跳投时，球在他头顶上方0.25 m处出手．问：球出手时，他跳离地面多高？3、某跳水运动员在进行10 m跳台跳水训练时，身体(看成一点)在空中的运动路线是如图所示的一条抛物线．在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面10m，入水处距池边的距离为4 m，同时运动员在距水面高度5 m以前，必须完成规定的翻腾动作，并调整好入水姿势时，否则就会出现失误．(1)求这条抛物线的函数关系式；(2)在某次试跳中，测得运动员在空中的运动路线是(1)中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为m，问此次跳水会不会失误？并通过计算说明理由．4、如图所示，是一条高速公路的隧道口在平面直角坐标系上的示意图，点A和A1、点B和B1分别关于y轴对称，隧道拱部分BCB1为一条抛物线，最高点C离路面AA1的距离为8米，点B离路面为6米，隧道的宽度AA1为6米．(1)求隧道拱抛物线BCB1的函数解析式．(2)现有一大型运货汽车，装载某大型设备后，其宽度为4米，车载大型设备的顶部与路面的距离均为7米，它能否通过这个隧道？请说明理由．5、某菜农搭建了一个横断面为抛物线形的蔬菜大棚，有关尺寸如图所示．(1)现建立如图所示的平面直角坐标系，试写出这条抛物线的函数表达式；(2)若这位菜农身高1.60m，则她在不弯腰的情况下，在大棚里横向活动范围有多长(精确到0.1m)？6、如图所示，有一座抛物线形拱桥，在正常水位时，水面AB的宽为20m，若水位上升3m，则水面CD的宽为10m．(1)建立如图所示的直角坐标系，试写出该抛物线的函数表达式；(2)现有一辆满载救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280km(桥长忽略不计)，货车正以40km/h的速度开往乙地，当行驶1h时，忽然接到紧急通知：前方连降暴雨，造成水位以0.25m/h的速度持续上涨(货车接到通知时水位在CD处，当水位达到桥拱最高点O时，禁止车辆通行)．试问：如果货车按原来的速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度最少为多少？7、如图所示，公园要造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA＝1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面距离最大，高度2.25m．若不计其他因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外？8、如图，在矩形ABCD中，AB＝6 cm，BC＝12 cm，点P从A出发，沿AB边向点B以1 cm/s的速度移动．同时Q 从B出发，沿BC边向C以2 cm/s的速度移动，如果P、Q两点分别到达B、C两点后就停止移动，回答下列问题：(1)运动开始第几秒时，△PBQ的面积等于8 cm2？(2)设运动开始到第t s时，五边形APQCD的面积为S cm2，写出S与t的函数关系式．(3)t为何值时，S最小？求出S的最小值9、某商店经营一批进价为10元的商品，据市场分析，每件售价15元，则一天可售55件，如果售价每降1元，则日销售量可增加3件，（为了方便结账，定价取整数）设销售单价为x元，日销售量为y件，日获利为w元。
二次函数应用题
1．某玩具厂计划生产一种玩具熊，每日最高产量为40只，且每日生产的玩具熊全部售出，已知生产x只玩具熊的成本为R（元），售价为每只P（元），且R、P与x之间的函数关系式分别为，．（1）当日产量为多少时，每日获得的利润为1750元？（2）当日产量为多少时，每日获得的利润最大？最大利润是多少？解：设每日产量为只，获得利润y元，则，即，其中，且x是整数．（1）当时，，解得，（舍）．（2）因为，所以当时，利润最大（元）．2．某旅行社有客房120间，每间客房的日租金为50 元，每天都客满．装修后欲提高租金，经调查，一间客房的日租金每增加5元，则客房每天少租6间，不考虑其他因素，每间客房的日租金提高到多少元时，客房的日租金的总收入最高？比装修前的日租金的总收入增加多少元？解：设日租金增加元，则收入，x是非负整数．即（x是非负整数）．当时，（元）．即日租金提高到75元时，总收入最高，比装修前增加750元．【总结】：例1、例2都是和利润相关的问题1、解决的步骤为：（1）将利润表示成某变量（通常是售价）的二次函数；（2）利用二次函数的最值求出利润的最大值或最小值，回答实际问题。
2、注意的问题（1）熟练掌握基本关系：每件的利润=每件的售价-每件的进价；总的利润=每件的利润×件数（或者总的利润=总的售价-总的进价）；（2）认真审题，如例1中，R（元）是总的成本，售价P（元）是每只的售价。
（3）求最大值或最小值时，要注意自变量的取值范围，当顶点的横坐标在自变量的取值范围之内时，在顶点处取得最值，而当顶点的横坐标不在自变量的取值范围之内时，通常在自变量的两端处取得最值，此时要画出草图辅助观察。
3、有一座抛物线形拱桥，在正常水位时水面AB的宽为20米，如果水位上升3米时，水面CD的宽是10 米．（1）建立以抛物线顶点为原点的直角坐标系，求此抛物线的解析式；（2）现有一辆载有救灾物质的货车从甲地经此桥到乙地，已知甲地到此桥280km（桥身忽略不计）．货车正以40km/h的速度开往乙地，当行驶一小时时，忽然接到紧急通知，前方连降暴雨，造成水位以每小时0.25m的速度持续上涨（货车接到通知时水位在CD处，当水位达到桥拱最高点时，禁止车辆通行）．问：货车以原来的速度行驶，能否安全通过此桥？若能，说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米？分析：（1）在平面直角坐标系中，要确定抛物线的解析式，需要知道抛物线上点的坐标，因此将题目中的条件转化为抛物线上点的坐标是解决问题的关键。
二次函数应用题
一、传播问题：1、某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染，求，，每轮感染中平均一台电脑能感染几台？若病毒得不到有效控制，三轮感染后，被感染的电脑会不会超过700台？2、有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?3、甲型H1N1流感病毒的传染性极强，某地因1人患了甲型H1N1流感没有及时隔离治疗，经过两天的传染后共有9人患了甲型H1N1流感，每天平均一个人传染了几人？如果按照这个传染速度，再经过5天的传染后，这个地区一共将会有多少人患甲型H1N1流感？二、增长率问题：平均增长（降低）率公式注意：（1）1与x 的位置不要调换（2）解这类问题列出的方程一般用直接开平方法1. 某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x ,列方程为_________________2. 某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为_____________3、雪融超市今年的营业额为280万元，计划后年的营业额为403.2万元，求平均每年增长的百分率？4、市政府为了解决市民看病难的问题，决定下调药品的价格，某种药品经过两次降价后，由每盒121元降到每盒100元，则这种药品平均每次降价的百分率为多少？2(1)a x b±=5、我国土地沙漠化日益严重，西部某市2003年有沙化土地100平方公里，到2005年已增至144平方公里。
请问：2003至2005年沙化土地的平均增长率为多少？三、面积问题：1、一块长和宽分别为40厘米和250厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体纸盒，使它的底面积为450平方厘米.那么纸盒的高是多少？2、如图某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长18m），另三边用木栏围成，木栏长35m。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五讲二次函数的应用题
解题步骤：
第一步设自变量；
第二步建立函数的表达式；
第三步确定自变量的取值范围；
第四步根据顶点坐标公式或配方法求出最大值或最小值（在自变量的取值范围内）
一．面积问题
例1.如图，用长20m的篱笆，一面靠墙（墙足够长）围成一个长方形的园子，怎样围才能使园子的面积最大？
最大面积是多少？
例2.已知某直角三角形的两直角边的和为2，则该直角三角形的面积可能达到的最大值是__________；斜边长的平方可能达到的最小值是__________。
基础练习
矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动．设运动时间为x秒，△PBQ的面积为y（cm2）. （1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值.
二．利润问题
例.某商店将进货每个10元的商品，按每个18元售出时，每天可卖60个，商店经理到市场上做一番调查后发现，若将这种商品的售价每提高1元，则日销售量就减少5个，为获得每日最大利润，则商品售价应定为每个多少元？
基础练习
某旅行社组团去外地旅游，30人起组团，每人单价800元．旅行社对超过30人的团给予优惠，即旅行团每增加一人，每人的单价就降低10元．你能帮助分析一下，当旅行团的人数是多少时，旅行社可以获得最大营业额？
综合提升
1.如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚
线折起，折成一个长方形形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）。
已知E、F在AB边
上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).
（1）若折成的包装盒恰好是个正方形，试求这个包装盒的体积V；
（2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？
2.班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
第四讲课后作业
1.小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
(2)当x是多少时，这个三角形面积S最大?最大面积是多少?
2.如图，在平面直角坐标系中，已知OA＝12厘米，OB＝6厘米，点P从O开始沿OA边向点A以1厘米/秒的速
度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动，如果P，Q同时出发，用t(秒)表示移动的时间(0≤t≤6)，那么
(1)设△POQ的面积为y，求y关于t的函数解析式；
(2)当△POQ的面积最大时，将△POQ沿直线PQ翻折得到△PCQ，试判断点C是否落在直线AB上？并说明理由．
3.为迎接中国世博会，某商家计划从厂家采购A ，B 两种产品共20件，产品的采购单价(元/件)是采购数量(件)的一次函数，下表提供了部分采购数量．
(1)设A 11 (2)经商家与厂家协商，采购A 产品的数量不少于B 产品数量的11
9，且A 产品采购单价不低于1200元，求该商
家共有几种进货方案；
(3)该商家分别以1760元/件和1700元/件的销售单价售出A ，B 两种产品，且全部售完，在(2)的条件下，求采购A 种产品多少件时总利润最大，并求最大利润．
三．综合提高
1.如图，四边形OABC 是边长为1的正方形，OC 与x 轴正半轴的夹角为15°，点B 在抛物线的图像上，则的值为（ ） A. B. C. D.
4.已知：如图m 、n 是方程x 2-6x+5=0的两个实数根，且m ＜n ，抛物线y=-x 2
+bx+c 的图象经过点A （m ，0）、B （0，n ）．
(1)求这个抛物线的解析式．
(2)设(1)中抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求出点C 、D 的坐标和△BCD 的面积.
6.如图，已知二次函数y=x 2
+bx+c 的图象经过两点C （-2，5）与D （2，-3），且与x 轴相交于A 、B 两点，其顶点为M ．
（1）求点M 的坐标； （2）求△ABM 的面积；
（3）在二次函数图象上是否存在点P ，使S △PAB =4/5S △MAB ？若存在，求出P 点的坐标；若不存在，请说明理由； （4）在二次函数图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变．得到一个新的图象，请你结合这个新的图象回答：当直线y=x+m （m ＜1）与此图象有两个公共点时，m 的取值范围是什么？
)0(2
<=a ax y a 3
2-
3
2
-
2-21
-。