整体法与隔离法经典习题
高一物理 必修一 整体法与隔离法典型题
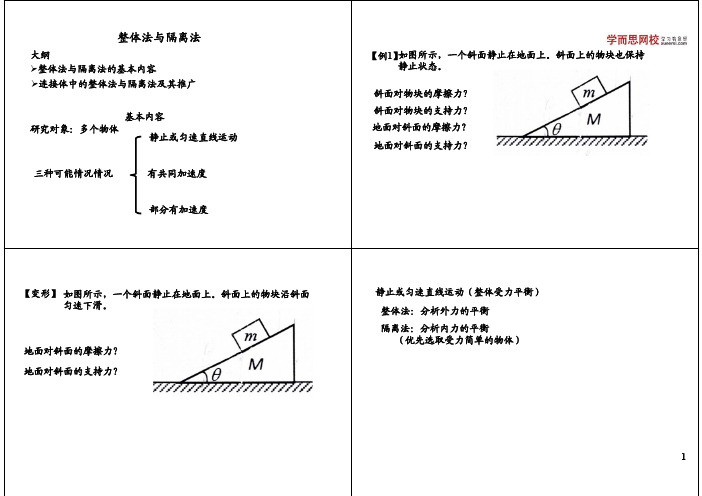
有共同加速度
部分有加速度
【变形】 如图所示,一个斜面静止在地面上。斜面上的物块沿斜面 匀速下滑。
静止或匀速直线运动(整体受力平衡) 整体法:分析外力的平衡 隔离法:分析内力的平衡 (优先选取受力简单的物体)
地面对斜面的摩擦力? 地面对斜面的支持力?
1
【例2】 如图所示,一个斜面静止在地面上。斜面上的物块也保持 静止状态。一水平向右的力F作用于物块。在F变大的过程 中,物块和斜面始终保持静止,则地面对斜面的支持力N 和摩擦力f的变化情况是 A. N变大,f不变 B. N变大,f变大 C. N不变,f变大 D. N不变,f不变
【变形】
如图所示,物体m位于动摩擦系数为μ的斜面上,斜面静止在 地面上,斜面的倾角为θ。现施加一水平力F作用于m上使其 沿斜面上滑。求地面对斜面摩擦力。
部分有加速度 整体法:整体合外力等于有加速度物体的合外力 (要会分解合外力) 隔离法:求内力 无需整体!直接隔离!
5
总结
研究对象:多个物体 整体法:分析外力平衡
【例6】如图所示,一个光滑斜面固定在地面上。斜面上有两个物 块A、B相互接触,一起沿斜面下滑,求B对A的压力。
3
【变形】如图所示,一个粗糙斜面固定在地面上。斜面上有两个物 块A、B相互接触,一起沿斜面下滑,物块和斜面之间的动 摩擦因数为μ,求B对A的压力。
【例7】如图所示,一个光滑斜面固定在地面上。斜面上有两个物 块A、B一起沿斜面下滑,两滑块接触面粗糙。求B对A的 摩擦力。
【例4】
如图所示,在两块相同的竖直木板间,有质量均为m的四 块相同的砖。用两个大小均为F的水平力压木板,使砖静止 不动,则左边木板对第一块砖和第二块砖对第三块砖的摩 擦力分别为( ) A.4mg, 2mg B.2mg, 0 C.2mg, mg D.4mg, mg
高中物理整体法隔离法解决物理试题题20套(带答案)

高中物理整体法隔离法解决物理试题题20套(带答案)一、整体法隔离法解决物理试题1.a、b两物体的质量分别为m1、m2,由轻质弹簧相连。
当用大小为F的恒力沿水平方向拉着 a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x1;当用恒力F竖直向上拉着 a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x2;当用恒力F倾斜向上向上拉着 a,使a、b一起沿粗糙斜面向上做匀加速直线运动时,弹簧伸长量为x3,如图所示。
则()A.x1= x2= x3 B.x1 >x3= x2C.若m1>m2,则 x1>x3= x2 D.若m1<m2,则 x1<x3= x2【答案】A【解析】【详解】通过整体法求出加速度,再利用隔离法求出弹簧的弹力,从而求出弹簧的伸长量。
对右图,运用整体法,由牛顿第二定律得整体的加速度为:;对b物体有:T1=m2a1;得;对中间图:运用整体法,由牛顿第二定律得,整体的加速度为:;对b物体有:T2-m2g=m2a2得:;对左图,整体的加速度:,对物体b:,解得;则T1=T2=T3,根据胡克定律可知,x1= x2= x3,故A正确,BCD错误。
故选A。
【点睛】本题考查了牛顿第二定律和胡克定律的基本运用,掌握整体法和隔离法的灵活运用.解答此题注意应用整体与隔离法,一般在用隔离法时优先从受力最少的物体开始分析,如果不能得出答案再分析其他物体.2.如图所示,质量为M的板置于水平地面,其上放置一质量为m的物体,物体与板,板与地面间的滑动摩檫系数分别为μ、2μ。
当作用在板上的水平拉力为F时能将板从物体下拉出,则F的取值范围为()A .F >mg μB .F >()m M g μ+C .F >2()m M g μ+D .F >3()m M g μ+ 【答案】D 【解析】 【详解】当M 和m 发生相对滑动时,才有可能将M 从m 下抽出,此时对应的临界状态为:M 与m 间的摩擦力为最大静摩擦力m f ,且m 运动的加速度为二者共同运动的最大加速度m a ,对m 有:m m f mg a g m mμμ===,设此时作用与板的力为F ',以M 、m 整体为研究对象,有:()()2m F M m g M m a μ'-+=+,解得()3F M m g μ'=+,当F F '>时,才能将M 抽出,即()3F M m g μ>+,故D 正确,ABC 错误。
整体法与隔离法例题

变式4:有一个直角支架AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑,AO上套有小环P,OB上套有小环Q,两环质量均为m,两环间有一根质量可忽略,不可伸长的细绳相连,并在某一位置平衡,如图3所示,现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态相比较,AO杆对P环的支持力 和 如图所示,光滑的金属球B放在纵截面为等腰三角形的物体A与竖直墙壁之间,恰好匀速下滑,已知物体A的重力是B的重力的6倍,不计球跟斜面和墙壁之间摩擦,问:物体A与水平面之间的动摩擦因数μ是多少?
( )
2、如图所示,质量为M的直角三棱柱A放在水平地面上,三棱柱的斜面是光滑的,且斜面倾角为θ。质量为m的光滑球放在三棱柱和光滑竖直墙壁之间,A和B都处于静止状态,求地面对三棱柱支持力和摩擦力各为多少?
(1)运动过程中轻绳与水平方向夹角θ;
(2)木块与水平杆间的动摩擦因数μ.
变式6:如图所示,一个底面粗糙,质量为m的斜面体静止在水平地面上,斜面体的斜面部分是光滑的,倾角为30°。现用一端固定的轻绳系一质量也为m的小球,小球静止时轻绳与斜面的夹角也是30°。试求:⑴当斜面体静止时绳的拉力大小?⑵若地面对斜面体的最大静摩擦力等于地面对斜面体支持力的k倍,为了使整个系统始终保持静止状态,k值必须满足什么条件?
A. 不变, 变大;
B. 不变, 变小;
C. 变大, 变大;
D. 变大, 变小。
变式5:如图所示,用轻质绝缘细线把两个带等量异种电荷的小球悬挂起来.今将该系统移至与水平方向成30”角斜向右上方向的匀强电场中,达到平衡时,表示平衡状态的图可能是( )
整体法隔离法经典习题 (1)

整体法与隔离法1.如图所示,顶端装有定滑轮的粗糙斜面体放在水平地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),现用水平向右的力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止,在此过程中下列说法正确的是( )A.水平力F增大B.斜面体所受地面的支持力一定不变C.物体A所受斜面体的摩擦力一定变大D.地面对斜面体的摩擦力一定变大.2,质量为m的物体在沿斜面向上的拉力F作用下,沿放在水平地面上的质量为M的粗糙斜面匀速上滑,此过程中斜面体保持静止,则地面对斜面()A.无摩擦力B.有水平向左的摩擦力大小为F·cosθC.支持力等于(m+M)gD.支持力为(M+m)g-F sinθ3.用轻质细线把两个质量未知的小球悬挂起来,如图甲所示.今对小球a持续施加一个向左偏下30°的恒力,并对小球b持续施加一个向右偏上30°的同样大的恒力,最后达到平衡.图乙中表示两个小球可能处于平衡状态的图是()4.有一直角支架AOB,AO 水平放置,表面粗糙;OB 竖直向下,表面光滑.AO 上套有小环P,OB 上套有小环Q,两环质量均为m.两环间由一根质量可忽略且不可伸长的细绳相连,并在某一位置平衡,如图所示.现将P 环向左移一小段距离,两环再次达到平衡,将移动后的平衡状态和原来的平衡状态比较,AO 杆对P 环的支持力F N 和细绳上的拉力F T 的变化情况是 ( )A.F N 不变,F T 变大B.F N 不变,F T 变小C.F N 变大,F T 变大D.F N 变大,F T 变小5.如图所示,两相同轻质硬杆1OO 、2OO 可绕其两端垂直纸面的水平轴O 、1O 、2O 转动,在O 点悬挂一重物M ,将两相同木块m 紧压在竖直挡板上,此时整个系统保持静止。
f F 表示木块与挡板间摩擦力的大小,N F 表示木块与挡板间正压力的大小。
若挡板间的距离稍许增大后,系统仍静止且1O 、2O 始终等高,则( )A .f F 变小B .f F 不变C .N F 变小D .N F 变大6.如图所示,轻绳的两端分别系在圆环A 和小球B 上,圆环A 套在粗糙的水平直杆MN 上.现用水平力F 拉着绳子上的一点O ,使小球B 从图中实线位置缓慢上升到虚线位置,但圆环A 始终保持在原位置不动.则在这一过程中,环对杆的摩擦力f 和环对杆的压力N 的变化情况是:( )A.f不变,N不变B.f增大,N不变C.f增大,N减小D.f不变,N减小,1.ABD 2. Bd 3.A 4. B 5. BD 6. B。
整体法与隔离法专题训练习题答案

整体法与隔离法专题训练答案liujianbo1.本题只有一个物体但有三个运动过程。
要考虑对过程用隔离法还是整体法。
适用的规律是动能定理。
先用隔离法:从A 到C 有mgh A + ACμmgcos α cos180°= E kc -0从C 到D CDμmgcos180° =E kd -E kc从D 到B -mgh b - BDμmgcosβ=0-E kdAC cos α=A'C BDcosβ=DB′三个方程相加得mg(h a -h b )- μmg( A'C +CD+ DB' )=0得μ= (h a -h b )/A'B‘=tan θm 作自由落体的条件是只受重力,故m 与M 间无弹力。
对m :H=gt 2/2 对M:S=at 2/2 当H/S=tan θ时F 有最小值。
故g/a=tan θ,a=gcot θF i =Mgcot2. (1)研究M 与m 组成的整体。
KA=(M+ m )a m ,a m =KA/(M+ m)再研究m ,是静摩擦力作为回复力。
f m = ma m =KA m/(M+ m)(2)根据机械能守恒,3. 常规方法是隔离法。
先研究m 。
(1)a=gsin θ 再研究M ,它的受力图如右。
静摩擦力最后画。
f=mgcos θsin θN=Mg+mgcos 2 θa=gsin θ- μ gcos θM 的受力图如下f 静=mgcos θ sin θ - μ mgcos 2θN=Mg+mg(1-sin 2 θ + μcos θ sin θ) ()2222121V m M MV +=mM MV V +=24.选择研究对象:因为A与B的加速度不同,本题宜用隔离法。
解:先研究B,画B的受力图。
v t2-v02=2as a=16m/s2 G+F f=ma F f=m(a - g)=0.3N再研究A 画A的受力图。
F n+F f=G a F n=1.7N 。
整体法和隔离法

整体法和隔离法
例1.如图所示,在两块相同的竖直木板间,有质量均为m 的四块相同的砖,用两个大小均为F 的水平力压木板,使砖静止不动,则左边木板对第一块砖,第二块砖对第三块砖的摩擦力分别为:( B )
A .4mg 、2mg
B .2mg 、0
C .2mg 、mg
D .4mg 、mg
【例2】如图所示,两个完全相同的重为G 的球,两球与水平地面间的动摩擦因数都是μ,一根轻绳两端固接在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳间的夹角为θ。
问当F 至少多大时,两球将发生滑动?
【解析】首先分析受力如图示,
选用整体法,由平衡条件得
F +2N=2
G ①
再隔离任一球,由平衡条件得T sin(θ/2)=μN ②
对O 点 2·T cos(θ/2)=F ③
①②③联立解之 例3
、如图所示,半径为R ,重为G 的均匀球靠竖直墙放置,左下方
有厚为h 的木块,若不计摩擦,用至少多大的水平推力F 推木块才能使球离开地面.
【解析】以球为研究对象,受力如图所示。
由平衡条件 N1cos θ=N2
2122θμθ
μctg Gctg F +=
N1sin θ=G
sin θ=(R-h)/R
再以整体为研究对象得:N2=F )
2()()(1sin cos cot 22
2h R h h R G
R
h R R h R G G G N F --=---====∴θ
θ
θ
1。
(完整版)整体法和隔离法典型例题

匀变速直线运动难点1.概念、规律、推论之间的联系与区别(1)一个重要概念:加速度0t v v v a t t-∆==∆ (2)三个重要规律: ①速度-时间规律:0t v v at =+②位移-时间规律:2012x v t at =+③速度-位移规律:222t v v ax -= (3)三个重要推论:①相邻相等时间内的位移差是定值,即:2x aT ∆= ②中间时刻的瞬时速度等于生程的平均速度,即:022tt v v v +=③中间位置的瞬时速度等于初速度与末速度的方均根值,即:2x v =(4)五个二级结论(仅适用于初速度为零的匀变速直线运动,请注意推导过程) ①第1s 、第2s 、…第ns 的速度之比12:::1:2::n v v v n =②前1s 、前2s 、…前ns 的位移之比22212:::1:2::n x x x n =③第1s 、第2s 、…第ns 的位移之比:::1:3::(21)N x x x n I =-④前1m 、前2m 、…前nm 所用时间之比12:::1:2::n t t t n =⑤第1m 、第2m 、…第nm 所用时间之比:::1:(21)::(1)N t t t n n I =---7、用电火花计时器(或电磁打点计时器)研究匀变速直线运动(A )(经常考试的实验)1、实验步骤:(1)把附有滑轮的长木板平放在实验桌上,将打点计时器固定在平板上,并接好电路 (2)把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着重量适当的钩码. (3)将纸带固定在小车尾部,并穿过打点计时器的限位孔(4)拉住纸带,将小车移动至靠近打点计时器处,先接通电源,后放开纸带. (5)断开电源,取下纸带(6)换上新的纸带,再重复做三次 2、常见计算:(1)2B AB BC T υ+=,2C BC CDT υ+=(2)2C B CD BCa T T υυ--==整体法和隔离法典型例题1.(2011·天津理综·T2)如图所示,A 、B 两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B 受到的摩擦力( )A. 方向向左,大小不变B. 方向向左,逐渐减小C. 方向向右,大小不变D. 方向向右,逐渐减小 【答案】选A .2.如图8所示,质量为M 的斜劈形物体放在水平地面上,质量为m 的粗糙物块,以某一初速度沿劈的斜面向上滑,至速度为零后又加速返回,而物体M 始终保持静止,则在物块m 上、下滑动的整个过程中 【 】(A )地面对物体M 的摩擦力方向没有改变 (B )地面对物体M 的摩擦力先向左后向右(C )物块m 上、下滑动时的加速度大小相同 (D )地面对物体M 的支持力总小于g m M )(+本题的正确答案是AD3.如图,质量为M 的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m 的小物块,小物块与斜面之间存在摩擦.用恒力F 沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力为( ) A .(M +m )gB .(M +m )g -FC .(M +m )g +F sin θD .(M +m )g -F sin θm FM θ • • •• •• O A B C D E3.07 12.3827.8749.62.77.40图2-54.有一个直角支架AOB ,AO 水平放置,表面粗糙, OB 竖直向下,表面光滑.AO 上套有小环P ,OB 上套有小环Q ,两环质量均为m ,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡,如图所示.现将P 环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO 杆对P 环的支持力F N 和摩擦力f 的变化情况是 ( )A .F N 不变,f 变大B .F N 不变,f 变小C .F N 变大,f 变大D .F N 变大,f 变小5(09年安徽卷)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。
整体法和隔离法专题训练 - 学生

第三章 第三课时 整体法隔离法专题训练一、选择题(共10小题,每小题6分,共60分,在每小题给出的四个选项中至少有一项符合题意,全部选对的得6分,漏选的得3分,错选的得0分)1.如图所示,一足够长的木板静止在光滑水平面上,一物块静皮肤止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为 ( )A .物块先向左运动,再向右运动B .物块向右运动,速度逐渐增大,直到做匀速运动C .木板向右运动,速度逐渐变小,直到做匀速运动D .木板和物块的速度都逐渐变小,直到为零2.如图所示,在倾角为θ的光滑斜面上有两个用劲度系数为k 的轻质弹簧相连的物块A 、B ,质量均为m ,开始时两物块均处于静止状态.现下压A 再静止释放使A 开始运动,当物块B 刚要离开挡板时,A 的加速度的大小和方向为 ( )A .0B .2g sin θ,方向沿斜面向下C .2g sin θ,方向沿斜面向上D .g sin θ,方向沿斜面向下3.如图所示是一种升降电梯的示意图,A 为载人箱,B 为平衡重物,它们的质量均为M ,上下均由跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中人的总质量为m ,匀速上升的速度为v ,电梯即将到顶层前关闭电动机,依靠惯性上升h 高度后停止,在不计空气和摩擦阻力的情况下,h 为( )A.v 22gB.(M +m )v 22mgC.(M +m )v 2mgD.(2M +m )v 22mg4.如图所示,小物块A 质量为M =10kg ,B 质量为m =2.5kg.A 、B 用一轻绳连接跨过无阻力的定滑轮且处于静止状态.A 与平台间动摩擦因数μ=0.25(与最大静摩擦因数相等).现用竖直向上的力F 拉A ,且F 由零线性增大至100N 的过程中,B 的下降高度恰为h =2m ,(A 未与滑轮相碰)则上述过程中的最大速度为(g =10m/s 2). ( )A .1m/sB .2m/sC .3m/sD .05.如图所示,某斜面体由两种材料拼接而成,BC 界面平行于底面DE ,两侧面与水平面夹角分别为30°和60°.已知一物体从A 点静止下滑,加速至B 点,匀速至D 点.若该物块静止从A 点沿另一侧面下滑,则有 ( )A .一直加速运动到E ,但AC 段的加速度比CE 段小B .AB 段的运动时间大于AC 段的运动时间C .将加速至C 点,匀速至E 点D .通过C 点的速率等于通过B 点的速率6.一条不可伸长的轻绳跨过质量可忽略不计的定滑轮,绳的一端系一质量m =15kg 的重物.重物静止于地面上,有一质量m 1=10kg 的猴子,从绳的另一端沿绳向上爬,如图所示,不计滑轮摩擦,在重物不离开地面的条件下,猴子向上爬的最大加速度为(g 取10m/s 2) ( )A .25m/s 2B .5m/s 2C .10m/s 2D .15m/s 27.如图(a)所示,水平面上质量相等的两木块A 、B 用一轻弹簧相连接,整个系统处于平衡状态.现用一竖直向上的力F 拉动木块A ,使木块A 向上做匀加速直线运动,如图(b)所示.研究从力F 刚作用在木块A 的瞬间到木块B 刚离开地面的瞬间这个过程,并且选定这个过程中木块A 的起始位置为坐标原点,则下图所示的图象中可以表示力F 和木块A 的位移x 之间关系的是 ( )8.如图所示的弹簧秤质量为m ,挂钩下面悬挂一个质量为m0的重物,现用一方向竖直向上的外力F 拉着弹簧秤,使其向上做匀加速直线运动,则弹簧秤的示数与拉力F之比为 ( )A .m 0:mB .m :m 0C .m 0:(m +m 0)D .m :(m -m 0)9.如图所示,一根轻质弹簧上端固定,下端挂一质量为m 0的秤盘,盘中有物体质量为m ,当盘静止时,弹簧伸长为l ,现向下拉盘使弹簧再伸长Δl 后停止,然后松开手,设弹簧总处在弹性限度内,则刚松开手时盘对物体的支持力等于 ( )A .(1+Δl l )(m +m 0)gB .(1+Δl l)mg C.Δl lmg D.Δl l (m +m 0)g10.如图所示,光滑水平面上放置质量分别为m 和2m 的四个木块,其中两个质量为m 的木块间用一不可伸长的轻绳相连,木块间的最大静摩擦力是μmg .现用水平拉力F 拉其中一个质量为2m 的木块,使四个木块以同一加速度运动,则轻绳对m 的最大拉力为 ( )A.3μmg 5B.3μmg 4C.3μmg 2D .3μmg二、论述、计算题(本题共3小题,共40分,解答时应写出必要的文字说明、计算公式和重要的演算步骤,只写出最后答案不得分,有数值计算的题,答案中必须明确数值和单位) 11.如图所示,把长方体分割成A、B两斜面体,质量分别为m A和m B,切面与水平桌面成θ角.两斜面体切面光滑,桌面也光滑.求水平推力在什么范围内,A不会相对B滑动?12.如图所示,在光滑的桌面上叠放着一质量为m A=2.0kg的薄木板A和质量为m B=3kg的金属块B.A的长度L=2.0m.B上有轻线绕过定滑轮与质量为m C=1.0kg的物块C相连.B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力.忽略滑轮质量及与轴间的摩擦.起始时令各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后放手,求经过多长时间B从A的右端脱离(设A的右端距离滑轮足够远,取g=10m/s2).13.一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端,如图所示,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右做加速运动时,求绳的拉力及斜面对小球的弹力.(g取10m/s2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整体法与隔离法经典习题
1.粗糙水平面上放置质量分别为m和2m的四个木块,其中两个质量为m的木块间用一不可
伸长的轻绳相连,木块间的动摩擦因数均为卩,木块与水平面间的动摩擦因数相同,可认为最大静摩擦力等于滑动摩擦力•现用水平拉力F拉其中一个质量为2m的木块,使四个木块一起匀速前进。
则需要满足的条件是()
A.木块与水平面间的动摩擦因数最大为「
B.木块与水平面间的动摩擦因数最大为 -
C.水平拉力F最大为2卩mg
D. 水平拉力F最大为6卩mg
2.如下图所示,重为G的匀质链条挂在等高的两钩上,并与水平方向成日角,试求:
(1)链条两端受到的力。
???
(2)链条最低处的张力
3.吊篮重300N人重500N绳子质量及其与滑轮摩擦不计,要使吊篮离地上升,则人的拉
力至少多大
4.有一直角支架AOBAC水平放置,0B竖直向下,表面光滑, 有小环P, OB上套有小环Q。
两环质量均为m两环间由一根忽略不可伸长的细绳相连,并在某一位置平衡,如图所示。
环向左移一小段距离,两环再次达到平衡,那么将移动后的态和原来的平衡状态比较,AO杆对P环的支持力N和细绳上的拉力T的变化情况是()
A.N不变,T变大
B.N不变,T变小
AO上套
质量可
现将P
平衡状A
的支持力为F 3,地面对A 的摩擦力为F 4,若F 缓慢增大而且整个装置仍保持静止,在此过
程中( )
A. F i 保持不变,F 3缓慢增大 B . F 2、F 4缓慢增大
C. F i 、F 4缓慢增大 D . F 2缓慢增大,F 3保持不变
8. 如图所示,质量为m 的物体在与斜面平行向上的拉力 F 作用下,沿着水平地面上质量为 C.N 变大,T 变大 C.N 变大,T 变小
5•将长方形均匀木块锯成如图所示的三部分,其中 对称,现将三部分拼在一起放在粗糙水平面上,当用与木
直的水平向右力F 作用时,木块恰能向右匀速运动,且 A 与B 、A 与C 均无相对滑动,图中 的9角及F 为已知,求A 与B 之间的压力为多少
6.如图所示,光滑的金属球B 放在纵截面为等边三角形的物体 A 与坚直墙之间,恰好匀速 下滑,已知物体A 的重力是B 重力的6倍,不计球跟斜面和墙之间的摩擦,问:物体 A 与
水平面之间的动摩擦因数 卩是多少
7.如图所示,质量为M 的直角三棱柱A 放在水平地面上,
三棱柱的斜面是光滑的,且斜面倾角为9.质量为m 的光滑
球B 放在三棱柱和光滑竖直墙之间.A 、B 处于静止状态,现对B 加一竖直
向下的力F ,F 的作用线过球心•设墙对
B 的作用力为只,B 对A 的作用力为F 2,地面对A
部分完全
块左侧垂 B
M的粗糙斜面匀速上滑,在此过程中斜面保持静止,则地面对斜面()
9. 如图所示,质量分别为m 、m 的两个物体通过轻弹簧连接,在力 F 的作用下一起沿水平 方向做匀速直线运动(m 在地面上,m 2在空中),力F 与水平方向成9角•则m 所受支持力 F N 和摩擦力F f 正确的是( )
10. 如图所示,重为8N 的球静止在与水平面成37°角的光滑斜面上,并通过定滑轮与重 4N 的物体A 相连,光滑挡板与水平而垂直,不计滑轮的摩擦,绳子的质量,求斜面和挡板所 受的
压力(sin37 0=0.6 )
A. F N = mg + mg — Fsin 9 C. F f = Feos 9
B. F N = mg + mg -Feos 9
D. F f = Fsin 9。
