(优选)第五版传热学课件第五
传热学5第五章
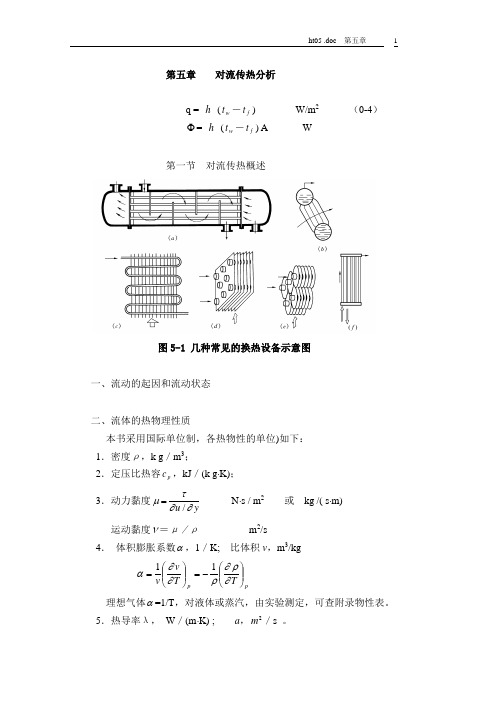
第五章 对流传热分析q = h (t w -t f ) W/m 2 (0-4)Φ= h (t w -t f ) A W第一节 对流传热概述图5-1 几种常见的换热设备示意图一、流动的起因和流动状态二、流体的热物理性质本书采用国际单位制,各热物性的单位)如下: 1.密度ρ,k g /m 3;2.定压比热容p c ,kJ /(k g ⋅K); 3.动力黏度/u yτμ∂∂=N ⋅s / m 2 或 kg /( s ⋅m)运动黏度ν=μ/ρ m 2/s 4. 体积膨胀系数α,1/K; 比体积v ,m 3/kgpp T T v v ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=∂ρ∂ρ∂∂α11 理想气体α=1/T ,对液体或蒸汽,由实验测定,可查附录物性表。
5.热导率λ, W /(m ⋅K) ; a ,m 2/s 。
三、流体的相变 四、换热表面几何因素()l c t t u f h p f w ,,,,,,,,μαρλ= (5-1)第二节 对流传热微分方程组一、对流传热过程微分方程式图5-2 对流传热过程xw x y t q ,⎪⎪⎭⎫ ⎝⎛-=∂∂λ W/2m (1)x x x f w x x t h t t h q ∆⋅=-=)( (2) x x t h ∆-=λ∂∂t y w x⎛⎝ ⎫⎭⎪, (5-2a) w t t -=θxw x x y h ,⎪⎪⎭⎫ ⎝⎛∆-=∂θ∂θλ (5-2b) 式中()∆θθθx wfx=-,其中θw =0,θf f w t t =-。
二、连续性方程图5-3 连续性方程的推导x 方向: d x M u y ρ≡d d xx x xM M M x x∂∂+≡+ y 方向: d y M v x ρ≡ d d yy y y M M M y y∂∂+≡+ 0u v x y∂∂∂∂+= (5-3)三、动量微分方程式图5-4 动量微分方程的推导(1) 微元体的质量×加速度: D d d d Ux y ρτD d u τ= u u uu v x y ∂∂∂∂τ∂∂++D d v τ= v v vu v x y∂∂∂∂τ∂∂++(2) 微元体所受的外力: 体积力: X d x d y Y d x d y表面力: (∂σ∂∂τ∂x y xx y +) d x d y (∂σ∂∂τ∂y x yy x+) d x d y x 方向: ρ(∂∂τ∂∂∂∂u u u x v u y ++) = X +∂σ∂∂τ∂x y xx y+y 方向: ρ(∂∂τ∂∂∂∂v u v x v vy ++) = Y +∂σ∂∂τ∂y x y y x+ρ(∂∂τ∂∂∂∂u u u x v u y ++) = X -∂∂px + μ∂∂∂∂2222u xu y +⎛⎝ ⎫⎭⎪⎪ (5-4a) ρ(∂∂τ∂∂∂∂v u v x v v y ++) = Y -∂∂py + μ∂∂∂∂2222v x v y +⎛⎝ ⎫⎭⎪ (5-4b)↓ ↓ (1) (2) (3) (4)(1)惯性力项,即质量与加速度之积;(2)体积力;(3)压强梯度;(4)黏滞力。
《传热学》(第五版)

第一章导热理论基础2已知:10.62()W m K λ=∙、20.65()W m K λ=∙、30.024()W m K λ=∙、40.016()W m K λ=∙求:'R λ、''R λ 解:2'3124124224259210 1.1460.620.650.016m K R W λσσσλλλ-⨯⨯⨯⨯⎛⎫∙=++=++⨯= ⎪⎝⎭'"232232560.265/0.650.024R m k W λσσλλ⨯⎛⎫=+=+=⋅ ⎪⎝⎭由计算可知,双Low-e 膜双真空玻璃的导热热阻高于中空玻璃,也就是说双Low-e 膜双真空玻璃的保温性能要优于中空玻璃。
5.6.已知:50mm σ=、2t a bx =+、200a =℃、2000b =-℃/m 2、45()Wm K λ=∙求:(1)0x q =、6x q = (2)v q解:(1)00020x x x dtq bx dx λλ====-=-= 3322452(2000)5010910x x x dtW q bx m dx σσσλλ-====-=-=-⨯⨯-⨯⨯=⨯(2)由220vq d t dx λ+=2332245(2000)218010v d t W q b m dxλλ=-=-=-⨯-⨯=⨯9.取如图所示球坐标,其为无内热源一维非稳态导热 故有:22t a t r r r r τ∂∂∂⎛⎫= ⎪∂∂∂⎝⎭00,t t τ==0,0tr r∂==∂ ,()f tr R h t t rλ∂=-=-∂ 10.解:建立如图坐标,在x=x 位置取dx 长度微元体,根据能量守恒有:x dx x Q Q Q ε++= (1)x dt Q dx λ=-+()x dx d dtQ t dx dx dxλ+=-++∙ 4()b b Q EA E A T Udx εεεσ===代入式(1),合并整理得:2420b fU d t T dx εσλ-= 该问题数学描写为:2420b f U d t T dx εσλ-= 00,x t T == ,0()x ldtx l dx ===假设的 4()b e x ldtfT f dx λεσ=-=真实的 第二章稳态导热3.解:(1)温度分布为 121w w w t t t t x δ-=-(设12w w t t >)其与平壁的材料无关的根本原因在 coust λ=(即常物性假设),否则t 与平壁的材料有关 (2)由 dtq dxλ=- 知,q 与平壁的材料即物性有关5.解: 2111222()0,(),w w ww d dt r dr drr r t t t t r r t t===>==设有:12124()11w w Q t t r r πλ=-- 21214F r r R r r λπλ-=7.已知:4,3,0.25l m h m δ=== 115w t =℃, 25w t =-℃, 0.7/()W m k λ=⋅ 求:Q解: ,l h δ ,可认为该墙为无限大平壁15(5)0.7(43)6720.25tQ FW λδ∆--∴==⨯⨯⨯= 8.已知:2220,0.14,15w F m m t δ===-℃,31.28/(), 5.510W m k Q W λ=⋅=⨯ 求:1w t解: 由 tQ Fλδ∆= 得一无限平壁的稳态导热312 5.510150.141520 1.28w w Q t t F δλ⨯=+=-+⨯=⨯℃ 9.已知:12240,20mm mmδδ==,120.7/(),0.58/()W m k W m k λλ=⋅=⋅3210.06/(),0.2W m k q q λ=⋅=求:3δ解: 设两种情况下的内外面墙壁温度12w w t t 和保持不变,且12w w t t >221313由题意知:1211212w w t t q δδλλ-=+122312123w w t t q δδδλλλ-=++再由: 210.2q q =,有121231212121230.2w w w w t t t t δδδδδλλλλλ--=+++得:123312240204()40.06()90.60.70.58mm δδδλλλ=+=⨯⨯+= 10.已知:1450w t =℃,20.0940.000125,50w t t λ=+=℃,2340/q W m ≤ 求:δ 解: 412,0.094 1.25102w w t t tq m m λλδ+∆==+⨯⨯41212[0.094 1.2510]2w w w w t t t t tmq qδλ+-∆==+⨯⋅ 44505045050[0.094 1.2510]0.14742340m +-=+⨯⨯⨯= 即有 2340/147.4q W m m mδ≤≥时有 11.已知:11120,0.8/()mm W m k δλ==⋅,2250,0.12/()mm W m k δλ==⋅33250,0.6/()mm W m k δλ==⋅求:'3?δ=解: '2121'3123112313,w w w w t t t t q q δδδδδλλλλλ--==+++由题意知:'q q =212tw 1tw 2q 11λ12λ23λ322即有:2121'3123112313w w w wt t t t δδδδδλλλλλ--=+++'33322λδδδλ=+ 0.6250505000.12mm =+⨯= 12.已知:1600w t =℃,2480w t =℃,3200w t =℃,460w t =℃ 求:123,,R R R R R R λλλλλλ解:由题意知其为多层平壁的稳态导热 故有: 14122334123w w w w w w w w t t t t t t t t q R R R R λλλλ----====∴112146004800.2260060w w w w R t t R t t λλ--===-- 223144802000.5260060w w w w R t t R t t λλ--===--33414200600.2660060w w w w R t t R t t λλ--===-- 14.已知:1)11012,40/(),3,250f mm W m k mm t δλδ==⋅==℃,60f t =℃ 220112,75/(),50/()h W m k h W m k λλ==⋅=⋅ 2)223,320/()mm W m k δλ==⋅ 3)2'23030,,70/()h W m k δδλλ===⋅求:123123,,,,,q q q k k k ∆∆∆ 解:未变前的122030102250605687.2/1113101754050f f t t q W m h h δλ---===⨯++++tw 1tw 4tw 2tw 3R 1R2R3R =R 1+R 2R3+t αt f221)21311121129.96/()1112101754050k W m k h h δλ-===⋅⨯++++ 21129.96(25060)5692.4/q k t W m =∆=⨯-= 21105692.45687.2 5.2/q q q W m ∆=-=-= 2)22321221129.99/()11131017532050k W m k h h δλ-===⋅⨯++++ 22229.99(25060)5698.4/q k t W m =∆=⨯-= 22205698.45687.211.2/q q q W m ∆=-=-= 3) 22330'101136.11/()131********k W m k h h δλ-===⋅⨯++++ 23336.11(25060)6860.7/q k t W m =∆=⨯-= 23306860.75687.21173.5/q q q W m ∆=-=-= 321q q q ∴∆∆>∆ ,第三种方案的强化换热效果最好 15.已知:35,130A C B mm mm δδδ===,其余尺寸如下图所示,1.53/(),0.742/()A C B W m k W m k λλλ==⋅=⋅求:R λ解:该空斗墙由对称性可取虚线部分,成为三个并联的部分R 1R 1R 1R2R3R 2R 2R3R311113222,A B C A B C R R R R RR R R R =++==++ 3321111311135101301020.1307()/1.53 1.53C A B A B C R R m k W δδδλλλ--⨯⨯∴=++=⨯+==⋅332322222335101301020.221()/1.530.742C A B A B C R m k W δδδλλλ--⨯⨯=++=⨯+=⋅2212115.0410()/1111220.13070.221R m k W R R λ-∴===⨯⋅⨯+⨯+16.已知:121160,170,58/()d mm d mm W m k λ===⋅,2230,0.093/()mm W m k δλ==⋅33140,0.17/(),300w mm W m k t δλ==⋅=℃,450w t =℃求:1)123,,R R R λλλ; 2) l q : 3) 23,w w t t . 解:1)4211111170lnln 1.66410()/2258160d R m k W d λπλπ-===⨯⋅⨯2222221117060lnln 0.517()/220.093170d R m k W d λδπλπ++===⋅⨯ 223332222111706080lnln 0.279()/2220.1717060d R m k W d λδδπλδπ++++===⋅+⨯+tw 1112323tw 4132R R R λλλ∴< 2) 2330050314.1/0.5170.279l i t t q W m R R R λλλ∆∆-====++∑ 3)由 121w w l t t q R λ-=得 4211300314.1 1.66410299.95w w l t t q R λ-=-=-⨯⨯=℃ 同理:34350314.10.279137.63w w l t t q R λ=+=+⨯=℃ 17.已知:1221211,,22m m d d δδλλ=== 求:'ll q q 解:忽略管壁热阻010121020122211ln ln 222d d R d d λδδδπλπλδ+++=++ '010122010122211ln ln 222d d R d d λδδδπλπλδ+++=++ '',l l t tq q R R λλ∆∆== (管内外壁温13,w w t t 不变)01012'20101'010*******22211lnln 22222211ln ln 222l l d d q R d d d d q R d d λλδδδπλπλδδδδπλπλδ+++++∴==+++++01010010101001241lnln 22241ln ln 22d d d d d d d d δδδδδδ++++=++++由题意知: 1001011[(2)]2m d d d d δδ=++=+ 2112011[(2)]32mm m d d d d δδ=++=+ 即:21010101232()m m d d d d d δδδ=⇒+=+⇒= (代入上式)3''15ln 3ln23 1.277ln 3ln 23l l q R q R λλ+∴===+ 即: '0.783l l q q ='21.7%l llq q q -∆==即热损失比原来减小21.7%。
传热学第五版课件完整版_图文

接触热阻的影响因素: 粗糙度
挤压压力 硬度匹配情形 空隙中介质的性质
减小接触热阻的措施: 表面尽量平整 增加挤压压力
两表面一软一硬 涂导热姆
第七节 二维稳态导热
应用领域:房间墙角,地下埋管,矩形保温层,短肋片
二维稳态导热微分方程: 二维稳态导热问题的研究手段:
解析法 数值法 形状因子法
第i层与第i+1层之间接触面的温度:
二、第三类边界条件
常物性时导热微分方程组如下:
根据第一类边界条件时的结果: (此时壁温tw1和tw2为未知) 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2,得:
单层平壁的热流密度:
多层平壁的热流密度:
第二节 通过复合平壁的导热
应用领域:空心砖,空斗墙
并解出其通解为 :
代入边界条件求出c1和c2,并代入通解,得出特解 :
等截面直肋的温度分布:
肋端过余温度:
肋片散热量:
当考虑肋端散热时,计算肋片散热量时可采用假想肋高 代替实际肋高 l
一维温度场假定的检验 :
请同学们思考一个问题:
肋高越大,肋的散热面积越大,因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行?若 可行,是否会有某些局限性?
一、等截面直肋的导热
一维简化的假设条件: 肋片的高度l远大于肋片的厚度δ, 因而厚度方向温差很小,
负内热源的处理方法—— 将y方向的对流散热量 等效转化为负内热源
断面周长: 断面面积:
进行负内热源处理后等截面直肋导热微分方程组如下:
(假定肋端绝热)
定义 :
令
—— 过余温度
:
使导热微分方程齐次化 :
第五版传热学课件

3.三种常见情况的简化:1Biblioteka 1 Xa.两无限大平行灰平壁:
1, 2
AEb1 Eb 2 1 1 1
1
2
1, 2
A1 Eb1 Eb 2 1 A1 1 1 1 A2 2
2 ,1
c.空腔与空腔内很小的内包壁面:
A1 X 1, 2 A1 X 1,5 A1 X 1,6
Ai X i , j Aik X ik , jp ——角系数的分解性
k 1 p 1
n
m
复杂情况下角系数的确定方法
——在图9-18,9-19,9-20的基础上, 利用角系数三个特性,对适用范围进行拓展
X 1, 2 A1 X 2,1 A2
1.辐射换热量计算式:
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 X 1, 2 A1 2 A2
2.系统发射率:
A1 Eb1 Eb 2 1, 2 S X 1, 2 A1 Eb1 Eb 2 1 1 A1 1 1 X A 1 1, 2 2 2 1 1 ——系统发射率 式中: S 1 1 1 X 1, 2 1 X 2,1 1 1 2
列出每个表面的辐射净热量方程
确定每两个表面间的角系数
三个黑表面组成空腔 的辐射网络图
方程组联立求解
重辐射面——参与辐射过程中没有净热量交换的绝热表面
重辐射面的特点:将投射过来的辐射能全部反射回去,并且是将 空间某一方向投射来的能量,转到空间的另一个方向上去。 重辐射面在网络图上的处理方法:不和外源相连接,形成浮动节点
n
——角系数的互换性
传热学课件第5章

第五章 对流换热原理
传热学C Heat Transfer
§5-1 对流换热概述
一、对流换热的定义和机理
对流换热:流体流过固体壁面时所发生的热 量传递过程。
机理:既有热对流,也有导热,不是基本的热量传 热方式。
传热学C Heat Transfer
二、牛顿冷却公式
hx— 壁面x处局 系部 W 数 ( m 表 2C ) 面
由以上得:
hx
tw
t
t y
y0,x
它揭示了对流换热问题的 本质
传热学C Heat Transfer
五、局部对流换热系数与边界层的关系
传热学C Heat Transfer
平均对流传热系数:
h 1 At
AhxtxdAx
对于长度为 l 的平板:
1. 定义:当流体流过固体壁面时, 由于流体粘性的作用,使得在固 体壁面附近存在速度发生剧烈 变化的薄层称为流动边界层或 速度边界层。
2. 速度边界层厚度d 的规定:速度等于99%主流 速度。
传热学C Heat Transfer
3. 特点:通常情况下,边界层厚度d是比壁面尺度l 小一个数量级以上的小量。 d << l
传热学C Heat Transfer
例如,对于外掠平板的对流换热现象,可以得到雷
诺数Re、普朗特数Pr和努赛尔数Nu。如果是
两个相似的外掠平板的对流换热现象,则必有:
R'eR"e Pr ' Pr" N'uN"u
根据相似的这种性质,在实验中就只需测量各准 则所包括的量,避免了测量的盲目性,解决了实验 中测量那些量的问题。
Gr gtL3 2
传热学课件第五章辐射换热理论

0
d
在相同的温度下以黑体的辐射力最大 ,
用Eb表示,则实际物体的辐射力E为
E = ε Eb
式中:ε 为物体的发射率(或黑度);
Eb为同温度下黑体的辐射力,W/m2。
二 、有效辐射 物体表面除了因本身的温度特性向外 界发出本身辐射外 ,其它物体投射到物体表 面上的投射辐射还有部分被反射。本身辐 射和反射辐射之和称为有效辐射,记为J,单 位为w/m2,即 J = E + ρ G 式中,E称为发射辐射或本身 辐射,ρ G为反射辐射,G称为该 表面接受到的投入辐射。 有效辐射在辐射换热的分析和计算中 非常重要。
Fb ( 01T ) 0.07025%, Fb ( 02T ) 8.88%
则 F b ( 1T 2T ) Fb ( 0 2T ) Fb ( 0 1T ) 8.88% 0.07025% 8.81%
结果分析:在灯丝发出的辐射能中,可见光只 占8.81%,其余91.19%属于不可见的红外辐射, 并转化为热能,散失到周围环境中,钨丝灯作为光 源其效率是很低的。
进行辐射换热计算时,需要计算物体辐射能 力的大小。对于黑体辐射可从普朗克定律积分得 出 Eb =σ bT4 W/m2 式中:σ b为黑体辐射常数,σ b=5.67×10-8W/ (m2·K4);T为黑体热力学温度,K。 上式也可 4 写为 T Eb c0 2 W/m 100 式中:c0为黑体辐射系数,c0=5.67。 上式表明黑体的辐射力与热力学温度的四次 方成正比,故又称为四次方定律。
首页
重点与难点
重点:
1. 热辐射的特点、热辐射表面的性质。 2. 辐射力、黑体、灰体、有效辐射等基本 概念。 3. 热辐射基本定律。 4. 气体辐射的特点。
传热学第五版课件完整版PPT课件
d 2t qV 0 2 dx
7.物性参数λ 、 ρ 、c均为常数,一维稳态温度场,无内热源:
d 2t 0 2 dx
第四节
通解
导热过程的单值性条件
特解
作用:用来对某一特定的导热过程进行进一步的具体说明
四种单值性条件:
几 何 条 件 时 间 条 件 物 理 条 件 边 界 条 件
δ,l,d……
q z
t z
第二节
导热系数
每种物质的导热系数可通过实验确定 常用物质可查表获取
一 般 规 律
固相>液相>气相 金属>非金属 晶体>无定形态 纯物质>有杂质物质 纯金属>合金
导热系数的主要影响因素:温度、压力
气体的导热系数:
随温度升高而增大(由于分子运动速度和比定容热容增大),
压力对其影响不大(密度增大但自由程减小)
第三节
导热微分方程式
研究目标:确定物体内的温度场
研究基础: 导热微分方程式=能量守恒定律+傅立叶定律 研究对象: 右 图 中 的 六 面 微 元 体
根据能量守恒定律: 导入和导出微元体的净热量+微元体中内热源的发热量 =微元体热能(内能)的增加
在一定时间dτ内: 导入微元体的净热量: 导出微元体的净热量:
t t t t c qV x x y y z z
——导热微分方程式
在几种特殊条件下对导热微分方程式的简化:
1.物性参数λ 、 ρ 、c均为常数:
q z dz q z q z dz z
q y
代入上式
再将傅立叶定律代入,得出: 三个方向导入与导出微元体的净热量:
传热学第五章
第五章 对流传热原理
第一节 概 述
对流传热种类 自然对流传热
空气 水 强迫对流传热 气体 高压水蒸汽
对流传热系数的大致范围
h[W/(m2﹒K)]
对流传热种类
水
3~10
液态金属
200~1000
气-液相变传热
水沸腾
20~100
水蒸汽凝结
500~3500
有机蒸汽凝结
表 5-1 h[W/(m2﹒K)] 1000~15000 3000~110000
第五章 对流传热原理
第二节 边界层概念
4、流动状态判据(P78)
(2)上述流体纵掠等温平壁中:
边界层由层流向湍流过渡的距离xc称为临界长度,对应的
临界雷诺数为
Re c
u xc
u xc
5 105
Re x Re c ,为层流边界层
Re x Re c ,为湍流边界层
综上所述,影响对流传热系数h的主要因素,可 定性地用函数形式表示为:
h=(v,tw,tf,λ,ρ,cp,η,αV,γ,lc,φ)
式中:γ为汽化潜热; lc为描述传热面大小的特征长度; φ为壁面的几何形状因素,包括形状、位置等。
第五章 对流传热原理
第一节 概 述
四、研究对流传热的方法(P76)
研究对流传热的方法,即确定对流传热系数h的方法大致有 以下四种:
例如,同一根圆管,管内流动和管外流动(横掠)的强迫对流 传热是截然不同的,如图5-1a)所示。
再如,同一水平壁自然对流散热,热面朝上时气流旺盛,热面 朝下时气流较弱,因此具有不同的传热强度,见图5-1b)
第五章 对流传热原理
第一节 概 述
图5-1 几何因素的影响
传热学第5章
如果Pr =1,则
St x
Cf , x 2
Cf St 2
以上两式称为雷诺比拟式
根据动量传递与热量传递之间的类比性,通过 理论分析建立起描述这两个传递现象的物理量之间 的关系式(称为比拟关系式),再由已知或比较容 易获得的动量传递的规律推测出热量传递的规律, 这种分析方法称为动量传递与热量传递的比拟法。 比拟法曾被广泛用于紊流换热问题的研究。
x
4.64 Re
1/ 2 x
精确解: 4.92 Rex 1/ 2
x
由速度分布及牛顿公式还可求得距前缘 x 处平 板表面的局部切应力和局部摩擦系数 2 0.323 u w,x Rex
Cf , x
w, x 1/ 2 0.646 Rex 2 u / 2
精确解: Cf , x 0.664 Rex 1/ 2
hl 令 Nu Y Y 0 Nu Y Y 0
hl
Y 0
Nu称为平均努塞尔数,等于壁面法线方向上的平 均无量纲温度梯度,大小反映平均对流换热的强弱。
2
对于常物性、无内热源、不可压缩牛顿流体平行 外掠平板稳态对流换热,du //dx=0,方程组简化为 u v U V 0 无量纲化 0 X Y x y 2 U U 1 2U u u u U V u v 2 X Y Re Y 2 x y y 2 1 2 t t t U V u v a 2 X Y Re Pr Y 2 x y y 式中 Re
特征数关联式中变量个数大为减少,更突出地反映相 关物理量之间的依赖关系及其对对流换热的综合影响。 3 外掠平板层流边界层微分方程精确解 对于常物性、 u v 0 无内热源、不可压 x y y = 0, u=v=0, u u 2u 缩牛顿流体平行外 t = tw, u v 掠等壁温平板稳态 x y y 2 y =∞, u=u∞ , t = t∞, 2 层流换热,数学模 t t t u v a 2 型为: x y y 4
传热学课件第5章
Convective Heat Transfer
本章重点内容
重点内容: (1)对流换热及其影响因素; (2)牛顿冷却公式; (3)用分析方法求解对流换热问题的实质; (4)边界层概念及其应用。
掌握内容: 对流换热及其影响因素;用分析方法求解对流换
热问题的实质。
了解内容: 比拟理论。
单位:W/(m2.K) 物理意义:当流体与壁面温度相差1K时、每 单位壁面面积上、单位时间内所传递的热量
如何确定h及增强换热的措施是对流换热的核
心问题
5-1 对流换热概说
5 对流换热的影响因素
(1)流动起因; (2)流动状态; (3)流体有无相变; (4) 换热表面的几何因素; (5)流体的热物理性质。
5-2 对流换热问题的数学描写
1 质量守恒方程(连续性方程)
流体的连续流动遵循质量守恒规律
y
沿x方向流入微元体的质量
M x udy
沿x方向流出微元体的质量
udy dy dx
u u dxdy
x
M xdx
Mx
M x x
dx
0
x
单位时间内沿x轴方向流入微元体的净质量:
Mx
M xdx
M x x
dx
h湍流 h层流
单相换热:
相变换热:凝结、沸腾、升华、凝固、融化等
h相变 h单相
5-1 对流换热概说
(4) 换热表面的几何因素: 内部流动对流换热:管内或槽内 外部流动对流换热:外掠平板、圆管、管束
5-1 对流换热概说
(5) 流体的热物理性质:
导热系数 [W/(m.K)] 比热容 c [J (kg C)]
贴壁处壁面 法线方向上 的流体温度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c p
tu dxdy
x
y方向对流入的净热量:y
y
y y
dy
cp
tv
y
dxdy
3.内能增量:
c p
t
dxdy
将1、2、3代入能量守恒关系式,得出:
2t x2
2t y 2
c p
tu
x
c p
tv
y
c p
t
应用连续方程将其简化,得出:
c
p
t
u
t x
v
t y
2t x2
2t y 2
Dt
或可写为:
a2t
c
p
t
u t x
v
t y
2t x 2
2t y 2
行简化
第三节 边界层换热微分方程组
研究目的—— 简化对流换热微分方程组
一、流动边界层
1.定义:
Ludwig Prandtl (1875-1953)
距离壁面
u0.99u 处以内的流体层
2.流动边界层的5个特点:
(1)边界层的厚度较之定型尺寸为极小量 l
将上式在x,y两个方向代入牛顿第二定律,得到Navier-Stokes方程:
x方向:
u
u
u x
v
u y
X
x
x
yx
y
y方向:
v
u
v x
v
v y
Y
y
y
xy
x
对于不可压缩流体:
表面法向应力
x y
p 2 p 2
u
x v
y
表面切向应力 yx
xy
u y
v x
将其代入Navier-Stokes方程,并采用连续方程化简,得到:
普朗特准则 Pr
a
三、数量级分析与边界层微分方程
数量级分析方法—— 将方程中各量和各项目量级的相对大小进行比较,舍去量级小的 量和项目,从而简化方程,使其可以求解
分析对象——二维稳态受迫层流,且忽略重力作用
分析基础——各基本参数的量级
u ~ 01,u ~ 01,t ~ 01,t ~ 01,l ~ 01, x ~ 01, ~ 0 , y ~ 0 ,t ~ 0t ~ 0
x
dx
y方向M
y
M dy
y v
My
dx M
y
y
dy
将以上四式代入质量守恒定律: M x M y M xdx M ydy
得出: u v 0 x y
三、动量微分方程式(N•S方程)
推导依据——牛顿第二定律F=ma
1.微元体的质量×加速度: dxdy DU d
DU 在两个方向的分量分别为:
对理想气体 1 T
Re增大——h增大
定性温度——换热中起主导作用的温度,以此特征 温度确定物性参数,可将物性参数按常数处理
三、流体的相变(凝结、沸腾、融化、凝固、升华、凝华)
冷凝器
锅炉
四、换热表面几何因素 (壁面尺寸、粗糙度、形状及与流体的相对位置)
定型尺寸——换热中有决定意义的尺寸,以此特征 尺寸作为分析计算的依据,能准确反映物体形状对 换热的影响
根据傅立叶定律:
x
t x
dy
y
t y
dx
x方向导入的净热量:
x
x
x x
dx
2t x2
dxdy
y方向导入的净热量:
y
y
y y
dy
2t y 2
dxdy
2.对流热量:
由左方进入微元体的焓值: x cptudy
由下方进入微元体的焓值: y cptvdx
x方向对流入的净热量:x
x
x x
dx
(优选)第五版传热学课件第 五
影响对流换热的因素
一、流动的起因和流动状态
起因
自然对流 受迫对流 混合对流
流动状态
层流 紊流
二、流体的热物理性质 (比热容、导热系数、密度、黏度、体积膨胀系数等)
比热容和密度大,单位体积流体能携带更多能量 导热系数大,流体内部导热能力强 黏度小,流体流动顺畅
h增大
体积膨胀系数 1 v 1 v T p T p
对流表面传热系数h的多参数函数
h f u,tw,t f , , cp , , , , l
对流换热情况分类
第二节 对流换热微分方程组
对流换热问题总的求解步骤(二维不可压缩牛顿型流体)
动量方程
能量方程
过程方程
已知条件
速度场
温度场
hx
h
一、对流换热过程微分方程式
推导依据:流体在贴壁处处于无滑移状态,贴壁流体层仅有导热发生
(2)边界层内速度梯度很大
u u y x
(3)边界层流态分为层流和紊流,紊流边界层紧靠壁处仍是层流,称层流底层
判断流态的准则——临界雷诺数
Re c
u xc
5105
(4)流场分为主流区和边界层区,主流可忽略黏性,边界层考虑流体黏性
(5)边界层法线方向压力梯度很小,边界层与主流区压力相同
p 0 y
对流换热微分方程组量级分析过程
1.连续方程: u v 0 x y
1 ? v ~ 0
1
2.x方向动量方程:
u
u x
v
u y
p x
2u x2
2u y 2
1111
1
根据傅立叶导热定律:
qx
t y
w,x
根据牛顿冷却定律: qx hx tw t f x hxtx
对流换热过程方程:
hx
tx
t y
w,x
x
y
w,x , 其中=t
tw
二、连续性方程
推导依据——质量守恒定律
各方向流进和流出微元体的质量流量:
x方向M
x
Mx dx M
udy
M x x
x方向:
u
u
u x
v
u y
X
p x
2u x 2
2u y 2
y方向:
v
u
v x
v
v y
Y
p y
2v x 2
2v y 2
对稳态流动:
惯性力
体积力 压强梯度 黏滞力
u v 0
当只有重力场作用时: X g x Y g y
四、能量微分方程式
推导依据—— 内能增量=导热热量+对流热量
1.导热热量:
d
五、对流换热微分方程组
hx
t x
t y
w, x
5个方程,5个未知数(h,u,v,t,p), 理论上存在唯一解
u
x
பைடு நூலகம்
v y
0
u
u u x
v
u y
X
p x
2u x 2
2u y 2
但由于方程组 过于复杂,实
v
u
v x
v
v y
Y
p y
2v x 2
2v y 2
际不可求解, 必须进一步进
d
Dux, y, u u x u y u u u v u
d
x y x y
Dvx, y, v v x v y v u v v v
d
x y x y
2.微元体所受的外力:(x,y两方向)
体积力YXddxxddyy
表面力
x
x
y
y
yx
y
xy
x
dxdy dxdy
根据伯努利方程:p x
dp dx
u
du dx
(量级分析方法的结论)
3.不同流动模型下边界层的描述: 管内受迫流动
受迫横向 外掠圆管
沿热竖壁 自然对流
二、热边界层
1.定义:
距离壁面 t
0.99 f 处以内的流体层
其中: t t f
2.与流动边界层的关系——取决于黏性系数与热扩散率的相对大小
